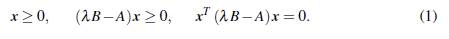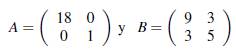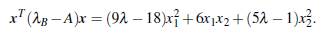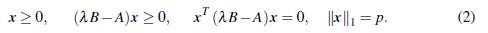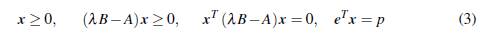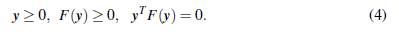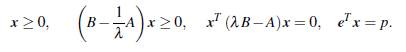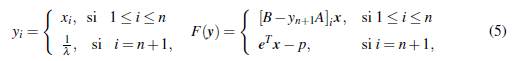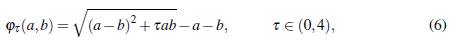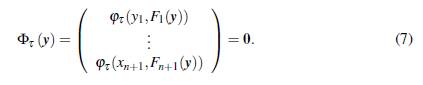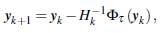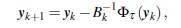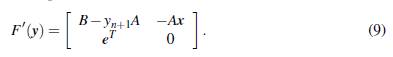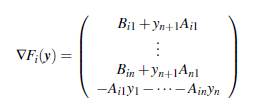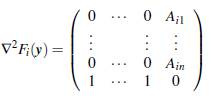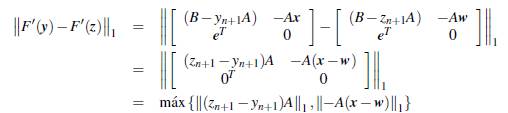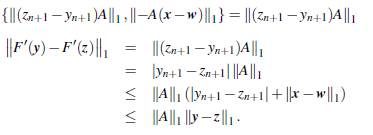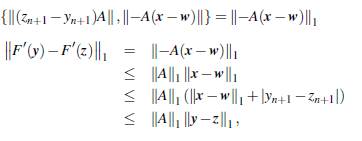Introducción
Sean A y B e ℝnxn, con B una matriz definida positiva. Ul problema de Valores Propios Complementarios, abreviadamente VPC(A,B), consiste en encontrar un escalar positivo λ y un vector x e ℝn , no nulo, tal que
Este problema tiene numerosas aplicaciones en ingenieríayfísica tales como, el estudio de la frecuencia de resonancia en estructuras y la estabilidad de sistemas dinamicos (Pinto da Costa, Martins, Figueiredo, y Judice, 2004).
Una solución al problema VPC(A, B) es un par (λ,x), donde X es llamado un valor propio complementario, y x es llamado vector propio complementario asociado a λ.
Como ocurre con los vectores propios convencionales, los vectores propios complementarios asociados a un valor propio complementario tambien forman un conjunto infinito, el cual es un cono convexo (Iusem, jUdice, Sessa, y Sarabando, 2019). Esto puede verse faícilmente con las siguientes matrices,
En este caso, las soluciones del problema VPC (A, B) son de la forma: (λ
1, x) = (2, (α, 0)
T
) y (λ
2,x) = (
Teniendo en cuenta que x ≥ 0, tenemos que
Si λ = 2 entonces x T (λB−A)x = 0 si, y solo si x 2 = 0 y x 1 ≥ 0.
Si λ = 1/5 entonces x T (λB−A)x = 0 si, y solo si x 1 = 0 y x 2 ≥ 0.
Mas aun, para los pares (X1,x) = (2, (α,0)
T
) y (X2,x) = (
Observe que, para cada valor propio hay infinitos vectores propios. Como es de esperarse, se prefiere un vector representante, como si fuera un "generador". Con el fin de obtener este vector propio complementario, el problema VPC (A, B), se puede transformar en el siguiente problema equivalente (Facchinei y Pang, 2003).
Dado p > 0 encontrar un escalar positivo λ y un vector x ∈ ℝ n tal que
Por la nonegatividad del vector x, se tiene que ∥x∥1 = Σ n k =1 xk, lo cual se puede expresar como e T x, donde e T = (1,. Así, el problema (2) se transforma en
que llamaremos problemaVPC2(A,B).
El caso particular, en el cual las matrices A y B son simétricas, generalmente se analiza independientemente, ya que pueden aplicarse métodos especiales para su solución (Iusem y cols., 2019); este tipo de problemas se les llama problema de valores propios complementarios simétrico. Cuando alguna de las matrices A o B no es simétrica, que es el caso más general, el problema es llamado no simétrico.
El problema VPC (A, B) puede reformularse como un problema de minimization con restricciones de complementariedad (Sherali y Tuncbilek, 1992), como uno de minimization global (Judice, Sherali, y Ribeiro, 2007) y como un problema de complementariedad no lineal (Facchinei y Pang, 2003). Nuestro interés esta en esta ultima reformulation debido a que existen algoritmos competitivos, en particular, tipo cuasi-Newton que permiten resolver en forma eficiente problemas de complementariedad no lineal y no han sido utilizados, hasta donde conocemos, para resolver problemas de valores propios complementarios.
En este artículo, consideramos el problema de los valores propios complementarios y su reformulation como un problema de complementariedad no lineal. Verificamos que este problema satisface ciertas hipótesis que permiten usar un algoritmo global cuasi-Newton propuesto en (Arias, Martínez, y Pérez, 2017) para resolver problemas de complementariedad no lineal en general. Implementamos dicho algoritmo adaptándolo al caso particular de los valores propios complementarios y realizamos un análisis numérico de su desempeño. Pruebas numéricas preliminares indican que es una buena alternativa para resolver dichos problemas.
El resto de este documento está organizado de la siguiente forma: en la siguiente sección, se reformula el problema de valores propios complementarios como uno de complementariedad no lineal, se mencionan métodos numéricos tradicionales para resolverlo y se introduce el algoritmo cuasi-Newton global que se usara para resolver indirectamente el VPC(A,B), luego, se verifica que el problema de valores propios complementarios satisface las hipótesis necesarias para que el algoritmo utilizado converja, posteriormente, se incluyen las pruebas numéricas que se realizaron para analizar la eficacia de esta estrategia y finalmente, se presentan algunos comentarios sobre el trabajo realizado.
Reformulación del VPC (A, B) como un problema de complementariedad no lineal
En general, dada F: ℝ n+1 - ℝ n+1, F (y) = (F 1 (y),...,F n+1 (y)) T , continuamente diferenciable, el Problema de Complementariedad No Lineal consiste en encontrar un vector y e ℝ n+1 que satisfaga las tres condiciones siguientes,
Veamos a continuación que, en efecto, el problema VPC2(A,B) puede reformularse como un problema de complementariedad no lineal.
A partir de (3), VPC2(A,B) puede expresarse de la siguiente forma (Júdice y cols., 2007): hallar λ > 0 y x ∈ ℝ n tal que
Haciendo un cambio de variable, se definen F: ℝn+1 - ℝn+1 y e Rn+1 tales que,
con lo cual, el problema VPC2(A, B), es de la forma (4); es decir, es un problema de complementariedad lineal.
Una estrategia de solución para problemas de complementariedad no lineal, tal vez, la más popular y ampliamente usada, consiste en reformularlo como un sistema de ecuaciones no lineales mediante ciertas funciones especiales, ϕ: ℝ2 → ℝ, llamadas funciones de complementariedad (Yong, 2010) que satisfacen la equivalencia, ϕ(a,b) = 0 ⇐⇒ a ≥ 0, b ≥ 0, ab = 0.
En este artículo usaremos la familia de funciones de complementariedad introducida en (Kanzow y Kleinmichel, 1998), y definida por,
la cual ha resultado competitiva en la reformulación de problemas de complementariedad (Arenas, Martínez, y Perez, 2014) (Perez, Arenas, Martínez, y Arias, 2019). Así, la reformulación del problema de valores propios complementarios puede, a su vez, reformularse como el siguiente sistema de ecuaciones no lineales no diferenciable
Este sistema se puede resolver mediante un método tipo Newton generalizado (Ferris y Pang, 1997; Facchinei y Pang, 2003; Kanzow y Kleinmichel, 1998) o cuasi-Newton (Arenas y cols., 2014; Arias y cols., 2017), entre otros (Arenas, Martínez, y Perez, 2020; Sanchez, Perez, y Martínez, 2021). En el primer caso, la iteración básica, es de la forma
donde Hk ∈ ∂Φ τ (y k ), es decir B k es una matriz en el jacobiano generalizado de Φ τ en y k (Clarke, 1975). En el caso, de un método cuasi-Newton, la iteración básica, es de la forma
donde B k ≈ Hk ∈ ∂Φτ (y k ) .
Por otra parte, con el fin de globalizar este tipo de algoritmos que resuelven sistemas de ecuaciones no lineales como el planteado en (7), se introduce una función de merito y se resuelve un problema de minimization (Dennis y Schnabel, 1996). La función de mérito natural y ampliamente usada es Ψ
τ
definida por Ψ
τ
(y) =
En (Arias y cols., 2017), los autores proponen un algoritmo global cuasi-Newton, concretamente un algoritmo secante de cambio mínimo, para resolver problemas de complementariedad no lineal, como el problema (8), el cual usa búsqueda lineal como estrategia de globalization. Este algoritmo mostro resultados excelentes al ser probado con funciones de difícil comportamiento numérico. Por ello, consideramos que es la mejor opción para resolver el problema VPC (A, B) vía la reformulation como un problema de complementariedad no lineal. En la experimentation numérica, presentamos más detalles de este algoritmo; en lo que sigue, nos referiremos a el como Algoritmo 1.
Verificación de hipótesis
El Algoritmo 1 converge con tasa superlineal, y esta convergencia esta condicionada a que satisfaga las siguientes hipotesis:
H.1 Existe una solution y* del sistema Φ T (y) = 0.
H.2 Las funciones F i son continuamente diferenciables y su gradiente es una funcion semi-suave.
H.3 La matriz jacobiana de F es Lipschitz continua en una vecindad de y*.
A continuation, analizaremos hasta que punto la función F satisface las hipótesis que requiere el Algoritmo 1 para alcanzar la convergencia. Para ello, usamos (5) y deducimos que la matriz Jacobiana de F, esta dada por
Estas expresiones nos facilitaran la verification de las hipótesis que garantizan la viabilidad del Algoritmo 1 para este problema particular.
H.1 En general, para determinar si un problema de complementariedad tiene solución, bastaría verificar que la función que define el problema es estrictamente monótona (Ferris y Pang, 1997); sin embargo, para el problema (4) con F definida en (5), este camino conduce a imponer condiciones muy fuertes sobre A y B para garantizar la monotonía de F y con ello, la solución al problema.
Una alternativa para garantizar la existencia de al menos una solución del problema VPC (A, B) es imponer condiciones menos restrictivas sobre A y B. Esto fue hecho en (Queiroz, Judice, y Humes, 2004), donde los autores demuestran que, si todas las componentes de A son positivas y B = I n , el problema VPC (A, B) tiene solución. Adicionalmente, si A es simétrica la solución es única. Este resultado, nos permite verificar la hipótesis H1 y diseñar experimentos numéricos, como veremos más adelante.
Vale la pena mencionar que la cantidad maxima de soluciones que puede tener el problema VPC (A, B) es n2n-1 (Seeger, 1999).
H.2 Las funciones F i son diferenciables. En efecto, cuando 1 ≤ i ≤ n, su respectivo gradiente está dado por
y, para n+1, el ∇Fi(y) es el vector de unos de n+1 componentes. Cada uno diferenciable, con además para 1 ≤ i ≤ n
y, para i = n +1, la ∇ 2 F i (y) es la matriz nula de orden n +1. Esto demuestra que cada gradiente ∇F i es continuamente diferenciable; por lo tanto, es también una función semisuave .
H.3 Probemos que F' es Lipschitz continua en todo su dominio. Sean y,z G ℝn+1 de tal forma que
Considérese la diferencia
por lo tanto, F' es Lipschitz continua con constante ∥A∥1.
Al satisfacer de manera razonable las hipótesis del algoritmo, se procede á mostrar los resultados numéricos.
Experimentación numérica
En esta sección, resolvemos numericamente la reformulation del problema VPC2(A, B) como un problema de complementariedad no lineal, el cual a su vez, lo hemos reformulado como el problema de minimization (8). Para ello usaremos el algoritmo propuesto en (Arias y cols., 2017), el cual hemos denominado en este documento Algoritmo 1. Este es un algoritmo cuasi-Newton, exactamente secante de cambio mínimo (Martínez, 1992), globalizado mediante una estrategia de busqueda lineal (Dennis y Schnabel, 1996). Para mayor claridad en la lectura de este documento lo incluimos a continuation.
El Algoritmo 1, hace un llamado al Algoritmo 2, que selecciona la actualización secante, que actualizara la matriz B k y que será usada en la siguiente iteración. Las actualizaciones que consideraremos son las siguientes: buena de Broyden (Broyden, 1965), mala de Broyden (Brown y Saad, 1994), Schubert (Schubert, 1970), COLUM (Martínez, 2000) e ICUM (Martínez, 1992).
Se considero como algoritmo para hacer las comparaciones respectivas el método de Newton generalizado, el cual llamaremos Algoritmo 3, y lo incluimos a continuación para claridad en la lectura de la sección. Por supuesto, aprovechamos la estructura del jacobiano de F indicada en (9) ya que, no es muy costosa su evaluación, ni su implementación.
Construcción de los problemas
Para construir los problemas VPC (A, B) usamos el lineamiento descrito en (Júdice y cols., 2007); es decir, dos categorías de problemas: simétricos y no simétricos; en todos, la matriz B es la identidad de tamaño n x n. La matriz A se construye como se indica en la Tabla 1, donde Escala significa el valor más grande que puede tomar cada componente de A, randn(n) es una matriz aleatoria de tamaño n x n y p esta dado por (3), generando un total de ocho configuraciones de parámetros.
Tabla 1 Selection de las matrices A y B en la experimentation.
| Tipo de problema | p | Escala | A | B |
|---|---|---|---|---|
| Simeítrico | 1 y6 | V= Escala x randn( n) | I n | |
| 1 y 50 | U= triu(V ) | |||
| A=U+U T | ||||
| No simétrico | 1 y6 | 1 y 50 | A= Escalax randn(n) | In |
Para escribir los códigos de los algoritmos y de las funciones objetivo de cada problema usamos el software Matlab® . Realizamos las pruebas numéricas en un computador Intel (R) Core (TM) i7-9700F CPU de 3.00 GHz.
Experimento preliminar
Uno de los interrogantes planteados antes de comenzar la experimentation fue el siguiente, ¿cual es el valor de x adecuado para la función ϕ τ definida en (6)? En (Kanzow y Klein-michel, 1998) se presento un algoritmo dinámico para variar x con buenos resultados, sin embargo, en el caso particular del problema VPC (A, B), en pruebas preliminares no se obtuvo un decrecimiento eficaz, al compararlo con el valor de x = 2 estático, el cual es un valor muy utilizado en funciones de complementariedad, esto llevo a diseñar el siguiente experimento.
Encontrar en cada paso el valor de x en el cual se pueda obtener el mayor decrecimiento de la función objetivo Ψ t . Para ello, se utilizaron diferentes valores de t desde 0.01 hasta 3.99 y se seleccionó para cada paso aquel valor de t en que se obtuvo el máximo descenso de Ψ t utilizando el método de Newton generalizado. Luego se repitió esta experiencia 10000 veces, los promedios de los 9110 ejecuciones exitosas se muestran en la Figura 1.
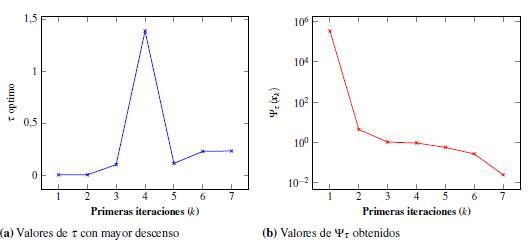
Figura 1 Valores de t que producen mayor decrecimiento y su respectivo Ψ t (x k ) en las primeras 7 iteraciones.
Podemos observar que el mayor decrecimiento se obtiene en las primeras 3 iteraciones, en los cuales λ toma valores muy pequeños, es por ello que hemos decidido realizar todos los experimentos con un valor de λ = 10-2.
Experimento principal
Realizamos para cada valor de n, cada valor de Escala y cada valor de p, 1000 ejecuciones; en cada ejecución se generó aleatoriamente un problema. El punto inicial y 0 también se genero aleatoriamente con el comando randn(n + 1,1). Cada uno de estos problemas, se resolvió con los algoritmos 1 y 2 respectivamente.
Los resultados más relevantes obtenidos en esta experimentación, se presentan en las Tablas 2 a 4, donde n, es el tamaño de las matrices A y B, p, es el valor de la constante dada en (3); escala, es el valor mas grande que puede tener cada componente de la matriz A; en cada una de las actualizaciones E, indica el porcentaje de éxitos con cada una de las actualizaciones; es decir, el número de veces que se obtuvo convergencia entre 1000 expresado como porcentaje; Iter, indica el promedio de iteraciones redondeado a un entero de las ejecuciones que tuvieron éxito; finalmente, tiempo indica el promedio de tiempo CPU redondeado a cuatro decimales en las ejecuciones que tuvieron éxito.
Tabla 2 Caso asimétrico con p = 1 y Escala = 1.
| Newton | Broyden B | Broyden M | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| n | P | E | Iter | tiempo | E | Iter | tiempo | E | Iter | tiempo |
| 2 | 97.1 | 16 | 0.0012 | 85.1 | 23 | 0.0016 | 27.9 | 10 | 0.0003 | |
| 3 | 99.1 | 14 | 0.0009 | 91.4 | 24 | 0.0017 | 28.1 | 12 | 0.0003 | |
| 4 | 99.4 | 13 | 0.0008 | 91.1 | 22 | 0.0014 | 24.2 | 13 | 0.0004 | |
| 5 | 99.5 | 12 | 0.0007 | 90.8 | 24 | 0.0016 | 24.9 | 14 | 0.0004 | |
| 10 | 99.7 | 13 | 0.0009 | 92.1 | 34 | 0.0025 | 17.9 | 18 | 0.0006 | |
| 20 | 99.7 | 16 | 0.0015 | 89.1 | 56 | 0.0063 | 9.9 | 22 | 0.0011 | |
| 30 | 99.9 | 20 | 0.0026 | 85.6 | 70 | 0.0098 | 8.3 | 24 | 0.0016 | |
| 50 | 98.1 | 23 | 0.0052 | 72.5 | 105 | 0.0246 | 5.1 | 27 | 0.0030 | |
| 100 | 92.5 | 26 | 0.0297 | 47.3 | 123 | 0.1364 | 2.1 | 31 | 0.0207 | |
| Schubert | COLUM | ICUM | ||||||||
| n | p | E | Iter | tiempo | E | Iter | tiempo | E | Iter | tiempo |
| 2 | 35.7 | 13 | 0.0007 | 76.9 | 21 | 0.0017 | 34.7 | 9 | 0.0003 | |
| 3 | 33.4 | 15 | 0.0008 | 80.3 | 19 | 0.0013 | 30.2 | 11 | 0.0004 | |
| 4 | 33.8 | 16 | 0.0007 | 77.5 | 19 | 0.0012 | 28.8 | 11 | 0.0004 | |
| 5 | 32.0 | 17 | 0.0007 | 74.7 | 22 | 0.0015 | 24.2 | 13 | 0.0004 | |
| 10 | 17.9 | 26 | 0.0019 | 52.0 | 27 | 0.0018 | 13.1 | 15 | 0.0006 | |
| 20 | 5.9 | 41 | 0.0043 | 21.0 | 30 | 0.0024 | 8.5 | 17 | 0.0010 | |
| 30 | 2.5 | 47 | 0.0073 | 14.5 | 31 | 0.0033 | 7.1 | 18 | 0.0013 | |
| 50 | 0.7 | 39 | 0.0068 | 7.4 | 33 | 0.0061 | 4.0 | 20 | 0.0024 | |
| 100 | 0.1 | 27 | 0.0254 | 4.5 | 36 | 0.0418 | 2.5 | 19 | 0.0138 | |
En los resultados presentados en la Tabla 2 se destacan las actualizaciones Broyden M.e ICUM por su rapidez de convergencia, sin embargo, tienen poco éxito, por lo cual afirmamos que no son muy efectivas al tomar valores iniciales aleatorios, si el problema tuviese una forma de iniciar el algoritmo en una vecindad pequeña de la solución esta falencia pudiera ser superada. Por otro lado, los métodos de Newton generalizado y Broyden B son los métodos más eficaces para este caso no simétrico con valores pequenos de las entradas de la matriz A.
Tabla 3 Caso asimétrico con p = 6y Escala = 50.
| Newton | Broyden B | Broyden M | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| n | P | E | Iter | tiempo | E | Iter | tiempo | E | Iter | tiempo |
| 2 | 6 | 77.4 | 14 | 0.0007 | 24.0 | 54 | 0.0030 | 0.8 | 18 | 0.0013 |
| 3 | 6 | 78.6 | 14 | 0.0006 | 10.0 | 59 | 0.0047 | 1.1 | 18 | 0.0012 |
| 4 | 6 | 80.6 | 14 | 0.0007 | 4.4 | 59 | 0.0050 | 0.6 | 35 | 0.0031 |
| 5 | 6 | 81.1 | 14 | 0.0007 | 2.7 | 42 | 0.0033 | 1.3 | 24 | 0.0024 |
| 10 | 6 | 82.4 | 14 | 0.0008 | 1.7 | 41 | 0.0035 | 0.8 | 54 | 0.0064 |
| 20 | 6 | 84.5 | 15 | 0.0012 | 0.5 | 81 | 0.0129 | 0.5 | 42 | 0.0067 |
| 30 | 6 | 82.9 | 16 | 0.0017 | 0.4 | 106 | 0.0246 | 0.2 | 51 | 0.0088 |
| 50 | 6 | 83.3 | 17 | 0.0030 | 0.5 | 107 | 0.0327 | 0.4 | 75 | 0.0293 |
| 100 | 6 | 86.9 | 19 | 0.0178 | 1.3 | 52 | 0.0793 | 0.3 | 101 | 0.1431 |
| Schubert | COLUM | ICUM | ||||||||
| n | p | E | Iter | tiempo | E | Iter | tiempo | E | Iter | tiempo |
| 2 | 6 | 0.7 | 23 | 0.0021 | 34.9 | 49 | 0.0040 | 0.4 | 20 | 0.0012 |
| 3 | 6 | 0.0 | - | - | 15.4 | 66 | 0.0056 | 0.5 | 11 | 0.0004 |
| 4 | 6 | 0.2 | 50 | 0.0056 | 7.5 | 50 | 0.0037 | 0.4 | 12 | 0.0004 |
| 5 | 6 | 0.5 | 15 | 0.0004 | 3.3 | 56 | 0.0044 | 0.1 | 12 | 0.0004 |
| 10 | 6 | 0.1 | 17 | 0.0007 | 1.1 | 27 | 0.0015 | 0.2 | 18 | 0.0007 |
| 20 | 6 | 0.2 | 13 | 0.0006 | 0.7 | 29 | 0.0018 | 0.1 | 22 | 0.0011 |
| 30 | 6 | 0.0 | - | - | 0.3 | 13 | 0.0010 | 0.2 | 13 | 0.0009 |
| 50 | 6 | 0.4 | 25 | 0.0031 | 0.0 | - | - | 0.0 | - | - |
| 100 | 6 | 0.0 | - | - | 0.1 | 40 | 0.0361 | 0.0 | - | - |
Los resultados de la Tabla 3 muestran que el método más eficiente en el caso no simétrico con entradas menores o iguales que 50, sigue siendo el método de Newton generalizado, seguido por la actualización de Broyden B también la actualización ICUM es la que converge mas rapidamente, aunque tiene poco exito.
Tabla 4 Caso simétrico con p =1 y Escala = 1.
| Newton | Broyden B | Broyden M | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| n | P | E | Iter | tiempo | E | Iter | tiempo | E | Iter | tiempo |
| 2 | 100.0 | 13 | 0.0032 | 90.0 | 21 | 0.0017 | 50.0 | 10 | 0.0003 | |
| 3 | 100.0 | 14 | 0.0009 | 90.0 | 17 | 0.0009 | 20.0 | 9 | 0.0002 | |
| 4 | 100.0 | 10 | 0.0004 | 90.0 | 34 | 0.0035 | 0.0 | - | - | |
| 5 | 100.0 | 10 | 0.0004 | 90.0 | 29 | 0.0018 | 20.0 | 14 | 0.0004 | |
| 10 | 100.0 | 16 | 0.0010 | 100.0 | 44 | 0.0042 | 10.0 | 15 | 0.0005 | |
| 20 | 100.0 | 40 | 0.0055 | 80.0 | 46 | 0.0047 | 0.0 | - | - | |
| 30 | 100.0 | 32 | 0.0052 | 60.0 | 68 | 0.0091 | 0.0 | - | - | |
| 50 | 90.0 | 42 | 0.0115 | 70.0 | 116 | 0.0302 | 20.0 | 28 | 0.0033 | |
| 100 | 70.0 | 17 | 0.0109 | 30.0 | 160 | 0.1602 | 0.0 | - | - | |
| Schubert | COLUM | ICUM | ||||||||
| n | p | E | Iter | tiempo | E | Iter | tiempo | E | Iter | tiempo |
| 2 | 30.0 | 17 | 0.0017 | 70.0 | 23 | 0.0024 | 30.0 | 6 | 0.0014 | |
| 3 | 10.0 | 7 | 0.0002 | 70.0 | 23 | 0.0017 | 70.0 | 11 | 0.0004 | |
| 4 | 0.0 | - | - | 50.0 | 16 | 0.0006 | 30.0 | 14 | 0.0005 | |
| 5 | 30.0 | 14 | 0.0004 | 60.0 | 27 | 0.0015 | 30.0 | 12 | 0.0004 | |
| 10 | 10.0 | 16 | 0.0005 | 50.0 | 70 | 0.0114 | 10.0 | 23 | 0.0008 | |
| 20 | 0.0 | - | - | 20.0 | 23 | 0.0018 | 0.0 | - | - | |
| 30 | 0.0 | - | - | 10.0 | 18 | 0.0015 | 10.0 | 26 | 0.0022 | |
| 50 | 0.0 | - | - | 10.0 | 21 | 0.0026 | 0.0 | - | - | |
| 100 | 0.0 | - | - | 0.0 | - | - | 0.0 | - | - | |
De la Tabla 4 deducimos que para el caso simétrico, el método de Newton generalizado es el más indicado, por efectividad y eficiencia, en contraste, el método de Shubert no parece ser recomendable para problemas de tamaño mayor a 5. También llama la atención que en muchos casos no se alcanza la convergencia en algunos métodos cuasi-Newton, salvo el método Broyden Bueno, que es muy confiable.
Comentarios finales
En este artículo, utilizamos un método cuasi-Newton para resolver el problema de valores propios complementarios basado en su reformulation como un problema de complementariedad no lineal. Un método de este tipo es una buena alternativa cuando las derivadas del sistema son muy costosas o difíciles de obtener. Particularmente en este caso no es muy costoso su computo, aun así, por las valiosas aplicaciones que tiene el reducir el tiempo de ejecución es un incentivo para utilizar esta propuesta.
Como pudimos verificar en los resultados de las pruebas numéricas, la cantidad de experimentos numéricos que se hicieron fue bastante amplia, por lo cual podemos concluir que los métodos cuasi-Newton aplicados a este problema pueden ser competitivos frente al método de Newton generalizado, especialmente el método de Broyden Bueno. Por otro lado también observamos que al aumentar la dimension del problema el número de éxito se reduce considerablemente, creemos que la razón de este fenómeno es que la norma del vector solución es igual a p y al ser muy pequeno (1 o 6) y la dimension muy grande, obliga a que cada componente del vector solución sea casi cero, lo cual genera problemas de estabilidad en el algoritmo.
Por otro lado, en cuanto a la selection del "mejor" valor de T en (6) todavía que da mucho por hacer. Dicho lo anterior concluimos que este algoritmo es una buena alternativa, pues el costo computacional es menor en comparación con el método de Newton generalizado.