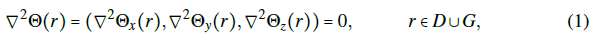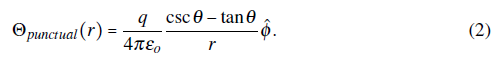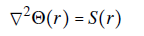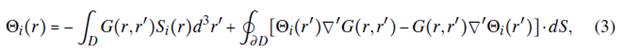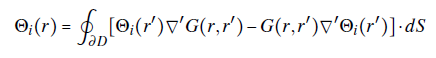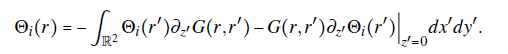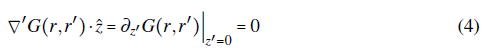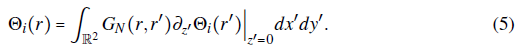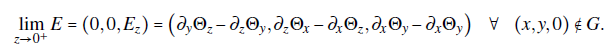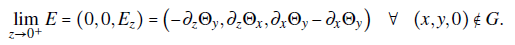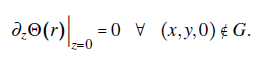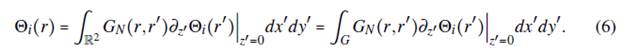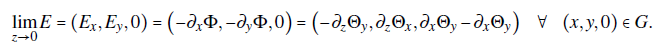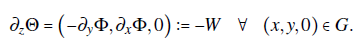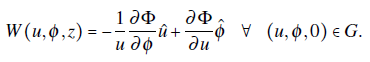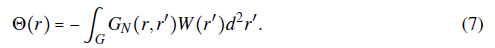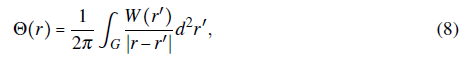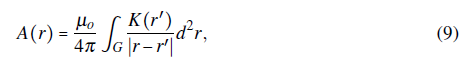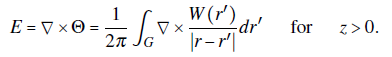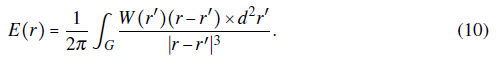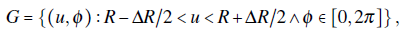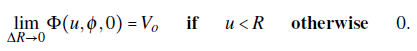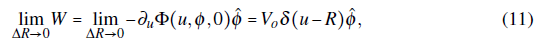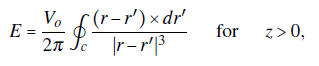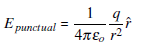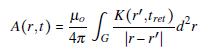Introduction

In this document, we study a system composed of two metal sheets with a gap G in between (see Fig.1-left). The sheets lie on the xy-ptaie, and a constant potential difference is enforced in-between. For convenience, the potentials of the inner and outer sheets are V _o and zero, respectively. This system is commonly referred to as gape p Surface Electr o de (SE) (^{House, 2008}; ^{Salacar et al, 2019}, 2022; ^{Schmied, 2010}) and it plays an important role to model the static electric nelds in SE ion traps where ion-trap networks including arrays of SE are also) promising candidates in quantum processing (^{Chiaverini et al, 2005}; ^{Seidelin et al._; 2006}; ^{Daniilidis et al., 2011}; ^{Kim et al., 2011}; ^{Hong et al., 2017}; ^{Mokhberi et al., 2017}; ^{Tao et al., 2018}; ^{Van Mourik et al., 2020})

The surface electrode also has practical relevance in antenna theory. For instance, when considering a time-varying voltage between the sheets. If the system is fed with a harmonic voltage source V(t) = V _o exp (iωt) of angular frequency o, then the SE will radiate electromagnetic waves that will mostly depend on the geometry of the gap G and ω. This time-dependent version of the SE is a type of dipole-blade antenna (^{Balanis, 2015}; ^{Hicks et al., 2012}). Those antennas play a role in astronomic radio-telescopes (^{Mozdzen et al., 2017}). Here we restrict our description to the stationary case. However, the electrostatic of the SE is also important since in the low-frequency limit (ω/c << 1, with c the velocity of light) the time-dependent solutions tend to the electrostatic profiles times harmonic phases.

In this article, we are interested in the electric field inside the charge-free region D = {ℝ³: z > 0} and the surface charge density on the sheets {ℝ²: z = 0} \ G. The boundary of the region of interest D is denoted as dD. Authors of Ref. (^{Oliveira & Miranda, 2001}) have shown that the electric field E in D can be computed via a Biot-Savart-like law when the gap region is infinitely thin. They proved the relationship by using analogies with magneto-statics, specifically by comparing the scalar magnetic potential of a planar loop carrying a steady current and the electric potential of the electrostatic system.

The alternative strategy in this article consists in writing the electric field E = ∇×Θ as the curl of a vector potential Θ in the free-charge region, where the electric field is divergeceless ∇⋅E = 0. Since the Laplacian of the electric vector potential is ∇²Θ = ∇×Θ−∇(∇⋅Θ), it can be reduced to the simpler equation

because every time-independent electric field is irrotational ∇xE = 0 and one can impose a Gaussian Gauge condition ∇ - Θ = 0 on the vector potential. The electric potential vector has been employed in different contexts where the use of Θ can be advantageous in comparison with the scalar electric potential i.e. numerical studies via Finite Element Method for electrostatics (^{Semenov et al., 2006}), and engineering problems (^{Landis, 2002}; ^{Stark et al., 2015}; ^{Albanese & Rubinacci, 1990}; ^{Zhang & Wang, 1999}). We show that solving the Laplace's equation (1) together with Neumann boundary conditions on the finite gap will equally derive in the Biot-Savart law like formula: An integral description of the electric field without resorting to the magneto-statics analogy.

The classical approach to derive the electric field of planar surface electrodes in Ref. (^{Oliveira & Miranda, 2001}) has been to map the traditional Dirichlet problem onto the much simpler Biot-Savart-like problem: The integral expression for the electric field due to an arbitrarily shaped planar region kept at a fixed electric potential and embedded in a grounded plane. A similar approach has been proved efficient in (^{Salazar et al., 2019}). As shown in Ref. (^{Salazar et al., 2020}), one can obtain the Biot-Savart law without solving the Laplace's equation. That alternative derivation is by employing the Helmholtz decomposition and Green's theorems. The current proposal is a first attempt to understand the transient phenomenon, being the difference regarding the previously published works on this subject by the authors.

Many contemporary applications such as antennas, electron traps, and microprocessor boards include this phenomenology and require efficient descriptions of the electric field. Indeed, SE are a promising candidates to build ion-trap networks suitable for large-scale quantum processing (^{Seidelin et al., 2006}; ^{Chiaverini et al., 2005}; ^{Daniilidis et al., 2011}; ^{Kim et al., 2011}; ^{Hong et al., 2017}; ^{Mokhberi et al., 2017}; ^{Tao et al., 2018}; ^{Van Mourik et al., 2020}). The remaining parts of this article derive the Biot-Savart law with the alternative approach.

Solution of the Laplace's equation

In this section, we formulate the system in terms of the vector potential 0 to calculate the electric field in the free-charge space. For a single punctual charged particle this vector potential takes the following form¹

A plot of this vector potential is shown in Fig. 1-right. One can understand that the battery (responsible for the difference potential V _o between the electrode sheets) removes negative charges from the inner metal sheet and transfers them to the outer sheet. The total electric vector potential of the system comes from a superposition of individual electric vector potentials (of each punctual charge on the sheets). Since Eq. (2) does not have z-component one can expect that total vector potential fulfills Θ • z^ = 0.

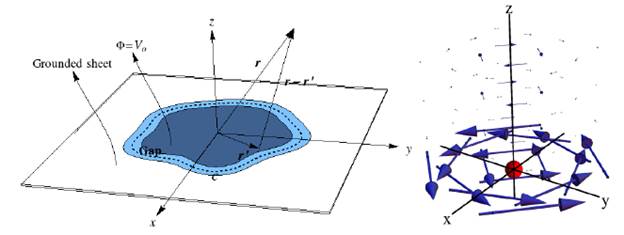
Figura 1 The physical system. A gaped SE is composed of two flat sheets at different electric potentials separated by a gap in between (left). Electric vector potential of a punctual charged particle (right). 

In the free-charge region the vector potential 0 satisfies the Laplace's equation Eq. (1). The Laplacian equation is a particular case of the more-general Poisson equation

where S is a source vector term. The analytical solution of the previous problem can be obtained through the Green's function,

with the {i} = {x,y, z} notation and G(r, r') the Green's function. Since there are no electric charges in D the source term in the Laplace' s equation is zero. Therefore, the surface term is the only integral that contributes in Eq. (3):

This last result can be written in Cartesian coordinates by only considering the surface contribution of the electrodes laying on the xy- plane,

In order to close the problem, we shall consider the Neumann boundary conditions for the vector potential on the xy-plane. Thus, the Green's function can be designed to satisfy G = Gn(r, r'), with

on the xy-plane. Hence, the definition of the vector potential simplifies to the solution of

Note also that the electric field on the metallic sheets is computed from the curl of the vector potential. The electric field may be calculated by approaching the sheets on the xy-plane from the z-direction:

For the single static punctual source, the z-component of the vector potential is exactly zero Θ _puntual (r) ∙ z^= 0 (see Eq. 2). The same occurs to the global vector potential due to the charge distributions on the metallic sheets. That is explained since the global vector potential is the superposition of potentials due to punctual charges. Therefore, Θ_z (r) = 0, and

The previous result implies that

It means that the normal derivative of the vector potential on the xy-plane is zero everywhere except on the gap region, hence

On the other hand, the electric field on the gap region between the sheets can be also computed by evaluating the limit

As a result, the z-derivative of the vector potential on the gap ∂ _z Θ=--W is related to the scalar potential, as follows

It is convenient to write vector W in polar coordinates r = (u,φ, z)) on the gap region, as follows

Thus, Eq. (6) takes the form

Now, regarding the definition of the Green's function in Eq. (7), one can use the method of images and propose G _N (r, r') as the function of two punctual identical charges symmetrically placed at z and -z’, 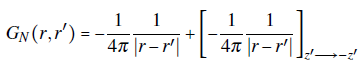, hence .

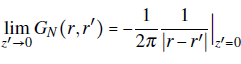It can be shown straightforwardly that this definition of the Green's function fulfills the boundary condition in Eq. (4). Finally, by replacing the previous Green's function definition into Eq. (7) the vector potential can be written as

which is the solution of the Laplace's equation of the electric vector potential imposing Neumann boundary conditions on the gap region G. One can observe that electric vector potential in Eq. (8) is mathematically equivalent to the standard vector potential in magnetostatics A(r) (^{Jackson, 1999}), computed from

with K(r') a steady surface density current and B - ∇x A the magnetic field. In fact, both vector potentials A and 0 can be used to compute the B and E fields in the free-space. If we study Eq. (9), one could state that electric currents are sources of the magnetic vector potential in a Coulomb-like way. Similarly, spatial variations on the electric scalar potential would be the sources of 0(r) according to Eq. (8). Unfortunately, these interpretations are quite subjective since both vectors potentials are not physically observable under a classical viewpoint since they are not unique: Vector potentials depend on a certain gauge choice (i.e. a Coulomb gauge).

Thus, the electric field is found from the curl of the vector potential,

Using the vector identity ∇×[λ(r, r′)F(r′)] = ∇λ ×F(r′) with λ = ∣r − r′∣⁻¹,, one finally obtains the Biot-Savart like law

The electric field in Eq. (10) is the electrostatic analogue of the magnetic field due to a closed ribbon on the G region carrying a constant surface density current K(r). An analogous role is played by W(r) in the SE electrostatic system. The Biot-Savart-like in Eq. (10) provides an integral solution of the electric field when the W(r) field is known. That is exactly the gapless limit case, where electrodes are ininitely close each other. In general, W(r) is unknown and it must be constructed over G for gaped SE. In those cases W(r) can be computed by approximating the scalar electric potential Φ on the gap region. One strategy to approximate Φ on the gap forces the zero charge condition on the mid trajectory on the gap. That strategy has been originally developed for the circular gaped SE in (^{Schmied, 2010}). The same approach can be applied for arbitrary geometry gaped SE (^{Salazar et al., -2022}). Therefore, one can understand the vector potential approach Θ here presented as a versatile way to find solutions in electrostatics. It fits better the nature of gaped SE problems rather than the traditional electric scalar potential Φ.

The gapless limit

In the gapless limit, the G region is ininitely thick and it becomes a closed loop c. For instance, if G is an annular region of ΔR thickness

then G becomes a circular loop of radius R in the ΔR -+ 0 limit. In this limit, one can also compute the W vector since the potential on z = 0 is

Hence, the W vector is computed from

where the derivative of the unit step function is a Dirac delta function. Replacing Eq. (11) into the surface integral Eq. 10, it becomes the following loop integral

where the c loop is counter-clock-wisely defined with respect to the z-axis. The result also is valid for an arbitrary closed loop. The central result in Ref. (^{Oliveira & Miranda, 2001}) is recovered from Eq. (10) in the gapless limit.

Conclusions

The electric field of planar metal sheets under a constant potential difference separated by a gap region has been studied in this article. The electric field is merely a Biot-Savart like integral on the gap region. The integral expression has been the solution of the Laplace's equation of the electric vector potential associated with the electric field under Neumann boundary conditions on the gap. In that sense, the vector potential formulation has described the electric field of planar surface electrodes instead of the scalar potential approach. We have proved that results in Ref. (^{Oliveira & Miranda, 2001}) can be equally derived from Eq. (10) in the particular case of an infinitely thin gap.

As a future work, one can study the non-stationary surface electrode where the metal sheets are set to a time dependent scalar potential. This type of system is also important for engineering since it is basically a dipole blade radiator. In that case, the electric vector potential Θ(r) satisfies a wave equation which is essentially a 4-dimensional Laplacian under an appropriate way to chose the Gauge. In this document we showed that it is possible to determine the electric field of the system by solving the Laplace's equation for the electric vector potential. It is known that a time-dependent generalization of the magnetic vector potential in Eq. (9) concerns the retarded solution of the wave equation (^{Jackson, 1999}).²

The question is if there exist a retarded version of the electric vector potential 0 which enable us to compute the radiated electric field via E(r, t) = ∇×Θ (r, t). Resembling over Eqs. (8) and (9), one can expect that the electric vector potential would certainly have a retarded formula for the dynamic propagation case. As a future work we expect to generalize the strategy presented in this document to find the time-dependent version of the electric vector potential.

The present article demonstrated another plausible approach to studying the gaped SE advantageous regarding Ref. (^{Salazar et al., 2020}) since it becomes mathematically simpler. That is constructing the electric vector potential from a superposition of vector potentials of individual static charges (see Fig. 1-right) on the metallic sheets and a Coulomb gauge condition. Results in Ref. (^{Salazar et al., 2020}) have been alternatively derived here and framed under an analytical strategy suitable to be generalized for time-dependent versions of the gaped SE.