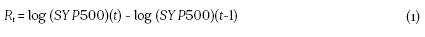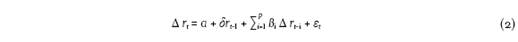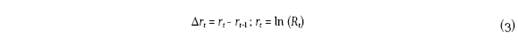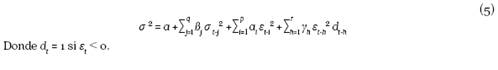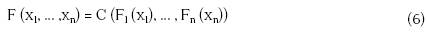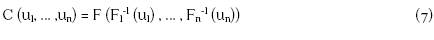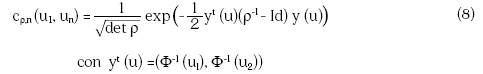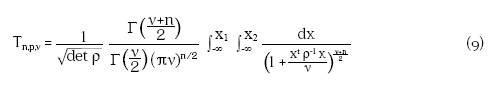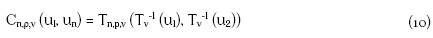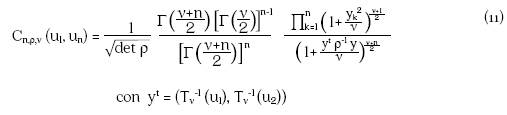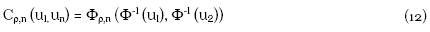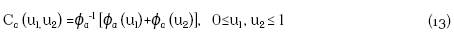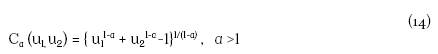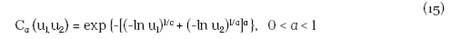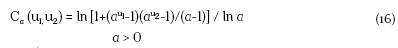Cambios importantes en el contexto financiero global (regulación, evolución tecnológica e innovación financiera) han impactado, crecientemente, la interrelación de los mercados financieros, sobre todo de las bolsas de valores, aumentando la probabilidad de efecto contagio, especialmente, entre aquellos que sostienen diversos nexos económicos y comerciales. Tal es el caso de los mercados pertenecientes al Tratado de Libre Comercio de América del Norte (TLCAN), los cuales se han caracterizado por tener una progresiva relación a partir de la firma de dicho tratado.
La crisis financiera global, cuyo principal antecedente es la crisis subprime, ha puesto de manifiesto la cohesión y fragilidad de los mercados de capital ante desequilibrios externos, incrementando la atención sobre la naturaleza de las interrelaciones bursátiles, su evolución y cambios abruptos en la intensidad de estas ante eventos extremos o momentos de calma e incertidumbre.
El contagio y dependencia financieros son temas tratados recurrentemente en la literatura, debido al impacto de dichos fenómenos en la formulación de políticas económicas, la localización eficiente de activos, y el desarrollo de estrategias de diversificación y cobertura del riesgo. Dichos temas atañen tanto a inversionistas como a las autoridades económicas, así como a académicos y profesionales que se encuentran profundamente relacionados con el campo de las finanzas.
La presente investigación se suma a las ya existentes, aportando evidencia empírica sobre cambios en la dependencia condicional entre los mercados de capitales de los países pertenecientes al TLCAN, los cuales apuntan a develar la existencia de efecto contagio, durante el más reciente y profundo desequilibrio bursátil a nivel internacional: la crisis financiera global. Para lograr dicho objetivo, se utiliza una metodología relativamente reciente y complementaria, que integra dos modelos generalizados autorregresivos con heterocedasticidad condicional (GARCH y TARCH), y la estimación vía cópulas.
El estudio abarca de 2003 a 2018, subdividido en tres períodos: antes, durante y después de la crisis financiera global, permitiendo determinar si hubo cambios en la dependencia condicional, si dichos cambios sugieren la presencia de efecto contagio y cuál fue la magnitud de dicho efecto. La estructura del trabajo es la siguiente: después de la presente introducción, se revisa la literatura relacionada; la tercera sección describe los datos y la metodología; la siguiente presenta y analiza los resultados de la estimación; y la quinta sección concluye.
Revisión de la literatura
El contagio y dependencia financieros son temas extensamente tratados en la literatura. En términos empíricos, se han desarrollado diversas aproximaciones para analizar los cambios en las relaciones entre diversos mercados financieros. El término contagio hace referencia, en su acepción más general, al incremento en la relación entre dos mercados, a partir de un desequilibrio o shock. Otro concepto ampliamente utilizado es aquel de interdependencia, fenómeno caracterizado por la existencia de altos niveles de relación entre mercados.
Ambos temas han sido probados a lo largo de la literatura. Por ejemplo, Bennet y Kelleher (1988), King y Wadhwani (1990), y Musumeci y Sinkey (1990) encontraron evidencia de efecto contagio en el crash de 1987, originado en Estados Unidos. Frankel y Schmukler (1996), al igual que Calvo, Leiderman y Reinhart (1996), analizaron el impacto de la crisis de 1994. Por su parte, Chiang, Jeon y Li (2007), y Baig y Goldfajn (1999) estudiaron la transmisión de la crisis asiática; mientras Baig y Goldfajn (2001), y Haile y Pozo (2008) investigaron los efectos de la crisis rusa; y Aloui, Aïssa y Nguyen (2011), Dimitriou, Kenourgios y Simos (2013), y Bekaert, Ehrmann, Fratzscher y Mehl (2014) analizaron el contagio causado por la más reciente -y aún no resuelta- crisis financiera global (CFG), cuyos efectos tuvieron como principal antecedente la denominada “crisis subprime”.
Forbes y Rigobon (2002), Loretan y English (2000), y Boyer, Gibson y Loretan (1997) han demostrado que la correlación convencional puede conducir a resultados sesgados e inadecuados en la modelación de relaciones financieras, debido a que no captura hechos estilizados en las series (como heteroscedasticidad, colas pesadas, conjuntos de volatilidad, memoria larga y asimetría). Además, la correlación lineal puede arrojar resultados espurios (Forbes y Rigobon, 2002; Baur, 2003). Para superar dichas limitaciones, se propone una metodología basada en la teoría de cópulas, la cual arroja mejores estimaciones, ajustándose para capturar el comportamiento de las series financieras.
Otros estudios, como aquellos realizados por Cheung, Fung y Tsai (2010), sugirieron que, en la crisis financiera global no solo ocurrió contagio, sino que también hay evidencia de que, en algunos mercados, la interdependencia se hizo más fuerte durante los momentos de crisis. En esta misma dirección, Samarakoon (2011) afirmaba que, durante dicha crisis, se encontraron efectos de ambos fenómenos (interdependencia y contagio) en mercados emergentes. Los resultados apuntaron a que el fenómeno de interdependencia estaba más ligado con los desequilibrios generados en Estados Unidos, mientras que el contagio estaba relacionado con los shocks provenientes de economías emergentes.
En dirección contraria a las investigaciones presentadas al inicio de esta sección, existen otras, como aquellas desarrolladas por Forbes y Rigobon (2002), donde se argumentó que, al estimar la correlación condicional, se pudo encontrar que no existió contagio en el crash de Estados Unidos en 1987, la crisis mexicana y la asiática, entre algunos países como: Estados Unidos, Canadá, Japón, Reino Unido y Alemania, sino que ha sido un fenómeno de interdependencia, debido a que la correlación entre dichos mercados se ha mantenido en niveles altos, en los períodos previos y posteriores a dichos eventos.
Como se observa en la literatura previamente analizada, los resultados respecto a la relación entre mercados financieros en episodios de incertidumbre son mixtos, debido a que estos dependen del tipo de análisis empírico que se lleve a cabo. En este sentido, se han desarrollado análisis complementarios, cada vez más refinados, con la intensión de obtener evidencia más acertada.
Algunos de los modelos que se han utilizado para configurar los cambios en la dependencia entre mercados financieros son aquellos de tipo Autorregresivo con Heteroscedasticidad Condicional (ARCH, por sus siglas en inglés). Dentro de dichos estudios, se encuentran aquellos que incluyen en el análisis a países en desarrollo, como aquel realizado por Marçal, Valls Pereira, Martin y Nakamura (2011), quienes investigaron el efecto contagio durante la crisis mexicana y asiática; sus resultados apuntaron a que los efectos se esparcieron de Asia a Latinoamérica, pero no en dirección opuesta.
Otro estudio que incluye tanto a países desarrollados como emergentes es aquel elaborado por Celik (2012), quien encontró que, durante la crisis financiera global, existió efecto contagio para la mayoría de los países bajo estudio; sin embargo, aquellos que sufrieron mayor efecto fueron los mercados emergentes. En esta misma dirección, Chittedi (2015) analizó los cambios en las relaciones entre los mercados de valores de India y Estados Unidos, a partir de la CFG; la evidencia señala que hubo un incremento importante en los niveles de correlación, durante las fechas cercanas a los efectos de dicha crisis.
Otra de las aplicaciones de los modelos ARCH, relacionada con los temas de contagio y dependencia, fue aquella implementada por Billio y Caporin (2005), quienes estimaron la correlación incondicional y los parámetros necesarios para analizar procesos de Markov no observables. Los resultados obtenidos son comparados con la evidencia de modelos de correlación condicional dinámica (DCC) y correlación condicional constante (CCC).
Además de los modelos ARCH, los fenómenos de contagio e interdependencia han sido aproximados empíricamente a través de la estimación de relaciones de dependencia entre mercados empleando cópulas. Rodríguez (2007) usó la metodología de cópula con parámetro cambiante, para analizar el efecto de la crisis mexicana y asiática en las relaciones entre los mercados latinoamericanos y del este asiático. Los resultados apuntaron a que hubo efecto contagio en ellos.
Chen, Wei, Lang, Lin y Liu (2014) emplearon cópulas multifractales para analizar la estructura de dependencia entre los mercados de valores de Estados Unidos y China. La evidencia empírica sugirió que el efecto contagio comenzó en Estados Unidos y tuvo una repercusión en el mercado chino. Empleando la misma metodología que Chen et al. (2014), Moreno (2017) investigó sobre el contagio financiero en una muestra de países europeos y latinoamericanos, donde sus resultados indicaron la presencia de contagio entre los países bajo estudio.
Otro estudio que incluyó la metodología de cópulas para analizar la relación de dependencia entre mercados, fue el realizado por Nguyen, Bhatti y Henry (2017), donde se analizó si los mercados de Vietnam y China fueron afectados por los desequilibrios generados en el estadounidense. Los hallazgos revelaron efectos diferenciados para los mercados de Vietnam y China, existiendo gran potencial de diversificación.
Con base en lo anterior, se puede señalar que los modelos de la familia ARCH y las cópulas son aproximaciones empíricas que permiten analizar a detalle los cambios en la relación de dependencia entre los mercados de valores. Dentro de los estudios que han empleado la metodología de Cópula- GARCH, se encuentra el de Su (2017), quien analizó la dependencia de cola y el riesgo de contagio entre los mercados de Taiwan, Corea del Sur, Estados Unidos, China y el índice global europeo MSCI Europe. Los resultados sugirieron efectos diferenciados de la crisis subprime y de la crisis de la deuda soberana griega, en términos de los estados de tendencia y salto del riesgo de contagio.
Mokni y Mansouri (2017), por su parte, estudiaron la relación entre los principales mercados de valores a nivel mundial, donde la evidencia indicó que la estructura de dependencia fue afectada en el largo plazo en la volatilidad. Otros estudios, anteriores a los mencionados, que emplearon la metodología Cópula-GARCH para estudiar la dependencia en mercados financieros, fueron los de Wei y Zhang (2004), Jondeau y Rockinger (2006), Huang, Lee, Liang y Lin (2009), y Aloui, Aïssa y Nguyen (2013).
El presente trabajo se une a los esfuerzos académicos antes citados, con el objetivo de analizar la dependencia condicional entre los mercados de valores de los países que componen el bloque TLCAN. El análisis propuesto incluye una metodología, relativamente innovadora y complementaria, denominada Cópula-GARCH, en la cual se estima la volatilidad de las series a partir de modelos de la familia ARCH, uno simétrico (GARCH) y otro asimétrico (TARCH) y, una vez estimada la volatilidad, se aproxima la relación de dependencia entre dichas series por medio de la cópula.
Metodología y descripción de los datos
La estimación del modelo Cópula-GARCH se realizó empleando los datos de los principales índices bursátiles de México (IPC), Canadá (TSX) y Estados Unidos (S&P500), para el período enero/2004- marzo/2018, todos ellos en dólares, para incluir el efecto del tipo de cambio. Igualmente, todas las series fueron homologadas, eliminando los días en los cuales los mercados no operaron. La muestra total incluyó 3425 datos diarios, divididos en tres subperíodos: precrisis (ene/2004-jul/2007), crisis (ago/2007-dic/2012)11 y poscrisis (ene/2013-mar/2018).
Los modelos GARCH y todas sus posibles variantes se han planteado como instrumentos de análisis idóneos en el estudio de las variables financieras, ya que permiten modelar las características de las series financieras (asimetría, exceso de curtosis, conjuntos de volatilidad, por mencionar algunas). La modelación de la volatilidad se realiza a partir de modelos autorregresivos con varianza condicional GARCH (1,1) y TARCH (1,1). Para la modelación de las series, son utilizados rendimientos diarios de los índices bursátiles, los cuales son estimados a través de la diferencia de los logaritmos naturales del precio de cierre de dos días consecutivos de operación, es decir:
Una condición necesaria para la aplicación del modelo es que las series sean estacionarias, es decir, que no presenten raíz unitaria. Para probar que dicha condición se cumple, es aplicada la prueba propuesta por Dickey y Fuller (1979; 1981), la cual, en honor a ambos, se denomina ADF. Siendo Rt el rendimiento diario de las series, la prueba ADF consiste en una regresión de la primera diferencia de las series contra las series con k rezagos, como se describe a continuación:
La hipotesis nula es H0: δ = 0 y H1: δ < 1.
Modelo GARCH. En cuanto a la estimación de la varianza σ2 , en el modelo GARCH, desarrollado por Bollerslev (1986) y Taylor (1986), la varianza condicional depende no solo de los cuadrados de las perturbaciones, sino también de las varianzas condicionales de períodos anteriores (Casas Monsegny y Cepeda Cuervo, 2008). Así, la varianza condicional del modelo GARCH (p, q) es especificada como:
Donde es necesario que se cumplan las siguientes condiciones, para asegurar que la varianza condicional sea positiva: a 0 > 0, a 1, a 2 , ... a q ≥ 0 y ß 1 , ß 2 , ß 3 , ... ß q ≥ 0 .
Este modelo también es conocido como GARCH simétrico, ya que se asume que los cambios negativos impactan en la misma magnitud que las variaciones positivas. A ht se le denomina varianza condicional, pues es estimada a partir de información pasada relevante. Los coeficientes rezagados del GARCH ßi indican que los efectos de cambios en la varianza condicional toman largo tiempo en desaparecer, a esta propiedad de la serie se le denomina persistencia en la volatilidad. Grandes valores en el coeficiente de error del GARCH aj indican que la volatilidad reacciona intensamente a los movimientos del mercado. Si el valor de (a+ß) es cercano y menor a la unidad, significa que un choque recibido en el tiempo t persistirá en períodos futuros. Un alto valor implicará que la serie tiene memoria larga (Joshi, 2012). Posteriormente, el modelo es probado para efecto ARCH, usando la prueba ARCH-LM. Si el resultado de esta prueba resulta no significativo, el modelo será adecuado (Joshi, 2012).
Modelo TARCH. Para detectar el efecto de la asimetría, han sido desarrollados numerosos modelos, entre los que se encuentran: EGARCH de Nelson (1991); GJR-GARCH de Glosten, Jagannathan y Runkle (1993); T-GARCH de Zakoian (1994); APARCH, desarrollado por Ding, Granger y Engle (1993); PNP- GARCH, utilizado por Bae y Karolyi (1994); y T-GARCH, por Hsin (2004). Dichos modelos son mayormente utilizados en la modelización de volatilidades, ya que capturan de forma diferenciada los efectos de los shocks positivos y negativos, siendo útiles tanto en períodos de estabilidad como de incertidumbre.
Para el caso del TARCH, que es el modelo en cuestión, la especificación generalizada de la ecuación de varianza condicional está dada por:
En este modelo, si ε t-i > 0 los valores positivos del residuo se interpretan como buenas noticias ε t-i < 0 y los valores negativos del residuo representan malas noticias. De igual manera, el efecto sobre la varianza condicional genera que las buenas noticias tengan un impacto de a 1; y las malas, un efecto de a 1 + γ 1. Si γ 1 > 0. Las malas noticias incrementan la volatilidad, lo cual se conoce como efecto apalancamiento o leverage. Si γ 1 ≠ 0 el impacto de las noticias es asimétrico (Joshi, 2012).
Cópula. Una cópula es una función con las siguientes propiedades:
Así, se puede definir la cópula como una distribución multivariada dentro del intervalo [0,1]n con marginales uniformes, teniendo en consideración cómo se deriva una cópula de una distribución multivariada continua. Por tanto, la cópula es la función de distribución multivariada original, con una transformación hacia una marginal univariada (Sosa, Bucio y Cabello, 2015).
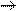 Sea una función de distribución n-dimensional F con distribuciones marginales continuas F1,..., Fn, existe una única n-cópula C: [0,1]n [0,1] tal que:
Sea una función de distribución n-dimensional F con distribuciones marginales continuas F1,..., Fn, existe una única n-cópula C: [0,1]n [0,1] tal que:
El teorema de Sklar (1973) permite combinar las marginales, para formar una distribución multivariada. Dada una distribución F con marginales multivariantes F1, ..., Fn, la función:
es automáticamente una -cópula. Esta cópula es la de la distribución multivariada . Mediante este teorema, Sklar (1973) señaló que, para cada función de distribución multivariada, se puede derivar fácilmente una cópula. Existen diversas familias, siendo las de mayor utilización en temas financieros las elípticas y Arquimedianas, por sus bondades y características.
Cópulas elípticas. Las cópulas elípticas han sido de las más utilizadas en aplicaciones financieras (Hernández y Sánchez, 2009; Hammoudeh, Nguyen, Reboredo y Wen, 2014) y tienen la particularidad de ser de tipo simétrico. Dentro de esta familia de cópulas, destacan la t-Student y la Gaussiana, que derivan de funciones multivariadas que poseen los mismos nombres. La densidad de dichas cópulas se encuentra representada por:
De manera particular, la cópula gaussiana está determinada por el conocimiento de la matriz del coeficiente de correlación ρ.
Cópula t-Student. Sea una distribución t-Student -dimensional Tn,p,ν con ν grados de libertad y una matriz ρ
La cópula t-Student es
Donde Tν es la distribución univariada t-Student con ν grados de libertad.
La densidad de la cópula t-Student es
La cópula t-Student, al igual que la Gaussiana, se basa en el parámetro de correlación ρ; así como en los grados de libertad.
Cópula Gaussiana. La n-cópula Gaussiana con matriz de correlación ρ, se describe a través de la siguiente ecuación:
Donde Ф denota la distribución Normal (acumulada) y Фρ,n denota la distribución Gaussiana estándar -dimensional con matriz de correlación ρ.
Cópulas Arquimedianas. Las cópulas bivariadas de tipo arquimediano son representadas de la siguiente forma:
donde ɸ
a
es convexa y decreciente tal que 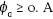 . A la función ɸ
a
se le denomina generador de la cópula Ca y la inversa del generador
. A la función ɸ
a
se le denomina generador de la cópula Ca y la inversa del generador 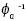 es la transformada de Laplace de una variable latente denotada γ, la cual induce la dependencia a. Por ello, la selección de un generador da como resultado diferentes cópulas dentro de esta familia. Por la naturaleza de la presente investigación, se hace referencia a las cópulas Clayton, Gumbel y Frank.
es la transformada de Laplace de una variable latente denotada γ, la cual induce la dependencia a. Por ello, la selección de un generador da como resultado diferentes cópulas dentro de esta familia. Por la naturaleza de la presente investigación, se hace referencia a las cópulas Clayton, Gumbel y Frank.
Cópula Clayton. La cópula bivariada de este tipo esta especificada como:
con generador ϕ a (t) t 1-a -1, y transformada de Laplace ϕa -1 (s) = (1+s) 1/(1-a) .
Cópula Gumbel. La cópula bivariada perteneciente a la familia Gumbel es:
con generador ϕ a (t) = (-ln t) 1/a , y transformada de Laplace ϕ a -1 (s) = exp {- sa }.
Cópula Frank. Esta cópula bivariada se especifica como:
con generador 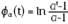 , y transformada de Laplace
, y transformada de Laplace 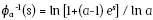
Estimación de los parámetros de la cópula. Existen diversas metodologías para la estimación de los parámetros de la cópula. En el presente, se utiliza el de máxima verosimilitud, ya que este mecanismo permite estimar los parámetros para cualquier tipo de cópula, maximizando su función de log-verosimilitud. De esta manera, dados el conjunto de marginales y una cópula, la función de log- verosimilitud puede ser maximizada obteniendo, de esta forma, el estimador de máxima verosimilitud,
Evidencia empírica
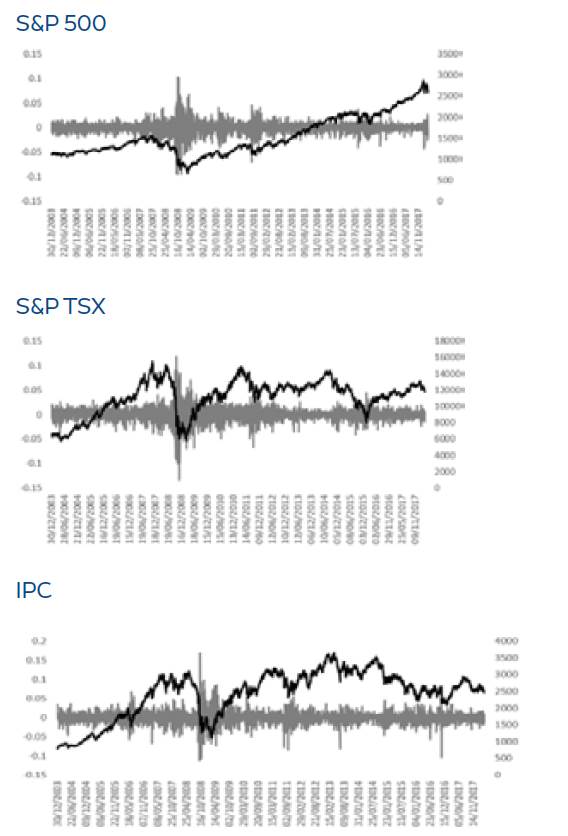
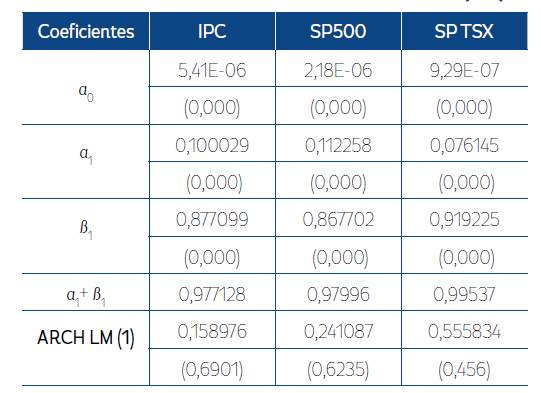
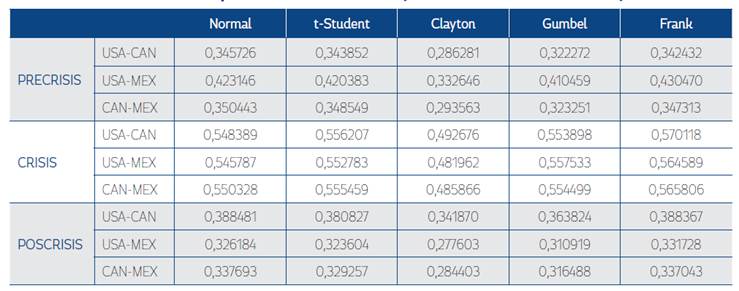
Los datos representados en la Figura 1 revelan el comportamiento de los índices bajo estudio, en niveles y rendimientos logarítmicos, calculados a partir de la ecuación (1). En dicha figura, se puede observar que las series en niveles presentan comportamiento similar, en términos de una caída abrupta en el tercer trimestre del año 2008, período en el cual se globalizó la crisis subprime. Igualmente, se presentan caídas conjuntas menores a finales del año 2015 y principios del 2016, lo cual, aparentemente, se debe a la respuesta de los mercados ante las noticias originadas a partir del Brexit y la crisis de la deuda en Grecia. En términos de los rendimientos de los índices, los períodos de las caídas de los bursátiles coinciden con conjuntos de volatilidad.
La Tabla 1 presenta los estadísticos descriptivos de las series en rendimientos. Como es de esperarse, el mercado de valores mexicano es aquel con la mayor rentabilidad, seguido del estadounidense y el canadiense. El mercado con la mayor variabilidad, medida como la desviación estándar, es el de México, seguido por el de Canadá y EE. UU. Las series presentan sesgo negativo y leptocurtosis; las distribuciones tienen colas pesadas y son puntiagudas. La prueba de Jarque Bera muestra que las series son no normales.
Tabla 1 Estadísticos descriptivos
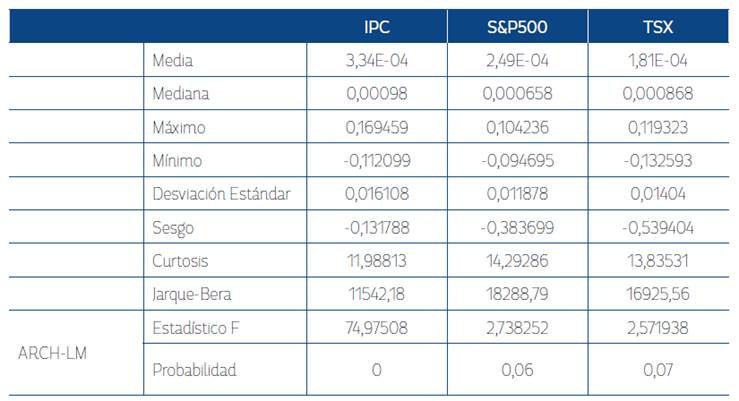
Nota: la prueba estadística ARCH-LM es el multiplicador de Lagrange usado para la detección del efecto ARCH. Bajo la hipótesis nula de no heteroscedasticidad, dicho termino se distribuye como λ 2(k). Elaboración propia.
La Tabla 1 muestra los resultados de la prueba ARCH-LM, los cuales indican la presencia de efecto ARCH para todas y cada una de las series bajo estudio, ya que la probabilidad asociada a los mismos es menor a 0,1. Dado que los modelos de la familia GARCH son aptos para la modelación de series leptocúrticas, se emplea uno de dichos modelos de tipo simétrico y uno asimétrico, para la modelación de la volatilidad de las series.
Tabla 2 Resultado de la prueba Dickey Fuller Aumentada
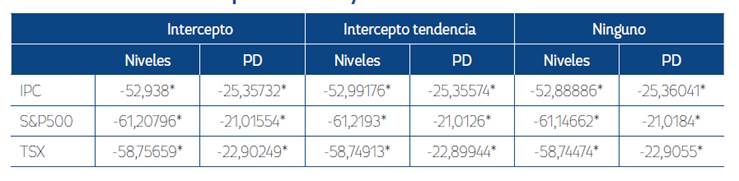
Nota: la hipótesis nula de la prueba ADF es que las series tienen raíz unitaria. El valor crítico de MacKinnon al nivel de significancia del 1 % es -3,44. * Nivel de significancia del 1%. Elaboración propia.
La condición de estacionariedad es examinada a través de la prueba de Dickey Fuller Aumentada (ADF, por sus siglas en inglés). Los resultados de la Tabla 2 sugieren que la hipótesis nula de la presencia de raíz unitaria es rechazada, ya que los valores de los índices bursátiles son mayores que el valor crítico de MacKinnon al 1 % de significancia. Por lo tanto, se confirma que las series son estacionarias tanto en niveles (logaritmos) como en primeras diferencias. Una vez que se cumple con la condición necesaria de que las series no tengan raíz unitaria, se lleva a cabo la modelación, a través de los modelos GARCH y TARCH.
Resultados del modelo GARCH y TARCH. Como se observa en la Tabla 3, todos los parámetros estimados a través del modelo GARCH (1,1) son positivos y estadísticamente significativos, con una probabilidad menor a 0,05. Además, el valor del resultado de la estimación del parámetro ß1 es mayor, en todos los casos, que el de a1, y en la suma a1+ ß1 el resultado es inferior y muy cercano a uno. Esto significa que se garantiza la condición de que el proceso ARCH es estacionario; es decir, la varianza no crece de forma indefinida. El hecho de que el coeficiente de retardo de la varianza condicional ß1 sea mayor que el coeficiente de error a1 implica que hay persistencia de los shocks con efectos en el largo plazo, lo que significa que la volatilidad no decae rápidamente, sino que tiende a permanecer, y su efecto se desvanece poco a poco.
Tabla 4 Resultados del modelo TARCH (1,1)
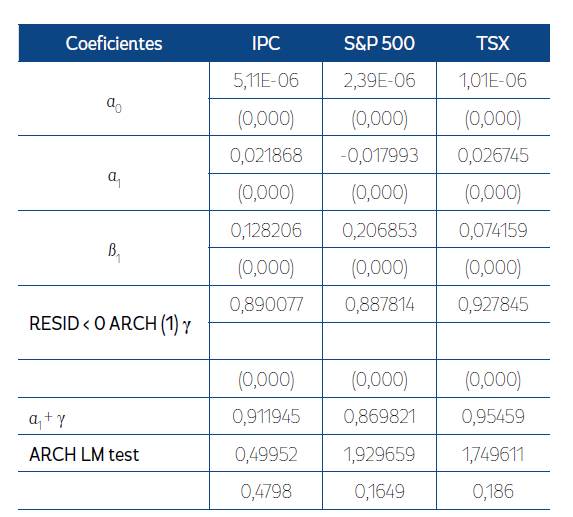
Nota: valores entre paréntesis representan las probabilidades. Elaboración propia.
Los resultados del modelo TARCH son presentados en la Tabla 4, donde se observa que el término de apalancamiento (γ) representado por RESID<0 ARCH (1) es mayor a cero y estadísticamente significativo, lo cual refuerza el supuesto de que los impactos positivos y negativos tienen efectos diferenciados en la volatilidad de los rendimientos bursátiles diarios. Las noticias buenas tienen un impacto de a1, mientras que las malas tienen un impacto a1+ γ; es decir, su impacto es mayor que el de las buenas en todos los mercados financieros analizados.
Por su parte, los valores del estadístico ARCH-LM con un rezago, para ambos modelos GARCH y TARCH, son no significativos estadísticamente, ya que la probabilidad asociada es mayor al 0,05, rechazando la presencia de efecto ARCH después de la aplicación del modelo, lo cual sugiere que los modelos son adecuados y que proveen buen ajuste. Igualmente, para ambos modelos (GARCH y TARCH) se realiza la prueba Ljung-Box, donde los valores de probabilidad obtenidos, para los tres mercados, son mayores de 5 %, lo cual indica que los residuales del modelo no presentan autocorrelación serial.
Una vez que se estima la volatilidad condicional, los valores de los residuales de ambos modelos son empleados para analizar la estructura de dependencia entre los diversos mercados, a través de tres subperíodos: antes, durante y después de la crisis.
Resultados de la cópula. La Tabla 5 y la Figura 2 muestran los resultados del parámetro de dependencia condicional, empleando los residuales del modelo GARCH, tanto para las cópulas elípticas (t-Student y normal) como para las Arquimedianas (Clayton, Gumbel y Frank). Los resultados señalan que, para todas las cópulas, el parámetro de dependencia es inferior en los períodos previo y posterior a la crisis. Lo anterior evidencia la existencia de contagio bursátil entre el bloque TLCAN.
Cabe señalar que la estructura de dependencia condicional que muestra mayor fuerza es aquella existente entre los mercados de Estados Unidos y México, la cual registra valores cercanos al 0,4 (promedio de los diversos parámetros de cópula), en el período previo a la crisis; 0,55, en el de crisis; y 0,31, en el posterior a la crisis; dichas cifras representan un incremento de 38 % en el parámetro de dependencia. En segundo lugar, en términos de magnitud, se encuentra la relación de dependencia entre Estados Unidos y Canadá, cuyo valor previo a la crisis es 0,328; durante la crisis, 0,544; y posterior a la crisis, de 0,373; los niveles asociados a dichos períodos, para el caso de la relación Canadá y México, son 0,333; 0,542, y 0,321, respectivamente.
Retomando el análisis de los datos presentados previamente, el nivel de dependencia condicional entre Estados Unidos-Canadá y Estados Unidos-México es sumamente parecido. Los resultados difieren en relación con el trabajo realizado por Díaz y Bucio (2018), donde se analiza la dependencia entre los rendimientos diarios de los mercados bursátiles del TLCAN, a diferencia del presente, que investiga la estructura de dependencia condicional, a partir de medir la volatilidad por medio de modelos GARCH. Lo anterior revela que el comportamiento de los mercados, en cuanto a sus variaciones (riesgo) debido a cambios en el mercado estadounidense es casi igual, lo que podría significar que la volatilidad de los mercados de México y Canadá tienen un parámetro de riesgo sistemático casi idéntico ante cambios en la volatilidad del estadounidense.
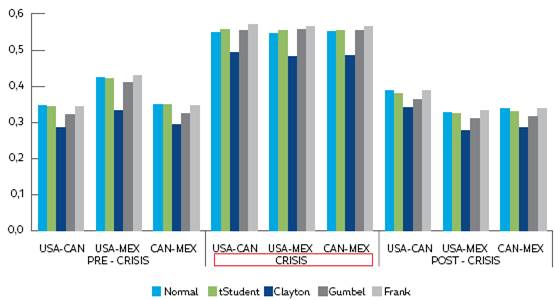
Elaboración propia con datos de la investigación
Figura 2 Evolución de la dependencia condicional (GARCH) en los mercados del TLCAN
Tabla 6 Parámetros de dependencia condicional (empleando residuales modelo TARCH)
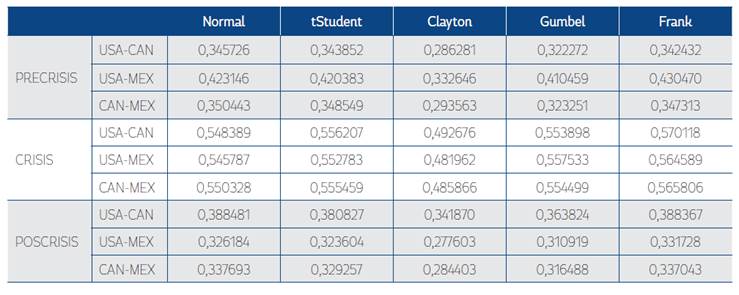
Nota: elaboración propia.
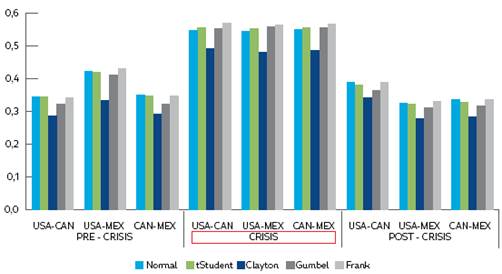
Elaboración propia con datos de la investigación
Figura 3 Evolución de la dependencia condicional-TARCH en los mercados del TLCAN.
Los resultados de la dependencia condicional (Tabla 6 y Figura 3), estimada a partir de los residuales del modelo TARCH, son levemente inferiores a aquellos obtenidos a partir del modelo simétrico GARCH, lo cual significa que la estructura de dependencia considerada a partir de la cópula, teniendo en cuenta asimetría en la volatilidad (las malas noticias tienen mayor impacto en ella que las positivas de la misma magnitud), describe niveles inferiores, en relación a aquella que no toma en cuenta el efecto apalancamiento. Dichos resultados apuntan a que la asimetría en la volatilidad de los mercados bajo estudio es muy parecida, por lo que la dependencia entre los mercados se ve apenas erosionada al incluir la respuesta asimétrica de las series. El hecho de que la dependencia condicional considerando asimetría sea menor que la que no lo hace responde al hecho de que la asimetría en los mercados es de distinta magnitud, como se aprecia en la Tabla 4.
Conclusiones
Las crisis financieras son fenómenos sumamente trascendentales. Uno de los espacios en los cuales se manifiestan afectaciones importantes es el mercado de valores, lugar de interconexión y obtención de recursos, sobre todo, para las unidades productivas de una economía. Los cambios en los precios de los títulos, que se derivan de la transmisión de desequilibrios, añaden riesgo a los mismos, incrementando el rendimiento asociado a dichos instrumentos y, por ende, el costo ligado al financiamiento. En referencia a lo anteriormente señalado, la presente investigación es de gran relevancia para los inversionistas, empresas que cotizan en bolsa y para aquellos tomadores de decisiones y hacedores de política económica.
El objetivo de la presente investigación es analizar la dependencia condicional entre los mercados de valores del bloque TLCAN, permitiendo identificar la existencia de efecto contagio a través del incremento en el nivel de dependencia en momentos de inestabilidad bursátil. Para lograr dicho fin, se modeló la volatilidad de las series a partir de un modelo simétrico GARCH y uno asimétrico. Una vez que fue modelada la volatilidad condicional, se estimó la estructura de dependencia a partir de cópulas Arquimedianas y elípticas, para tres subperíodos: antes, durante y después de la crisis financiera global.
Los resultados de los modelos GARCH y TARCH apuntaron a que ambos son idóneos para la modelación de la volatilidad de las series, las cuales presentan memoria larga y asimetría; es decir, que el efecto de un shock tarda mucho en desvanecerse y que las noticias malas tienen mayor impacto en la volatilidad que aquellas positivas de la misma magnitud. Los modelos fueron probados y señalaron la existencia de un ajuste adecuado.
La dependencia condicional, estimada a partir de los residuales del modelo GARCH, señaló que existe un incremento de alrededor de 38 % en el período de crisis, respecto al período previo y posterior. Igualmente, los resultados sugirieron que la dependencia condicional entre México- Estados Unidos y Canadá-Estados Unidos es muy parecida, lo cual implica que la volatilidad de ambos mercados tiene el mismo nivel de respuesta ante variaciones del mercado estadounidense. Esta conclusión es sumamente relevante, en términos de la construcción de portafolio y la localización de inversiones, con miras de diversificar el riesgo.
Para los gestores de inversión, el incremento de la dependencia entre mercados durante períodos de crisis disminuye el efecto de la diversificación de portafolio internacional. Lo anterior debería ser tomado en cuenta para realizar estrategias en función de la etapa del ciclo económico en el que se encuentre. Igualmente, la medición del riesgo del mercado debe ajustarse, ya que en épocas de crisis existe mayor volatilidad y asimetría en la misma, teniendo mayores efectos, en el mercado, las malas noticias (caídas en los índices) que aquellas positivas.
Por otra parte, la dependencia condicional, calculada mediante los residuales del modelo TARCH, es levemente inferior a la estimada a partir de modelos GARCH, lo cual significa que la modelación de la asimetría en la volatilidad tiene un leve efecto en el nivel de dependencia.
Finalmente, cabe anotar que el contagio financiero es un tema que debe seguir siendo estudiado, ya que aún existen aspectos que no se han descifrado en torno al mismo. Una mayor comprensión del fenómeno llevará a un mejor diseño de los planes y programas de prevención de crisis, aminorando el efecto de las mismas e, incluso, permitiendo que se eviten. En este sentido, algunas líneas de investigación futura podrían ser el análisis del contagio financiero con otras metodologías -como el cálculo de la matriz de correlación incondicional-, estudiar la dependencia entre diversos mercados a nivel global, e investigar las relaciones entre diversos activos (bonos, acciones, mercaderías, etc.).