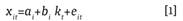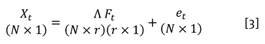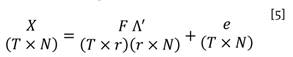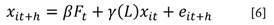Introducción
Tal y como es señalado por Mitchell, Brockett y Mendoza (2013), la modelación y pronóstico de tasas de mortalidad ha sido un área activa de investigación al menos desde que Graunt (1662) examinara la mortalidad en Londres, con el fin de crear un sistema de alerta sobre el incremento de la incidencia (y el posterior declive) de la peste bubónica. El principal aporte del trabajo de Graunt consistió en mostrar que a pesar de que la longitud de la vida individual es incierta, es posible predecir patrones de mortalidad a nivel agregado, es decir, para grupos de personas. La modelación teórica sobre las tasas de mortalidad se siguió perfeccionando con los aportes de Moivre (1725), y sobre todo Gompertz (1825), quien mostró cómo formular un sistema de ecuaciones en diferencias cuya solución lleva a una curva de supervivencia doble-exponencial (conocida como la curva de Gompertz), que actualmente se utiliza para predecir el comportamiento de las tasas de mortalidad de personas de edades muy avanzadas (Gavrilov y Gavrilova, 2011).
Estas construcciones son de naturaleza estática, sin embargo, hoy se entiende que las tasas de mortalidad son series de tiempo dinámicas, que evolucionan estocásticamente de período a período. De esta forma, mientras que los modelos estáticos sirven para predecir las tasas de mortalidad en un período específico, se quedan cortos al momento de proyectar la evolución temporal de las tasas y es necesario recalibrarlos, de cuando en cuando, para acomodar cambios en la estructura de tales tasas de mortalidad. Es por esto que los modelos estadísticos de series de tiempo han cobrado un papel relevante en las décadas más recientes, para lograr un pronóstico dinámico óptimo de las tasas de mortalidad.
Dado lo anterior, actualmente, tal y como lo señalan Haberman y Renshaw (2012) mucha de la investigación que se lleva a cabo en términos del pronóstico de tasas de mortalidad, en la literatura actuarial y demográfica, se basa en métodos de extrapolación que capturan los patrones históricos de tales tasas, valiéndose de estructuras predictivas paramétricas o no paramétricas, y que pueden ser extrapoladas fácilmente siguiendo modelos tradicionales de series de tiempo. La más utilizada de estas estructuras es el modelo de Poisson de estructura log-bilineal, propuesto por Brouhns, Denuit y Vermunt (2002) y Renshaw y Haberman (2006), el cual a su vez es una generalización del modelo originalmente propuesto por Lee y Carter (1992). Este último se basa en una estructura de predicción paramétrica, que consta de efectos idiosincráticos por edad y efectos comunes de mortalidad, que afectan a todos los grupos de edad simultáneamente.
En este documento se expone el modelo de Lee-Carter, actualmente el más popular para el pronóstico de tasas de mortalidad y se le contextualiza dentro de la clase de modelos por factores. Un modelo por factores es uno en el que la dinámica de una serie, en este caso de una tasa de mortalidad, consta de dos partes: un componente idiosincrático y un componente común. Este componente común es un factor no observable, que afecta todas las tasas de mortalidad simultáneamente y debe ser estimado al mismo tiempo que los parámetros del sistema. También se aplica aquí el modelo de Lee-Carter para el pronóstico de las tasas de mortalidad de Cali de 2013 a 2030, lo cual constituye un aporte en sí mismo, ya que estas pueden servir como insumo para la elaboración de cálculos actuariales y de políticas públicas en la ciudad.
La literatura en Colombia, sobre el pronóstico de tasas de mortalidad utilizando modelos por factores es escasa, una excepción es el estudio de Reyes-Sierra (2010) en el que se estiman varios modelos por factores con las tasas de mortalidad agregadas para Colombia. La intención de la autora es, principalmente, el estudio de los efectos en términos de carga fiscal en pensiones para la Nación, debido al envejecimiento de la población. Así como la influencia de la sobremortalidad masculina en los pronósticos de carga fiscal por este concepto. La autora simula varios escenarios de costo fiscal y compara el error cuadrático medio de varias estrategias de pronóstico, dentro de las cuales se cuenta el modelo de Lee-Carter.
En este documento, a diferencia del de Reyes-Sierra (2010), se trabaja con datos municipales, pertenecientes a Santiago de Cali. Para Cali, los estudios demográficos son escasos y se remontan hasta trabajos que cuentan hoy con más de dos décadas como el de Bayona (1990). A pesar de los años transcurridos, sigue siendo el estudio de Bayona (1990) un referente para el análisis demográfico en la región. Muchos de los análisis que se hacen allí, por ejemplo en términos de la pronunciada sobremortalidad masculina de la ciudad, el desperdicio de años de vida debido a muertes violentas (por homicidios y suicidios) en hombres de rangos de edad entre 15 y 30 años, y las mejoras significativas en las tasas de mortalidad de los adultos mayores, son hoy tan esclarecedores de los datos, como lo eran en ese entonces. No obstante, el objetivo de este trabajo no es la dilucidación de los efectos causales detrás de las dinámicas de mortalidad en la ciudad, sino el pronóstico de las mismas, y la exploración detallada de las tendencias recientes de las tablas de vida.
Este documento se organiza así: en la primera sección, después de esta introducción, se presenta el modelo de Lee-Carter; en la segunda se le contextualiza dentro de la clase de los modelos por factores; en la tercera se realiza una estimación con los datos de Santiago de Cali y se presentan los principales resultados del estudio. En la cuarta y última se concluye.
El modelo de Lee-Carter
El de Lee y Carter (1992) es un modelo estadístico ampliamente utilizado en la literatura sobre demografía y actuaria, desde que fue propuesto por lo autores hace un par de décadas, para la estimación y pronóstico de tasas específicas (y globales) de mortalidad y la construcción de tablas de vida (Deaton y Paxson, 2004).
Ha sido usado como punto de referencia para pronósticos de población (Hollman, Mulder y Kallan, 2000); recomendado por diversos organismos de naciones desarrolladas como el Panel de Consultores Técnicos de Seguridad Social en Estados Unidos (Lee y Miller, 2001), o la Investigación Continua de Mortalidad en el Reino Unido (Continuous Mortality Investigation, 2004). La literatura académica, por su parte, se ha alineado en torno a él y a modelos relacionados, de forma tal que su uso se ha extendido a diversas naciones alrededor del mundo, en cuanto se ha tornado una herramienta indispensable dentro de la formulación de políticas públicas relacionadas con el pronóstico de la expectativa de vida de una población específica y el pronóstico de sus tasas de mortalidad .
Formalmente, sea xit = ln mit el logaritmo natural de la tasa de mortalidad específica del grupo i en el período t. Se tiene que el modelo puede ser planteado en términos de un vector a y un vector b a lo largo de la dimensión transversal (edades discriminadas por sexo y rangos de edad), y un vector k a lo largo de la dimensión temporal, de forma tal que:
Adicionalmente, deben cumplirse las restricciones de que ∑ i bi =1 y ∑ t kt =0 de manera que ai son promedios temporales simples de los logaritmos de las tasas de mortalidad específicas. Estas restricciones son necesarias para la identificación del sistema, tal y como se hará evidente en la siguiente sección del documento.
Nótese que kt es un índice dinámico, variante en el tiempo, que mide el nivel de mortalidad general. eai es la forma general de la mortalidad a través de las edades, dentro la estructura de mortalidad analizada. bi indica cuál tasa de mortalidad declina rápidamente, y cuál lo hace lentamente en respuesta a cambios en el factor k ( dln(mit )/dt=bi dk/dt ). En principio, bi podría ser negativo para algunas edades indicando que la mortalidad en esas edades podría incrementarse cuando esta cae para el resto de edades. No obstante, en la práctica este no parece ser el caso en el largo plazo, tal y como lo señalan Lee y Carter (1992) y como se puede apreciar en la sección que contiene la evidencia empírica de este documento. De hecho, solo se encuentran valores negativos de este parámetro para un grupo de edad, dentro del grupo de hombres (14-19 años), como se verá más adelante.
Debido a que el modelo se ajusta sobre los logaritmos de las tasas de mortalidad, no es posible que se presente el caso de tasas de mortalidad negativas en el pronóstico, lo cual es una característica muy conveniente del mismo.
El término de error ε it con media 0 y varianza σε 2 refleja las influencias históricas específicas asociadas con cada rango de edad (condicional al sexo) que no son capturadas por el modelo. Para cualquier valor de kt , el modelo ajustado define un conjunto de tasas de mortalidad que pueden ser usadas para la derivación de tablas de mortalidad y tablas de vida.
La estrategia de estimación del modelo, sobre la cual se volverá más adelante, consiste en utilizar una descomposición de valor singular (SVD por sus siglas en inglés), puesto que el método de mínimos cuadrados ordinarios no puede ser aplicado directamente sobre [1], al no existir en esta ecuación regresores predeterminados (el índice kx debe ser también estimado en el proceso ).
La popularidad del modelo de Lee-Carter con respecto a modelos tradicionales de series de tiempo ARIMA, utilizados para el pronóstico de las tasas específicas de mortalidad en estimaciones independientes, se debe a la inclusión del término kt que es común a todas las tasas. Este solo varía en el tiempo y no transversalmente, entre grupos. De esta forma, se reduce la cantidad de parámetros a ser estimados, a la vez que se impone un comportamiento acompasado entre las tasas, impidiendo que el pronóstico en intervalos largos de tiempo se disperse. Evitando así la configuración de patrones implausibles en la práctica.
Tal y como es señalado por Girosi y King (2007), kt corresponde al primer componente principal del sistema, y por tal razón el modelo de Lee-Carter puede ser visto como un caso específico del modelo de caminata aleatoria multivariado con deriva. También es posible entender kt como una tendecia estocástica común, impuesta sobre el sistema, lo cual emparenta el modelo de Lee-Carter con la literatura de CVAR (Vectores Autorregresivos Cointegrados) o con los modelos VEC (vectores de corrección de error), donde bi está relacionado con el vector de cointegración del sistema.
Modelos por factores
En esta sección se introducen los modelos por factores, muy populares en la econometría contemporánea y se presenta el modelo de Lee-Carter como un caso específico de estos, con el fin de ganar alguna intuición adicional sobre el mismo.
Siguiendo a Bai y Ng (2008), sea N el número de unidades de sección cruzada y T el número de observaciones en el tiempo , para i=1,…,N y t=1,…,T, el modelo por factores estáticos (MFE) se define como:
eit se refiere al término de error idiosincrático, λ i correspondiente a las cargas de los factores. Este vector contiene los pesos que la unidad i asigna a cada uno de los correspondientes r factores comunes Ft . Cit= λ i Ft es conocido como el componente común del modelo. Si adicionalmente se define Xt =(x 1 t ,x 2 t ,…, xNt )’ y Λ=(λ1,…,λN )’, en forma vectorial para cada período se tendrá que:
donde et=(e1t ,e2t ,…,eNt )’. Nótese que a pesar de que el modelo es específico en cuanto a la relación estática entre xit y Ft , Ft mismo puede ser un vector dinámico. En el caso en que Ft y Xt sean conjuntadamente estacionarios, Ft puede pensarse como el producto de una dinámica que sigue una representación de vectores autorregresivos (VAR):
A(L) es un polinomio en el operador de rezagos. El modelo de factores estáticos es implementado en numerosos estudios alrededor del mundo que tienen como objetivo pronosticar tasas de mortalidad por cohortes de edades y sexo, tal como en el caso de Alonso (2008), Delwarde, Denuit, Guillén y Vidiella-i-Anguera (2006), Cossette, Delwarde, Denuit, Guillot y Marceau (2007), Lemoine (2015) o Bisetti y Favero (2014). Nótese que si se hace L=1 y A(1)=lr, donde lr es la matriz identidad de orden r, el modelo en [4] se convierte en una caminata aleatoria multivariada, como la propuesta por Girosi y King (2007). Si además imponemos que r=1, estaremos en presencia del modelo de Lee y Carter (1992) expuesto en la ecuación 1.
En el caso general Ft puede contener factores estacionarios y no estacionarios como ocurre en Peña y Poncela (2004, 2006) o en Bai y Ng (2004). No obstante, para las aplicaciones empíricas es conveniente restringir la atención a los casos en los cuales todos los factores son estacionarios o aquellos en los cuales todos ellos comparten la misma tendencia estocástica. Esto es especialmente relevante cuando se tiene un N grande, y las pruebas de cointegración basadas en la representación VAR de lo sistemas tienen un pobre desempeño, debido a la cantidad enorme de parámetros que se deben estimar en el VAR .
Adicionalmente se tiene que si las perturbaciones en [2] pueden estar débilmente correlacionadas, se habla de un modelo aproximado por factores, mientras que si estas se exigen ortogonales, se está en presencia de un modelo exacto por factores. Los modelos aproximados por factores son muy populares en econometría (Stock y Watson, 2006), pero los modelos exactos por factores han sido más utilizados en la literatura actuarial. El modelo de Lee-Carter es en su versión original uno de estos.
Identificación
En notación matricial el modelo puede ser escrito como:
donde X=(X 1',…,X t ' ) y F=(F 1,…., FT ). Claramente F y Λ no son identificables por separado. Para cualquier matriz arbitraria de dimensión (r×r) con determinante distinto de cero, H, se tiene que FΛ'= FHH -1 Λ' =F* Λ'*, donde F *= FA y Λ*=ΛH-1, y por tanto el modelo por factores será observacionalmente equivalente a X = F*Λ'* + e. Es debido a lo anterior que se deben imponer r 2 restricciones, con el fin de fijar de forma única F y Λ (Bai & Wang, 2015). Muchas alternativas se han propuesto en la literatura para llevar a cabo esta tarea.
Por ejemplo, Harvey (1989), Zuur, Fryer, Jolliffe, Dekker & Beukema (2003) y Holmes et al. (2014) proponen la siguiente: en las primeras N - 1 filas de Λ, el valor λ en la j-ésima columna y en la i-ésima fila se hace igual a cero si j>i. El intercepto se restringe de forma tal que cada serie de tiempo en FT tenga una media temporal de cero (de t=0 a t=T) . La matriz de segundos momentos E[e’e] se obliga a igualar a una identidad de orden N, IN .
Por otra parte, la estimación de los factores a través de componentes principales (PC) o SVD, generalmente impone la normalización dada por 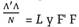 diagonal. Las cuales son suficientes para la identificación del sistema.
diagonal. Las cuales son suficientes para la identificación del sistema.
Estimación
Una alternativa para estimar el modelo en [2] - [4] consiste en usar PC o equivalentemente SVD, para estimar los factores y las cargas de los mismos .
Otra forma de estimación eficiente de [2] - [4], bajo el supuesto de errores gaussianos, surge cuando se nota que [3] y [4] pueden ser pensados como una representación de estado-espacio, donde la ecuación de transición sigue un proceso markoviano de primer orden. El vector no observable está dado por [4], mientras que [2] es la ecuación de medida en el sistema. Por lo tanto, el modelo puede ser estimado por máxima verosimilitud, a través del algoritmo de maximización de expectativas o recurriendo a otros optimizadores numéricos (Hamilton, 1994; Holmes et al., 2014). El filtro de Kalman es el estimador óptimo en este caso de los parámetros del sistema, y el suavizador de Kalman puede ser utilizado para estimar el vector no observable de factores, que en el caso del modelo de Lee-Carter corresponde al índice de mortalidad general kt.
Pronóstico
Tal y como lo señalan Stock y Watson (2006) el pronóstico del modelo por factores se puede llevar a cabo a través de una regresión simple de los factores estimados sobre adelantos de la variable que se quiere estimar. Es decir, el pronostico de h-períodos adelante se puede realizar directamente a través de una regresión de xit + h sobre los factores estimados en el paso anterior, así:
En el caso del modelo de Lee-Carter, este pronóstico corresponde sencillamente a la extrapolación del factor no observable kt y el cálculo de la mortalidad implicada en xit + h , de acuerdo con los parámetros ax , bx ∈ β. La inclusión de los rezagos de xit + h = ln mxt + h es opcional.
Estimación del modelo de Lee-Carter para Santiago de Cali
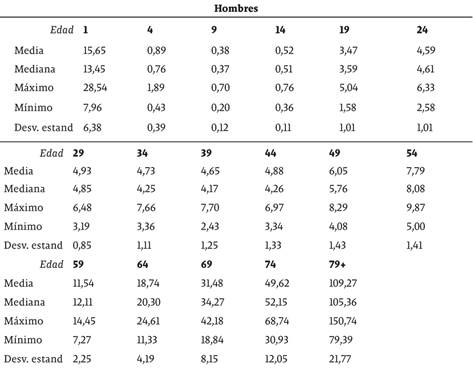
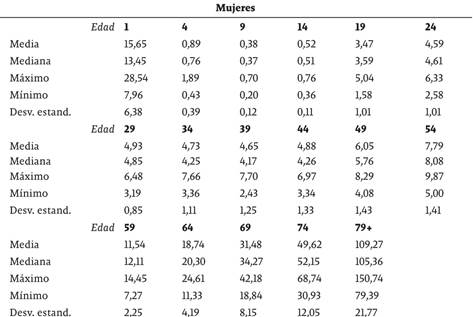
Los datos de las tasas de mortalidad por géneros y según los rangos de edad especificados en la tabla 1 se obtuvieron directamente de la Secretaría de Salud Municipal de Cali, con una frecuencia anual desde 1985 hasta 2012. En las tablas 4 y 5 de los anexos se presentan los estadísticos descriptivos asociados. Los datos disponibles presentan la limitación de que solo se encuentran discriminados por quinquenios y además es imposible estudiar la mortalidad en las edades más avanzadas, al estar agregadas todas las tasas de mortalidad después de los 79 años en una misma categoría.
El gráfico de las tasas en logaritmos tranversal y temporalmente, se presenta en la figura 1(a) 1(b).
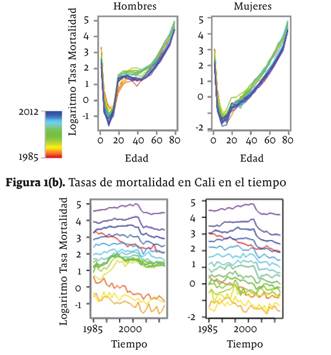
Fuente: elaboración propia, con base en información suministrada por la Secretaría de Salud Municipal de Cali
Figura 1(a) Tasas de mortalidad Cali por edades y sexo: 1985-2012
Como se puede observar, tanto para hombres como para mujeres, las tasas de mortalidad han presentando importantes reducciones durante el período de estudio. Lo anterior es consistente con lo encontrado en la literatura internacional (Figg, 2008) y está relacionado con el proceso de desarrollo económico y las consecuentes mejoras en términos clínicos, higiénicos y epidemiológicos que se han presentando desde inicios del siglo pasado alrededor del mundo, y en particular en Colombia. No obstante, también es evidente la diferencia en la dinámica de las tasas de mortalidad para los hombres en los rangos entre 14 y 25 años y el resto de la población. Para estos rangos de edad de hombres, en contraste con lo encontrado para las mujeres, las tasas de mortalidad son en promedio más altas de lo que eran 40 años antes. Se tiene que sus tasas específicas de mortalidad se deterioraron sustancialmente hasta mediados de los años de 1990 y solo a partir de esa fecha empezaron a reducirse en consonancia con las del resto de la población. Este es un fenómeno muy distinto al que se aprecia para economías desarrolladas, en las cuales todas las tasas de mortalidad han presentado decrecimientos generalizados tanto para hombres como para mujeres en el siglo actual. Esta particularidad seguramente está vinculada con las dinámicas sociales de violencia y homicidios de la ciudad, especialmente acentuadas en estos grupos específicos de la población (Bayona, 1990), pero su comprensión requiere de un estudio causal de los factores determinantes de la muerte.
Otros patrones que surgen de la comparación sí son acordes con lo encontrado para otras regiones del mundo. Por ejemplo, la forma de “joroba” que presentan las tasas de mortalidad de los hombres a partir del grupo 1 hasta el grupo 4, y que no se presentan en las tasas de mortalidad para mujeres en los mismos rangos de edad, se asocian con un mayor número de accidentes de tráfico masculinos y homicidios en esos rangos de edad, que en el resto de la población. Por lo demás, las tasas tanto de hombres como de mujeres se reducen después del año de edad, hasta los 14, fecha a partir de la cual se incrementan sostenidamente, conforme la edad avanza.
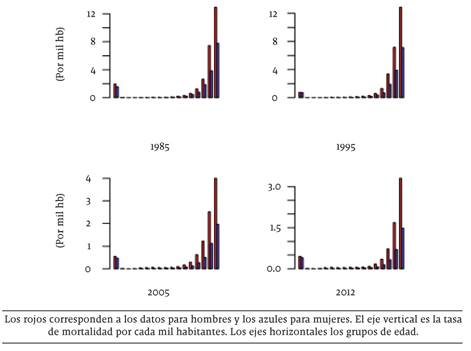
En la figura 2 se presentan las tasas de mortalidad por sexo y rangos de edad en cuatro cortes transversales de la información, para los años 1985, 1995, 2005 y 2012. Como se puede apreciar, una vez más se pone de manifiesto la reducción acentuada en todos los grupos de las tasas de mortalidad medias. No obstante, en este gráfico es más fácil ver que las reducciones no han sido proporcionales, siendo más pronunciadas para las mujeres que para los hombres. También es evidente que las reducciones en los niveles de las tasas de mortalidad son más pronunciadas en los grupos de menor edad, particularmente los menores de un año, y en los de edad más avanzada, en especial a partir de los 60 años de edad.
Modelo estimado
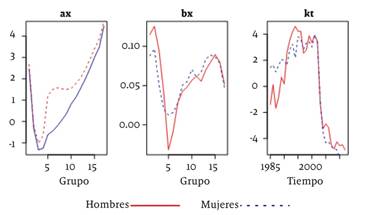
De la estimación del modelo expresado en la ecuación 1 con los datos para Santiago de Cali se tiene la figura 3. Es posible ver cómo los factores propios asociados con las tasas de mortalidad de forma idiosincrática, recogidos en el factor ax , presentan patrones frecuentemente hallados en la literatura internacional. Tanto para hombres como para mujeres, este factor decrece a partir del grupo 2 (entre 1 y 4 años), y solo se empieza a incrementar de nuevo a partir del grupo 4 (10 a 14 años). Lo anterior es consistente con el análisis de las figuras 1 y 2.
En el análisis del índice ax también se detecta un comportamiento típico del gráfico para los hombres (línea sólida). Se trata de una “joroba” entre los grupos 5 y 8 que corresponde, como se mencionó antes, con el incremento del número de muertes por accidentes de tránsito en esos grupos y presumiblemente también se asocia con dinámicas de violencia de la ciudad.
En cuanto al índice bx , que indica la sensibilidad de las tasas de mortalidad específicas ante la tendencia general de la mortalidad, se tiene que los comportamientos de los grupos son heterogéneos. Por su parte, los grupos de mayores edades, tanto para hombres como para mujeres, son más sensibles antes las reducciones de la tasa de mortalidad general. En particular los grupos que más responden ante reducciones en las tasas de mortalidad general son los grupos 11, 12 y 13 (máximos locales del gráfico de bx ), lo cual indica que para las personas entre los 45 y los 59 años de edad, las reducciones en las tasas de mortalidad general que se han presentando a partir de 1994 (índice kt ) han sido más acentuadas que para los otros grupos.
No obstante, es sin lugar a dudas en los grupos 1 y 2 (menores de 1 año y entre 1 y 4 años) donde esta reducción de la mortalidad ha sido más acentuada en los últimos 40 años, ya que los coeficientes de estos grupos son los más altos de la muestra.
Por su parte, se tiene que la tendencia general de la mortalidad a partir de 1994 ha sido marcadamente decreciente, de lo cual da cuenta la evolución de los índices kt , para ambos sexos. Como se mencionó antes, el índice kt indica el factor común, no observable, que determina el comportamiento de las tasas de mortalidad específicas en su conjunto. Está relacionado con las posibles relaciones de cointegración del sistema y, por lo tanto, da cuenta de una relación de largo plazo entre todas las tasas de mortalidad. Como en este estudio se estimaron dos modelos, uno para hombres y otro para mujeres, se tienen dos índices kt . Ambos presentan comportamientos similares: muestran un incremento desde inicios de la muestra en 1985 hasta 1994, en el cual empiezan a reducirse. Lo anterior indica que solo a partir de ese año se presenta el patrón comúnmente encontrado en la literatura internacional de reducción continua en la tendencia común de las tasas de mortalidad, propia del avance en los estadios de desarrollo de las naciones.
Este es un tema ampliamente documentado internacionalmente, por ejemplo en los estudios clásicos de Wilmoth (1998a), Oeppen y Vaupel (2002) y White (2002). En todos estos casos, mediante la cuantificación de las tendencias centrales como la expectativa de vida, se ha documentado una tendencia al alza en la extensión de la longevidad humana, que no parece tener una cota fácil de establecer. Este es un hallazgo que se mantiene, aun cambiado las tendencias centrales que se usen en el análisis, tal y como lo han demostrado autores como, por ejemplo, Canudas-Romo (2008, 2010) y Horiuchi, Ouellette, Cheung y Robine (2013). Estos autores enfocan sus análisis en medidas alternativas de longevidad como la moda de la edad de muerte y la mediana en la distribución de la longitud de la vida. Otros autores más (Bongaarts y Feney, 2002, 2003; Bongaarts, 2005) han propuesto medidas de la expectativa de vida que presentan ajustes ante la naturaleza cambiante de las tasas de mortalidad, llegando a conclusiones similares en términos generales.
También es notable que el comportamiento de los índices para hombres y para mujeres se hace más homogéneo a partir de ese año, ya que antes de esa fecha ambos subían, pero a distintos ritmos.
Finalmente, ya que las estimaciones se realizaron a través de descomposiciones de valor singular, es posible entender los índices kt como los primeros componentes principales de las tasas de mortalidad de hombres y mujeres. Por tanto, es posible calcular la cantidad de la variabilidad en los datos que es recogida por los mismos. Recuérdese que si se tienen N variables en el sistema, se tendrán N componentes principales ortogonales, y por tanto en ese caso es posible determinar qué porcentaje de la variabilidad total en el sistema es explicada por cada componente principal. El componente principal asociado con el mayor valor propio de la matriz de varianzas y covarianzas Xt (centrada) explica la mayor cantidad de la variabilidad, y se toma como índice kt .
En el caso de las tasas de mortalidad de mujeres, este recoge 65,5% de la variabilidad total del sistema. Por su parte, en el caso de las tasas de mortalidad de hombres, este recoge 53,7% de la variabilidad total del sistema. Ambos valores son altamente significativos, si se tiene en cuenta que en promedio sería de esperar que cada componente principal recogiera 5,9% de la variabilidad total. Lo cual se interpreta como un buen ajuste del modelo de Lee-Carter a la muestra.
Tablas de mortalidad proyectadas
Las proyecciones para el modelo de Lee-Carter son relativamente sencillas; se extrapola por simulación el componente kt y luego se aplican los índices ax , bx estimados, para obtener el valor futuro de cada tasa de mortalidad.
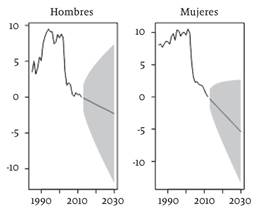
Las simulaciones proyectadas del índice kt se presentan en la figura 4. Los intervalos de confianza son muy amplios puesto que se trata de una caminata aleatoria y además son relativamente pocos los datos para Santiago de Cali, en comparación con regiones europeas o norteamericanas, que generalmente cuentan con datos en períodos de más de cien años. De ahí que se planteen en este documento los pronósticos de las tasas de mortalidad solo hasta el año 2030 (18 años desde 2012) y no a 50 años, como es habitual para naciones desarrolladas, con el fin de evitar pronósticos demasiado imprecisos.
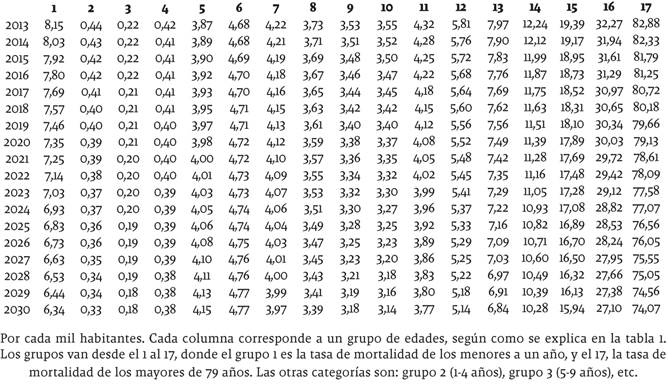
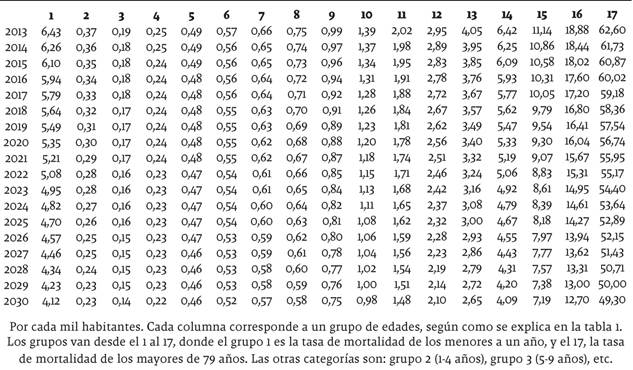
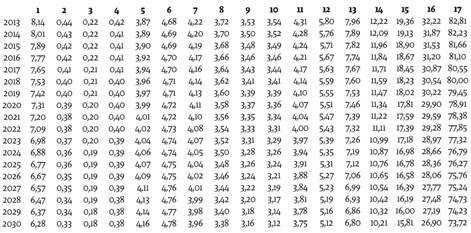
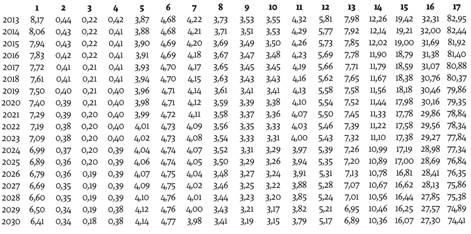
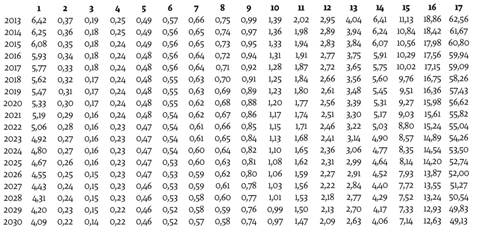
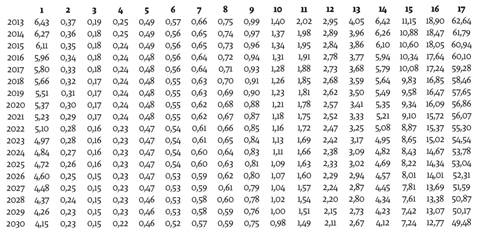
En las tablas 2 y 3 se presentan los pronósticos puntuales (medios) de cada tasa de mortalidad por rango de edad y sexo, discriminada según los grupos explicados en la tabla 1. En las tablas 6 a 9 en los anexos se presentan los intervalos de confianza de estas predicciones al 95%, los cuales están asociados con los riesgos de longevidad y mortalidad en la literatura actuarial. También se presentan los gráficos de cada tasa de mortalidad junto con su pronóstico en la figura 5.

Fuente: elaboración propia
Figura 5 Tasas de mortalidad y su pronóstico: Santiago de Cali, 1985-2030
De acuerdo con las tendencias que describen las series de las tasas de mortalidad para hombres y mujeres, en la ciudad de Cali durante las décadas más recientes, el modelo de Lee-Carter nos invita a esperar contínuas mejoras en términos de reducción de la mortalidad en la ciudad, durante los próximos años, para la mayoría de los grupos de edad analizados. Esta reducción de la mortalidad, que lleva consigo incrementos en los indicadores de duración de la vida, tales como la expectativa de vida al nacer, o calculada en distintas edades, es un fenómeno generalizado que ha sido ampliamente documentado en la literatura.
Por ejemplo, Riley (2001) reporta un incremento en la expectativa de vida al nacer alrededor del mundo, desde 1800 hasta 2000, de cerca de 30 años. Este incremento ha sido especialmente pronunciado para los países desarrollados. Este autor explora además los factores relacionados con el ensanchamiento de la duración de la vida, los cuales incluyen aspectos de salud pública, medicina, desarrollo económico, nutrición, educación, condiciones de las viviendas, entre otras. Por su parte, Oeppen y Vaupel (2002) también argumentan a favor de una tasa de crecimiento constante en el aumento de la longevidad humana, durante el último siglo. De hecho, estos autores encuentran que los límites en la expectativa de vida parecen incrementarse de forma regular, lo cual hace muy difícil pronosticar un límite para la duración de la vida humana. Otros autores, como White (2002), respaldan tal afirmación y presentan evidencia de que un modelo con una tasa de mejora constante en términos de la reducción de la mortalidad, se ajusta de forma satisfactoria a los indicadores de duración de la vida. No obstante algunos estudios recientes como Dong, Milholland y Vigj, J. (2016) argumentan que el ritmo de expansión de la longevidad humana parece haber empezado a estancarse. Se trata de un tema abierto en la literatura, que para el caso de regiones pertenecientes a economías no desarrolladas, aun se encuentra completamente inexplorado.
No obstante, del análisis de la tabla 2, y sobre todo de la figura 4, resalta un hecho que no constituye un patrón generalizado en el mundo, con relación al pronóstico de tasas de mortalidad, sino que más bien responde a condiciones sociales propias del Valle del Cauca, y en especial de Santiago de Cali. Esto es, las tasas de mortalidad de los hombres en los grupos 5 y 6, es decir, entre los 15 y los 19 años, y entre los 20 y 24 años de edad, no presentan signos claros de disminución en las próximas décadas y, de hecho, podrían incrementarse ligeramente. Este fenómeno está asociado, tal y como se mencionó anteriormente, con altas tasas de homicidios y accidentalidad en esos rangos de edad, para la población masculina.
Estos dos hechos: tasas de mortalidad a la baja para la mayoría de los rangos de edad, y tasas estancadas en los rangos medios, podrían llevar al aceleramiento en el proceso de envejecimiento de la población de Cali, y a la exacerbación de los retos sociales que este fenómeno trae consigo. Por ejemplo, al incremento en las razones de dependencia económica, ya que las personas en edad de trabajar serían menos en términos relativos, en los próximos años, que aquellas por fuera de la edad de trabajar (como es el caso de los niños y adultos mayores).
Las dinámicas de envejecimiento de la población, que se derivan, por un lado de una reducción en las tasas de mortalidad de los adultos mayores (tal y como se observa en los pronósticos para el caso de Cali), y por otro, de un número cada vez mayor de individuos llegando a los rangos de edad más altos (como consecuencia de un desplazamiento hacia abajo de toda la curva de mortalidad), tienen importantes implicaciones para el funcionamiento del sistema pensional de las naciones y de sus políticas de bienestar. Una población que se envejece representa un reto, no solamente porque los individuos viven más tiempo, sino también porque las personas viejas mueren cada vez a edades más avanzadas. Esta concentración en la edad de muerte debe cambiar los puntos de vista tradicionales con respecto a la evolución de la longevidad e invitan a reexaminar la viabilidad de los esquemas de pensiones actualmente operantes en el país.
Esta transformación demográfica de la sociedad, sobre la cual se presenta evidencia en este documento, ha sido estudiada por autores como Branca et al. (2009), para el caso de las economías desarrolladas. Este autor señala el incremento en la morbilidad y la discapacidad, y consecuentemente, la necesidad de crear una red de tratamiento y cuidados de salud adecuada, como algunos de los retos que se derivan del proceso de envejecimiento poblacional. Los retos impuestos por este tipo de transformación son muy altos incluso para las economías desarrolladas occidentales, e involucran la necesidad de integrar hospitales y territorios, la necesidad de ofrecer servicios tales como las residencias asistidas, hospitales de cuidado diario, casas de cuidado, centros de Alzheimer, cuidados integrados en el hogar y mayor número de profesionales y técnicos de la salud. Estos retos son aun más formidables para países como Colombia y ciudades como Cali, donde los rubros de financiamiento para enfrentarlos serán aun más escasos que en el mundo desarrollado.
Si queremos estar preparados para un mundo en el que una de cada cinco personas tendrán más de 65 años, y muchos de ellos tendrán más de 85 años, las transformaciones sociales que se deben perseguir no son pequeñas, tal y como lo señala Waite (2004), quien afirma que estos hombres y mujeres son más propensos a vivir en casas de cuidado, a presentar discapacidades sustanciales, y falta de recursos financieros. Este es un panorama cierto, sobre el que la región debe empezar a discutir.
Conclusiones y futuras extensiones
En este documento se presenta una aplicación del modelo de Lee y Carter (1992) para la modelación y el pronóstico de las tasas de mortalidad de Cali, en el período 1985-2030. Estos pronósticos tienen en cuenta la estructura común de las tasas y se ajustan relativamente bien a la muestra de estudio, como se puede inferir del porcentaje de variabilidad total que recogen entre 53% y 65%; ajustándose más para el caso de las tasas de mortalidad de las mujeres que de los hombres.
Una de las limitaciones del modelo de Lee-Carter es que los pronósticos que se realizan con base en el mismo serán más acertados en la medida en que las series de mortalidad en el sistema estén cointegradas. Esto ha sido explorado en épocas recientes en la literatura actuarial (Chuliá, Guillén & Uribe, 2016) llevando a la exploración de propuestas alternativas de pronóstico, que en algunos contextos superan al modelo original. No obstante, una de las ventajas del método utilizado aquí es que permite el pronóstico de tasas que son coherentes entre sí, al depender de una misma tendencia estocástica subyacente.
Los patrones de mortalidad en Cali se ajustan en buena medida a los hallazgos para otras regiones del mundo. Se han presentando importantes reducciones en la mayor parte de las tasas de mortalidad específicas durante el período analizado y se pronostican, por ende, futuras reducciones para casi todos los grupos de edad. Una excepción a este ajuste lo representan los grupos de edad entre los 14 y 30 años, de hombres. En estos, las tasas de mortalidad de hecho se incrementaron entre 1985 y 1994, y no es que se hayan reducido sustancialmente a partir de esa fecha, razón por la cual el modelo de Lee-Carter no pronostica reducciones particulares en estas tasas en el futuro cercano y, por el contrario, en algunos casos, pronostica incrementos (ver grupo 5 en la figura 4).
Las tablas de mortalidad aquí presentadas pueden servir como insumo para actuarios o formuladores de políticas públicas. Debido al carácter metodológico de la presente investigación, muchos datos quedan sueltos sobre las causas detrás de los comportamientos detectados. Sobre esto se espera que la literatura sobre demografía avance en el futuro. También es necesario expandir este tipo de análisis a otras regiones de Colombia