De la subordinación a la hegemonía.
Sobre la legitimación epistemológica de las matemáticas en la filosofía natural en el siglo XVII^*

Felipe Ochoa^**

^* El presente artículo recoge de manera parcial resultados de la investigación doctoral patrocinada por Colciencias, titulada Mathematics, natural philosophy, and providentialtheology: aninquiry into the ontological problem of the causation of gravityforce in Newton'sphysics. Asimismo, de una investigación en curso sobre los debates en torno a las matemáticas en los siglos XVI y XVII, adelantada en el Instituto de Filosofía de la Universidad de Antioquia, Medellín, Colombia. Deseo agradecer a los jurados de esta publicación por sus amables recomendaciones que hicieron posible mejorar este artículo.

^** Ph.D. Instituto de Filosofía, Universidad de Antioquia, Medellín, Colombia.
Correo electrónico: feochoa@quimbaya.udea.edu.co.

Recibido: 25 de abril de 2013 - Revisado: 24 de julio de 2013 - Aceptado: 25 de septiembre de 2013

Este artículo analiza la legitimación epistemológica de las matemáticas en la filosofía natural en el siglo XVII. En el Renacimiento se alegó que las matemáticas no cumplían con los criterios aristotélicos de cientificidad, ya que no explicaban las causas eficientes y finales. Así, sus críticos inspirados en la tradición aristotélica rechazaron los primeros intentos de matematizar la filosofía natural. Se examinan las condiciones epistemológicas implicadas en el debate sobre la cientificidad de las matemáticas y su pertinencia para la filosofía natural. Se hace un recorrido historiográfico de la matematización de la naturaleza para ofrecer nuevos elementos de ponderación respecto a una caracterización históricamente más contextual y filosóficamente más conceptual del surgimiento de la ciencia moderna.

Palabras clave

Matemáticas, filosofía de las matemáticas, ciencia moderna, Piccolomini, Clavius, Barozzi, Pereira.

From Subordination to Hegemony
On the Epistemological Legitimation of Mathematics in Natural Philosophy of XVII Century

This article analyzes the epistemological legitimation of mathematics in natural philosophy in the seventeenth century. In the Renaissance it was claimed that mathematics does not meet the Aristotelian criteria of scientificity, and that it did not explain the efficient and final causes. So, its critics, inspired by the Aristotelian tradition, rejected the first attempts to mathematize natural philosophy. The epistemological conditions involved in the debate are examined on the scientific nature of mathematics and its relevance to natural philosophy. A historiographical tour of the mathematization of nature is made to provide new weighing elements with respect to a historically and philosophically more conceptual characterization of the emergence of modern science.

Key Words

Mathematics, philosophy of mathematics, modern science, Piccolomini, Clavius, Barozzi, Pereira.

De la subordination à l'hégémonie.
Sur la légitimation epistemologique des mathématiques dans la philosophie naturelle au siècle XVII

Cet article analyse la légitimation épistemologique des mathématiques dans la philosophie naturelle au XVIIe siècle. Durant la Renaissance on a allégué que les mathématiques ne s'acquittaient pas des critères de scientificité aristotélicienne, puisqu'elles n'expliquaient pas les causes efficientes et finales. Ainsi, ses détracteurs, inspirés par la tradition aristotélicienne ont rejeté les premières tentatives de « mathématiser » la philosophie naturelle. Dans cette recherche, on examine les conditions épistémologiques impliquées dans le débat sur le scientificité des mathématiques et de sa pertinence pour la philosophie naturelle. Egalement, on fait un parcours historiographique de la « mathématisation » de la nature pour offrir de nouveaux éléments de pondération par rapport à une caractérisation historiquement plus contextuelle et philosophiquement plus conceptuelle du surgissement de la science moderne.

Mots-clés

Mathématiques, philosophie des mathématiques, science moderne, Piccolomini, Clavius, Barozzi, Pereira.

Da subordinação à hegemonía.
Sobre a legitimação epistemológica das matemáticas na filosofía natural do século XVII

Este artigo analisa a legitimação epistemológica das matemáticas na filosofía natural no século XVII. No Renascimento alegou-se que as matemáticas não cumpriam com os critérios aristotélicos de cientificidade, já que não explicavam as causas eficientes e finais. Deste modo, os seus críticos inspirados na tradição aristotélica rejeitaram as primeiras tentativas de matematizar a filosofía natural. Examinam-se as condições epistemológicas envolvidas no debate sobre a cientificidade das matemáticas e a sua pertinência para a filosofía natural. Faz-se uma viagem historiográfica da matematização da natureza para oferecer novos elementos de ponderação sobre uma caracterização historicamente mais contextual e filosoficamente mais conceitual no surgimento da ciência moderna.

Palavras chave

Matemáticas, filosofía das matemáticas, ciência moderna, Piccolomini, Clavius, Barozzi, Pereira.

La matematización de la filosofía natural ha sido considerada una de las características más sobresalientes de la revolución científica del siglo XVII, al igual que el surgimiento del método experimental. Ahora, si bien es cierto que esta última ha sido objeto de polémicas entre los especialistas, en lo que parece haber consenso es sobre la matematización de la naturaleza. Se admite que el cambio de la explicación cualitativa aristotélica de los fenómenos naturales por la matemática, constituye la ruptura entre las filosofías naturales antigua y moderna.

En este sentido, según las narrativas tradicionales, la postulación de una tierra planetaria por Copérnico en De revolutionibus orbium coelestium (1543) se desarrolló y consolidó por Kepler, Galileo, Descartes y Newton. También conforme con estos relatos, la tesis copernicana dio origen a la creación de una nueva física que en los Principios matemáticos de la filosofía natural (1687) de Newton tendría su realización. Estas narrativas las llamaré heroicas, en tanto se concentran en exclusiva en los grandes nombres y en las excepcionales proezas de su pensamiento. Por otra parte, más recientes son las narrativas que analizan desde un espectro más amplio de influencias, obstáculos y transformaciones, las condiciones de emergencia y consolidación de la ciencia moderna. A estas las llamaré revisionistas, por cuanto ofrecen una comprensión que desde la perspectiva heroica quedan sin resolverse.

En las narrativas revisionistas una de sus consecuencias más extremas es la negación de la rúbrica, y con ello, del hecho, del nacimiento de la ciencia moderna: la revolución científica. Si bien un error de las narrativas heroicas es ofrecernos una imagen sospechosamente coherente del origen de la ciencia moderna, un desacierto de las revisionistas en su versión extrema, es la negación del surgimiento de la ciencia moderna en el siglo XVII. Para citar un ejemplo, Betty Dobbs (2000), la historiadora de Newton, ha llegado a poner en cuestión la existencia de la revolución científica, y más aún, que Newton sea su más elevada expresión. Esta visión crítica de la revolución científica podría pensarse afín a la de los historiadores que sugieren fuertes vínculos entre las tradiciones de investigación medieval, renacentista y moderna, en lo experimental y lo matemático (Crombie, 1952). Respecto a Dobbs y los partidarios de su tesis, las filiaciones de Newton con la filosofía y la teología antiguas les llevan a considerar al pensador más como un reaccionario que como un revolucionario, porque sus estudios vistos en conjunto apuntan más hacia la restauración del conocimiento primordial, la prisca sapientia, que hacia una nueva ciencia¹. Ahora, a propósito de las reconstrucciones heroicas, la creación de una física que sistematiza los fenómenos celestes y terrestres, y la predilección de lo cuantitativo sobre lo cualitativo, son argumentos suficientemente sólidos como para exigir una postura correctiva a la tesis que niega este cambio de actitud frente al conocimiento de los fenómenos naturales² .

A pesar de este estado de cosas, sorprende que existan dos posiciones antagónicas frente a lo que ocurrió en los siglos XVI y XVII, sin que ninguna de ellas se enfoque en un aspecto fundamental de lo que en el fondo está en debate: la legitimación epistemológica de las matemáticas en el estudio de la filosofía natural. Esto resulta aún más llamativo si se considera que ambas narrativas resaltan las condiciones de emergencia de la "ciencia moderna", en cuanto a sus objetos de estudio, enfoques metodológicos y problemas suscitados por las ciencias físico-matemáticas, llamadas a ser el modelo de legitimidad científica y paradigma de racionalidad de todo saber que aspire a ciencia. En efecto, desde la visión heroica, tal fenómeno es algo dado; para los historiadores revisionistas, difícilmente es algo que hayan explorado (Yolder, 1988).

Como es habitual en la historiografía sobre la matematización de la filosofía natural en el siglo XVII, la mirada al Renacimiento es un punto de partida adecuado cuando se trata de comprender mejor dicho fenómeno. Como tal, se ha valorado porque su producción intelectual suministró elementos claves para la revolución científica; o desestimado, debido a la multiplicidad de enfoques filosóficos. Tales enfoques, sostiene un notable historiador, se vinculan más por una imaginación desbordante que por una nueva sistematización del conocimiento y una nueva visión del mundo. Así, para Alexandre Koyré (1997) esta fue "la época de la más burda y profunda superstición" (p. 41), carente de una teoría que diera cuenta de los nuevos hechos que se observaban y de la erudición alcanzada. Para él, el desarrollo de una teoría explicativa de los fenómenos es condición central para la constitución de la ciencia, y el reemplazo de la ciencia aristotélica la ve, grosso modo, en los desarrollos de Galileo y Kepler a partir de Copérnico, y en la síntesis de Newton (Koyré, 1965).

Ahora, si bien es cierto que los defensores de la tesis continuista pueden establecer continuidades entre el Renacimiento y la Modernidad, también hay argumentos que señalan discontinuidades (o quizá rupturas) entre estos dos periodos. Así pues, es posible advertir temas y problemas que dominaron la esfera intelectual -entendida en su sentido más amplio- del siglo XII al siglo XVII. Entre otros, podrían enumerarse la continua exploración y reactivación de las antiguas escuelas filosóficas, el papel central del análisis de Aristóteles para los planes de estudio -complementado con la crítica de su papel educativo y los intentos de reformar y modernizar al interior la tradición aristotélica-, la rivalidad entre optimismo metafísico y el voluntarismo, que se remonta a Avicena y Ockham, sin olvidar los intentos de matematización de la ciencia natural iniciados por R. Grosseteste y Roger Bacon en Oxford (siglo XII) y su renovación en el siglo XVII por Leibniz y Gassendi, así como el permanente debate acerca de la autonomía de la filosofía y su apropiada relación con la teología y las creencias religiosas (Sorell, 1993). Sin embargo, la aceptación de la cosmología copernicana, el establecimiento de la filosofía mecánica y, sobre todo, la creación de la física-matemática, sirven de fronteras para distinguir la nueva ciencia de su predecesora (Hall, 1952; Hall, 1981).

Aunque no se puede hablar de una sola ciencia, o de modo más preciso, de una sola "filosofía de la naturaleza" durante el Renacimiento, este periodo sí ofrece elementos epistemológicos claves para comprender la matematización de la naturaleza. Quizá una razón para que Koyré subestimara el Renacimiento se debe a la proliferación de teorías rivales a la filosofía aristotélica-escolástica. Asimismo, a que existieron saberes que contrastan de forma drástica con la letanía de la nueva racionalidad de la experimentación matemáticamente expresada, como la filosofía oculta, la demonología y la magia a las que se asocian la alquimia, la herejía y la superstición. Pese a ello, estudios recientes amplían y profundizan nuestro conocimiento de estas prácticas³.

Ahora bien, el debate sobre la legitimidad de las matemáticas en la filosofía natural es un episodio menos tratado por los historiadores de la ciencia moderna, pero de hecho, los filósofos del Renacimiento, en gran medida inspirados en la tradición aristotélica, fueron particularmente importantes en la legitimación epistemológica de la matematización de la filosofía natural (Biagioli, 1989; Dear, 1995; Mancosu, 1996)⁴.

Mi objetivo es concentrarme en el tránsito de las matemáticas, en la jerarquía del conocimiento, de la subordinación a la filosofía natural, al papel rector que llegó a desempeñar sobre esta, es decir, a su hegemonía. Me refiero en concreto a la polémica sobre la certeza y cientificidad de las matemáticas, conocida como la Quaestio de certitudine mathematicarum. Pretendo abordar la matematización de la naturaleza a partir de las condiciones epistemológicas implicadas en el debate; en otras palabras, abordaré aquí una perspectiva revisionista de las condiciones de emergencia de este enfoque hacia el estudio de la naturaleza, señalando algunos obstáculos que hubo de superar, así como otros problemas que suscitó. De ser correcto que la matematización de la naturaleza es un componente incontestable del surgimiento de la ciencia moderna, una mirada a los aspectos que se indican ofrecerá elementos de análisis para una caracterización de la ciencia moderna históricamente más contextual y filosóficamente más conceptual⁵.

Los temas de la Quaestio conforman todo un trasfondo teórico que señala las condiciones de emergencia de la matematización de la naturaleza, y ofrecen el tenor de las disputas sobre cómo las matemáticas se instituyeron como lenguaje de la ciencia moderna. Surgida del contexto de revisión crítica de la filosofía aristotélica en el que se contrastó con las alternativas posibles gracias a la reconstitución de los antiguos trabajos de las matemáticas griegas, es válido notar que el recurso a figuras de autoridad como Aristóteles, Platón, Euclides y Proclo entre otros, dominó la escena en un sentido muy afín a las prácticas persuasivas de la escolástica.

Una segunda característica se relaciona con la negación de la naturaleza científica de las matemáticas, por un grupo de científicos aristotélicos, que dio origen a la discusión sobre la causalidad de las demostraciones matemáticas sometidas a las exigencias de los Analíticos segundos de Aristóteles (1988).

La tercera característica avanza hacia el establecimiento de una nueva política del conocimiento que defiende la legitimidad de la incorporación de las matemáticas en la filosofía natural (física), en el contexto de las distinciones de los saberes conforme a sus objetos de estudio. De hecho, la cuestión sobre las relaciones entre física y matemáticas puede declararse tan antigua como la filosofía misma. En su Física y en los Analíticos segundos, Aristóteles (1988) estableció un contexto para las discusiones sobre las relaciones y distinciones entre física y matemáticas, así como para los debates sobre la naturaleza de las matemáticas mixtas. Tal contexto perduró hasta el Renacimiento e incluso, hasta el siglo XVII. A decir verdad, el impulso esencial para matematizar la filosofía natural le debe más a los debates (por caso la Quaestio) sobre las matemáticas mixtas, que al supuesto platonismo de Galileo, como sostiene Koyré (1997). En este sentido, bien puede decirse que la Quaestio representa la discusión epistemológica sobre la extensión del uso de las matemáticas a dominios más allá de los aceptados por Aristóteles, como la astronomía, la óptica y la música.

Para finalizar, una cuarta característica tiene que ver con la ontología de las entidades matemáticas y su nexo con el mundo natural. Esta última es importante, dado que en gran medida los debates epistemológicos en torno a la matematización de la naturaleza, tienen como eje las tensiones entre si las matemáticas ofrecen solo una descripción de la naturaleza, o brindan una explicación causal de la misma en el sentido aristotélico (formal, material, eficiente y final).

Las Cuestiones mecánicas seudo aristotélicas pueden considerarse el punto de inicio de la revalorización epistemológica de las matemáticas durante el Renacimiento. La primera traducción al latín (1517) se debe a Vittore Fausto, la segunda (1525) a Niccolò Leonico Tomeo y la tercera (1547) a Alessandro Piccolomini (1508-1579). A su traducción, Piccolomini añadió un Commentarium de certitudine mathematicarum disciplinarum (Comentario sobre la certeza de las disciplinas matemáticas), donde rebate la antigua y apreciada opinión de que las matemáticas dan el ejemplo más preclaro de cientificidad. Para su tesis, Piccolomini se apoya en el contexto aristotélico de ciencia, entendida como conocimiento causal de lo que depende aquello que se sabe, siendo las demostraciones su constatación.

En Analíticos segundos I, 13 Aristóteles distingue dos tipos de demostraciones: del qué y del porqué. La primera procede de las causas a los efectos, y la segunda explica los efectos por las causas. La más relevante, para Aristóteles (1988), es esta última, en tanto más idónea para la demostración científica.

Ahora bien, en su "Proemio" a la Física de Aristóteles (1995), Averroes introdujo un tercer tipo de demostración, la potissima, comprendida como la demostración que proporciona al mismo tiempo el conocimiento de la causa y el efecto. Piccolomini tomó esta demostración para declarar que las demostraciones matemáticas no cumplen este criterio -que se considera la regla de oro de las demostraciones- invalidando así su cientificidad. Así, confrontadas con las demostraciones potissimae, las matemáticas no tienen el grado más elevado de certeza. Además, siendo las demostraciones el núcleo del conocimiento científico, y dado que las matemáticas no se ajustan a los requerimientos de las demostraciones potissimae, bien podría decirse que no son ciencias según el cuadro epistemológico de Piccolomini. De manera similar, Benito Pereira (1535-1610), en consonancia con Piccolomini, llegó a negar el estatuto de cientificidad de las matemáticas, sosteniendo en De communibus ómnium rerum naturaliumprincipiis affection ibus que:

Tener ciencia es adquirir conocimiento de algo a través de la causa que hace que la cosa sea lo que es, y la ciencia es el efecto de la demostración. Pero la demostración más perfecta debe depender de lo 'per se' y propio de lo demostrado. Efectivamente, lo accidental y común se excluye de las demostraciones perfectas. Pero el matemático no considera la esencia de la cantidad, ni trata sus afecciones surgidas de su esencia, ni las declara por las causas propias basadas en la cantidad, ni hace demostraciones a partir de lo propio y 'per se', sino por predicados accidentales y comunes. En consecuencia, la doctrina matemática no es propiamente ciencia (Pereira, 1591, p. 24).

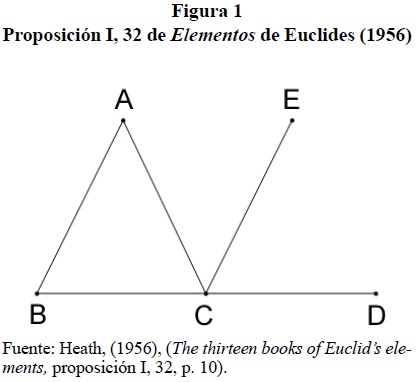
La estrategia para negar la cientificidad de las matemáticas consiste en someter los teoremas difíciles de interpretar causalmente al modelo de las demostraciones potissimae, y de ellos el locus classicus es la proposición I, 32 de los Elementos de Euclides, quien afirma: "en todo triángulo, si se prolonga uno de sus lados, el ángulo externo es igual a los dos ángulos internos y opuestos, y los tres ángulos internos del triángulo son iguales a dos rectos" (Heath, 1956, p. 316). La prueba de esta proposición es de la siguiente forma: propongamos el triángulo ABC (figura 1). Prolónguese BC hasta llegar a D. Trácese en C una paralela a BA, dígase CE. Apelando a los teoremas previos se obtendrá que BAC = ACE y ECD = ABC. De esta manera, ABC + ACB + CAB = ACB + ACE + ECD = dos ángulos rectos.

Dos modos de interpretar esta prueba llevan a conclusiones opuestas: a) según la tradición escolástica, es causal porque la definición de triángulo le confiere su esencia, determinando formalmente sus propiedades y b) según los críticos de la cientificidad de las matemáticas, la dificultad de separar la causa de sus propiedades invalida la potencia de la prueba, porque apelar a segmentos auxiliares al triángulo hace que no sea propiamente causal. La primera postura se funda en que los teoremas son deducciones de los primeros principios en los que se manifiestan, además de la generación de las figuras, sus atributos esenciales. Pero este argumento entra en conflicto con la segunda interpretación, la de Piccolomini y Pereira, que rechaza el recurso a elementos auxiliares. En este sentido, afirma Pereira (1591): "el geómetra prueba que el triángulo tiene tres ángulos iguales a dos rectos basado en que el ángulo externo, resultante de extender el lado del triángulo, es igual a dos ángulos del mismo triángulo que se opone" (p. 26).

La oposición entre estas interpretaciones radica en cómo se comprenda la demostración potissima. Para la tradición escolástica, cimentada en la autoridad de Aristóteles, las matemáticas -y en el presente caso, la geometría- ofrecen demostraciones potissimae, como se afirma en Analíticos segundos I, 14. Para la tradición crítica del Renacimiento, es decir, Piccolomini, Pereira y los jesuitas de Coimbra, la demostración perfectísima debe dar cuenta a la vez de la causa y el efecto.

Las Cuestiones mecánicas suscitaron el interés de matemáticos y humanistas por la aplicabilidad de las matemáticas a la mecánica en sus aspectos teórico y práctico. De hecho, Benedetti, Cardano, Tartaglia y Galileo las estudiaron; y desde el punto de vista práctico también fueron valoradas por estudiosos de la navegación y la arquitectura. Por otra parte, si bien esta obra le debe su difusión a la tradición humanista italiana, su interés se extendió a Portugal, Alemania e Inglaterra, y su inclusión en el Corpus aristotelicum por Aldus (1495-1498) se pudo haber interpretado como una amenaza para la filosofía natural, pues en ella se sugiere la matematización de la física, o surge su posibilidad. Además, en los métodos de conocimiento aristotélico y escolástico imperaba la separación de los saberes conforme sus objetos de estudio; para el presente caso, debe prevalecer la clara separación entre el análisis de la cantidad y la magnitud de la aritmética y la geometría, del análisis del movimiento (física) que le corresponde a la filosofía natural que es causal en sentido estricto (Funkenstein, 1986).

Es comprensible, entonces, que los ataques a la cientificidad de las matemáticas estuvieran articulados por una política conservadora del conocimiento, que insistía en preservar tal separación y en enfatizar que las matemáticas no son filosofía natural, subordinándola a esta. Tampoco resulta extraño que esta distinción, subyacente a la revalorización epistemológica de las matemáticas, estuviera liderada por profesores de filosofía natural como Benito Pereira, quien impartió cursos de filosofía natural en el Colegio Romano. En este sentido, la Quaestio representa un episodio especial en la transición hacia un ideal universal de conocimiento inspirado, articulado y dirigido por las matemáticas. Dicho episodio lo constatan las respuestas a Piccolomini y sus partidarios por una serie de matemáticos italianos como Pietro Barozzi, Giuseppe Biancani y Christopher Clavius, pero aun es más significativo que trascendiera estas fronteras y fuese debatido por el lógico polaco Martin Smiglecki y por matemáticos británicos como John Wallis e Isaac Barrow.

Sus posturas ante la Quaestio además de concentrarse en la reinstalación de las matemáticas en el contexto de las ciencias causales aristotélicas, también se enfocaron en su institucionalización en el plan de estudios de la filosofía como parte integral. Más importante todavía, defendieron una ontología de las entidades matemáticas que, aunque abstracta de la materia sensible, está inmersa en ella y da cuenta de la estructura de la naturaleza.

Clavius, profesor de matemáticas en el Colegio Romano, desarrolló allí su carrera desde 1565 hasta su muerte en 1612. Su papel en la Quaestio se circunscribió a promover la enseñanza de las matemáticas en las universidades y a exaltar su dignidad al rango de la metafísica y la filosofía natural en los estudios superiores. Vale recordar que las matemáticas formaban parte del quadrivium (aritmética, geometría, música y astronomía), y algunas veces se incluían en el trivium en los cursos de lógica. Tanto el quadrivium como el trivium constituían la formación preliminar a la filosofía, la cual suministraba los fundamentos para abordar la teología, la medicina y las leyes. En este esquema es comprensible la apología de Clavius de las matemáticas como parte integral de la filosofía.

El impacto de Clavius se manifestó principalmente en la Ratio studiorum, aprobada en 1599 en el Colegio Romano, documento que consigna sus pronunciamientos sobre la dignidad y necesidad de la promoción de las matemáticas en la universidad. En la Parte IV de la Ratio (versión de 1586) señala la utilidad y potencia explicativa de las matemáticas para las demás ciencias.

Las disciplinas matemáticas proporcionan y explican a los poetas el ascenso y descenso de los cuerpos celestes; a los historiadores la forma y distancia de los lugares; a los analíticos (analyticis) ejemplos de demostraciones sólidas; a los líderes políticos técnicas fácilmente admiradas para administrar bien los asuntos domésticos y militares; a los físicos las formas y distinciones de las revoluciones celestes, la luz, los colores, los medios transparentes, los sonidos; a los metafísicos el número de las esferas y de inteligencias; a los abogados y a los clérigos el hábito de reconocer el tiempo con precisión (Clavius, 1586, citado por Smolarski, 2002b, p. 461).

Enfatizando las matemáticas como clave para comprender la realidad física y su aplicabilidad en asuntos prácticos, Clavius destaca su valor más allá del papel pedagógico en estudios preliminares a la filosofía y las promueve a herramienta esencial, incluso para la formación profesional de teólogos, legistas y médicos.

Pero más significativo resulta que su objetivo se dirigiera a disolver la ruptura existente entre la filosofía natural (físicos) y las matemáticas (analyticis). Así, su enfoque contrasta con el también jesuita del Colegio Romano Benito Pereira, quien se alineó con Piccolomini negando la cientificidad de las matemáticas, con el objeto de preservar la distinción respecto a la filosofía natural y mantener la superioridad de esta sobre aquellas. Los argumentos que Clavius expone recurren a Aristóteles y Platón, por ejemplo. Así, en su In disciplinas mathematicas prolegomena defiende la inclusión de las matemáticas:

Puesto que las matemáticas tratan cosas consideradas aparte de toda materia sensible -aunque en sí mismas están inmersas en ella- es evidente que guardan un lugar intermedio entre la metafísica y la ciencia natural, si consideramos su objeto según la demostración de Proclo. Pues el objeto de la metafísica está separado de toda materia, tanto en la cosa como en la razón; el objeto de la física está unido efectivamente a la materia sensible, tanto en la cosa como en la razón; por lo cual, dado que el objeto de las disciplinas matemáticas se considera libre de toda materia -aunque esta se encuentra en la cosa misma- se establece claramente que son intermedias entre las otras dos (Clavius, 1612, p. 5).

Este pronunciamiento se concentra en la legitimidad de las matemáticas en el ámbito de la filosofía, pero en In sphearumloanis Sacro Bosco commentarium (Clavius, 1612) afirma incluso la superioridad científica de las matemáticas respecto a la metafísica y la filosofía natural, porque mientras que en estas abundan la multiplicidad de opiniones, la unanimidad de las demostraciones matemáticas le confieren una certeza y cientificidad incontestables (Dear, 1995).

Con apoyo en una estrategia similar, en Modus qua disciplinas mathematicae in scholis Societatis possent promouei (Modo por el que se pueden promover las disciplinas matemáticas en la escuela de la Sociedad [Jesuita]) (Clavius, 1586, citado por Smolarski, 2002a) Clavius describe la instrucción de las matemáticas y la interacción de profesores y alumnos con los estudios de filosofía, así como entre quienes la imparten y reciben, resaltando primero la asistencia y discusión por parte de los profesores de matemáticas a las disputationes y eventos similares de filosofía, para mostrar la conexión entre estos saberes y remediar así el que:

Hasta ahora los estudiantes [parecieran] despreciar estas ciencias por la simple razón de que piensan que no son de valor e incluso que son inútiles, ya que a quien las enseña nunca se le invita a actos públicos con otros profesores (p. 467).

La eventual retroalimentación que surge de esta interacción beneficia la filosofía natural, porque según Clavius, "sin las matemáticas esta [la filosofía natural] es débil e imperfecta" (p. 467), indicando así su necesidad para la correcta comprensión del resto de la filosofía. Aquí el juicio de Clavius de nuevo se soporta en argumentos de autoridad, lo cual se manifiesta en su alusión a Platón, Aristóteles y otros, para quienes un requisito fundamental para una comprensión adecuada de asuntos filosóficos requería saberes sólidos en matemáticas. Por esta razón

Sería de gran ayuda si los instructores de filosofía omitieran cuestiones de poco beneficio para la comprensión de las cosas de la naturaleza, y no denigraran de la autoridad de las matemáticas entre los estudiantes, como son esas cuestiones que enseñan según las cuales las matemáticas no son ciencias, que no tienen demostraciones, que se abstraen del ser (ens) y del bien (bonum) etc. Pues la experiencia constata que esto obstruye enormemente a los estudiantes, y para nada son útiles; debido especialmente a que los instructores difícilmente pueden enseñarlas (lo cual se sabe aparte de lo que otros han dicho más de una vez) sin llegar a ridiculizarlas (Clavius, 1586, citado por Smolarski, 2002a, p. 468).

El enfoque de Clavius tiene como punto de inscripción la organización de los saberes como la conciben básicamente Aristóteles y Platón, aunque el lugar que estos le confieren a las matemáticas en la jerarquía del saber no sea la misma. Asimismo, destaca el beneficio que la filosofía natural obtiene de su estudio. De esta manera evita entonces los cuernos del dilema sobre la cientificidad o no de las matemáticas, propuesto por la crítica sobre la causalidad. De hecho, al tener que pronunciarse al respecto, Clavius describe la estructura lógica de las matemáticas para sustentar su cientificidad. Así, en In disciplinas mathematicas prolegomena, la parte introductoria a su edición de los Elementos de Euclides, manifiesta:

Mientras cada doctrina, y cada disciplina, se producen a partir [del] conocimiento preexistente como lo afirma Aristóteles, y demuestran sus conclusiones a partir de principios particulares asumidos y consentidos; no obstante, ninguna ciencia demuestra sus principios, según Aristóteles y otros filósofos. Las disciplinas matemáticas ciertamente tendrán sus principios a partir de los cuales, toda vez propuestos y consentidos, confirman sus problemas y teoremas (Clavius, 1612, p. 9).

Esta manera de afirmar la legitimidad de las matemáticas sería adoptada por una serie de promotores jesuitas como Christopher Scheiner (1575-1650), quien al principio de su disertación aseguró que las matemáticas demuestran sus conclusiones científicamente, por axiomas, definiciones, postulados y suposiciones, de donde resulta claro que se llaman ciencias (Scheiner, 1614). Así, la adecuación de las matemáticas a la cientificidad aristotélica parece suficiente para evitar el debate sobre las causas. Pero si Euclides presenta los ejemplos por antonomasia de demostración científica, las dificultades radican en la acomodación del objeto de las matemáticas a la estructura formal del modelo aristotélico de ciencia (Dear, 1995).

Precisamente Biancani, discípulo de Clavius, abordó este problema en De mathematicarum natura dissertatio (1615). Esta obra es la primera refutación sistemática a los ataques de Piccolomini y Pereira sobre la cientificidad de las matemáticas. La Dissertatio aparece como apéndice al Aristotelis loca machanica donde comenta los pasajes matemáticos que se ligan con el corpus aristotélico. Se divide en cinco capítulos. El primero trata del objeto de estudio de las matemáticas puras (aritmética y geometría) y aplicadas (astronomía, óptica, mecánica y música); el segundo, del problema de la causalidad en matemáticas y si hacen uso del tipo más perfecto de demostración (potissima); el tercero, de la excelencia obtenida de su estudio; el cuarto, de la vindicación de las matemáticas de algunas calumnias que se le han proferido; y el quinto trata sobre las matemáticas aplicadas. A modo de conclusión, el tratado enumera las demostraciones del primer libro de los Elementos, indicando el tipo de causa que usa cada una de ellas. Pese a la importancia general de la Dissertatio, aquí me limitaré a analizar los dos primeros capítulos, que se conectan con la ontología y epistemología, comenzando con la causalidad en matemáticas y luego con la naturaleza de sus objetos.

El capítulo segundo de la Dissertatio "sobre el término medio de las demostraciones geométricas y aritméticas i. e., si son demostraciones perfectas", inicia con una erudita lista de autores de filosofía que nunca dudaron de la perfección de las demostraciones matemáticas, y que por el contrario las tomaron como ilustración de demostraciones perfectas según Aristóteles. Además de citar a Aristóteles mismo, Biancani menciona a Platón, Proclo, Averroes, Temistio, Toleto y Zarabella. Contrasta sus pronunciamientos con los de Piccolomini. Luego ofrece pruebas en beneficio de las matemáticas, analizando el tipo de pruebas causales empleadas (materiales y formales), excluyendo las eficientes y finales. La demostración perfecta -expresa Biancani- es aquella que, además de brindar la causa propia e idónea de lo que se debe demostrar, evidencia que su propiedad procede de dicha causa, característica cardinal de las demostraciones matemáticas, a lo cual añade el autor: "esta causa en aritmética y geometría es material cuando hace uso de una totalidad como su término medio; o formal cuando el término medio es la definición del sujeto o la propiedad" (Biancani, 1615, p. 14).

Respecto a las causas eficientes, refiriéndose a quienes, como Pereira, sostienen que deben usarse, Biancani (1615) refuta, pues apunta que es una equivocación puesto que "no se dan cuenta de que tales líneas o particiones no son el término medio de estas demostraciones, sino que se ofrecen para encontrarlas y su conexión con la propiedad ha de ser probada" (p. 14). En definitiva, sobre las causas finales, puesto que tradicionalmente se excluyen de las demostraciones matemáticas, Biancani no las aborda. Ahora, el no ocuparse de las causas eficientes y finales en matemáticas no es debilidad en la argumentación sino, antes bien, demostración de que no está inventando un enfoque al respecto y que por el contrario, coincide con la tradición medieval de la demostración que se concentró en la causalidad material y formal.

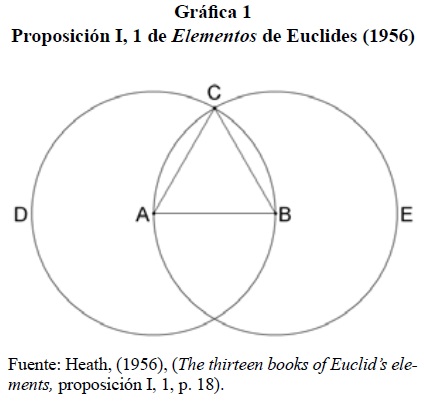
Para aclarar que las matemáticas recurren a estos dos tipos de causalidad, Biancani explica que existen causas formales, y para ello fija la proposición I, 1 de los Elementos: "construir un triángulo equilátero sobre una recta finita dada" (Heath, 1956, p. 241). En este caso se procede así: pongamos que en la línea recta que es AB (gráfica 1), se trazan dos círculos con radios iguales a AB en cada uno de los extremos en los centros A y B. Digamos que C sea uno de los puntos donde los círculos forman una intersección. Por último, se conectan A con B, y C con B.

A, B y C formarán un triángulo equilátero, en tanto sus lados son iguales al radio del mismo círculo y, de esta manera, iguales entre sí. Para Biancani,

Ya que esta demostración no es la prueba de un teorema, sino la solución a un problema, deberíamos saber que nuestros oponentes ignoran completamente que en cada problema se señala algo mediante la construcción de algunas líneas. Por ejemplo, en este caso Euclides enseña por qué al trazar ciertos círculos alrededor de una línea dada, y al trazar ciertas líneas como prescritas, obtenemos un triángulo equilátero como resultado obvio para cualquiera que considere el asunto. Así que estas líneas, en tanto radios de esos círculos, de ninguna manera son extrínsecas a la demostración; al contrario, son su sujeto (Biancani, 1615, p. 16).

El núcleo del argumento es la explicación de círculo, la definición I, 15 que afirma un círculo es una figura plana comprendida por una línea tal que todas las rectas que caen sobre ella desde un punto de los que están dentro de la figura, son iguales entre sí. Esta definición hace las veces de causa formal de la prueba.

Sobre la causalidad material, Biancani ilustra su uso con la debatida proposición I, 32 a que se aludió en las críticas de Pereira a las matemáticas por aplicar elementos auxiliares. Biancani sostiene que aquí se procede por causas materiales en tanto la igualdad del todo se infiere de la igualdad de las partes.

La Dissertatio es significativa porque desarrolla una apología de la certeza y cientificidad de las matemáticas en el contexto aristotélico del conocimiento científico, y más aún cuando se interpreta en tanto análisis de la práctica de los matemáticos y cómo el modelo causal aristotélico puede, legítimamente, aplicársele. No obstante:

Estos esfuerzos están destinados a no ser conclusivos porque, como sabemos hoy, la estructura silogística no es suficiente para capturar adecuadamente la mecánica de un argumento matemático informal, y sin tal análisis había mucho lugar para probables análisis sobre los mismos teoremas que entrarán en conflicto (Mancosu, 1996, p. 17).

Lejos de reforzar la idea de una historiografía triunfalista, según la cual en un mismo renglón no se puede hablar de la visión de la batalla de los vencedores y los vencidos, lo que ello resalta son las condiciones de emergencia de las matemáticas como herramienta lingüística de la ciencia moderna, temas sobre los que volveré después de estudiar lo concerniente a la ontología de las entidades matemáticas.

Para comprender mejor los argumentos sobre el lugar de las matemáticas en la jerarquía del conocimiento, conviene recordar cómo consideraron los objetos de los que se ocupan y su conceptualización ontológica, tanto los críticos como los defensores. La ontología de las entidades matemáticas de Piccolomini y Pereira está influenciada por la comprensión averroísta de la cantidad en tanto característica más general de la materia, la teoría de la abstracción aristotélica y la posición intermedia de las matemáticas entre la metafísica y la filosofía natural. En palabras de Piccolomini (1576), la cantidad inherente a la materia prima, previa a su actualización es "cantidad abstracta" o "cantidad indeterminada", por lo cual las matemáticas trabajan con el ente más simple. Así, aun cuando por ello Piccolomini le confiere la certeza que estas alcanzan, sus demostraciones no las considera científicas, lo cual ilustra con la proposición I, 32. En contraste, dado que la filosofía natural se ocupa de la realidad de la materia, formal y materialmente, su lugar en la jerarquía del conocimiento es superior a las matemáticas; incluso las matemáticas mixtas o aplicadas, que investigan fenómenos naturales como el sonido y la luz, las considera desprovistas de cientificidad. Para constatarlo recurre a la astronomía mediante el ejemplo de la esfericidad de la tierra, caso en el cual mientras al filósofo natural le corresponde investigar las causas esenciales inherentes a la naturaleza, el astrónomo tiene en cuenta solo sus propiedades matemáticas. Así, cuando este considera

[...] que el cielo es esférico, o que la Tierra es redonda, no necesita conocer la verdadera naturaleza y su sustancia, sino que solo a partir de las posiciones, figuras y aspectos vistos en el cielo argumenta que son de tal forma [...]. Por esta razón puede concluirse que aunque la ciencia de las cosas naturales a veces se entrelaza con otras ciencias al tratarse del mismo objeto, o al demostrar cierta conclusión, no obstante el filósofo natural difiere de ellos porque nunca separa los conceptos de las formas de aquellos de su propio tema, trata ambas naturalezas como relacionadas mutuamente, a saber, materia y forma, que son los dos principios y causas intrínsecas de las cosas naturales (Piccolomini, 1576, pp. 24v-25r).

Pereira incluso va más lejos negando que la cantidad tenga vínculo alguno con las sustancias sensibles o con toda sustancia. Este es el núcleo de su crítica a la posición intermedia de las matemáticas; a su vez es el centro de su ataque a la doctrina platónica de la reminiscencia, según la cual las entidades matemáticas son innatas al alma. En el ámbito de la Quaestio la consecuencia más negativa para las matemáticas es que al disociar la cantidad de toda sustancia cierra la posibilidad de que sus demostraciones sean causales. Así las cosas, la certeza de las matemáticas queda restringida a su estructura lógica, en contraste con las demostraciones de la filosofía natural que, en efecto, son potissimae por tratar sustancias reales y materiales. Los pronunciamientos de Pereira están dirigidos a preservar la superioridad de la filosofía natural sobre las matemáticas y a enfatizar la separación de estos saberes, lo que estaba en riesgo a raíz de las Cuestiones mecánicas y de las lecturas neoplatónicas de la ontología de las entidades matemáticas que conforman en gran medida las respuestas durante la Quaestio.

En este sentido, por ejemplo, Francesco Barozzi (1537-1604), profesor veneciano de matemáticas, defendió la posición intermedia de estas conforme a la disposición de las ciencias, según la dignidad de los entes que estudia. Para Barozzi, la teología conserva el primer lugar, las matemáticas el segundo y la filosofía natural el tercero. Esta jerarquización se basa en una lectura platónica en la que Barozzi se inspira en Proclo. También Pietro Catena (1501-1576) consideró las entidades matemáticas inteligibles invocando la teoría de la reminiscencia, justificando así la naturaleza puramente intelectual de su conocimiento. Para beneficio de las matemáticas, Catena inclusive proclamó la superioridad de las demostraciones matemáticas respecto a las potissimae, y decretó que el conocimiento de las cosas naturales solo es posible a través de los métodos matemáticos.

Aquí creo conveniente manifestar la divergencia de enfoques entre Platón y la lectura neoplatónica de Catena. Mientras que para el primero el conocimiento de las matemáticas se dirige de la abstracción de lo mundano y hacia la contemplación de las formas, para el segundo las matemáticas se dirigen al discernimiento del mundo natural. Como se infiere, adonde se orienta el conocimiento por medio de las matemáticas es opuesto en Platón y Catena, y esta misma posición puede observarse en Galileo, quien concibe las matemáticas solo como un lenguaje que facilita la comprensión de la naturaleza, no guiado a la contemplación de las formas.

Volvamos ahora a Biancani y su caracterización ontológica de las entidades matemáticas. El primer capítulo de la Dissertatio demuestra la existencia de las entidades matemáticas y, además, señala que sus definiciones son esenciales y causales. Para ello, el autor parte de cuáles son los objetos de las matemáticas, a saber, la cantidad discreta (matemática) y la magnitud continua (geometría), pero desde un punto de vista finitista:

El geómetra y el aritmético consideran la cantidad no absolutamente, sino en cuanto delimitada, como son para el geómetra las líneas finitas rectas o curvas en la cantidad continua; y las superficies delimitadas de las cuales resultan varias figuras, como el círculo, el triángulo, etc.; y, finalmente, los sólidos, de nuevo delimitados, que constituyen diferentes figuras sólidas como la pirámide, el cubo, el cono, el cilindro etc. Lo mismo puede observarse de manera análoga en la cantidad discreta, esto es, en los números, considerados por los aritméticos en cuanto delimitados (Biancani, 1615, p. 6).

Quienes critican las pruebas geométricas se equivocan porque conciben su objeto como absoluto, como el caso del filósofo natural y el metafísico; pero no debe ser así, puesto que el estudio de la cantidad inteligible del matemático difiere de la sensible del filósofo natural. Para Biancani el que las matemáticas traten en abstracto la cantidad les confiere cierta perfección, llamada perfección matemática, que lo lleva a desarrollar sus argumentos sobre la existencia de las entidades matemáticas contra quienes afirman su inexistencia como Pereira, que sostiene que las figuras geométricas no se adecúan al reino físico. Para Biancani ello se debe a la tosquedad e imperfección de la materia sensible y a su imposibilidad de asimilar tal perfección, de tal suerte que "aunque estas figuras perfectas matemáticas no existan en la naturaleza de las cosas, existen en la mente del Autor de la Naturaleza [...] como arquetipos exactos de sus ideas" (Biancani, 1615, p. 6), investigadas por los matemáticos. Este pasaje de Biancani puede verse como de inspiración platónica para el desarrollo de su argumentación, o como enfoque aristotélico, en tanto que explota la interpretación escolástica de las "formas" correspondientes a las ideas de Dios en la línea del aristotelismo cristianizado.

Dos observaciones finales sobre Biancani. Primero, como lo afirman Mancosu (1996) y Feldhay (1998), el finitismo implícito en el tratamiento de la magnitud continua de la geometría, si bien se explica al interior de la práctica matemática de su época, encontraría serios problemas en los desarrollos de la geometría en figuras de magnitudes infinitas como el sólido infinito de Torricelli, y en los desarrollos de los indivisibles e infinitesimales en matemáticas. Segundo, como parte de las políticas del conocimiento -por lo menos en la comunidad de los matemáticos jesuitas- Biancani llega a establecer unas fronteras más específicas entre las matemáticas, a las que les restituye su dignidad epistemológica, y la filosofía natural, como parte de una estrategia de control disciplinar. Esto deja abierto el problema de la aplicabilidad de las matemáticas al conocimiento de la naturaleza, el cual se resuelve (o disuelve) en los desarrollos de la Quaestio con Wallis (1693-1699) y Barrow (1734).

La contribución de Wallis a la Quaestio surge como respuesta a la Lógica de Smiglecki (1618), que se da en el tercer capítulo de su Mathesis universalis sive arithmeticum opus integrum titulado "Sobre las demostraciones en matemáticas. Donde se demuestra que las matemáticas son verdaderamente ciencias" (1693-1696). Las posiciones que Wallis debate son la naturaleza imaginaria de las entidades matemáticas y la negación de la posibilidad de que sus demostraciones se lleven a cabo por causas verdaderas. Estos argumentos, a mi juicio, son la indicación más reveladora de cómo los postulados de la Quaestio de modo progresivo se concentraron más en la naturaleza misma de la argumentación matemática y su práctica en el siglo XVII, que en su adecuación al modelo aristotélico-escolástico de cientificidad. Así, respecto a que las entidades matemáticas no existen en la naturaleza y que permanecen separadas de ella, Wallis, al igual que Smiglecki, afirma la suficiencia de su potencialidad, pero a diferencia suya, enfatiza más el carácter abstracto de las entidades matemáticas que su separación, a fin de reducir la brecha que las separa de los objetos físicos. Así escribe:

Una cosa es abstraer y otra negar. El matemático abstrae las magnitudes del cuerpo físico, pero no las niega; no afirma más la existencia de la cantidad en el cuerpo físico, que lo que el físico afirma de la existencia de la sustancia corpórea sin la cantidad. En consecuencia, las entidades matemáticas existen, o pueden existir, no solo en la imaginación sino en realidad; no en sí mismas sino en el cuerpo físico, aunque se consideren en abstracto (Wallis, 16931696, p. 21).

Sobre la causalidad de las demostraciones, primero lleva a cabo una interesante redefinición de lo que debe ser una demostración científica que tendrá importantes consecuencias:

Digo que aunque sea cierto lo que se afirma, a saber, que las demostraciones matemáticas no se realizan mediante una causa verdadera y próxima, no obstante son suficientemente científicas si se realizan por una causa más distante, por un efecto, o por otro término medio tomado de otra parte de la demostración, y que con certeza se concluya lo que se afirma sin que pueda ser de otra forma. Para que la demostración sea científica es suficiente que provenga de la naturaleza de la cosa por un medio necesario [...]. Smiglecki, ni ninguno otro que conozca, negará que las matemáticas puras sean ciencias, aunque no les confiera la mayor perfección demostrativa (p. 22).

La idea de que las pruebas matemáticas no guardan el mismo grado de perfección, constituye en verdad una clara reconfiguración a propósito de las clases de demostraciones que, sin embargo, tienen el mismo grado de certeza para Wallis. Según su jerarquización, la potissima estaría representada por la del por qué, luego por la de qué y para finalizar, la prueba por contradicción o prueba por reducción al absurdo. Tradicionalmente, las dos primeras se han denominado directas u ostensivas, y la tercera indirecta.

En la fase de la Quaestio previa a Wallis, las pruebas por reducción al absurdo no eran consideradas científicas, entendiendo por científico, causal en el contexto aristotélico. Para Proclo estas:

Siempre alcanzan una conclusión manifiestamente imposible, opuesta a lo que se admite. En algunos casos las soluciones entran en conflicto con las nociones comunes, los postulados o las hipótesis (de que parten); en otros casos, contradicen las proposiciones previamente establecidas (Proclo, s.f. citado por Heath, 1956, p. 136).

Estas pruebas se usan en geometría para demostrar teoremas inversos como la proposición I, 6 de los Elementos a partir de la proposición I, 5. Barozzi y Biancani, que defendieron la causalidad de las pruebas ostensivas, no consideraron causales las de reducción al absurdo; y otro actor de la Quaestio, David Rivaltus, las tomó como causales en el sentido de Smiglecki: como relativas al conocimiento.

En Wallis, el cambio de perspectiva sobre la causalidad en las demostraciones matemáticas, prueba que la filosofía de las matemáticas se estaba constituyendo en una consideración de ellas como lenguaje de la ciencia, transformando su análisis y práctica en algo ya diferente al de la ciencia aristotélica, articulada por el razonamiento silogístico. Según Mancosu (1992), "esta distinción es mucho más cercana a la fenomenología del discurso matemático, y a la experiencia del matemático, que cualesquiera de las distinciones con soporte en el criterio causal" (p. 255). Esta reconfiguración sobre las matemáticas se evidencia y especifica más aún en Isaac Barrow.

En las Lecciones de matemáticas (en Latín, 1683; traducción inglesa, 1734) dictadas entre 1664 y 1666, Barrow (1734) dedicó un formidable espacio a la causalidad en matemáticas, respondiendo así al debate que inició en 1547 Piccolomini. A diferencia de Wallis, que se concentró solo en la Lógica de Smiglecki, Barrow cita fuentes directas de la polémica -como Pereira y Biancani-, pero aclara que no pretende defender la legitimidad de las matemáticas como ciencias -las juzga como scientiae por excelencia- sino demostrar su utilidad para la filosofía natural. Así pues, su papel en la Quaestio es proclamar la hegemonía de las matemáticas en la filosofía natural del siglo XVII. Esta actitud no es novedosa en la época en que Barrow escribe sus Lectures. La matematización de la naturaleza en cuanto a mecánica ya había empezado con Galileo y el estudio de la caída libre, por mencionar solo un ejemplo. Lo significativo de los pronunciamientos de Barrow, empero, radica en que su apología a las matemáticas y a la excelencia que de ellas proclama, tiene unos componentes metafísicos específicos, como su voluntarismo teológico, que relaciona su filosofía de las matemáticas con el estudio experimental de la naturaleza, prefigurando así aspectos de gran importancia de la filosofía natural de Isaac Newton. En este sentido, es conveniente destacar la inclusión de Barrow a propósito de la hegemonía de las matemáticas que, como bien se sabe, en los Principia de Newton lleva a cabo su realización. Así pues, terminaré este análisis de la matematización de la naturaleza, articulado por la filosofía de las matemáticas de los actores que aquí se trataron, con estos aspectos de los pronunciamientos de Isaac Barrow, mentor de Newton.

La Lección V comienza con el reconocimiento de que la certeza de las matemáticas no es algo que se hubiera puesto en cuestión en exclusiva con Pereira (y por extensión con Piccolomini) sino que se retrotrae a la antigüedad griega. En aquel entonces los escépticos dudaron de la certeza de los axiomas de las matemáticas obtenidos de forma inductiva. A esta objeción responde Barrow negando que todos los principios en matemáticas se obtengan así y, de hecho, afirma:

Puede anotarse que, en la mayoría de las cosas en matemáticas, aunque pueda tenerse la ocasión de contemplarlas con los sentidos, no surgen sin embargo inmediata y directamente a partir de ellos, sino que su existencia y cualidad se infieren y comprenden a partir de la sola razón (Barrow, 1734, p. 75).

No obstante, la sensación no queda por completo excluida de la aritmética y la geometría, puesto que puede ser útil para probar la posibilidad de las hipótesis matemáticas. Para tal efecto:

Una sola observación sensible puede dar testimonio suficiente de que cada magnitud que tratan los matemáticos puede tener existencia real; y no se necesita mucho para ello, sino que un solo testimonio de los sentidos dará abundante evidencia de que todas las hipótesis matemáticas son posibles, que las magnitudes pueden oponerse, dividirse, moverse, llenar el espacio, etc. (Barrow, 1734, pp. 75-76).

Hay valiosas consecuencias de esta declaración, que dan cuenta de la transformación de la filosofía y práctica matemáticas en el siglo XVII.

1. Se declara el vínculo indisoluble entre las matemáticas y la experiencia. Si bien en las discusiones previas, las apologías a las matemáticas estaban dirigidas a señalar el importe que la experiencia podría obtener a partir de estas, ahora la situación aparece invertida: la experiencia se subordina a las matemáticas, sirviéndole de beneficio a ellas.

2. La comprensión de la experiencia también cambió. Mientras que en el sentido aristotélico esta resulta de repetidas percepciones: de la repetición a la memoria, y de las varias memorias a la experiencia general de un particular, con Barrow invocar la experiencia se orienta hacia afirmaciones generales, no universales y, por último, en contraste con el reporte de las experiencias referidas en el sentido aristotélico hacia cómo ocurren las cosas, la reconfiguración de la experiencia según Barrow se refiere a cómo algo había ocurrido. Desde esta perspectiva, la experiencia singular del matemático podría hacerse general, e incluso universal, salvo que un hecho (experiencia) contrario(a) obligara a revisar la hipótesis (Dear, 1995). A modo de digresión puede anotarse que esta forma de generalización-universalización es un elemento primordial de la metodología de Newton.

3. El binomio potencial-actual de la ontología de las entidades matemáticas se transforma en un realismo matemático en Barrow, en tanto "que todas las figuras geométricas imaginables realmente son inherentes en cada partícula de la materia [...] de hecho y en la máxima perfección, aunque no aparente en los sentidos" (Barrow, 1734, p. 76). Esta afirmación es contraria a Biancani, quien sostenía que las entidades matemáticas solo existen en la mente. Para Barrow, no se trata de la mera potencialidad como parte de la teoría de producción de posibles cosas futuras, sino, más precisamente, de la potencia de la voluntad divina. Así las cosas, su voluntarismo teológico lo limita en su discusión de las causas matemáticas al ámbito de la causalidad formal:

Las demostraciones matemáticas son eminentemente causales, lo cual se sigue a partir de que solo llegan a sus conclusiones a partir de axiomas que demuestran las afecciones principales y más universales de todas las cantidades, y a partir de definiciones que declaran las generaciones constitutivas y pasiones esenciales de las magnitudes particulares. En consecuencia, las proposiciones que surgen de tales supuestos principios, deben seguirse de las esencias y causas íntimas de las cosas (Barrow, 1734, p. 83).

Las causas materiales no se toman en cuenta en las Lecciones V y V7. Respecto de las eficientes y finales, como se ha observado, históricamente no han sido objeto de tratamiento en la Quaestio en particular, ni en las teorías medievales de la demostración general. En Barrow (1734), ello se debe a su teología.

Cada acción de una causa eficiente, como su efecto consecuente, depende de la libre voluntad y poder de Dios Todopoderoso, quien puede impedir a su placer el influjo y eficacia de cualquier causa; tampoco existe efecto alguno confinado a una sola causa, sino que puede producirse por otras innumerables. Por ello es posible que pueda haber una causa sin efecto, o un efecto sin causa peculiar que le confiera a una cosa su existencia. Por tanto, no puede haber argumentación a partir de la causa eficiente al efecto, ni por el contrario del efecto a la causa que se rija por leyes necesarias (pp. 88-89).

La teología de Barrow apoya su tratamiento de la causalidad en matemáticas, el cual como lo enuncia la cita anterior a esta, constituye una redefinición en su práctica de las matemáticas. Toda vez que opera la asimilación de la causalidad formal en la demostración matemática, queda excluido cualquier otro tipo, el cual no será más que "mera ficción, que no se fundamenta en argumento alguno, ni se confirma por ningún ejemplo" (Barrow 1734, p. 100). En conclusión, a las demostraciones de las matemáticas, Barrow (1734) sostiene que en ellas es donde se pueden encontrar las más perfectas.

La radical transformación que se manifiesta en la apreciación de las matemáticas para Barrow, no puede considerarse solo como una reinstalación de su dignidad, como fue tradicionalmente hasta Piccolomini.

La subordinación de las matemáticas a la filosofía natural en el esquema aristotélicoescolástico se había reconfigurado hacia la hegemonía de las matemáticas sobre la filosofía natural; otro cambio paralelo es el rompimiento en Barrow de la vieja dicotomía matemáticas puras/matemáticas mixtas. La cantidad, discreta (aritmética) o continua (geometría), había colonizado los objetos del mundo natural. Así:

En realidad cada uno de los objetos [matemáticos] [es] a la vez inteligible y sensible en un aspecto diferente. Inteligible en cuanto la mente aprehende y contempla sus ideas universales, y sensible cuando concuerdan con los objetos particulares manifestados a los sentidos (Barrow 1734, p. 19).

De acuerdo con esta concepción de los objetos de las matemáticas, concluye Barrow (1734) el carácter que bien podría llamarse omnicomprensivo de estas en toda la filosofía natural, pues "no existe rama alguna de la filosofía natural que no pueda arrogarse el título [de matemáticas] para sí, puesto que no hay ninguna en que la consideración de la cantidad esté completamente excluida" (p. 21).

Diez años después de la muerte de Barrow aparecerían los Principios matemáticos de la filosofía natural de Isaac Newton, título que inequívocamente expresa la hegemonía de las matemáticas en la filosofía natural. En efecto, el papel de las matemáticas en la mecánica racional de los Principios de Newton indica asimismo que los criterios desde los que se entendían términos como "explicación" e "inteligibilidad" habían adquirido una nueva significación (Ochoa, 2012). En este sentido, la causalidad, núcleo del ataque a la cientificidad de las matemáticas por Piccolomini y Pereira, había quedado por fuera de las exigencias centrales del pensamiento científico de finales del siglo XVII; otro tanto ocurriría con la causalidad física del concepto central de la obra de Newton: la gravitación universal. Como observa Gingras (2001) "la publicación de los Principia de Newton marca un comienzo de este cambio donde las explicaciones matemáticas llegaron a prevalecer sobre las mecánicas cuando estas últimas no se ajustaban a los cálculos" (p. 398).

El análisis expuesto aquí acerca de uno de los muchos debates sobre la legitimidad epistemológica de las matemáticas de la filosofía natural en los siglos XVI y XVII, solo presenta una de las facetas de este complejo proceso del ascenso en la jerarquía del conocimiento y el papel regente en la filosofía natural. Como se deja ver, es un primer paso de la matización del eslogan de las grandes narrativas según el cual, la revolución científica del siglo XVII fue posible gracias a las matemáticas. En efecto, hay algo de verdad en este eslogan, pero esta es más variada y compleja de lo que su enunciación refleja. De hecho, la historiografía sobre los orígenes de la ciencia moderna precisamente desafía la generalización implícita en esta suposición y la aparente facilidad explicativa descrita por la matematización de la filosofía natural. En este contexto, hay otros elementos que ameritan un estudio más detallado que, por limitaciones de espacio, no es posible tratarlos aquí, como la metafísica comprendida en el principio de acuerdo con cual el mundo obedece a una constitución en pondere, numero et mensura, o en el que la creación implícitamente está conformada en un orden geométrico. La denominada matematización de la naturaleza y, en concreto, de la filosofía natural, está llamada a revalorarse, lo que, por lo demás, ya ha arrojado sus primeros resultados (Roux, 2010)⁶.

¹ En este sentido, llama la atención que en una época en la que abundaron obras con títulos que aludían a la novedad, su ausencia en los escritos de Newton desde la metodología científica hasta la teología, desde la alquimia hasta las matemáticas, sea notable. De hecho, su Nueva teoría sobre la luz y los colores (1672) constituye la excepción. Aunque esta suspicacia quizá dé lugar a sutiles reflexiones, puede confrontársela con una opuesta: las obstinadas luchas de Newton por la novedad y autoría de sus descubrimientos matemáticos.

² Sobre la reevaluación de la revolución científica véase Osler (2000). El análisis de la historiografía de Newton en cuanto a sus límites y alcances, puede verse en Ochoa (2001) y Orozco (2007; 2009).

³ Véanse, por ejemplo, Vickers (1984), Clark (1997), Newman y Grafton (2001), Moran (2005), Newman (2006), entre otros.

⁴ En particular importantes, sin que ello vaya en detrimento de las concepciones platónicas, neoplatónicas y pitagóricas que de igual modo ejercieron un papel determinante en la incorporación de las matemáticas en la filosofía natural.

⁵ La matematización de la naturaleza, proceso al que subyace una profunda complejidad, no ha sido abordada de manera sistemática, de tal forma que se articulen la filosofía y epistemología de las matemáticas con los contextos locales y sociales de producción de conocimiento, ya sean institucionales, ideológicos y políticos. Estos enfoques, que pueden llamarse conceptualista y contextualista, aún no producen tratamiento sistemático. Empero, en el ámbito contextualista, Peter Dear (1995) dedica buena parte de su obra a desarrollar una "narrativa heurística" de la revolución científica, con base en cómo la filosofía natural llegó a ser matemática, haciendo una reconstrucción histórica desde la sociología del conocimiento. Aquí pretendo llamar la atención sobre lo necesario de abordar ambos aspectos en los análisis del surgimiento de la ciencia moderna. Ahora, dado que una síntesis tal de este episodio que involucre los aspectos mencionados podría arrojar como resultado una narrativa totalizante que deja por fuera posibles objetos de análisis, se apunta como término medio a la consideración de ambos aspectos en igual importancia. Esta problemática historiográfica requiere un tratamiento más amplio que el ofrecido aquí. Véanse Jardine (1986), Guicciardini (1989), Dear (1995), Mancosu (1996), Pycior (1997), Blay (1998) y Dobbs (2000).

⁶ Muestra de ello es el número monográfico de Earlyscience, 15(4) de 2010.

Aristóteles. (1988). Tratados de Lógica: (Órganon) II: sobre la interpretación. Analíticos primeros. Analíticos segundos. Madrid: Gredos.         [ Links ]

Aristóteles. (1995). Física (Trad. G. De Echandía). Madrid: Gredos.         [ Links ]

Barrow, I. (1734). The Usefulness of Mathematical Learning Explained and Demonstrated: Being Mathematical Lectures Read in the Public Schools of Cambridge. Londres: S. Austen.         [ Links ]

Biagioli, M. (1989). The social status of Italian mathematicians, 1450-1600. History of Science 27:41-95.         [ Links ]

Biancani, G. (1615). De mathematicarum natura dissertatio. Bolonia: B. Cocchi.         [ Links ]

Blay, M. (1998). Reasoning with the Infinite: From the Closed World to the Mathematical Universe. Chicago: University Press.         [ Links ]

Clark, S. (1997). Thinking with Demons: The idea of witchcraft in early modern Europe. Oxford: Clarendon Press.         [ Links ]

Clavius, C. (1612). Opera mathematica (Vols. 1-5). Mainz: Reinhard Eltz.         [ Links ]

Crombie, A. C. (1952). Augustine to Galileo: The History of Science, A.D. 400-1650. London: Falcon.         [ Links ]

Dear, P. (1987). Jesuit mathematical science and the reconstitution of experience in the early seventeenth century. Studies in History and Philosophy of Science 18(2):133-175.         [ Links ]

Dear, P. (1995). Discipline and Experience. The Mathematical Way in the Scientific Revolution. Chicago: University Press.         [ Links ]

Dear, P. (1998). The Mathematical Principles of Natural Philosophy: Toward a Heuristic Narrative for the Scientific Revolution. Configurations 6(2):173-193.         [ Links ]

Dobbs, B.J. (2000). Newton as Final cause and First Mover. En M. Osler (Ed.), Rethinking the scientific revolution (pp. 25-39). New York, NY: Cambridge University Press.         [ Links ]

Feldhay, R. (1998). The use and abuse of mathematical entities: Galileo and the Jesuits revisited. En P. K. Machamer (Ed.), The Cambridge companion to Galileo (pp. 80-145). Cambridge: Cambridge University Press.         [ Links ]

Funkenstein, A. (1986). Theology and the scientific imagination from the Middle Ages to the seventeenth century. Princeton: Princeton University Press.         [ Links ]

Gingras, Y. (2001). What did Mathematics do to Physics?. History of Science 39:383-416.         [ Links ]

Guicciardini, N. (1989). The development of Newtonian calculus in Britain, 1700-1800. New York: Cambridge University Press.         [ Links ]

Hall, A. R. (1981). From Galileo to Newton. New York: Dover.         [ Links ]

Hall, M. B. (1952). The Establishment of the Mechanical Philosophy. Bruges: St. Catherine Press.         [ Links ]

Heath, T. L. (1956). The Thirteen Books of Euclid's Elements. New York: Dover Publications.         [ Links ]

Jardine, N. (1986). Epistemology of the sciences. En C. B. Schmitt, Q. Skinner & E. Kessler (Eds.), The Cambridge history of Renaissance philosophy (pp. 685-711). Cambridge: Cambridge University Press.         [ Links ]

Koyré, A. (1965). The significance of the Newtonian synthesis. En Newtonian studies (pp. 3-24). Cambridge: Cambridge University Press.         [ Links ]

Koyré, A. (1994). From the Closed World to the Infinite Universe. Baltimore: Johns Hopkins University Press.         [ Links ]

Koyré, A. (1997). La aportación científica del Renacimiento. En Estudios de historia del pensamiento científico (pp. 41-50). México: Siglo XXI Editores.         [ Links ]

Mancosu, P. (1992). Aristotelian Logic and Euclidean Mathematics: Seventeenth Century Developments of the Quœstio de Certitudine Mathematicarum. Studies in History and Philosophy of Science 23(2):241-265.         [ Links ]

Mancosu, P. (1996). Philosophy of Mathematics and Mathematical Practice in the Seventeenth Century. New York: Oxford University Press.         [ Links ]

Moran, B.T. (2005). Distilling Knowledge: Alchemy, Chemistry, and the Scientific Revolution. Cambridge: Harvard University Press.         [ Links ]

Newman, W.R. (2006). Atoms and Alchemy: Chymistry and the experimental origins of the scientific revolution. Chicago: University of Chicago Press.         [ Links ]

Newman, W.R. & Grafton, A. (2001). Secrets of Nature: Astrology and Alchemy in Early Modern Europe. Cambridge: MIT Press.         [ Links ]

Ochoa, F. (2001). Newton heteróclito: Problemas y límites del historiar a Sir Isaac Newton. Estudios de Filosofía 24:63-78.         [ Links ]

Ochoa, F. (2012). Mathematics, Natural Philosophy, and Providential Theology: An inquiry into the ontological problem of the causation of gravity force in Newton's physics. (Tesis Doctoral, Instituto de Filosofía, Universidad de Antioquia).         [ Links ]

Orozco, S. (2007). Modelos interpretativos del corpus newtoniano: Tradiciones historiográficas del siglo XX. Estudios de Filosofía 35:227-256.         [ Links ]

Orozco, S. (2009). Isaac Newton y la reconstitución del palimpsesto divino. Medellín: Editorial Universidad de Antioquia.         [ Links ]

Osler, M. J. (2000). Rethinking the Scientific Revolution. Cambridge: Cambridge University Press.         [ Links ]

Pereira, B. (1591). De communibus omnium rerum naturalium principiis et affectionibus, libriquindecim. Venetiis: Andream Muschium.         [ Links ]

Piccolomini, A. (1576). La prima parte della filosofia naturale. Roma: Daniel Zaneti, & Compagni.         [ Links ]

Pycior, H. (1997). Symbols, Impossible Numbers, and Geometric Entanglements: British Algebra Through the Commentaries on Newton's Universal Arithmetick. New York: Cambridge University Press.         [ Links ]

Roux, S. (2010). Forms of Mathematization (14th-17th Centuries). Early Science and Medicine 15(4-5):319-337. doi: 10.1163/157338210X516242        [ Links ]

Scheiner, C. (1614). Disquisitiones mathematicae de controuersii set nouitatibus astronomicis. Ingolstadii: Elisabetham Angermariam.         [ Links ]

Smiglecki, M. (1618). Lógica Martini Smiglecii: Selectis disputationi bus et quaestioni bus illustrata. Ingolstadii: Eder.         [ Links ]

Smolarski, D. C. (2002a). Historical Documents, Part II. Two Documents on Mathematics. Science in Context 15(3):465-470. doi: 10.1017/S0269889702000583        [ Links ]

Smolarski, D.C. (2002b). Historical Documents, Part I. Sections on mathematics from the various editions of the Ratio Studiorum. Science in context 15(3):459-64. doi:10.1017/S0269889702000571        [ Links ]

Sorell, T. (1993).The Rise of Modern Philosophy: The Tension between the new and traditional philosophies from Machiavelli to Leibniz. Oxford: Clarendon Press.         [ Links ]

Vickers, B. (1984). Occult and Scientific Mentalities in the Renaissance. Cambridge: Cambridge University Press.         [ Links ]

Wallis, J. (1693-1699). Johannis Wallis Oxoniensi Opera mathematica: tribus volumini buscontenta. Oxford: Theatro Sheldoniano.         [ Links ]

Yolder, J. G. (1988). Unrolling time: Christiaan Huygens and the Mathematization of Nature. Cambridge: Cambridge University Press.         [ Links ]

Para citar este artículo use: Ochoa, F. (2013). De la subordinación a la hegemonía. Sobre la legitimación epistemológica de las matemáticas en la filosofía natural en el siglo XVII. Revista Civilizar Ciencias Sociales y Humanas, 13(25), 157-176.