Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Pensamiento Psicológico
Print version ISSN 1657-8961
Pensam. psicol. vol.12 no.2 Cali July/Dec. 2014
Writing Times in Three Digit Numerals: Relation between Times and Syntactic Structure of Verbal Expressions Dictated1
Tiempos de escritura en numerales de tres dígitos: relación entre el tiempo y la estructura sintáctica de las expresiones verbales dictadas
Tempos de escritura em numerais de três dígitos: relação entre a tempo e a estrutura sintática das expressões verbais ditadas
Diego Fernando Guerrero2
Mariela Orozco-Hormaza3
Rafael G. Hurtado4
Universidad del Valle, Cali (Colombia)
Universidad Nacional de Colombia, Bogotá (Colombia)
1This research was supported by Colciencias under Grant 110645221365.
2Magíster. Instituto de Psicología, Calle 13 No 100-00, edificio 385, 4to. piso, oficina 4002, Cali-Colombia. Correspondencia: diego.guerrero@correounivalle.edu.co
3Ph.D.
4Ph.D.
Received: 23/05/2013 Accepted: 01/06/2014
Para citar este artículo/ to cite this article
Guerrero, D. F., Orozco-Hormaza, M. y Hurtado, R. G. (2014). Writing Times in Three Digit Numerals: Relation between Times and Syntactic Structure of Verbal Expressions Dictated. Pensamiento Psicológico, 12(2), 57-64. doi: 10.11144/Javerianacali.PPSI12-2.wttd
Abstract
Objective. This study evaluates in three-digit numerals how the writing times between digits (Inter Digit Jump - IDJ) adjust to the predictions deduced from the transcoding models proposed by Power and Dal Martello (1990) and Barrouillet, Camos, Perruchet and Seron (2004), who explain the writing of numerals in children. Method. The study had the participation of twenty five (25) first grade children who wrote down spoken verbal numerals in three-digit numerals correctly; the duration of the Inter-Digit Jump was analyzed for four types of numerals during the course of four sessions. Results. The results of the ANOVAs showed that in the four types of numerals, the duration in the first IDJ is greater than in the second IDJ, and that the shortest durations tended to take place prior to writing the zero digit. Conclusion. These findings best fit the predictions based on the model by Barrouliet et al., (2004), which assumes that the chain of digits is produced and stored in a buffer to be subsequently produced by the graphomotor procedures, showing that in three-digit numerals the IDJ duration reflects more the production program than the syntactic structure of the verbal numerals dictated.
Keywords: Number transcoding, graphomotor procedures, arabic numerals, verbal numerals.
Resumen
Objetivo. El presente estudio evalúa el ajuste de los tiempos en las pausas entre dígitos, en la escritura de numerales arábigos, con las predicciones que se derivan de los modelos de transcodificación de Power y Dal Martello (1990) y Barrouillet, Camos, Perruchet y Seron (2004), quienes explican el proceso de transcodificación de numerales en niños. Método. En el estudio participaron 25 niños de primer grado que escribían correctamente numerales de tres dígitos a partir de un dictado, se analizó el tiempo de las pausas entre dígitos para cuatro tipos de numeral en cuatro sesiones de trabajo. Resultados. Los análisis de varianza ANOVA mostraron que en los cuatro tipos de numerales la duración en la primera pausa es mayor que en la segunda y que los menores tiempos tienen lugar antes de escribir el dígito cero. Conclusión. Estos resultados se ajustan mejor a las predicciones basadas en el modelo de Barrouliet et al. (2004), el cual supone que la cadena de dígitos se produce y almacena en una memoria intermedia para luego ser producida por los procedimientos de grafomotores, lo que sugiere que en los numerales de tres dígitos los tiempos en las pausas entre dígitos reflejan el programa motor de escritura más que la estructura sintáctica de los numerales verbales dictados.
Palabras clave: Transcodificación numérica, procedimientos grafomotores, numerales arábigos, numerales verbales.
Resumo
Escopo. O presente estudo avalia o ajuste dos tempos nas pausas entre dígitos na escritura de numerais arábicos, com as predições que são derivadas dos modelos de trans-codificação de Power e Dal Martello (1990) e Barrouillet, Camos, Perruchet e Seron (2004), que explicam o processo de trans-codificação de numerais em crianças. Metodologia. No estudo participaram 25 crianças do primeiro ano que escreviam corretamente numerais de três dígitos a partir de um ditado, foi analisado o tempo das pausas entre dígitos para quatro tipos de numeral em quatro sessões de trabalho. Resultados. Os análises de variância ANOVA mostraram que nos quatro tipos de numerais a duração na primeira pausa é maior que na segunda e que os menores tempos têm lugar antes de escrever o dígito zero. Conclusão. Estos resultados ajustam-se melhor para as predições baseadas no modelo Barrouliet et al. (2004), no qual supõe que a cadeia de dígitos é produzida e armazenada numa memória intermédia para depois ser feita pelos procedimentos grafomotores, o que sugere que nos numerais de três dígitos os tempos nas pausas entre dígitos refletem o programa motor de escritura mais que a estrutura sintática dos numerais verbais ditados.
Palavras chave: Trans-codificação numérica, procedimentos grafomotores, numerais arábicos, numerais verbais.
Introduction
Two types of models describing numerical transcoding from the verbal format to the Arabic format have been proposed: the semantic and asemantic models (Seron & Noël, 1995). Semantic models assume that writing numerals from a dictation requires an intermediate representation that specifies the amount expressed verbally (McCloskey, 1992; McCloskey & Caramazza, 1987; McCloskey, Caramazza & Basilli, 1985; McCloskey & Macaruso, 1995; Power & Dal Martello, 1990), whereas asemantic models are based on production rules applied to primitive lexical structures and do not require a semantic representation (Barrouillet et al., 2004; Dehaene, 1992; Seron & Nöel, 1995). This work focuses on two of the models proposed that account for the transcoding process in children: the verbal semantic model by Power and Dal Martello (1990) and the Developmental, Nonsemantic, and Procedural Model for Transcoding from verbal to Arabic Numerals (ADAPT) proposed by Barrouillet et al. (2004).
For Power and Dal Martello (1990), transcoding is divided in understanding and production process. Understanding refers to the construction of an internal semantic representation derived from the verbal expression. For example, to write "three-hundred twenty five", the expert subject constructs a representation of the type: ((C100*C3) + (C10* C2) + C5), representing the primitive number concepts (C100, C3, C10, C2, and C5) and the relations of product (*) and sum (+). In the second state, production corresponds to the activation of chains and chain operators from the semantic representation; the number concepts activate the digits or chains of digits, e.g., the C5, C2, and C3 concepts activate the "5", "2", and "3" digits and the C10 and C100 concepts activate the "0" and "00" chains respectively, the relation of product activates the concatenation operator " & " and the sum the overwriting operator "#"; thus, the concatenation generates the X (3&00) and Y (2&0) chains, and the overwriting operator overwrites the digit "5" in the Y chain (20#5) and then the resulting "25" chain is overwritten in the final zeros of X (300#25), generating the "325" chain. According to the model, intermediate representation is constructed from the segmentation made by the subject of the lexical-syntactic structure of the verbal expression; this permits stating that when the lexical-syntactic structures are different, then different representation types should be presented and, hence, different forms of constructing the numeral.
Previous transcoding studies (Granà, Lochy, Girelli, Seron & Semenza, 2003; Lochy, Pillon, Zesiger & Seron, 2002; Seron & Fayol, 1994) have specifically introduced evidence that supports Power and Dal Martello's model, especially regarding to McCloskey's adult transcoding model. Generally, the studies found that the lexical-syntactic structure of verbal expression affects second grade Belgium and Wallonia children's writing; specifically the syntactic structure determines different levels of success (Seron & Fayol, 1994). Lochy et al. (2002) found that the syntactic structures associated with the absence of expression of amount in different positions, which is transcribed as "0", affects the correct writing in adult with brain damage. Granà et al. (2003) found that with university students the writing times of Arabic numerals seem to depend on the syntactic structure of the numeral dictated.
Seron and Fayol (1994) found that in the three-digit numerals, the level of success depends on the syntactic structure of the numeral, with the highest levels of success in the Unit-Hundred numerals (UH, e.g., five-hundred), followed by the Hundred-Unit (HU, e.g., one-hundred five5), and the Hundred-Teens (HT, e.g., one-hundred thirteen) and with the lowest levels in the Hundred-Decade (HD, e.g., one-hundred forty). Although no significant differences were found, Seron and Fayol suggest that the greatest difficulty in writing corresponds to numerals represented as product, and which need the overwriting operator (i.e., HU, HT and HD).
Lochy et al. (2002) found that the syntactic structure of the verbal numerals affected the writing times between digits (Inter Digit Jump). The results showed that when writing "1200", the time in the first IDJ (i.e., between the first and second digits) is longer when the verbal expression was of the type "one-thousand two-hundred" (UMUH) than when it was dictated as "twelve hundred" (ThH). Following Power and Dal Martello's model, these authors propose that the first expression would generate the semantic representation <C1*C1000> + <C2*C100> and the union of digits 1 and 2 corresponded to an overwriting (1000 # 200). In the second type of expression the intermediate representation would be <(C10*C2)*C100> and digits 1 and 2 would be joined by the concatenation operation (1&2&00). In seconds, the IDJ time differences were found among zero-ending numerals (ThH and UMUH) and numerals without zero (UMUHDU); the greatest times were presented in the second type. The authors suppose that this is due to the use of the overwriting operator for the digits corresponding to the DU expressions present in the UMUHDU numerals and absent in the ThH and UMUH numerals.
Granà et al. (2003) found that the structure of the verbal expression affects the writing of Arabic numerals, particularly the production of zeros corresponding to the lack of an amount in the dictated numeral. In intermediate numerals with zeros like "three-thousand one" (UMU, 3001) there was a tendency for more errors than in numerals with final zeros like "four-thousand three-hundred twenty" (UMUH, 4320). For these authors, the zeros from the first type correspond to syntactic zeros that are constructed by overwriting "#": in the case of "3001" by the overwrite of the "1" digit in the "3000" chain; in the second case or lexical zeros, production depends on direct recovery of long-term memory (LTM), of the "20" chain corresponding to "twenty". Granà et al. (2003) assume that verbal expressions of the TENS class (twenty, thirty, forty [...] ninety) will generate primitive number concepts in the subjects that derive from the direct recovery of the corresponding chains (20, 30, 40... 90).
Barrouillet's model (Barrouillet et al., 2004) is presented in two versions: the basic (ADAPTBASIC) and advanced (ADAPTADV) models. The basic model describes the transcoding process up to numeral 99, while the advance model describes the transcoding process up to six-digit numerals. For the ADAPTADV model the verbal numerical expression is coded in a phonological representation analyzed with a PARSER, which segments the representation into units corresponding to primitive lexicals (units, teens, and tens) and separators like "hundred" and "thousand", the primitive lexicals activate digital representations associated in LTM, and together with the separators are maintained in the Working Memory (WM); the production system reads the contents of the WM and control-action procedures generate the numerical chain to be produced (Barrouillet et al., 2004; Camos, 2008). For example, when transcoding "two-hundred four", the first step corresponds to codifying in the phonological code segmented by the Parser, and which produces the segments "two", "hundred", and "four". The primitive lexicals "two" and "four" activate the graphemic representations associated in LTM ("2" and "4"). The production system reads the primitive lexical "two" and a procedure is activated (P1), which recovers the digital representation "2" and starts the construction of the chain, it then reads the "hundred" unit, and given that there is no representation associated, it activates a P2 procedure that adds two slots to the chain stored in WM, generating the chain "2_ _", the following unit "four" activates a procedure (P1) that recovers the representation "4" and inserts it at the end of the chain "2 _ 4"; finally, without further information to be read, a P4 procedure fills the empty spaces with zeros, generating the "204" chain, then the chain constructed is "stored in a buffer prior to its subsequent transcription by graphomotor procedures" (pp. 370-371).
The main purpose of this study is evaluate the adjustment of the Inter Digit Jump (IDJ) times in writing three-digit Arabic numerals using Power and Dal Martello (1990) and Barrouliet et al. (2004) models for children trasncodification from spoken verbal to Arabic numerals. For this reason, we analyzed IDJ duration in four types of three-digit numerals: Unit-Hundred (UH), Unit-Hundred Unit (UHU), Unit-Hundred Decade (UHD), and Unit- Hundred Decade-Unit (UHDU).
According to Power and Dar Martello's model, we hypothesize that the longest duration must be presented in the use of the overwriting operation: in the first IDJ, the longest duration is expected in the UHD and UHDU numerals, whose second digit is constructed by overwriting (U00#D0 and U00# DU); for the second IDJ, the longest duration is expected in the UHU numerals whose third digit is constructed by overwriting (U00 # U) than in the remaining numerals. When comparing the duration between the first and the second IDJ for each numeral, the first IDJ is expected to be higher in the UH, UHD, and UHDU numerals, and the second IDJ is expected higher in the UHU numerals.
For Barrouliet et al's. model (2004), we hypothesize that the duration of the IDJs reflect the motor program more than the numeral's construction operations, bearing in mind that for the model the chain is first constructed and then stored in a buffer to be produced later. It is expected that in all numerals the duration of the first IDJ is greater than the second IDJ. An additional aspect is the type of digit to be written, keeping in mind that the program to write the "0" digit is much easier than for the rest of the digits (Lochy et al., 2002), it is expected that when comparing among the numerals, the first IDJ appears in the shortest time in UH numerals (written with two zeros) followed by UHD and UHU numerals (written with one zero), and the longest duration in UHDU numerals (written without a zero); for the second IDJ, it is expected that the longest duration appears in UHDU and UHU numerals, whose third digit is different from zero.
Method
Participants
An experimental design was used to study a group of 65 children attending the first grade in a private school. The children lived in a socio-economic middle-class neighborhood located in Cali, Colombia. Their mean age, including both males and females, was six years seven months with a 3-month standard deviation. Twenty-five children (mean age = 6.5; SD = 5 months), who wrote correctly over 90% of the numerals in the four sessions, were selected for this study.
The children were assigned a task and interviewed individually. Each child participated in four sessions at two-week intervals. This study was approved by the Ethics Committee of the University where the first author belongs, following the guidelines of the Code of Ethics of Helsinki. This was a non-invasive study and was carried out with the consent and cooperation from both the school leadership and parents', and the participation was entirely voluntary.
Instruments
In each session, a battery of 27 numerals of three-digits was dictated to be written in Arabic format. The numerals dictated were chosen from a higher order than those traditionally taught to first graders (i.e., numerals between 10 and 99). The numerals were classified according to Seron & Fayol (1994) categories as: 5 UHDU numerals (XXX), like "doscientos cuarenta y seis6; 4 UHD numerals (XX0), like "doscientos cuarenta"; 9 of the type UHU (X0X), like "doscientos seis"; and 9 UH numerals (X00), like "two hundred".
Procedure
To apply the task of numeral dictation, three researchers were trained to modulate their voices and reach the maximum homogeneity in the dictation. The average duration of the sessions was 20 minutes; at the beginning of each session, the children were familiarized with the task. For the dictation, four random sequences were constructed with the 27 numerals and each sequence was randomly assigned to each child in each of the four application sessions. The written production was captured by using a USB Pen Table (WACOM-Intuos 2 PLATINUN, accuracy: +/- 0.25 mm) and monitored by a Mac SpellWrite 2.6b software (Cottrell, 1999).
Data Analysis
The correctly written three-digit productions were selected for analysis. During each production, duration time was taken for each IDJ; the first IDJ was considered as the time in milliseconds between lifting the pencil upon ending digit 1 and supporting it to start writing digit 2; for the second IDJ, time was analyzed between digits 2 and 3. For each distribution, the contrast Kolmogorov-Smirnov test with normal distribution was performed, finding that the times behaved normally at significant level alpha = 0.05.
Results
Between sessions and types of numeral analysis of inter digit jump duration
The duration was analyzed independently for each position of the IDJ (first or second) with four types of numerals (UH, UHU, UHD, and UHDU) x 4 sessions (1st, 2nd, 3rd, and 4th) Anova with repeated measurements in the two factors.
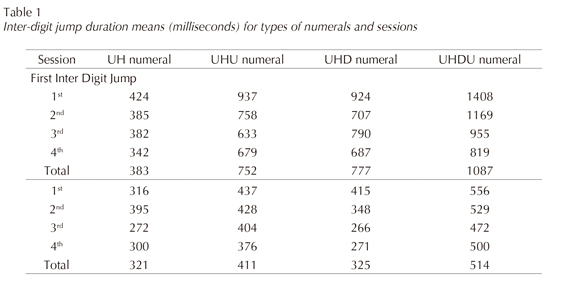
At the first IDJ, located between the first and the second digit (X_XX), the ANOVA revealed the following effects: type F(3, 72) = 55.293, p < 0.001; session F(3, 72) = 9.452, p < 0.001; and interaction type x session F(9, 72) = 2.288, p = 0.018. Post hoc Tuckey's HSD showed that duration contrast was statistically significant between UH and UHU numerals (p < 0.001), UH and UHD numerals (p < 0.001), UH and UHDU numerals (p < 0.001), UHDU and UH numerals (p < 0.001), and UHDU and UHD numerals (p < 0.001). As can be seen from Table 1, in the first IDJ duration a UH numeral (383 ms) was shorter than the duration for UHU (752 ms) and UHD numerals (777 ms), which were shorter than for UHDU numerals (1087 ms). At the significant level alpha = 0.05, Post hoc Tuckey's HSD showed that the first session was different from the 2nd, 3rd, and 4th sessions, and the 4th session differed from the 2 nd session.
At the second IDJ, located between the second and the third digit (XX_X), the ANOVA revealed the following effects: type F(3, 72) = 14.151, p < 0.001; session F(3, 72) = 2.833, p = 0.044; no interaction between type x sessions was found. Post hoc Tuckey's HSD showed statistically significant between UHDU and UH numerals (p < 0.001), UHDU and UHU numerals (p = 0.001), UHDU and UHD numerals (p < 0.001), UHU and UH numerals (p = 0.004), and UHU and UHD numerals (p = 0.019). As noted in Table 1, the duration for a UHDU numeral (514 ms) was higher than that for a UHU numeral (411 ms), which were higher than UHD (325 ms) and UH numerals (321 ms). Post hoc Tuckey's HSD showed that the 3rd session was significantly different from the 1st and 2nd sessions (p < 0.05).
Fourth session analysis of inter digit jump duration
To analyze the four types of numerals and the differences between the first and second IDJ duration, the 4th session was selected, because that presented a shorter IDJ duration. For the first IDJ, the duration was analyzed with four types of numerals (UH, UHU, UHD, and UHDU); one-way ANOVA revealed the effect of type of numeral F(3, 72) = 19.215, p < 0.001. The post hoc Tuckey's HSD showed significant differences between UH and UHU numerals (p < 0.001), UH and UHD numerals (p < 0.001), and UH and UHDU numerals (p < 0.001). In UH numerals (342 ms), the duration was shorter than in UHU (679 ms), UHD (687 ms), and UHDU numerals (819 ms).
For the second IDJ duration, one-way ANOVA revealed the effects of the type of numeral F(3, 72) = 10.362, p < 0.001. The post hoc Tuckey HSD showed statistically significant between UHDU and UH numerals (p = 0.001), UHDU and UHU numerals (p = 0.006), UHDU and UHD numerals (p < 0.001), and UHU and UHD numerals (p = 0.005). In UHDU numerals (500 ms) the duration was longer than in UHU (376 ms), UH (300 ms), and UHD numerals (271 ms).
To evaluate the differences between the IDJ in each type of numeral, the duration was compared by using a t test for dependent samples. The results showed significant differences between the first and the second IDJ duration in UHU (t (24) = 5.604; p < 0.001), UHD (t (24) = 6.543; p < 0.001), and UHDU numerals (t (24) = 4.233; p < 0.001).
Discussion
In general, the results are consistent with the idea that the three-digit chain is generated and stored in a buffer to be produced, as suggested by Barrouliet et al's model. The results show that in the first IDJ, the duration is longer in UHDU numerals (X_XX), which involve a writing program of two digits different from zero and different amongst themselves, the second duration occurs in numerals with one zero digit, the UHD numerals (X_X0) and UHU numerals (X_0X) and, finally, the shortest time occurs in UH numerals (X_00) with two zero digits. In the second IDJ, the duration tends to be higher in the UHDU (XX_X) and UHU numerals (X0_X) than in the UH (X0_0) and UHD numerals (XX_0); a longer time is present in numerals whose third digit is different from zero. These results suggest that the duration in IDJ does not directly reflect the rules or representations generated by the syntactic structure of the numerals dictated, which seems to reflect aspects of the motor program in writing Arabic numerals, such as the ease of writing the zero digit (Lochy et al., 2002).
The results of the fourth session show the same tendency of the general analysis; in the first IDJ, the duration was shorter before writing two zero digits (UH); in the second IDJ, the duration was longer before writing the third digit in the UHDU numerals (XX_X). These results show that the duration tends to be longer before writing quantity digits; the first IDJ presents the shortest time in numerals with double zero (X_00), while in the second IDJ the longest time occurs in numerals with double digit of quantity (XX_X). The contrast between the first and second IDJ shows that in the UHU, UHD, and UHDU numerals the first pause is significantly longer than the second; in UH numerals the same tendency is noted, but no differences are found. Similar to the prior results, this behavior best fits that expected by Barrouiliet et al's model, which shows that times do not adjust to the presence of the overwriting operation.
Lochy et al. (2002) have suggested that in four-digit numerals the presence of longer durations in IDJs is due to the type of syntactic structure dictated. The authors found that when dictating conventional expressions like "one-thousand two-hundred" and non-conventional expressions like "twelve-hundred", whose Arabic production is the same "1200", the first IDJ was longer in the conventional expressions than in the non-conventional expressions; this is due to the use of overwriting. In conventional expressions, the second digit was constructed by the overwriting operation (1000#200), while in non-conventional expressions the second digit is generated by concatenation (1&2&00), influencing in a longer time for conventional expressions, i.e., the duration of the IDJ had as a cause the type of chain operator used. An alternate interpretation comes from the model by Barrouliet et al. (2004); when the authors propose their transcoding algorithm, they keep in mind the limited resources of WM and state that for transcoding effects it is possible that subjects carry out partial transcriptions "the application of certain rules may permit direct transcription before the complete chain of digits has been formed" (Barrouliet et al., 2004, p. 375), for the "twelve-hundred" case, the presence of the "hundred" separator and the high frequency of the expression "twelve" could generate the direct production of the "12" chain, which could explain the shorter time in writing the digit "2" in these types of numerals.
A behavior that could indicate what occurs when writing three-digit numerals, is that of the time intervals in writing between letters (InterLetter Intervals - ILI); prior studies have shown that the longer durations tend to occur in the limits of the orthographic syllables (Kandel, Hérault, Grosjacques, Lambert & Fayol, 2009; Soler & Kandel, 2010). Soler and Kandel (2010) found that, in disyllabic words, the duration of ILIs diminished in the letters belonging to the second syllable. The authors suggest that in the first syllable, the longest times occur because of the simultaneous processing of the letters to be produced in the initial syllable and the letters corresponding to the final syllable (Soler & Kandel, 2010). This phenomenon may be equivalent to what occurs in UHDU, UHD, and UHU numerals, where the first IDJ is longer than the second. The results could suggest that the longer time in the first interval reflects the segmentation made by the processing system guided by the "hundred" separator, and that parallel to writing the second digit, the production system prepares the writing of the third digit.
The conclusions of this study are limited to three- digits numerals, and could not extend to another numerals. For the purpose of progressing with understanding of transcoding process, there is clearly a need for more systematic experimental studies that highlight the transcoding in higher order numerals.
Acknowledgments
This research was funded by Colciencias under grant 110645221365. The authors thank Oscar Ordoñez for his acute reading and recommendations for the drafting of this article.
Pie de página
5The expression "one-hundred" corresponds to the French numeral "Cent", the remaining UH numerals UH start with the expressions from the ONES lexical class (deux, trois, quatre, cinq, six, sept, huit, and neuf) and are accompanied by a Multiplier Word (Cent).
6In Spanish two different expressions are used for hundred: "cien", that corresponds to the English expression "one hundred" and "cientos" that corresponds to hundred as either a multiplier word (McCloskey, 1992), or a "product relation" (Seron & Fayol, 1994, p. 283), or a "separator" (Barrouillet et al., 2004, p. 379). Another difference is that in Spanish only one word is used to designate the hundred numerals: "doscientos". From a morphological point of view, "dos" (two) is a prefix, and "cientos", a suffix; in English and other languages, two words are used, i.e., two hundred, three hundred, etc.
References
Barrouillet, P., Camos, V., Perruchet, P. & Seron, X. (2004). ADAPT: A Developmental, Nonsemantic, and Procedural Model for Transcoding from Verbal to Arabic numerals. Psychological Review, III(2), 368-394. doi: 10.1037/0033-295X.11 1.2.368. [ Links ]
Camos, V. (2008). Low Working Memory Capacity Impedes Both Efficiency and Learning of Number Transcoding in Children. Journal of Experimental Child Psychology, 99, 37-57. doi: 10.1016/j.jecp.2007.06.006. [ Links ]
Cottrell, D. (1999). SpellWrite Version 1.6 [Computer software and manual] [ Links ].
Dehaene, S. (1992). Varieties of Numerical Abilities. Cognition, 44, 1-42. doi: 10.1016/0010-0277(92)90049-N. [ Links ]
Granà, A., Lochy, A., Girelli, L., Seron, X., & Semenza, C. (2003). Transcoding Zeros Within Complex Numerals. Neuropsychologia, 41, 1611-1618. doi: 10.1016/S0028-3932(03)00109-X. [ Links ]
Kandel, S., Hérault, L., Grosjacques, G., Lambert, E., & Fayol, M. (2009). Orthographic vs. Phonologic Syllables in Handwriting Production. Cognition, 110, 440-444. doi: 10.1016/j.cognition.2008.12.001. [ Links ]
Lochy, A., Pillon, A., Zesiger, P., & Seron, X. (2002). Verbal Structure of Numerals and Digits Handwriting: New Evidence from Kinematics. The Quarterly Journal of Experimental Psychology, 55A(1), 263-288. doi: 10.1080/02724980143000271. [ Links ]
McCloskey, M. (1992). Cognitive Mechanisms in Numerical Processing: Evidence from Acquired Dyscalculia. Cognition, 44, 107-157. doi: 10.1016/0010-0277(92)90052-J. [ Links ]
McCloskey, M., & Caramazza, A. (1987). Cognitive Mechanisms in Normal and Impaired Number processing. In G. Deloche & X. Seron (Eds.), Mathematical Disabilities: A cognitive neuropsychological perspective. Hillsdale, NJ: Erlbaum. [ Links ]
McCloskey, M., & Macaruso, P. (1995). Representing and Using Numerical Information. American Psychologist, 50, 331-363. doi: 10.1037/0003-066X.50.5.351. [ Links ]
McCloskey, M., Caramazza, A., & Basili, A. (1985). Cognitive Mechanism in Number Processing and Calculation: Evidence from dyscalculia. Brain and Cognition, 4, 171-196. doi: 0.1016/0278-2626(85)90069-7. [ Links ]
Power, R. J. D., & Dal Martello, M. F. (1990). The dictation of Italian Numerals. Language and Cognitive Processes, 5, 237-254. doi: 10.1080/01690969008402106. [ Links ]
Seron, X., & Nöel, M. P. (1995). Transcoding Numbers from the Arabic Code to The Verbal One or vice versa: How many routes? Mathematical Cognition, 1, 215-243. [ Links ]
Seron, X., & Fayol, M. (1994). Number Transcoding in Children: A Functional Analysis. British Journal of Developmental Psychology, 12, 281-300. doi: 10.1111/j.2044-835X.1994.tb00635.x [ Links ]
Soler, O., & Kandel, S. (2010). A Longitudinal Study of Handwriting Skills in Pre-scholars: The Acquisition Of Syllable Oriented programming strategies. Reading & Writing: An Interdisciplinary Journal (Advance online publication). doi: 10.1007/s11 145-010-9251-1 [ Links ]













