Pruebas de bondad de ajuste en distribuciones simétricas, ¿qué estadístico utilizar?^*

Goodness of Fit Tests for Symmetric Distributions, which Statistical Should I Use?

Ignacio Pedrosa^**
Joel Juarros-Basterretxea^***
Adán Robles-Fernández^****
Julia Basteiro^*****
Eduardo García-Cueto^******
Universidad de Oviedo, España

^*Artículo de investigación
^**Facultad de Psicología. Correo electrónico: npedrosa@cop.es
^***Facultad de Psicología. Correo electrónico: juarrosbasterretxea.j@gmail.com
^****Facultad de Psicología. Correo electrónico: roblesfernandez.a@gmail.com
^*****Facultad de Psicología. Correo electrónico: jlbasteiro@gmail.com
^******Facultad de Psicología. Correo electrónico: cueto@uniovi.es

Recibido: marzo 24 de 2014 | Revisado: octubre 18 de 2014 | Aceptado: octubre 18 de 2014

Para citar este artículo

Pedrosa, I., Juarros-Basterretxea, J., Robles-Fernández, A., Basteiro, J., & García-Cueto, E. (2015). Pruebas de bondad de ajuste en distribuciones simétricas, ¿qué estadístico utilizar? Universitas Psychologica, 14(1), 245-254. http://dx.doi.org/10.11144/Javeriana.upsy13-5.pbad

Resumen

El uso de pruebas no paramétricas resulta recomendable cuando los datos a analizar no cumplen los supuestos de normalidad y homocedasticidad. Sin embargo, la suposición de la normalidad de los datos o el empleo de pruebas de bondad de ajuste que no son adecuadas para el tamaño muestral empleado son aspectos habituales. Este hecho implica, en muchas ocasiones, el uso de pruebas estadísticas no ajustadas al tipo de distribución real y, consecuentemente, el establecimiento de conclusiones erróneas. Por ello, en el presente estudio se ha analizado el poder de detección de cinco pruebas de bondad de ajuste (Kolmogorov-Smirnov, Kolmogorov-Smirnov-Lilliefors, Shapiro-Wilk, Anderson-Darling y Jarque-Bera) en distribuciones simétricas con seis tamaños muestrales entre 30 y 1000 participantes generados mediante una simulación Monte Carlo. Los resultados muestran una tendencia conservadora generalizada a medida que se incrementa el tamaño muestral. En cuanto a los tamaños muestrales, las pruebas con un mejor poder de detección de la no normalidad son Kolmogorov-Smirnov-Lilliefors y Anderson-Darling para muestra pequeñas, la prueba de Kolmogorov-Smirnov si se emplean tamaños muestrales medios (200 participantes) y la prueba de Shapiro-Wilk cuando se analizan muestras superiores a 500 participantes. Además, la prueba clásica de Kolmogorov-Smirnov se considera absolutamente ineficaz independientemente del tamaño muestral.

Palabras clave: bondad de ajuste; distribución normal simétrica; tamaño muestral; simulación Monte Carlo; Kolmogorov-Smirnov

Abstract

The use of nonparametric tests is recommended when the data do not meet the assumptions of normality and homoscedasticity. However, the assumptions of normality of the data or the use of goodness of fit tests that are not appropriate for the assessed sample are common aspects. In many cases, this implies the use of statistical tests unadjusted for the real data distribution and, consequently, the establishment of inaccurate conclusions. Therefore, in this paper the detection power of five tests of goodness of fit (Kolmogorov-Smirnov-Lilliefors, Kolmogorov-Smirnov, Shapiro-Wilk, Anderson-Darling and Jarque -Bera) in symmetric distributions is analysed in six sample sizes between 30 and 1000 participants generated by Monte Carlo simulation. Results show a marked conservative tendency as the sample size becomes larger. Regarding sample sizes to detect non-normality: analysing small samples the best results are provided by Kolmogorov-Smirnov-Lilliefors and Anderson-Darling tests, if the sample is medium-sized (200 participants) the Kolmogorov-Smirnov, and when samples are over 500 participants the Shapiro-Wilk test is recommended. In addition, the classic test of Kolmogorov-Smirnov is considered absolutely ineffective regardless the sample size.

Keywords: goodness of fit; symmetric normal distribution; sample size; Monte Carlo simulation; Kolmogorov-Smirnov test

Dentro del ámbito de investigación aplicado de las ciencias de la salud y de la psicología en particular, la inmensa mayoría de las investigaciones llevadas a cabo en el campo aplicado suelen utilizar pruebas estadísticas paramétricas. Todas ellas (coeficiente de correlación de Pearson, ANOVA, ANCOVA, prueba de t, estadístico Z, análisis factorial, etc.) presuponen la normalidad —univariada o multivariada— de las distribuciones de las puntuaciones en la población. La violación del supuesto de normalidad hace que las interpretaciones de los resultados no sean las que, a priori, se podrían deducir del uso de las pruebas en sí mismas.

Aun siendo cierto que diferentes estudios señalan que muchas de estas pruebas paramétricas han demostrado ser robustas cuando se violan tanto el supuesto de normalidad como el de homocesdasti-cidad (Finch, 2005; Lemeshko & Lemeshko, 2008), desde hace más de 50 años los diferentes expertos en metodología recomiendan el uso de pruebas no paramétricas cuando los datos sobre los que se trabaja no cumplen dichos supuestos (Zimmerman, 1998).

Sin embargo, la realidad es que cuando se lleva a cabo la investigación aplicada, la mayor parte de investigadores emplean pruebas paramétricas, suponiendo habitualmente la normalidad de los datos y sin ningún tipo de comprobación sobre este supuesto (Erceg-Hurn & Mirosevich, 2008; Romáo, Delgado, & Costa, 2010). De hecho a la hora de trabajar con datos empíricos, resulta habitual que estos violen el supuesto de normalidad (Choi, 2005; Strasak, Zaman, Marinell, Pfeiffer, & Ulmer, 2007). Así, ya Micceri (1989) demostró cómo a pesar de asumir este supuesto, tras examinar 440 conjuntos de datos, ninguno de ellos se ajustaba realmente a una distribución normal.

Esta es una cuestión que debería estar presente a la hora de iniciar cualquier estudio, ya que las pruebas estadísticas citadas anteriormente son de uso frecuente en todo tipo de campos sustantivos de la psicología a la hora de llevar a cabo la adaptación de instrumentos de medida (e. g. Pedrosa, García-Cueto, Suárez-Álvarez, & Pérez Sánchez, 2012), el estudio del efecto de unas condiciones experimentales sobre una conducta específica (e. g. Tavares Tadaiesky & Zagury Tourinho, 2012), el análisis de la relación entre diversas variables (e. g. Suárez-Álvarez, Campillo-Álvarez, Fonseca-Pedrero, García-Cueto, & Muñiz, 2013), etc.

En este sentido, como se ha dicho, esta comprobación se entiende como un paso previo al tratamiento de los datos que en la mayoría de ocasiones, no llega a realizarse, ya sea bien al presuponer una robustez a las pruebas que se utilizan, que no siempre poseen, o bien por desconocimiento o desidia del propio investigador. Por el contrario, en aquellas situaciones en donde se comprueba la normalidad de la distribución, es común el empleo de pruebas de bondad de ajuste de uso generalizado que se encuentran accesibles en los paquetes estadísticos de tratamiento de datos más populares.

En alusión a dicho software, cabe destacar el paquete estadístico SPSS como uno de los más utilizados dentro del área de las ciencias de la salud de manera global y de la psicología en particular. Aunque mediante este programa, el estudio de la normalidad puede realizarse aplicando tres pruebas estadísticas: Kolmogorov-Smirnov (K-S), la prueba de K-S tras aplicar la corrección de Lilliefors (K-S-L) y Shapiro-Wilk (S-W), resulta también frecuente que la primera de ellas sea la más utilizada sin que el investigador conozca, en numerosas ocasiones, las otras pruebas alternativas que el software ofrece y que, como se muestran más adelante, presentan un poder de detección más elevado que la prueba de K-S.

Así pues, la comprobación del supuesto de normalidad presenta una importancia destacada, ya que como indican Steinskog, Tj0stheim y Kvam-st0 (2007), muchos procedimientos estadísticos requieren, o funcionan mejor, cuando el supuesto de normalidad se cumple, lo que influye directamente sobre las inferencias y estimaciones de los resultados obtenidos.

De este modo por ejemplo, el trabajo de Schucany y Ng (2006) muestra cómo la selección de las pruebas estadísticas adecuadas y ajustadas al tipo de distribución real con que se trabaja, provoca una reducción del error tipo I. Por tanto, la comprobación del supuesto de normalidad y la posterior elección de las pruebas estadísticas que se deben emplear implicarían a nivel práctico, consecuencias destacables si se piensa por ejemplo, en la aplicación de un tratamiento médico o psicológico.

Asumiendo entonces la relevancia del estudio de la normalidad en la investigación teórica y empírica, los trabajos en torno a las pruebas de bondad de ajuste han sido numerosos, desarrollándose más de 40 estadísticos diferentes (Henderson, 2006; Yazici & Yolacan, 2007).

En esta línea, se han llevado a cabo multitud de investigaciones en las que se analiza la eficacia de las diferentes pruebas de normalidad en base a una amplia gama de características como por ejemplo, el tipo de distribución, el tamaño muestral o la variación de los parámetros muestrales, entre otras (e. g., Frey, 2009; García-Cueto, Gallo & Miranda, 1998; Meintanis & Hlávka, 2010; Shin, Jung, Jeong, & Heo, 2012; Zghoul, 2010). Estos trabajos han demostrado cómo el poder para detectar desviaciones de la normalidad de las diferentes pruebas puede ser significativamente diferente dependiendo de la naturaleza de la no normalidad sobre la que se trabaje (Romáo, et al., 2010).

Dentro de esta variedad de pruebas existentes, la prueba de K-S es una de las más clásicas en el estudio de la normalidad y en esencia, se basa en el concepto de la función de distribución empírica y sus propiedades como aproximación de la función de distribución teórica cuando se trabaja sobre variables continuas y se conocen todos los parámetros muestrales. Así, esta prueba compara la función de distribución teórica con la empírica y calcula un valor de discrepancia máxima entre ambas distribuciones, proporcionando un valor p, asociado a la probabilidad de obtener una distribución que discrepe tanto como la observada si verdaderamente se hubiera obtenido una muestra aleatoria, de tamaño n, de una distribución normal (Chakravarti, Laha, & Roy, 1967).

Sin embargo, esta prueba cuenta con ciertas limitaciones que restringen su aplicación, entre las que destacan el hecho de que si los parámetros de posición, escala y forma de la distribución se calculan a partir de los datos, la región crítica de la prueba no es válida, por lo que estos deben determinarse mediante simulación. Además la prueba muestra una mayor sensibilidad en el centro de la distribución que en las colas (Thadewald & Buning, 2007). Por otra parte, a estas dos limitaciones hay que añadir su tendencia conservadora, provocando que la hipótesis nula se acepte en un número excesivamente elevado de ocasiones (Shahabuddin, Ibrahim, & Jemain, 2009; Steinskog, et al., 2007).

Con la intención de mejorar la prueba de K-S, Lilliefors (1967) propuso una modificación de la misma (K-S-L) sustentada sobre los mismos principios estadísticos, pero específica para aquellos casos en donde la media y la varianza son desconocidas. De este modo, se evita el efecto que provoca, como ocurre en el caso de K-S, la estimación de los parámetros de la muestra (Steinskog, et al., 2007) y se recomienda por tanto, como el estadístico más apropiado para dichos casos (Oztuna, Elhan, & Tuccar, 2006).

En último lugar, la prueba de Shapiro-Wilk (Shapiro & Wilk, 1965) es una de las más consolidadas y con mayor potencia estadística entre las existentes actualmente (Arcones & Wang, 2006). Su fundamento estadístico está basado en una gráfica de probabilidad en la que se considera la regresión de las observaciones sobre los valores esperados de la distribución hipotetizada, en donde su estadístico W representa el cociente de dos estimaciones de la varianza de una distribución normal.

Esta prueba ha demostrado de manera general, resultados adecuados en comparación a las pruebas clásicas (Arcones & Wang, 2006), pero especialmente cuando se trabaja con distribuciones de colas cortas (Thadewald & Buning, 2007) y con un tamaño muestral inferior a 30, ya que muestra una alta variabilidad cuando se modifican tanto la simetría como el tamaño muestral de la distribución, especialmente entre 20 y 50 participantes (Yazici & Yolacan, 2007).

Por otro lado, diferentes investigaciones han señalado la adecuada potencia estadística de otras dos pruebas de bondad de ajuste que, si bien no están implementadas en muchos de los programas estadísticos más populares, sí resulta fácil obtener el software para su aplicación a través de la web, como son las pruebas de Jarque-Bera (J-B) y AndersonDarling (A-D).

La prueba de J-B se formula bajo la hipótesis nula de normalidad de los residuos, siguiendo una distribución %² con dos grados de libertad, al derivar esta de la suma de cuadrados de dos normales estandarizadas asintóticamente independientes (Jarque & Bera, 1987). Esta prueba ha demostrado una alta consistencia general, pero especialmente cuando se trabaja con muestras grandes y distribuciones simétricas y de colas largas (Thadewald & Buning, 2007; Yazici & Yolacan, 2007).

Ligada a esta prueba, se ha desarrollado una corrección de la misma (Urzúa, 1996), sin embargo, se ha demostrado que esta no mejora de manera significativa la potencia estadística de la prueba clásica de Jarque-Bera (Thadewald & Buning, 2007).

Finalmente, la prueba de Anderson-Darling supone una modificación del test de Cramervon Mises, que se basa en la diferencia de cuadrados entre las distribuciones pero, en su caso, otorga una mayor relevancia a los datos existentes en las colas de la distribución (Farrel & Rogers-Stewart, 2006). Así, diferentes autores han señalado esta prueba como la más potente estadísticamente (Arshad, Rasool & Ahmad, 2003; Shahabuddin, et al., 2009) cuando se alude a pruebas basadas en las funciones de distribución empíricas (EDF; Dufour, Farhat, Gardiol, & Khalaf, 1998), destacando respecto a las demás, como ocurría con J-B, cuando se trabaja con distribuciones simétricas y cuando la muestra tiende a aumentar (Yazici & Yolacan, 2007).

A pesar de que, como se ha comentado, existen diversas características que afectan al poder de detección de estas pruebas, en el presente estudio únicamente se ha valorado la variación del tamaño muestral por ser precisamente la variable a la que el investigador otorga mayor relevancia en los estudios aplicados en psicología en los que, generalmente, las variables siguen distribuciones normales y donde, por regla general, el investigador no llega a analizar el resto de variables que definen a la propia distribución.

Así pues, el objetivo del presente trabajo es comprobar la precisión de las pruebas estadísticas para la comprobación de la normalidad de los datos más utilizados en el campo de la psicología cuando, bajo unos parámetros de distribución estándar, se modifica el tamaño muestral de las distribuciones. Con ello se pretende determinar qué pruebas estadísticas resultan más adecuadas para cada caso particular. En este sentido, se analiza en qué medida las diferentes pruebas cumplen el error tipo I, de modo que si se trabajase sobre distribuciones normales a un nivel de confianza del 95%, debería rechazarse la hipótesis nula exactamente en un 5% de los casos, pudiendo así establecer qué pruebas son más conservadoras y liberales en función del tamaño muestral.

El hecho de seleccionar únicamente este nivel de confianza se debe a que, en primer lugar, es el nivel más habitual a la hora de realizar investigación aplicada y por otro lado, a que elevar el nivel de confianza al 99% no se entiende como recomendable debido al riesgo de incrementar notablemente el error tipo II y aceptar todas las distribuciones como normales.

Además, se pretender comprobar la consistencia en la detección de la prueba K-S-L y S-W en función del programa estadístico empleado.

Para ello, se han empleado las cinco pruebas estadísticas previamente definidas en base a los criterios ya citados. Así, se considera relevante analizar la precisión de las pruebas de K-S, K-S-L y Shapiro-Wilk por formar parte del paquete estadístico con mayor difusión dentro del ámbito psicológico y por otro lado, las pruebas de Anderson-Darling y Jarque-Bera porque, siendo fáciles de obtener y aplicar estadísticamente, ambas han demostrado resultados muy positivos cuando se trabaja con distribuciones gaussianas (Thadewald & Buning, 2007; Yazici & Yolacan, 2007) como es el caso del presente trabajo.

Material y método

Material

Con el objetivo de analizar el comportamiento de las diferentes pruebas de bondad de ajuste seleccionadas en el presente estudio en función de los diferentes tamaños muestrales, se diseñó un experimento de simulación mediante el método Monte Carlo.

Se generaron un total de 1_,880,000 datos, divididos en 6000 muestras (1000 réplicas por cada tamaño muestral), los cuales variaron desde 30 sujetos -con el objetivo de comprobar el funcionamiento de las diferentes pruebas en grupos pequeños— hasta un tamaño muestral de 1000 participantes, pasando por 50, 100, 200 y 500.

El hecho de establecer en 1000 sujetos el tamaño muestral máximo se debe a que se ha demostrado que la distribución de la probabilidad asociada al estadístico de contraste es estable cuando se trabaja con una muestra superior a este número de participantes (Steinskog, et al., 2007).

Todas las muestras simuladas siguieron una distribución normal estandarizada (μ=0 y σ=1), variando exclusivamente en su tamaño.

Método

La generación de los datos se llevó a cabo bajo las condiciones de normalidad y los estadísticos descriptivos anteriormente expuestos. Para ello, se empleó el método de simulación Monte Carlo mediante el software Multivar (Aguinis, 1994).

Una vez simulados los datos, se aplicaron las cinco pruebas de normalidad anteriormente especificadas en cada uno de los seis tamaños muestrales generados con la finalidad de comprobar el porcentaje de veces que cada una de ellas rechazaba la hipótesis nula de normalidad de las distribuciones. Al analizar los datos a un nivel de confianza determinado, se ha tenido en cuenta el error máximo para el cálculo del intervalo confidencial.

Análisis de datos

Las diferentes pruebas estadísticas fueron ejecutadas mediante el paquete estadístico SPSS, el cual ofrece la posibilidad de aplicar las pruebas de Shapiro-Wilk, Kolmogorov-Smirnov y Kolmogorov-Smirnov una vez aplicada la corrección de Lilliefors.

Por otro lado, las pruebas de Anderson-Darling y Jarque-Bera se utilizaron mediante la macro XLStat habilitada para el programa Microsoft Excel.

De manera añadida, también mediante esta macro, se aplicaron las pruebas K-S-L y S-W con el objetivo de replicar los resultados con los obtenidos mediante el SPSS, cuya sintaxis informática es ciega para el usuario y los programas fuente inaccesibles.

Resultados

Tras generar las 6000 muestras mediante la simulación y aplicar las pruebas estadísticas previamente explicitadas, se calculó el porcentaje de veces que cada prueba rechazaba la hipótesis nula en cada tamaño muestral. Puesto que en el estudio se ha asumido un nivel de confianza de 95%, el poder de detección de las pruebas será más adecuado cuando el error tipo I se aproxime al 5%.

En la Tabla 1 se muestran, en primer lugar y en letra cursiva, el porcentaje de rechazos de la hipótesis nula en las pruebas estadísticas de Shapiro-Wilk, Anderson-Darling, Kolmogorov-Smirnov-Liliefors y Jarque-Bera mediante el software XLStat. A continuación, se pueden observar los resultados obtenidos mediante el programa estadístico SPSS empleando las pruebas de Kolmogorov-Smirnov-Liliefors, Kolmogorov-Smirnov y Shapiro-Wilk.

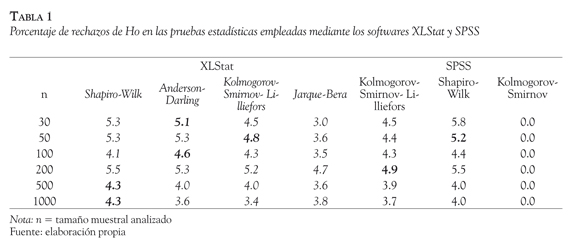
Además, se han señalado en negrita aquellos casos en los que, para cada tamaño muestral analizado, se ha alcanzado el mejor poder de detección de todas las pruebas utilizadas.

Como previamente se ha expuesto, al analizar los datos a un nivel de confianza determinado, se ha calculado el intervalo confidencial en torno a la proporción obtenida y se ha comprobado de este modo, si el porcentaje de rechazos del error tipo I por las diferentes pruebas de bondad de ajuste es el adecuado teniendo en cuenta el error máximo de estimación. En este caso, el E = 0.014 por lo que, debido a la mínima modificación que realmente produce sobre las proporciones de rechazo al nivel de las centésimas, se decidió prescindir del intervalo confidencial.

Si se observan los resultados de la prueba de K-S, se comprueba que el uso de este estadístico conlleva la aceptación de la hipótesis nula en todos los tamaños muestrales analizados. Inicialmente se detectó un funcionamiento anómalo de esta prueba, ya que la hipótesis de normalidad se aceptaba en todos los casos excepto en el tamaño muestral de 500 participantes, en donde se rechazaba en 1.9% de ocasiones. Debido a la importante diferencia respecto al resto de muestras analizadas y con el objetivo de comprobar si estos resultados se debían al efecto del artefacto con que se simularon las muestras, se decidió generar nuevamente la totalidad de muestras con un software diferente —empleando el propio XLStat— para posteriormente probar de nuevo el ajuste de la distribución a la normal. Los resultados, como se puede comprobar en la Tabla 1, muestran que la prueba K-S no permite rechazar la hipótesis nula en ningún caso, desapareciendo así la citada anomalía.

Discusión y conclusiones

Analizando cada una de las pruebas estadísticas empleadas se pueden obtener diferentes conclusiones que en algunos casos difieren respecto a los trabajos hasta ahora publicados.

En primer lugar se confirma una de las principales limitaciones de la prueba de K-S como es su tendencia excesivamente conservadora, al igual que se ha demostrado en trabajos precedentes, provocando que la hipótesis nula se acepte en la totalidad de las ocasiones (Shahabuddin, et al., 2009; Steinskog, et al., 2007).

Esta cuestión, como se apuntaba en la parte introductoria, supone un problema relevante ya que dentro del ámbito psicológico, esta es una de las pruebas más utilizadas tanto por ser una de las más clásicas como, fundamentalmente, por estar implementada en el programa estadístico SPSS. Esta cuestión conlleva, como ya se ha comentado, implicaciones directas en cuanto a las pruebas estadísticas empleadas para el tratamiento de los datos y las conclusiones de estas derivadas. Por ello, se puede concluir que a pesar de su amplio uso y su fácil accesibilidad, constituye la prueba estadística menos adecuada para comprobar la normalidad de las distribuciones en todos los casos.

La prueba de K-S-L surgió en su momento como una mejora respecto al estadístico K-S (Steinskog, et al., 2007). A pesar de seguir mostrando una tendencia conservadora, como ocurre en el caso de K-S, esta prueba sí permite rechazar la hipótesis nula en un porcentaje determinado de casos en función del tamaño muestral. De manera general, se observa como esta tendencia conservadora se incrementa a medida que aumenta el número de participantes, agudizándose esta en el caso de emplear el programa XLStat, excepto en muestras de tamaño superior a 500 participantes.

Si se alude a la prueba de S-W, los resultados corroboran el hecho de que su poder de detección es superior respecto a las pruebas clásicas citadas en los párrafos previos, aproximándose en mayor medida al 5% de casos rechazados esperado de manera general (Arcones & Wang, 2006).

Sin embargo, esta prueba muestra su mejor poder de detección en muestras de 50 participantes y no en muestras pequeñas como señalan algunos trabajos previos (Yazici & Yolacan, 2007) siendo de hecho, la más liberal a la hora de analizar tamaños muestrales reducidos (menores de 50) que, aunque no muestra los mejores resultados, sí cuenta con un poder de detección razonable. Por otra parte, contrariamente a lo esperado, es la prueba que presenta un mejor funcionamiento cuando la muestra tiende a incrementar su tamaño, destacando como el mejor estadístico cuando se analizan muestras a partir de 500 participantes.

En cuanto al estadístico de J-B, este solo muestra un alto poder de detección en tamaños muestrales en torno a 200 participantes, siendo excesivamente conservador en todos los casos restantes, incluso más que la prueba K-S-L. Además, los resultados no se ajustan a lo esperado en cuanto a que resultan contrarios a lo expuestos en trabajos precedentes, los cuales destacan como principal características su alta consistencia general, especialmente en muestras simétricas como es el presente caso (Tha-dewald & Buning, 2007; Yazici & Yolacan, 2007), sin destacar como la mejor prueba en ningún caso.

En último lugar, respecto a la prueba A-D, los resultados muestran cómo esta es la mejor prueba cuando se analizan distribuciones simétricas y de tamaño pequeño (n=30). Sumado a esto, los datos concuerdan con trabajos que han señalado esta prueba como la más potente a nivel estadístico (Arshad, et al., 2003; Shahabuddin, et al., 2009) ya que de manera general, tiende a presentar un mejor poder de detección en todos los casos, exceptuando únicamente aquellos en los que la muestra es excesivamente grande, en donde continúa la tendencia general de incrementar su carácter conservador.

Teniendo en cuenta ambos programas estadísticos, las pruebas que ofrece el software SPSS presentan, prácticamente en su totalidad, una tendencia más conservadora respecto a los resultados ofrecidos por la aplicación XLStat, tendiendo a aceptar así la hipótesis nula en un mayor número de ocasiones.

En primer lugar, teniendo en cuenta todos estos resultados de manera global, cabe destacar que todas las pruebas incrementan su tendencia conservadora a medida que aumenta el tamaño de la muestra, reduciéndose así el número de casos en que se rechaza la hipótesis nula.

De manera específica, se ha comprobado que las pruebas de J-B y K-S no muestran una capacidad de detección adecuada independientemente del tamaño muestral. En el caso de esta última, los resultados son especialmente preocupantes, puesto que se trata de una de las pruebas más empleadas a nivel general y el hecho de aceptar prácticamente en todos los casos, la hipótesis nula, acarrea directamente el uso inadecuado de pruebas estadísticas paramétricas teniendo que tener especial cuidado con las conclusiones derivadas del estudio.

En función del tamaño muestral analizado, las pruebas de K-S-L y A-D son las que muestran una mejor capacidad de detección en muestras pequeñas, aproximándose, en mayor medida al 5% esperado. En cuanto a tamaños muestrales medios (200 participantes) se considera la prueba de K-S-L como las más adecuada. Por último, cuando se analizan muestras de gran tamaño (superiores a 500 participantes), se considera la prueba de S-W como la mejor para poner a prueba la hipótesis nula y comprobar el ajuste de los datos a la distribución normal.

Además, globalmente, la prueba de S-W ha demostrado ser una de las más consistentes a la variación muestral, al contar con un poder de detección razonable y muy cercano al 5% esperado cuando se modifica el tamaño muestral.

Por otro lado, respecto al software empleado, a pesar de ser un programa de uso sencillo y generalizado, el SPSS ha demostrado una tendencia especialmente conservadora, en este caso respecto al XLStat, lo que conlleva, como ya se ha desarrollado, una aceptación de la hipótesis nula en un mayor número de casos provocando en muchos casos un uso indebido de pruebas estadísticas paramétricas. De hecho, si se analizan todos los tamaños muestrales dentro del programa SPSS, este solo presenta en dos ocasiones las pruebas estadísticas con un mejor poder de detección, en los casos de las pruebas S-W y K-S-L cuando se cuenta con 50 y 200 participantes, respectivamente.

Esta cuestión pone de relevancia el hecho de que los resultados deberían ser completamente independientes del programa estadístico empleado, puesto que se parte de un estadístico claramente definido y se emplean sobre él los mismos datos en ambos casos. Por tanto, esta discrepancia en los resultados obtenidos hace pensar que la aplicación del estadístico difiere en función del software, siendo imposible comprobar su cálculo por la falta de transparencia citada previamente en cuanto a la sintaxis empleada.

Como conclusión, se considera esencial la elección tanto del programa estadístico que se desea utilizar para el análisis estadístico como principalmente, de la prueba estadística que se debe utilizar en función del tamaño muestral con que se lleve a cabo la investigación. En el caso específico de la prueba de bondad de ajuste, se entiende como un problema el hecho de que uno de los paquetes estadísticos más generalizados aporte una prueba estadística que no presenta una consistencia mínimamente razonable.

De cara a futuros trabajos en esta línea de investigación, se entiende como importante el hecho de calcular, además de la capacidad de detección, la potencia estadística de cada una de las pruebas de bondad de ajuste, así como su comportamiento en función del tipo de distribución.

Referencias

Aguinis, H. (1994). A quickbasic program for generating correlated multivariate random normal scores. Educational and Psychological Measurement, 54(3), 687-689.         [ Links ]

Arcones, M. A., & Wang, Y. (2006). Some new tests for normality based on U-processes. Statistics and Probability Letters, 76, 69-82. http://dx.doi.org/10.1016/j.spl.2005.07.003        [ Links ]

Arshad, M., Rasool, M.T., & Ahmad, M.I. (2003). Anderson Darling and modified Anderson Darling tests for Generalized Pareto Distribution. Pakistan Journal of Applied Sciences, 3(2), 85-88.         [ Links ]

Chakravarti, I.M., Laha, R.G., & Roy, J. (1967). Kolmogorov-Smirnov (K-S) test. En Handbook of Methods of Applied Statistics, Volume I (pp. 392394). New York: Wiley.         [ Links ]

Dufour, J.M., Farhat, A., Gardiol, L., & Khalaf, L. (1998). Simulation-based finite sample normality tests in linear regressions. The Econometrics Journal, 1(1), 154-173.         [ Links ]

Erceg-Hurn, D. M., & Mirosevich, V. M. (2008). Modern robust statistical methods: an easy way to maximize the accuracy and power of your research. The American psychologist, 63(7), 591-601. http://dx.doi.org/10.1037/0003066X.63.7.591        [ Links ]

Farrell, P.J., & Rogers-Stewart, K. (2006). Comprehensive study of tests for normality and symmetry: extending the Spiegelhalter test. Journal of Statistical Computation and Simulation, 76(9), 803-816. http://dx.doi.org/10.1080/10629360500109023        [ Links ]

Finch, H. (2005). Comparison of the performance of nonparametric and parametric MANOVA test statistics when assumptions are violated. Methodology, 1(1), 27-38. http://dx.doi.org/10.1027/16141881.1.1.27        [ Links ]

Frey, J. (2009). Unbiased goodness-of-fit tests. Journal of Statistical Planning and Inference, 139, 3690-3697. http://dx.doi.org/10.1016/j.jspi.2009.04.017        [ Links ]

García-Cueto, E., Gallo P., & Miranda, R. (1998). Bondad de ajuste en el análisis factorial confirmatorio. Psicothema, 10, 717-724.         [ Links ]

Henderson, A. R. (2006). Testing experimental data for univariate normality, Clinica Chimica Acta, 366(1,2), 112-129.         [ Links ]

Jarque, C.M., & Bera, A. K. (1987). A test for normality of observations and regression residuals. International Statistical Review, 55, 163-172. http://dx.doi.org/10.2307/1403192        [ Links ]

Lemeshko, B., & Lemeshko, S. (2008). Power and robustness of criteria used to verify the homogeneity of means. Measurement Techniques, 51 (9), 950-959. http://dx.doi.org/10.1007/s11018-008-9157-3        [ Links ]

Lilliefors, H. (1967). On the Kolmogorov-Smirnov test for normality with mean and variance unknown. Journal of the American Statistical Association, 62(318), 399-402. http://dx.doi.org/10.2307/2283970        [ Links ]

Meintanis, S.G., & Hlávka, Z. (2010). Goodness-of-Fit Tests for Bivariate and Multivariate Skew-Normal Distributions. Scandinavian Journal of Statistics, 37, 701-714.         [ Links ]

Micceri, T. (1989). The unicorn, the normal curve, and other improbable creatures. Psychological Bulletin, 105, 156-166. http://dx.doi.org/10.1037//0033-2909.105.1.156        [ Links ]

Oztuna, D., Elhan, A.H., & Tuccar, E. (2006). Investigation of four different normality tests in terms of type I. Error rate and power under different distributions. Turkish Journal of Medical Sciences, 36(3), 171-176.         [ Links ]

Pedrosa, I., García-Cueto, E., Suárez-Alvarez, J., & Pérez Sánchez, B. (2012). Adaptación española de una Escala de Apoyo Social percibido para deportistas. Psicothema, 24(3), 470-476.         [ Links ]

Romáo, X., Delgado, R., & Costa, A. (2010). An empirical power comparison of univariate goodness-of-fit tests for normality. Journal of Statistical Computation and Simulation, 80(5), 545-591.         [ Links ]

Schucany, W.R., & Ng, H.K.T. (2006). Preliminary goodness-of-fit tests for normality do not validate the one-sample Student t. Communications in Statistics, Theory and Methods, 35, 2275-2286.         [ Links ]

Shahabuddin, F.A.A., Ibrahim, K., & Jemain, A.A. (2009). On the Comparison of Several Goodness of Fit tests under Simple Random Sampling and Ranked Set Sampling. World Academy of Science, Engineering and Technology, 54, 77-80.         [ Links ]

Shapiro, S.S., & Wilk, M.B. (1965). An analysis of variance test for normality (complete sampies). Biometrika 52(3,4), 591-611. http://dx.doi.org/10.2307/2333709        [ Links ]

Shin, H., Jung, Y., Jeong, C., & Heo, J.H. (2012). Assessment of modified Anderson-Darling test statistics for the generalized extreme value and generalized logistic distributions. Stochastic Environmental Research and Risk Assessment, 26, 105-114.         [ Links ]

Steinskog, D.J., Tj0stheim, D.B., & Kvamst0, N.G. (2007). A Cautionary Note on the Use of the Kolmogorov-Smirnov Test for Normality. Monthly Weather Review, 135(3), 1151-1157. http://dx.doi.org/10.1175/MWR3326.1        [ Links ]

Strasak, A. M., Zaman, Q., Marinell, G., Pfeiffer, K. P., & Ulmer, H. (2007). The use of statistics in medical research: A comparison of The New England Journal of Medicine and Nature Medicine. American Statistician, 61, 47-55.         [ Links ]

Suárez-Alvarez, J., Campillo-Alvarez, A., Fonseca-Pedrero, E., García-Cueto, E., & Muñiz, J. (2013). Professional training in the workplace: The role of achievement motivation and locus of control. Spanish Journal of Psychology. En imprenta.         [ Links ].

Tavares Tadaiesky, L., & Zagury Tourinho, E. (2012). Effects of support consequences and cultural consequences on the selection of interlocking behavioral contingencies. Revista Latinoamericana de Psicología, 44(1), 121-131.         [ Links ]

Thadewald, T., & Buning, H. (2007). Jarque-Bera Test and its Competitors for Testing Normality - A Power Comparison. Journal of Applied Statistics, 34(1), 87-105. http://dx.doi.org/10.1080/02664760600994539        [ Links ]

Urzúa, C. (1996). On the correct use of omnibus tests for normality. Economics Letters, 53, 247-251.         [ Links ]

Yazici, B., & Yolacan, S. (2007). A comparison of various tests of normality. Journal of Statistical Computation and Simulation, 77(2), 175-183.         [ Links ]

Zimmerman, D. (1998). Invalidation of parametric and nonparametric statistical tests by concurrent violation of two assumptions. Journal of Experimental Education, 67(1), 55-68. http://dx.doi.org/10.1080/00220979809598344        [ Links ]

Zghoul, A. A. (2010). A goodness of fit test for normality based on the empirical moment generating function. Communications in Statistics-Simulation and Computation, 39(6), 1292-1304.         [ Links ]