Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Universitas Psychologica
Print version ISSN 1657-9267
Univ. Psychol. vol.14 no.3 Bogotá July/Sept. 2015
https://doi.org/10.11144/Javeriana.upsy14-3.prpd
Precisión en la recuperación de parámetros, con datos ordinales, en el Análisis de Estructura de Covarianza y el Modelo de Rutas mediante Mínimos Cuadrados Parciales*
Accuracy on Parameter Recovery, with Ordinals Data, of Structure Covariance Analysis and Partial Least Squares Path Modeling
Edgardo Daniel Miranda-Zapata**
Universidad de la Frontera, Chile
Miguel Ángel Ruiz-Díaz***
Universidad Autónoma de Madrid, España
*Artículo de investigación. FONDECYT de Iniciación 2013, N° 11130722. Beca Presidente de la República de Chile (2008), de la Comisión Nacional de Investigación Científica y Tecnológica de Chile (CONICYT).
**Autor de correspondencia. E-mail: edgardo.miranda@ufrontera.cl
Recibido: 25 de abril de 2014 | Revisado: 26 de marzo de 2015 | Aceptado: 26 de marzo de 2015
Para citar este artículo
Miranda-Zapata, E., & Ruiz, M. A. (2015). Precisión en la recuperación de parámetros, con datos ordinales, en el Análisis de Estructura de Covarianza y el Modelo de Rutas mediante Mínimos Cuadrados Parciales. Universitas Psychologica, 14(3), 985-996. http://dx.doi.org/10.11144/Javeriana.upsy14-3.prpd
Resumen
Se compara la precisión en la recuperación de parámetros del Análisis de Estructura de Covarianza (ACOV) y el Modelo de Rutas mediante Mínimos Cuadrados Parciales (PLS-PM), en un modelo simple con variables manifiestas simuladas con escala ordinal de cinco puntos. Se utiliza un diseño experimental, manipulando el método de estimación, tamaño muestral, nivel de asimetría y tipo de especificación del modelo. Se valora la media de las diferencias absolutas para el modelo estructural. ACOV presenta estimaciones más precisas que PLS-PM, en distintas condiciones experimentales. Cuando se utiliza un tamaño muestral pequeño, ambas técnicas son igualmente precisas. Se sugiere utilizar ACOV frente a PLS-PM. Se desaconseja fundamentar la elección de PLS-PM frente a ACOV en la utilización de una muestra pequeña.
Palabras clave: Análisis de estructura de covarianza; precisión; modelo de ecuaciones estructurales; modelo de rutas mediante mínimos cuadrados parciales; recuperación de parámetros; variables manifiestas ordinales
Abstract
The accuracy on parameter recovery is compared between Structure Covariance Analysis (ACOV) and Partial Least Squares Path Modeling (PLS-PM), with simulated ordinals data with 5 points, in a simple model. An experimental design is used, controlling the estimation method, sample size, skewness level and model specification. Mean absolute differences are used to assess accuracy for the structural model. ACOV provided more accurate estimates of the structural parameters than PLS-PM in different experimental conditions. With a small sample size, both techniques are equally accurate. Using ACOV against PLS -PM is suggested. PLS choosing ACOV instead based on the use of a small sample size is not recommended.
Keywords: structure covariance analysis; accuracy; structural equation modeling; partial least squares path modeling; parameter recovery; ordinal manifest variables
Introducción
Habitualmente se distinguen dos aproximaciones de Modelos de Ecuaciones Estructurales (MEE): la aproximación basada en covarianzas, dentro de la cual se encuentra la técnica de Análisis de Estructura de Covarianza ([ACOV]; Jõreskog, 1970, 1979), y la aproximación basada en componentes, dentro de la cual se encuentra el Modelo de Rutas mediante Mínimos Cuadrados Parciales ([PLS-PM]; Wold, 1977, 1980).
ACOV es la técnica de MEE que ha presentado un mayor desarrollo y es la más popular hasta el momento (López & López, 2006). Lo que, en parte, ha sido favorecido por ser la primera técnica en ser planteada formalmente y la primera en presentar un programa estadístico informático que la aplica: LISREL, desarrollado por Jõreskog y van Thillo (1972), y que sigue siendo actualizado hasta la fecha (Jõreskog & Sôrbom, 2006). En contraposición, PLS-PM solo ha contado con el programa informático LVPLS, desarrollado por Jan-Bernd Lohmõller, desde 1984. En la actualidad, ambos tipos de modelado cuentan con diversos programas específicos de análisis o han sido incluidos como rutinas de paquetes de análisis de datos, entre los cuales se encuentran: AMOS (Arbuckle, 1994), CALIS (SAS Institute Inc., 2008), EQS (Bentler, 1995), Mplus (Muthén & Muthén, 1998-2010) y R v. 2.14.0 (R Development Core Team, 2011) con los paquetes "sem" v. 3.0-0 (Fox, Nie, & Byrne, 2012) y "lavaan" (Rosseel, 2012), para ACOV; y PLS-Graph (Chin, 2001), R v. 2.14.0 (R Development Core Team, 2011) con los paquetes "plspm" (Sánchez & Trinchera, 2012) y "semPLS" (Monecke & Leisch, 2012), SmartPLS (Ringle, Wende, & Will, 2005) y XLSTAT (Addinsoft, 2009), para PLS-PM.
PLS-PM es planteada como una alternativa para la estimación de parámetros frente a las restricciones de distribución normal que presenta ACOV cuando se utiliza con el método de máxima verosimilitud (Jõreskog & Wold, 1982). Ambas técnicas de MEE han sido compradas en diversas ocasiones (Areskoug, 1982; Chin, 1995; Fornell & Bookstein, 1982; Jõreskog & Wold, 1982; Reinartz, Haenlein, & Henseler, 2009; Wold, 1982a). Los planteamientos apuntan a que ambas técnicas son más complementarias que competitivas, desatacando que el propósito de ACOV es estudiar la estructura de las relaciones entre variables, reflejada en la matriz de varianzas y covarianzas, mientras que PLS-PM tiene como objetivo principal maximizar la varianza explicada de las variables dependientes del modelo. Así la utilización de PLS-PM es más apropiada para situaciones en las cuales el interés fundamental del investigador es predecir las variables latentes del modelo o identificar de manera exploratoria las relaciones existentes entre ellas, mientras que la utilización de ACOV debe ser escogida cuando el propósito recae en confirmar relaciones teóricamente asumidas (Haenlein & Kaplan, 2004; Reinartz et al., 2009).
Ambas técnicas de MEE comparten las convenciones de representación gráfica del modelo, la formulación lineal de las relaciones entre los indicadores y variables latentes, y la inclusión en el modelo de errores de medida y de estimación. Entre las diferencias, se encuentra que el método de estimación de máxima verosimilitud de ACOV asume la distribución normal conjunta, mientras que PLS-PM no realiza supuestos distribucionales.
Cabe destacar que existen otros métodos de estimación de ACOV que no requieren del cumplimiento del supuesto de normalidad multivariante (p. ej., mínimos cuadrados no ponderados, distribución asintóticamente libre y mínimos cuadrados de escala libre). Las estimaciones de ACOV en muestras grandes con distribución normal multivariante, han resultado ser más eficientes que las estimaciones de PLS-PM (Fornell & Bookstein, 1982), mientras que las estimaciones del PLS-PM no presentan problemas en la identificación del modelo, son eficientes en muestras pequeñas, aun estimando modelos complejos y logran la convergencia más rápidamente (Fornell & Bookstein, 1982; Jõreskog & Wold, 1982). Por otra parte, se plantea que las estimaciones de parámetros de PLS-PM presentan una mayor eficiencia y sesgo, frente a las estimaciones del ACOV, tendiendo a subestimar los parámetros del modelo estructural y a sobreestimar los parámetros del modelo de medida (Chin, 1995; Hulland, Ryan, & Rayner, 2010).
La diferencia clave de PLS-PM respecto de ACOV es la definición explícita de las variables latentes, como una combinación ponderada de sus indicadores por parte del primero (Wold, 1982b), de manera similar a como se define el modelo de Componentes Principales (Chin, 1995), lo cual ha conllevado que se le denomine MEE basado en componentes, a veces también llamado MEE basado en la varianza. Por su parte, ACOV propone la definición de los indicadores como una combinación de las variables latentes y, además, plantea la necesidad de estimar las comunalidades como en el modelo de Factor Común (Chin, 1995), lo que ha conllevado que se le denomine MEE basado en factores, a veces también llamado MEE basado en covarianzas.
Un trabajo destacable, en el que se basa este estudio, es el realizado por Hwang, Malhotra, Kim, Tomiuk y Hong (2010). En su estudio, realizaron una simulación comparando la eficiencia de tres técnicas de MEE: ACOV, PLS-PM y Análisis Generalizado de Componentes Estructurales, con datos simulados con escala de intervalos, en un modelo que incluía efectos cruzados. Los autores encontraron que la única condición determinante en la recuperación adecuada de los parámetros fue la especificación correcta del modelo. En concreto, cuando el modelo se encontraba correctamente especificado, ACOV recuperó los parámetros sin sesgo y recuperó mejor los parámetros que PLS-PM. Sin embargo, cuando el modelo se encontraba incorrectamente especificado, PLS-PM recuperó mejor los parámetros, aun cuando ambas aproximaciones presentaron sesgo en sus estimaciones. ACOV sobreestimó los parámetros: los del modelo estructural en el límite del rango aceptable (10 %) y los del modelo de medida fuera del rango aceptable, mientras que PLS-PM subestimó los parámetros del modelo estructural dentro del rango aceptable y sobreestimó los parámetros del modelo medida fuera del rango aceptable.
En los estudios que comparan ACOV con PLS-PM, se suelen utilizar datos simulados con escala de intervalos (p. ej., Fornell & Bookstein, 1982; Reinartz et al., 2009). Aunque actualmente se han realizado estudios con variables en escala ordinal (p. ej., Barroso, Cepeda, & Roldán, 2010; Hulland et al., 2010), estos han utilizado ACOV con el método de estimación de Máxima Verosimilitud (ML), a pesar del planteamiento de Fornell y Bookstein (1982) y Forero, Maydeu-Olivares y Gallardo-Pujol (2009) sobre la conveniencia de utilizar el método de estimación de Mínimos Cuadrados No Ponderados (ULS) sobre la matriz de correlaciones policóricas, cuando las variables manifiestas se encuentren medidas en escala ordinal. Un estudio que compara ambas técnicas de MEE, utilizando ACOV con el método de estimación ULS es el realizado por Tenenhaus, Mauger y Guinot (2010). Sin embargo, las variables manifiestas utilizadas se encuentran en escala dicotómica.
El presente estudio persigue profundizar en la comparación de las técnicas de MEE más utilizadas, ACOV y PLS-PM, utilizando condiciones extremas de asimetría y tamaño muestral, que superan las utilizadas por Hwang et al. (2010); además se utilizan variables manifiestas con escala ordinal, condición que se considera habitual en el ámbito de investigación aplicada en las ciencias del comportamiento y de la salud. A la vez, se utiliza el método de estimación que se ha planteado como más eficiente para las estimaciones con ACOV cuando se utilizan variables ordinales, superando las limitaciones de estudios previos. Cabe señalar que en el presente estudio se utilizarán dos niveles de especificación de modelos: más especificado y menos especificado. Estos niveles se fundamentan en la precisión realizada por Mulaik (2009) respecto al error que implica hablar de un "modelo mal especificado" cuando se libera un parámetro que es cero en la población, ya que al liberar un parámetro del modelo nada es especificado, de hecho, el modelo es menos especificado.
Método
Se diseñó un estudio de recuperación de parámetros mediante simulación de muestras sintéticas. Se consideró pertinente valorar el efecto conjunto de cuatro factores: Técnica de definición del MEE, con dos niveles: ACOV y PLS-PM; Especificación del modelo con dos niveles: más especificado y menos especificado; Asimetría con tres niveles: nula (0), media (1.25) y alta (2) y Tamaño muestral con cuatro niveles: muy pequeño (50), pequeño (100), mediano (300) y grande (500). Estos niveles de asimetría y tamaños muestrales incluyen los niveles utilizados por Hwang et al. (2010), buscando superar las limitaciones señaladas por los autores al respecto, incorporando un nivel mayor para la asimetría (2) y un tamaño muestral menor (50). Se planteó un diseño completo para la combinación de los niveles de los factores.
El modelo poblacional utilizado (Figura 1) incluye tres variables latentes (una exógena y dos endógenas) y nueve variables manifiestas reflectivas (tres por cada variable latente). La variable latente exógena (e) tiene un efecto directo sobre una de las variables latentes endógenas (η1), la cual a su vez tiene un efecto directo sobre la otra variable latente endógena (η2). Este modelo es una variación del modelo utilizado por Bollen, Kirby, Curran, Paxton y Chen (2007) y Hwang et al. (2010), para evaluar la recuperación de parámetros con distintos métodos de estimación utilizando variables manifiestas con escala de intervalos. Se excluyeron los efectos cruzados (cross-loadings) de las variables latentes hacia las variables manifiestas, para considerar una estructura lo más simple posible para el modelo de medida.
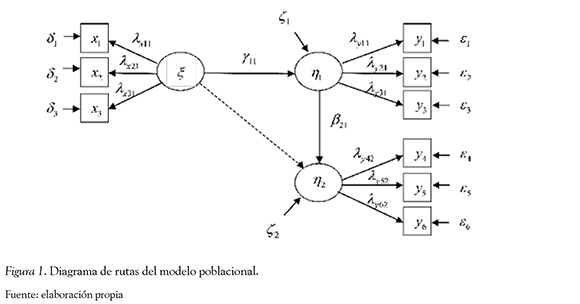
Se valoraron dos niveles de especificación del modelo en los parámetros estimables: más especificado (se especifica el modelo poblacional) y menos especificado (se estima también el parámetro y21, y que no ha sido especificado en la generación de las muestras, ver Figura 1). Este factor se definió como efecto intragrupo.
Ambos factores intragrupo se combinaron dentro de las cuatro combinaciones posibles intergrupo. Por tanto, los cuatro factores se combinan en un diseño (2x2x3x4), siendo los dos primeros factores intergrupos y los dos segundos intragrupos.
Para cada una de las muestras simuladas, se estiman los parámetros teóricos del modelo. De las estimaciones obtenidas, se valoran el porcentaje de soluciones que convergen y el porcentaje de soluciones impropias, para cada una de las condiciones experimentales consideradas y para el total de muestras generadas. Se determinó un máximo de 100 iteraciones para la convergencia de las soluciones, y se consideró que una solución es impropia cuando una o más varianzas son negativas o cuando uno o más parámetros estimados presentan valores superiores a 1 en valor absoluto, de acuerdo con la comprobación técnica propuesta por Bollen (1989). Las muestras que presentan soluciones que no convergen o soluciones impropias son excluidas de los análisis posteriores del estudio por ser consideradas no válidas, tal como en el estudio de Forero et al. (2009).
Para valorar la distancia entre los parámetros estimados y los parámetros poblacionales expresada en la misma escala de los parámetros (precisión), se calculó la Media de las Diferencias Absolutas (MAD) entre el parámetro estimado y el parámetro poblacional, para el Modelo Estructural y del Modelo de Medida, de acuerdo con:
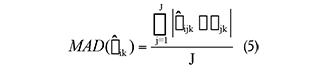
Luego, a través de un ANOVA de medidas repetidas se comparan las medias del MAD del Modelo Estructural, en las réplicas válidas por condición experimental. Valores menores de MAD implican una menor distancia entre la estimación del parámetro y el valor del parámetro poblacional.
Análisis
Para la estimación de parámetros con ACOV se utiliza el programa LISREL v.8.8 (Jõreskog & Sõrbom, 2006), calculando la matriz de correlaciones policóricas con PRELIS y utilizando como método de estimación Mínimos Cuadrados No Ponderados, de acuerdo con lo planteado por Forero et al. (2009).
Para el análisis con PLS-PM, se utiliza el entorno de programación para análisis estadístico R v. 2.14.0 (R Development Core Team, 2011), con el paquete "plspm" (Sánchez & Trinchera, 2012). Considerando que estudios previos (Tenenhaus, Esposito Vinzi, Chatelin, & Lauro, 2005; Ringle, Gõtz, Wetzels, & Wilson, 2009) han comprobado la ausencia de diferencias en las estimación de parámetros al utilizar los distintos esquemas para la estimación de parámetros de PLS-PM y el planteamiento de Esposito Vinzi, Trinchera y Amato (2010), se opta por utilizar el esquema de rutas, al ser el único que considera la dirección de las relaciones como han sido establecidas en el modelo de rutas predictivo.
Para la automatización de los análisis en todas las condiciones, se utiliza el programa Visual Fox Pro 9.0, a través del cual se ejecutan las sentencias de análisis de LISREL y R, y además se extraen las estimaciones estandarizadas de los parámetros desde los archivos de resultados de cada programa.
Se realizan los 24 000 análisis de estimación (6 000 muestras x 2 aproximaciones de MEE x 2 especificaciones del modelo). Los datos resultantes se analizaron utilizando el programa SPSS versión 15. El modelo de análisis utilizado fue un Análisis de Varianzas (ANOVA) de medidas repetidas con 2 factores intragrupos (técnicas de MEE y especificación del modelo) y con 2 factores intergrupos (nivel de asimetría y tamaño de la muestra), utilizando como variable dependiente el promedio de las diferencias absolutas por condición para los parámetros del modelo estructural.
Para evaluar la relevancia estadística de los resultados, se desestimó la utilización del valor de la significación estadística observada (valor p), debido a la gran cantidad de réplicas utilizadas y la influencia que tiene sobre el valor p el tamaño de la muestra. Por dichos motivos se optó por considerar el tamaño del efecto como valor de comparación, teniendo en cuenta solo los efectos correspondientes a un tamaño del efecto al menos mediano (η = 0.06), de acuerdo con Cohen (1988). Se informa el valor de Eta cuadrado que asume esfericidad, considerando que éste, es el mismo valor que se obtuvo para Greenhouse-Geisser, Huynh-Feldt y Límite-inferior.
Resultados
El porcentaje de estimaciones convergentes en el total de réplicas fue muy elevado tanto para la técnica ACOV (97.35 %) como para la técnica PLS-PM (98.24 %). El menor porcentaje de convergencia por condición fue de 79.2 % para ACOV con el modelo menos especificado, asimetría de 2 y tamaño muestral de 50; condición en la que PLS-PM presentó un 86.8 % de soluciones que convergieron. Se tuvo que descartar un 4 % del total de réplicas por falta de convergencia.
PLS-PM presentó un 0.2 % de soluciones impropias, en cambio ACOV presentó un 15.2 % de soluciones impropias del total de réplicas. El mayor porcentaje de soluciones impropias (62.2 %) lo presentó ACOV en la condición de modelo menos especificado, con asimetría de 2 y un tamaño muestral de 50, instancia en que PLS-PM presentó un 0.8% de soluciones impropias.
Las réplicas que presentaron soluciones impropias no fueron consideradas en los análisis posteriores. En total se desestimó la utilización de un 17.7 % de las réplicas, considerando las 4 938 réplicas válidas para los análisis posteriores.
Precisión
En el ANOVA de medidas repetidas (2x2x3x4) que valoraba el MAD de las estimaciones estandarizadas de los parámetros del Modelo Estructural (Tabla 1), no se evidenciaron interacciones de tercer orden con tamaños del efecto medianos o superiores. Se encontraron el siguiente efecto de interacción de segundo orden.
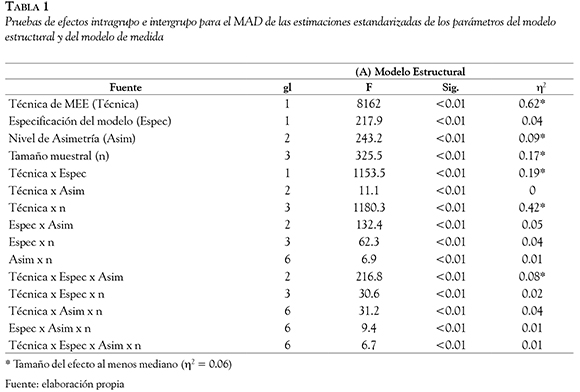
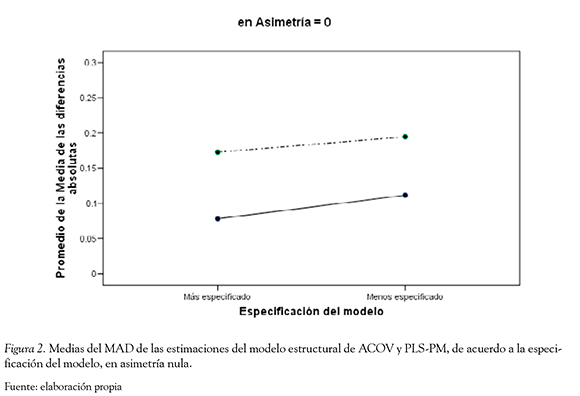
Interacción entre la técnica de MEE, la especificación del modelo y el nivel de asimetría (η2 = 0.08). Las estimaciones de ACOV presentaron un menor promedio de MAD, que las estimaciones de PLS-PM, en las dos modalidades de especificación del modelo, cuando se utilizaron los distintos niveles de asimetría. La diferencia entre el MAD de ACOV y PLS-PM fue menor con el modelo menos especificado y dicha diferencia disminuyó en la medida que aumentaba el nivel de asimetría. La diferencia entre el MAD de las técnicas con el modelo más especificado aumentó en la medida que aumentó el nivel de asimetría (Figuras 2, 3 y 4).
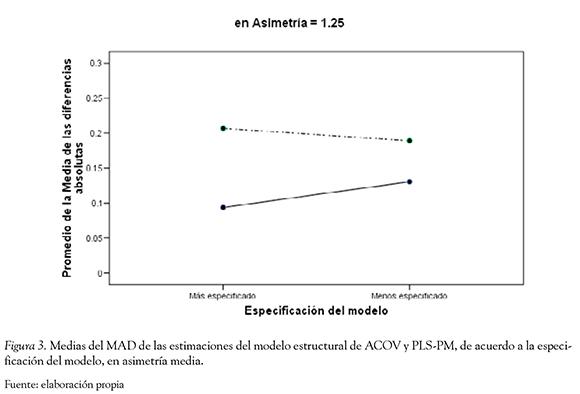
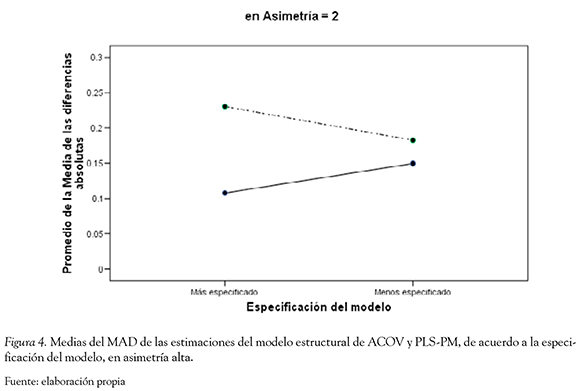
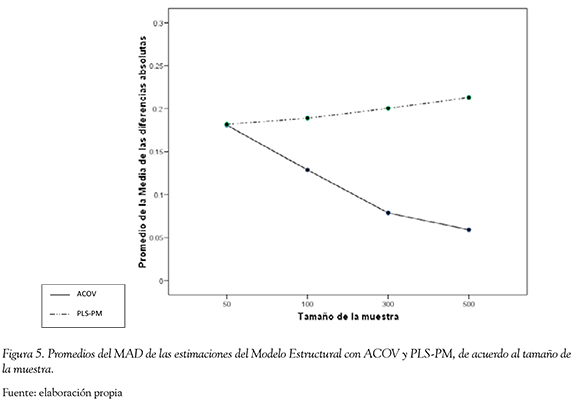
Además se encontró el efecto de interacción de primer orden entre la Técnica de MEE y tamaño de la muestra (η2= 0.42). El promedio del MAD de las estimaciones de ACOV fue menor que el promedio del MAD de PLS-PM cuando se utilizaron tamaños muestrales muy grandes, grandes y medianos. El promedio de MAD de PLS-PM tendió a aumentar en la medida que disminuía el tamaño muestral, y el promedio del MAD de ACOV tendió a aumentar en la medida que disminuía el tamaño de la muestra, llegando a niveles similares a los presentados por PLS-PM cuando el tamaño de las muestras fue pequeño. Así, las diferencias entre los promedios de los MAD disminuyó en la medida que disminuyó el tamaño muestral (Figura 5).
Por último, al analizar las estimaciones obtenidas de cada uno de los parámetros del Modelo Estructural, cuando se utiliza el modelo menos especificado. Respecto del parámetro γ21 PLS-PM presenta estimaciones superiores (x = 0.11; dt = 0.10; ET = 0.001) que las estimaciones de ACOV (x = 0.02; dt = 0.19; ET = 0.003), con η2 = 0.27. Las estimaciones de PLS-PM del parámetro γ11 presentaron un sesgo negativo en el rango del 28 % al 38%, en cambio ACOV presentó un sesgo dentro del rango aceptable (η2 = 0.18). Las estimaciones de PLS-PM del parámetro β21 presentaron un sesgo negativo en el rango del 33 % al 42 %, en cambio ACOV presentó un sesgo dentro del rango aceptable η2 = 0.13.
Discusión
El presente estudio evalúa la precisión en la recuperación de parámetros de las dos técnicas de MEE más extendidas: ACOV y PLS-PM. Al analizar un modelo definido mediante variables manifiestas medidas en escala ordinal, en distintas condiciones de especificación del modelo, tamaño muestral y nivel de asimetría.
El principal aporte del presente estudio se encuentra en la inclusión de variables manifiestas en escala ordinal y la utilización del método que ha demostrado ser más eficiente para la estimación de parámetros para ACOV en estas condiciones: ULS sobre la matriz de correlaciones policóricas (Forero et al., 2009), instancia poco investigada en el ámbito de la comparación de técnicas de MEE; y en el caso de haber sido estudiada, se ha utilizado el método de estimación especificado en los programas estadísticos por defecto (Máxima Verosimilitud). Este estudio supera dicha deficiencia. Además se superan algunas de las limitaciones señaladas por Hwang et al. (2010), en cuanto a los niveles de asimetría y tamaño muestral, incluyendo un nivel de asimetría mayor que el nivel máximo de asimetría utilizado por los autores e incluyendo un tamaño muestral menor que el mínimo utilizado por los autores.
Los resultados evidencian que cerca de un sexto del total de las estimaciones de los parámetros realizadas con ACOV presentan soluciones impropias, frente al 0.2 % de PLS-PM.
En cuanto a la precisión en la estimación de parámetros los resultados evidencian efectos de la asimetría y el tamaño muestral, a diferencia de los hallazgos de Hwang et al. (2010), en los que solo se evidenció un efecto de la especificación del modelo. En el Modelo Estructural, ACOV presentó una menor diferencia absoluta promedio entre las estimaciones y los parámetros poblacionales (MAD), que PLS-PM en ambas modalidades de especificación del modelo, en los tres niveles de asimetría. Así también el promedio del MAD de las estimaciones de ACOV fue menor que el promedio del MAD de PLS-PM cuando se utilizaron tamaños muestrales muy grandes, grandes y medianos. Cuando se utilizó un tamaño muestral pequeño ambas técnicas obtuvieron valores similares de MAD.
En el Modelo de Medida ACOV presentó una menor diferencia absoluta promedio entre las estimaciones y los parámetros poblacionales (MAD), que PLS-PM en condición de asimetría nula y tamaños muestrales grande (n = 300) y muy grande ( n = 500). Al aumentar el nivel de asimetría los valores de MAD de PLS-PM se asemejan a los valores de MAD de ACOV. Con tamaños muestrales mediano y pequeño ambas técnicas presentan diferencias promedio similares en los distintos niveles de asimetría utilizados en este estudio.
La tendencia de PLS-PM a sobreestimar el parámetro del Modelo Estructural que fue fijado a 0 en el modelo poblacional, es decir la tendencia a identificar efectos directos donde no los hay, y a presentar un sesgo negativo en los otros parámetros del Modelo Estructural, es decir la tendencia a indicar que la relación existente entre las variables latentes es menos intensa de lo que realmente es. Tendrá efectos negativos a la hora de realizar un análisis de mediación. Por lo cual, para este tipo de análisis se sugiere elegir ACOV.
Como conclusión se plantea que la estimación de parámetros de ACOV presenta menores diferencias entre los parámetros estimados y los parámetros poblacionales (MAD) que PLS-PM, cuando se utilizan tamaños muestrales grande, mediano y pequeño. Así, se plantea que las estimaciones de ACOV son más precisas que las estimaciones de PLS-PM. Sin embargo, con un tamaño muestral muy pequeño ambas técnicas presentan valores similares. Por lo que la tendencia a utilizar PLS-PM, fundamentada en la utilización de un tamaño muestral pequeño (Hair et al., 2012; Gefen, Straub, & Boudreau, 2000; Marcoulides, 2006), no es avalada por los resultados de este estudio y es desaconsejada.
Las principales limitaciones del presente estudio son la utilización de un modelo demasiado simple, con valores elevados e invariantes para los parámetros, lo cual, al ser poco habitual en investigaciones aplicadas, puede limitar la generalización de los resultados encontrados. Además, parece ser recomendable utilizar tamaños de efecto más elevados para determinar un efecto relevante.
Como sugerencia para futuros estudios sobre esta temática, se sugiere incorporar distintos niveles para la escala ordinal, pudiendo incorporar además distintas escalas de medida para las variables manifiestas (p. ej., ordinal y de intervalos), modelos con distintos niveles de complejidad, distintos valores de los parámetros poblacionales y/o indicadores de tipo formativo.
Referencias
XLSTAT 2009 [Software de computación]. París: Addinsoft. Disponible en http://www.xlstat.com/en/products/xlstat-plspm/ [ Links ]
Arbuckle, J. (1994). AMOS: Analysis of moment structures. Psychometrika, 59(1), 135-137. [ Links ]
Areskoug, B. (1982). The first canonical correlation. Theoretical PLS analysis and simulation experiments. En K. G. Jõreskog & H. Wold (Eds.), Systems under indirect observation (Part II, pp. 95-117). Amsterdam: North-Holland. [ Links ]
Barroso, C., Cepeda, G., & Roldán, J. L. (2010). Applying maximum likelihood and PLS on different sample sizes: Studies on SERVQUAL model and Employee Behaviour model. En V. Esposito Vinzi, W. W. Chin, J. Henseler & H. Wang (Eds.), Handbook of Partial Least Squares. Concepts, methods and applications (pp. 427-447). Berlin: Springer-Verlag. [ Links ]
Bentler, P. M. (1995). EQS Structural Equations Program manual. Encino, CA: Multivariate Software. [ Links ]
Bollen, K. A. (1989). Structural equations with latent variables. New York: Wiley. [ Links ]
Bollen, K. A., Kirby, J. B., Curran, P. J., Paxton, P. M., & Chen, F. (2007). Latent variable models under misspecification. Two-stages least squares (2SLS) and Maximum likelihood (ML) estimators. Sociological Methods and Research, 26(1), 48-86. [ Links ]
Bollen, K. A., & Long, J. S. (1993). Testing structural equation models. Newbury Park, CA: Sage Publications. [ Links ]
Chin, W. W. (1995). Partial Least Squares is to LISREL as principal components analysis is to common factor analysis. Technology Studies, 2(2), 315-319. [ Links ]
Chin, W. W. (2001). PLS-Graph user's guide Version 3.0. Houston: Soft Modeling Inc. [ Links ]
Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2nd ed.). Hillsdale, NJ: Erlbaum. [ Links ]
Esposito Vinzi, V., Trinchera, L., & Amato, S. (2010). PLS path modeling: From foundations to recent developments and open issues for model assessment and improvement. En V. Esposito Vinzi, W. W. Chin, J. Henseler & H. Wang (Eds.), Handbook of Partial Least Squares. Concepts, methods and applications (pp. 47-82). New York: Springer-Verlag. [ Links ]
Forero, C. G., Maydeu-Olivares, A., & Gallardo-Pujol, D. (2009). Factor analysis with ordinal indicators: A Monte Carlo study comparing DWLS and ULS estimation. Structural Equation Modeling, 16 (4), 625-641. [ Links ]
Fornell, C., & Bookstein, F. L. (1982). Two structural equation models: LISREL and PLS applied to consumer exit-voice theory. Journal of Marketing Research, 19(4), 440-452. [ Links ]
Fox, J., Nie, Z., & Byrne, J. (2012). Sem: Structural equation models. Disponible en http://cran.r-project.org/web/packages/sem/index.html [ Links ]
Gefen, D., Straub, D., & Boudreau, M. (2000). Structural equation modeling and regression: Guidelines for research practice. Communications of the Association for Information Systems, 4(7), 1-78. Disponible en http://www.cis.gsu.edu/∼dstraub/Papers/Resume/Gefenetal2000.pdf
Haenlein, M., & Kaplan, A. (2004). A biginner's guide to partial least squares analysis. Understanding Statistics, 3(4), 283-297. [ Links ]
Hulland, J., Ryan, M. J., & Rayner, R. K. (2010). Modeling customer satisfaction: A comparative performance evaluation of covariance structure analysis versus partial least squares. En V. Esposito Vinzi, W. W. Chin, J. Henselery & H. Wang (Eds.), Handbook of Partial Least Squares. Concepts, methods and applications (pp. 307-325). Berlin: Springer-Verlag. [ Links ]
Hwang, H., Malhotra, N., Kim, Y., Tomiuk, M., & Hong, S. (2010). A comparative study on parameter recovery of three approaches to structural equation modeling. Journal of Marketing Research, 47(4), 699-712. [ Links ]
Jõreskog, K. G. (1970). A general method for estimating a linear structural equation system. ETS Research Bulletin Series, 1-41. doi: 10.1002/j.2333-8504.1970.tb00783.x [ Links ]
Jõreskog, K. G. (1979). Structural equation models in the social sciences: Specification, estimation and testing. En J. Magidson (Ed.), Advances in factor analysis and structural equation models (pp. 105-127). New York: University Press. [ Links ]
Jõreskog, K. G., & Sõrbom. D. (2006). LISREL 8.8 for Windows [Computer software]. Lincolnwood: Scientific Software International, Inc. [ Links ]
Jõreskog, K. G., & van Thillo, M. (1972). LISREL: A general computer program for estimating a linear structural equation of unmeasured variables (Report N° ETS-RB-72-56). Princeton, NJ: Educational Testing Service. [ Links ]
Jõreskog, K. G., & Wold, H. (1982). The ML and PLS techniques for modeling with latent variables: Historical and comparative aspects. En K. G. Jõreskog & H. Wold (Eds.), Systems under indirect observation: Causality, structure, prediction, (Part I, pp.263-270). Amsterdam: North-Holland. [ Links ]
Lohmõller, J. B. (1984). LVPLS program manual. Cologne, Germany: Zentralarchiv für Empirische Sozialforschung, Universitát zu Kõln. [ Links ]
López, L. M., & López, J. M. (2006). Estudio comparado de las estimaciones de dos versiones del modelo de aceptación de la tecnología (TAM) mediante los programas AMOS y PLS. Investigaciones Europeas, 12(3), 95-110. [ Links ]
Marcoulides, G. A. (2006). PLS: A silver bullet? MISS Quarterly, 30(2), iii-ix. [ Links ]
Monecke, A., & Leisch, F. (2012). semPLS: Structural Equation Modeling Using Partial Least Squares. Journal of Statistical Software, 48(3), 1-32. Disponible en http://www.jstatsoft.org/v48/i03/paper [ Links ]
Mulaik, S. A. (2009). Linear Causal Modeling with Structural Equations. Boca Raton, FL: Chapman & Hall/CRC. [ Links ]
Muthén, L., & Muthén, B. (1998-2010). Mplus user's guide (6th ed.). Los Angeles, CA: Muthén & Muthén. Disponible en http://www.statmodel.com/download/usersguide/Mplus Users Guide v6.pdf [ Links ]
R Development Core Team. (2011). R: A language and environment for statistical computing [Software computacional]. Vienna, Austria: R Foundation for Statistical Computing, http://www.r-project.org/ [ Links ]
Reinartz, W., Haenlein, M., & Henseler, J. (2009). An empirical comparison of the efficacy of covariance-based and variance-based SEM. International Journal of Research in Marketing, 26(4), 332-344. [ Links ]
Ringle, C. M., Gõtz, O., Wetzels, M., & Wilson, B. (2009). On the use of formative measurement specifications in structural equation modeling: A Monte Carlo simulation study to compare covariance-based and Partial Least Squares Model estimation methodologies (Research Memorandum No 14). Maastricht University, Maastricht Research School of Economics of Technology and Organization (METEOR). Disponible en http://mpra.ub.uni-muenchen.de/15390/ [ Links ]
Ringle, C. M., Wende, S., & Will, A. (2005). SmartPLS (Version 2.0) [Software de computación]. Hamburgo: University of Hamburg. [ Links ]
Rosseel, Y. (2012). lavaan: An R package for structural equation modeling. Journal of Statistical Software, 48(2), 1-36. Disponible en http://www.jstatsoft.org/v48/i02/paper [ Links ]
SAS Institute Inc. (2008). SAS/STAT® 9.2 User's Guide. Cary, NC: SAS Institute Inc. [ Links ]
Sánchez, G., & Trinchera, L. (2012). pls-pm: Partial Least Squares data analysis method. R package version 0.2-2. Disponible en http://cran.r-project.org/web/packages/plspm/index.html [ Links ]
Tenenhaus, M., Esposito Vinzi, V., Chatelin, Y., & Lauro, C. (2005). PLS path modeling. Computational Statistics & Data Analysis, 48(1), 159-205. doi: 10.1016/j.csda.2004.03.005 [ Links ]
Tenenhaus, M., Mauger, E., & Guinot, C. (2010). Use of ULS-SEM and PLS-SEM to measure a group effect in a regression model relating two blocks of binary variables. En V. Esposito Vinzi, W. W. Chin, J. Henseler & H. Wang (Eds.), Handbook of Partial Least Squares. Concepts, methods and applications (pp. 125-140). Berlin: Springer-Verlag. [ Links ]
Wold, H. (1977). On the transition from pattern cognition to model building. En R. Henn & O. Moeschlin (Eds.), Mathematical economics and Game Theory: Essays in honor of Oskar Morgenstern (pp. 536-549). Berlin: Springer-Verlag. [ Links ]
Wold, H. (1980). Model construction and evaluation when theoretical knowledge is scarce: Theory and application of partial least squares. En J. Kmenta & J. Ramsey (Eds.), Evaluation of econometric models (pp. 47-74). New York: Academic Press. [ Links ]
Wold, H. (1982a). systems under indirect observation using pls. en c. fornell (ed.), a second generation of multivariate analysis (Vol. 1, pp. 325-347). New York: Praeger Publishers. [ Links ]
Wold, H. (1982b). Soft modeling: The basic design and some extensions. En K. G. Jõreskog & H. Wold (Eds.), Systems under indirect observation (Part II, pp. 1-54). Amsterdam: North-Holland. [ Links ]













