Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Iteckne
Print version ISSN 1692-1798
Iteckne vol.10 no.1 Bucaramanga Jan./June 2013
Dinámica Estocástica o Compleja con Información Incompleta: Una Revisión desde el Control
Stochastic or Complex Dynamics with Missing Data: A Review on Control
Amalia Dávila Gómez1, Alejandro Peña Palacio2, Paula Andrea Ortiz Valencia3, Edilson Delgado Trejos4
1 Esp. Docencia Investigativa, FUNLAM. Docente TC, Investigadora Grupo TecnoeInfo, Fundación Universitaria. Luis Amigó - FUNLAM, Medellín, Colombia. amalia.davilago@amigo.edu.co.
2 PhD en Ingeniería, UPB. Docente TC, Investigador Grupo GIMSC, Escuela de Ingeniería de Antioquia. Medellín, Colombia. pfjapena@gmail.com.
3 MSc en Ingeniería Automática, UPB. Docente TC, Facultad de Ingenierías, Investigador GAE, Instituto Tecnológico Metropolitano ITM, Medellín, Colombia. paulaortiz@itm.edu.co.
4 PhD en Ingeniería LI Automática, Universidad Nacional de Colombia. Investigador Lab. MIRP, Instituto Tecnológico Metropolitano ITM, Medellín, Colombia. edilsondt@gmail.com.
RESUMEN
El control de procesos con dinámica estocástica o compleja es exitoso siempre y cuando se pueda estimar un modelo que se ajuste bien al comportamiento, sin embargo, esta suposición pierde validez en aplicaciones donde la información del sistema es reducida o incompleta, muy comunes en ambientes reales de la industria. La literatura presenta diferentes esquemas de control, siendo los modelos neuro-difusos los que reportan mejor desempeño. Estos modelos conjugan la capacidad de adaptación que tienen las redes neuronales con la robustez de los motores de inferencia que tiene la lógica difusa, para modelar el conocimiento de expertos mediante reglas de aprendizaje, identificar dinámicas complejas y aumentar la adaptabilidad del sistema a perturbaciones que en la práctica tienden a ser de naturaleza estocástica sumado, a veces, que la información del sistema sea restringida. Este artículo presenta una revisión sobre dificultades y soluciones derivadas del control de sistemas estocásticos o complejos con información incompleta. Se revisan las estructuras de control cuando la dinámica del sistema presenta vaguedad en los datos, la evolución hacia técnicas adaptativas, y el desempeño de las redes neuro-difusas ante procesos estocásticos o complejos con incertidumbre en los datos. De forma preliminar se establece que el control de este tipo de sistemas debe estar compuesto por modelos híbridos soportados en rutinas de optimización y análisis probabilístico que garanticen el tratamiento de las incertidumbres sin afectar el desempeño de las estructuras de control y la consistencia en la precisión.
PALABRAS CLAVE: Control adaptativo, sistemas estocásticos, redes neuronales, lógica difusa, modelos neurodifusos, información incompleta.
ABSTRACT
Control theory for processes with stochastic or complex dynamics has a successful performance as long as a model can be adjusted to the system behavior, although for real applications in the industry, where data can be reduced or incomplete, this statement may not be true. Different control schemes have been proposed and the literature reports promising results with neural fuzzy models. These models combine the adaptability of neural networks with the robust inference of fuzzy logic, in order to model expert knowledge by learning rules, identify complex dynamics and enhance the control adaptability when stochastic disturbances are present, which sometimes cause incomplete system data. This paper presents a review on the difficulties and solutions related to the control of stochastic or complex systems with incomplete data. This study, initially, discusses the control structures when the system data present notable uncertainty levels. Next, different adaptive control schemes are presented, and finally, nonlinear and stochastic control approaches based on neural fuzzy systems are reviewed. Thereby, in a preliminary way, this review establishes that a system under the conditions mentioned above should be controlled by hybrid models supported on probabilistic routines and optimization procedures in order to appropriately consider the stochastic disturbances and the uncertainty levels without reducing the control performance and yielding consistent accuracy.
KEYWORDS: Adaptive control, stochastic systems, neural networks, fuzzy Logic, neuro-fuzzy models, incomplete system data.
1. INTRODUCCIÓN
Los sistemas de control prestan una atención importante hacia los procesos dinámicos, aun a los que por razones particulares adoptan naturaleza estocástica, debido a que la mayoría de sistemas pueden entrar en episodios de comportamiento inesperado y no lineal [1]. Por ejemplo, en muchas industrias existen condiciones tan adversas que ocasionan altas pérdidas de información [2] y que los sistemas embebidos adquieran naturaleza estocástica [3]. En algunos casos, estos asuntos llegan a impedir la automatización de procesos que pueden involucrar alto riesgo para la salud de los operarios [4] o acciones que manualmente son difíciles de lograr con exactitud [5]. También puede ocurrir que el modelo del sistema en un momento dado no corresponda al inicial y esto ocasione fallas o variaciones no deseadas en los procesos [6]. En este sentido, la literatura reciente deja ver una progresiva tendencia hacia la inteligencia computacional, a través de modelos híbridos basados en redes neuronales [7] y lógica difusa [8] para la identificación autoajustable y el control multi-objetivo de procesos, a partir sólo de las entradas y las salidas del sistema [9].
Uno de los aspectos más atractivos y conocidos de los sistemas expertos es que evita la necesidad de rigurosos modelos matemáticos mediante una base de conocimiento que posee información de uno o más expertos en el área específica [10], de forma que expresiones analíticas muy complejas pueden ser remplazadas por descripciones lingüísticas auto explicadas en la estrategia de control [11]. Las nuevas tendencias sugieren combinar estratégicamente estas técnicas de inteligencia artificial con esquemas de control tradicionales [7], puesto que la industria actual necesita sistemas de control con memoria, capacidad de respuesta ante eventos inesperados, parámetros autoajustables y decisiones automáticas soportadas por bases de conocimiento dinámicas [12]. En este contexto, se ha incrementado el interés por los modelos neuro-difusos, y las principales razones son: a) el buen desempeño de las redes neuronales; b) la integración del conocimiento de expertos; y c) Las ventajas de extraer conocimiento a partir del conjunto de datos bajo el formato de reglas [13]. Así, los modelos difusos pueden ser adaptables o fijos [14] y se pueden combinar fácilmente con modelos bien conocidos de aprendizaje neuronal que reportan buen desempeño, entre ellos: redes de mapas auto-organizativos (SOM), Redes de Hopfield y aprendizaje por cuantificación vectorial (LVQ) [9]. Una combinación neurodifusa que ha ganado popularidad es el Sistema de Inferencia Neuronal Difuso Adaptativo (ANFIS) [15], que por su sistema de inferencia provee un mecanismo intuitivo y de alto nivel para representar el conocimiento mediante relaciones difusas de aprendizaje [16]. Aunque es conocido el buen desempeño de los modelos neuronales, difusos y neuro-difusos en aplicaciones automáticas, se presentan fuertes restricciones cuando se requiere implementar la identificación y control en sistemas cuyas perturbaciones le inducen dinámica estocástica [17] y más cuando no se cuenta con todos los datos, dada la dificultad de observar y seguir todos los estados operacionales [18].
En este artículo se presenta una revisión sobre las dificultades y soluciones derivadas del control de sistemas estocásticos o complejos cuando la dinámica del proceso presenta vaguedad en los datos. Se busca principalmente determinar los campos que aún quedan abiertos en esta área del conocimiento, a fin de inquietar hacia nuevas investigaciones que logren soluciones fácilmente adoptables por el sector industrial. Este estudio se presenta en el marco del proyecto de investigación PM10204, financiado por el ITM de Medellín.
II. SISTEMAS ESTOCÁSTICOS CON INFORMACIÓN INCOMPLETA: PERSPECTIVA DE CONTROL
Los sistemas estocásticos tienen una dinámica regida por patrones de comportamiento que aparte de contener cambios inesperados son variantes en el tiempo [2]. Todas las estrategias de modelado y control para este tipo de sistemas hacen hincapié en el análisis de la incertidumbre, porque en la medida en que un sistema se vuelve más complejo, también se hace más difícil el gobierno de su dinámica, por el incremento de la incertidumbre de cada variable [18]. Es así como el error de medición acumulada, las interacciones inciertas entre los subsistemas, y demás aspectos que incrementan la incertidumbre de un sistema, dificultan las tareas de modelado y control de procesos que de forma global adoptan patrones de comportamiento estocástico [19]. Aunque las incertidumbres provienen de diferentes fuentes, usualmente comparten características comunes, algunas son de naturaleza no lineal y otras de naturaleza estocástica [20]. Además, es frecuente que se involucren las siguientes causas: a) falta de claridad y conocimiento de los datos que surgen a partir del modelado y/o control, b) vaguedad en la transmisión y procesamiento de la información [18], c) vaguedad de los datos que proviene de la baja resolución de sensores o medición inapropiada [21], y d) la naturaleza estocástica del entorno que dificulta el análisis global del sistema [1]. En general, la teoría de control estocástico funciona bien siempre y cuando un modelo estocástico estándar esté disponible para ser ajustado, sin embargo, esta suposición puede no ser válida en aplicaciones de procesamiento con información reducida [22]. Así, la teoría general de control puede garantizar el rendimiento del sistema mediante la aplicación de un modelo matemático relativamente preciso de incertidumbre [23], pero limitaciones relacionadas al acceso completo de los datos hacen difícil la tarea en aplicaciones reales, donde las condiciones adversas pueden inducir patrones de comportamiento estocástico [18].
Numerosos métodos han surgido en los últimos años para el tratamiento de dinámicas de alta complejidad sobre modelos estocásticos. Por ejemplo, en [24] se propone un algoritmo híbrido inteligente de generación y asignación de espacios de probabilidad, donde luego de ser analizado el historial de los datos, se demuestra mediante ejemplos numéricos que el error no excede el 1.9% para diferentes configuraciones de parámetros del algoritmo, verificándose así su robustez y efectividad. Así también, el filtro de Kalman extendido, ampliamente usado para la estimación de ruidos aleatorios, en [25] es implementado exitosamente en aplicaciones de administración de energía dentro de un sistema de redes estocásticas, se obtienen errores de estimación del estado de la carga alrededor del 0.6%. Sin embargo, el rendimiento de este tipo de técnicas puede verse seriamente afectado frente a las limitaciones que producen las incertidumbres y la ausencia de datos, tales como: fallas numéricas, mala la calibración de los parámetros, vago seguimiento de la referencia real y alta sensibilidad a la incertidumbre de ganancia, información, estimación y escalamiento, según se describe en el estudio reportando en [21].
Los sistemas de control difuso han demostrado su capacidad para manejar incertidumbres mediante el mapeo de datos inciertos a un dominio lingüístico, y la fácil integración con las bondades de la computación neuronal para mejorar su rendimiento [26], sin embargo, la expresión lingüística puede no ser suficiente para mantener adecuadamente el desempeño del control frente a perturbaciones que inducen naturaleza estocástica al sistema, de manera que métodos de inferencia difusa, como Mamdani y Takagi Sugeno (TS) [16], no siempre aseguran resultados favorables bajo entornos estocásticos con información incompleta [27]. En [26], se observa mediante simulaciones de Monte Carlo que la integración de rutinas probabilísticas, para el análisis de incertidumbre, permite reducir el error en el 50%.
La perspectiva de control de los sistemas estocásticos con información incompleta cuenta con una variedad de métodos alternativos que han sido reportados en la literatura con buenos resultados de desempeño. Tal es el caso del Sistema Wavelet Probabilístico (PWS), presentado en [28], el cual se propone para modelar e identificar sistemas dinámicos desconocidos con naturaleza estocástica y datos incompletos. El PWS usa una función wavelet de 3 dominios que hace un balance entre probabilidad, tiempo y frecuencia, para lograr un esquema de modelado robusto cuando la información de los datos es pobre, pues supera al sistema wavelet (WS) tradicional en ambientes de dinámica estocástica y datos ruidosos. Los resultados para diferentes experimentos, se presentan en términos del error cuadrático medio (MSE) y se destaca que el error de identificación logrado con el PWS, oscila en la mitad del que se logra para el WS tradicional y es aún menor que el obtenido con una red neuronal de base radial (RBF). En particular, para uno de los experimentos, los resultados de MSE fueron: 71.48, 114.06 y 317.67 para PWS, WS y RBF, respectivamente. En [29] se propone una variación del teorema de Wonham para implementar un sistema de control óptimo por realimentación, considerado el problema de regulación estocástica para sistemas lineales con ruido dependiente de control y de estado. La validación sobre un sistema con información incompleta perturbado por ruido gaussiano arrojó mejores resultados que los obtenidos en sistemas con información completa. Desde otra perspectiva, el problema de las relaciones de preferencia difusa con información incompleta es estudiado en [30], con mínimos cuadrados para la toma de decisiones. Mediante la transformación entre la relación de preferencia multiplicativa y difusa, se desarrolló un modelo de mínimos cuadrados para obtener el vector de prioridad colectiva entre las relaciones de preferencia incompletas en máquinas de toma de decisión múltiple. A fin de comparar, se extendió el modelo a casos de preferencia difusa con información completa mediante máquinas de toma de decisión simple y múltiple, encontrándose que el método propuesto es factible y efectivo.
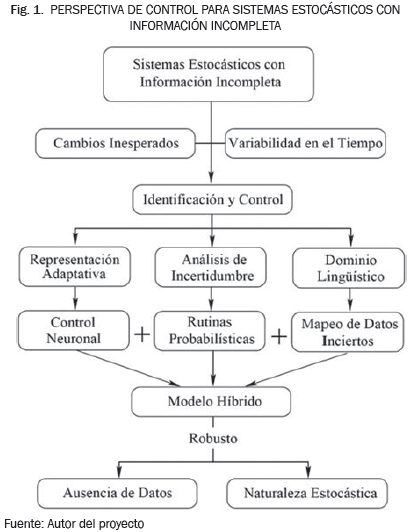
De acuerdo con la revisión presentada en esta sección, la Fig. 1 ilustra de manera general la perspectiva de control de sistemas estocásticos con información incompleta, donde aún quedan abiertas oportunidades de investigación al observar la importancia de analizar la incertidumbre inherente del proceso, o inducida por el entorno, mediante rutinas probabilísticas. Asimismo, la inclusión de un sistema de representación adaptativa (e.g., computación neuronal) y un dominio lingüístico amplio y suficiente que facilite el mapeo de datos inciertos. Desde el punto de vista de la aplicación, en términos de la viabilidad para ejecutar computacionalmente las técnicas, se resalta la necesidad de integrar los métodos de inteligencia computacional con procedimientos híbridos de representación y toma de decisiones en una plataforma conjunta, a fin de contrarrestar la ausencia de datos y la naturaleza estocástica de las interacciones de los subsistemas, al integrar además meta-algoritmos de optimización para disminuir el costo de cómputo.
III. ESQUEMAS ADAPTATIVOS PARA EL CONTROL DE SISTEMAS COMPLEJOS
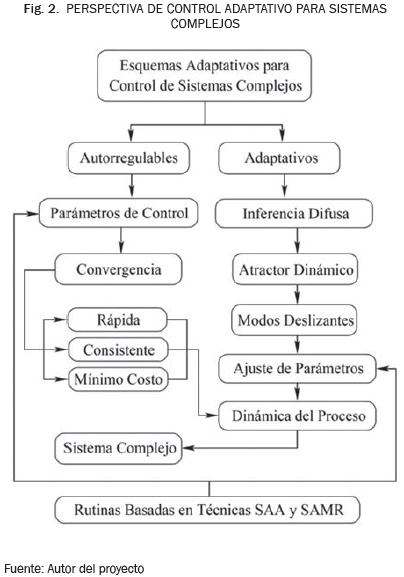
La evolución de la teoría de control ha logrado el desarrollo de técnicas, tanto de identificación auto-regulable como adaptativas mediante herramientas de cómputo [31]. El concepto adaptativo surge cuando se incorporan a la máquina, de forma estructural, habilidades humanas para la toma de decisiones, y en este contexto, se diseña un controlador cuyos parámetros son ajustados continuamente frente a los cambios en la dinámica del proceso, de forma que puede ser de dos tipos: directo e indirecto [32]. La mayoría de los esquemas adaptativos de control se han aplicado como extensiones de la técnica convencional PID [33]. De forma que los procedimientos involucrados en la sintonización automática de cada uno de los parámetros del controlador hacen parte de las rutinas que convierten un esquema de control clásico en control adaptativo [34] y fueron desarrollados originalmente para resolver los inconvenientes surgidos en procesos complejos que tienden a cambiar sus condiciones operativas a través del tiempo y a veces de manera inesperada [35]. La Fig. 2 presenta una perspectiva general de control adaptativo para sistemas complejos como resultado de la revisión de este tema en la literatura que se presenta a continuación.
La literatura reporta diferentes esquemas de control adaptativo para sistemas dinámicos complejos que consideran el enfoque desde la inteligencia computacional. Un estudio presentado en [36] propone ajustar el modelo de referencia de un controlador descentralizado mediante rutinas adaptativas y modos deslizantes aplicados a un sistema MIMO no lineal. Este diseño toma en cuenta la capacidad de aproximación universal que tienen los sistemas borrosos Takagi - Sugeno (TS).
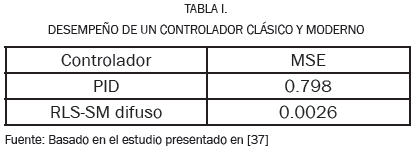
De manera experimental, se presenta la ventaja de no requerir conocimiento previo del límite superior del término de incertidumbre y, de forma analítica, el sistema de control difuso en lazo cerrado demuestra ser globalmente estable en el sentido de que todas las señales implicadas están delimitadas con errores de seguimiento que convergen a cero. De igual manera, en [37] se presenta el diseño de un controlador basado en Lógica Difusa Adaptativa (AFL) y Modos Deslizantes (SM), el cual es entrenado con la técnica de Mínimos Cuadrados Recursivos (RLS). El problema de la variación de parámetros es resuelto con el controlador adaptativo y se utiliza un regulador interno PI para lograr que el control de velocidad de un motor de inducción, con un torque de carga de 5 Nm, sea realizado por medio de las corrientes de estator y no mediante la variación de los voltajes. Adicionalmente, se usó el modelo del motor en las coordenadas de flujo orientado del rotor para comprobar la eficiencia del controlador, así como el error cuadrático medio (MSE) para comparar el desempeño entre un controlador PID convencional y el controlador difuso RLS-SM. Los resultados obtenidos se muestran en la Tabla I.
Es importante anotar que los esquemas adaptativos también han experimentado progresos importantes en el procesamiento de señales derivadas de sistemas complejos como los fisiológicos (señales electrocardiográficas y los potenciales evocados cerebrales, entre otros) y en aplicaciones a sistemas de telecomunicaciones [38]. Sin embargo, las aplicaciones sobre procedimientos autoajustables para estrategias de control de sistemas dinámicos complejos cada vez son más frecuentes, aun cuando las perturbaciones pueden llegar a adoptar naturaleza estocástica [39].
En [40] se presenta un estudio desde dos perspectivas de adaptación para estrategias de control con varianza mínima generalizada de dos grados de libertad (GMV2DOF). El primero es desde el modelo del proceso, donde se utiliza un estimador de mínimos cuadrados con algoritmos recursivos para el diseño del autoajuste directo; y el segundo utiliza una técnica difusa Mamdani para la programación de parámetros GMV2DOF basada en interpretaciones analíticas y físicas de la robustez del sistema. Se demostró que existen ventajas con la programación difusa cuando se requiere adaptar el sistema de control a procesos complejos desconocidos. En otro estudio expuesto en [41], se diseña un controlador adaptativo difuso soportado en la técnica backstepping para el control de temperatura de una clase de reactores con tanque agitado continuo (CSTRs), los cuales son sistemas fuertemente inestables. Se utiliza la lógica difusa para estimar las condiciones de concentración dependientes y otros parámetros del sistema que tienen alto nivel de incertidumbre. Los resultados muestran que el sistema controlado en lazo cerrado se lleva a un estado de operación asintóticamente estable y el error de aproximación por perturbación externa es mínimo. Un trabajo inspirado por la alta complejidad embebida en los datos de carga eléctrica es descrito en [42], donde se presenta una combinación de esquemas difusos adaptativos, redes de mapas auto-organizativos (SOM), también llamadas redes de Kohonen, y sistemas de regresión por vectores de soporte (SVR), con el fin de obtener simultáneamente altos niveles de precisión e interpretabilidad en la predicción de la carga eléctrica. El éxito de este modelo consistió en la inclusión de una base comprensible de conocimiento humano, y la construcción de una función de pertenencia difusa homogénea para cada subgrupo. Adicionalmente, se mostró una comparación con diferentes modelos matemáticos y se probó la eficiencia del desempeño con datos reales, donde los resultados confirmaron la validez del método propuesto.
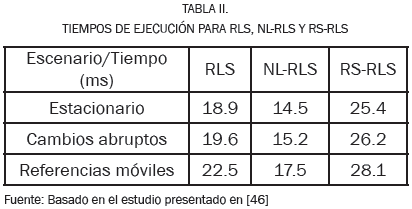
Desde hace tres décadas, se ha tenido reporte del buen impacto en procesos industriales de los Sistemas Auto-Ajustables (SAA) y Sistemas Adaptativos con Modelo de Referencia (SAMR) [43]. Los SAA fueron propuestos conceptualmente en [44], y establecidos experimentalmente en [45], donde el autoajuste se basa en el conocimiento del modelo para adaptarse a los cambios mediante procedimientos recursivos asociados a los parámetros del proceso. Sin embargo, el principal inconveniente es que la estabilidad no puede ser asegurada de manera global. En los últimos años, esta técnica ha sido combinada con otros métodos de identificación basados en mínimos cuadrados recursivos (RLS), obteniéndose notables niveles de desempeño en términos de precisión, sensibilidad y tiempo de autoajuste ante procesos estacionarios, dinámicas con cambios abruptos y seguimiento de referencias móviles [46]. En la Tabla II se observa la comparación entre los tiempos de ejecución bajo las mismas condiciones de cómputo para los métodos RLS, RLS no lineal (NLRLS) y RLS de sensibilidad reducida (RS-RLS).
De manera alternativa, los SAMR se basan en que el comportamiento del proceso sea idéntico a un modelo de referencia. Así, cuando existe una diferencia entre la entrada y la salida, el mecanismo de adaptación intenta minimizarla con el ajuste de los parámetros del regulador, tal y como se propone en [47], permitiendo que el sistema responda de forma apropiada ante perturbaciones inesperadas variables en el tiempo. En el contexto de sistemas complejos, la literatura reporta numerosos trabajos basados en técnicas SAA y SAMR, mediante estructuras híbridas con rutinas modernas de inteligencia computacional, donde se reportan soluciones promisorias para el control de sistemas no lineales inestables, en ambientes que además inducen apreciables niveles de incertidumbre [33], [48]. Por su parte, los esquemas de Control Adaptivo de Modelo Múltiple (MMAC) han ganado un buen lugar de preferencia en aplicaciones sobre procesos complejos. La teoría de MMAC establece que un sistema complejo desconocido puede llegar a ser la combinación de un conjunto finito de sistemas lineales invariantes en el tiempo, de manera que el ajuste a las respuestas no lineales del sistema real podría lograrse mediante la inclusión de un modelo de incertidumbre acotado, aditivo o multiplicativo. En [49] se presenta un estudio donde se analizan esquemas MMAC y se establece que si el número de modelos es suficientemente grande y está uniformemente distribuido en el espacio de parámetros, el método ofrece una respuesta rápida y precisa. Asimismo, diferentes procedimientos son propuestos para lograr buenos resultados usando un número de modelos significativamente pequeño. Sin embargo, las aplicaciones reales en la industria, donde los sistemas dinámicos tienden a ser considerablemente complejos, exigen que el número de modelos se incremente si se quiere sostener un desempeño favorable en términos de identificación y control del proceso.
De acuerdo con la revisión de los trabajos mencionados en esta sección y desde el punto de vista de la aplicación orientada a la viabilidad para ejecutar computacionalmente las técnicas, es importante resaltar que los sistemas complejos, por sus características dinámicas, requieren ser controlados mediante esquemas adaptativos que dependen fuertemente de la eficiencia de las técnicas de autoajuste que optimizan los parámetros del controlador. Esta es la razón por la que muchos de los esfuerzos reportados en la literatura reciente, se concentran en la obtención de rutinas de optimización que ofrezcan una convergencia de autoajuste cada vez más rápida, consistente y de mínimo costo operacional y computacional, pues buscan máximo rendimiento en términos de precisión y sensibilidad, para su aplicación en tiempo real.
IV. MODELOS NEURO-DIFUSOS PARA EL CONTROL DE SISTEMAS COMPLEJOS CON INCERTIDUMBRE
Ya es bien conocido en la literatura que las redes neuronales, debido a la capacidad de adaptación de sus elementos procesales (i.e., neuronas), están dotadas de una dinámica que constantemente cambia para ajustarse a nuevas condiciones, mediante procedimientos basados en iteraciones que conforman la etapa de entrenamiento [9], [7]. Se han propuesto diferentes modelos híbridos que combinan las fortalezas de las redes neuronales y la lógica difusa (i.e., modelos neurodifusos) para el control de sistemas complejos que incluyen apreciables niveles de incertidumbre, debido a la facilidad que tienen para combinar el razonamiento difuso con el manejo de información incierta [50], [51]. Es, por tanto, que los modelos neuro-difusos son entendidos en la literatura como una herramienta potente que posee los méritos de bajo nivel para el aprendizaje, junto a la potencia de cálculo de las redes neuronales, además del pensamiento de alto nivel, similar al humano, que ofrece el razonamiento lógico de las técnicas difusas [52].
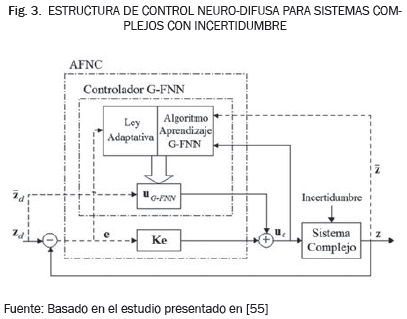
En orden de controlar sistema complejos cuando existen niveles de incertidumbre en los parámetros de operación, en [53] se propone un esquema de control neuronal difuso adaptativo por modos deslizantes enriquecido con rutinas auto-organizativas. En este esquema, la fase de entrenamiento estructural posee la habilidad de generar y eliminar en línea las reglas difusas requeridas para lograr la estructura neuronal óptima, y la fase de entrenamiento paramétrico ajusta los pesos de interconexión de la red neuronal a fin de lograr un desempeño de aproximación favorable. El entrenamiento paramétrico es basado en funciones de Lyapunov, de forma que se pueda garantizar la estabilidad del sistema. De manera similar, en [54] se aborda el diseño y análisis de un sistema de control adaptativo neuro-difuso robusto para la sincronización de sistemas caóticos con incertidumbre. El sistema propuesto se compone de una etapa de identificación lograda por una red neuro-difusa (NFN) de cuatro capas y un controlador supervisado que concentra su esfuerzo en atenuar los efectos del error de aproximación. El identificador NFN es también el regulador principal utilizado para la valoración en línea de las incertidumbres compuestas. Este estudio resuelve los problemas relacionados con la convergencia de la red y la estabilidad de la sincronización adaptativa mediante el método directo de Lyapunov, bajo la suposición de que el estado del sistema principal genera las trayectorias de referencia, a pesar de la incertidumbre que se embebe en la dinámica operativa del sistema. Otros estudios se concentran en una de las tareas más exigentes que tiene la ingeniería de control, relacionada con el diseño efectivo de controladores robustos en tiempo real para sistemas complejos de múltiples entradas y múltiples salidas (MIMO), especialmente cuando se requieren mecanismos de reacción rápida frente a perturbaciones externas fuertes con altos niveles de incertidumbre. En la Fig. 3, se ilustra el enfoque presentado en [55], donde se propone un esquema de control neurodifuso adaptativo (AFNC) basado en un algoritmo de aprendizaje genético con redes neuro-difusas (G-FNN) para la identificación y control de un sistema MIMO no lineal.
El controlador de la Fig. 3 cuenta con las siguientes características: a) estructura neuronal difusa auto-organizativa, i.e., las reglas pueden ser generadas o borradas de manera automática; b) capacidad de aprendizaje en línea para aplicaciones sobre sistemas MIMO no lineales con incertidumbre; c) velocidad de aprendizaje rápida; d) control adaptativo; e) control robusto con estabilidad global establecida según el método de Lyapunov. Este estudio concluyó que los modelos neuro-difusos adaptativos ofrecen una tasa de convergencia rápida y demuestran capacidad suficiente para manejar los errores de modelado y perturbaciones externas en sistemas no lineales con incertidumbre. De manera complementaria, en [56] se toma el mismo enfoque de la estructura mostrada en la Fig. 3, pero en este caso se consideran los sistemas complejos de una entrada y una salida (SISO) con incertidumbre, y se propone la implementación de un controlador difuso adaptativo por modos deslizantes (AFSMC). El procedimiento basado en lógica difusa se usa para aproximar la función del sistema complejo desconocido y el algoritmo AFSMC se diseña para usarse como técnica de control. De acuerdo con la teoría de Lyapunov, se establece una función continua para eliminar la acción del ruido de la señal de control. La simplicidad de este método facilita su implementación y, en general, el esquema de control garantiza la estabilidad asintótica global si todas las señales son uniformemente acotadas. Los resultados de este estudio dejan ver que el AFSMC supera notablemente en términos de rendimiento al controlador por modos deslizantes tradicional. Otro estudio reportado en [57], presenta el esquema de un control difuso de estructura variable por modos deslizantes con el objetivo de regular la velocidad de un motor en las unidades de un filtro de ventilación, el cual se caracteriza por su alta no linealidad, variabilidad en el tiempo y naturaleza multivariable compleja. Los resultados de este estudio muestran el buen desempeño del esquema propuesto de control a este tipo de sistemas en términos de robustez en la estabilidad lograda, como en los apropiados márgenes conseguidos en la respuesta transitoria. En [58], otro estudio analiza la viabilidad de los controladores basados en Sistemas de Inferencia Neuro-Difusa Adaptativa (ANFIS) para el control de sistemas complejos con incertidumbre, y han encontrado que estos sistemas tienen la capacidad de dividir los datos en grupos para incrementar el nivel de adhesión a ellos y producir mayor poder de adaptación, velocidades de respuesta más rápidas, y una mayor precisión y robustez ante perturbaciones inesperadas. Adicionalmente a esto, la literatura reporta numerosos estudios que proponen derivaciones o extensiones de la estructura de control presentada en la Fig. 3, donde se destaca la forma en que los modelos neuro-difusos son potenciados con el poder de optimización que tienen los algoritmos genéticos [59]. En [60], por ejemplo, se presenta la integración de un Algoritmo Genético de forma Reducida (RGA) con un Controlador Neuro-difuso de Adaptación Indirecta, en un sólo algoritmo denominado RIAFC y aplicado a sistemas complejos con incertidumbre. Se incluye una función de ajuste en el RGA para sintonizar los parámetros en línea y evaluar la estabilidad del sistema en lazo cerrado, además de incorporarse un controlador supervisado en el RIAFC para garantizar que los estados del sistema sean limitados a la región estable. Los resultados confirman la factibilidad y aplicabilidad del método propuesto en aplicaciones reales, como la ventaja de incluir mecanismos de optimización tan potentes como son los algoritmos genéticos.
De acuerdo con los estudios revisados en esta sección, numerosas aplicaciones de control han sido propuestas mediante modelos neuro-difusos en sistemas complejos con incertidumbre para obtener diferentes grados de eficiencia. Como un primer aspecto, es importante mencionar que respecto a otras técnicas de control, las ventajas de los modelos neuro-difusos son evidentes si se considera que ya no es requerida la obtención precisa de modelos matemáticos del proceso, además de contar con la posibilidad de incluir el conocimiento de expertos en la ley de control [61]. Un segundo aspecto a considerar tiene que ver con las dificultades que tienen los modelos neurodifusos para lograr el autoajuste adecuado de sus parámetros, puesto que los procedimientos de auto-sintonización aún reportan problemas para la inicialización de los parámetros de operación, o en algunos casos, la velocidad de aprendizaje y adaptación es muy lenta en relación con la velocidad del proceso a controlar. Visto de una manera general, se puede decir que el mal ajuste de los parámetros puede reducir la flexibilidad y la capacidad de procesamiento numérico del controlador, convirtiendo el sistema en ineficiente o redundante. En particular, si los parámetros relacionados con el número de capas ocultas o el número de reglas difusas son muy grandes, se vuelve prohibitiva la implementación del sistema en tiempo real, por lo que no habría ningún interés desde la industria para este tipo de soluciones. Como tercer y último aspecto de esta sección, es importante notar la resaltable capacidad que tienen los modelos neuro-difusos para capturar la dinámica directa e inversa de los procesos complejos, con incertidumbres y variantes en el tiempo; además de demostrar alta versatilidad y robustez para las operaciones de control. Sin embargo, desde el punto de vista de la aplicación orientada a la viabilidad de cómputo para ejecutar las técnicas, no siempre es fácil recolectar la suficiente información de un sistema complejo con incertidumbres, para la fase de entrenamiento de las redes, desde el mismo lugar de operación cuando el ambiente industrial es adverso, además de la dificultad asociada a la complejidad de procesamiento que exige contener en un conjunto reducido de expresiones lingüísticas todas las variaciones posibles de un proceso real. Por esto el diseño de estrategias para entrenar efectivamente sistemas neurodifusos con conjuntos reducidos y no balanceados de datos, es un campo que sigue abierto en la literatura.
V. MODELOS NEURO-DIFUSOS PARA SISTEMAS ESTOCÁSTICOS CON INFORMACIÓN INCOMPLETA
Las redes neuronales han sido usadas para un gran número de aplicaciones en control de sistemas que presentan respuesta estocástica cuando son sometidos a determinadas condiciones de entrada, y muchas de esas aplicaciones dependen de la estabilidad de la misma red [62], [63], [64], [65]. Tomado en cuenta que los sistemas reales son generalmente afectados por una cantidad considerable de perturbaciones externas, es muy importante tomar en cuenta los efectos estocásticos para asegurar las condiciones de estabilidad de las redes neuronales, incluido los efectos de retardo por transmisión [66], [67]. De otra parte, los sistemas de control automático han recibido contribuciones importantes de procedimientos basados en modelos difusos, los cuales tienen como objetivo alcanzar mejores niveles de precisión, dimensionalidad y simplicidad en la estructura de los sistemas no lineales. Comparado con los modelos matemáticos convencionales, la ventaja de los modelos difusos consiste en tener la posibilidad de construirlos con el mínimo esfuerzo matemático derivado del sistema, además de la capacidad que tienen para aproximarse a una clase amplia de sistemas no lineales [16]. Como se ha comentado en secciones anteriores de esta revisión, el concepto de incorporar lógica difusa dentro de una red neuronal ha crecido y se ha popularizado en los temas de investigación por su buen desempeño y amplio rango de aplicabilidad [68], [69], [70]. Sin embargo, se ha demostrado que ciertas perturbaciones estocásticas (e.g., del tipo de Ornstein-Uhlenbeck con reversión a la media) podrían desestabilizar este tipo de redes [20], por lo que se ha propuesto analizar las propiedades de pasividad del sistema en orden de determinar los márgenes de estabilidad [71], [72]. La presencia de factores inevitables, como es el error de modelado, aparición inesperada de perturbaciones externas y la fluctuación de parámetros durante la implementación física, inducen a las redes neuronales incertidumbres y variaciones en los componentes, que afectan considerablemente la pasividad del sistema completo. En este sentido, con el fin de analizar la incertidumbre que puede llegar a ser inducida en una red neuronal, se han propuesto procedimientos simples que consisten en asumir parámetros en ciertos intervalos [73], [74]. Es importante resaltar que la teoría de pasividad fue originada del análisis de circuitos y se ha convertido en una herramienta útil para analizar la estabilidad de los sistemas [75]. El análisis de pasividad de los modelos de control neuro-difuso ha sido ampliamente discutido en varios trabajos de la literatura [76], [77], [78]. La extensión de este análisis para aplicaciones que involucran ausencia de información o incertidumbres en las variables estocásticas con retrasos es estudiado en [79], donde dichas incertidumbres se asumen acotadas en conjuntos compactos dados y las redes neuro-difusas usan una función de activación generalizada que descarta presunciones de acotamiento, monotonía y diferenciabilidad. Se propone la construcción de un funcional Lyapunov-Krasovskii propio y la combinación del método de la matriz libremente ponderada con técnicas de análisis estocástico, en orden de obtener nuevas condiciones de pasividad dependiente de los retardos y en función de desigualdades matriciales lineales (LMIs), lo cual puede ser resuelto mediante paquetes numéricos estándar. Los resultados reportan que una red neuronal difusa estocástica con incertidumbres satisface la condición de pasividad dependiente de retardos robustamente hasta una cota superior permitida de τ = 0.9897, la cual es menos conservativa que otras reportadas en la literatura. Un estudio presentado en [80] discute el tratamiento de la estabilidad global y exponencial de la incertidumbre estocástica mediante modelos neuro-difusos Takagi-Sugeno, donde se explota el poder que tienen las redes para representar los modelos variantes en el tiempo y a partir del enfoque Lyapunov-Krasovskii se obtienen las condiciones de estabilidad. También se incluyen técnicas basadas en LMIs para demostrar la exactitud de los resultados teóricos. Este estudio deja abierto el caso de múltiples variables con tiempo de retardo, incluido tanto los retrasos discretos y distribuidos, como los efectos ocasionados en términos de estabilidad. En [81] se aplican modelos neuro-difusos a cadenas de suministro inmersas en un ambiente estocástico, donde a pesar que la información es reducida o algunas veces incompleta, se logra un pronóstico realista en relación con los costos y presupuestos, así como el menor número de suministro de la cadena de valor respecto a la demanda. Este método ofrece resultados que sugieren su aplicación a casos reales y aun puede ampliarse para la consideración de múltiples productos con más canales de información o considerarse un mayor número de variables por aproximaciones neurodifusas para lograr mayor fidelidad en el modelo. Otro estudio se presenta en [82], donde se implementa un método denominado Red Neuronal Difusa Estocástica (SFNN), el cual está formado por un algoritmo genético a fin de obtener soluciones al problema de la relación entre la cantidad y la calidad del agua en un depósito, dado que no existen muchas técnicas para este tipo de optimización y se presentan limitaciones en relación al acceso completo de la información, promoviendo otra cantidad de limitaciones operativas. El modelo propuesto fue probado para diferentes funciones recursivas y la optimización fue llevada a cabo usando 6 diferentes SFNN, lo cual permitió mejoras potenciales en la calidad del agua a través de medios de control hidráulico. Esta técnica basada en SFNN ya había sido propuesta en [83], donde fue definida como un modelo neuro-difuso entrenado estocásticamente, que puede alcanzar soluciones "quasi" óptimas, e intenta superar los inconvenientes involucrados en el trabajo con los modelos de programación dinámica estocástica. Las incertidumbres inducidas por la información incompleta son tratadas mediante la probabilidad condicional de los eventos difusos. Los resultados mostraron la viabilidad del uso de las SFNN y las bondades que ofrecen en términos de optimización. Finalmente, en esta revisión vale la pena destacar el buen desempeño que ofrecen las redes ANFIS con análisis de frontera estocástica (ANFIS-SFA), las cuales son recomendadas para aplicaciones reales donde están involucrados problemas de complejidad, ambigüedad, vaguedad en los datos, dinámica estocástica y componentes difusas, que con frecuencia dificultan los procesos de control. Un estudio reportado en [84], presenta una adaptación del método ANFIS-SFA para el análisis del comportamiento y predicción del consumo de gas natural a largo plazo. Se entrenan los datos con ANFIS, mediante seis modelos distintos basados en diferentes entradas y se comparan los modelos con respecto a la media del error absoluto porcentual. Se usa un modelo auto-regresivo para proyectar el Producto Interno Bruto (PIB) y la población para el período 2008-2015. Estos datos proyectados se utilizan como entrada del modelo ANFIS y el SFA se usa para examinar el comportamiento del consumo de gas en años anteriores y establecer tendencias para los años próximos. En este estudio se resalta el enfoque ANFIS-SFA, el cual demuestra su capacidad para manejar la complejidad, la incertidumbre y el azar en un sistema estocástico.
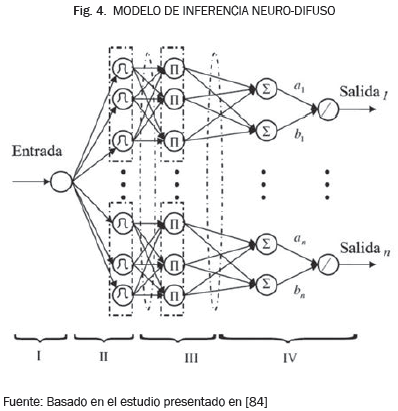
Los sistemas reales obedecen a una dinámica multivariada e interactuante, que fácilmente es influenciada, perturbada o integrada por incertidumbres de diversas clases, las cuales inducen naturaleza estocástica al proceso global y algunas veces llegan a afectar la completitud de los datos. De acuerdo con la revisión presentada en esta sección, los modelos neuro-difusos cuentan con las características dinámicas suficientes para superar los inconvenientes inherentes a la dinámica estocástica de los sistemas que además no cuentan con información completa de sus variables de proceso. En general, los modelos neurodifusos ofrecen una gran flexibilidad para optimizar diferentes tipos de funciones recursivas, dado que las reglas de decisión difusa y los parámetros de relación entre ellas pueden tomarse desde una gama amplia de posibilidades. Adicionalmente, la literatura reporta numerosas formas en que estos modelos pueden ser potenciados al integrar otros esquemas derivados del análisis estadístico, evolutivo o de la teoría de información. La Fig. 4 presenta el esquema de un modelo de inferencia neuro-difuso, el cual permite intuir ventajas relacionadas con el enorme potencial en aplicaciones de control estocástico para sistemas con información incompleta. Entre las principales ventajas, se pueden destacar la adaptabilidad, flexibilidad, robustez y facilidad matemática, en tareas que exijan el desarrollo de soluciones en el marco de una fácil implementación. Sin embargo, desde el punto de vista de la aplicación orientada a la viabilidad para ejecutar computacionalmente las técnicas quedan muchos campos abiertos en la literatura, en relación con la optimización de la topología del modelo o del mismo proceso de entrenamiento.
VI. CONCLUSIONES Y RECOMENDACIONES
En la práctica se ha vuelto frecuente encontrar sistemas cuyo entorno de operación induce fuertes perturbaciones de naturaleza compleja o estocástica, donde resulta afectada de manera considerable la observabilidad de todos los estados. En este artículo se presenta una revisión sobre el control de sistemas estocásticos o complejos con información incompleta, donde se destaca la necesidad de crear nuevos modelos que permitan mejorar el manejo de la incertidumbre cuando los datos son reducidos o incompletos. De acuerdo con las tendencias de la literatura en sistemas de control, este tipo de sistemas puede soportarse en las bondades que ofrecen las redes neurodifusas, en orden de asegurar el seguimiento de dinámicas pre-establecidas, dada la robustez que aportan los motores de inferencia difusa y la capacidad de adaptación que tienen las redes neuronales. En este sentido, se resaltó la tendencia actual de integrar en una plataforma conjunta los métodos de inteligencia computacional, con procedimientos híbridos de representación, optimización y toma de decisiones, a fin de contrarrestar la ausencia de datos y la naturaleza estocástica de las interacciones de los subsistemas. Aunque desde el punto de vista de la aplicación, se resaltan dificultades importantes relacionadas con la complejidad de procesamiento, donde se abren nuevas oportunidades de investigación orientadas a obtener mayor viabilidad de cómputo para la ejecución de las técnicas.
La revisión sobre esquemas adaptativos de control para sistemas complejos identificó que la mayoría de las técnicas son en alguna medida derivaciones o extensiones del esquema de control convencional PID, donde predominan las aplicaciones híbridas por modos deslizantes. Debido a que estos esquemas dependen fuertemente de la eficiencia de las técnicas de autoajuste, las cuales optimizan los parámetros del controlador, se percibe la necesidad de aumentar los esfuerzos investigativos enfocados al mejoramiento de estas técnicas, buscando facilidades de implementación en tiempo real sin comprometer los niveles de precisión y robustez.
La revisión presentada sobre modelos neurodifusos permitió resaltar su capacidad para capturar la dinámica directa e inversa de procesos complejos, con incertidumbres y variantes en el tiempo; además de demostrar alta versatilidad y robustez para diversas aplicaciones de control. También se detectaron las dificultades que tienen estos modelos para lograr el autoajuste óptimo de sus parámetros, puesto que los procedimientos de auto-sintonización siguen reportando problemas respecto a criterios adecuados de inicialización. Este inconveniente algunas veces provoca que la velocidad de aprendizaje y adaptación sea muy lenta en relación con la velocidad del proceso a controlar.
Al enfocar la revisión de los modelos neurodifusos hacia sistemas estocásticos con información incompleta, se destaca la facilidad con que estos modelos pueden ser altamente potenciados a partir de la integración con otros esquemas de procesamiento, e.g., para aprovechar las ventajas que ofrece el análisis estadístico, evolutivo o la teoría de información, a fin de estructurar soluciones más robustas y confiables, aunque no siempre pueda asegurarse la fácil implementación. En general, se puede concluir de la literatura, que los modelos neuro-difusos cuentan con las características dinámicas suficientes para superar los inconvenientes inherentes a la dinámica estocástica, en sistemas que además pueden tener el inconveniente de no contar con la información completa de sus variables de proceso.
AGRADECIMIENTOS
Este artículo se presenta en el marco del proyecto de investigación PM10204, financiado por el Instituto Tecnológico Metropolitano -ITM de Medellín.
REFERENCIAS
[1] W. H. Gao and F. Q. Deng, "Parameter-dependent robust stability for nonlinear distributed delay stochastic systems with polytopic-type uncertainties," in Proc. 2009 Conference on Machine Learning and Cybernetics, Vol. 6, pp. 3684-3689. [ Links ]
[2] A. Hossain, Z. A. Choudhury and S. Suyut, "Statistical Process Control of an Industrial Process in Real Time," IEEE Transactions on Industry Applications, Vol. 32, No. 2, pp. 243-249, Apr. 1996. [ Links ]
[3] P. Liu and H. Li, "Approximation of stochastic processes by T-S fuzzy systems," Fuzzy Sets and Systems, Vol. 155, No. 2, pp. 215-235, Oct. 2005. [ Links ]
[4] A. Toola, "The safety of process automation," Automatica, Vol. 29, No. 2, pp. 541-548, Mar. 1993. [ Links ]
[5] J. C. Rodríguez-Gamboa, E. S. Albarracín and E. Delgado-Trejos, "Quality Control Through Electronic Nose System," in Modern Approaches to Quality Control, A. B. Eldin, Ed., Rijeka Croatia: InTech, 2011, pp. 505-522. [ Links ]
[6] K. L. Hsieh, L. I. Tong and M. C. Wang, "The application of control chart for defects and defect clustering in IC manufacturing based on fuzzy theory," Expert Systems with Applications, Vol. 32, No. 3, pp. 765-776, Apr. 2007. [ Links ]
[7] R. Del-Hoyo, B. Del-Brío, N. Medrano and J. Fernández, "Computational intelligence tools for next generation quality of service management," Neurocomputing, Vol. 72, No. 16-18, pp. 3631-3639, Oct. 2009. [ Links ]
[8] Y. V. Pehlivanoglu and O. Baysal, "Vibrational genetic algorithm enhanced with fuzzy logic and neural networks," Aerospace Science and Technology, Vol. 14, No. 1, pp. 56-64, 2012. [ Links ]
[9] I. S. Baruch, R. Beltran, J. L. Olivares and J. M. Flores, "A fuzzy-neural multi-model for nonlinear systems identification and control," Fuzzy Sets and Systems, Vol. 159, No. 20, pp. 2650-2667, Oct. 2008. [ Links ]
[10] J. Sanz, A. Fernández, H. Bustince and F. Herrera, "A genetic tuning to improve the performance of Fuzzy Rule-Based Classification Systems with Interval-Valued Fuzzy Sets: Degree of ignorance and lateral position," International Journal of Approximate Reasoning, Vol. 52, No. 6, pp. 751-766, Sep. 2011. [ Links ]
[11] V. Novák, "Reasoning about mathematical fuzzy logic and its future," Fuzzy Sets and Systems, Vol. 192, No. 1, pp. 25-44, Apr. 2012. [ Links ]
[12] N. R. Abburi and U. S. Dixit, "A knowledge-based system for the prediction of surface roughness in turning process," Robotics and Computer-Integrated Manufacturing, Vol. 22, No. 4, pp. 363-372, Aug. 2006. [ Links ]
[13] F. Villada, E. García and J. D. Molina, "Electricity Price Forecasting using Neuro-Fuzzy Networks," Información Tecnológica, Vol. 22, No. 6, pp. 111-120, 2011. [ Links ]
[14] P. M. Marusak, "Advantages of an easy to design fuzzy predictive algorithm in control systems of nonlinear chemical reactors," Applied Soft Computing, Vol. 9, No. 3, pp. 1111-1125, Jun. 2009. [ Links ]
[15] L. Naderloo, R. Alimardani, M. Omid, F. Sarmadian, P. Javadikia, M. Y. Torabi, and F. Alimardani, "Application of ANFIS to predict crop yield based on different energy inputs," Measurement, Vol. 45, No. 6, pp. 1406-1413, Jul. 2012. [ Links ]
[16] T. Takagi and M. Sugeno "Fuzzy identification of systems and its application to modeling and control," IEEE Transactions on Systems, Man, and Cybernetics, Vol. 15, No. 1, pp. 116-132, Jan. 1985. [ Links ]
[17] A. Zhang, "Robust Reliable Fuzzy Control for Uncertain Markovian Jump Singular Systems," in Proc. 5th Int. Conf. Fuzzy Systems and Knowledge Discovery (FSKD'08), Vol. 1, pp. 406-410, Oct. 2008. [ Links ]
[18] H. X. Li and Z. Liu, "A Probabilistic Fuzzy Logic System: learning in the stochastic environment with incomplete dynamics," in Proc. 2009 IEEE Int. Conf. Systems, Man and Cybernetics (SMC'09), pp. 383-388. [ Links ]
[19] S. Ushida, "Control performance improvements due to fluctuations in dynamics of stochastic control systems," in Proc. 50th IEEE Conf. on Decision and Control and European Control Conf. (CDC-ECC'11), pp. 1430-1436, 2011. [ Links ]
[20] H. Yang and L. Sheng, "Robust stability of uncertain stochastic fuzzy cellular neural networks," Neurocomputing, Vol. 73, No. 1-3, pp. 133-138, Dec. 2009. [ Links ]
[21] T. Shibata, "The impacts of uncertainties in a real options model under incomplete information," European Journal of Operational Research, Vol. 187, No. 3, pp. 1368-1379, Jun. 2008. [ Links ]
[22] S. K. Mitter, "Filtering and stochastic control: A historical perspective," IEEE Control Systems, Vol. 16, No. 3, pp. 67-76, Jun. 1996. [ Links ]
[23] P. Dorato, "A historical review of robust control," IEEE Control Systems Magazine, Vol. 7, No. 2, pp. 44-47, Apr. 1987. [ Links ]
[24] J. Zhou and B. Liu, "New stochastic models for capacitated location-allocation problem," Computers and Industrial Engineering, Vol. 45, No. 1, pp. 111-125, Jun. 2003. [ Links ]
[25] L. Xu, J. Wang and Q. Chen, "Kalman filtering state of charge estimation for battery management system based on a stochastic fuzzy neural network battery model," Energy Conversion and Management, Vol. 53, No. 1, pp. 33-39, Jan. 2012. [ Links ]
[26] H. Li, and Z. Liu, "A Probabilistic Neural-Fuzzy Learning System for Stochastic Modeling," IEEE Transactions on Fuzzy Systems, Vol. 16, No. 4, pp. 898-908, Aug. 2008. [ Links ]
[27] Z. Chen, L. Zhao and K. Lee, "Environmental risk assessment of offshore produced water discharges using a hybrid fuzzy-stochastic modeling approach," Environmental Modelling and Software, Vol. 25, No. 6, pp. 782-792, Jun. 2010. [ Links ]
[28] Z. Liu, H. X. Li, and Y. Zhang, "A Probabilistic Wavelet System for Stochastic and Incomplete Data-Based Modeling," IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, Vol. 38, No. 2, pp. 310-319, Apr. 2008. [ Links ]
[29] F. Carravetta and G. Mavelli, "Suboptimal stochastic linear feedback control of linear systems with state-and control-dependent noise: The incomplete information case," Automatica, Vol. 43, No. 5, pp. 751-757, May. 2007. [ Links ]
[30] Z. W. Gong, "Least-square method to priority of the fuzzy preference relations with incomplete information," International Journal of Approximate Reasoning, Vol. 46, No. 2, pp. 258-264, Feb. 2008. [ Links ]
[31] V. A. Akpan and G. D. Hassapis, "Nonlinear model identification and adaptive model predictive control using neural networks," ISA Transactions, Vol. 50, No. 2, pp. 177-194, Apr. 2011. [ Links ]
[32] G. Stein and G. N. Saridis, "A parameter-adaptive control technique," Automatica, Vol. 5, No. 6, pp. 731-739, Nov. 1969. [ Links ]
[33] K. K. Tan, T. H. Lee and X. Jiang, "Robust on-line relay automatic tuning of PID control systems," ISA Transactions, Vol. 39, No. 2, pp. 219-232, Apr. 2000. [ Links ]
[34] Y. Lim, R. Venugopal and A. G. Ulsoy, "Auto-tuning and adaptive control of sheet metal forming," Control Engineering Practice, Vol. 20, No. 2, pp. 156-164, Feb. 2012. [ Links ]
[35] R. Hoskinson, K. Van den Doel and S. Fels, "Realtime adaptive control of modal synthesis," in Proc. 2003 Conf. on New Interfaces for Musical Expression (NIME'03), pp. 99-103. [ Links ]
[36] H. Gu, T. Zhang and Q. Shen, "Decentralized model reference adaptive sliding mode control based on fuzzy model," Journal of Systems Engineering and Electronics, Vol. 17, No. 1, pp. 182-186, Mar. 2006. [ Links ]
[37] S. Sánchez and E. Giraldo, "Speed control of induction motor using fuzzy recursive least squares technique," Revista Tecno Lógicas, Vol. 2008, No. 21, pp. 99-111, Dec. 2008. [ Links ]
[38] D. S. Brito, E. Aguiar, F. Lucena, R. C. S. Freire, Y. Yasuda and A. K. Barros, "Influence of low frequency noise in adaptive estimation using the LMS algorithm," Signal Processing, Vol. 89, No. 5, pp. 933-940, 2009. [ Links ]
[39] Z. Cao, Q. Mu, L. Hu, Y. Liu and L. Xuan, "Improve the loop frequency of liquid crystal adaptive optics by concurrent control technique," Optics Communications, Vol. 283, No. 6, pp. 946-950, Mar. 2010. [ Links ]
[40] A. S. Silveira, J. E. N. Rodríguez and A. A. R. Coelho, "Robust design of a 2-DOF GMV controller: A direct self-tuning and fuzzy scheduling approach," ISA Transactions, Vol. 51, No. 1, pp. 13-21, Jan. 2012. [ Links ]
[41] S. Salehi and M. Shahrokhi, "Adaptive fuzzy backstepping approach for temperature control of continuous stirred tank reactors," Fuzzy Sets and Systems, Vol. 160, No. 12, pp. 1804-1818, Jun. 2009. [ Links ]
[42] J. Che, J. Wang and G. Wang, "An adaptive fuzzy combination model based on self-organizing map and support vector regression for electric load forecasting," Energy, Vol. 37, No. 1, pp. 657-664, Jan. 2012. [ Links ]
[43] K. J. Aström, "Theory and applications of adaptive control - A survey," Automatica, Vol. 19, No. 5, pp. 471-486, Sep. 1983. [ Links ]
[44] R. E. Kalman, "Design of a self-optimizing control system," Transactions of the American Society of Mechanical Engineers, Vol. 80, pp. 468-478, Sep. 1958. [ Links ]
[45] K. J. Aström and B. Wittenmark, "On self-tuning regulators," Automatica, vol. 9, no. 2, pp. 185-199, Mar. 1973. [ Links ]
[46] A. Navia and R. Díaz, "Adaptive sigmoidal plant identification using reduced sensitivity recursive least squares," Signal Processing, Vol. 91, No. 4, pp. 1066-1070, Apr. 2011. [ Links ]
[47] W. Wang and B. Tang, "A fuzzy adaptive method for intelligent control," Expert Systems with Application, Vol. 16, No. 1, pp. 43-48, Jan. 1999. [ Links ]
[48] B. F. Wu, L. S. Ma, J. W. Perng and H. I. Chin, "Absolute stability analysis in uncertain static fuzzy control systems with the parametric robust Popov criterion," in Proc. 2008 IEEE Int. Conf. Fuzzy Systems (FUZZIEEE' 08), pp. 1325-1330. [ Links ]
[49] K. S. Narendra and Z. Han, "Location of models in multiple-model based adaptive control for improved performance," in Proc. 2010 American Control Conference (ACC'10), pp. 117-122. [ Links ]
[50] H. Han, C. Y. Su and Y. Stepanenko, "Adaptive control of a class of nonlinear systems with nonlinearly parameterized fuzzy approximators," IEEE Transactions on Fuzzy Systems, Vol. 9, No. 2, pp. 315-323, Apr. 2001. [ Links ]
[51] A. Loria and A. Zavala, "Adaptive tracking control of chaotic systems with applications to synchronization," IEEE Transactions on Circuits and Systems I, Regular Papers, Vol. 54, No. 9, pp. 2019-2029, Sep. 2007. [ Links ]
[52] Y. G. Leu, W. Y. Wang and T. T. Lee, "Robust adaptive fuzzy-neural controllers for uncertain nonlinear systems," IEEE Transactions on Robotics and Automation, Vol. 15, No. 5, pp. 805-817, Oct. 1999. [ Links ]
[53] C. F. Hsu, "Self-organizing adaptive fuzzy neural control for a class of nonlinear systems," IEEE Transactions on Neural Networks, Vol. 18, No. 4, pp. 1232-1241, Jul. 2007. [ Links ]
[54] C. S. Chen and H. H. Chen, "Robust adaptive neuralfuzzy-network control for the synchronization of uncertain chaotic systems," Nonlinear Analysis: Real World Applications, Vol. 10, No. 3, pp. 1466-1479, Jun. 2009. [ Links ]
[55] Y. Gao and M. J. Er, "Online adaptive fuzzy neural identification and control of a class of MIMO nonlinear systems," IEEE Transactions on Fuzzy Systems, Vol. 11, No. 4, pp. 462-477, Aug. 2003. [ Links ]
[56] S. Wang, L. Hou, L. Dong and H. Xiao, "Adaptive fuzzy sliding mode control of uncertain nonlinear SISO systems," Procedia Engineering - International Conference on Advances in Engineering, Vol. 24, pp. 33-37, 2011. [ Links ]
[57] Y. Wang, J. Song and B. Zhang, "Fuzzy Sliding-Mode Variable Structure Control for Fan Filter Units' Motor Speed Regulation System," Procedia Engineering - CEIS2011, Vol. 15, pp. 969-973, Aug. 2011. [ Links ]
[58] A. Meharrar, M. Tioursi, M. Hatti and A. Boudghéne, "A variable speed wind generator maximum power tracking based on adaptative neuro-fuzzy inference system," Expert Systems with Applications, Vol. 38, No. 6, pp. 7659-7664, Jun. 2011. [ Links ]
[59] J. Javadi-Moghaddam and A. Bagheri, "An adaptive neuro-fuzzy sliding mode based genetic algorithm control system for under water remotely operated vehicle," Expert Systems with Applications, Vol. 37, No. 1, pp. 647-660, Jan. 2010. [ Links ]
[60] Y. G. Leu, Y. W. Wang and I. H. Li, "RGA-based on line tuning of BMF fuzzy-neural networks for adaptive control of uncertain nonlinear systems," Neurocomputing, Vol. 72, No. 10-12, pp. 2636-2642, Jun. 2009. [ Links ]
[61] M. Landín, R. C. Rowe and P. York, "Advantages of neurofuzzy logic against conventional experimental design and statistical analysis in studying and developing direct compression formulations," European Journal of Pharmaceutical Sciences, Vol. 38, No. 4, pp. 325-331, Nov. 2009. [ Links ]
[62] T. Ensari and S. Arik, "New results for robust stability of dynamical neural networks with discrete time delays," Expert Systems with Applications, Vol. 37, No. 8, pp. 5925-5930, Aug. 2010. [ Links ]
[63] H. Shao, "Novel delay-dependent stability results for neural networks with time-varying delays," Circuits, Systems, and Signal Processing, Vol. 29, No. 4, pp. 637-647, Aug. 2010. [ Links ]
[64] F. O. Souza, and R. M. Palhares, "Interval time-varying delay stability for neural networks," Neurocomputing, Vol. 73, No. 13-15, pp. 2789-2792, Aug. 2010. [ Links ]
[65] J. Tian and X. Zhou, "Improved asymptotic stability criteria for neural networks with interval time-varying delay," Expert Systems with Applications, Vol. 37, No. 12, pp. 7251-7525, Dec. 2010. [ Links ]
[66] S. Blythe, X. Mao and X. Liao, "Stability of stochastic delay neural networks," Journal of the Franklin Institute, Vol. 338, No. 4, pp. 481-495, Jul. 2001. [ Links ]
[67] H. Huang and J. Cao, "Exponential stability analysis of uncertain stochastic neural networks with multiple delays," Nonlinear Analysis: Real World Applications, Vol. 8, No. 2, pp. 646-653, Apr. 2007. [ Links ]
[68] T. W. Huang, "Exponential stability of fuzzy cellular neural networks with distributed delays," Physics Letters A, Vol. 351, No. 1-2, pp. 48-52, Feb. 2006. [ Links ]
[69] B. Liu and P. Shi, "Delay-range-dependent stability for fuzzy BAM neural networks with time-varying delays," Physics Letters A, Vol. 373, No. 21, pp. 1830-1838, May. 2009. [ Links ]
[70] X. Y. Lou and B. T. Cui, "Robust asymptotic stability of uncertain fuzzy BAM neural networks with time-varying delays," Fuzzy Sets and Systems, Vol. 158, No. 24, pp. 2746-2756, Dec. 2007. [ Links ]
[71] H. Li, B. Chen, C. Lin and Q. Zhou, "Mean square exponential stability of stochastic fuzzy Hopfield neural networks with discrete and distributed time-varying delays," Neurocomputing, Vol. 72, No. 7-9, pp. 2017-2023, Mar. 2009. [ Links ]
[72] L. Sheng, M. Gao and H. Yang, "Delay-dependent robust stability for uncertain stochastic fuzzy Hopfield neural networks with time-varying delays," Fuzzy Sets and Systems, Vol. 160, No. 24, pp. 3503-3517, Dec. 2009. [ Links ]
[73] Z. Shu and J. Lam, "Global exponential estimates of stochastic interval neural networks with discrete and distributed delays," Neurocomputing, Vol. 71, No. 13-15, pp. 2950-2963, Ago. 2008. [ Links ]
[74] W. Su and Y. Chen, "Global robust exponential stability analysis for stochastic interval neural networks with time-varying delays," Communications in Nonlinear Science and Numerical Simulation, Vol. 14, No. 5, pp. 2293-2300, May. 2009. [ Links ]
[75] W. Lin and C. I. Byrnes, "Passivity and absolute stabilization of a class of discrete-time nonlinear systems," Automatica, Vol. 31, No. 2, pp. 263-267, Feb. 1995. [ Links ]
[76] X. W. Liu, "Passivity analysis of uncertain fuzzy delayed systems," Chaos, Solitons and Fractals, Vol. 34, No. 3, pp. 833-838, Nov. 2007. [ Links ]
[77] J. Liang, Z. Wang and X. Liu, "Robust passivity and passification of stochastic fuzzy time-delay systems," Information Sciences, Vol. 180, No. 9, pp. 1725-1737, May. 2010. [ Links ]
[78] J. Fu, H. Zhang, T. Ma and Q. Zhang, "On passivity analysis for stochastic neural networks with interval time-varying delay," Neurocomputing, Vol. 73, No. 4-6, pp. 795-801, Jan. 2010. [ Links ]
[79] P. Balasubramaniam and G. Nagamani, "Global robust passivity analysis for stochastic fuzzy interval neural networks with time-varying delays," Expert Systems with Applications, Vol. 39, No. 1, pp. 732-742, Jan. 2012. [ Links ]
[80] M. Syed-Ali and P. Balasubramaniam, "Exponential stability of uncertain stochastic fuzzy BAM neural networks with time-varying delays," Neurocomputing, Vol. 72, No. 4-6, pp. 1347-1354, Jan. 2009. [ Links ]
[81] A. T. Gumus and A. F. Guneri, "A multi-echelon inventory management framework for stochastic and fuzzy supply chains," Expert Systems with Applications, Vol. 36, No. 3, pp. 5565-5575, Apr. 2009. [ Links ]
[82] P. Chaves and T. Kojiri "Deriving reservoir operational strategies considering water quantity and quality objectives by stochastic fuzzy neural networks," Advances in Water Resources, Vol. 30, No. 5, pp. 1329-1341, May. 2007. [ Links ]
[83] P. Chaves, T. Kojiri and T. Hori, "Stochastic Operation for Multi-purpose Reservoir Using Neuro-Fuzzy Systems," Annuals of Disas. Prev. Res. Inst., No. 48B, 14 pp., 2005. [ Links ]
[84] A. Azadeh, S.M. Asadzadeh, M. Saberi, V. Nadimi, A. Tajvidi and M. Sheikalishahi, "A Neuro-fuzzy-stochastic frontier analysis approach for long-term natural gas consumption forecasting and behavior analysis: The cases of Bahrain, Saudi Arabia, Syria, and UAE," Applied Energy, vol. 88, No. 11, pp. 3850-3859, Nov. 2011. [ Links ]