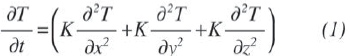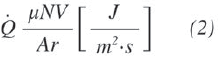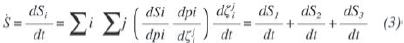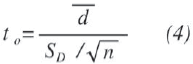Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Iteckne
versão impressa ISSN 1692-1798
Iteckne vol.10 no.2 Bucaramanga jul./dez. 2013
Modelamiento del proceso de desgaste de un tribómetro pin-disco: Flash temperature y mecanismos de disipación
Wear modelling of a pin-on-disk tribometer: Flash temperature and dissipation mechanisms
Juan Sebastián Rudas F1, Lina María Gómez E2, Alejandro Toro3
1 MSc en Ingeniería, Investigador Grupo GTS, Investigador Grupo de investigación en Procesos Dinámicos. Universidad Nacional de Colombia, Colombia. jsrudas@unal.edu.co.
2 Ph. D. Docente Universidad Nacional de Colombia, Investigador. Grupo de investigación en Procesos Dinámicos. Universidad Nacional de Colombia, Colombia. limage@unal.edu.co.
3 Ph. D., Docente Universidad Nacional de Colombia, Investigador Grupo GTS. Universidad Nacional de Colombia, Colombia. aotoro@unal.edu.co.
RESUMEN
El desgaste de un material en una superficie de trabajo tiene profundas consecuencias económicas relacionadas con inactividad de maquinaria y pérdida de producción. El desgaste deslizante ha sido un problema altamente estudiado desde diferentes enfoques con el fin de predecir la tasa de desgaste de uno o de ambos metales participantes en el par tribológico. En este artículo se desarrolla un modelo semifísico de base fenomenológica de pares deslizantes con fines de predecir la tasa de desgaste. La metodología utilizada brinda como estructura del modelo matemático diferentes ecuaciones de balance que describen los fenómenos vinculados directamente con la pérdida de material, como lo son elevados cambios térmicos y el aumento de la entropía del sistema deslizante (primer y segunda principio de la termodinámica). Con el modelo desarrollado se logra predecir la tasa y el volumen de desgaste, además de la energía generada y disipada en el par deslizante.
PALABRAS CLAVE: Desgaste, degradación termodinámica, modelado, tribología.
ABSTRACT
The wear from a work surface has profound economic consequences related to downtime and loss of production machinery. Sliding wear problem has been highly studied from different approaches in order to predict the wear rate of one or both metals from tribological pair. This paper develops a phenomenological based semiphysical model to sliding pairs for wear rate prediction. The methodology employed provides for mathematical model structure as balance equations that describe different phenomena linked to the loss of material, such as high thermal dynamic and increased the entropy from sliding system (first and second law of thermodynamics). Model simulation shows that obtained model can predict the wear rate, the generation and disipation energy into sliding pair.
KEYWORDS: Modeling, thermodynamical degradation, tribology, wear.
1. INTRODUCCIÓN
El uso intensivo de modelos en la ingeniería moderna es más que evidente. Los avances en la capacidad de computación han catapultado el desarrollo de modelos cada vez más detallados y precisos, que luego se utilizan en diseño, optimización, control y diagnóstico de fallas, entre otras tareas.
Entre las tres grandes familias de modelos (fenomenológicos, empíricos y semifísicos), la facilidad de obtención de los modelos empíricos ocultó posibilidades importantes de las otras dos familias de modelos. De otro lado, el requisito del conocimiento detallado de todos los fenómenos, ha hecho que los modelos fenomenológicos sean escasos en ingeniería. La tercera familia (modelos semifísicos), solo empezó a demostrar sus verdaderas utilidades hasta que la potencia de cómputo alcanzó capacidad suficiente para resolver numéricamente sistemas de varias ecuaciones diferenciales y algebraicas simultáneamente.
En el modelado del proceso de desgaste ocurre una situación similar, existe una gran abundancia de modelos empíricos reportados en la literatura, de los cuales en la mayoría las variables involucradas para predecir la tasa de desgaste están relacionadas con propiedades mecánicas (área real de contacto, módulo de Young, radio de Poisson etc.) [2], [3] y el punto de operación del proceso de deslizamiento (velocidad, carga, geometría, etc.) [4]-[6]. Los modelos semifísicos de base fenomenológica (MSBF) han desempeñado un papel importante en el estudio del proceso de desgaste, aplicando metodologías determinadas se han desarrollado modelos estáticos [6], modelos que relacionan la dinámica del desgaste en función de ecuaciones constitutivas que representan fenómenos de abrasión, adhesión y fatiga [7], [8], modelos dinámicos [9] y simulaciones computacionales con fines de entender y predecir el fenómeno de desgaste generado por la fricción [10]-[12].
En los últimos años se ha realizado un acercamiento metodológico próximo al modelamiento de las dinámicas termomecánicas presentes en un par deslizante [4], [13]-[15]. Se han propuesto ecuaciones constitutivas donde se describen los diferentes mecanismos de desgaste en función de la energía disipada [16], [17]. También se tienen estudios donde se presentan correlaciones entre el área real de contacto con la energía generada y su posterior disipación dentro de los sólidos en contacto [18]-[20]. Sin embargo no se tienen estudios que relacionen directamente las variables clásicas del proceso (coeficiente de fricción, la carga y la velocidad) con la temperatura y su implicación con el aumento en la tasa de desgaste de un proceso, dado que la dinámica de los procesos térmicos que se presentan en el par deslizante hace intrincado su estudio por las metodologías convencionales de desarrollo de modelos.
Los MSBF son altamente generalizables ya que su estructura se basa en la fenomenología subyacente del proceso estudiado, por tanto, aunque cambien la entrada de energía, o se utilicen diferentes materiales, la fenomenología estudiada no cambia y sigue rigiendo el proceso, solo restaría modificar los parámetros de los nuevos materiales o la magnitud de las entradas de energía. Por tanto, un modelado de un proceso desde la fenomenología que lo rige hace que el modelo sea escalable y generalizable.
En este artículo se presenta el desarrollo de un MSBF del proceso de desgaste que se lleva a cabo en un ensayo de desgaste en el tribómetro Pin-Disco con el fin de describir los fenómenos relevantes y predecir la taza de desgaste. En la Sección 2 se describe la metodología utilizada para desarrollar el modelo, en la Sección 3 se describe el desarrollo del modelo, en la Sección 4 se presentan los resultados de simulación y la validación y, finalmente, en la Sección 5 se presentan las conclusiones.
2. METODOLOGÍA PARA EL DESARROLLO DE MODELOS SEMIFÍSICOS DE BASE FENOMENOLÓGICA
Se dice que este tipo de modelo es de Base Fenomenológica ya que su estructura se basa en los balances de energía, masa y cantidad de movimiento, y Semifísico porque agrega a la estructura formulaciones empíricas para varios de sus parámetros [23]. Los balances de materia, de energía y de cantidad de movimiento (o cualquier entidad balanceable) relacionan las variables más significativas de un proceso brindándole la estructura al MSBF con un fundamento fenomenológico. La estructura del modelo se complementa con ecuaciones para los parámetros del modelo, estas ecuaciones, denominadas ecuaciones constitutivas, en su mayoría son de carácter empírico (correlaciones desde datos experimentales) o representación de fenómenos de transporte. A continuación se describen algunos conceptos relevantes y se detalla la metodología para el desarrollo del MSBF.
2.1. Conceptos asociados con los Modelos Semifísicos de Base Fenomenológica
A continuación se definen algunos conceptos que se utilizan en la descripción de la metodología.
Sistema de Proceso. Según Hangos & Cameron [24] es una abstracción del proceso a la manera de un sistema, con lo cual se puede aplicar al proceso todas las herramientas de representación y análisis de sistemas matemáticos existentes.
Objetivo del modelado. Es la intencionalidad del modelador, respecto la semejanza que quiere conservar entre el proceso real y el resultado teórico. Esta intención, normalmente se ata con la cualidad más tangible del modelo desarrollado, ya sea representación, descripción, explicación y/o predicción.
Criterio de validación. Es la manera de comprobar la fidelidad, para la cualidad predefinida, del modelo respecto al proceso real. Si esta fidelidad no existe, no habrá manera de darle legalidad al modelo ante sus potenciales usuarios [23].
2.2. Metodología para el desarrollo de Modelos Semifísicos de Base Fenomenológica
El método que se desarrolla en este artículo está basado en el propuesto en [1], [23], que a su vez se basaron en metodologías propuestas en [24], [25]. El procedimiento de modelado está dado por los siguientes pasos:
- Elaboración de una descripción, ya sea verbal, ya sea un diagrama de flujo del proceso o ambas.
- Precisar un nivel de detalle, según el propósito que se desea con el modelo, es decir: ¿Qué preguntas responderá el modelo?
- Definir sistemas de proceso y relacionar estos sistemas, ya sea de forma descriptiva, verbal o en diagrama de bloques.
- Aplicar el principio de conservación adecuado, según la entidad que se desee balancear, sobre cada sistema de proceso.
- Hallar las ecuaciones constitutivas que permitan calcular el mayor número de parámetros en cada sistema de proceso.
- Obtención del modelo computacional y solución del modelo matemático.
- Validación del modelo para diferentes condiciones de operación y evaluación de su desempeño.
3. MODELO SEMIFÍSICO DE BASE FENOMENOLÓGICA DEL PROCESO DE DESGASTE EN UN TRIBÓMETRO PIN-DISCO
La metodología indicada en la Sección 2 es aplicada al tribómetro Pin-Disco con el fin de describir las variables relevantes del proceso, su interacción y predecir la taza de desgaste. El modelo desarrollado es validado con datos de un ensayo de laboratorio. Para el desarrollo del modelo se considera que en el ensayo Pin-Disco ocurre un proceso de deslizamiento en seco. A continuación se detallan cada uno de los pasos de la metodología descrita en la Sección 2.2.
3.1. Descripción del proceso
En el caso del estudio del desgaste por deslizamiento se han diseñado y construido dispositivos que emulen dicho proceso [21]; entre estos dispositivos se desarrolló el tribómetro Pin-Disco en el cual se miden y controlan algunas de las variables que intervienen en el proceso, poniendo a prueba durante determinado tiempo los materiales específicos del estudio para realizar una posterior caracterización. Con esta metodología se pretende emular el proceso de desgaste con el fin de obtener una probeta que presente el mismo mecanismo de desgaste del proceso original.
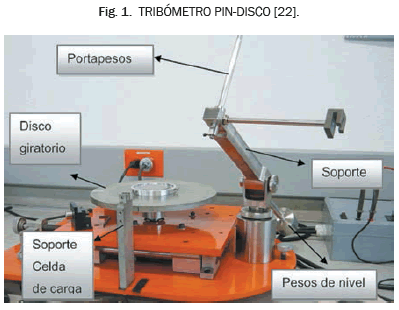
El modelo que se desarrolla en este trabajo viene de la abstracción de un ensayo de laboratorio para estudiar el desgaste generado por el deslizamiento en seco de sólidos metálicos. El tribómetro Pin-Disco, presentado en la Fig. 1, es un dispositivo versátil que permite medir las propiedades de fricción y desgaste de combinaciones de materiales con y sin lubricante, bajo condiciones variables de carga y velocidad de deslizamiento. El tribómetro Pin-Disco consiste de un Disco giratorio fabricado de uno de los materiales bajo ensayo y de un pin cilíndrico o esférico y estático, sometido a una determinada carga.
3.2. Nivel de detalle del modelo
El nivel de detalle del modelo es definido como macroscópico. No se intenta representar procesos microscópicos, ni fenómenos atomísticos.
3.3. Sistemas de procesos del Pin-Disco
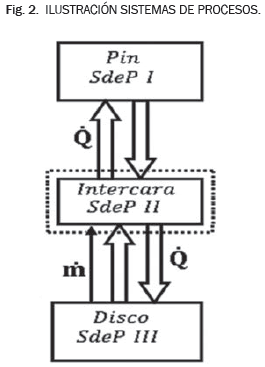
Como el modelo es de carácter macroscópico se pueden tomar tres sistemas de proceso (SdeP). En la Fig. 2 se presenta el diagrama de los sistemas de proceso y sus interacciones. El primer sistema de proceso (SdeP I) corresponde al Pin, el cual se asume como un cuerpo infinito o sumidero perfecto y que posee una dureza considerablemente superior a la del Disco. El sistema de proceso II (SdeP II) corresponde a la superficie de contacto entre el Pin y el Disco, o intercara del Pin y el Disco. El sistema de proceso III (SdeP III) corresponde al Disco.
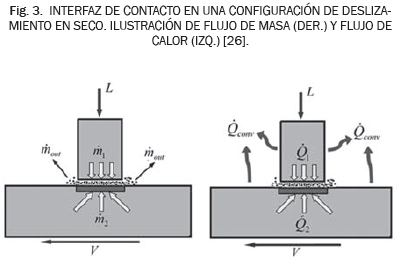
Estos sistemas de procesos se corresponden con los plateados en [26] y que se ilustran en la Fig. 3, las diferencias radica en que el Pin no disipa calor al entorno por considerarse un sumidero perfecto y que del Pin no se desprende masa por su alta dureza comparada con la del Disco.
3.4. Aplicar el principio de conservación adecuado
A continuación se detallan los balances de conservación aplicados a cada sistema de proceso.
3.4.1. Sistema de Proceso I: El Pin
En el Sistema de Proceso I no se aplica ningún principio de conservación por considerarse un sumidero perfecto.
3.4.2. Sistema de Proceso II: El Disco
En el Sistema de Proceso II se realiza un balance de energía de parámetros distribuidos. Basado en la primera ley de la termodinámica, el estamento de esta ecuación se rige bajo el principio físico de la conservación de la Energía. El propósito del desarrollo de este modelo de transferencia térmica es identificar y cuantificar la magnitud y la dinámica de la energía generada por el contacto deslizante. En la Tabla I se indican las condiciones de frontera del Disco, debido a la simetría geométrica, sólo se modela la mitad del Disco, de ahí la condición de frontera cara axisimétrica.
En la ecuación (1) se indica el balance de energía dinámico en parámetros distribuidos
Donde K es la conductividad térmica del material, en este caso Ti6Al4V, x, y y z son las coordenadas geométricas espaciales y, finalmente, T es la temperatura en el sólido.
Cuando el Pin se desliza sobre el Disco, el resultado inevitable de la fricción es la liberación de calor. A altas velocidades de deslizamiento se libera una gran cantidad de energía [17]. Casi todo el calor liberado en el proceso de fricción en un deslizamiento en seco entre sólidos es generado sobre la interfaz de contacto y disipado en el interior de los sólidos a través de las rugosidades en contacto [21].
3.4.3. Sistema de Proceso III: La intercara
En la intercara es donde se lleva a cabo, como tal, el proceso de desgaste. Este sistema de proceso está compuesta por una capa muy delgada del Pin y otra muy pequeña del Disco, a pesar de su pequeño tamaño (~40µm), la energía generada por el contacto presenta elevadas magnitudes (~500KW/m2) y presenta dinámicas instantáneas (~50µsg), por tanto, medir esta energía en campo resulta prácticamente imposible. Se plantea realizar los balances de energía y de entropía, con el fin de poder describir adecuadamente los fenómenos térmicos y disipativos que ocurren en el proceso de desgaste.
El balance de energía es descrito en (2), y se asume que toda la energía generada por el contacto es disipada dentro del volumen de control. El calor generado por unidad de área por segundo está dado en [27].
Donde µ es el coeficiente de fricción, N es la carga, V es la velocidad de deslizamiento y Ar es el área real de contacto. La ecuación (2) describe el trabajo generado por el contacto entre las pequeñas rugosidades de las dos superficies, dicho trabajo se disipa como calor en el Disco.
El balance de entropía se indica en (3), en el balance intervienen procesos de degradación disipativos pi, donde cada pi=pi(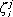 ) describe la energía, el trabajo, la deformación plástica, la fractura, la generación de grietas o el calor característico del proceso y depende de una serie de variables fenomenológicas dependientes del tiempo
) describe la energía, el trabajo, la deformación plástica, la fractura, la generación de grietas o el calor característico del proceso y depende de una serie de variables fenomenológicas dependientes del tiempo 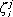 =
=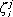 (t),j=1,2,...,m. Cada proceso de degradación genera una entropía irreversible Si=Si{pi(
(t),j=1,2,...,m. Cada proceso de degradación genera una entropía irreversible Si=Si{pi(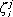 )}. La ecuación (3) es la suma de todos los procesos disipativos considerados en esta investigación para el proceso de desgaste.
)}. La ecuación (3) es la suma de todos los procesos disipativos considerados en esta investigación para el proceso de desgaste.
3.5. Ecuaciones constitutivas y parámetros
En el proceso de desgaste por contacto deslizante se presenta diferentes mecanismos de degradación dados a su vez por diferentes mecanismos de disipación de energía y generación de entropía. En la Tabla II se presentan las ecuaciones constitutivas relacionadas con los procesos disipativos, algunos de los cuales hacen parte de la sumatoria en (3). En la Tabla II también se presentan otras ecuaciones constitutivas utilizadas en el cálculo de algunos parámetros necesarios para definir el comportamiento plástico de los sólidos.
Para este modelo se debe tener en cuenta parámetros geométricos del sistema y las propiedades de los materiales involucrados en el desgaste (Titanio grado 5 -Ti6Al4V- como Disco y Carburo de Tungsteno Cobalto -Wc/Co- como Pin). En la Tabla III se indican los valores de los parámetros utilizados en los balances planteados en el aparte anterior.
3.6. Solución del modelo matemático - modelo computacional
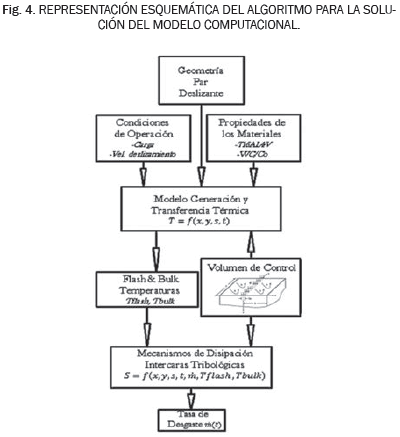
En la Fig. 4 se presenta el algoritmo utilizado para solucionar el modelo computacional. Inicialmente se deben ingresar todos los parámetros relacionados con la geometría del par deslizante, las condiciones de operación y las propiedades de los materiales (parámetros que se presentan en la Tabla III). Con estos parámetros se soluciona el problema de generación, tránsito y transferencia de energía del par deslizante mediante integración explícita. Con la solución de este primer problema se logra identificar dos variables Tflash y Tbulk, temperatura flash y temperatura bulk respectivamente [27]. Y finalmente, con estas variables se soluciona, en la misma geometría y volumen de control, el balance de entropía calculando la energía disipada por cada mecanismo de degradación y obtener la tasa de desgaste de sistema.
3.7. Validación del modelo
La validación es al menos una manera de comprobar la fidelidad y la precisión entre el modelo desarrollado y el proceso real del cual se ha realizado la abstracción. Los resultados y la validación del modelo se muestran en la Sección 4.
4. RESULTADOS DE SIMULACIÓN, VALIDACIÓN Y ANÁLISIS DEL MODELO DESARROLLADO
Para realizar las simulaciones y los experimentos en el tribómetro se tomaron como punto de operación un compendio entre las condiciones experimentales desarrolladas en [28] y las tomadas en [29] presentadas en la Tabla III.
4.1. Resultados de simulación
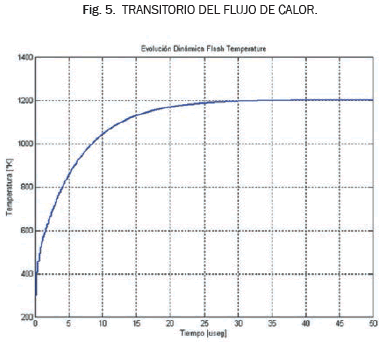
En la Fig. 5 se presenta el comportamiento dinámico de la Temperatura Flash (1), se observa que su tiempo de estabilización es corto El disco alcanza temperaturas de hasta 1200K para una velocidad de deslizamiento de V=0.16m/seg.
El tiempo de estabilización del flujo de calor es aproximadamente 40 µseg , una respuesta dinámica "instantánea", comparado con el tiempo de duración del ensayo. El flujo de calor es generado específicamente por el contacto entre las asperezas, donde la concentración de esfuerzos y tensiones hacen que se genere un delta de energía, bien llamado, una "Flash Temperature" Esta temperatura ha sido planteada, entre otros autores, como Stachowiak y Batchelor [21].
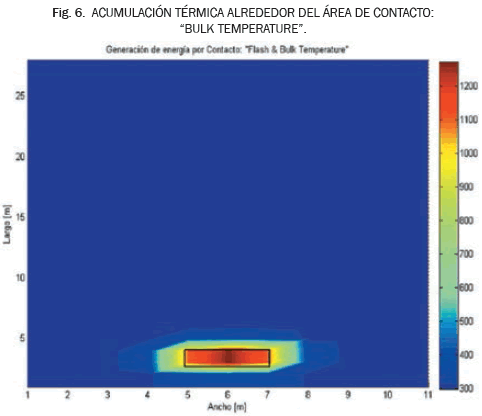
Por otro lado, aunque la dinámica de la "Flash Temperature" sea tan veloz en el volumen alrededor del área real de contacto, se almacena suficiente energía para aumentar la temperatura de estas regiones circundantes en unos cuantos grados y por consiguiente, aumenta la tasa de disipación de energía; a la temperatura del volumen que ha acumulado dicho calor se le conoce como "Bulk Temperature" o temperatura de volumen la cual es igual a Tbulk=337 [K]. La simulación de la temperatura Bulk se presenta en la Fig. 6, siendo la estela alrededor del rectángulo que representa el área de contacto.
4.2. Validación del modelo
Para la validar el modelo se compara los resultados obtenidos en la simulación con los resultados de un ensayo de desgaste realizado en el laboratorio de Tribología de la Universidad Nacional de Colombia por [22] en un tribómetro Pin-Disco. Los resultados de los ensayos de laboratorio y los resultados de las simulaciones se presentan en la Tabla IV. Se puede observar que el volumen removido obtenido con el modelo es muy cercano a los resultados de la experimentación en el laboratorio, inclusive para cambios en la velocidad de deslizamiento y de carga. Sin embargo se realiza una comparación entre los resultados experimentales con los resultados de las simulaciones, presentados en la Tabla IV, teniendo en cuenta que los resultados de ambos experimentos son dependientes o pareados, por el hecho de tener el mismo punto de operación. Para dicha comparación y validación del modelo se utilizó el estadístico definido por (4).
Donde,
to: Estadístico de Prueba
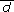 : Promedio muestral de las diferencias
: Promedio muestral de las diferencias
SD: Desviación estándar muestral de las diferencias
n: Tamaño de la muestra
Con el anterior estadístico de prueba se calcula el valor-p (significancia observada o calculada) y se compara con la significancia predefinida que se denota por alfa (α). Si la significancia observada es mayor que la significancia predefinida existe una alta probabilidad de que los resultados, tanto el experimental en laboratorio como el experimental en simulación, sean idénticos o muy parecidos. Para las comparaciones realizadas en este trabajo se define un valor de alfa del 5 % (α=0.05).
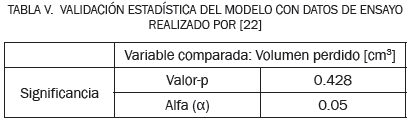
En la Tabla V se presenta los resultados del cálculo de la significancia calculada con los resultados presentados en la Tabla IV. Se observa que el cálculo del valor-p es mayor con respecto al valor predefinido de α.
Es así como el cálculo de la significancia permite afirmar que: los resultados obtenidos por el modelo propuesto y los datos adquiridos en el ensayo de desgaste son idénticos estadísticamente. Los resultados obtenidos indican errores bajos del modelo (entre 8 - 10 %), en su calidad de predicción. Con la información anterior se logra validar el modelo propuesto en este trabajo, afirmando que el modelo desarrollado logra predecir la tasa de desgaste, la temperatura generada y el volumen removido en un proceso de deslizamiento entre sólidos en seco.
4.3. Análisis del modelo desarrollado
Tal como se indica en la Sección 2 una de las ventajas de los MSBF es que permiten identificar claramente las variables relevantes del proceso, de acuerdo con las cantidades balanceables. En el proceso de deslizamiento en seco las variables relevantes son: la temperatura flash, la temperatura bulk y la entropía. Debido al contacto entre el Pin y el Disco se ocasiona una fuerza de fricción que aporta calor un flujo de calor a las piezas en contacto. El balance de energía en el Disco (1) evidencia que hay dos temperaturas relevantes en el proceso y que ya han sido descritas en la literatura. La Temperatura flash con una dinámica instantánea pero de magnitud suficientemente alta para calentar sus alrededores ocasionando el calentamiento del Disco, que es descrito por la Temperatura bulk, de un orden de magnitud menor que la Temperatura flash. El gradiente térmico dado por la diferencia entre las temperaturas flash y bulk inestabilizan temodinámicamente el Disco y tiende a aumentar la energía del sistema. Un material (o ambos) perteneciente al par deslizante responde de manera que inicia a consumir (o dispar) toda o parte de la energía acumulada con el fin de re-organizar o reestabilizar el equilibrio perdido. Los materiales responden de diferentes maneras: generando grietas, nuevas áreas y superficies, realizando transiciones entre mecanismo de desgaste y en la generación de desechos o pérdida de material, entre otros. Cada uno de estos mecanismos de disipación de energía aumenta la tasa de entropía del material. Es decir, la relación entre el aumento de la entropía del sistema está directamente relacionado con el comportamiento de la tasa de desgaste del par deslizante. Es así, como en este trabajo se cuantifico la energía disipada por diferentes mecanismos disipativos y se pudo lograr identificar un volumen de masa removido por el contacto deslizante en seco de dos metales.
5. CONCLUSIONES
En este artículo se implementó una metodología para el desarrollo de modelos semifísicos de base fenomenológica con la cual se obtuvo un modelo capaz de explicar los fenómenos que se llevan a cabo en la interfaz y subsuperficie de contacto de pares deslizantes, y predecir la tasa de desgaste y el volumen removido en el proceso. El modelo desarrollado representa el proceso de desgaste que se realiza en un ensayo de desgaste a escala de laboratorio en un tribómetro Pin-Disco, en cuyos materiales pertenecientes al par deslizante fueron WC/Co y Ti6Al4V. Los modelos semifísicos de base fenomenológica son altamente generalizables y constituyen una herramienta robusta en la representación, descripción, explicación y predicción de procesos.
El contacto entre las rugosidades de las superficies pertenecientes al par deslizante producen microzonas de contacto donde se generan elevados esfuerzos alrededor de una pequeña área de contacto provocando a su vez deltas térmicos, llamados "flash temperaturas", que ocasionan la inestabilidad de sistema y, por consiguiente, el aumento de la entropía del mismo. La cuantificación de la entropía generada por diferentes mecanismos y, micromecanismos de desgaste, dentro del volumen de control brindaron la estructura para el desarrollo del modelo capaz de cuantificar la pérdida de material.
REFERENCIAS
[1] C. A. Gómez, Y. A. Calderón y H. Álvarez, "Construcción de modelos semifísicos de base fenomenológica. Caso proceso de fermentación" Rev. Bio. Agro, vol. 6 no. 2, pp. 28-39. 2008. [ Links ]
[2] H. A. Abdel-aal, "The deduction of friction-induced temperatures from thermal strain measurements in the dry sliding of metallic pairs", Therm Science, vol. 38, pp. 160-174, 1999. [ Links ]
[3] C. Guang-Neng Dong, M. Hua, J. Li and B. Kong, "Temperature field and wear prediction for UHMWPE acetabular", Material and Design, vol. 28, pp. 2402-2416, 2007. [ Links ]
[4] R. A. Singh, G. S. V. L. Narasimham and S. K. Biswas, "Estimation of surface temperature of a pin wearing on a disk", Tribology Letters, vol. 12, no. 4, pp. 203-207, 2002. [ Links ]
[5] E.-Sung Yoon, H. Kong and O.-kwan Kwon, "Evaluation of frictional characteristics for a pin-on-disk apparatus with different dynamic parameters", Wear, vol. 203/204, pp. 341-349, 1997. [ Links ]
[6] D.-cheol Ko and B-min Kim, "Development of an analytical scheme to predict the need for tool regrinding in shearing processes", International Journal, vol. 40, pp. 1329-1349, 2000. [ Links ]
[7] A. Yevtushenko, O. Ukhanska, and R. Chapovska, "Friction heat distribution between a stationary pin and a rotating disc", Wear vol. 196, pp. 219-225, 1996. [ Links ]
[8] D. M. Kennedy and M. S. J. Hashmi, "Methods of wear testing for advanced surface coatings and bulk materials", Journal of Materials Processing Technology, vol. 77, pp. 246-253, 1998. [ Links ]
[9] H. K. Hong and C.S. Liu, "Coulomb friction oscillator: Modelling and responses to armonic loads and base excitations", Journal of Sound and Vibration, vol. 229, no. 5, pp. 1171-1192, 2000. [ Links ]
[10] S. K. Wang and J. Woodhouse, "The frequency response of dynamic friction: A new view of sliding interfaces", Journal Mechanics and Physics of Solids, vol. 59, pp. 1020-1036, 2011. [ Links ]
[11] S. L. Rice and F.A. Moslehy, "Modeling friction and wear phenomena", Wear, vol. 206, pp. 136-146, 1997. [ Links ]
[12] V. Hegadekatte, N. Huber and O. Kraft, "Modeling and simulation of wear in a pin on disc tribometer", Tribology Letters, vol. 24, no. 1, pp. 51-60, 2006. [ Links ]
[13] J. Jiang, F. H. Stott and M. M. Stack, "The role of triboparticulates in dry sliding wear", Tribology International, vol. 31, no. 5, 245-256, 1998. [ Links ]
[14] F. H. Stott, "High-temperature sliding wear of metals", Tribology International, vol. 35, pp. 489-495, 2002. [ Links ]
[15] H. A. Abdel-aal, "The correlation between thermal property variation and high temperature wear transition of rubbing metals", Wear, vol. 237, pp. 147-151, 2000. [ Links ]
[16] M.D Bryant, M.M Khonsari and F.F Ling, "On the thermodynamics of degradation", Proceedings of the Royal Society A, vol. 464, pp. 2001-2014. 2008. [ Links ]
[17] N. Aderghal, T. Loulou, A. Bouchoucha, and P. Rogeon, "Analytical and numerical calculation of surface temperature and thermal constriction resistance in transient dynamic strip contact", Applied Thermal Engineering, vol. 31, no. 8, pp. 1527-1535, 2011. [ Links ]
[18] M. Nosonovsky, "Entropy in Tribology: in the Search for Applications", Entropy, vol. 12, pp. 1345-1390. 2010. [ Links ]
[19] C. Basaran and C.Y. Yan, "A thermodynamic framework for damage mechanics of solder joints", J. Elect. Pack, vol. 120, pp. 379-384, 1998. [ Links ]
[20] A. Zmitrowicz, "Wear patterns and laws of wear - a review", Journal of Theoretical and Applied Mechanics, vol. 44, no. 2, pp. 219-253, 2006. [ Links ]
[21] G.W Stachowiak and A. W Batchelor, "Engineering tribology", Tribology Series 24 , ED. Elsevier science publishers B.V. 1993. [ Links ]
[22] R. Arrubla y C. Ochoa, "Evaluación del desempeño tribológico del par Wc/co - Ti6al4v mediante pruebas tipo pin-disco en contacto no lubricado", Tesis de Grado En Ingeniería Mecánica, Universidad Nacional De Colombia, 2011. [ Links ]
[23] H. Alvarez, R. Lamanna, P. Vega and S. Revollar, "Metodología para la Obtención de Modelos Semifísicos de Base Fenomenológica Aplicada a una Sulfitadora de Jugo de Caña de Azúcar", Revista Iberoamericana de Automática e Informática Industrial RIAI, vol. 6, pp. 10-20, 2009. [ Links ]
[24] K. Hangos and I. Cameron, "Process Modelling and model analysis" Ed. Academic Press. 2001. [ Links ]
[25] K.M. Hangos, J. Bokor, G. Szederkényi and M. di Bernardo, "Analysis and control of nonlinear process systems", Springer-Verlag London Limited, vol. 42. No. 10, pp. 1829-1831, 2006. [ Links ]
[26] A.B., Aghdam and M.M., Khonsari, "On the correlation between wear and entropy in dry sliding contact", Wear, vol. 270, no. 11-12, pp. 781-790, 2011. [ Links ]
[27] J.S. Rudas, J.H. Urrea, L.M. Gómez and A.O. Toro, "Correlación entre la dinámica de la temperatura "flash" y la temperatura "bulk" generada durante el deslizamiento de pares metálicos", Mecánica Computacional, vol. 31, pp. 2119-2131, 2012. [ Links ]
[28] A. Molinari, G. Straffelini, B. Tesi and T. Bacci, "Dry sliding wear mechanisms of the Ti6Al4V alloy", Wear, vol. 208, pp. 105-112, 1997. [ Links ]
[29] H. A. Abdel-aal, "On the interdependence between kinetics of friction-released thermal energy and the transition in wear mechanisms during sliding of metallic pairs", Wear, vol. 254, pp. 884-900, 2003. [ Links ]