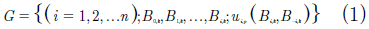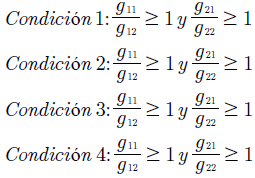Juego de selección de access point basado en restricciones de ancho de banda

Access point selection game based on bandwidth restrictions

Evelio Astaiza-Hoyos¹, Héctor Fabio Bermúdez-Orozco², Luis Freddy Muñoz-Sanabria³

1 Ph. D (c). Ciencias de la Electrónica. Universidad del Quindío. Armenia, Colombia. eastaiza@uniquindio.edu.co.
2 M. Sc. Electrónica y Telecomunicaciones. Universidad del Quindío. Armenia, Colombia. hfbermudez@uniquindio.edu.co.
3 M. Sc. en Computación. Universidad del Cauca. Fundación Universitaria de Popayán. Popayán, Colombia. lfreddyms@fup.edu.co.

RESUMEN

En este artículo se presentan los resultados del estudio de la selección de un punto de acceso inalámbrico en redes 802.11 multicelda, las cuales se enfrentan actualmente a la progresiva saturación del espectro radioeléctrico, debido a la masificación de usuarios. Este problema es abordado desde la perspectiva de la teoría de juegos no cooperativos, en la cual los usuarios (dispositivos transmisores) son los jugadores y los posibles valores discretos de ancho de banda definidos en el sistema, las estrategias que estos tienen para jugar, por lo cual, para la canalización definida en 802.11g, y considerando solamente los canales no traslapados, se identifican tres casos dependiendo del número de canales o cantidad de ancho de banda que el usuario elija. Para la solución del juego se introduce el concepto de Equilibrio de Nash (NE), se comprueba la existencia de este en el modelo planteado y se propone un algoritmo diseñado en la herramienta matemática computacional Matlab → que permite resolver el problema de asociación bajo este concepto. Particularmente, en este juego se busca la maximización de la utilidad para cada usuario, con el fin de encontrar desde esta perspectiva la solución al problema planteado, en este escenario, se verifica que el punto de acceso seleccionado bajo la perspectiva del equilibrio de Nash será aquel que presente las mejores condiciones de ganancia de canal utilizando la estrategia del máximo ancho de banda disponible.

PALABRAS CLAVE: Ancho de banda, equilibrio de nash, juegos no cooperativos, redes 802.11, selección de punto de acceso, teoría de juegos.

ABSTRACT

This article describes the results of the selection of a access point in 802.11 wireless networks multicell, which are currently facing the progressive saturation of the radio spectrum due to overcrowding User. This problem is addressed from the perspective of the theory of noncooperative games where users (transmitter devices) are the players and the possible discrete values of bandwidth defined in the system, strategies that they have to play, whereby, for the channeling defined in 802.11g, and considering only the nonoverlapping channels, three cases are identified depending on the number of channels or amount of bandwidth the user to choose. For game solution concept of Nash Equilibrium (NE) is introduced, the existence of the proposed model is verified and the computational algorithm designed in Matlab mathematical tool proposed, that solves the problem of association under this concept. Particularly, in this game seeks to maximize the utility for each user, in order to find from this perspective, the solution to the problem raised, in this scenario, it is verified that selected access point from perspective of Nash equilibrium will be the one to present the best channel conditions gain using the strategy of using the maximum available bandwidth.

KEYWORDS: Bandwidth, nash equilibrium, noncooperative games, 802.11 wireless networks, access point selection, game theory.

1. INTRODUCCIÓN

Uno de los problemas que enfrenta actualmente la tecnología Wi-Fi es la progresiva saturación del espectro radioeléctrico debido a la masificación de usuarios, lo cual responde al hecho de que en muchos escenarios desarrollados, la distribución de usuarios en el área geográfica es no uniforme. Tal es el caso de grandes áreas como universidades y campos corporativos, aeropuertos y centros comerciales, en los cuales la concentración de usuarios, que requieren diferentes tasas de transferencia, puede variar significativamente dependiendo de los horarios. Una alta concentración en un área localizada incrementa la carga en un punto de acceso (AP) en esta área, resultando una reducción del ancho de banda disponible por usuario y en la congestión del medio inalámbrico, generándose efectos indeseados como pérdida de paquetes y el aumento del retardo extremo a extremo. Lo anterior, dado el mecanismo de selección de AP que se tiene en este tipo de redes, el cual, garantiza que un transmisor selecciona el AP del que percibe el mayor nivel de potencia (AP más cercano). Es por ello, que el objetivo de este trabajo es desarrollar un algoritmo que permita a cada usuario seleccionar de manera egoísta el AP que ofrece el equilibrio óptimo que le permita maximizar su tasa de transferencia de información, en busca de garantizar calidad del servicio (QoS). Sin embargo, no siempre estas condiciones garantizan alcanzar una calidad de servicio requerida desde la perspectiva de estrategias de utilización del ancho de banda disponible que le permita acceder a los servicios requeridos en la red.

Por ello, el objetivo de esta investigación ha sido el diseño de un algoritmo basado en el Equilibrio de Nash (NE) que permite resolver el problema de selección de un AP en redes 802.11 para asegurar que todos los usuarios en la red alcancen la mejor tasa de transferencia de información basada en restricciones de ancho de banda.

2. ANTECEDENTES Y ESTADO ACTUAL

Hasta la fecha, el conocimiento del estado del arte de las aplicaciones en redes inalámbricas de la teoría de juegos, se resume en las siguientes contribuciones: En [1] se modela la selección de un AP como un juego caracterizado por los equilibrios de Nash, en el cual se analiza el impacto de las decisiones egoístas que toma cada usuario en búsqueda del AP que le ofrezca un equilibrio óptimo entre la carga y la distancia a ser recorrida. En [2] se analiza una red inalámbrica con gran número de usuarios, considerando dos casos en la elección egoísta de una Estación Base (BS). En primer lugar, la BS asigna el mismo tiempo a sus usuarios, lo que se traduce en un único NE; y en segundo lugar, la BS asigna el mismo rendimiento dando como resultado múltiples NE que puede llegar a ser ineficientes y traducirse en una baja utilidad. Por otra parte, en [3] se modela la interacción de varios dispositivos como jugadores racionales egoístas interesados en maximizar su propia eficiencia espectral con el objetivo de obtener conectividad inalámbrica mediante el uso de un conjunto de BS en forma de un juego no cooperativo. Se analizan dos escenarios: 'BS seleccionada' en el cual se obtiene un NE y segundo, 'BS compartida' presentándose múltiples NE. Usando la dinámica de mejor respuesta, se proporcionan algoritmos completamente descentralizados, que siempre convergen en un NE para ambos juegos. Otras aplicaciones se describen en [4], [12].

3. TEORÍA DE JUEGOS

En términos generales e intuitivos, la Teoría de Juegos estudia situaciones de conflicto y cooperación a las que se denomina juegos, analizando los comportamientos estratégicos de los jugadores que pueden darse mediante decisiones individuales (como en los juegos no cooperativos), o bien mediante acuerdos entre los participantes (como en los juegos cooperativos).

Un juego consiste en un conjunto de individuos racionales (jugadores), un conjunto de movimientos (o estrategias) disponible para esos jugadores y una especificación de recompensas (o pagos) para cada combinación de estrategias. El objetivo, entonces, es tener un perfil de estrategias con las cuales obtener el mejor resultado posible, es decir, la mayor utilidad, teniendo en cuenta que este resultado no solo depende de las acciones propias sino también de las de los otros participantes [13].

4. EQUILIBRIO DE NASH

Existen distintos conceptos de solución a un juego, basados en dos clases de argumentos, los argumentos de dominación y los argumentos de equilibrio. En la solución de juegos mediante argumentos de dominación se busca eliminar las estrategias que se supone un jugador racional nunca utilizaría, puesto que le generaban ganancias inferiores ante cualquier creencia que pudiera tener sobre el comportamiento de los rivales. Sin embargo, estos conceptos han permitido en la mayoría de los casos simplificar en alguna medida los elementos por analizar, pero no se alcanza un resultado claro en la mayoría de las situaciones. Las soluciones mediante argumentos de equilibrio son quizás los conceptos de solución más importantes, en los cuales se espera que los jugadores jueguen un perfil de estrategias constituido por modos razonables de jugar, llegando al equilibrio de Nash.

El Equilibrio de Nash (NE) es un perfil de estrategias del que ningún jugador desearía desviarse, es decir, del que ningún jugador se arrepiente de la decisión tomada, ya que está formado por estrategias que son óptimas ante las estrategias del resto de jugadores. Sin embargo, esto no significa que en un NE cada jugador esté alcanzando el mejor resultado posible, sino el mejor resultado condicionado por el hecho que los demás jugadores jueguen las estrategias indicadas para ellos en dicho perfil. El NE busca maximizar la utilidad y es un estado de la red en la que los usuarios no pueden mejorar su tasa de transferencia de información por cambiar unilateralmente el AP al cual están realizando la conexión.

Definición 1. (Equilibrio de Nash) NE: En el juego G = {(i = 1,2,...n); B_0,k, B_1,k,...B_i,k; u_i,p(B_i,k, B_-i,k)}, se dice que el perfil de estrategias puras (b_0,k,b_1,k,...b_i,k) es un NE si para cada jugador u_i,p(b_0,k*,...,b_i-1,k*, b_i,k*, b_i+1,k*,...b_n,k*) ≥ u_i(b_0,k*,...,b_i-1,k*, b_i,k, b_i+1,k*,...b_n,k*) para todo b_i,k de B_i,k. Es decir, para cada jugador i,b_i,k, es una respuesta óptima a b*_-i,k) - [14].

5. MODELO DEL SISTEMA

El sistema del problema planteado es modelado como un juego no cooperativo, estático con información completa, en el cual cada jugador toma una posición egoísta buscando maximizar sus utilidades mediante las estrategias que tenga para jugar, y es estático, ya que las decisiones se toman simultáneamente. La Fig. 1 representa el modelo de juego basado en la estructura de una red inalámbrica de 2x2, es decir, 2 AP y 2 usuarios, el cual es extensible a un escenario n x n ya que comparte las mismas características, para definir el juego, se considera un canal de acceso múltiple (MAC) [19] vectorial sin memoria, que se supone invariante en el tiempo dentro del cual cada jugador selecciona su estrategia, se realiza una referencia a una topología de red y existen múltiples transmisores, en el cual cada transmisor simultáneamente envía múltiples flujos de bits independientes a un receptor, en este artículo, se trabaja solamente con el caso especial del canal MAC, en el cual los canales del transmisor al receptor se descomponen en un conjunto de subcanales independientes y no traslapados.

El juego es denotado por:

donde i hace referencia a los jugadores o usuarios de la red, B_i,k el ancho de banda asociado a la cantidad de canales k seleccionados por el jugador que equivale a cada una de las posibles estrategias que tiene disponible cada jugador y u_i,p es la función de utilidad con la que el jugador i al conectarse al punto de acceso p obtendrá los pagos de acuerdo con sus decisiones tomadas B_i,k.

La comunicación inalámbrica entre los usuarios del juego planteado está regida por el estándar 802.11g, el cual ofrece un gran ancho de banda en el rango de frecuencia de 2,4 GHz con codificación OFDM [15], [16]. Esta banda de frecuencias comprende 11 canales disponibles que no son completamente independientes, un canal se superpone y produce interferencia hasta un canal a 4 canales de distancia. Por tal motivo con el fin de evitar las interferencias causadas por el solapamiento se definen las estrategias del juego como el ancho de banda disponible en el mejor de los casos por los tres canales 1, 6 y 11 los cuales se encuentran lo suficientemente separados para no presentar interferencia entre sí. Aclarando que cada jugador puede elegir como estrategias 1 canal (20MHz), 2 canales (40MHz) o 3 canales (60MHz). Entonces, el perfil de estrategia del juego para un usuario es el vector:

Donde 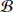= (20MHz, 40MHz, 60MHz) es el conjunto de todos los posibles anchos de banda (cantidad de canales) que un jugador puede utilizar como estrategia en el juego.

Para seleccionar una función que permita modelar el comportamiento de las tasas de transferencia de información de acuerdo con las características del canal, es necesario que esta relacione conceptos como capacidad, ancho de banda, potencia y ruido. Por tal motivo, en este trabajo se define la función de utilidad para todos los jugadores como su eficiencia espectral, es decir, la relación entre su velocidad de transmisión de Shannon y el ancho de banda disponible B en cada punto de acceso p:

Entre las variables que conforman (3) se encuentra la potencia P. En este caso, se considera que la máxima potencia que puede manejar el receptor, es un número entero de veces la potencia máxima de transmisión de un terminal de usuario para el escenario puntual a trabajar, y sin perder generalidad se considera por simplicidad que ese número entero es 1 y que la potencia de entrada máxima (Pin_max) del AP es igual a la potencia emitida por una tarjeta de red inalámbrica de un computador portátil cercana a los 32mW.

Por otra parte se tiene la ganancia g_j,k que en un canal de comunicaciones generalmente representa las perdidas por propagación de la señal, por esta razón toma valores inferiores a la unidad y, por lo tanto, no funciona como una ganancia sino como una atenuación de la señal causada por dicho fenómeno. Para obtener los valores de ganancia se hace uso de la función "rand" de Matlab → [17], con la cual se generan números aleatorios con media 0 y varianza 1 uniformemente distribuidos.

6. METODOLOGÍA PARA LA SOLUCIÓN DEL JUEGO

Una vez definido el modelo del juego, se realiza la búsqueda de las soluciones de este, guiado por los siguientes pasos de la estructura de solución propuesta:

• Verificación de la Existencia del Equilibrio de Nash (NE).
• Elaboración de la matriz de utilidades.
• Obtención de la mejor respuesta (BR) para cada caso.
• Solución del juego mediante el NE.

6.1 Existencia del Equilibrio de Nash

Antes de iniciar la solución del juego planteado mediante la búsqueda de los puntos de equilibrios de Nash, es pertinente probar si efectivamente dichos puntos de equilibrios existen. Para esto, se cuenta con distintos teoremas con los cuales se puede comprobar o no tal existencia, e incluso la referencia [18] plantea una metodología estructurada para la determinación de esta, indicando qué teoremas se deben emplear según el tipo de juego y el contexto de aplicación. El teorema 1, se escoge para demostrar la existencia del NE, ya que se ajusta a las condiciones y características por el juego aquí presentado y definidas en [18], dicho teorema ha sido demostrado en [1], [3], [13], [18], [22].

Teorema 1. Existencia del equilibrio de Nash (EN). Sea el juego G = {(i = 1,2,...n); B_0,k, B_1,k,...B_i,k; u_i(B_i,k, B_-i,k)} tal que, para todo jugador i, se cumple: B_i,k es un subconjunto no vacío, compacto y convexo de un espacio R^k.u_i es continua en todo su dominio 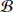= B_0,kXB_1,kX...XB_i,k, y es cuasicóncava en la variable b_i,k. Si se cumplen estas condiciones, o el juego G es finito existe al menos un EN en estrategias mixtas [19].

Como resultado de aplicar el teorema 1 sobre la función de utilidad definida en (3), dado que esta es continua en todo el dominio de estrategias y cuasicóncava, y el conjunto de estrategias B_i,k es un subconjunto no vacío, compacto y convexo de un espacio R^k, y además el juego es finito, por lo tanto se dice que existe al menos un equilibrio de Nash para el juego planteado en estrategias mixtas.

6.2 Elaboración de la matriz de utilidades

La Teoría de Juegos dedica gran parte de sus estudios a los llamados juegos bipersonales, es decir, con dos jugadores, en el cual es bastante útil el análisis matricial. El análisis matricial hace uso de la "Matriz de Pagos" que corresponde a una representación de las situaciones que pueden ser generadas por las alternativas de decisión y acción de dos jugadores. De este modo cada intersección o combinación de la alternativa elegida por un jugador y la alternativa elegida por otro, crea un punto de coordenadas que posee un valor, y se convierte en un premio para cada jugador o en un castigo si el premio tiene valor negativo. La matriz de utilidad general para el juego aquí planteado se muestra a continuación y depende básicamente de la estrategia B_i,k que el jugador elija:

La utilidad (eficiencia espectral) para cada jugador, la cual se muestra en la Tabla I, es denotada como u_i,p^k, donde i: jugador, p: punto de acceso y k: estrategia, y es la utilidad obtenida por el jugador al conectarse al AP p con una estrategia de ancho de banda k (cantidad de canales), y B es el ancho de banda máximo manejado por cada AP, para este caso 60MHz.

6.3 Obtención de la mejor respuesta

A continuación se analizan los conjuntos de perfiles de estrategias que contienen el (los) punto(s) de equilibrio de Nash, para encontrarlo(s) es necesario aplicar la dinámica de mejor respuesta, mediante la evaluación de bajo qué condición, cada usuario maximiza su utilidad dado que el otro usuario ha seleccionado un punto de acceso, como se muestra a continuación:

De la dinámica de mejor respuesta, se generan las siguientes condiciones mediante las cuales se evalúa el equilibrio de Nash para cada estrategia seleccionada por cada jugador, lo cual implica la selección de un AP.

De acuerdo con las condiciones 1 a 4 se identifican 3 casos en los cuales se evalúa el equilibrio de Nash, los casos identificados son:

Caso 1:

Caso 2

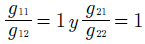
Caso 3

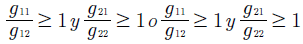
El caso 1 identifica un escenario en el cual los dos usuarios tienen su mejor canal sobre el mismo AP, lo cual implica que los dos jugadores seleccionan el mismo AP para realizar su transmisión, y dado que el máximo ancho de banda manejado por cada AP es 60MHz, y denotando el máximo ancho de banda que un usuario puede seleccionar sobre un AP como B_i,kmax = 60MHz , luego, en este caso los perfiles de estrategias son de la forma (B_i,k, B_i,kmax - B_i,k) o de la forma (B_i,kmax - B_i,k, B_i,k), si g11 > g21 o g12 > g22 el equilibrio de Nash es (B_i,kmax, 0), pero si g11 > g21 o g12 > g22 el equilibrio de Nash es (0, B_i,kmax), ya que el usuario que tenga el mejor canal seleccionará la estrategia que permite maximizar su utilidad, que en este caso es jugar B_i,kmax y dado que los dos jugadores seleccionan el mismo AP, el otro jugador no tiene otra alternativa más que no transmitir.

El caso 2 identifica un escenario en el cual los dos usuarios se pueden conectar a cualquier AP y se esperaría que si el jugador 1 se conecta al AP1 lo haga utilizando el máximo ancho de banda para maximizar su utilidad, por lo tanto, el jugador 2 se conectaría al AP2 utilizando el máximo ancho de banda, o viceversa; sin embargo, este caso es improbable, dado que las ganancias de canal son realizaciones de variables aleatorias que siguen distribuciones continuas, razón por la cual, la probabilidad que las ganancias sean exactamente iguales es igual a cero y por lo tanto el caso 2 no sea real.

El caso 3 identifica un escenario en el cual cada usuario se conecta a un AP diferente, por ejemplo el jugador 1 selecciona el AP1 y por lo tanto el jugador 2 selecciona el AP2, por lo que, la estrategia que maximiza la utilidad de cada jugador es seleccionar el máximo ancho de banda posible para cada AP el cual es B_i,kmax = 60MHz .

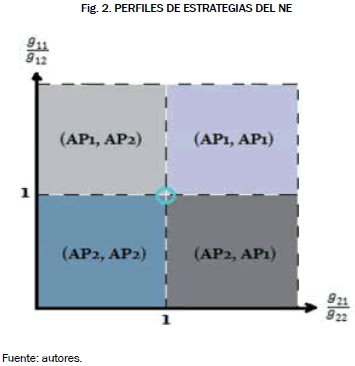
En la Fig. 2, se muestran los perfiles de estrategias para cada escenario y las selecciones realizadas de acuerdo con el escenario, y a los equilibrios y selecciones, se procede a la realización del algoritmo que permite la selección del AP basado en las estrategias de ancho de banda que decida jugar.

7. RESULTADOS

Para evaluar cada una de las ecuaciones obtenidas en la matriz de utilidades y teniendo en cuenta los criterios establecidos para las variables que intervienen en la función de utilidad, considerando las posibles estrategias de ancho de banda y las características del canal presentadas en el instante de tiempo en el cual se desarrolla el juego.

En el modelo del juego existe un número determinado de canales en paralelo, los cuales están limitados por el mismo nivel de potencia máxima. El objetivo principal es distribuir la potencia total entre los canales con el fin de maximizar la eficiencia espectral de cada uno de ellos. Este concepto asignación óptima de potencia en canales paralelos se realiza mediante el algoritmo de Water-Filling [23], [24].

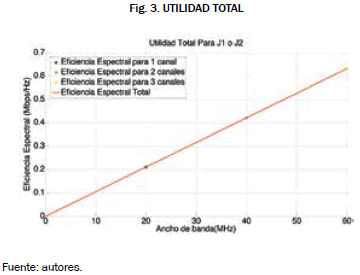
El funcionamiento del algoritmo del Equilibrio de Nash requiere, entonces, la suma de las eficiencias espectrales obtenidas por los dos jugadores para cada una de sus estrategias, y que las ganancias de los AP elegidos sean iguales. Por lo tanto la Fig. 3 muestra la eficiencia espectral (Mbps/Hz) contra las estrategias de ancho de banda (MHz). La línea roja (utilidad total) muestra la suma de las utilidades de los dos jugadores, sus valores se presentan en la Tabla II y los asteriscos indican en cada caso los pagos para cada estrategia aplicada.

Tabla II

Para simular los equilibrios de Nash es necesario que las ganancias de los canales no sean iguales independientemente de si los dos jugadores eligen igual o diferente Access Point, Por lo tanto, para efectos de simulación se optó por un valor de ganancia arbitraria que como bien se mencionó anteriormente debe ser menor a 1, indicando una atenuación o pérdidas por propagación, los cuales se muestran en la Tabla III.

La Fig. 4 muestra que los equilibrios de Nash que se obtienen cuando las ganancias de los AP son aleatorias, el valor de la utilidad está dado por la función de utilidad. Con el NE se garantiza maximizar la utilidad pero no se garantiza una eficiencia energética, dado que estos puntos de equilibrio se dan para la potencia máxima emitida por la tarjeta de red inalámbrica del dispositivo de acuerdo con el modelo de canal MAC vectorial y al algoritmo de asignación óptima de potencia wáter filling.

8. CONCLUSIONES

Se logró determinar a través del método de solución del Equilibrio de Nash que la ganancia del canal es un factor totalmente influyente en la eficiencia espectral de este cuando la variación de la función de utilidad es únicamente la estrategia ancho de banda. Por lo tanto, se obtuvo para cada estrategia un equilibrio de Nash que se alcanza cuando las ganancias de los AP elegidos son iguales.

El Equilibrio de Nash no permite garantizar una eficiencia energética, ya que las estrategias obtenidas como solución para cada uno de los usuarios corresponden al máximo nivel de potencia emitido por la tarjeta de red inalámbrica del dispositivo electrónico. De este modo se consumirá bastante potencia en el dispositivo lo que disminuiría el tiempo de duración de su batería si se utiliza este concepto de solución.

Se determinó que desde el punto de vista de la eficiencia espectral el Equilibrio de Nash garantiza tasas de transferencia que están muy por encima de las mínimas requeridas por cada usuario bajo condiciones de utilización de servicios individuales, por ejemplo, para realizar una video conferencia es suficiente con 256Kbps, en la Tabla II se verifica que la eficiencia espectral es del orden de 0.3161 Mbps/Hz en equilibrio, lo cual implica que el usuario utiliza 60MHz de ancho de banda y, por lo tanto, tiene una capacidad disponible de 18.966 Mbps, la cual es muy superior a los 256Kbps requeridos. Debido a que el ancho de banda del canal es fijo (20MHz) y no se reparte entre los usuarios, existe una gran proporción de ancho de banda que no es utilizada aun cuando la actividad que el usuario desea desempeñar en la red requiera una tasa de transmisión alta. De este modo se concluye que el Equilibrio de Nash presenta grandes problemas en cuanto a la optimización en la asignación de recursos espectrales.

TRABAJOS FUTUROS

La selección de AP en redes 802.11 es una problemática a la cual se enfrenta actualmente la tecnología Wi-Fi debido a la masificación de usuarios. Por tanto, son numerosos los trabajos en búsqueda de métodos de solución efectivos para este problema que pueden ser abordados incluso desde la perspectiva de la Teoría de Juegos. Sería bastante interesante la elaboración de un trabajo futuro que busque la unificación de los parámetros potencia y ancho de banda, permitiendo así garantizar QoS bajo condiciones totales de capacidad. Otro trabajo puede enfocarse en resolver el mismo problema bajo restricciones de ancho de banda, utilizando otros conceptos de solución como el equilibrio de satisfacción y el equilibrio de satisfacción eficiente.

REFERENCIAS

[1] K. Mittal, E. Belding and S. Suri, "A game theoretic analysis of wireless access point selection by mobile users", Computer Communications Journal, vol. 31, n°1, pp. 2049-2062, 2008.         [ Links ]

[2] L. Jiang, S. Parekh, J. Walrand, "Base station association game in multi-cell wireless networks," in Wireless Communications and Networking Conference 2008, Las Vegas, pp. 1616-1621, 2008.         [ Links ]

[3] Perlaza, S. Belmega, E. Lasaulce, S. Debbah, M. "On the base station selection and base station sharing in self-configuring networks," in 3rd ICST/ACM International Workshop on Game Theory in Communication Networks. Pisa, Italy, October 2009.         [ Links ]

[4] Li-Hsing Yen, Jia-Jun Li, and Che-Ming Lin, "Stability and fairness of native AP selection games in IEEE 802.11 access networks," in Wireless and Optical Communications Networks (WOCN), Colombo, pp. 1-5, 2010. DOI: 10.1109/WOCN.2010.5587341.         [ Links ]

[5] Lin Gao, Xinbing Wang, Gaofei Sun and Youyun Xu, "A game approach for cell selection and resource allocation in heterogeneous wireless networks," in Sensor, Mesh and Ad Hoc Communications and Networks (SECON), 8th Annual IEEE Communications Society Conference, Salt Lake City, UT., pp. 530-538, 2011. DOI: 10.1109/SAHCN.2011.5984939.         [ Links ]

[6] E. Jocelyne, F. Martignon and E. Altman, "Joint pricing and cognitive radio network selection: a game theoretical approach," in Modeling and Optimization in Mobile, Ad Hoc and Wireless Networks (WiOpt), 10th International Symposium, Paderborn, Germany, pp. 49-53, 2012.         [ Links ]

[7] D. L. Trujillo, "Selección de Access Point en redes 802.11 garantizando mínima capacidad para QoS: una perspectiva desde la teoría de juegos no cooperativos," thesis, Universidad del Quindío, Armenia, Colombia. 2012.         [ Links ]

[8] D. Monderer, "Potential Games." Games and Economic Behavior, vol. 14, pp. 124-143, 1996.         [ Links ]

[9] S. Ross and B, Chaib-Draa, "Learning to play a satisfaction equilibrium," in Computer Science Department. PLT Bdg, Laval University, Quebec, PQ, Canada, 2010.         [ Links ]

[10] I. Menache and A. "Network games. Theory, models, and dynamics," Jean Walrand, Series Editor, pp. 69, 2010.         [ Links ]

[11] D. Amzallag, R. Bar-Yehuda, D. Raz, and G. Scalosub, "Cell Selection in 4G Cellular Networks," in Proceeding of the Annual IEEE 27th INFOCOM, Hong Kong, pp. 700-708, 2008.         [ Links ]

[12] P. Mertikopoulos, E. Belmega, A. Moustakas, and S. Lasaulce, "Dynamic power allocation games in parallel multiple access channels," in VALUETOOLS '11 Proceedings of the 5th International ICST Conference on Performance Evaluation Methodologies and Tools, Brussels, Belgium, pp. 332-341, 2011.         [ Links ]

[13] Grupo de Investigación Eumednet. Universidad de Málaga, Introducción a la teoría de juegos. 2012 [Online]. Available: http://www.eumed.net/cursecon/juegos/index.htm.         [ Links ]

[14] J. Pérez, J. Jimeno, and E. Cerdá, "El equilibrio de Nash" Teoría de Juegos, Cap. 2, Madrid, España: Pearson, 2004, p. 89.         [ Links ]

[15] H. Rohling, OFDM Concepts for Future Communication Systems, New York: Springer Heidelberg, 2011, p. 5.         [ Links ]

[16] R. Nee, R. Prasad, OFDM for Wireless Multimedia Communications. Artech House, 2000, p. 229.         [ Links ]

[17] M. Rodríguez, Introducción Rápida a Matlab y Simulink para Ciencia e Ingeniería. Ediciones Díaz de Santos, S.A. Madrid, 2003.         [ Links ]

[18] S. Lasaulce, M. Debbah and E. Altman, "Methodologies for analyzing equilibria in wireless games," Signal Processing Magazine, IEEE, vol. 26, no. 5, pp. 41-52, 2009. DOI 10.1109/MSP.2009.933496.         [ Links ]

[19] J. Pérez, J. Jimeno, and E. Cerdá, "Teoremas de existencia del equilibrio de Nash", Teoría de Juegos, Cap. 3. Madrid, España: Pearson, 2004, pp. 170-175.         [ Links ]

[20] E. Astaiza. "Introducción a la teoría de juegos en comunicaciones inalámbricas, Cap. 5 Existencia del Equilibrio de Nash", Univ. del Quindío, Armenia, Quindío, 2013, pp. 25-26.         [ Links ]

[21] D. Monderer, "Potential games," Games and Economic Behavior, vol. 14, pp. 124-143, 1996.         [ Links ]

[22] R. Cheng and S. Verdu, "Gaussian multiaccess channels with isi: capacity region and multiuser water-filling," IEEE Trans. On Info. Theory, vol. 39, no. 3, pp. 773-785, May. 1993.         [ Links ]

[23] C. E. Shannon. Communication theory of secrecy systems. Bell Syst. Tech. J., vol. 28, pp. 656-715, 1949.         [ Links ]

[24] M. S. Pinsker. Information and Stability of Random Variables and Processes. Izd. Akad. Nauk, 1960. Translated by A. Feinstein, 1964.         [ Links ]