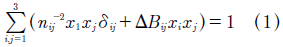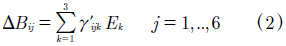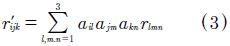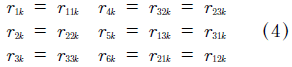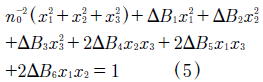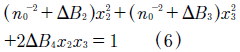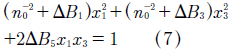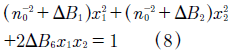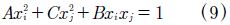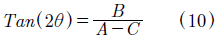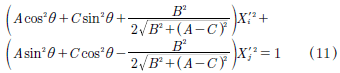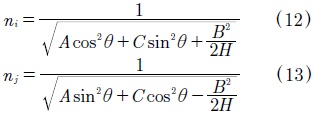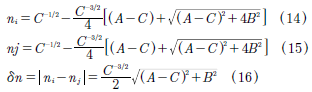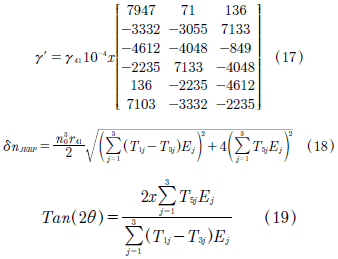Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Iteckne
versão impressa ISSN 1692-1798
Iteckne vol.14 no.1 Bucaramanga jan./jun. 2017
Crystallographic cut that maximizes of the birefringence in photorefractive crystals
Corte cristalográfico que maximiza la birrefringencia en cristales fotorrefractivos
Jorge Enrique Rueda-Parada1
1 Ph. D. Natural Science, Physic. Universidad de Pamplona. Pamplona, Colombia. jorgeenriquerueda@gmail.com.
ABSTRACT
The electro-optical birefringence effect depends on the crystal type, cut crystal, applied electric field and the incidence direction of light on the principal crystal faces. It is presented a study of maximizing the birefringence in photorefractive crystals of cubic crystallographic symmetry, in terms of these three parameters. General analytical expressions for the birefringence were obtained, from which birefringence can be established for any type of cut. A new crystallographic cut was encountered; the birefringence value is greater than PROM, PRIZ and HUIGNARD commercial cuts.
KEYWORDS: Photorefractive crystals; Birefringence; electro-optical effect.
RESUMEN
La birrefringencia por efecto electro-óptico depende del tipo de cristal, del corte del cristal, del campo eléctrico aplicado y de la dirección de incidencia de la luz sobre las caras principales del cristal. Se presenta un estudio de maximización de la birrefringencia en cristales fotorrefractivos de simetría cristalográfica cúbica, en términos de estos tres parámetros. Expresiones analíticas generales para la birrefringencia fueron obtenidas, a partir de las cuales se puede establecer la birrefringencia de cualquier tipo de corte. Un nuevo corte cristalográfico fue encontrado, cuyo valor de birrefringencia es mayor que los cortes comerciales PROM, PRIZ y HUIGNARD.
PALABRAS CLAVE: Cristales fotorrefractivos; Birrefringencia; Efecto electro-óptico.
1. INTRODUCTION
The photorefractive crystals are light modulators, electro-optical and photoconductive, and have optical memory [5],[12],[13]. These materials are of particular interest related to dynamic holography and optical amplification applications, between others [4]-[7], [9]-[21]. The optical efficiency of these materials depends on the direction of light propagation through the birefringence of the same material, and the applied electric field [5],[12]. The crystal cut refer to the principal crystal faces, each of which is parallel to a particular crystallographic plane. Thus, each cut corresponds to a maximum birefringence and thus a maximum optical efficiency. Using the numerical Newton-Raphson method [8] was determined the cut that maximizes the birefringence in cubic crystals with 3m23 symmetry. The methodology can be applied to other crystallographic symmetries. The results were compared with the birefringence in PROM, HUIGNARD and PRIZ commercial cuts [4]-[7].
2. SOLUTION OF THE PROBLEM
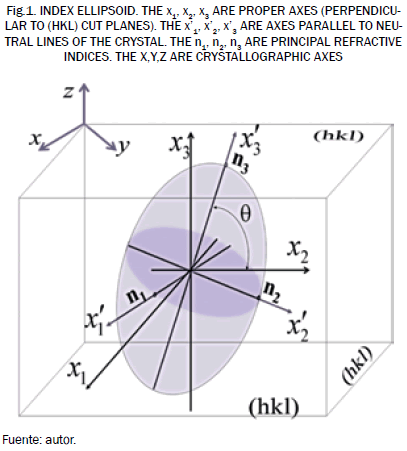
The solution of the problem from the mathematical model of index ellipsoid [1], defined by (1):
where the first term of this equation represents the undisturbed state of the crystal, and second term is the ΔBij disturbed state. The nij parameter is the refractive index tensor, and xi,j are spatial coordinates. With δij = 0 if i  j, and δij = 1 if i = j. Figure. 1 is a scheme that defines index ellipsoid. It is presented the solution for the particular case of isotropic crystals (n11 = n22 = n33 = no) [1],[2], that exhibit electro-optic effect of the first order, where the perturbation (electro-optic effect) is given by (2):
j, and δij = 1 if i = j. Figure. 1 is a scheme that defines index ellipsoid. It is presented the solution for the particular case of isotropic crystals (n11 = n22 = n33 = no) [1],[2], that exhibit electro-optic effect of the first order, where the perturbation (electro-optic effect) is given by (2):
Where γ'ijk is the electro-optic tensor (EOT) in the proper axes system of the crystal, and Ek is the electric field applied perpendicularly to principal faces crystal.
In equation (3), the rlmn electro-optic tensor is given in the (x,y,z) system. This transformation is applied when the proper axes are not parallel to (x,y,z) axes:
where i,j,k = 1..3, and ail,jm,kn are the coefficients of the transformation R(α,β,γ) matrix as a function of the Euler angles [3]. These angles define the crystal cut. Also in (3), due to symmetry of the EOT can be applied the next contraction of indexes (4):
Then, eighteen terms of electro-optical tensor are obtained in the system of proper axes. For the particular study of this work, the non-zero and equal terms are r41 = r52 = r63. This tensor is given in a (x,y,z) system, axes parallel to the [100], [010], [001] crystallographic directions. The birefringence can be calculated from equation (1) given in the proper axes system of the crystal:
Equation (5), it can be considered three illumination directions perpendicular to the (h,k,l) planes cut (Fig. 1):
Case 1. Illumination parallel to the x1 axes:
Case 2. Illumination parallel to the x2 axes:
Case 3. Illumination parallel to the x3 axes:
Equations (6) to (8) represent indices planes parallel to the (0,x2,x3), (x1,0,x3) and (x1,x2,0) crystal faces, respectively. Moreover, the equations (6) to (8) have the form (9),
with i  j, and B
j, and B  0, and where:
0, and where:
We can assume that the proper axes do not coincide with neutral lines, and then it facilitates to find general expressions for the birefringence. These solutions must be transformed to coordinates of the neutral lines. Assuming that the neutral lines are rotated to an θ angle with relation to its proper axes, then (11):
Coefficients of the (11) define the ni and nj principal indices refraction, thus:
Where ni = n2 and nj = n3 for Case 1; ni = n1 and nj = n3 for Case 2; ni = n1 and nj = n2 for Case 3; with 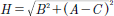 . If (12) and (13) are expanded into Taylor series, then we can obtain:
. If (12) and (13) are expanded into Taylor series, then we can obtain:
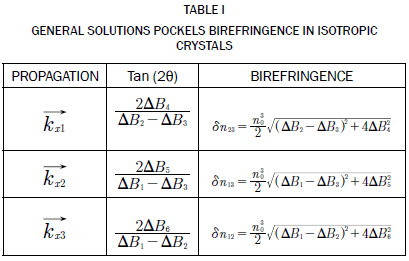
Table I contains general expressions obtained for the birefringence and the orientation of the neutral lines.
3. ALGORITHM OF THE NUMERICAL METHOD AND RESULTS
With these before expressions, we can calculate the birefringence of the crystal. The following is the algorithm for the numerical calculations:
- Define a cut: R(α,β,γ).
- Calculate r'ijk.
- Calculate the perturbation with three field components, equation (2).
- Calculate the birefringence (for each interest case of the Table 1).
- Check if the birefringence is the maximum, then finishes.
In the birefringence numerical maximization process, we can use the three equations of birefringence (Table I). The other part, It was used as input parameters, the EOT of a BSO crystal (r41 = 4 pm/V) and three electric field components. The Newton-Raphson routine seeks maximum birefringence between the three expressions of the Table I, and in terms of the cut angle defined by [α;β;γ]. The software system output reports the cut angles [α;β;γ], the elements of the perturbation vector, and r'ijk. Equations (17) to (19) are results of numerical maximization of the birefringence process.
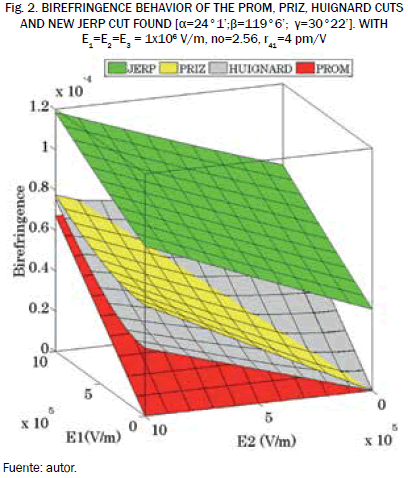
The maximization algorithm was implemented in Fortran, where 1x10-6 rad precision was used to the [α;β;γ] angles. We found that the birefringence is maximum for [α = 24°1'; β = 119°6'; γ = 30°22'] cut, with the light propagation on the kx2 direction. The equations (18) and (19) are the maximum birefringence and orientation of the neutral lines, respectively. Fig. 2 shows the numerical results of birefringence found with related to PROM, PRIZ, and HUIGNARD traditional cuts, and new cut (JERP). Table II contains the birefringence of the new cut compared with the traditional cuts.
4. CONCLUSIONS
It has been maximized the birefringence of photorefractive materials, in terms of the cutting of the principal crystal faces. It has been encountered a new cut, which was evaluated for four directions of the applied electric field, and the three main directions of propagation of light in the crystal. In all cases tested, the birefringence of the new cut is greater than PROM, PRIZ, and HUIGNARD commercial cuts. Furthermore, the general analytical expressions of birefringence were found. From these new expression can be studied, with less difficulty, analytically or numerically any birefringence crystal cubic crystallographic structure.
REFERENCES
[1] I. P. Kaminow, E. H. Turner, "Electrooptic Light Modulators", Appl. Opt., 5, 10, 1966. [ Links ]
[2] J. Nye, "Proprietés Physiques de Cristaux", Ed. Masson, 1985. [ Links ]
[3] H. Goldstein, J. Safko, "Classical Mechanics", Third Edition, Addison-Wesley (2002). [ Links ]
[4] S. Hou, D. Oliver, Pockels Readout Memory Using BSO, App. Lett., 18, 325, 1971. [ Links ]
[5] J. Huignard, F. Micheron, "High-sensitivity read-write volume Bi12SiO20 and Bi12GeO20 crystal", App.Phys. Lett., 29, 591, (1976). [ Links ]
[6] D. Casasent, F. Caimi, A. Khomenko, "Soviet Priz spatial light modulator", App. Opt., 20, 4215, 1981. [ Links ]
[7] D. Casasent, F. Caimi, M. P. Petrov, A. V. Khomenko, "Applications of the Priz light modulator", Applied Optics, 21, 21, (1982). [ Links ]
[8] J. Tjalling, "History of the newton-raphson method", SIAM Review, 37, 4, 1995. [ Links ]
[9] Li, C.-S., Zeng, Z. He, X.-L., "Optical voltage sensor using bismuth silicate crystal grown by hydrothermal method", Journal of Optoelectronics Laser, 25, 2, 2014. [ Links ]
[10] X. He, H. Zhou, W. Zhou, Z. Hu, C. Zhang, H. Huo, J. Wang, (...), F. Lu, "Solubility and optical activity of Bi12SiO20 crystals", Journal of Crystal Growth, 351, 1, 2012. [ Links ]
[11] Li, C., Cui, X., Yoshino, T. "Optical electric-power sensor by use of one bismuth germanate crystal", Journal of Lightwave Technology, 21, 5, 2003. [ Links ]
[12] A. R. Salazar, E. Jorge, J. E. Rueda, "Modification of the exchange of energy in BSO at equal optimized coupling constant", Optics Communications 212, 2002. [ Links ]
[13] M. Tebaldi, J. E. Rueda, N. Bolognini, "Talbot interferometer based on a birefringence grating", Optics Communications 185, 2000. [ Links ]
[14] J. E. Rueda, M. Tebaldi, S. Granieri, N. Bolognini, "Implementation of a photorefractive correlator based on a fake zoom lens", Optik, 113, 7, 2002. [ Links ]
[15] J. A. Gómez, H. G. Lorduy, A. Salazar, "Novel procedure for the simultaneous determination of the Debye length and electro-optic coefficient for an optically active BSO crystal", Optics Communications, 284, 460, 2011. [ Links ]
[16] J. A. Gómez, H. G. Lorduy, A. Salazar, "Improvement of the dynamic range of a fiber specklegram sensor based on volumen speckle recording in photorefractive materials", Optics and Laser in Engineering, 49, 473, 2011. [ Links ]
[17] J. A. Gómez, H. Lorduy, A. Salazar, "Influence of the volume speckle on fiber specklegram sensors based on four-wave mixing, Lorduy in photorefractive materials", Optics Communications, 284, 1008, 2011. [ Links ]
[18] J. E. Rueda, A. Romero, "Optical cryptography using Fresnel diffraction and phase conjugation", Dyna, 80, 181, 2013. [ Links ]
[19] V. H. Arístizabal, A. Hoyos, N. D. Gómez, J. A. Gómez, "Effect of Wavelength on Metrological Characteristics of Non-Holographic Fiber Specklegram Sensor", Photonic Sensors, 1, 1, 2015. [ Links ]
[20] A. Keshavarz, Z. Abbasi, "Spatial soliton pairs in an unbiased photovoltaic-photorefractive crystal circuit", Spring, 1, 1, 81, 2016. [ Links ]
[21] M. A. A. Khushaini, A.B-M.A. Ibrahim, "On the optical bistability of ferroelectrics via two-wave mixing: Beyond the slowly varying envelope approximation", Optics Communications, 381, 384, 2016. [ Links ]