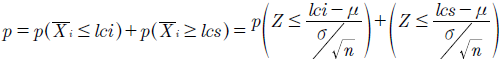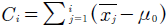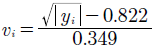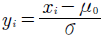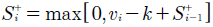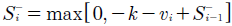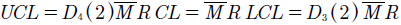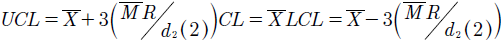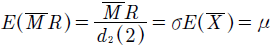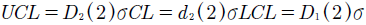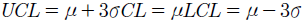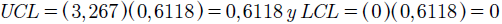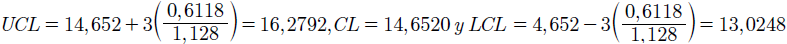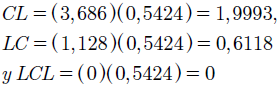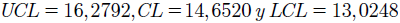1. INTRODUCCIÓN
Las cartas de control para procesos estadísticos son utilizadas frecuentemente para monitorear una característica de calidad e identificar irregularidades en las medidas de localización y variabilidad aplicadas, que pueden presentarse como cambios repentinos o graduales en los datos de estudio. Comúnmente, en el caso univariado se utilizan las cartas de control Shewhart, CUSUM y EWMA, cuya variación se supone que sigue una distribución normal.
En este artículo se hará una aplicación a un método básico SPC, mediante la utilización de la Carta CUSUM para monitorear la variabilidad del pH en el uso de fungicidas en la protección de plantas. La carta de CUSUM es una alternativa ante la insensibilidad de los corrimientos pequeños del proceso en las cartas de control de Shewhart, debido a que va acumulando información obtenida de las muestras anteriores y de esta manera puede detectar de forma más rápida pequeños cambios en el proceso1.
Douglas M. Hawkins2,3 creó un procedimiento para el estudio de la variabilidad implementando CUSUM. El propósito de este trabajo es aplicar el procedimiento presentado por Hawkins, estudiar la sensibilidad de los datos de un proceso real y comparar los resultados con la carta de control de Shewhart, mediante el cálculo de la longitud de corridas promedio (ARL), con la finalidad de detectar cuál de estas cartas es más sensible a estos cambios.
ARL permite establecer mediante el conteo de puntos, cuál de las cartas de control, en este caso univariado, detecta con más rapidez una señal de alarma, dado un incremento en la variabilidad en el monitoreo de la medida de variabilidad o en la medida de localización de una carta de control.
2. ESTADO DE ARTE
2.1 Fundamentación teórica
2.1.1 Principios básicos
Es el número de puntos graficados en la carta hasta que aparezca una señal fuera de control, cuando el proceso se monitorea en línea, es decir, se encuentra en Fase II, se conoce como longitud de corridas, se donará por RL. La longitud de corridas RL es una variable aleatoria con un comportamiento geométrico de la forma P(RL = x) = p(1 - p) x-1 , con un valor esperado de ARL = 1/p, donde en condiciones normales p = 0.0027, es definida como la probabilidad de que aparezca una señal de alarma. Esta longitud de corridas RL permite para cada una de las cartas de control evaluar su sensibilidad, realizando el conteo de tandas hasta que exista una señal de alarma o punto fuera de los límites; los estudios indican, por ejemplo: mayor potencia en detectar señales de alarma de la carta S en contraste con la carta R para cualquier incremento de la dispersión. En la carta de control Shewhart, p se define entonces como la probabilidad de que un punto se localice fuera de control, definida como:
La carta CUSUM fue propuesta por Page (1954), y el nombre de CUSUM se debe a que es una carta en la que se grafican las sumas acumuladas de las desviaciones con respecto al valor nominal de la característica de interés. Por ejemplo, suponer que se tienen muestras de tamaño n ≥ 1, y que x j es el promedio de la j-ésima muestra. Entonces, si μ 0 es el objetivo para la media del proceso, la carta de control de suma acumulada se construye graficando la cantidad4:
contra la muestra i, el estadístico C i se le llama a la suma acumulada hasta la i-ésima muestra, incluyéndola.
Esta carta constituye una forma rápida de determinar cuánto se aparta una unidad de producto de un estándar de fabricación establecido, determinando el valor aceptable e inaceptable de esta desviación, visualizándose la información en forma de gráfico. Las cartas de control de CUSUM permiten monitorear en forma continua las diferencias acumuladas de una característica cualitativa de un proceso determinado, que puede definirse como datos recogidos secuencialmente para permitir la detección temprana de desviaciones de un estándar establecido5,6. La principal ventaja de las cartas CUSUM es que puede detectar un cambio pequeño o persistente en el promedio del proceso, más rápidamente que una carta de control Shewhart Tabla I.
Tabla I BREVE EVOLUCIÓN DE LAS CARTAS DE CONTROL
| CRONOLOGÍA | CONTEXTUALIZACIÓN | ANÁLISIS |
|---|---|---|
| Carta de control 1920 | Empleado por primera vez por el Dr. Walter Shewhart en la Bell Telephone. | Utilizada para localizar los problemas ocurridos durante el proceso que puede ser por causas asignables (no aleatorias) o causas no asignables (aleatorias). |
| Cartas Control Mutivariante 1947 | La principal aportación en este campo fue la realizada por el profesor Harold Hotelling (1947), quien propuso una carta de control multivariante basado en la distancia de Mahalanobis (1936). | Las cartas de control multivariante, denominadas T2 de Hotelling, el cual monitorea la distancia entre el vector de promedios esperado y el vector de promedios observados, considerando su matriz de varianza covarianzas para evaluar el límite de control. |
| Cartas CUSUM 1954 | En esta carta se considera el componente de dependencia en el tiempo de las observaciones o estadísticos de control, introducido por E. S. Page (1954). | Estas cartas van acumulando información obtenida de las muestras anteriores; de esta forma pueden detectar con rapidez cambios pequeños en el proceso. |
| Carta Ewma 1959 | S. W. Roberts (1959) denominado carta de promedios móviles exponencialmente ponderados (EWMA). | Aplica como estadístico de control una ponderación asociada a las observaciones anteriores, para sensibilizar la carta cuando los cambios son pequeños. |
| CUSUM R 1963 | E.S. Page adopta la estadística de control R. | Introduce el estadístico de control del rango en las sumas acumuladas. |
| CP CUSUM 1999 | Acosta, Mejía, Pignatello y Reo utilizan la transformación normal inversa para determinar el estadístico de la carta CUSUM(17). | Para monitorear la variabilidad tomando como base la razón de verosimilitud. |
| Carta MCUSUM 1988 | Crosier presentó una versión multivariada de la carta CUSUM. | Las cartas multivariantes están sujetas al supuesto de normalidad multivariada que podría ser una limitación para los casos donde se rechace esta hipótesis. |
| Carta Mewma 1992 | Lowry a través de la extensión de la carta de control EWMA para el caso multivariante. | |
| CUSUM V 2002 | Petrodjo, Abdollahian y Narayan definen un estadístico de control Vt aproximado a una distribución chi-cuadrado(18). | Esta carta es más sensible que la carta CUSUM para la desviación S y el rango R. |
| DDChart | R. Liu aporta el diseño de la carta de control denominada cartas DDChart. | Cartas de control de tipo no paramétrico, basados en el concepto de profundidad de datos. |
Fuente: Los autores
En el campo de los herbicidas o protectores de planta, J.P. Lorente (2012) presenta la importancia de las cartas de control univariadas de Shewhart en la agricultura, afirmando a su vez las grandes dificultades en la implementación en este sector debido al desconocimiento en la aplicación de las herramientas estadísticas en el control de calidad19.
2.1.2 Carta de control CUSUM para la variabilidad
Las cartas de control CUSUM son utilizadas para monitorear la medida de variabilidad de un proceso. Supóngase que se desea monitorear la σ 2 de una característica de calidad tomando una muestra de x 1, x 2, x 3,…, x n de n variables independientes. Cuando el proceso está bajo control, tiene una distribución normal con media μ 0 y desviación estándar σ. Se supone que σ es conocida o que se cuenta con una estimación de la misma7.
Para evaluar la variabilidad, Hawkins (1981, 1993) sugiere crear una nueva cantidad estandarizada1,3,8:
Donde y i es el valor estandarizado de la variable aleatoria x i , y está dado por:
Hawkins sugiere que las v i son más sensibles a los corrimientos en la varianza que a los de la media. Puesto que la distribución bajo control de v i es aproximadamente N ~ (0,1), es posible establecer los siguientes CUSUM unilaterales (estadísticos de control) a escala estandarizada9:
donde S0 + = S0 - = 0
Para la aplicación de esta carta, es importante definir dos parámetros. El primero de ellos corresponde a K, conocido como valor de referencia (o tolerancia, o valor laxo), el cual determina la sensibilidad del gráfico y se obtiene como K = kσ. La elección de k depende del tamaño del corrimiento que quiere detectarse; es decir, k = ½δ donde δ es la magnitud del corrimiento en unidades de desviación estándar10.
Otro parámetro que se debe considerar es el intervalo de decisión H, criterio para decidir si el proceso está fuera de control. Se define H = hσ, donde σ es la desviación estándar de la variable muestral usada para formar la CUSUM. Por lo general, este valor suele ser cinco veces la desviación estándar del proceso σ. Cabe anotar, que diversos estudios analíticos3 recomiendan utilizar h = 4 o h = 5 y k = 0,5, ya que con estos valores se alcanzará una CUSUM que tiene un buen desempeño de la longitud promedio de la corrida (ARL).
En la Tabla II se muestra las longitudes promedio de las corridas bilaterales para h = 4 y h = 5 con k = 0,5 Para la carta de control, se debe tener en cuenta que si la desviación estándar del proceso aumenta, los valores de Si + igualmente aumentarán y terminaran por exceder el valor de h; por otro lado, si la desviación estándar disminuye, entonces los valores de Si + aumentarán y terminarán por exceder -h.
Tabla II DESEMPEÑO DE LA ARL DE LA CUSUM TABULAR CON k = ½ Y h = 4 o h = 5
| Corrimiento en la media (múltiplo de s) | h = 4 | h = 5 |
|---|---|---|
| 0.00 | 168 | 465 |
| 0.25 | 74.2 | 139 |
| 0.50 | 26.6 | 38.0 |
| 0.75 | 13.3 | 17.0 |
| 1.00 | 8.38 | 10.4 |
| 1.50 | 4.75 | 5.75 |
| 2.00 | 3.34 | 4.01 |
| 2.50 | 2.62 | 3.11 |
| 3.00 | 2.19 | 2.57 |
| 4.00 | 1.71 | 2.01 |
Fuente: D.C. Montgomery, Introduction to Statical Quality Control.
En estos casos, si Si + o Si - excede el intervalo de decisión H, se considera que el proceso está fuera de control, deberán buscarse las causas asignables que generaron este hecho y emprender cualquier acción correctiva.
Los valores de N+ y N- indican los períodos en que las sumas no han sido cero, en la carta CUSUM permite conocer cuando ha ocurrido el corrimiento. De esta manera permite contar hacia atrás desde un punto fuera de control hasta el período de tiempo en que la CUSUM subió de cero, para encontrar el primer período del proceso posterior al corrimiento.
Los cálculos de los ARL de la Tabla II se verificaron por simulación fijando una longitud promedio de corrida nominal o primaria ARL0 = 200, estableciendo el límite unilateral superior de control para la carta e intervalo de muestreo fijo. Se supuso que los esquemas trabajan en las condiciones de Fase II de control. El proceso de simulación se llevó a cabo mediante el programa de computación diseñado en lenguaje R, el cual compara simultáneamente para los valores de h cuatro (4) y (5). El algoritmo que se aplicó es el siguiente:
a) Inicialmente se evaluó el límite de control superior de referencia en cada uno de los esquemas, bajo un valor nominal ARL igual a 200, para los valores de h de cuatro y cinco. b) Una vez establecido el valor del límite superior de control, se generan los subgrupos cuyas observaciones provienen de una distribución normal con media y desviación conocida y se generaron grupos de observaciones provenientes de una distribución normal con desviación estándar modificada. c) Para cada muestra se calculó del estadístico de control para la variabilidad. d) Posteriormente en cada uno de los esquemas se compara su valor con el límite superior respectivo. Cada vez que el estadístico excedía al valor del límite superior respectivo, se detiene la simulación; de lo contrario, el proceso continuaba. e) Los pasos anteriores se replicaron 15000 veces, efectuando 1000 veces las mismas réplicas y los resultados obtenidos en cada iteración para un mismo esquema de control se promediaron, obteniendo así la longitud media de corridas ARL.
2.1.3 Carta de Shewhart para observaciones individuales
Con el fin de estimar la variabilidad debida a causas especiales cuando se presentan lecturas individuales que constituyen tendencias, Shewhart presenta la carta de control de observaciones individuales En esta carta se selecciona una observación por subgrupo de la característica de calidad de interés; y se monitorea la variabilidad mediante el rango móvil (MR).
Los límites históricos para el rango móvil están definidos como9
Los límites para la medida de localización en la Fase I, están dados por:
donde la media es 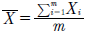 y el rango móvil
y el rango móvil 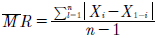 .
.
En esta primera parte se asume el desconocimiento de los parámetros de control (σ, μ). Cuando se presenta un hecho no aleatorio o asignable, los responsables del proceso deben encontrar una causa atribuible realizando las correcciones pertinentes para que esta situación no se presente. Luego, se debe eliminar la señal fuera de control, para determinar posteriormente los parámetros del proceso.
Subsiguientemente, en la Fase II la formulación de los límites de control para la medida de variabilidad están dados como:
La formulación para los límites estándar de control de la medida de localización, Fase II son en su orden:
3. APLICACIÓN EN EL USO DE FUNGICIDAS
Las plantas como cualquier ser vivo son susceptibles de enfermarse, estas enfermedades son las principales fuentes de daño de plantas y cultivos, causadas primeramente por organismos fitopatógenos. Siendo los hongos la principal causa de pérdida de cultivos a nivel mundial. En este sentido, se hace indispensable manejar adecuadamente las enfermedades de las plantas bajo un riguroso control que encierra desde la rotación de cultivos, selección de cultivares tolerantes o resistentes, época de siembra, nivel de fertilización, modificación del microclima, sanidad hasta la aplicación de fungicidas.
En este artículo se explicará qué son los fungicidas, por qué son necesarios, y la calidad de la mezcla fungicida; en esta última se resaltará la calidad del agua en función del pH y su efecto sobre la estabilidad y eficacia del fungicida. La importancia de este estudio es introducir en esta área las herramientas del control estadístico de proceso CEP, en la evaluación, monitoreo y análisis de la información mediante técnicas gráficas, como son las cartas de control, específicamente la carta CUSUM debido a su sensibilidad a pequeños cambios, por lo que se hace indispensable, en este caso, en la evaluación de características de calidad como el pH del fungicida.
A fin de comprender la importancia del pH en la estabilidad y eficacia de un fungicida, en un comienzo, es transcendental abordar el concepto de fungicida.
En este sentido, según Whindham (2016), un fungicida es un “Compuesto que mata o inhibe el crecimiento de hongos”12. Igualmente, en 13 se define a un fungicida como “un tipo particular de plaguicida que controla enfermedades fúngicas, inhibiendo o eliminando al hongo que causa la enfermedad”. Por otra parte, otros autores definen a un fungicida como “todos aquellos compuestos que pueden proporcionar resistencia a la planta huésped o que convierten el medio ambiente en un lugar inadecuado para el desarrollo y crecimiento del organismo infeccioso”14.
En un sentido general, existen tres razones principales por las cuales se utilizan los fungicidas:
Para controlar a la enfermedad durante el establecimiento y desarrollo de un cultivo.
Para incrementar la productividad de un cultivo y reducir sus daños.
Para mejorar el período de almacenamiento y la calidad de las plantas y los productos cosechados.
A lo que respecta a la calidad de la mezcla fungicida, se debe hacer hincapié a la preparación de la mezcla, ya que este aspecto es fundamental para asegurar la correcta distribución y estabilidad de los componentes por unidad de volumen. “A lo anterior debe sumarse la calidad del agua (esto en el caso de preparaciones en agua o en emulsión). Las características químicas del agua (pH y dureza, principalmente) pueden afectar la efectividad del (los) ingrediente (s) activo (s)”15.
La mayoría de los fungicidas, particularmente los organofosforados y los carbamatos atraviesan una reacción química en presencia de componentes alcalinos que destruyen su efectividad. Esta reacción es llamada hidrólisis alcalina y ocurre cuando el pesticida es mezclado con agua alcalina (con un pH mayor a 7). A mayor alcalinidad del agua, más rápido se desvanece la efectividad de los mismos. Por ejemplo, en un fungicida “X”, el tiempo para que ocurra el 50% de la hidrólisis a pH 8.0 es 63 minutos; a pH 7.0 ocurre en 386 minutos y a pH 6.0, 80 horas. Esto significa que si el pH de su agua es 8.0 y pasa una hora desde que agregó el fungicida al tanque y lo aplicó, el 50% de la materia activa ya está descompuesta. Pero si el agua tiene un pH 6.0, no perderá una cantidad significativa durante la aplicación16.
En definitiva, el grado de destrucción de una mezcla fungicida varía de acuerdo con la alcalinidad y la temperatura del agua y el tiempo en que la mezcla permanece en el tanque. Es aquí, donde radica la importancia de las mediciones de pH, característica que se ha tomado como ejemplo para este artículo, ya que permite asegurar que dicha hidrólisis pase lo más lento posible y asimismo asegurar la estabilidad y eficacia del producto. Cabe resaltar que estos valores de pH han sido modificados por una constante.
4. RESULTADOS
4.1 Aplicación carta CUSUM
En la Tabla III se presenta una muestra x i de la característica de calidad de interés (valores de pH), con μ = 14,6520 y σ = 0,4329. Igualmente se exhibe la cantidad estandarizada v i de cada muestra, obtenida mediante la ecuación (2), los estadísticos de control Si + y Si -, hallados con las fórmulas (4) y (5) respectivamente y los contadores N+ y N-.
Tabla III DESEMPEÑO DE LA ARL DE LA CUSUM TABULAR CON k = ½ Y h = 4 o h = 5
| Número del subgrupo | X i | Y i | V i | S i + | N + | S i - | N - |
|---|---|---|---|---|---|---|---|
| 1 | 14,790 | 0,319 | -0,738 | 0,000 | 0,000 | 0,238 | 1,000 |
| 2 | 14,640 | -0,028 | -1,878 | 0,000 | 0,000 | 1,616 | 2,000 |
| 3 | 14,730 | 0,180 | -1,139 | 0,000 | 0,000 | 2,255 | 3,000 |
| 4 | 14,160 | -1,137 | 0,699 | 0,199 | 1,000 | 1,055 | 4,000 |
| 5 | 14,970 | 0,735 | 0,101 | 0,000 | 0,000 | 0,455 | 5,000 |
| 6 | 14,625 | -0,062 | -1,640 | 0,000 | 0,000 | 1,595 | 6,000 |
| 7 | 15,660 | 2,329 | 2,017 | 1,517 | 1,000 | 0,000 | 0,000 |
| 8 | 14,025 | -1,448 | 1,093 | 2,110 | 2,000 | 0,000 | 0,000 |
| 9 | 15,030 | 0,873 | 0,322 | 1,932 | 3,000 | 0,000 | 0,000 |
| 10 | 14,340 | -0,721 | 0,077 | 1,510 | 4,000 | 0,000 | 0,000 |
| 11 | 14,700 | 0,111 | -1,401 | 0,000 | 0,000 | 0,901 | 1,000 |
| 12 | 14,190 | -1,067 | 0,605 | 0,105 | 1,000 | 0,000 | 0,000 |
| 13 | 15,030 | 0,873 | 0,322 | 0,000 | 0,000 | 0,000 | 0,000 |
| 14 | 14,640 | -0,028 | -1,878 | 0,000 | 0,000 | 1,378 | 1,000 |
| 15 | 14,640 | -0,028 | -1,878 | 0,000 | 0,000 | 2,757 | 2,000 |
| 16 | 14,325 | -0,755 | 0,135 | 0,000 | 0,000 | 2,122 | 3,000 |
| 17 | 15,435 | 1,809 | 1,498 | 0,998 | 1,000 | 0,123 | 4,000 |
| 18 | 14,475 | -0,409 | -0,523 | 0,000 | 0,000 | 0,146 | 5,000 |
| 19 | 14,640 | -0,028 | -1,878 | 0,000 | 0,000 | 1,525 | 6,000 |
| 20 | 13,995 | -1,518 | 1,175 | 0,675 | 1,000 | 0,000 | 0,000 |
Fuente: Autores.
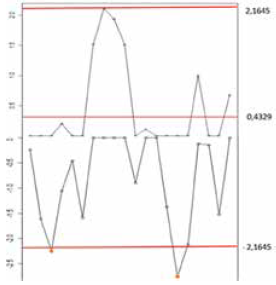
Con el fin de producir un buen desempeño de la ARL se supondrá que la magnitud del corrimiento que quiere detectarse es de δ = 1; por lo tanto, se define un valor de sensibilidad de la carta o referencia de k = 0,5 y además, se utiliza un intervalo de decisión de cinco veces la desviación estándar del proceso σ, es decir, UCL = 5(0,4329) = 2,1645, CL = 0,4329 y LCL = -5(0,4329) = -2,1645.
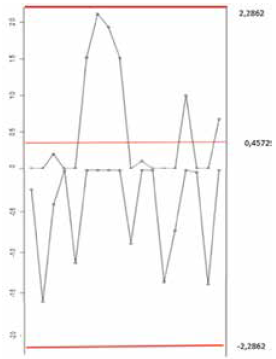
Al graficar los estadísticos de control Si + y Si - se obtienen dos puntos fuera de control, como se muestra en la Fig. 1. Estos puntos fuera de los límites poseen una causa asignable; por lo tanto, son eliminados.
Se procede de nuevo a evaluar y graficar los estadísticos de control para los datos restantes, como se observa Tabla IV.
Tabla IV APLICACIÓN CARTA CUSUM PARA LOS SUBGRUPOS RESTANTES
| Número del subgrupo | X i | Y i | V i | S i + | N + | S i - | N - |
|---|---|---|---|---|---|---|---|
| 1 | 14,790 | 0,319 | -0,738 | 0,000 | 0,000 | 0,238 | 1,000 |
| 2 | 14,640 | -0,028 | -1,878 | 0,000 | 0,000 | 1,616 | 2,000 |
| 3 | 14,160 | -1,137 | 0,699 | 0,199 | 1,000 | 0,416 | 3,000 |
| 4 | 14,970 | 0,735 | 0,101 | 0,000 | 0,000 | 0,000 | 0,000 |
| 5 | 14,625 | -0,062 | -1,640 | 0,000 | 0,000 | 1,140 | 1,000 |
| 6 | 15,660 | 2,329 | 2,017 | 1,517 | 1,000 | 0,000 | 0,000 |
| 7 | 14,025 | -1,448 | 1,093 | 2,110 | 2,000 | 0,000 | 0,000 |
| 8 | 15,030 | 0,873 | 0,322 | 1,932 | 3,000 | 0,000 | 0,000 |
| 9 | 14,340 | -0,721 | 0,077 | 1,510 | 4,000 | 0,000 | 0,000 |
| 10 | 14,700 | 0,111 | -1,401 | 0,000 | 0,000 | 0,901 | 1,000 |
| 11 | 14,190 | -1,067 | 0,605 | 0,105 | 1,000 | 0,000 | 0,000 |
| 12 | 15,030 | 0,873 | 0,322 | 0,000 | 0,000 | 0,000 | 0,000 |
| 13 | 14,640 | -0,028 | -1,878 | 0,000 | 0,000 | 1,378 | 1,000 |
| 14 | 14,325 | -0,755 | 0,135 | 0,000 | 0,000 | 0,743 | 2,000 |
| 15 | 15,435 | 1,809 | 1,498 | 0,998 | 1,000 | 0,000 | 0,000 |
| 16 | 14,475 | -0,409 | -0,523 | 0,000 | 0,000 | 0,023 | 1,000 |
| 17 | 14,640 | -0,028 | -1,878 | 0,000 | 0,000 | 1,401 | 2,000 |
| 18 | 13,995 | -1,518 | 1,175 | 0,675 | 1,000 | 0,000 | 0,000 |
| 19 | 14,790 | 0,319 | -0,738 | 0,000 | 0,000 | 0,238 | 1,000 |
| 20 | 14,640 | -0,028 | -1,878 | 0,000 | 0,000 | 1,616 | 2,000 |
Fuente: Autores.
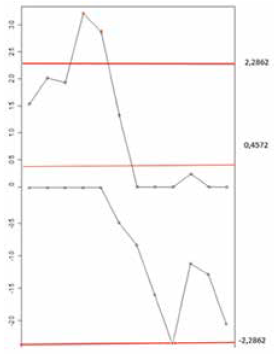
El proceso se encuentra en un estado de estabilidad estadística con parámetros μ = 14,6483 y σ = 0,4572. Los límites de control están dados por UCL = 5(0,4572) = 2,2862, CL = 0,4572 y LCL = -5(0,4572) = -2,2862.
Finalmente, se hace control a la nueva información seleccionada del proceso; tomando como referente estos límites estandarizados, Tabla V.
Tabla V APLICACIÓN CARTA CUSUM A LOS DATOS DE CONTROL
| Número del subgrupo | X i | Y i | V i | S i + | N + | S i - | N - |
|---|---|---|---|---|---|---|---|
| 1 | 15,720 | 2,344 | 2,031 | 1,531 | 1,000 | 0,000 | 0,000 |
| 2 | 15,270 | 1,360 | 0,986 | 2,017 | 2,000 | 0,000 | 0,000 |
| 3 | 15,075 | 0,933 | 0,413 | 1,930 | 3,000 | 0,000 | 0,000 |
| 4 | 15,600 | 2,081 | 1,778 | 3,208 | 4,000 | 0,000 | 0,000 |
| 5 | 15,000 | 0,769 | 0,158 | 2,866 | 5,000 | 0,000 | 0,000 |
| 6 | 14,745 | 0,211 | -1,038 | 1,328 | 6,000 | 0,538 | 1,000 |
| 7 | 14,775 | 0,277 | -0,847 | 0,000 | 0,000 | 0,885 | 2,000 |
| 8 | 14,715 | 0,146 | -1,261 | 0,000 | 0,000 | 1,646 | 3,000 |
| 9 | 14,715 | 0,146 | -1,261 | 0,000 | 0,000 | 2,407 | 4,000 |
| 10 | 14,115 | -1,166 | 0,739 | 0,239 | 1,000 | 1,168 | 5,000 |
| 11 | 14,490 | -0,346 | -0,669 | 0,000 | 0,000 | 1,337 | 6,000 |
| 12 | 14,715 | 0,146 | -1,261 | 0,000 | 0,000 | 2,099 | 7,000 |
Fuente: Autores.
En la Fig. 3 se muestra la carta de control CUSUM para estos datos sometidos a control.
4.2 Aplicación carta SHEWHART
En la Tabla VI se presenta la información histórica de la característica de calidad x i . Así, como los valores de MR para los 20 subgrupos.
Tabla VI INFORMACIÓN DE LA MEDICIÓN DE pH Y APLICACIÓN CARTA SHEWHART
| Número del subgrupo | X i | MR |
|---|---|---|
| 1 | 14,790 | |
| 2 | 14,640 | 0,150 |
| 3 | 14,730 | 0,090 |
| 4 | 14,160 | 0,570 |
| 5 | 14,970 | 0,810 |
| 6 | 14,625 | 0,345 |
| 7 | 15,660 | 1,035 |
| 8 | 14,025 | 1,635 |
| 9 | 15,030 | 1,005 |
| 10 | 14,340 | 0,690 |
| 11 | 14,700 | 0,360 |
| 12 | 14,190 | 0,510 |
| 13 | 15,030 | 0,840 |
| 14 | 14,640 | 0,390 |
| 15 | 14,640 | 0,000 |
| 16 | 14,325 | 0,315 |
| 17 | 15,435 | 1,110 |
| 18 | 14,475 | 0,960 |
| 19 | 14,640 | 0,165 |
| 20 | 13,995 | 0,645 |
Fuente: Autores.
Al aplicar la fórmula (6), se obtienen los límites de control históricos para el rango móvil. Dados por:
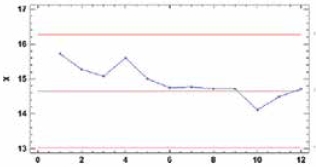
Igualmente, se hallan los límites de control histórico para la media, definido en la ecuación (7) como
El proceso se encuentra estabilizado estadísticamente; así que, se estiman los parámetros con la fórmula (8) σ = 0,5424 y μ = 14,6520. El siguiente paso es hacer control con los datos de la Tabla VII.
Tabla VII APLICACIÓN CARTA SHEWHART A LOS DATOS DE CONTROL
| Número del subgrupo | X i | MR |
|---|---|---|
| 1 | 15,720 | |
| 2 | 15,270 | 0,450 |
| 3 | 15,075 | 0,195 |
| 4 | 15,600 | 0,525 |
| 5 | 15,000 | 0,600 |
| 6 | 14,745 | 0,255 |
| 7 | 14,775 | 0,030 |
| 8 | 14,715 | 0,060 |
| 9 | 14,715 | 0,000 |
| 10 | 14,115 | 0,600 |
| 11 | 14,490 | 0,375 |
| 12 | 14,715 | 0,225 |
Fuente: Autores.
Primeramente, se evalúan los límites estándar del rango móvil, correspondientes a la ecuación (9)
Seguidamente, se hallan los límites estándar de la media, definidos por la ecuación (10), como,
5. ANÁLISIS DE LOS RESULTADOS
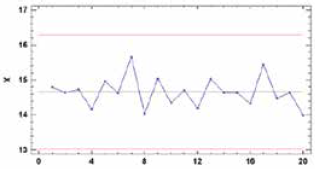
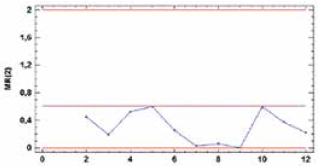
Es importante resaltar el comportamiento de las cartas Shewhart y CUSUM en la Fase I de estabilización estadística o estudio inicial. En el caso de carta MR de Shewhart, específicamente la medida de variabilidad, el comportamiento sugiere una variabilidad que permite asumir una estabilización de la carta; comportamiento de estabilización más diciente en la carta de la medida de localización, donde la aleatorización alrededor de la media es evidente.
Se puede indicar que para la carta tradicional de Shewhart MR, la estimación de los parámetros es fácil de establecer. El caso de la carta univariada CUSUM difiere en forma importante bajo la misma información, obsérvese en la carta, Fig. 2, a pesar de eliminar los subgrupos que presentan señales de alarma debido a causas asignables, detectadas en el monitoreo del proceso; el comportamiento de las tandas indican una gran variabilidad debido a que existen puntos cercanos a los límites de control establecidos. Es decir, la estabilización de la carta es compleja, permite señalar de esta forma un proceso que requiere de intervención para lograr una mejor estabilización.
En la Fase II o Fase de control, de acuerdo con la Tabla II, un corrimiento de una desviación se detectaría en 10.4 muestras para la carta CUSUM, en comparación con la carta de control de Shewhart para mediciones individuales MR que requeriría 43.96 subgrupos o puntos, en promedio, para detectar ese corrimiento. Es decir, la potencia de la carta CUSUM en detectar cambios pequeños en el proceso, permite sugerir en el caso práctico de estudio, una gráfica acertada a las condiciones del proceso.
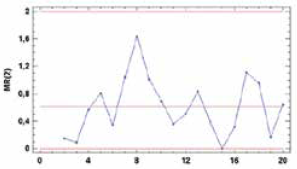
Esto se demuestra con la información sometida a control, la carta Shewhart MR, no detecta a lo largo del proceso señales de alarma o fuera de control, por el contrario, sugiere un mejoramiento en el proceso al disminuir la variabilidad de este, Fig. 6. Mientras que la carta CUSUM muestra tres (3) puntos fuera de control para los primeros subgrupos, mejor sensibilidad al detectar más señales de alarma en contraste con la carta MR de Shewhart, como también una tendencia decreciente pronunciada; lo que indica un estado fuera de control denominado cambio de nivel. Esta tendencia también es detectada en la carta Shewhart MR pero en forma suavizada. Esta mejor potencia en detectar señales de alarma de la carta CUSUM, se debe a que combina información de varias muestras y por lo tanto, es más eficiente al detectar cambios pequeños de la medida de variabilidad.
6. CONCLUSIONES
La toma de decisiones para el mejoramiento de los procesos se basa en la información generada por las cartas de control. Así, una carta de control deberá ser capaz de detectar la magnitud del cambio que ocurre en el proceso, con la intención de realizar las mejoras o cambios, que realmente el proceso requiera. En este artículo se aplicó la carta CUSUM para la medida de variabilidad en una muestra de potencial de hidrógeno pH, en protectores de plantas.
El estudio comparó la carta tradicional MR de Shewhart, con respecto a la CUSUM: se observó en esta última, una longitud de corrida promedio ARL menor que la carta de Shewhart. Esto indica que la propuesta CUSUM varianza posee mayor sensibilidad en detectar señales de alarma que la carta tradicional de Shewhart para observaciones individuales.