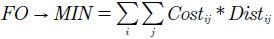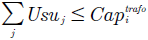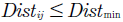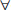1. INTRODUCCIÓN
Los sistemas de distribución eléctrica constituyen una de las partes importantes dentro de un sistema eléctrico, ya que son las primeras en ser consideradas para la planeación y expansión de estos; a su vez, representan el enlace final del sistema eléctrico con los usuarios1. Por lo que es de gran importancia mantener los sistemas en un óptimo funcionamiento con estándares de servicio y calidad, también se debe considerar la expansión del sistema de distribución para permitir la cobertura en el abastecimiento de energía eléctrica a los usuarios dentro de sus áreas de servicio2. Dado que los sistemas se encuentran en constante crecimiento y expansión según investigaciones realizadas, por lo que es de valor analizar métodos que nos permitan cumplir estos requerimientos. Uno de estos métodos implica el uso de la planificación en las redes de distribución, ya que pueden ser empleadas tanto en redes aéreas como en redes soterradas; para la aplicación de la planeación en las redes de distribución eléctrica habitualmente se encuentran tres tipos: planeamiento de expansión, planeamiento de operación y planeamiento de construcción nueva3.
Para el planeamiento de las redes de distribución se debe conocer la región geográfica de emplazamiento y la potencia instalada de cada carga, con el objetivo de encontrar rutas y configuraciones óptimas para su despliegue4, para el diseño de las redes no solo se debe considerar la carga actual, sino también la carga que se espera exista dentro de un horizonte de tiempo; lo que significa que el problema de diseño es dotado de cierta incertidumbre5. Cabe recalcar que en el diseño de las redes de distribución pueden darse de forma radial o en malla; sin embargo, por cuestiones prácticas en la ingeniería la gran mayoría de las redes de distribución funcionan como redes radiales, dado que el análisis implica menor complejidad6. En cuanto a los datos exactos de los usuarios las empresas de distribución presentan inconvenientes, dado que con el constante crecimiento de la demanda el levantamiento de la información se vuelve difícil; por lo tanto, se utilizó la plataforma OpenStreetMap (OSM) en busca de información real con el fin de exponer al modelo a condiciones prácticas de enrutamiento en escenarios típicamente urbanos7.
Planificar una red de distribución eléctrica minimizando los costos de instalación y operación es una actividad compleja, puesto que existe una gran variedad de alternativas técnicas viables; conllevando al uso de herramientas de optimización y así permitir ahorrar importantes recursos a las empresas de distribución, debido a la magnitud de las inversiones requeridas. El problema de la planificación de las redes de distribución se establece claramente como un problema de naturaleza combinatoria con funciones no lineales, donde la función objetivo es la de minimizar los costos, sujeta a restricciones técnicas de operación del servicio de energía eléctrica8), (9.
Comúnmente se utilizan modelos matemáticos fundamentados en heurísticas para la solución del planeamiento en las redes de distribución, ya que estos permiten calcular y encontrar soluciones cercanas a la óptima; sin embargo, existen otros modelos matemáticos que usan procesos evolutivos y de pronóstico que permiten encontrar soluciones óptimas, tales como: método matemático de programación y algoritmo aleatorio de optimización (algoritmo genético, algoritmo de colonia de hormigas y algoritmo de enjambre de partículas), estos son algoritmos mejorados que sirven específicamente para la aplicación en la planeación de las redes de distribución10. A pesar de ello, la evolución de los algoritmos tradicionales todavía afronta dificultades relacionadas con las características combinatorias del problema de planificación de las redes de distribución, puesto que existe una gran cantidad de variables involucradas en el proceso11.
Para nuestro estudio se consideró el uso de algoritmos basados en heurísticas con el objetivo de minimizar los costos relacionados con los recursos empleados en la construcción de la red de distribución, usando procesos de crecimiento controlado que permita hacer una cobertura de todos los usuarios, conociendo la capacidad de los transformadores y buscando mediante el uso de un árbol mínimo de Steiner el enrutamiento de la topología de la red. El árbol mínimo de Steiner o mínimum Steiner tree se encuentra basado en la teoría de grafos y puede ser resuelto por diversos algoritmos, incluyendo el algoritmo de Dijkstra12, hallando la ruta o el camino más corto con el fin de que todos los usuarios del sistema eléctrico se puedan conectar a la red de distribución13.
En adelante, el artículo se estructura de la siguiente manera; en la sección II se abarca temas relacionados con la planeación óptima de las redes de distribución. En la sección III se describe el modelo de optimización para la planeación de la red de distribución propuesto, la sección IV engloba el análisis pertinente a los resultados obtenidos de la optimización, con la ubicación de los transformadores óptimos georreferenciados y la construcción de la topología de la red. Por último, en la sección V se concluye el artículo.
2. PLANEACIÓN DE REDES AÉREAS DE DISTRIBUCIÓN ELÉCTRICA
2.1 Redes de distribución eléctrica
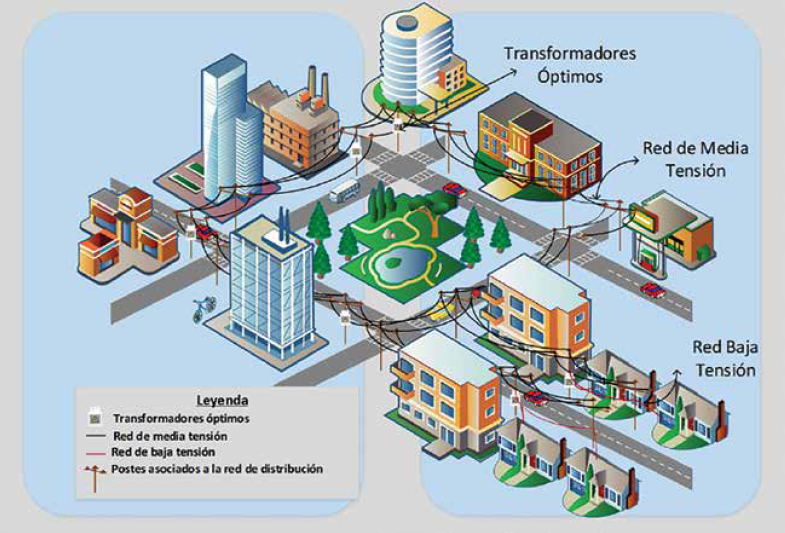
En la literatura la planeación de un sistema de distribución eléctrico aéreo o soterrado se expone a diversos impedimentos de construcción, englobando limitaciones técnicas y ambientales10; por lo que es de gran importancia que la red de distribución pueda adaptarse a las características del diseño general de la ciudad o área funcional en la que va a operar, ajustándose al patrón general de la ciudad14. Así pues, tradicionalmente las redes de distribución se proyectan de forma radial y aérea, debido a que el diseño técnico y económico es relativamente bajo en relación con un diseño de una red soterrada15; estos costos pueden reducirse significativamente o a su vez pueden ser evitados considerando simultáneamente datos geográficos y rutas de líneas existentes dentro de la planeación de las redes. La implementación de las restricciones geográficas proporciona un filtrado y procesamiento de la materia prima de datos geográficos, dando como resultado posibles enrutamientos con el objetivo de obtener datos de entrada de referencia para la planificación de la red16.
El diseño de una red de distribución eléctrica se la puede identificar como un grafo denotado por G = (V, E) el cual contiene todas las posibles rutas y conexiones para el enrutamiento de la red; este grafo se lo extrae del mapa de la ciudad donde se va a realizar la planeación. Donde V es el conjunto de nodos o vértices (se incluyen cargas, transformadores, intersecciones de los enlaces y subestaciones) y E es el conjunto de elementos designados como aristas (conexión del medidor inteligente hacia la red de baja tensión del sistema de distribución)17), (18; se denota que los puntos Steiner son los puntos de conexión del medidor inteligente más conocidos como acometida. Cada una de las conexiones tiene un peso definido correspondiente al cálculo de la distancia que existe entre cada vértice, dicha distancia es calculada con la fórmula de Haversine, puesto que tiene mayor exactitud cuándo se usa en puntos georreferenciados19.
2.1.1 Árbol de Steiner
Se ha encontrado que la explicación de los árboles de Steiner puede ser bastante comprensible sin que esto implique que la resolución del método sea simple, de hecho, el problema es de tipo NP-hard, ya que no requiere tratamiento de tipo polinomial. Para el efecto de comprender el objetivo se ha de suponer la existencia de una cantidad determinada de puntos que se deben enlazar, primeramente, se debe considerar el árbol mínimo de expansión inicial, con esto se obtiene el camino más corto de los puntos existentes, una vez realizado el MST (mínimum spanning tree), se crea una cantidad de puntos auxiliares aleatorios denominados puntos de Steiner (Stp) para reducir la longitud total; con los Stp obtenidos se crea un nuevo árbol de conexión denominado árbol de Steiner20.
El árbol de Steiner ha sido empleado en aplicaciones de ingeniería, ya que permite encontrar el camino global más corto, para poder superar la deficiencia existente en los algoritmos de optimización basados en teoría de grafos; y detalla en encontrar un árbol con un peso mínimo para un grafo y un conjunto de vértices. Para la resolución del problema del árbol mínimo de Steiner, según investigaciones, existen varios métodos, tales como el de la distancia más larga y un algoritmo de planificación jerárquica basado en análisis de las topologías de las redes21), (22.
2.2 Capacidad y cobertura de zonas georreferenciadas de las redes de distribución eléctrica
El despliegue de cada uno de los transformadores deberá considerar los principales problemas de cobertura y capacidad que ocurren dentro de una red de distribución eléctrica, para lo cual tomará coordenadas de las casas más cercanas, de tal forma que los enlaces sean óptimos y no se permita recorrer distancias excesivamente grandes. Uno de los principales objetivos es el empleo de ubicaciones georreferenciadas para cada dispositivo eléctrico que se vaya a implementar. Para lo cual se ha planteado un margen de cobertura y una capacidad que permite albergar cierta cantidad de usuarios, conociendo los sitios factibles en que se puedan ubicar cada uno de los transformadores23.
3. FORMULACIÓN DEL PROBLEMA
Para solventar el problema existente en la planeación óptima de las redes aéreas de distribución se plantea un modelo matemático basado en heurísticas, el cual nos permite minimizar la cargabilidad de los transformadores de distribución mediante la restricción de conexión de los usuarios, a su vez el modelo también plantea la reducción del uso de conductores en la implementación de la red de distribución eléctrica considerando costos; todo eso se realiza bajo un escenario georreferenciado. Los usuarios que se pueden conectar a los transformadores de distribución variable, cabe denotar que los valores utilizados son con fines explicativos; esto nos permite identificar las distintas particiones que se van a hacer en la parte de bajo voltaje para poder solventar con las necesidades técnicas y económicas de energía a los usuarios, tal como se puede observar en la Fig. 1.
Con el fin de alcanzar lo antes mencionado se plantea el uso de clusterización por medio del Algoritmo de K-Medoids seccionando el total de los usuarios en grupos más pequeños para la restricción de conexión hacia los transformadores, esto nos permite encontrar un centroide para cada grupo; con este centroide obtenido se verifica si es el punto más óptimo de ubicación del transformador.
Para realizar el procedimiento de la conexión de estos grupos de usuarios se optó por la utilización de un árbol mínimo de Steiner, que radica en la selección de un punto más cercano a la vivienda sobre la red de distribución y posterior la creación de dicho punto de Steiner. El punto de Steiner es agregado a los nuevos puntos existentes de conexión. Teniendo en cuenta que una vez creados los nuevos puntos existentes de conexión a base de los puntos de Steiner se modifica la conectividad de los usuarios hacia los transformadores más cercanos. Con lo cual mediante una variación del algoritmo de Dijsktra se logra interconectar los puntos Steiner hacia el punto más óptimo de ubicación de los transformadores.
Lo anteriormente explicado nos da la metodología para la creación de la red de baja tensión; en cambio para la conexión de los transformadores hacia la red de media tensión se utiliza el algoritmo de Dijsktra, ya que este nos permite encontrar el camino más corto al menor costo, debido a criterios de diseño, el cual no considera todas las calles como lugares de ubicación para la red eléctrica. Para el diseño de la red de distribución eléctrica se tiene como variables de inicio el número de usuarios N, donde se encuentran asociados las coordenadas de latitud y longitud de las viviendas, T coordenadas de ubicación de los transformadores. El modelo planteado elije de forma óptima donde ubicar y desplegar los transformadores, con el fin de que se logre una conectividad al cien por ciento de todos los usuarios. Denotamos que el problema de planeación óptima de redes aéreas de distribución tiene como función objetivo (1).
Donde:
Cost ij es el costo unitario asociado al trayecto del punto i al punto j.
Dist ij distancia del punto i al punto j.
Para lo cual se han considerado ciertas restricciones que nos permita cumplir con las condiciones de minimizar los costos y reducir el uso de recursos en la instalación de las redes de distribución:
La ecuación (2) nos permite limitar el número de usuarios que se pueden conectar a los transformadores que se crean, la restricción (3) se cumple la condición de que los enlaces para el árbol mínimo de Steiner sean al menor costo ya que se limita la distancia. Las variables utilizadas en el modelo matemático para la planeación óptima se pueden observar en la Tabla l.
Tabla I. TABLA DE VARIABLES
| Xc, Yc | Vector de coordenadas (latitud y longitud) de cada vivienda |
| N | Número de viviendas |
| Distmin | Distancia mínima |
| Distij | Distancia euclidiana calculada |
| G | Matriz de conectividad |
| calles | Coordenadas de todos los puntos de las calles |
| S | Conjunto de coordenadas de los circuitos por transformador |
| T | Conjunto de transformadores óptimos por cir- cuito |
| nodos_calles | Puntos Steiner usados para la construcción del árbol de Steiner |
| Xcon, Ycon | Coordenadas de la ubicación de los centroides de las viviendas dadas por la clusterización |
| C | Clúster obtenido en la clusterización de los no- dos_calles |
| Idx | Identificación de cada clúster |
Posteriormente se define el pseudocódigo que nos va ayudar a resolver el problema planteado para lograr una conectividad de todos los usuarios a la red de distribución.
Tabla II. ALGORITMO 1
La respuesta del algoritmo 1, mostrado en la Tabla II variará dependiendo del escenario que se va a analizar; la segunda fase es la construcción de la red de bajo y medio voltaje, la cual se observa a continuación:
Tabla III. ALGORITMO 2
4. ANÁLISIS DE RESULTADOS
En la Fig. 2 se puede apreciar el comportamiento del modelo frente a varios escenarios de capacidad en los transformadores para lo cual se tiene valores de capacidad de 16, 27, 38, 49, 60, 71 y 82; en cada uno de los escenarios propuestos se dispone de distintas densidades poblacionales de 97, 194, 291, 388 y 486 clientes.
Los resultados obtenidos nos permiten diagnosticar distintas opciones en el despliegue de las redes aéreas de distribución; se advierte que el modelo tiene la capacidad de ser escalable, ya que nos permite modificar ciertos parámetros obteniendo resultados óptimos para cada escenario.
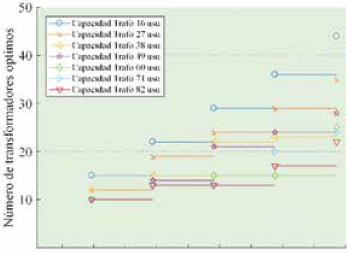
Hay que destacar que cuan mayor sea el número de usuarios, la cantidad de transformadores óptimos que se despliegan depende directamente de la capacidad que se le asigne a cada uno; así podemos suponer que cuando la capacidad es mayor, el número de transformadores que el modelo escoja va a ser el menor y por consecuente el más óptimo. En la Fig. 3 muestra el comportamiento de la planeación mediante el uso de un árbol mínimo de expansión para la red de media tensión, en dicho modelo se considera las esquinas como punto de conexión de los usuarios, por lo cual obliga a que la expansión sea ineficiente y a su vez más costosa.
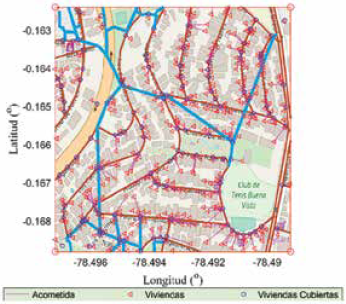
En contraste la Fig. 4 evidencia una planeación similar con la diferencia que se han incluido los puntos Steiner, permitiendo realizar conexiones ortogonales de los usuarios hacia la red de distribución. El uso de las conexiones ortogonales en lugar de los tramos diagonales reduce la utilización del conductor, cabe recalcar que en algunos casos las conexiones siguen siendo diagonales, ya que por cuestiones de limitaciones del mapa o de la ubicación del usuario el modelo encontró dichos puntos de conexión como los más cercanos. Es importante mencionar que para el caso mostrado en la Fig. 4 se han tomado en consideración 486 usuarios, con la creación de 22 transformadores, que a su vez buscan conectarse entre sí para formar la red de media tensión, considerando los puntos Steiner para generar la ruta. Observando que la línea roja es la formación de la red de media tensión, los cuadrados morados nos muestran la ubicación del despliegue de los transformadores óptimos y a su vez se puede observar los puntos Steiner que son las extensiones de los usuarios para la conexión a la red que se encuentran graficados de distintos colores para denotar los distintos tipos de los circuitos de baja tensión.
La Fig. 5 es un claro ejemplo de cómo la planeación puede ser escalada para grupos de usuarios variantes, diferentes tipos de mapas y en función a ello cambiarán el número de transformadores óptimos por ubicarse. Para lo que se plantea el uso de un nuevo mapa bajo las condiciones iniciales de 1483 usuarios; se advierte las variaciones en cuanto al ruteo de la red de media tensión y puntos Steiner creados, dado que en un distinto mapa los usuarios se encuentran bajo distintas coordenadas.
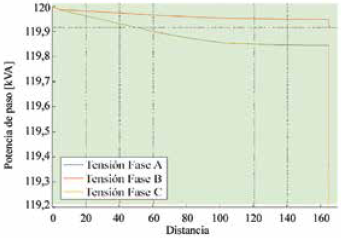
Una vez obtenidas las directrices de la planeación, se procedió a la simulación utilizando el software Cymdist, allí se pudo visualizar de mejor manera el comportamiento de dicho sistema; con lo cual se analizaron varios parámetros técnicos, tal como se presenta en la Fig. 6, que es el resultado del perfil de voltaje, denotando que a mayor distancia la variación de voltaje va a ir decayendo conforme se vaya alejando de la fuente. Esta variación se puede observar en la red de bajo voltaje considerando el número de cargas que se conecta a cada fase.
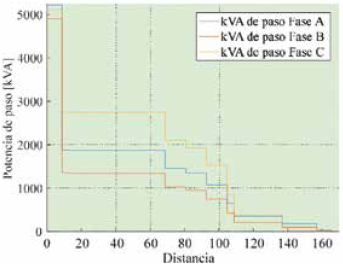
Otro de los resultados que se obtuvo fue el perfil en kVA que se observa en la Fig. 7, se puede interpretar como el comportamiento que tiene la potencia a lo largo de la distancia de recorrido, ya que nos permite visualizar la variación que esta presenta frente a las cargas conectadas a la red de distribución y de paso en cada fase, coincidiendo en similitudes con la Fig. 6. En el que con el paso de la distancia los valores empiezan a decaer.
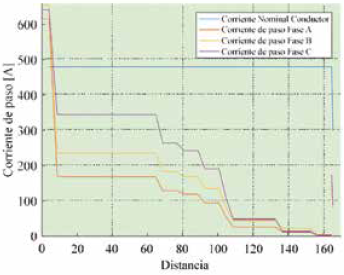
Una de las consideraciones principales de diseño es la corriente que circula por el sistema, ya que con esta se debe escoger los conductores que van a soportarla, es por ello que en la Fig. 8 se aprecia la corriente de circulación por los conductores obtenida en la simulación en el software Cymdist, observando un vínculo entre la corriente y la distancia desde la fuente hacia las cargas o usuarios.
5. CONCLUSIONES
La variación del crecimiento de la demanda de un sistema de distribución genera cambios en la planeación de un determinado lugar geográfico, delimitando la posibilidad de mantener crecimientos controlados de los usuarios; el presente trabajo brinda la oportunidad de analizar diferentes escenarios a los que se podría enfrentar una empresa distribuidora para poder implementar en la planeación futura del sistema.
El uso de un árbol de Steiner llega a ser más confiable en la búsqueda de un enrutamiento de menor costo, ya que, a diferencia de un árbol mínimo de expansión, este método inserta nuevos puntos con el fin de utilizar mejores rutas que disminuya la cantidad de conductor que se va a utilizar y por lo tanto minimizar el costo de implementación.
El uso de la plataforma OpenStreetMap proporciona una gran cantidad de información sobre aspectos geográficos y datos relevantes acerca de edificaciones emplazadas en una localidad, es de gran importancia poder filtrar y distinguir los datos para aprovechar al máximo los recursos obtenidos en la búsqueda para realizar una planeación, ya que así se evita errores que puedan producir un mal levantamiento de información, considerando la heterogeneidad de datos arrojados por la plataforma podrían alterar el rendimiento del algoritmo.
El algoritmo planteado permite optimizar los recursos que se van a utilizar en la construcción de las redes áreas de distribución; además de ubicar los sitios candidatos de instalación de los transformadores. De esta forma se obtiene una cobertura del cien por ciento de todos los usuarios.