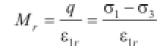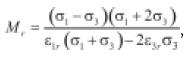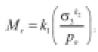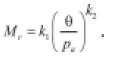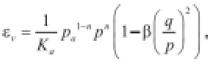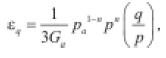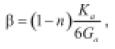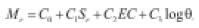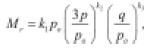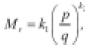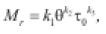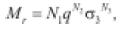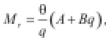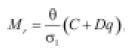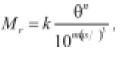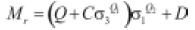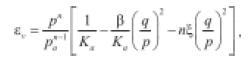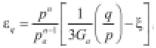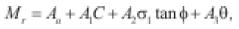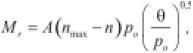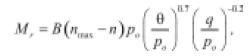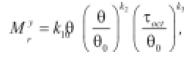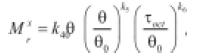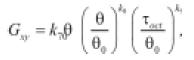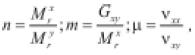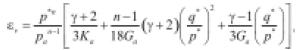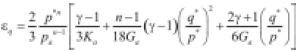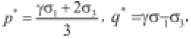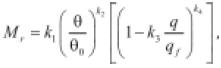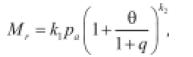Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Ingenierías Universidad de Medellín
Print version ISSN 1692-3324On-line version ISSN 2248-4094
Rev. ing. univ. Medellin vol.6 no.11 Medellín July/Dec. 2007
COMPORTAMIENTO RESILIENTE DE MATERIALES GRANULARES EN PAVIMENTOS FLEXIBLES: ESTADO DEL CONOCIMIENTO
RESILIENT BEHAVIOR OF GRANULAR MATERIALS IN FLEXIBLE PAVEMENTS: STATE OF THE ART
Hugo Alexander Rondón Quintana1; Fredy Reyes Lizcano2
1 Facultad de Ingeniería Civil - Universidad Católica de Colombia. Director de Investigaciones. Ingeniero civil de la Universidad Francisco de Paula Santander, Magíster en Ingeniería Civil de la Universidad de Los Andes (Bogotá D. C.) y candidato a doctor en Ingeniería de la Universidad de Los Andes (Bogotá D. C.). Dirección: Dg. 47 No. 15-50, sede El Claustro, Bogotá D. C., Colombia. Tel: (57-1) 2853876, Fax: (57-1) 2858792. e-mail: harondon@ucatolica.edu.co.
2 Departamento de Ingeniería Civil --Pontificia Universidad Javeriana. Director Especialización en Geotecnia Vial y Pavimentos. Ingeniero civil de la Pontificia Universidad Javeriana, D. E. A. École Nationale Supérieure de Mécanique, Nantes (Francia), Ph. D. en Ingeniería, Laboratoire Central de Ponts et Chaussées y École Nationale Supérieure de Mécanique, Nantes (Francia). Dirección: Calle 40 No. 5-50, Edif. José Gabriel Maldonado, Bogotá D.C., Colombia. Tel: (57-1) 3208320 Ext. 5270, Fax: (57-1) 3208320 Ext. 5398. e-mail: fredy.reyes@javeriana.edu.co
Resumen
Los vehículos que circulan sobre una estructura de pavimento inducen ciclos de carga y descarga que generan dentro de las capas granulares deformaciones recuperables (resilientes) y permanentes (plásticas). La ingeniería de pavimentos ha venido desarrollando estudios desde la década de los 60 con el fin de intentar comprender el comportamiento elastoplástico que experimentan materiales granulares cuando conforman capas de base y subbase en estructuras flexibles. La mayor parte de las investigaciones que se han realizado en esta área se han concentrado en estudiar su comportamiento resiliente. El estado del conocimiento de estudios desarrollados para medir la respuesta resiliente y la deformación permanente en materiales granulares es presentado en dos artículos por separado. En este primer artículo se presenta la forma como ha sido estudiado el comportamiento resiliente de materiales granulares y se discuten los factores que influyen en dicho comportamiento. Al final del artículo se presenta la evolución de las ecuaciones matemáticas desarrolladas a partir de resultados de estudios teóricos y experimentales. Un estado del conocimiento sobre el fenómeno de deformación permanente es presentado en un segundo artículo.
Palabras clave
Comportamiento resiliente, estado del conocimiento, materiales granulares, pavimentos flexibles.
Abstract
When vehicles move on a pavement structure, they induce load cycles that generate resilient and permanent strains inside granular layers. Since the 60's, pavement engineering has developed studies in order to understand the elasto-plastic behavior that granular materials experiment on base and sub-base layers of flexible pavements. Most of the researches that have been made in this area have concentrated in studying their resilient behavior. A state of the art about the behavior of granular materials in flexible pavements is presented in two separate papers. This first paper tries on resilient stress-strain characteristics of such materials. The mathematical equations found in the literature to predict the resilient behavior are listed, and their advantages and shortcomings are reviewed. The permanent strain characteristics of unbound aggregates are considered in another paper.
Key Words
Resilient behavior, state of the art, granular materials, flexible pavements.
INTRODUCCIÓN
En una estructura de pavimento flexible cada eje de carga genera en las capas de base y subbase (compuestas por materiales granulares no tratados) deformaciones tanto resilientes (recuperables) como permanentes (plásticas). Sin embargo, para el cálculo de esfuerzos y deformaciones, gran parte de los métodos de diseño mecanicistas de pavimentos emplean ecuaciones elásticas lineales. Suponer que el comportamiento de materiales granulares es completamente elástico conduce a una respuesta aproximada, correspondiente quizá a muy bajos niveles de esfuerzos. Además, en este tipo de ecuaciones elásticas se impide considerar un módulo de rigidez del material dependiente del nivel de esfuerzo aplicado, como lo demuestra la evidencia experimental (p. e., Hicks & Monismith, 1972; Barksdale, 1972; Boyce, 1980; Brown & Pappin, 1981; Karasahin et al., 1993; Tatsuoka et al., 1999; Lekarp et al., 2000; COST 337, 2000; Wermeister et al., 2001; Garnica et al., 2002; Werkmeister 2003, Rahim & George, 2005; Tong Li & Baus, 2005).
Por lo anterior, y con el fin de entender mejor el comportamiento de estos materiales bajo carga cíclica, la ingeniería de pavimentos ha venido desarrollando dos tipos de estudios en el nivel macromecánico, generalmente por separado. El primero de ellos y sobre el cual se ha realizado mayor investigación desde la década de los 60 se concentra en el desarrollo de ecuaciones matemáticas que predigan la evolución de la deformación resiliente y de las variables asociadas a la rigidez elástica del material (módulo resiliente Mr, módulo volumétrico K y el de cortante G) cuando experimentan diversas trayectorias de carga cíclica. Una vez desarrollada la ecuación se introduce en ecuaciones constitutivas elásticas, con el fin de predecir la deformación que experimentará la capa granular. Estas ecuaciones son conocidas como elásticas no lineales, y suponen que en cada ciclo de carga, la deformación permanente es pequeña, comparada con la deformación resiliente. Algunas de ellas son: ecuaciones no lineales (Brown & Pell, 1967; Hicks & Monismith, 1972; Boyce, 1980), anisotrópicas no lineales elásticas (Tutumluer & Thompson, 1997; Hornych et al., 1998; Tatsuoka et al., 1999; Adu-Osei et al., 2001; Hicher & Chang, 2006), hiperelásticas (Hoff & Nordal, 1999; Taciroglu & Hjelmstad, 2002). El segundo tipo de estudio busca desarrollar ecuaciones matemáticas que permitan predecir la deformación permanente a partir del estado de confinamiento y del número de ciclos de carga a los cuales es solicitada una muestra en el laboratorio. Estas ecuaciones son consideradas como empíricas (p. e., Barksdale, 1972; Sweere, 1990; Lekarp et al., 2000). Algunas incluyen la influencia del esfuerzo desviador (p. e., Lashine et al., 1971; Gidel et al., 2001) y otras son basadas en la mecánica de suelos: 'Three-surface kinematic hardening model' (Hau et al., 2005), elastoplásticos (Wolff, 1992; Wolff & Visser, 1994; Hicher et al., 1999; Chazallon, 2000; Takeuchi et al., 2004; Habiballah et al., 2004; Habiballah & Chazallon, 2005).
Otra metodología de estudio intenta comprender fenómenos físicos del comportamiento de materiales granulares en el nivel micromecánico para poder entender el comportamiento en el nivel macromecánico. Esta metodología emplea herramientas computacionales denominados programas de elementos discretos (DEM por sus siglas en inglés). Tal vez los primeros reportes sobre validación del uso de esta herramienta son los de Cundall (1978) y Cundall & Strack (1979). Son muy pocos lo estudios que se han realizado en el nivel micromecánico en esta área en comparación con los estudios en el nivel macro. Algunos de ellos pueden ser consultados en Khogali & Zeghal (2000), Zeghal (2000), Khogali & Zeghal (2003), Alonso-Marroquín & Hermann (2004), Alonso-Marroquín et al. (2004), Zeghal (2004), García-Rojo & Hermann (2004), Saussine et al. (2004), García-Rojo et al. (2005), Kim et al. (2005). Esta herramienta de investigación tiene como principales desventajas:
• Requiere de alta velocidad y capacidad para almacenamiento de información.
• Para el caso de un pavimento donde los ciclos de carga son elevados (en algunos casos superiores a 3x107), simulaciones en el nivel micromecánico no son posibles con la tecnología actual.
• Solo son tenidos en cuenta como mecanismos de desplazamiento la rotación y el deslizamiento entre partículas.
• En el nivel micromecánico la confrontación de los resultados numéricos de las simulaciones con la evidencia experimental es mucho más difícil que para el caso macromecánico.
• Para las simulaciones, conocer a priori las diferentes formas y tamaños de las partículas en un material granular es complejo, y el grado de complejidad aumenta cuando se debe tener en cuenta que de acuerdo con la forma como es compactado puede adquirir estructuras totalmente diferentes.
• Condiciones ambientales y contenido de finos no son tenidos en cuenta en las simulaciones.
A pesar del amplio número de investigaciones en estas áreas el comportamiento elastoplástico de estos materiales aún no ha sido totalmente entendido (Brown, 1996; Lekarp et al., 1996; Uzan, 1999; Lekarp et al., 2000; Collins & Boulbibane, 2000; Werkmeister et al., 2002; Werkmeister 2003; Dawson, 2003). Específicamente, existe un amplio progreso en la predicción de la respuesta resiliente, pero es menos exitoso en la predicción de la deformación permanente (Dawson et al., 2000). En este artículo se presentan, de manera resumida, los resultados teóricos y experimentales de estudios llevados a cabo para evaluar el comportamiento resiliente de materiales granulares empleados para conformar capas de base y subbase en estructuras de pavimento flexibles. Especialmente se presentarán los resultados para evaluar el módulo resiliente ya que la mayoría de estudios en esta área se ha concentrado en su medición y evaluación. Por tal motivo, el artículo inicia con una breve definición de este parámetro mecánico. Un estado del conocimiento similar fue elaborado para aquellos estudios tendientes a medir y evaluar la deformación permanente que experimentan estos materiales bajo carga cíclica. Ambos estados del conocimiento son presentados por separado.
MÓDULO RESILIENTE
Seed et al. (1955, Garnica et al., 2001) introdujo el término módulo resiliente (Mr) como la relación que existe entre la magnitud del esfuerzo desviador cíclico 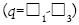
(1)
σ1 es el esfuerzo cíclico axial, σ3 es la presión de confinamiento y ε3r es la deformación horizontal resiliente. La ecuación (1) es aplicable para el caso en el cual la presión de confinamiento se mantiene constante. Cuando esta presión varía, se usa la ecuación elástica generalizada de Hooke obteniendo:
(2)
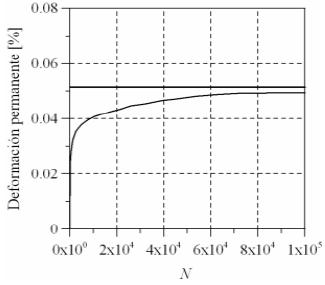
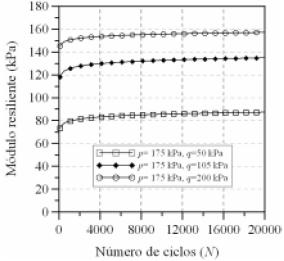
Durante la ejecución de ensayos triaxiales cíclicos se observa que después de un cierto número de ciclos de carga, el material tiende a poseer casi en su totalidad deformaciones resilientes (debido principalmente a la densificación del material como se observa en la figura 1). En este punto el módulo que se obtiene llega a ser aproximadamente constante y se supone que el comportamiento del material es elástico. Es a este módulo constante al que se le denomina módulo resiliente.
Figura 1. Curva típica de un ensayo triaxial cíclico (Werkmeister et al., 2001).
FACTORES QUE INFLUYEN EN EL COMPORTAMIENTO RESILIENTE
Influencia del esfuerzo
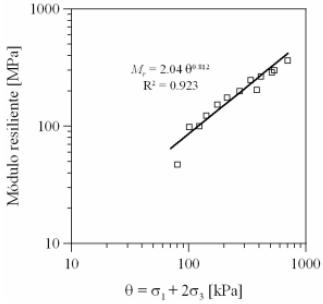
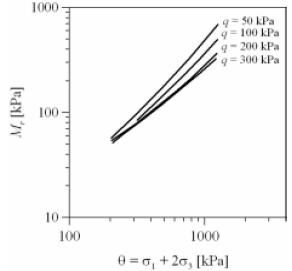
Con respecto a la magnitud del esfuerzo ha sido ampliamente demostrado que el valor del módulo resiliente (Mr) depende principalmente de la presión de confinamiento y mantiene una relación de proporcionalidad directa con la suma de esfuerzos principales 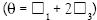
Figura 2. Variación del módulo resiliente con 
Brown (1974), citando los estudios realizados sobre materiales granulares en la Universidad de California a finales de la década de los 60, menciona que el módulo no es sensiblemente afectado por el esfuerzo desviador, siempre y cuando no se aproxime al esfuerzo de falla. Khedr (1985) observó de manera general un incremento del módulo cuando se aumenta la magnitud del esfuerzo, pero en algunos especimenes, cuando la magnitud del esfuerzo desviador era baja (menor a 70 kPa) y éste se incrementaba, la tendencia era a disminuir la rigidez.
Figura 3. Variación del módulo resiliente con £ y el esfuerzo desviador (q). Brown, 1974.
Figura 4. Variación del módulo resiliente con el esfuerzo desviador (q) (Reyes & Rondón, 2007)
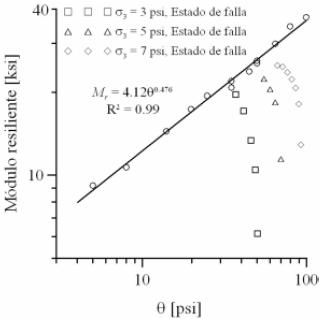
Van Niekerk et al. (2002) realizaron ensayos sobre materiales producto de demolición de edificios (concreto y mampostería) y observaron que el valor del módulo se incrementa inicialmente de manera lineal con θ. Sin embargo, cuando la magnitud de θ es muy alta (debido a que el esfuerzo desviador es cercano al valor de falla monotónica) la tendencia del módulo es a decrecer con un aumento en el esfuerzo desviador. Similar observación había sido reportada años atrás por Elliott & David (1989), realizando ensayos triaxiales sobre tres materiales granulares distintos (figura 5).
Figura 5. Módulo resiliente de una grava densa (Elliott & David, 1989).
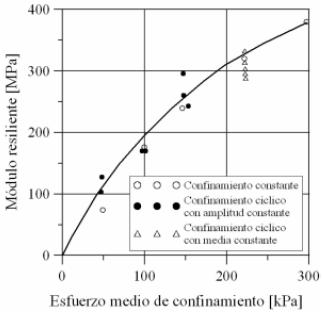
Zeghal (2004) realizó una simulación numérica del ensayo de módulo resiliente en un DEM. La investigación usó el DEM para replicar el comportamiento del espécimen durante su preparación y ensayo. Las simulaciones muestran que el DEM es capaz de reproducir los resultados del ensayo de una manera cualitativa. 16 simulaciones de ensayos triaxiales cíclicos empleando 4 presiones de confinamiento diferentes y 4 esfuerzos desviadores demostraron que el módulo resiliente aumenta con un incremento en la presión de confinamiento. Se muestra, además, que el esfuerzo desviador tiene alta influencia sobre la magnitud del módulo cuando la presión media 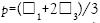
Influencia del contenido de agua
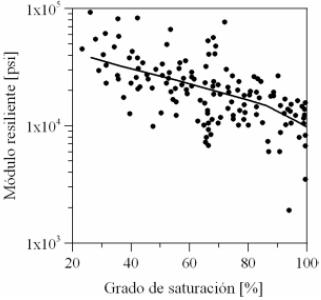
Experimentalmente ha sido ampliamente reportado que el valor del módulo resiliente disminuye cuando se aumenta la cantidad de agua en el material granular Hicks & Monismith (1971), Barksdale & Hicks (1973), Rada & Witczak (1981), Barksdale & Itani (1989), Dawson et al. (1996), Paute & Hornych (1996), Balay et al. (1997), Tian et al. (1998), Dawson et al. (2000), Khogali & Zeghal (2000), Tong Li & Baus (2005) (Figura 6). Thom & Brown (1987) mencionan que la presencia de agua en un material granular genera efectos lubricantes entre las partículas, desarrollando un incremento en la deformación y disminución de la rigidez del material. Pappin et al. (1992) observaron que una reducción en la saturación del material disminuye las deformaciones de corte resilientes y, por lo tanto, genera un incremento en la rigidez. Además, concluyen que el comportamiento esfuerzo deformación resiliente de materiales granulares saturados es idéntico al seco cuando se permite el drenaje en el ensayo. Heydinger et al. (1996) y Tian et al. (1998) no encontraron una tendencia consistente de la influencia del contenido de agua sobre el módulo resiliente de materiales distintos. Lekarp et al. (2000) mencionan que con altos contenidos de agua el material granular pierde succión, generando disminución de las fuerzas de contacto entre partículas y, por lo tanto, de la rigidez. Lo anterior, basado en los estudios realizados por Dawson et al. (1996) en donde se concluye que existe un valor óptimo de contenido de agua en el cual la rigidez es máxima (debido a la presencia de succión entre las partículas). Si el contenido de agua aumenta con respecto al óptimo, la succión entre as partículas se pierde, seguida por un incremento en la presión de poros lo cual causa disminución en la rigidez. De manera similar, Coronado et al. (2005) reportan que el módulo es mayor cuando el contenido de agua decrece por que se incrementan las fuerzas de capilaridad entre los meniscos de las partículas. Basado en estudios realizados con un simulador de vehículo pesado, Theyse (2002) concluye que la entrada de agua a las capas granulares de base y subbase genera una disminución notoria del valor del módulo resiliente. Él reportó una disminución por encima del 60% en el valor del módulo cuando se incrementa el grado de saturación desde 20% hasta 90%. Magnusdottir & Erlingsson (2002) compactaron una muestra granular con 3 humedades diferentes (por debajo del óptimo de humedad), y a pesar de que la muestra con mayor humedad era la más densa, ésta presentó los valores más bajos de módulo. En ese mismo estudio reportan la evolución del módulo con diferentes grados de saturación y se puede observar que existe un contenido de agua óptimo para el cual la rigidez es máxima y luego de este óptimo la rigidez tiende a disminuir.
Figura 6. Influencia de la saturación sobre el Mr. θ=10 psi y N=159 (Rada & Witczak, 1981).
Influencia de la densidad
En general, la literatura reporta un aumento de la rigidez cuando el material granular es más denso (p. e., Hicks & Monismith, 1971; Barksdale & Hicks, 1973; Barksdale & Itani, 1981; Kolisoja, 1997; Dawson et al., 2000; van Niekerk et al., 2002; Khogali & Zeghal, 2003) (ver Figura 7). Allen & Thompson (1974), Rada & Witczak (1981) y Khogali & Zeghal (2000) concluyen que aunque un incremento en densidad genera un incremento del módulo, el efecto es pequeño comparado con la influencia de la magnitud del esfuerzo o el contenido de agua. Allen & Thompson (1974) y Barksdale & Itani (1989) concluyen que en general el efecto de la densidad sobre el comportamiento resiliente de materiales granulares es más evidente para bajos valores de q. A altos niveles de esfuerzo, el efecto de incrementar el módulo gracias a un incremento en densidad es menos evidente. De acuerdo con Janoo & Bayer (2001) y Janoo et al. (2004) el efecto de la densidad sobre la rigidez es mínimo cuando el material granular presenta entre el 75% y el 100% de sus partículas fracturadas. Sin embargo, cuando las partículas fracturadas presentes en el material están en el rango de 0% a 50% el efecto de la densidad puede ser importante. Theyse (2002) reportó un incremento del 10% en el valor del módulo cuando la densidad de un material granular incrementó de 82.6 a 87.5% de la densidad máxima de compactación del ensayo Proctor.
Figura 7. Efecto de la densidad sobre el módulo (Magnusdottir & Erlingsson, 2002).
Influencia de la granulometría, tamaño máximo, cantidad de finos y forma de la partícula
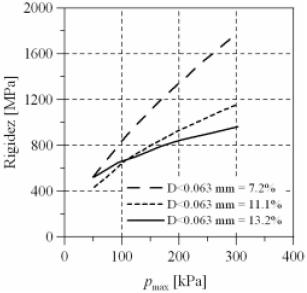
En general, la literatura reporta un incremento en el módulo resiliente cuando las partículas son más angulares Hicks & Monismith (1971), Barksdale & Hicks (1973), Allen & Thompson (1974), Barkasdale & Itani (1989), Dawson et al. (2000). Hicks & Monismith (1971), Barksdale & Itani (1989), Tutumluer et al. (2003) concluyen que entre mayor es la presencia de finos en un material granular la rigidez tiende a disminuir. Similar observación es reportada por Magnusdottir & Erlingsson (2002) (Figura 8), pero mencionan que el conocimiento general en esta área es que materiales densos bien gradados usualmente tienen la más alta resistencia mecánica con contenidos de finos por debajo de 9%. Coronado et al. (2005) reportan un incremento notable en el módulo resiliente cuando el contenido de finos aumenta de 7% a 10%. Barksdale & Hicks (1973), realizando ensayos cíclicos sobre materiales triturados y parcialmente triturados, reportan que el módulo disminuyó con el aumento de finos para el caso del material parcialmente triturado, y aumentó para el caso del material totalmente triturado. Rada & Witczak (1981) basados en estudios realizados sobre 6 materiales granulares diferentes concluyen que no existe una tendencia general de la evolución del valor del módulo con el contenido de finos y su grado de influencia depende del tipo de material estudiado.
Sweere (1990) concluye que, dependiendo del tipo de material y granulometría escogida, el tamaño del espécimen puede influir en las mediciones del módulo resiliente. Él reportó que la rigidez en ensayos triaxiales cíclicos con especímenes de 40 cm de diámetro presenta en algunos materiales, alrededor del 70% del valor de rigidez cuando se realiza el mismo ensayo con especímenes de 15 cm de diámetro. Similar observación es reportada por Janoo & Bayer (2001) y Janoo et al. (2004) para el caso de un material con diferente angularidad (100%, 50% y 0% de material triturado). Ellos obtuvieron sobre especímenes con diámetro de 15 cm módulos entre 35-50% más altos que aquellos obtenidos sobre especímenes con diámetro de 30 cm. Observaron que la angularidad de las partículas tiene una leve influencia sobre la respuesta resiliente, pero los resultados de los ensayos cuando se emplean especímenes de 30 cm de diámetro son contradictorios a aquellos que emplean especímenes con 15 cm.
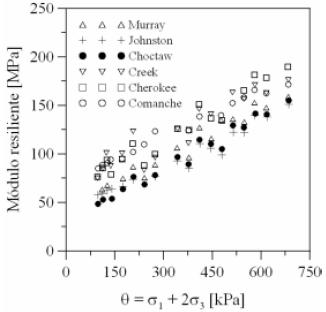
Thompson & Smith (1990) observaron pequeñas diferencias en los valores del módulo resiliente de 7 tipos de materiales granulares distintos. Para un q = 20 psi el valor de módulo osciló entre 28.6 a 35.4 ksi (197.5 MPa - 244.4 MPa). Heydinger et al. (1996) por el contrario, reportan que el módulo resiliente varía significativamente con el tipo de material empleado. Zaman et al. (1994) realizaron ensayos triaxiales cíclicos con presión de confinamiento constante (PCC) sobre 6 materiales granulares distintos utilizados para la construcción de carreteras en Oklahoma (USA). La granulometría de los materiales y el nivel de esfuerzo durante los ensayos eran iguales y la conclusión del estudio fue que los materiales presentaron diferencias entre el 20% y el 50% en el valor del módulo resiliente (figura 9). Además, en ese mismo estudio concluyen que el efecto de la granulometría no es significativo en comparación con la magnitud del esfuerzo aplicado.
Figura 8. Efecto del contenido de finos sobre el módulo Magnusdottir & Erlingsson, 2002.
Figura 9. Efecto del tipo de material sobre el módulo Zaman et al. (1994).
Kamal et al. (1993) y Kolisoja (1997) reportan que materiales con granulometrías gruesas y mayor tamaño de partículas presentan generalmente mayor módulo, menor deformación volumétrica y de corte resiliente que las finas. Basados en ensayos triaxiales cíclicos sobre 3 materiales granulares (caliza, grava-arena y concreto reciclado), Lekarp & Isacsson (2001) reportaron de manera general un pequeño incremento del módulo resiliente cuando los materiales presentaban mayores tamaños máximos de partículas, a excepción del concreto reciclado. Theyse (2002) concluye que el tamaño máximo de partículas no tiene efecto sobre el módulo resiliente (para un rango entre 19.5 y 37.5 mm) y observó un ligero incremento de la rigidez cuando las partículas son más angulares y presentan mayor textura. Además reportó que existe un contenido de finos óptimos (9%) en el cual se obtiene la mayor rigidez en el material.
Thom & Brown (1988), Brown & Selig (1991) concluyen que agregados con gradación uniforme son más rígidos que aquellos bien gradados. Garnica & Gómez (2001), Van Nieker (2002), por el contrario, reportan que agregados bien gradados son más rígidos que los uniformemente gradados. Raad et al. (1992) realizando ensayos triaxiales cíclicos no drenados sobre 4 materiales granulares saturados concluyen que agregados con gradación abierta son más resistentes a la elevación de la presión de poros (y por lo tanto, a la disminución de la rigidez) que materiales densamente gradados. Sin embargo, cuando realizaron los mismos ensayos sobre muestras no saturadas, observaron que materiales con granulometría densa presentan mayor rigidez que las abiertas. Plaistow (1994, citado de Lekarp et al., 2000), menciona que el efecto de la granulometría sobre el comportamiento resiliente es importante cuando se controla el contenido de agua y la densidad. Heydinger et al. (1996) evaluaron el efecto de la granulometría (abierta y cerrada) sobre el valor del módulo resiliente de 3 materiales granulares diferentes (caliza, grava y ceniza). La caliza presentó mayor módulo cuando se empleó granulometría abierta mientras la ceniza presentó mayor módulo cuando se utilizó granulometría cerrada. Para el caso de la grava no se encontró una tendencia satisfactoria. Tian et al. (1998) evaluaron la variación del módulo resiliente para un material con 3 granulometrías distintas (gruesa, intermedia y fina) y observaron que la granulometría intermedia experimentó mayor rigidez (50% mayor que la granulometría fina y 10% mayor que la gruesa).
Kolisoja et al. (2002) estudiaron el efecto del contenido de finos sobre el módulo resiliente en materiales secos, que han adsorbido agua y en aquellos que experimentan ciclos de congelamiento-secado. Ellos observaron una pequeña disminución del valor del módulo con el incremento en el contenido de finos para materiales que han adsorbido agua o presentan ciclos de congelamiento secado. Los mayores módulos se obtienen con el material en estado seco y los menores cuando experimentan ciclos de congelamiento-secado.
Basados en ensayos tipo PCC sobre granulares tipo gneiss, Uthus et al. (2005) concluyen que el comportamiento resiliente de estos materiales con baja cantidad de finos y altos coeficientes de gradación (entre mayor sea este coeficiente el material presenta menor coeficiente de uniformidad) son menos sensitivas al agua que las muestras con alto contenido de finos y bajos coeficientes de gradación.
Kumar et al. (2006) realizaron ensayos monotónicos y cíclicos sobre 4 materiales granulares utilizados para conformar capas de subbase de estructuras flexibles. El material que presentaba el mayor CBR (60.7%, Californian Bearing Ratio) experimentó menor rigidez bajo carga cíclica que los demás que presentaban CBR entre 9.1 y 47.2%.
Influencia de la frecuencia de carga e historia de esfuerzo
Kalcheff & Hicks (1973) no encontraron un efecto significativo sobre las características resilientes de 4 materiales granulares cuando se realizaron ensayos cíclicos con distintas secuencias de carga. De acuerdo con Brown & Hyde (1975) y Theyse (2002), la historia de esfuerzo no afecta el valor del módulo resiliente en materiales granulares.
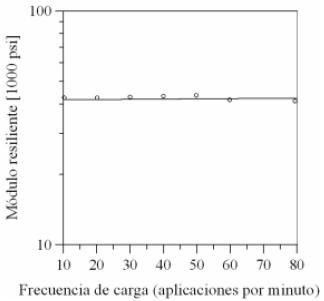
Kalcheff & Hicks (1973) observaron que el cambio en la respuesta resiliente de 4 materiales granulares bien gradados es mínimo, cuando se ensayan en un rango de frecuencias de carga entre 0.04 y 1.0 Hz (figura 10). Similar observación fue reportada por Allen & Thompson (1974) ensayando 3 materiales granulares con frecuencias entre 0.04 y 10 Hz, Brown (1974) con frecuencias entre 0.01 y 10 Hz, Boyce (1976) con frecuencias entre 0.1 y 20 Hz, Thom & Brown (1987) con frecuencias entre 0.1 y 3.0 Hz y por Theyse (2002) con frecuencias entre 0.3 y 1.0 Hz. En general, la frecuencia de carga no afecta el comportamiento resiliente de materiales granulares (Rada & Witczak, 1981; Lekarp et al., 2000).
Figura 10. Efecto de la frecuencia de carga sobre el módulo resiliente (Kalcheff & Hicks, 1973).
Influencia del tipo de ensayo
Allen & Thompson (1974) concluyen que los ensayos PCC producen valores de módulo similares y en algunos casos ligeramente más altos que aquellos producidos en ensayos triaxiales cíclicos con presión de confinamiento variable (PCV), y la diferencia de estos resultados disminuye cuando la suma de esfuerzos principales aumenta. Brown & Hyde (1975) obtuvieron valores similares de módulo cuando realizaron ensayos PCC y PCV (figura 11).
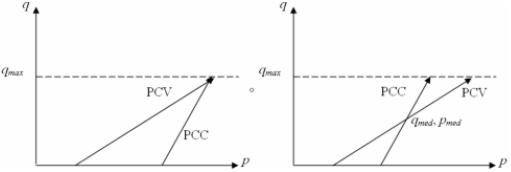
En ambos estudios las trayectorias de esfuerzos fueron diferentes, como se observa en la figura 12. Es importante tener en cuenta que a pesar de que la trayectoria de esfuerzo utilizada por Brown & Hyde (1975) es más representativa para comparar el comportamiento del material granular en ensayos PCC y PCV (debido a que presentan el mismo esfuerzo desviador medio qmed, presión media pmed y máximo esfuerzo desviador qmax), solo fue comparada una sola trayectoria lo cual limita el análisis y las conclusiones.
Figura 11. Variación del módulo resiliente con el tipo de ensayo, Brown & Hyde (1975).
Figura 12. Esfuerzos utilizados por a) Allen & Thompson (1974), b) Brown & Hyde (1975)
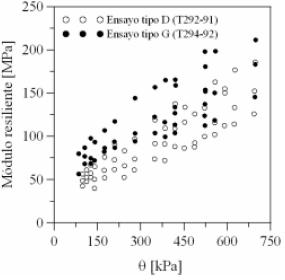
Nataatmadja & Parkin (1989) observaron diferente comportamiento esfuerzo - deformación resiliente cuando se realizaban ensayos PCC o PCV. Por lo anterior desarrollaron ecuaciones diferentes de evolución del módulo para ambos ensayos (ecuaciones 13 y 14). Zaman et al. (1994) y Mohammad et al. (1994) compararon los resultados de dos tipos de ensayos cíclicos tipo PCC sobre un mismo material granular y obtuvieron valores diferentes de módulo resiliente como se observa en la figura 13. La diferencia en los ensayos eran las trayectorias de esfuerzos utilizadas (AASHTO T292-91 y T294-92).
Figura 13. Variación del módulo resiliente con 
Anisotropía
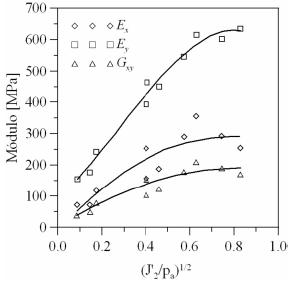
En una capa de base o subbase de un pavimento flexible los materiales granulares experimentan anisotropía debido a las distintas formas, tamaños de partículas y método de depositación (inherente), y por efectos de compactación y carga en las diferentes direcciones (inducida). Propiedades anisotrópicas de materiales granulares han sido reportadas desde la década de los 70. Moore et al. (1970), Barksdale & Hicks (1973), Allen & Thompson (1974), Hoque et al. (1996), Tutumluer & Thompson (1997), Hoque & Tatsuoka (1998), Adu-Osei et al. (2001), Seyhan et al. (2005) reportaron que en los materiales granulares la rigidez lateral es menor en comparación con la vertical (Figura 14). Hornych et al. (2000) basados en ensayos triaxiales cíclicos sobre una caliza y un granito concluyen que la relación entre la rigidez lateral y la vertical en estos materiales fue de 0.54 y 0.66, respectivamente.
Figura 14. Variación de la rigidez vertical (Ey) y lateral (Ex) en un material granular. J'2 es la segunda invariante del tensor de esfuerzo desviador Adu-Osei et al. (2001).
Muhunthan et al. (2000) desarrollaron un equipo para analizar la microestructura de materiales granulares. Ellos realizaron ensayos sobre muestras densas de arena Ottawa, arena silícea y esferas de vidrio, y concluyeron que los especímenes tienen más vacíos en la dirección horizontal que en la vertical. Seyhan & Tutumluer (2002) realizaron ensayos PCV sobre 13 materiales granulares los cuales fueron clasificados como 'buenos' y 'pobres' basados en sus propiedades mecánicas. El objetivo de los ensayos era medir la relación entre la rigidez horizontal y vertical (Mrh y Mrv respectivamente) que experimentan estos materiales bajo cargas cíclicas. De los resultados concluyen que materiales con buenas propiedades mecánicas presentan valores más bajos de Mrh/Mrv que aquellos con menores propiedades, pero cuando el nivel de esfuerzo incrementa los materiales con buenas propiedades incrementan esta relación y los de baja calidad tienden a disminuirla.
Kim et al. (2005), basados en estudios en el nivel micromecánico sobre 6 materiales granulares con 3 gradaciones y 3 contenidos de agua distintos, concluyen que en el rango de anisotropía inherente (donde no son inducidos esfuerzos), la relación entre la rigidez horizontal y la vertical (Ex/Ey) está en el rango de 0.4 - 1.0. Además, concluyen:
• El tipo de agregado, orientación y forma de las partículas tienen un sustancial efecto sobre el comportamiento de materiales granulares y sobre el nivel de anisotropía.
• Agregados con partículas alargadas son más anisotrópicos.
• El nivel de anisotropía decrece cuando el material es más angular y con alta textura.
ECUACIONES RESILIENTES (ELÁSTICAS NO LINEALES)
A continuación se presenta la evolución de las ecuaciones elásticas no lineales más utilizadas para la estimación del módulo y las deformaciones resilientes.
• Dunlap (1963), Monismith et al. (1967): tiene en cuenta que el módulo resiliente varía con la magnitud de la presión de confinamiento (σ3):
(3)
po es una presión de referencia (100 kPa) y k1, k2 son parámetros del material obtenidos por medio de regresión. Desventajas de la ecuación: no tiene en cuenta la influencia del esfuerzo desviador (Uzan, 1985; Nataatmadja & Parkin, 1989; Tutumluer & Thompson, 1997; Garg & Thompson, 1997), se basa en la realización de ensayos triaxiales cíclicos con presión de confinamiento constante donde solo el esfuerzo vertical axial es cíclico; se supone que la relación de Poisson es constante y no es adecuada para predecir deformación volumétrica y de corte (Seed, 1990; COST 337, 2000; Lekarp et al., 2000).
• K-q (Brown & Pell, 1967; Hicks & Monismith, 1971; Hicks & Monismith, 1972): es similar a la ecuación (3), solo que ésta tiene en cuenta que el módulo varía con el nivel de esfuerzo inducido al material. Debido a su simplicidad, es la ecuación más utilizada para estimar el módulo resiliente.
(4)
θ es la suma de esfuerzos principales, pa es una presión de referencia (100 kPa) y k1, k2 son parámetros del material obtenidos por regresión. Las desventajas de la ecuación son similares a las de la ecuación (3). Incluso algunos investigadores mencionan que en muchos casos esta ecuación es inexacta para los rangos probables de esfuerzos que se presentan in situ ya que fue calibrada en ensayos cíclicos con trayectorias de esfuerzo donde la presión de confinamiento era constante (Brown, 1974; Brown & Hyde, 1975; Brown & Pappin, 1981; Uzan, 1985; Sweere, 1990; Brown, 1996; Gomes-Correia et al., 1999; Gomes-Correia, 2000; COST 337, 2000; Kim, 2004). May & Witczak (1981) basados en medidas de deflexión tomadas de 3 pistas de ensayo construidas en Maryland (USA), reportaron que el módulo resiliente de las capas granulares medido in situ es función no solamente de la magnitud de esfuerzos principales sino también de las deformaciones de corte generadas por el esfuerzo desviador. Maree et al. (1982) realizaron estudios experimentales sobre materiales granulares con un simulador de vehículo pesado (HVS) y concluyen que aunque la tendencia general de la rigidez es a aumentar con el incremento en θ, una ecuación como la (4) presenta correlaciones muy pobres entre lo medido experimentalmente y la simulación.
• Boyce (1980): denominado por Boyce como modelo G-K. Se basa en la realización de ensayos triaxiales cíclicos con presión de confinamiento variable. Es una ecuación en 3D que tiene en cuenta la influencia que tiene la relación q/p (esfuerzo desviador y presión media, respectivamente), sobre el comportamiento resiliente de materiales granulares. Además, tiene en cuenta que la relación de Poisson () varía con la carga cíclica aplicada.
(5)
(6)
(7)
ev es la deformación volumétrica, eq es la deformación por cortante, b es un potencial elástico y Ka, Ga, n son parámetros del material. Boyce (1980) hace claridad que histéresis o campos plásticos son excluidos de la ecuación, y si el material experimenta deformaciones permanentes, éstas deben ser calculadas por separado. La deficiencia de la ecuación se presenta cuando el material granular experimenta altos niveles de esfuerzo lo cual genera valores altos de deformación resiliente (COST 337, 2002). Ecuaciones similares pueden ser consultados en Brown & Pappin (1981), Lekarp et al. (2000) y Pappin & Brown (1980) (denominado modelo de contorno). Este tipo de ecuaciones presentan como principal desventaja que sus parámetros son de difícil determinación experimental.
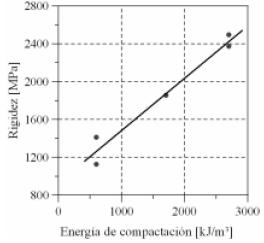
• Rada & Witczak (1981): proponen la ecuación (8) basados en el análisis de resultados de 271 ensayos triaxiales cíclicos realizados por 10 institutos de investigación. Esta ecuación relaciona el módulo resiliente con el grado de saturación (Sr), la energía de compactación (EC) y la suma de esfuerzos principales (θ).
(8)
Ci, son los parámetros del material obtenidos por medio de regresión.
• Uzan (1985): Introduce el esfuerzo desviador en la ecuación (4).
(9)
p es la presión media, q es el esfuerzo desviador, po es la presión de referencia (100 kPa) y los ki son parámetros del material. Las desventajas de la ecuación son similares a las de la ecuación (3) solo que ésta tiene en cuenta la influencia del esfuerzo desviador. Ecuaciones similares (10, 11 y 12) son presentadas por Tam & Brown (1988), Heydinger et al. (1996) y Pezo (1993, citado de Lekarp et al., 2000), respectivamente:
(10)
(11)
(12)
Para el caso triaxial 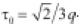
• Nataatmadja & Parkin (1989): desarrollaron ecuaciones diferentes para predecir la evolución del módulo resiliente cuando se emplean ensayos PCC y PCV (ecuaciones 13 y 14, respectivamente).
(13)
(14)
θ es la suma de esfuerzos principales y A, B, C, D son parámetros del material.
• Elliott & David (1989): observaron para niveles de esfuerzo superiores al estático de falla que la ecuación (4) no puede predecir la evolución del módulo resiliente. Modificaron, entonces, la ecuación k-q relacionando el módulo con la suma de esfuerzos principales (θ) y la relación entre el esfuerzo desviador y la resistencia monotónica del material (s).
(15)
k, n, m son parámetros del material obtenidos por regresión.
• Queck (1992), Gleitz (1996): relaciona el módulo resiliente con la magnitud del esfuerzo principal mayor y menor (

(16)
Q, Qi, C y D son parámetros del material.
• Jouve & Elhannani (1994): es una versión modificada de la ecuación de Boyce (1980) la cual tiene en cuenta efectos anisotrópicos en materiales granulares.
(17)
(18)
x es un parámetro que tiene en cuenta el nivel de anisotropía del material. Si x=0 el material es isotrópico y las ecuaciones (17) y (18) se convierten en las ecuaciones (5) y (6), respectivamente.
• Zaman et al. (1994): relaciona el módulo resiliente con la cohesión (C), el ángulo de fricción (£) y la suma de esfuerzos principales (q).
(19)
Ai, son parámetros del material obtenidos por regresión.
• Kolisoja (1997): modificó las ecuaciones (4) y (9) para que tuvieran en cuenta el efecto que tiene la porosidad del material (n) sobre la rigidez.
(20)
(21)
nmax es la porosidad máxima que puede alcanzar el material y A, B son parámetros.
• Tutumluer & Thompson (1997), Adu-Osei et al. (2001): ecuación similar a la (9) en 3D, pero tiene en cuenta el comportamiento anisotrópico que experimentan materiales granulares.
(22)
(23)
(24)
En la ecuación (22) el módulo resiliente calculado es en la dirección y y en la ecuación (23) en la dirección x. Los ki son los parámetros del material obtenidos por regresión. Para introducir las ecuaciones en un programa de elementos finitos, se requiere calcular además los parámetros n, m y m:
(25)
nxx y nxy son la relación de Poisson (la primera componente es la dirección de la carga aplicada y la segunda la dirección de la deformación).
• Hornych et al. (1998): ecuaciones similares a las presentadas por Jouve & Elhannani (1994).
(26)
(27)
(28)
γ es un parámetro que tiene en cuenta el nivel de anisotropía del material. Si γ=1 el material es isotrópico y las ecuaciones (26) y (27) se convierten en las ecuaciones (5) y (6), respectivamente. Este tipo de ecuaciones tiene como principal limitación que los parámetros son de difícil obtención experimental.
• Van Niekerk et al. (2002): observaron sobre muestras de material proveniente de demolición de edificios (concreto y mampostería), rigidización a bajos niveles de esfuerzo y ablandamiento a altos niveles (desviador acercándose a la falla monotónica).
(29)
θ0 es una presión de referencia, q es el esfuerzo desviador, qf es el esfuerzo desviador de falla y ki son los parámetros del material obtenidos por regresión.
• Rahim & George (2005): proponen una ecuación empírica que tiene en cuenta el efecto del esfuerzo, la densidad, el grado de uniformidad y el contenido de agua y finos de materiales granulares sobre el módulo.
(30)
(31)
θ es la suma de esfuerzos principales, q es el esfuerzo desviador, pa es la presión atmosférica, γd es la densidad seca, w es el contenido de agua, #200 es el porcentaje del material que pasa el tamiz No. 200 en un ensayo granulométrico y cu es el coeficiente de uniformidad.
En general, las ecuaciones anteriores son incapaces de predecir deformaciones permanentes. Estas ecuaciones simulan deformaciones obtenidas en ensayos cíclicos una vez el material granular alcanza la fase estable o de postcompactación (deformaciones resilientes casi en su totalidad) de la figura 1. Por lo anterior, pueden ser empleados para el cálculo de las deformaciones a tensión que se producen en la capa asfáltica (fatiga), y con cierto grado de confianza, para el cálculo de la deformación o desplazamiento en capas granulares cuando los niveles de esfuerzo cíclico son bajos y se pueda alcanzar la fase estable. Niveles bajos de esfuerzo pueden ser obtenidos en estructuras de pavimentos flexibles cuando la capa asfáltica es gruesa y de alta rigidez; las propiedades mecánicas del material granular son muy buenas en comparación con el nivel de esfuerzo aplicado o cuando la carga impuesta por los vehículos es pequeña. Cuando la magnitud del esfuerzo cíclico es alta, las ecuaciones elásticas pueden perder validez y confiabilidad para la predicción de la deformación o el desplazamiento.
De manera general, la literatura reporta una mejor predicción de la respuesta resiliente de materiales granulares cuando se utilizan ecuaciones que involucran efectos anisotrópicos (p.e., Tutumluer & Thompson, 1997; Gomes-Correia et al., 1999; Adu-Osei et al., 2001; Tutumluer et al., 2003; Kim, 2004; Kim et al., 2005; Masad et al., 2006). Estudios reportados por Gomes-Correia (2000), COST 337 (2000) y Neves & Gomes-Correia (2004),, donde se comparan medidas de deformación resiliente en pistas de prueba con simulaciones empleando ecuaciones elásticas lineales, y no lineales demuestran que la modelación resiliente es menos satisfactoria cuando se usan ecuaciones lineales elásticas ya que parece ser que tienden a sobreestimar la deformación. Además demuestran que las ecuaciones que emplean parámetros volumétricos y de corte (como la de Boyce, 1980) y que pueden simular anisotropía (Jouve & Elhannani, 1994; Hornych et al., 1998) presentan la mejor predicción. Por último, concluyen que la condición de no linealidad y anisotropía comienza a ser más importante cuando la capa granular es gruesa y el espesor de la capa asfáltica es delgada.
Algunos investigadores recomiendan en las modelaciones de estructuras de pavimento el empleo de ecuaciones elastoplásticas e hipoplásticas en vez de las elásticas lineales o no lineales (p.e., Balay & Kabré, 1996; Guezouli et al., 1996; Van Schelt et al., 1996; Uzan, 1999, Rondón & Lizcano, 2006). Jouve & Guezouli (1996) realizaron simulaciones numéricas empleando 4 programas de elementos finitos (FENLAP - University of Nottingham, DIANA - Delft University of Technology, NOEL - Université de Nantes y CESAR - Laboratoire Central des Ponts et Chaussées) para modelar el comportamiento de una misma estructura de pavimento y comparar los resultados de mediciones realizadas in situ con aquellos obtenidos en las simulaciones. Para el cálculo de esfuerzos y deformaciones en la capa asfáltica y la subrasante, se empleó una ecuación constitutiva elástica lineal, y para las capas de base y subbase se utilizó una ecuación elástica no lineal. Reportan como conclusión general del estudio que para obtener una mejor predicción del esfuerzo en estructuras de pavimentos es necesario el empleo de ecuaciones más sofisticadas tales como las elastoplásticas. En un estudio similar, pero empleando 5 ecuaciones constitutivas diferentes (1 elástica lineal, 3 elásticas no lineales y una elastoplástica) para modelar las capas granulares de una estructura de pavimento, Jouve & Guezouli (1996a) concluyen que ecuaciones elastoplásticas predicen mejor los esfuerzos que se producen en una estructura de pavimento, pero mencionan que para la estimación de la deformación permanente es necesario realizar modificaciones a la ecuación (especialmente cuando la magnitud de la carga es alta). Rondón & Lizcano (2006) realizaron simulaciones numéricas empleando el programa de elementos finitos Abaqus, con el fin de comparar los resultados obtenidos de modelar la capa de base granular de un pavimento flexible empleando una ecuación elástica lineal y una hipoplástica. Ellos concluyen que los valores de deformación vertical pueden ser subestimados cuando se utilizan ecuaciones elásticas lineales, debido a que esta ecuación no tiene en cuenta (como sí lo hace la hipoplasticidad) que los materiales granulares exhiben un comportamiento no lineal y que desde el inicio del proceso de carga se generan deformaciones tanto resilientes como permanentes
CONCLUSIONES
Pocos estudios en el nivel micromecánico han sido desarrollados para estudiar el comportamiento elastoplástico que experimentan materiales granulares bajo carga cíclica en comparación con los estudios en el nivel macro. Estudios para evaluar como la fricción, rigidez y dinámica entre partículas afectan los parámetros resilientes en un material granular deben ser realizados con el fin de entender fenómenos observados en el nivel macro.
Los principales factores que afectan las propiedades resilientes de materiales granulares son la magnitud de las cargas cíclicas y el contenido de agua. Otros factores que lo afectan son la densidad, el número, duración y frecuencia de carga, el tipo de ensayo, la gradación, naturaleza mineralógica y contenido de finos, el tamaño máximo y la forma de la partícula sólida. La mayoría de los estudios consultados presentan similares conclusiones cuando reportan la forma como algún factor influye sobre las propiedades resilientes de materiales granulares. Sin embargo. en algunos casos, investigadores reportan conclusiones contradictorias (p. e., influencia de la magnitud del esfuerzo desviador, contenido de finos y la granulometría). En general, la rigidez de materiales granulares se incrementa cuando la presión de confinamiento, la magnitud de esfuerzos y la densidad aumentan. Para altos grados de saturación, la tendencia del valor del módulo es a disminuir cuando se incrementa la cantidad de agua en el material. Sin embargo, algunos estudios han demostrado que existe un valor óptimo de contenido de agua en el cual la rigidez alcanza su mayor valor. La duración y frecuencia de carga no tienen un efecto significativo sobre las propiedades resilientes. Materiales con partículas angulares presentan mayor rigidez que aquellos con partículas redondeadas. El efecto de la granulometría y contenido de finos no es claro y en muchos casos se presenta contradicción reportando su influencia. Aunque efectos anisotrópicos sobre materiales granulares han sido reportados desde la década de los 70, muy pocos estudios teóricos y experimentales han sido desarrollados en esta área.
La gran variedad de ecuaciones presentadas muestran el grado de complejidad que existe para entender el comportamiento de estos materiales. La mayor parte de las mismas se han concentrado en determinar la relación entre el módulo resiliente y el nivel de esfuerzo. Pocas ecuaciones han sido desarrolladas para estimar el comportamiento resiliente en 3D. La tendencia actual es desarrollar ecuaciones elásticas no lineales que tengan en cuenta el comportamiento anisotrópico de materiales granulares. Como conclusión general en esta área se reporta que la predicción de la respuesta resiliente es mejor cuando se utilizan ecuaciones de este tipo.
BIBLIOGRAFÍA
1. ADU-OSEI, A., LITTLE, D. N. & LYTTON, R. L. (2001). Cross-anisotropic Characterization of Unbound Granular Materials. Transportation Research Record, 1757, Transportation Research Board, Washington, D. C., 82-91. [ Links ]
2. ALLEN, J. J. & THOMPSON, M. R. (1974). Resilient Response of Granular Materials Subjected to Time-Dependent Lateral Stresses. Transportation Research Record, 510, Transportation Research Board, Washington, D. C., 1-13. [ Links ]
3. ALONSO-MARROQUÍN, F., GARCÍA-ROJO, R. & HERRMANN, H. J. 2004. Micromechanical Investigation of granular ratcheting. Proceedings of the International Conference on Cyclic Behavior of Soils and Liquefaction Phenomena, Bochum (Germany), 3-9. [ Links ]
4. ALONSO-MARROQUÍN, F. & HERMANN, H. J. 2004. Ratcheting of Granular Materials. The American Physical Society. 92:5. [ Links ]
5. BALAY, J., GOMES-CORREIA, C., JOUVE, P., HORNYCH, P. & PAUTE, J.-L. 1997. Mechanical Behaviour of Soils and Unbound Granular Materials, Modelling of Flexible Pavements - Recent Advances. Proceedings 8th International Conference on Asphalt Pavements, Seattle, Vol. 1, 823-842. [ Links ]
6. BALAY, J. & KABRÉ, H. 1996. Modelization of Flexible Pavements with César-LCPC FEM Program. Flexible Pavement. Ed. Gomes-Correia Correia, Balkema, Rotterdam, 185-192. [ Links ]
7. BARKSDALE, R. D. 1972. Laboratory Evaluation of Rutting in Basecoarse Materials. Proceedings of the 3rd International Conference on Asphalt Pavements, Vol. 1, 161-174. [ Links ]
8. BARKSDALE, R. D. 1984. Performance of Crushed-Stone Base Courses. Transportation Research Record, 954, Transportation Research Board, Washington, D. C., 78-87. [ Links ]
9. BARKSDALE, R. D. & HICKS, R. G. 1973. Evaluation of Materials for Granular Base Courses. 3rd Interamerican Conference on Materials - Technology, Brazil, 134-143. [ Links ]
10. BARKSDALE, R. D. & ITANI, S. Y. 1989. Influence of Aggregate Shape on Base Behaviour. Transportation Research Record, 1227, Transportation Research Board, Washington, D. C., 173-182. [ Links ]
11. BOYCE, H. R. 1980. A Non-linear Model for the Elastic Behaviour of Granular Materials under Repeated Loading. Proceedings International Symposium on Soils under Cyclic and Transient Loading, Swansea, U.K., Vol. 1 285-294. [ Links ]
12. BOYCE, J. R. 1976. The Behaviour of a Granular Material under Repeated Loading. Ph. D., Thesis, University of Nottingham. [ Links ]
13. BROWN, S. F. 1974. Repeated Load Testing of a Granular Material. Journal of the Geotechnical Engineering Division, Vol. 100, No. 7, 825-841. [ Links ]
14. BROWN, S. F. 1996. Soil Mechanics in Pavement Engineering. The 36th Rankine Lecture of the British Geotechnical Society, Géotechnique 46, No. 3, 383-426. [ Links ]
15. BROWN, S. F & HYDE, A. F. L. 1975. Significance of Cyclic Confining Stress in Repeated-load Triaxial Testing of Granular Material. Transportation Research Record, 537, Transportation Research Board, Washington, D. C., 49-58. [ Links ]
16. BROWN, S. F. & PAPPIN, J. W. 1981. Analysis of Pavements with Granular Bases. Transportation Research Record, 810, Transportation Research Board, Washington, D. C., 17-23. [ Links ]
17. BROWN, S. F. & PELL, P. S. 1967. An Experimental Investigation of the Stresses, Strains and Deflections in a Layered Pavement Structure Subjected to Dynamic Loads. Proc., 2nd Int. Conf. Struct. Des. of Asphalt Pavements, 487-504. [ Links ]
18. BROWN, S. F. & SELIG, E. T. 1991. The Design of Pavement and Rail Track Foundations. Cyclic Loading of Soils, Chapter 6, 249-305. [ Links ]
19. CHAZALLON, C. 2000. An Elastoplastic Model with Kinematic Hardening for Unbound Aggregates in Roads. Unbound Aggregates in Road Construction - UNBAR 5, Dawson editor, Balkema, Rotterdam, 265-270. [ Links ]
20. COLLINS, I. F. & BOULBIBANE, M. 2000. Geomechanical Analysis of Unbound Pavements Based on Shakedown Theory. Journal of Geotechnical and Geoenvironmental Engineering, Vol. 126, 50-59. [ Links ]
21. CORONADO, O., FLEUREAU, J.-M., GOMES CORREIA, A. & CAICEDO, B. 2005. Influence of Suction on the Properties of two Granular Road Materials. 7th International Conference on the Bearing Capacity of Roads, Railways and Airfields, Norway. [ Links ]
22. COST 337. 2000. Unbound Granular Materials for Road Pavements, Final Report of the Action. Luxembourg: Office for Official Publications of the European Communities. [ Links ]
23. CUNDALL, P. A. 1978. BALL - A Program to Model Granular Media Using the Distinc Element Method. Technical Note, Advanced Technology Group, Dames & Moore, London. [ Links ]
24. CUNDALL, P. A. & STRACK, O. D. L. 1979. A Discrete Numerical Model for Granular Assemblies. Géotechnique, 29 (1), 47-65. [ Links ]
25. DAWSON, A. R. 2003. Cumulative Damage and its Applicability to Low Volume Road Pavements. Internationales Kolloquium Prüfung, Bewertung und Bemessung von Straßenbefestigungen, Technische Universitat Dresden. [ Links ]
26. DAWSON, A. R., MUNDY, M. J. & HUHTALA, M. 2000. European Research into Granular Material for Pavement Bases and Subbases. Transportation Research Record, 1721, Transportation Research Board, Washington, D. C., 91-99. [ Links ]
27. DAWSON, A. R., PAUTE, J. L & THOM, N. H. 1996. Mechanical Characteristics of Unbound Granular Materials as a Function of Condition. Flexible Pavement. Ed. Gomes Correia, Balkema, Rotterdam, 35-44. [ Links ]
28. DUNLAP, W. A. 1963. A Report on a Mathematical Model Describing the Deformation Characteristics of Granular Materials. Tech. Rep. No. 1, Proj. 2-8-62-27, Texas Transp. Inst., Texas A&M University, College Station, Tex. [ Links ]
29. ELLIOTT, R. P. & DAVID, L. 1989. Improved Characterization Model for Granular Bases. Transportation Research Record, 1227, Transportation Research Board, Washington, D. C., 128-133. [ Links ]
30. GANDARA, J. A. & NAZARIAN, S. 2006. Characterization of Rutting Potential of Texas Bases Through Laboratory and Small Scale Tests. TRB 85th Annual Meeting of the Transportation Research Board, Washington D. C., pp. 15. [ Links ]
31. GARCÍA-ROJO, R. & HERMANN, H. J. 2004. Shakedown of Unbound Granular Material. Institute for Computer Applications 1, University of Stuttgart (Germany), pp. 9. [ Links ]
32. GARCÍA-ROJO, R., ALONSO-MARROQUÍN, F. & HERMANN, H. J. 2005. Characterization of the Material Response in the Granular Ratcheting. Institute for Computer Applications 1, University of Stuttgart (Germany), pp. 14. [ Links ]
33. GARG N. & THOMPSON M. R. 1997. Triaxial Characterization of Minnesota Road Research Project Granular Materials. Transportation Research Record, 1577, Transportation Research Board, Washington, D. C., 27-36. [ Links ]
34. GARNICA, P. A. & GÓMEZ, L. J. 2001. Deformaciones Permanentes en Materiales Granulares para la Sección Estructural de Carreteras. Publicación Técnica No. 176, Secretaría de Comunicaciones y Transportes (SCI) - Instituto Mexicano del Transporte (IMT). Sanfandila, México, pp. 46. [ Links ]
35. GARNICA, P. A., GÓMEZ, L. J. & SESMA, M. J. 2002. Mecánica de Materiales para Pavimentos. Publicación Técnica No. 197, Secretaría de Comunicaciones y Transportes (SCI) - Instituto Mexicano del Transporte (IMT). Sanfandila, México, pp. 234. [ Links ]
36. GARNICA, P. A., PÉREZ, G. N. & GOMES, L. A. 2001. Módulo de Resiliencia en Suelos Finos y Materiales Granulares. Publicación Técnica No. 142, Secretaría de Comunicaciones y Transportes (SCI) - Instituto Mexicano del Transporte (IMT). Sanfandila, México, pp. 58. [ Links ]
37. GIDEL, G., HORNYCH, P., CHAUVIN, J., BREYSSE, D. & DENIS, A. 2001. A New Approach for Investigating the Permanent Deformation Behavior of Unbound Granular Material Using the Repeated Load Triaxial Apparatus. Bulletin Des LaboratoiresDes Ponts et Chaussées, 5-21. [ Links ]
38. GLEITZ, T. 1996. Contribution to the Mathematical Determination of the Stress-Strain Behaviour of Unbound Structural Layers by Means of Triaxial Tests. Flexible Pavement. Ed. Gomes Correia, Balkema, Rotterdam, 273-279. [ Links ]
39. GOMES-CORREIA, A. 2000. Modelling Unbound Granular Materials. Recommendations for Pavement Design. Technical University of Lisbon - IST. [ Links ]
40. GOMES-CORREIA, A. & GILLETT, S. 1996. A Large Triaxial Apparatus for the Study of Granular Materials under Repeated Loading Used at LNEC. Flexible Pavement. Ed. Gomes Correia, Balkema, Rotterdam. 45-51. [ Links ]
41. GOMES-CORREIA, A., HORNYCH, P. & AKOU, Y. 1999. Review of Models and Modelling of Unbound Granular Materials. Unbound Granular Materials - Laboratory testing, In-situ testing and modelling, Gomes Correia, A. (Ed.), A.A. Balkema, Rotterdam, 3-15. [ Links ]
42. GUEZOULI, S., ELHANNANI, M. & JOUVE, P. 1996. NOEL: A Non Linear Finite Element Code for Road Pavement Analysis. Flexible Pavements, Ed. Gomes Correia, Balkema, Rotterdam. 193-200. [ Links ]
43. HABIBALLAH, T. & CHAZALLON, C. 2005. An Elastoplastic Model Based on the Shakedown Concept for Flexible Pavements Unbound Granular Materials. Int. J. Numer. Anal. Meth. Geomech., 29:577-596. [ Links ]
44. HABIBALLAH, T., CHAZALLON, C. & HORNYCH, P. 2004. Simplified Model Based on the Shakedown Theory for Flexible Pavements. Proc., of the 6th International Symposium on Pavements Unbound, 191-198. [ Links ]
45. HAU, K. W., MCDOWELL, G. R., ZHANG, G. P. & BROWN, S. F. 2005. The Application of a Three-Surface Kinematic Hardening Model to Repeated Loading of Thinly Surfaced Pavements. Granular Matter, 7: 145-156. [ Links ]
46. HEYDINGER, A. G., XIE, Q., RANDOLPH, B. W. & GUPTA, J. D. 1996. Analysis of Resilient Modulus of Dense- and Open-Graded Aggregates. Transportation Research Record, 1547, Transportation Research Board, Washington, D. C., 1-6. [ Links ]
47. HICHER, P.-Y & CHANG, C. S. 2006. Anisotropic Nonlinear Elastic Model for Particulate Materials. Journal of Geotechnical and Geoenvironmental Engineering, Vol. 132, No. 8, 1052-1061. [ Links ]
48. HICHER, P., DAOUADJI, A. & FEDGHOUCHE, D. 1999. Elastoplastic Modelling of the Cyclic Behaviour of Granular Materials. Unbound Granular Materials - Laboratory testing, In-situ testing and modelling, Gomes Correia, A. (Ed.), A.A. Balkema, Rotterdam, 161-168. [ Links ]
49. HICKS, R. G. & MONISMITH, C. L. 1972. Prediction of the Resilient Response of Pavements Containing Granular Layers Using Non-linear Elastic Theory. Proceedings of the 3rd International Conference on Asphalt Pavements, Vol. 1, 410-429. [ Links ]
50. HICKS, R. G., & MONISMITH, C. L. 1971. Factors Influencing the Resilient Properties of Granular Materials. Hwy. Res. Rec. 345, 15-31. [ Links ]
51. HOFF, I. & NORDAL, R. S. 1999. Constitutive Model for Unbound Granular Materials Based in Hyperelasticity. Unbound Granular Materials - Laboratory Testing, In-situ Testing and Modelling, Gomes Correia editor, Balkema, Rotterdam, 187-196. [ Links ]
52. HOQUE, E. & TATSUOKA, F. 1998. Anisotropy in Elastic Deformation of Granular Materials. Soils and Foundations, Vol. 38, No. 1, 163-179. [ Links ]
53. HOQUE, E., TATSUOKA, F. & SATO, T. 1996. Measuring Anisotropic Elastic Properties of Sand Using a Large Triaxial Specimen. Geotechnical Testing Journal, GTJODJ, Vol. 19, No. 4, 411-420. [ Links ]
54. HORNYCH, P., KASAI, A. & QUIBEL, A. 2000. Modelling of Full Scale Experiment of Two Flexible Pavement Structures. International Symposium on Unbound Aggregates in Roads, 359-367. [ Links ]
55. HORNYCH, P., KAZAI, A. & PIAU, J.-M. 1998. Study of the Resilient Behaviour of Unbound Granular Materials. Proc. BCRA'98, Trondheim, Nordal & Refsdal editor's, Vol. 3, 1277-1287. [ Links ]
56. JANOO, V. C. & BAYER, J. J. 2001. The Effect of Aggregate Angularity on Base Course Performance. Technical Report ERDC/CRREL TR.01-12, Vermont Agency of Transportation, US Army Corps of Engineers, pp. 31. [ Links ]
57. JANOO, V., BAYER, J. J. & BENDA, C. C. 2004. Effect of Aggregate Angularity on Base Material Properties. Journal of Material in Civil Engineering, Vol. 16, No. 6, 614-622. [ Links ]
58. JOUVE, P. & GUEZOULI, S. 1996. Comparison and Harmonized Development of Some Finite Element Programs. Flexible Pavement. Ed. Gomes Correia, Balkema, Rotterdam, 147-163. [ Links ]
59. JOUVE, P. & GUEZOULI, S. 1996a. Evolution and Recommendations for Finite Element Programs. Flexible Pavement. Ed. Gomes Correia, Balkema, Rotterdam, 165-169. [ Links ]
60. JOUVE, P. & ELHANNANI, M. 1994. Application des modèles non linéaires au calcul des chaussées souples. International Bulletin de liaison des Laboratoires des Ponts et Chaussées, No. 190, Paris, 39-55. [ Links ]
61. KALCHEFF, I. V. & HICKS, R. G. 1973. A Test Procedure for Determining the Resilient Properties of Granular Materials. Journal of Testing and Evaluation, JTEVA, Vol. 1, No. 6, 472-479. [ Links ]
62. KAMAL, M. A., DAWSON, A. R., FAROUKI, O. T., HUGHES, D. A. B. & SHA'AT, A. A. 1993. Field and Laboratory Evaluation of the Mechanical Behavior of Unbound Granular Materials in Pavements. Transportation Research Record, 1406, Transportation Research Board, Washington, D. C., 88-97. [ Links ]
63. KARASAHIN, M., DARSON, A. R. & HOLDEN, J. T. 1993. Applicability of Resilient Constitutive Models of Granular Materials for Unbound Base Layers. Transportation Research Record, 1406, Transportation Research Board, Washington, D. C., 98-107. [ Links ]
64. KHEDR, S. 1985. Deformation Characteristics of Granular Base Course in Flexible Pavements. Transportation Research Record, 1043, Transportation Research Board, Washington, D. C., 131-138. [ Links ]
65. KHOGALI, W. E. I. & ZEGHAL, M. 2003. A Comprehensive System for Characterising Granular Materials: Providing Material Input for Pavement Design. Annual Conference of the Transportation Association of Canada, pp. 12. [ Links ]
66. KHOGALI, W. E. I. & ZEGHAL, M. 2000. On the Resilient Behaviour of Unbound Aggregates. Unbound Aggregates in Road Construction, Nottingham, England, 29-34. [ Links ]
67. KIM, SUNG-HEE. 2004. Determination of Aggregate Physical Properties and its Effect on Cross-Anisotropic Behavior of Unbound Aggregate Materials. Ph. D., Thesis, Texas A&M University, pp. 243. [ Links ]
68. KIM, SUNG-HEE; LITTLE, DALLAS N. & MASAD, EYAD. 2005. Simple Methods to Estimate Inherent and Stress-Induced Anisotropy of Aggregate Base. Trasnportation Research Record, 1913, Transportation Research Board, Washington D. C., 24-31. [ Links ]
69. KOLISOJA, P. 1997. Resilient Deformation Characteristics of Granular Materials. Ph. D., Thesis, Tampere University of Technology. [ Links ]
70. KOLISOJA, P., SAARENKETO, T., PELTONIEMI, H. & VUORIMIES, N. 2002. Laboratory Testing of Suction and Deformation Properties of Base Course Aggegates. Transportation Research Record, 1787, Transportation Research Board, Washington D. C., 83-89. [ Links ]
71. KUMAR, P., CHANDRA, S. & VISHAL, R. 2006. Comparative Study of Different Subbase Materials. Journal of Materials in Civil Engineering, Vol. 18, No. 4, 576-580. [ Links ]
72. LASHINE, A. K., BROWN, S. F. & PELL, P. S. 1971. Dynamic Properties of Soils. Department of Civil Engineering, University of Nottingham (England). [ Links ]
73. LEKARP, F. & ISACSSON, U. 2001. The Effects of Grading Scale on Repeated Load Triaxial Test Results. International Journal of Pavement Engineering, Vol. 2, 85-101. [ Links ]
74. LEKARP, F., RICHARDSON, I. R. & DAWSON, A. 1996. Influences on Permanent Deformation Behavior of Unbound Granular Materials. Transportation Research Record, 1547, Transportation Research Board, Washington D. C., 68-75. [ Links ]
75. LEKARP, F., ULF, I. & DAWSON, A. R. 2000. State of the art. I: Resilient Response of Unbound Aggregates. Journal of Transportation Engineering. 126:1, 66-75. [ Links ]
76. LUZIA, R. C. & PICADO - SANTOS, L. 2004. Study of the Unbound Crushed Materials Behavior in Road Pavements. Cyclic Behaviour of Soils and Liquefaction Phenomena, Proc. of CBS04, Bochum, 167-172. [ Links ]
77. MAGNUSDOTTIR, B. & ERLINGSSON, S. 2002. Repeated Load Triaxial Testing for Quality Assessment of Unbound Granular Base Course Material. Proceedings, 9th Nordic Aggregate Research Conference, Reykjavik, Iceland, pp. 5. [ Links ]
78. MAREE, J. H., VAN ZYL, N. J. W. & FREEME, C. R. 1982. Effective Moduli and Stress Dependence of Pavement Materials as Measured in Some Heavy Vehicle Simulator Tests. Transportation Research Record, 852, Transportation Research Board, Washington D. C., 52-60. [ Links ]
79. MASAD, S., LITTLE, D. & MASAD, E. 2006. Analysis of Flexible Pavement Response and Performance Using Isotropic and Anisotropic Material Properties. Journal of Transportation Engineering, Vol. 132, No. 4, 342-349. [ Links ]
80. MAY, R. W. & WITCZAK, M. W. 1981. Effective Granular Modulus to Model Pavement Responses. Transportation Research Record, 810, Transportation Research Board, Washington D. C., 1-9. [ Links ]
81. MOHAMMAD, L. N., PUPPALA, A. J. & ALAVILLI, P. 1994. Influence of Testing Procedure and LVDT Location on Resilient Modulus of Soils. Transportation Research Record, 1462, Transportation Research Board, Washington D. C., 91 - 101. [ Links ]
82. MONISMITH, C. L., SEED, H. B., MITRY, F. G., & CHAN, C. K. 1967. Prediction of Pavement Deflections from Laboratory Tests. Proc., 2nd Int. Conf. Struct. Des. of Asphalt Pavements, 109-140. [ Links ]
83. MOORE, W. M., BRITTON, S. C. & SCRIVNER, R. H. A 1970. Laboratory Study of the Relation of Stress to Strain for a Crushed Limestone Base Material. Texas Transportation Institute, Collage Station, Res. Rept. 99 - 5F. [ Links ]
84. MORGAN, J. R. 1966. The Response of Granular Materials to Repeated Loading. Proc., 3rd Conf., ARRB, 1178-1192. [ Links ]
85. MUHUNTHAN, B., MASAD, E. & ASSAAD, A. 2000. Measurement of Uniformity and Anisotropy in Granular Materials. Geotechnical Testing Journal, Vol. 23, 423-431. [ Links ]
86. NATAATMADJA, A. & PARKIN, A. K. 1989. Characterization of Granular Materials for Pavements. Canadian Geotechnical Journal, 26, 725-730. [ Links ]
87. NEVES, J. M. C. & GOMES CORREIA. 2004. Behaviour of Granular Materials: Field Results versus Numerical Simulations. Proc., of the 6th International Symposium on Pavements Unbound. 97-106. [ Links ]
88. PAPPIN, J. W. & BROWN, S. F. 1980. Resilient Stress Strain Behavior of a Crushed Rock. Proceedings, International Symposium on Soils Under Cyclic and Transient Loading, Swansea, Great Britain, Vol. 1, 169-177. [ Links ]
89. PAPPIN, J. W., BROWN, S. F. & O'REILLY, M. P. 1992. Effective Stress Behaviour of Saturated and Partially Saturated Granular Material Subjected to Repeated Loading. Geotechnique, Vol. 42, No. 3, 485-497. [ Links ]
90. PAUTE, J.-L. & HORNYCH, P. 1996. Influence of Water Content on the Cyclic Behaviour of a Silty Sand. Flexible Pavement. Ed. Gomes Correia, Balkema, Rotterdam, 121-134. [ Links ]
91. PEZO, R. F. 1993. A general method of reporting resilient modulus tests of soils - A Pavement Engineer's Point of View. 72nd Annual Meeting of the TRB. [ Links ]
92. QUECK, U. 1992. Grundlagen zur Berechnung der Spannungs-Verformungszustände Ungebundener Konstruktionschichten als Teil Flexibler Befestigungen im Strassenbau. Dissertation, TU Dresden, Germany. [ Links ]
93. RAAD, L., MINASSIAN, G. H. & GARTIN, S. 1992. Characterization of Saturated Granular Bases under Repeated Loads. Transportation Research Record, 1369, Transportation Research Board, Washington D. C., 73-82. [ Links ]
94. RADA, C. & WITCZAK, W. M. 1981. Comprehensive Evaluation of Laboratory Resilient Moduli Results for Granular Materials. Transportation Research Record, 810, Transportation Research Board, Washington D. C., 23-33. [ Links ]
95. RAHIM, A. M. & GEORGE, K. P. 2005. Models to Estimate Subgrade Resilient Modulus for Pavement Design. International Journal of Pavement Engineering, Vol. 6, 89-96. [ Links ]
96. REYES, F. & RONDÓN, H. A. 2007. Caracterización Mecánica de Granulares de Pavimentos en Triaxiales Cíclicos. Revista Ingeniería de Pavimentos (Actualmente en revisión), Argentina. [ Links ]
97. RONDÓN, H. A. & LIZCANO, A. 2006. Modeling of a Flexible Pavement Structure Applying the Hypoplastic Constitutive Law. GeoCongress 2006, (ASCE) Atlanta (USA). [ Links ]
98. SAUSSINE, G., CHALET C., GAUTIER, P. E., DUBOIS, F., BOHATIER, C. & MOREAU, J. J. 2004. Modelling Ballast under Cyclic Loading Using Discrete Element Methods. Cyclic Behaviour of Soils and Liquefaction Phenomena, Proc. of CBS04, Bochum, 649-658. [ Links ]
99. SEYHAN, U. & TUTUMLUER, E. 2002. Anisotropic Modular Ratios as Unbound Aggregate Performance Indicators. Journal of Materials in Civil Engineering, Vol. 14, No. 5, 409-416. [ Links ]
100. SEYHAN, U., TUTUMLUER, E. & YESILYURT, H. 2005. Anisotropic Aggregate Base Inputs for Mechanistic Pavement Analysis Considering Effects of Moving Wheel Loads. Journal of Materials in Civil Engineering, Vol. 17, No. 5, 505-512. [ Links ]
101. SWEERE, G. T. 1990. Unbound Granular Bases for Roads. Ph. D. Thesis, University of Delft. Netherlands, pp. 429. [ Links ]
102. TACIROGLU, E. & HJELMSTAD, K. D. 2002. Simple Nonlinear Model for Elastic Response of Cohesionless Granular Materials. Journal of Engineering Mechanics, Vol. 128, 969-978. [ Links ]
103. TAKEUCHI, Y., KOYANAGAWA, M., MAKI, T., NISHIZAWA, T. & ENDO, K. 2004. Fundamental Study on Permanent Deformation Analysis of Granular Base Course Material Using Elasto-Plastic Model. Proc., of the 6th International Symposium on Pavements Unbound, 69-78. [ Links ]
104. TAM, W. A. & BROWN, S. F. 1988. Use of the Falling Weight Deflectometer for in situ Evaluation of Granular Materials in Pavements. Journal of Transportation Engineering. Proc., 14th ARRB Conf., Vol. 14, Part 5, 155-163. [ Links ]
105. TATSUOKA, F., ISHIARA, M., UCHIMURA, T. & GOMES CORREIA, A. 1999. Non-linear Resilient Behaviour of Unbound Granular Materials Predicted by the Cross-Anisotropic Hypo-Quasi-Elasticity Model. Unbound Granular Materials - Laboratory testing, In-situ testing and modelling, Gomes Correia editor, Balkema, Rotterdam, 197-206. [ Links ]
106. THEYSE, H. L. 2002. Stiffness, Strength, and Performance of Unbound Aggregate Materials: Application of South African HVS and Laboratory Results to California Flexible Pavements. Report produced under the auspices of the California Partnered Pavement Research Program for the California Department of Transportation. University of California, pp. 76. [ Links ]
107. THOM, N. H., & BROWN, S. F. 1987. Effect of Moisture on the Structural Performance of a Crushed-Limestone Road Base. Transportation Research Record, 1121, Transportation Research Board, Washington D. C., 50-56. [ Links ]
108. THOM, N. H., & BROWN, S. F. 1988. The Effect of Grading and Density on the mechanical Properties of a Crushed Dolomitic Limestone. Proc., 14th ARRB Conf., Vol. 14, Part 7, 94-100. [ Links ]
109. THOMPSON, M. R. & SMITH, K. L. 1990. Repeated Triaxial Characterization of Granular Bases. Transportation Research Record, 1278, Transportation Research Board, Washington D. C., 7-17. [ Links ]
110. TIAN, P., ZAMAN, M. M. & LAGUROS, J. G. 1998. Variation of Resilient Modulus of Aggregate Base and Its Influence on Pavement Performance. Journal of Testing and Evaluation, JTEVA, Vol. 26, No. 4, 329-335. [ Links ]
111. TONG LI & BAUS, R. L. 2005. Nonlinear Parameters for Granular Base Materials from Plate Tests. Journal of Geotechnical and Geoenvironmental Engineering, Vol. 131, No. 7, 907-913. [ Links ]
112. TUTUMLUER, E., LITTLE, D. N. & KIM, S. H. 2003. Validated Model for Predicting Field Performance of Aggregate Base Courses. Transportation Research Record, 1837, Transportation Research Board, Washington D. C., 41-49. [ Links ]
113. TUTUMLUER, E. & THOMPSON, M. R. 1997. Anisotropic Modelling of Granular Bases in Flexible Pavements. Transportation Research Record, 1577, Transportation Research Board, Washington D. C., 18-26. [ Links ]
114. UTHUS, L., HOFF, I., & HORVLI, I. 2005. A Study on the Influence of Water and Fines on the Deformation Properties of Unbound Aggregates. Proceedings, 7th Internacional Conference on the Bearing Capacity of Roads, Railways and Airfields, Trondheim (Norway). [ Links ]
115. UZAN, J. 1985. Characterization of Granular Material. Transportation Research Record, 1022, Transportation Research Board, Washington D. C., 52-59. [ Links ]
116. UZAN, J. 1999. Permanent Deformation of a Granular Base Material. Transportation Research Record, 1673, Transportation Research Board, Washington D. C., 89-94. [ Links ]
117. VAN NIEKERK, A. A., MOLENAAR, A. A. A. & HOUBEN, L. J. M. 2002. Effect of Material Quality and Compaction on the Mechanical Behavior of Base Course Materials and Pavement Performance. 6th International Conference Bearing Capacity of Roads, Railways and Airfields, 1071-1081. [ Links ]
118. VAN SCHELT, W., VOS, E., GALJAARD, P. J. & HENDRIKS, M. A. N. 1996. The Non-linear Elastic Model of Boyce: An Evaluation of the Model in the FEM-Program DIANA. Flexible Pavement. Ed. Gomes Correia, Balkema, Rotterdam, 201-206. [ Links ]
119. WERKMEISTER, S. 2003. Permanent Deformation Behaviour of Unbound Granular Materials in Pavement Constructions. Ph. D., thesis, University of Technology, Dresden, pp. 189. [ Links ]
120. WERKMEISTER, S., DAWSON, A. & WELLNER, F. 2001. Permanent Deformation Behaviour of Granular Materials and the Shakedown Concept. Transportation Research Record, 1757, Transportation Research Board, Washington D. C., 75-81. [ Links ]
121. WERKMEISTER, S., NUMRICH, R., DAWSON, A. & WELLNER, F. 2002. Deformation Behaviour of Granular Materials under Repeated Dynamic Load. Journal of Environmental Geomechanics - Monte Veritá, 215-223. [ Links ]
122. WOLFF, H. 1992. Elasto-Plastic Modelling of Granular Layers. Research Report RR92/312, Department of Transport, South Africa. [ Links ]
123. WOLFF, H. & VISSER, A. T. 1994. Incorporating Elasto - Plasticity Granular Layers Pavement Design. Proc.Instn. Civil Engineering Transportation, 105, 259-272. [ Links ]
124. ZAMAN, M., CHEN, D. & LAGUROS, J. 1994. Resilient Moduli of Granular Materials. Journal of Transportation Engineering, Vol. 120, No. 6, 967-988. [ Links ]
125. ZEGHAL, M. 2000. A Discrete Element Study of the Resilient Behavior of Granular Materials. 14th ASCE Engineering Mechanics Conference, Austin - Texas, pp. 5. [ Links ]
126. ZEGHAL, M. 2004. Discrete-Element Method Investigation of the Resilient Behavior of Granular Materials. Journal of Transportation Engineering. Vol. 130, 503-509. [ Links ]
127. ZEGHAL, M. 2003. Effect of Compaction on the Resilient Behaviour of Granular Materials: an Analytical Study. 16th ASCE Engineering Mechanical Conference, University of Washington, Seattle, pp. 3. [ Links ]
Recibido: 03/03/2007
Aceptado: 24/09/2007