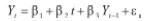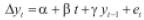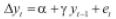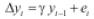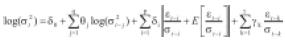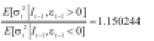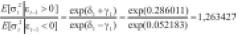Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Ingenierías Universidad de Medellín
Print version ISSN 1692-3324On-line version ISSN 2248-4094
Rev. ing. univ. Medellin vol.6 no.11 Medellín July/Dec. 2007
ESTUDIO DE EFECTOS ASIMÉTRICOS Y DÍA DE LA SEMANA EN EL ÍNDICE DE VOLATILIDAD 'VIX'1
STUDY OF ASYMMETRIC AND DAY OF THE WEEK EFFECTS IN 'VIX'* VOLATILITY INDEX
Pilar Beatriz Álvarez Franco2; Diego Alexánder Restrepo3; Fredy Ocaris Pérez4
2 Ingeniera Financiera de la Universidad de Medellín. Contacto: pbalvarez@valoresbancolombia.com
3 Docente del Departamento de Finanzas de la Universidad EAFIT. Contacto: drestr16@eafit.edu.co
4 Docente de Ingeniería Financiera de la Universidad de Medellín. Contacto: foperez@udem.edu.co
1Este artículo es derivado del proyecto de investigación 'Modelación de la volatilidad condicional heteroscedástica de series de tiempo financieras', financiado por la Vicerrectoría de Investigaciones de la Universidad de Medellín.
Resumen
En este trabajo se estudian los efectos asimétricos y día de la semana en el Índice de Volatilidades VIX de la Chicago Board Option Exchange del 02/01/2003 al 30/03/2007. Se utilizan modelos GARCH asumiendo innovaciones gaussianas, t-student y de la distribución generalizada de los errores (GED). Para las innovaciones gaussianas se utiliza el método de Quasi Máxima Verosimilitud. Se encuentra que un modelo EGARCH(1,1) y un modelo TGARCH con regresores exógenos para el día lunes e innovaciones con distribución GED y t-Student, respectivamente, se ajustan bien a los datos. Ambos modelos indican que existen efectos asimétricos en la serie y que en el día lunes la volatilidad del mercado medida con el VIX es mayor que en los demás días. Dado que en la literatura se encuentra que los días lunes los rendimientos son menores, estos resultados apoyan la hipótesis de que los rendimientos de los activos financieros están correlacionados negativamente con su volatilidad.
Palabras clave
Modelos GARCH, efectos asimétricos, VIX, efecto día de la semana.
Abstract
In this work, we study asymmetric and day of the week effects in the Chicago Board Option Exchange's Volatility Index -VIX- from 01/02/2003 to 03/302007. We use GARCH models assuming Gaussian, t-Student and Generalized Error Distribution (GED) innovations. To Gaussian innovations, we use the Quasi-Maxima-Likelihood Method. The results show evidence in favor of asymmetric and day of the week effects. An EGARCH model with GED errors and a TGARCH model with t-Student Distribution fit well the data. We used exogenous variables for the mean of the process, representing the first day of the week, to explore the day of the week effects. Our results suggest that on Mondays the market volatility is higher than in other days. This supports the thesis that returns are negatively correlated with volatility.
JEL Classification: C52, C53, G10, G32
Key Words
GARCH Models, Asymmetric Effects, Day of the Week Effect, Volatility Index, VIX.
INTRODUCCIÓN
La modelación de series financieras y en especial de su volatilidad es un campo de creciente investigación en finanzas (Engle, 2004; Christoffersen y Diebold, 2000; Andersen et al. 2003; Fleming, Kirby y Ostdiek, 2001). La presencia de efectos asimétricos y de día de la semana en estas series ha sido documentada extensamente en la literatura (Engle y Ng, 1993; Rabemananjara y Zakoian, 1993; Zakoian, 1994; Nelson, 1991; Glosten, 1993; Braun, Nelson y Sunier, 1995 ; Field, 1931; French, 1980; Cross, 1973; Chen y Singal, 2003; Chan et al. 2004; Aggarwal y Rivoli, 1989; Arsad Coutts, 1997; Chang, Pinegar y Ravichandran, 1993; Mehdian y Perry, 2001.). Estos estudios muestran que la distribución de los rendimientos de precios de activos está en función del día de la semana y, además, presentan reacciones asimétricas en su volatilidad, dependiendo de la dirección que tomen los precios.
Este artículo se centra en la modelación de la media y la varianza del Índice VIX, utilizando modelos de series de tiempo ARIMAX, GARCH, TGARCH; EGARCH, GARCH-M y PGARCH. El índice de volatilidad de la CBOE (Chicago Board Option Exchange) 'VIX' es un indicador que mide de cerca las expectativas de volatilidad del mercado del S&P500. Es calculado utilizando información en tiempo real de las cotizaciones, tanto de compra como de venta, del mercado de opciones sobre el S&P500. Para su cálculo se usan las opciones con los dos vencimientos más cercanos superiores a ocho días, y luego se pondera para hacerlo equivalente a una volatilidad esperada para los próximos 30 días. El índice se cotiza en puntos porcentuales, tal como se publica una desviación estándar, por ejemplo, el día 30 de marzo del 2007 el índice cerró en 14.64, que equivale a una volatilidad del 14,64%.
El cálculo del índice es independiente de cualquier modelo de valoración; usa una fórmula que promedia los precios ponderados de las opciones at-the-money y out-the-money, puts y calls para derivar la volatilidad esperada. La fórmula del VIX separa la volatilidad esperada de otros factores que afectan el precio de las opciones, tales como cambios en el precio del subyacente, pago de dividendos, tasas de interés y tiempo al vencimiento. De esta forma, el VIX ofrece una manera para que los inversionistas transen volatilidades simple y directamente sin tener que lidiar con otros factores de riesgo, que de otra forma podrían tener un impacto en el valor de las posiciones en opciones sobre el S&P500. Por esta razón, el índice es utilizado como una medida aproximada de la evolución de la volatilidad en el mercado y, consecuentemente, del nivel de aversión al riesgo de los inversionistas.
Conocer el comportamiento del VIX y hacer pronósticos sobre el mismo ha sido un objeto de estudio en años recientes, debido a la posibilidad de inferir las expectativas del mercado sobre su evolución en el corto plazo. En este trabajo se pretende establecer si el VIX presenta efectos asimétricos (apalancamiento) y de día de la semana. Este último efecto está asociado a que la volatilidad es más alta en algunos días de la semana, sobre todo en aquellos donde existe una acumulación de información superior a la de otros días, atribuible a diferentes factores. Los resultados del trabajo permiten que el mismo contribuya a la literatura existente sobre la correlación negativa entre los rendimientos y la volatilidad de los activos financieros.
El artículo se divide en cuatro partes. La primera presenta una revisión de la literatura sobre efectos día de la semana y asimétricos en la varianza de las series de tiempo financieras, así como los principales estudios realizados sobre el VIX. La segunda revisa la teoría a los modelos de series de tiempo utilizados en este estudio. La tercera parte muestra los datos y e ilustra la metodología empleada. La cuarta parte presenta los resultados del trabajo, y por último se presentan las principales conclusiones. En los anexos se presentan algunos resultados que apoyan la investigación.
REVISIÓN DE LA LITERATURA
Efecto día de la semana
Un hecho estilizado sobre los rendimientos de los activos financieros ampliamente documentado es que los mismos varían en función de los días de la semana. Fields (1931) investiga si los rendimientos de los días que preceden un día festivo son más bajos que los demás días de la semana. Una posible explicación a este fenómeno es que los especuladores prefieren cerrar sus posiciones en dichos días para no soportar la incertidumbre asociada a los días en que los mercados permanecen cerrados. Sin embargo, Fields no encuentra evidencia que soporte dicho argumento. Cross (1973) y French (1980) estudian este efecto sobre el índice S&P500. En sus estudios encuentran que, en promedio, los días lunes tienen un rendimiento negativo y que los días miércoles y viernes presentan los mayores rendimientos. Thaler (1987) documenta que en los meses de enero los rendimientos tienden a ser más altos que en los demás meses del año. Wang et al. (1997) reportan que los rendimientos tienden a ser negativos los días lunes e inferiores a los de los demás días de la semana.
Rogalski (1984) encuentra que los menores rendimientos de los días lunes se deben a que el precio de apertura de ese día es menor que el precio de cierre del día viernes. Durante los días lunes, en promedio, los precios suben desde el precio de apertura hasta el de cierre. Por esta razón, el efecto atribuido al día lunes se convierte en un efecto atribuible a los fines de semana. Este autor también encuentra que dicho efecto tiende a revertirse en los fines de semana de enero. El efecto lunes se presenta también en los mercados de renta fija. Gibbons y Hess (1981) encuentran que los días lunes los rendimientos sobre los T-Bill son significativamente menores que en otros días. Otros estudios reportan efectos similares en los mercados de futuros (Dyel y Marbely, 1986). Jaffe y Westerfield (1985) encuentran que los retornos para los mercados accionarios japonés y australiano son menores los días martes.
Otros estudios, en línea con los anteriores, encuentran que el efecto lunes o de fin de semana es significativo para la mayoría de los mercados donde se ha investigado5. No obstante, Dubois y Louvet (1996) reportan que en los años más cercanos y anteriores a 1992 dicho efecto desapareció en el mercado americano. Recientemente, y dada la importancia de los mercados de productos derivados, la investigación sobre el efecto día de la semana se ha trasladado al cambo de la volatilidad de los rendimientos. Berument y Kyimaz (2001) aportan evidencia acerca de que la volatilidad de los rendimientos de los activos financieros está en función de los días de la semana. Estos autores encuentran que ambos efectos se encuentran presentes en el índice S&P500 entre 1973 y 1997.
La mayoría de los efectos investigados sobre la volatilidad se refieren a los efectos asimétricos, no obstante, los efectos debidos a los días de la semana en la ecuación de la volatilidad no habían sido estudiados hasta el trabajo de Berument y Kyimaz (2001). La aproximación de Berument y Kyimaz implica utilizar modelos ARMAX-GARCH para estimar la ecuación de la media y de la varianza de los rendimientos logarítmicos diarios del S&P500. Para capturar el efecto del día de la semana incluye variables dummy para cada día, tanto en la ecuación de la media como en la de la varianza. Sus resultados indican que los días lunes hay un menor rendimiento que los días viernes. En el día miércoles se observa el mayor rendimiento promedio. Así mismo, documentan que los días viernes se presenta la mayor volatilidad y los días miércoles y jueves la menor. No se encuentra evidencia sobre efectos asimétricos en la volatilidad.
Efectos asimétricos en la volatilidad
La literatura sobre los efectos asimétricos en los rendimientos de los activos financieros ha tomado un gran impulso en los últimos años. Este efecto se refiere a que los retornos y la volatilidad de los mismos se correlacionan negativamente. Sin embargo, la evidencia empírica al respecto es mixta. French, Schwert y Stambaugh (1987), Campbell y Hentschel (1992) encuentran que dicha correlación es positiva. De otro lado, Turner, Startz y Nelson (1989), Glosten, Jannathan y Runkle (1993) y Nelson (1991) encuentran que la correlación es negativa.
El efecto de asimetría se relaciona con el efecto apalancamiento. No obstante, como señalan Bekaert y Wu (2000) y Wu (2001), la asimetría en la ecuación de la varianza que tienen los choques negativos respecto a los positivos sobre la misma no se explica enteramente por el efecto apalancamiento. Existen otras variables difíciles de identificar que tienen el mayor impacto en la misma. Sin embargo, determinar si el efecto asimétrico se debe al apalancamiento o no ha quedado en un segundo plano, pues es más importante conocer el efecto en sí mismo. Como señalan Poon y Granger (2003), estudios recientes demuestran que la autocorrelación de la volatilidad tiende a aumentar en épocas de mercados bajistas y crisis financieras. Los modelos TGARCH de Glosten et al. (1993) y los EGARCH de Nelson (1991) capturan adecuadamente los efectos asimétricos presentes en la volatilidad de los rendimientos financieros.
Brooks, Henry y Persand (2002) utilizan modelos asimétricos para evaluar su importancia en el establecimiento de ratios de cobertura con futuros financieros. Encuentran que dichos modelos se desempeñan de forma superior a los modelos no simétricos para coberturas dentro de la muestra. Sin embargo, no hay una mejora significativa en coberturas por fuera de muestra.
Modelación del VIX
La literatura sobre modelos de series de tiempo aplicados al índice VIX es amplia. Recientemente, Bali y Weinbaum (2007) realizan la modelación del índice VIX introduciendo los modelos de volatilidad condicional extrema (EVT) y modelos GARCH. Su trabajo se centra en la habilidad de estos modelos para pronosticar la evolución del VIX en el corto plazo. Encuentran que los modelos EVT superan los pronósticos con los modelos GARCH más utilizados en la literatura.
Majmudar y Baneerjee (2004) modelan el VIX con diferentes modelos APGARCH y casos específicos del mismo. Utilizan datos diarios de cierre del VIX desde 1990 hasta 2003. Encuentran que el modelo EGARCH se desempeña mejor que sus competidores para pronosticar el VIX. Dong (2006) utiliza modelos GARCH y redes neuronales para pronosticar el VIX desde abril de 1990 hasta junio de 2006. Concluye que los modelos de pronóstico con base en redes neuronales son más exactos. Fernandes, Medeiros y Scharth (2006) examinan las propiedades estadísticas del VIX utilizando modelos de árboles de transición suavizada autorregresiva (STAR) y modelos no lineales de procesos autorregresivos heterogéneos (HAR) conjuntamente con modelos ARIMA y ARFIMA. Encuentran que los modelos STAR tienen un mejor desempeño en el pronóstico del VIX.
Engle y Gallo (2002) aplican modelos GARCH para modelar el VIX, reportan que dichos modelos se desempeñan bien y son de utilidad en la predicción del VIX para periodos cortos de tiempo. En su estudio, combinan modelos GARCH con un modelo de errores multiplicativo, es decir, el VIX es un proceso aleatorio producto de un factor escalar (que depende de los datos más recientes de la serie) y una variable estandarizada aleatoria positiva y de variables exógenas; los errores se distribuyen según una distribución gamma.
De otro lado, en un estudio similar, Cecconi, Gallo y Lombardi (2002) investigan qué modelos se ajustan mejor en la predicción del VXN, un índice similar al VIX pero para el mercado NASDAQ. En este estudio, los resultados permiten soportar que los modelos GARCH son adecuados para capturar las características de la volatilidad de este índice, incluso en tiempos de turbulencias.
Awartani y Corradi (2003) estudian la capacidad de los modelos GARCH para pronosticar la volatilidad del VIX para diferentes horizontes de tiempo haciendo hincapié en los efectos asimétricos. Encuentran que los modelos GARCH (1,1) tienen un desempeño inferior a los modelos TGARCH (1,1) para pronósticos de un periodo. Encuentran lo mismo para horizontes de pronóstico más amplios, no obstante, el componente de asimetría no parece tener tanto efecto como en el caso del pronóstico para un solo periodo. El modelo GARCH se desempeña bien ante otros modelos que no incluyen efectos asimétricos.
Ahoniemi (2006) modela la volatilidad implícita del VIX con el propósito de obtener pronósticos que sirvan para la transacción de opciones en el mercado. El ajuste de los pronósticos se evalúa contra alternativas de inversión basada en simulación para establecer el precio estimado de las opciones. Encuentra que un modelo ARIMA (1,1,1) con regresores exógeneos como el S&P500 y el MSCI tiene poder predictivo respecto a la dirección que toma el VIX. Este modelo predice la dirección correcta del VIX en el 60% de las veces. Estrategias basadas en los pronósticos para 15 meses reportan rendimientos positivos.
Becker et al. (2005) aplican varios modelos de la familia GARCH a la predicción de la volatilidad implícita en el índice VIX. El propósito de su estudio era determinar si la información no atribuible a los pronósticos basados en dichos modelos era relevante para ser considerada en la evolución futura del índice. Encuentran que dichos pronósticos no contienen información diferente a la reflejada en las series históricas.
Ogus (2002) pone a prueba la ineficiencia de los mercados de opciones sobre el S&P500 utilizando estrategias de inversión basadas en pronósticos con modelos GARCH. Encuentra que, al controlar por costos de transacción, dichas estrategias generan rendimientos positivos. Resalta que los modelos GARCH se desempeñan bien debido a su flexibilidad para incorporar efectos asimétricos y no lineales en la volatilidad. En línea con estos hallazgos, Rubio y Moroni (2004) encuentran que los modelos GARCH aplicados a índices como el VIX mejoran la capacidad de predicción de la volatilidad.
En la revisión de la literatura no se encontraron estudios que analicen conjuntamente los efectos asimétricos y de día de la semana para el VIX. Este estudio pretende contribuir a la literatura internacional sobre este aspecto.
MODELOS DE VOLATILIDAD CONDICIONAL GENERAL AUTORREGRESIVOS
En este trabajo se eligen algunos modelos a priori para capturar el comportamiento del VIX y a continuación se procede con su validación. Estos modelos son ampliamente utilizados en la literatura y se conocen con la denominación de modelos de heteroscedasticidad general autorregresivos GARCH (p,q)6. Se utilizan principalmente para modelar la varianza del proceso analizado (Tsay, 2002).
Modelos GARCH
Los modelos GARCH(p,q) tienen la siguiente especificación:
El orden 'p' está asociado a la dependencia temporal de la varianza de la serie con los choques aleatorios al cuadrado ocurridos 'p' periodos atrás. El orden 'q' de la ecuación de la varianza está asociado a la dependencia temporal de la misma en el periodo 't' al valor que haya tomado en 'q' periodos anteriores. Los errores cumplen con las condiciones αt convencionales de independencia y distribución con media cero y varianza constante. Los εt corresponden a los errores para la ecuación de la media condicional, los cuales claramente dependen de la volatilidad condicional del proceso.
Los modelos ARCH (p) son un caso especial de los modelos GARCH (p,q) y vienen definidos por la siguiente ecuación:
En este caso, la varianza condicional del proceso depende de los choques aleatorios en periodos pasados. El parámetro δ0 debe ser mayor que cero y los δi deben ser mayores o iguales a cero. La suma de todos los parámetros debe ser inferior a la unidad para garantizar la condición de estacionariedad de la varianza. La distribución de los errores αt es desconocida, pero normalmente se asume normal o t-Student.
Para el caso del modelo GARCH (p,q) se deben cumplir las mismas restricciones sobre los parámetros, incluyendo aquellos asociados a la varianza condicional de periodos pasados. En estos modelos, la esperanza y la varianza incondicionales vienen dadas por las siguientes expresiones:
La media incondicional es cero y la varianza incondicional es constante y diferente de cero cuando se cumplen las restricciones sobre los parámetros. La media condicional y la varianza condicional del GARCH(p,q) vienen dadas por las siguientes expresiones:
Extensiones de los modelos GARCH han sido propuestas por diferentes autores. A continuación se presenta la especificación de los modelos de Glosten et al. (1993) y Nelson (1991) que se utilizarán en este estudio.
Modelos TGARCH
Los modelos Threshold GARCH (T-GARCH) (GJR, 1993) tienen la siguiente especificación:
Donde:
I - t-k=1 si εt < 0 y 0 en otro caso.
En este modelo las 'buenas' εt - i > 0 y las 'malas' noticias εt - i < 0, tienen efectos diferentes en la varianza condicional; las 'buenas' noticias tienen un impacto δi, mientras que las 'malas' tienen un impacto δi + γk si γk> 0. De esta forma las malas noticias incrementan la volatilidad y se dice que hay un efecto apalancamiento de orden i-th. Es decir si γi ≠ 0, el impacto de las noticias es asimétrico7.
Modelos EGARCH
Los modelos EGARCH o GARCH exponenciales nacen a partir de la publicación de Nelson (1991) sobre heteroscedasticidad condicional en los modelos de rentabilidad de activos. Dicho autor propone una nueva forma funcional a partir de la observación de las deficiencias de los ya ampliamente actualizados modelos tipo ARCH. En su artículo critica tres elementos de los procesos ARCH: 1) Las restricciones de no negatividad de los parámetros son difíciles de lograr en muchas ocasiones, 2) los modelos GARCH no permiten estimar convenientemente el efecto de apalancamiento financiero que aparece en la realidad. 3) los modelos GARCH Integrados, IGARCH, son difíciles de llevar a la práctica, siendo confuso el término de persistencia en varianza condicional, cuestionamiento planteado por Engle y Bollerslev (1986).
Nelson propone una nueva especificación más general sobre la varianza condicional heteroscedástica que da nombre a los GARCH exponenciales o EGARCH (p,q). Dicha especificación de la varianza condicional trata de capturar la asimetría existente entre los retornos positivos y los negativos; esto se conoce como efecto apalancamiento. Estos modelos tienen la siguiente especificación general:
El lado izquierdo de la ecuación es el logaritmo de la varianza condicional. Lo anterior implica que el efecto apalancamiento es exponencial en vez de cuadrático, a diferencia de lo que sucede en los modelos TGARCH. En consecuencia, los pronósticos de la varianza condicional serán siempre no negativos. La presencia de efecto apalancamiento puede ser probada bajo la hipótesis nula de γk = 0 contra la alternativa γk< 0. El impacto es asimétrico si γk ≠ 0. Cuando εt -k es negativo y γk< 0 la varianza será mayor que cuando γk > 08.
Otro de los grandes aportes del artículo de Nelson (1991) sobre los modelos EGARCH hace referencia a la función de distribución de la perturbación aleatoria. Con frecuencia, las series a las que se aplica el modelo tipo ARCH muestran una distribución con mayor apuntamiento que el de una normal y con colas 'más gruesas'. Es por ello que se plantea aquí una forma tal que la función de densidad del proceso admita, como caso especial, una distribución normal; pero que, al tiempo, permita otros tipos de funciones. El autor propone emplear la función de distribución GED: Generalized Error Distribution (distribución generalizada de las perturbaciones); la función de densidad de la GED se define como
Donde Γ(·) es la función gamma, λ = [2(-2/v) Γ (1 / υ) / Γ (3 / υ)]1/2 y υ es el parámetro que determina si la función de densidad de las perturbaciones es de colas gruesas. Cuando υ = 2, las perturbaciones se distribuyen como una normal. Si υ < 2, la distribución de los errores tiene colas más gruesas que las de la normal (por ejemplo, si υ = 1, la distribución es una exponencial doble) y, para υ > 2, la distribución de los errores es de colas más delgadas que las de la normal (por ejemplo, si υ → ∞, la distribución de los errores es una uniforme en el intervalo (-31/2, 31/2).
Modelos GARCH en Media, GARCH-M
Otros modelos de gran importancia son los modelos GARCH-M, los cuales tienen la siguiente especificación:
Como se observa, la varianza de los retornos se involucra en la ecuación de la media para representar que éstos están relacionados linealmente con el riesgo. Algunas variantes de este modelo especifican la ecuación de la media de la siguiente manera:
Donde la desviación y el logaritmo de la varianza entran en la ecuación de la media.
La ecuación de la varianza condicional de estos modelos es la siguiente:
Donde los parámetros y las variables tienen la interpretación habitual. La especificación general de este modelo permite incluir parámetros que recojan la asimetría debida al apalancamiento tal como en los modelos T-GARCH y EGARCH.
Modelos Power GARCH, PGARCH
Los modelos Power GARCH, PGARCH, tienen la siguiente especificación:
La diferencia con los modelos GARCH radica en que el parámetro γ (Power) no se asume igual a 2, sino que se estima conjuntamente con los demás. Si γ = 2 los modelos GARCH son un caso especial y comparte con estos todas las extensiones posibles.
DATOS Y METODOLOGÍA
La serie de datos del VIX comprende 1069 observaciones del valor de cierre para los días hábiles entre lunes y viernes desde el 02/01/2003 hasta el 30/03/2007. Los datos se extrajeron de la CBOE y todos corresponden a la nueva metodología de cálculo del VIX implementada por dicha entidad. Los regresores exógenos son variables dummys construidas para indicar el día de la semana.
La metodología utilizada corresponde a la empleada por Box y Jenkins (1974), Engle (1982) y Bollerslev (1986). En primer lugar se analiza la estacionariedad de la serie y posteriormente se procede a estimar por máxima verosimilitud el modelo ARIMA que mejor se ajuste al proceso generador de datos. Para la modelación de la varianza se utiliza la estimación por máxima verosimilitud y quasi máxima verosimilitud - QML propuesta por Bollerslev y Wooldridge (1992) cuando se asumen errores gaussianos9. Ante la presencia de exceso de curtosis y distribuciones de los retornos del VIX con colas pesadas se estiman los modelos asumiendo errores t-student y de la Función Generalizada de Errores (GED).
Se estiman varias alternativas de modelos GARCH, PGARCH, APGACH, TGARCH y EGARCH y se selecciona el mejor modelo con base en los criterios de información de Akaike y Schwarz.
RESULTADOS
Comportamiento del S&P500 y el VIX
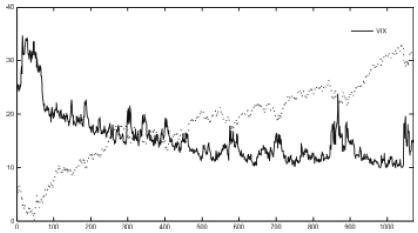
Durante largos períodos de tiempo el VIX y el S&P500 han presentado una alta correlación negativa (-0.84) como puede observarse en el gráfico 1.
En los periodos en los que el S&P500 aumenta (disminuye) la volatilidad se reduce (aumenta). Lo anterior es un hecho empírico que se corrobora fácilmente. Además, cuando el mercado experimenta una caída, el VIX reacciona más fuertemente que cuando experimenta un aumento; esto se conoce como el efecto apalancamiento es uno de los hechos que se investiga en este trabajo.
Fuente: Elaboración de los autores
Grafico 1. Serie VIX vrs Serie S&P
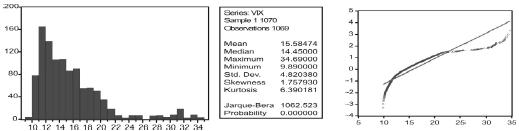
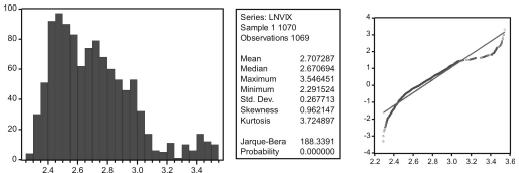
En los gráficos A1 y A2 de los anexos se muestran los histogramas de frecuencias del VIX y del logaritmo natural del VIX (LNVIX). Asimismo, se presentan las estadísticas descriptivas más importantes y el gráfico Quantile-Quantile correspondiente contra su contraparte teórica de una distribución normal.
Como puede observarse, el estadístico Jarque Bera rechaza la hipótesis nula de que el VIX o el LNVIX se distribuyan según una distribución normal. Los gráficos Q-Q corroboran esta aserción, dado que su forma empírica se aleja significativamente de la línea teórica asociada a la distribución normal. En el histograma de frecuencias se puede notar que existen valores atípicos en la cola derecha de la distribución, lo cual puede indicar que asumir innovaciones gaussianas para las perturbaciones de los modelos puede subestimar la probabilidad de observar estos valores atípicos. En este caso, si los modelos derivados se utilizan para el cálculo de la volatilidad se estaría subestimando la misma.
Identificación de los modelos ARIMA-GARCH
El gráfico A3 en los anexos presenta la relación entre el rango y la media de los rendimientos logarítmicos del VIX. Este gráfico se utiliza para determinar si la serie es estacionaria en varianza. Como se observa los valores se encuentran muy dispersos, lo cual es un indicador de la no estacionariedad en varianza, por tanto se decide aplicar una transformación Box-Cox y trabajar con la serie en logaritmos naturales. En ese gráfico se evidencia que a medida que aumenta la media, aumenta la dispersión, por lo tanto, la serie no es estacionaria en varianza y apoya la elección de tomar logaritmos naturales para estabilizarla.
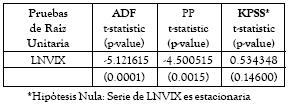
Las pruebas de raíz unitaria para determinar estacionariedad10 en media que se utilizaron fueron las de Dickey y Füller, Phillips y Perron (1988) y Kwiatkowski et al. (1992) (KPSS). En el anexo B se presenta cómo se implementa el Test de Dickey y Fuller estándar (Diekey y Füller, 1979). La tabla A1 presenta los resultados de las pruebas. Como se detalla en el anexo B, dado que la serie del LNVIX es estacionaria en tendencia, se procedió a crear una variable Wt = LNVIX - ( β0 + β1t) que fuera estacionaria en media. El mejor modelo que se ajusta a esta variable Wt es un AR (9) con rezagos estadísticamente significativos de orden uno y nueve.
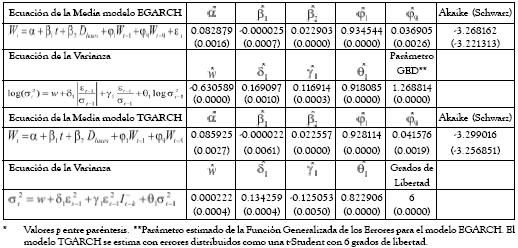
Según los criterios de información de Akaike y Schwarz, los mejores modelos que permiten estimar la volatilidad condicional heteroscedástica son un ARMAX-EGARCH(1,1) y un ARMAX-TGARCH(1,1) los cuales se presentan en la tabla 111. No se encontró evidencia a favor de los modelos GARCH-M y PAGARCH, otros modelos estimados se presentan en la tabla A2 del anexo C.
Tabla 1. Modelos ARMAX-EGARCH y TGARCH con el mejor ajuste.*
De acuerdo con los criterios de información de Akaike y Schwarz el mejor modelo sería el TGARCH (1,1). No obstante, como se muestra más adelante, en los pronósticos extramuestrales el modelo EGARCH produce un error cuadrático medio menor.
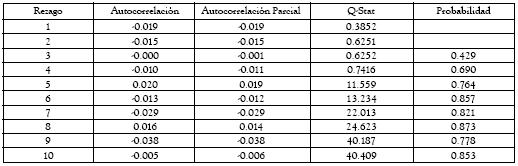
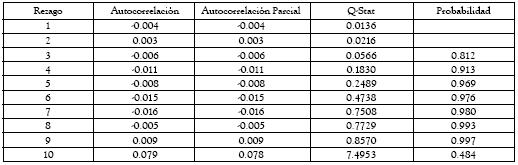
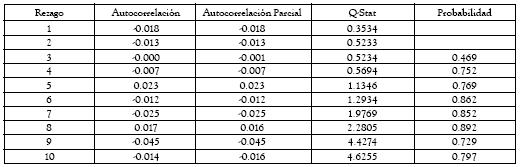
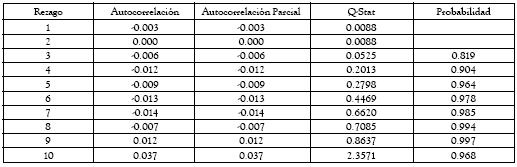
Todos los modelos se validaron según los procedimientos convencionales. Las tablas A4a, A4b, A5a, A5b, A6 y A7 presentan las pruebas de Ljung-Box y LM para los residuales de los modelos EGARCH y TGARCH. Como se puede apreciar, las especificaciones de los modelos en la tabla 1 cumplen con los supuestos básicos exigidos. Por consiguiente, a partir de dichos modelos se pueden inferir los resultados que se presentan en la siguiente sección.
Asimetría y efecto día de la semana en el VIX
El índice VIX presenta respuestas asimétricas en la ecuación de la varianza; esto se debe a que γ1 ≠ 0 para los modelos estimados. De acuerdo al modelo TGARCH, I -t-1= 1 si εt< 0 y 0 en otro caso. Así, cuando εt-1 > 0 y εt-1< 0, se tendrán respuestas diferentes en la varianza condicional del VIX. Tratándose del VIX, el cual es una medida de la volatilidad del mercado de opciones sobre el S&P500, una buena (mala) noticia se asocia al hecho de que la volatilidad disminuya (aumente), es decir a que el índice VIX caiga (suba). Así, una buena noticia ocurre cuando εt-1< 0 y una mala noticia cuando εt-1> 0, pues si εt-1< 0 implica que I -t-1= 1, y dado que γ1 = -0.125053 el impacto será de (δ1 + γ1 )ε2t-1 = (0.134259 - 0.125053)ε2t-1 = 0.009206ε2t-1. De otro lado, si εt-1> 0 esto implica que I -t-1= 0 y el impacto en la varianza condicional será igual a δ1ε2t-1 = 0.134259ε2t-1. Por esta razón, cuando hay un impacto positivo al VIX (el VIX sube), la volatilidad será aproximadamente 15.0244% superior que cuando el impacto es negativo (el VIX baja)12.
Según el modelo EGARCH, γ1 = 0.116914. Así, cuando εt-1> 0 la varianza condicional del VIX será mayor, pues en este caso, el parámetro γ1 se encuentra multiplicado por εt-1 y no por ε2t-1. Este resultado es análogo al del modelo TGARCH. Cuando las noticias son favorables, εt-1< 0 el impacto es menor. Por lo anterior, en el modelo EGARCH cuando el VIX sube, la volatilidad será aproximadamente un 26,3427% superior a cuando el VIX baja13.
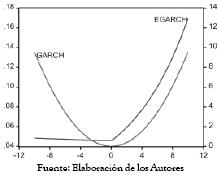
El gráfico 2 presenta el efecto asimétrico que tiene la volatilidad condicional del VIX ante impactos positivos y negativos del mismo tamaño con el modelo EGARCH. En estos se observa fácilmente como los choques positivos conllevan a una mayor varianza condicional. También se observa que en el modelo GARCH (1,1), los choques aleatorios negativos dan como resultado una varianza que es simétrica respecto a la existencia de choques positivos. Con base en lo anterior, y dado que el parámetro de asimetría resulta ser significativo, el modelo EGARCH es capaz de capturar el efecto asimétrico en la volatilidad que presentan los choques (noticias) positivos o negativos. Si se utiliza un modelo simétrico se estaría subvalorando y sobrevalorando consistentemente.
Fuente: Elaboración de los Autores
Gráfico 2. Efecto asimétrico modelo EGARCH
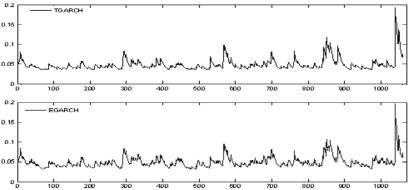
Los gráficos 4 y 5 muestran las series de la volatilidad condicional del VIX con los modelos estimados. Como se aprecia en dichos gráficos, el comportamiento de la volatilidad con ambos modelos es similar. La media de la volatilidad con el modelo EGARCH es de 2.13% diaria, lo que equivale aproximadamente a 33.67% anual. Para el modelo TGARCH es de 3.64% y 57.496%, respectivamente. La volatilidad medida como la desviación estándar histórica del VIX es de 4.82% diaria y 76.22% anual. La diferencia entre los modelos EGARCH y TGARCH se debe principalmente al mayor efecto que tiene en una y otra serie la asimetría en la varianza condicional.
Fuente: Elaboración de los autores
Gráficos 4 y 5. Volatilidad condicional del VIX con los modelos TGARCH y EGARCH
El día en que la volatilidad del VIX es más alta corresponde al 27 de febrero de 2007.
Ahora, la ecuación de la media de ambos modelos tiene la misma estructura. Sin embargo, el valor de los parámetros asociados a cada variable difiere levemente. Según los modelos estimados, el valor del VIX en el tiempo t depende positivamente del valor que toma el día anterior y nueve días hacia atrás. Es importante ver, que el impacto del día anterior es bastante alto, cercano a 0.93, lo cual indica una alta dependencia del valor del día anterior, pero no así del valor de nueve días antes.
El fenómeno más interesante de analizar es el impacto que sobre el valor del índice tiene el día de la semana. En ambos modelos estimados, el parámetro asociado al día lunes es estadísticamente significativo e igual a 0.02290314. Lo anterior indica que el valor del VIX tiende a ser mayor en los días lunes respecto a los demás días de la semana. De acuerdo con la revisión de la literatura, se encuentra evidencia a favor de que los días lunes los rendimientos de los activos financieros tienden a ser negativos, además, los días lunes en promedio dichos rendimientos son menores que en los demás días de la semana. Así, es de esperarse que si la hipótesis de la correlación negativa entre los rendimientos y la volatilidad de los activos financieros se cumple, los días lunes exista una mayor volatilidad en comparación con los demás días de la semana.
Los resultados de este trabajo presentan evidencia a favor de dicha hipótesis, pues, dado que el VIX es una medida aceptada de la volatilidad del mercado, el hecho de que el día lunes el índice tiende a ser más alto comparado con los demás días de la semana, apoya la existencia de una mayor volatilidad durante dicho día y en consecuencia una correlación negativa con los rendimientos en ese mismo día.
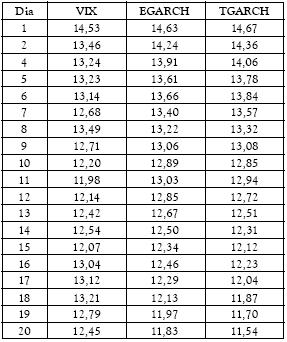
Pronósticos extramuestrales con los modelos estimados
La tabla 2 presenta los pronósticos extramuestrales para 20 días de negociación del mes de abril de 2007.
Tabla 2. Pronósticos extramuestrales
El modelo que mejor se desempeña en los pronósticos extramuestrales es el EGARCH. Bajo el criterio de la raíz del error cuadrático medio, el modelo EGARCH (RMSE=0.64) es mejor que el modelo TGARCH (RMSE = 0.74), por tanto, los intervalos de confianza serán más amplios si el pronóstico se realiza con el modelo TGARCH. Al observar las medidas de capacidad predictiva del modelo, el modelo EGARCH tiene mejor bias proportion y variance proportion.
CONCLUSIONES
En este trabajo se modeló el índice VIX desde el 01/01/2003 hasta el 30/03/2007 mediante modelos GARCH. Los resultados del trabajo sugieren que el mejor modelo para explicar el comportobstante, un modeamiento de la media y la varianza condicional del VIX es un modelo ARIMAX-EGARCH (1,1) con errores de una función generalizada de errores. No lo ARIMAX-TGARCH (1,1) se desempeña de forma similar y permite corroborar los resultados del estudio. Otras especificaciones de los modelos como los GARCH-M y PGARCH no presentan un buen ajuste.
Los Test de Dickey-Füller Aumentado, Phillips y Perron y KPSS indicaron que el logaritmo del VIX forman un proceso estacionario alrededor de una tendencia. Por esta razón, fue necesario incorporar un regresor que represente dicha tendencia en la ecuación de la media de ambos modelos, cuyo parámetro asociado resulta significativo en todos los casos. De igual manera se incorporaron regresores que permitieran evidenciar si en la serie del VIX se presentan efectos día de la semana. Como resultado se obtuvo que el día lunes el VIX tiende a presentar incrementos que son estadísticamente superiores a los de los demás días de la semana. Según estos modelos, el VIX se puede explicar adecuadamente a partir de un proceso autorregresivo de orden uno y nueve, y de dos regresores exógenos, la tendencia y el día lunes de la semana.
En la ecuación de la varianza condicional se encontró evidencia a favor de la existencia de efectos asimétricos. Tanto en el modelo EGARCH como en el TGARCH los parámetros asociados a los efectos asimétricos son significativos. Además, dichos parámetros tienen el signo que apoyan las conclusiones más importantes del trabajo. Específicamente, los signos de los parámetros asociados a la asimetría permiten concluir que la varianza condicional del VIX es superior cuando la volatilidad en el mercado aumenta, que cuando disminuye. Para el caso del modelo EGARCH, la varianza condicional es un 26.3427% superior cuando el VIX sube que cuando éste cae. En el modelo TGARCH dicha cifra es de 15.0244%. Los pronósticos extramuestrales de dichos modelos para horizontes inferiores a 30 días resultan ser satisfactorios, pues son bastantes cercanos a los valores reales.
En la literatura se encuentra evidencia a favor de que en los días lunes los rendimientos de los activos tienden a ser menores, comparados con los de los demás días de la semana. Los resultados de nuestro estudio sugieren, que si el VIX es un buen indicador de la volatilidad del mercado, entonces, la volatilidad los días lunes tiende a ser mayor. Tomando conjuntamente los dos anteriores hechos empíricos, este trabajo corrobora la tesis de que los rendimientos de los activos financieros se correlacionan negativamente con su volatilidad y contribuyen a soportar la literatura existente en este sentido.
ANEXOS
Anexo A. Estadísticas descriptivas del VIX
Gráfico A1. Histograma, Gáfico Q-Q y estadísticas descriptivas VIX 02/01/2003 al 30/03/2006.
Gráfico A2. Histograma, Gáfico Q-Q y estadísticas descriptivas LNVIX 02/01/2003 al 30/03/2006.
Anexo B. Pruebas de estacionariedad de la variable
- Series Estacionarias en tendencia y estacionarias en diferencia
Muy pocas series temporales reales pertenecientes al mundo financiero son estacionarias. Los motivos de la falta de estacionariedad suelen ser que presentan tendencia, varianza no constante, entre otras.
Afortunadamente, es posible transformar muchas series financieras no estacionarias en otras aproximadamente estacionarias, mediante operaciones algebraicas adecuadas.
Suponga que se tiene el siguiente proceso
- Tendencia determinística
Si β ≠ 0, β2 ≠ 0 y β3 = 0, entonces la ecuación (1) es de la forma Yt = β1 + β2 t + εt. Para que dicho proceso sea estacionario, se debe estimar la tendencia y después, al proceso dado, se le resta dicha tendencia, de la forma 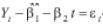
- Caminata aleatoria
Si β1= 0, β2 = 0 y β3 = 1, entonces la ecuación (1) es de la forma Yt = Yt-1 + εt. Para que dicho proceso sea estacionario, se debe diferenciar una vez, de la forma Yt = Yt-1 = εt. Por tanto dicho proceso es estacionario al diferenciarse una vez, es decir, el proceso Yt es estacionario en diferencia.
Existen otras situaciones, sin embargo, para los propósitos de este trabajo sólo es necesario conocer las diferencias entre las series estacionarias en tendencia y estacionarias en diferencia, pues la primera situación se encuentra presente en la serie de las diferencias logarítmicas del VIX. Para establecer si dicha serie es estacionaria, se utiliza el procedimiento el Test de Dickey y Fuller estándar, el cual se describe a continuación.
Un proceso yt = ρ yt-1 + x't δ + et es estacionario si |ρ| < 1. Donde x't son regresores exógenos opcionales que pueden ser una constante, una tendencia o ambos. En caso contrario |ρ| ≥ 1 se dice que el proceso es no estacionario y, por tanto, la varianza del proceso incrementa con el paso del tiempo. Para detectar si el proceso tiene raíz unitaria, Dickey y Füller evalúan la hipótesis nula de que ρ = 1 contra la alternativa de que ρ< 1. Para esto sustraen de la ecuación yt = ρ yt-1 + x'tδ + et , yt-1. Lo cual resulta en Δyt = γ yt-1+ x'tδ + et donde γ = ρ -1.
Lo anterior implica especificar las siguientes regresiones para la variable yt:
La hipótesis nula es γ = 0, lo cual implica que ρ = 1 contra la alternativa de que γ < 0 lo cual implica ρ < 1. Se debe observar si los parámetros asociados a x'tson significativos. Se puede observar el estadístico de Durbin y Watson para ver si los residuales son ruido blanco. No obstante, este estadístico sólo advierte la presencia de autocorrelación en los residuales de orden 1.
El Test estándar de Dickey y Füller sólo es válido si el proceso es AR(1). Cuando el proceso es AR(p) o tiene componentes MA(q) se corre el Test de Dickey y Füller Aumentado, el cual consiste en involucrar rezagos de las diferencias de yt que sean significativas de tal manera que los residuales sean ruido blanco.
Al realizar el Test de Dickey y Füller estándar incluyendo tendencia e intercepto, tendencia, intercepto ó ninguno, los errores no resultaron ser ruido blanco. Por tanto se procedió a correr el Test de Dickey y Füller Aumentado (ADF), Test de Philips y Perron y KPSS.
Fuente: CBOE. Cálculo de los autores
Tabla A1. Pruebas de Raíz Unitaria para la LNVIX
Como se observa se rechaza la hipótesis nula de que el logaritmo natural del VIX tenga raíz unitaria. Estos resultados confirman los del ADF, pues el p-valor del test de Philips y Perron es de 0.0015 inferior al 0.05. El estadístico del test de KPSS es 0.534388, mayor que los valores críticos asociados al mismo (la hipótesis nula de este test es que el proceso es estacionario, contrario a la hipótesis nula de ADF y Phiplips y Perron).
Sin embargo, los resultados mostraron que la serie LNVIX es estacionaria en tendencia, por tanto, es necesario estimar la tendencia y restarla a la variable LNVIX obteniendo una nueva serie que llamaremos Wt = LNVIX - ( β0 + β1t) para que así la serie quede estacionaria en media. Una vez se tiene la serie estacionaria en media se procede a la identificación del modelo ARMA. Para esto se utiliza el correlograma de Wt = LNVIX - ( β0 + β1t).
De acuerdo con el correlograma, los parámetros asociados a rezagos de la variable son significativos. Mediante el PACF es posible identificar los rezagos de una estructura AR que parecen ser significativos. Para este caso se seleccionaron como tales los rezagos 1, 3, 9 11 y 29. El correlograma no permite identificar una a simple vista una estructura para el orden del MA. Con el correlograma anterior se procedió a estimar el modelo ARMA que mejor se ajuste a la serie.
Siguiendo la metodología de Box-Jenkins se estimaron los siguientes modelos: AR(1), AR(3), AR(9), ARMA(9,29) y ARMA(3,29) adicionándoles la tendencia. Los parámetros de estos modelos resultan significativos y los residuales son ruido blanco. Sin embargo, el modelo con los valores para el criterio de Akaike y Schwarz es un AR(9) con rezagos estadísticamente significativos de orden 1 y 9. La Tabla A3 presenta los resultados de esta estimación.
Anexo C. Pruebas de validación de los modelos estimados
Tabla A2. Modelos Estimados
Tabla A3a. Pruebas de Ljung-Box sobre los residuales del modelo EGARCH
Tabla A3b. Pruebas de Ljung-Box sobre los residuales al cuadrado del modelo EGARCH
Tabla A4a. Pruebas de Ljung-Box sobre los residuales del modelo TGARCH
Tabla A4b. Pruebas de Ljung-Box sobre los residuales al cuadrado del modelo TGARCH
Tabla A5. ARCH Test: Modelo EGARCH. 10 rezagos
Tabla A6. ARCH Test: Modelo TGARCH. 10 rezagos
5 French (1980), Wang, Li y Ericsson (1997); Keim y Stambaugh (1984); Thaler (1987); Berument y Kiymaz (2001); Lakonishok y Levi (1982); Lakonishok y Maberly (1990); Jaffe y Westerfield (1985); Loudon, Watt y Yadav (2000), Dyl y Martin (1985); Fortune (1998); Gibbons y Hess (1998); Hansen , Lunde y Nason (2005); Platev, Lyroudi y Kanaryan (2003); Chukwuogor-Ndu (2006); Joshi (2006); Bhattacharya, Sarkar y Mukhopadhayay (2001); Savva, Osborn y Gill (2006); Bayar y Kan (2002); Basher y Sadorsky (2004) Cáceres, Maroto y Sales (2006); Balaban (1994), Choudhry (2001), Kamara (1997), entre otros.
6 Engle (1982), Bollerslev (1986).
7 Los modelos GARCH son un caso especial de los modelos TGARCH cuando el término Threshold (De asimetría) es cero.
8 El modelo anterior es el estimado en Eviews el cual difiere levemente del propuesto inicialmente por Nelson (1991), el cual es el siguiente:
Eviews tiene en cuenta el componente de asimetría que recoge el impacto de las buenas y las malas noticias en la ecuación de la varianza condicional mediante 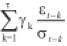
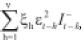
9 Esta estimación se utiliza cuando se sospecha que los residuales del modelo especificado no se distribuyen normalmente y se han estimado los parámetros bajo este supuesto. Aunque los parámetros estimados son consistentes, la matriz de covarianzas estimada no lo será. De esta manera los estadísticos de prueba para rechazar la significancia de los parámetros no estarían bien construidos y deben corregirse mediante la correción propuesta por estos autores. De esta manera, los parámetros estimados serán consistentes y los p-valores asociados muestran la verdadera probabilidad para rechazar o aceptar la significancia de los parámetros. En otras palabras, mediante esta estimación se asegura que la matriz de covarianzas es robusta ante la presencia de heteroscedasticidad y no normalidad en los residuales.
10 Una serie se dice estacionaria (en sentido débil) si la media y las autocovarianzas de la serie no dependen del tiempo.
11 representa el vector de regresores exógenos para la media que contiene una variable dummy para el día lunes.
12 Impacto de
13 Impacto de
14 Los parámetros asociados a los demás días de la semana no resultaron significativos.
BIBLIOGRAFÍA
1. AGGARWAL, Reena y RIVOLI, Pietra. 1989. seasonal and day-of-the-week effects in four emerging stock markets, The Financial Review, Vol. 24, Issue 4 (November 1989), Pages 541-550. [ Links ]
2. AHONIEMI, Katia. 2006. Modeling and forecasting implied volatility: an Econometric Analysis of the VIX Index. Helsinski School of Economics. Working Paper 129. [ Links ]
3. ANDERSEN, Torben G.; BOLLERSLEV, Tim; DIEBOLD, Francis X. y LABYS, Paul. 2003. Modeling and forecasting realized volatility. Econometrica, Vol. 71, No. 2. (Mar., 2003), pp. 579-625. [ Links ]
4. ARSAD, Zainudin y COUTTS, J. Andrew. 1997. Security price anomalies in the London International Stock Exchange: a 60 year perspective, Applied Financial Economics, Volume 7, Number 5, 1 October 1997, pp. 455-464. [ Links ]
5. AWARTANI, Basel M. A. y CORRADI, Valentina. 2003. Predicting the volatility of the S&P-500 stock index via GARCH Models: The role of asymmetries. University of Exeter Working Paper. [ Links ]
6. BALABAN, Ercan. 1994. Day of the week effects: new evidence from an emerging stock market. Applied Economics Letters 2, pp. 139-143. [ Links ]
7. BAYAR, Asli y ÖZGüR, Berk Kan. 2002. Day of the week effect: recent evidence from nineteen Stock Markets. Central Bank Review 2, pp. 77-90. [ Links ]
8. BASHER, Syed y SADORSKY, Perry. 2004. Day of the week effect in emerging stock markets. York University Working Paper. [ Links ]
9. BECKER, Ralf; CLEMENTS Adam E. y WHITE Scott I. WHITE. 2005. Forward looking information in S&P 500 options. School of Economics and Finance, Queensland University of Technology, Working Paper. [ Links ]
10. BEKAERT, Geert y GUOJUN, Wu. 2000. Asymmetric Volatility and Risk in Equity Markets. The Review of Financial Studies, Vol. 13, No. 1. (Spring, 2000), pp. 1-42. [ Links ]
11. BERUMENT, H. y KIYMAZ. H. 2001. the day of the week effect on stock market volatility. Journal of Economics and Finace. [ Links ]
12. BHATTACHARYA, Kaushik; SARKAR Nityananda y MUKHOPADHAYAY, Debabrata. Stability of the day of the week effect in return and in volatility at the indian capital market : a garch approach with proper mean specification. Reserve Bank of India Working Paper. [ Links ]
13. BOLLERSLEV, T. 1986. 'Generalized autoregresive conditional heteroscedasticity'. Journal of Econometrics, 31f, 307-327. [ Links ]
14. BOLLERSLEV, T. and WOOLDRIDGE, J. (1992). quasi-maximum likelihood estimation and inference in dynamics model with time varying covariances. Econometric Reviews, Vol. 11, 143 - 172. [ Links ]
15. BOX, G.E.P. y JENKINS, G.M. 1970. Time series analysis: forecasting and control. Holden-Day. [ Links ]
16. BRAUN, Phillip A.; NELSON Daniel B. y SUNIER Alain M. 1995. Good news, dad news, volatility, and betas. The Journal of Finance, Vol. 50, No. 5. (Dec., 1995), pp. 1575-1603. [ Links ]
17. BROOKS, Chris; ÓLAN T. Henry y PERSAND, Gita. 2002. The effect of asymmetries on optimal hedge ratios. The Journal of Business, Vol. 75, No. 2. (Apr., 2002), pp. 333-352. [ Links ]
18. CÁCERES, Rosa María; MAROTO SANTANA, Octavio y JORDÁN SALES, Lourdes. 2006. Day of the week effect on european stock markets. Internaitonal Research Journal of Finance and Economics 2, pp. 54-70. [ Links ]
19. CAMPBELL, John y HENTSCHEL, Ludger. 1991. No news is good news: an asymmetric model of changing volatility in stock returns. NBER Working Paper No. 3742. [ Links ]
20. CECONNI, M.; GALLO, G. M. y LOMBARDA, M. J. 2002. Garch base volatility forecasts for market volatility index. Dipartamento Di Statistica 'Giuseppe Parenti', Working Paper 2002/06. [ Links ]
21. CHAN, Su Han, LEUNG, Wai-Kin y WANG Ko. 2004. The impact of institutional investors on the monday seasonal, The Journal of Business, Volume 77, Number 4 (October 2004), pages 967-986. [ Links ]
22. CHANG, Eric C., PINEGAR, J. Michael y RAVICHANDRAN, r. 1993. International evidence on the robustness of the day-of-the-week effect, The Journal of Financial and Quantitative Analysis, Vol. 28, No. 4. (Dec., 1993), pp. 497-513. [ Links ]
23. CHEN, Honghui y SINGAL, Vijay, 2003. Role of speculative short sales in price formation: the case of the weekend effect, The Journal of Finance, Volume 58, Number 2, April 2003, pp. 685-706. [ Links ]
24. CHIAKU Chukwuogor-Ndu. 2006. Stock market returns analysis, day of the week effect, volatlity of returns: evidence from european financial markets 1997-2004. Internaitonal Research Journal of Finance and Economics 1, pp.112-124. [ Links ]
25. CHOUDHRY, Taufiq. 2000. Day of the week effect in emerging asian stock markets: evidence from the garch model. Applied Financial Economics 10, pp. 235-242. [ Links ]
26. CHRISTOFFERSEN, Peter F. y DIEBOLD Francis X. 2000. How relevant is volatility forecasting for financial risk management? The Review of Economics and Statistics, Vol. 82, No. 1. (Feb., 2000), pp. 12-22. [ Links ]
27. CHRISTOS S., Savva, OSBORN, Denise R. y GILL, Len. 2006. The day of the week effect in fifteen european stock markets. University of Manchester. Working Paper. [ Links ]
28. CROSS, F. 1973. The Behavior of Stock Prices on Fridays and Mondays. Financial Analysts Journal 29: 67-69. [ Links ]
29. DICKEY, D. and FULLER, W. 1979. Distribution of the estimates for autorregresive time series with unit root. Journal of American Statistical Association, 74 (June), 427 - 31. [ Links ]
30. DONG, Gang. 2006. Empirical test of forecasting vix index and profitability in trading vix derivatives. Claruth International Investment LLC, Working Paper. [ Links ]
31. DUBOIS, M. y LOUVET P. 1996. The day of the week effect: The international evidence. Journal of Banking and Finance 20 (1996), pp. 1463-1484. [ Links ]
32. DYL, E., and MABERLY, E. 1986. The daily distribution of changes in the price of stock futures. Journal of Futures Markets 6: 513-521. [ Links ]
33. ENGLE, Robert F. 1982. 'Autoregresive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation'. Econometrica, 50, 4, 987-1007. [ Links ]
34. ENGLE, R. y BOLLERSLEV, T. 1986. Modelling the persistence of conditional variances. Econometrics Review, 5, 1 1-50. [ Links ]
35. ENGLE, Robert y GALLO, Giampiero. 2002. A model for intradaily volatility and multiple indicators. ESEM 2002. [ Links ]
36. ENGLE, Robert F. y VICTOR, K. Ng. 1993. Measuring and testing the impact of news on volatility. The Journal of Finance, Vol. 48, No. 5. (Dec., 1993), pp. 1749-1778. [ Links ]
37. ENGLE, Robert. 2004. Risk and volatility: econometric models and financial practice. The American Economic Review, Vol. 94, No. 3. (Jun., 2004), pp. 405-420. [ Links ]
38. FERNANDES, Marcelo; Marcelo C. Medeiros y Marcel Scharth. 2006. Modeling And Predicting The Cboe Market Volatility Index. Queen Mary, University of London, Working Paper. [ Links ]
39. FIELDS, M. J. 1931. Stock prices: a problem in verification, The Journal of Business of the University of Chicago, Vol. 4, No. 4. (Oct., 1931), pp. 415-418. [ Links ]
40. FLEMING, Jeff; KIRBY, Chris y OSTDIEK, Barbara. 2001. The economic value of volatility timing. The Journal of Finance, Vol. 56, No. 1. (Feb., 2001), pp. 329-352. [ Links ]
41. FORTUNE, Meter. 1998. Weekends can be rough: revisiting the weekend effect in stock prices. Federal Reserve Bank of Boston, Working Paper 98-6. [ Links ]
42. FRENCH, Kenneth R. 1980. Stock returns and the weekend effect. Journal of Financial Economics, Volume 8, Issue 1, March 1980, Pages 55-69. [ Links ]
43. FRENCH, Kenneth R.; SCHWERT G. William y ROBERT F. Stambaugh.1987. Expected stock returns and volatility. Journal of Financial Economics, Volume 19, Issue 1, September 1987, Pages 3-29 [ Links ]
44. GIBBONS, Michael R. y HESS, Patrick. 1981. Day of the week effect and asset returns. The journal of Business Vol 54. No. 4., (Oct. 1981), pp. 579-596. [ Links ]
45. GLOSTEN, L. R.; JAGANNATHAN, R. y RUNKLE, D. E. On the relation between the expected value and the volatility of the nominal excess return on stocks,' Journal of Finance, 48, 1779-1801. [ Links ]
46. HANSEN, Peter; LUNDE Asger y NASON, James M. 2005. Testing the singnificance of calendar effects. federal reserve bank of atlanta, Working Paper No. 2005-2. [ Links ]
47. JAFFE, Jeffrey y WESTERFIELD, Randolph. 1985. The week-end effect in common stock returns: The International Evidence. The Journal of Finance, Vol. 40, No. 2. (Jun., 1985), pp. 433-454. [ Links ]
48. JOSHI, Nayan Khrisna. 2006. Day of the week effect: It is and industry specific phenomenon. Economic Journal of Nepal, Vol. 29, No. 1, pp. 1-12. [ Links ]
49. KAMARA, Avraham. 1997. New evidence on the monday seasonal in stock returns. The Journal of Business, Vol. 70. No. 1. (Jan., 1997), pp. 63-84. [ Links ]
50. KIYMAZ, H. y BERUMENT, H. 2003. The day of the week effect on stock market volatility and volume: International evidence. Review of Financial Economic. [ Links ]
51. KEIM, Donald B. y STAMBAUGH, Robert F. 1983. A further investigation of the weekend effect in stock returns. The Journal of Finance, Vol. 39, No. 3, Papers and Proceedings, Forty-Second Annual Meeting, American Finance Association, San Francisco, CA, December 28-30, 1983. (Jul., 1984), pp. 819-835. [ Links ]
52. KWIATKOWSKI, D., PHILLIPS, P., SCHMIDT, P. and SHIN, Y. 1992. Testing the null hypothesis of stationary against the alternative of a unit root. Journal of Econometrics, Vol. 54. 159 - 178. [ Links ]
53. LAKONISHOK, Josef y LEVI, MauriceI. 1982. Weekend effects on stock returns: a note. The Journal of Finance, Vol. 37, No. 3. (Jun., 1982), pp. 883-889. [ Links ]
54. LAKONISHOK, Josef y MABERLY, Edwin. 1990. The weekend effect: trading patterns of Individual and Institutional Investors. The Journal of Finance, Vol. 45, No. 1. (Mar., 1990), pp. 231-243. [ Links ]
55. LOUDON, Geoffrey F. et al. 2000. An empirical analysis of alternative parametric arch models. Journal of Applied Econometrics, Vol. 15, No. 2. (Mar. - Apr., 2000), pp. 117-136. [ Links ]
56. MAJMUDAR, Utkarsh y BANERJEE, Arnab. 2004. VIX Forescasting. Presented to the 40th Annual Conference of The Indian Econometrics Society. India February, 13-15, 2004. [ Links ]
57. MEHDIAN, Seyed y PERRY, Mark J. 2001. The reversal of the monday effect: new evidence from US equity markets, Journal of Business Finance & Accounting, Volume 28, Numbers 7-8, September/October 2001, pp. 1043-1065. [ Links ]
58. NELSON, D. B.. 1991. Conditional heteroskedasticity in asset returns: a new approach. Econometrica, 59, 347-370. [ Links ]
59. OGUS, Ayla. 2002. Pricing of S&P 100 Index Options Based on GARCH Volatility. Izmir University of Economics, Working Paper 02/01. [ Links ]
60. PATEV, Plamen y LYROUDI, Katerina. 2003. The day of the week effect in the central european trasition stock markets. University of Macedonia Working Paper. [ Links ]
61. PHILLIPS, P. and PERRON, P. 1988. Testing for a unit roots in time series regression. Journal of Econometrics 33, (June), 335 - 46. [ Links ]
62. POON, Ser-Huang y GRANGER Clive W. J. 2003. Forecasting volatility in financial markets: A Review. Journal of Economic Literature, Vol. 41, No. 2. (Jun., 2003), pp. 478-539. [ Links ]
63. RABEMANANJARA, R. y ZAKOIAN J. M. 1993. Threshold arch models and asymmetries in volatility. Journal of Applied Econometrics, Vol. 8, No. 1. (Jan. - Mar., 1993), pp. 31-49. [ Links ]
64. REINGANUM, Marc. 1983. Discussion: What the anomalies mean. The Journal of Finance, Vol. 39, No. 3, Papers and Proceedings, Forty-Second Annual Meeting, American Finance Association, San Francisco, CA, December 28-30, 1983. (Jul., 1984), pp. 837-840. [ Links ]
65. ROGALSKI, Richard J. 1984. New Evidence Regarding Day of The Week Returns over Traing and Non-Trading Periods: A Note. The Journal of Finance, Vol. 39, No. 5 (Dec., 1984), pp. 1603-1614. [ Links ]
66. RUBIO, Javier Giner y MORINI MARRERO Sandra. 2004. El índice VIX para la predicción de volatilidad: un estudio internacional. Working Paper 2004-10. [ Links ]
67. THALER, Richard. 1987. Anomalies: seasonal movements in security prices ii: weekend, holiday, turn of the month, and intraday effects. The Journal of Economic Perspectives, Vol. 1, No. 2. (Autumn, 1987), pp. 169-177. [ Links ]
68. TSAY, R. S. 2002. Analysis of financial time series. John Wiley and Sons, New York. [ Links ]
69. TURAN G., Balia y WEINBAUMB, David. 2007. A conditional extreme value volatility estimator based on high-frequency returns. Journal of Economic Dynamics & Control 31 (2007) 361-397. [ Links ]
70. TURNER, Christopher M., STARTZ, Richard, y NELSON, Charles R. 1989. A markov model of heteroscedasticity, Riskm and learning in the stock market. Journal of Financial Economics, Vol. 25, 3-22. [ Links ]
71. WANG, Ko; LI, Yuming y ERICKSON, Jhon. 1997. A new look at the monday effect. The Journal of Finance, Vol. 52, No. 5. (Dec., 1997), pp. 2171-2186. [ Links ]
72. WU, Guojun. 2001. The determinants of asymmetric volatility. The Review of Financial Studies, Vol. 14, No. 3. (Autumn, 2001), pp. 837-859. [ Links ]
73. ZAKOIAN, J. 1994. Threshold heteroskedastic models. Journal of Economic Dynamics and Control 18, 931 - 995. [ Links ]
Recibido: 15/08/2007
Aceptado: 29/08/2007













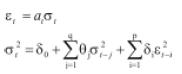
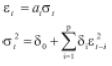
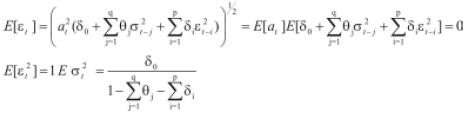
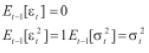
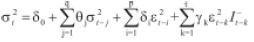
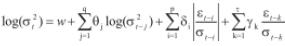
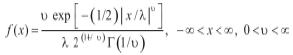
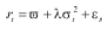
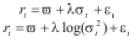
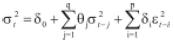
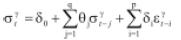
 .
.