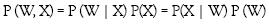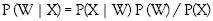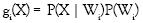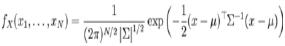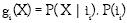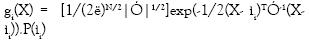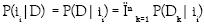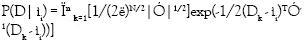Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Ingenierías Universidad de Medellín
Print version ISSN 1692-3324On-line version ISSN 2248-4094
Rev. ing. univ. Medellin vol.6 no.11 Medellín July/Dec. 2007
TEORÍA DE DECISIÓN BAYESIANA EN LOS CRITERIOS DE SIMILITUD UTILIZADOS EN LA SEGMENTACIÓN DE IMÁGENES DE RANGO
BAYESIAN DECISION THEORY IN SIMILARITY CRITERIA USED IN RANGE IMAGES SEGMENTATION
Díaz Idanis1; Montoya Diana2; Boulanger Pierre3
1 Facultad de Ingeniería. Universidad de Medellín, email:idiaz@udem.edu.co. Medellín, Colombia
2 Facultad de Ingeniería. Universidad de Medellín, email:dmmontoya@udem.edu.co. Medellín, Colombia
3 Department of Computing Science. University of Alberta, email: pierreb@cs.ualberta.ca. Edmonton, Alberta, Canadá
Resumen
El obtener una imagen segmentada correctamente sigue siendo un asunto sin resolverse. Por lo general los resultados obtenidos por un computador al segmentar una imagen contienen sobre-segmentaciones, sub-segmentaciones y bordes mal definidos. En gran parte, estos inconvenientes recaen sobre el criterio de similitud utilizado por los algoritmos de segmentación. En el presente artículo se hace un análisis de los criterios de similitud más utilizados en la literatura y de la utilización de criterios basados en la teoría de decisión bayesiana.
Palabras clave
Segmentación, imágenes de rango, teoría bayesiana
Abstract
To obtain a segment image is still not possible. Typically, results obtained by computer programs show over-segmentation and not well-defined edges. Most of these difficulties are believed to be due to similarity criteria used by segmentation algorithms. In this paper, there is an analysis of similarity criteria most used in literature and an analysis of criteria based on Bayesian decision theory.
Key Words
Segmentation, range images, Bayesian theory
INTRODUCCIÓN
Las imágenes de rango son un tipo especial de imagen que contiene información asociada a la posición y a la distancia en la que se encuentra cada punto de la escena representada, con respecto a un punto de refernecia. De esta manera, una imagen de rango contiene información sobre la estructura 3D de los objetos de la escena. Este tipo de imagenes son utilizadas en aplicaciones de la visión tridimensional como los sistemas de navegación róbotica, la construcción de modelos computacionales, entre otras.
Para la mayoría de los algoritmos de alto nivel de la visión por computador, el segmentar la imagen se ha convertido en un paso necesario, debido a que este procedimiento ayuda a simplificar la manipulacion de los datos, la complejidad geométrica de los objetos representados y el modelamiento computacional de los mismos. La segmentación de una imagen de rango consiste en dividir la imagen en regiones con las mismas propiedades geométricas o que pertenezcan a una misma superficie. Hoover, (Hoover, 1996), define la segmentación de una imagen de rango con un lenguage más formal, de la siguiente manera:
Si R es una imagen de rango completa, la segmentación consiste en dividir R en subregiones: R1, R2,....;Rn, tal que:
1. Ui=1nRi = R
2. Ri es una región conectada para i = 1,2,...,n y
3. Ri ∩ Rj = Φ para todo i y j, si i ≠ j
4. P(Ri) = TRUE para i = 1,2,...,n y
5. P(Ri ∪ Rj ) = FALSE para i =1,2,...,n
En donde P(Ri) es un predicado lógico o un conjunto de propiedades similares sobre los puntos de Ri , y Φ es el conjunto nulo.
En el estado del arte de la segmentación de imágenes de rango, los algoritmos propuestos se pueden clasificar de acuerdo con el procedimiento general que siguen, este puede ser: por crecimiento de regiones, por agrupamiento jerárquico o por agrupamiento por particionamiento. Cada uno de estos tipos de procedimientos, cuenta con un paso de selección de semillas o particionamiento inicial de la imagen en pequeñas regiones, y un criterio de similitud para tomar la decisión de unir dos regiones, o un elemento individual a una región ya conformada. El método utilizado para la selección de semillas y el criterio de similitud tienen una gran influencia en el desempeño de los algoritmos de segmentación. Cada algoritmo propuesto busca mejorar la calidad de las segmentaciones obtenida, ensayando diferentes métodos, planteamientos o variaciones de estos dos componentes.
En este trabajo se hace un análisis de las distintas formas de planteamiento de los criterios de similitud, que se observan en la literatura, resaltando el uso de un criterio bayesiano. En la siguiente sección se ilustrará el tipo de errores no deseados en la segmentación, que dependen en gran parte de la selección de un buen criterio de similitud. La sección 3 es una revisión de los tipos de criterios de similitud normalmente utilizados. En la sección 4, se hace una introducción a la teoría Bayesiana en problemas de clasificación. En la sección 5, se muestra el uso de la teoría Bayesiana en el diseño del criterio de similitud para el problema de la segmentación de imágenes de rango. Por último, la sección 6 es una conclusión general de este trabajo.
RESULTADOS NO DESEADOS EN UNA IMAGEN SEGMENTADA
Los principales errores que deben evitar los algoritmos de segmentación son: sobre-segmentación, esto es, cuando una región es dividida incorrectamente en varios segmentos: La sub-segmentación que se da cuando en una región realmente hay más de un segmento y la división no se realizó (Hoover, 1996). Y la mala definición de los bordes entre los segmentos.
Los errores en los resultados de las segmentaciones se deben, esencialmente, a la presencia de ruido en los valores de rango adquiridos en el proceso de sensado de las imágenes, y a las complejidades de las superficies; por ejemplo, las pequeñas concavidades en las imágenes conducen a sobre segmentaciones, lo cual se podría evitar con un criterio de similitud basado en un valor umbral que discrimine ciertas curvaturas o cambios en las orientaciones de las normales de los elementos a agrupar; pero al prevenir la sobre-segementación utilizando un umbral como criterio, se corre el riesgo de ocasionar sub-segmentaciones. Por otro lado, la falta de claridad o precisión en los límites entre los sub objetos de la imagen hace que el procedimiento de crecimiento o unión de regiones origine bordes que no definen la verdadera geometría de las regiones. En las siguientes figuras se ilustra este tipo de problemas:
Figura 1. Sobre-segmentación y sub-Segmentación (Hoover, 1996).
En la figura 1, el cuadrado de la izquierda representa una correcta segmentación, y el cuadrado de la derecha es una representación de la segmentación del mismo objeto, pero con algunos errores. En la imagen de la derecha, las regiones 12, 13, 14, 15 y 18 son sobresegmentaciones de la región 15 en la imagen de la izquierda, y la región 11 en la derecha es una sub-segmentación de las regiones 10, 11,12 y 13 de la izquierda.
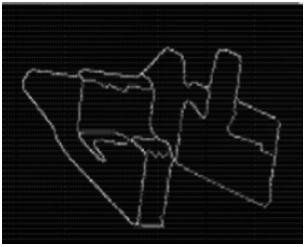
Figura 2. Bordes mal definidos (Díaz, 2005).
En la figura 2, cada uno de los segmentos de la imagen corresponden a las regiones encerradas por los bordes; sin embargo, en esta figura se puede ver la mala definición de los bordes que, por tratarse de imágenes de superficies planas rectangulares, deberían ser líneas rectas entre ellas.
CRITERIOS DE SIMILITUD
El criterio de similitud se utiliza para determinar si un elemento puede ser añadido a una región, usualmente, está basado en características geométricas de la imagen. Los criterios de similitud utilizados por los algoritmos de segmentación se pueden dividir en dos tipos, los que se basan en una métrica de error al ajustar un modelo paramétrico a los datos de cada región, y los que optimizan una función de distancia que mide la diferencia en la orientación de las normales, o en las curvaturas de las superficies, y la cercanía de los elementos.
Entre los algoritmos propuestos para la segmentación de imágenes de rango que utilizan un criterio de error basado en el ajuste de un modelo de superficie, se pueden mencionar los siguientes trabajos: Besl, 1988; Jiang, 1992; Lee, 1998; Koster, 2000; Zuckerberger, 2002; Boulanger, 2005; Vieira, 2005. Los modelos paramétricos más usados en este tipo de trabajos son: modelos polinomiales implícitos y los modelos parámetricos de superficies como los de Beizer. Básicamente, el procedimiento que siguen estos algoritmos es extraer pequeñas regiones semilla de la imagen a través de un método para un primer particionamiento, o seleccionando unos pocos puntos iniciales. Con los datos que conforman las pequeñas semillas, se calcula un modelo de superficie. Luego, se unen a cada una de las pequeñas regiones aquellos puntos, elementos u otras regiones que se ajusten o se aproximen al modelo que la representa. Cada vez que una región es modificada, se recalcula nuevamente el modelo. Se continúa con el proceso de unión, hasta que no se puedan unir más regiones, porque el error de ajuste sea mayor que un umbral preestablecido.
Por su parte, los algoritmos que optimizan una función de distancia se basan en las características geométricas de la imagen sin tener en cuenta el modelo polinomial que podría representar cada región. Entre los algoritmos de segmentación propuestos que trabajan con este tipo de criterios se pueden mencionar: Garland, 2001; Shlafman, 2002; Katz, 2003; Sander, 2003; Liu, 2004, Yamauchi, 2005. Las características geométricas en las que se basan los criterios de similitud de este tipo de propuestas son: la orientación de las normales, las curvaturas, las distancias geodésicas, y las distancias euclidianas. Los algoritmos que utilizan este tipo de criterios, igualmente parten de regiones semilla, a las que se les asignan una normal promedio o un valor de curvatura, que las represente. La idea general es unir, ya sea un punto sin agrupar a una región, o dos regiones pequeñas, vecinos y que, además, sus normales o curvaturas representativas sean similares. El objetivo de este tipo de algoritmos es minimizar la distancia entre el elemento representativo y los respectivos puntos de cada región.
Tanto el criterio de similitud basado en el ajuste de un modelo polinomial, como el basado en las características geométricas de las regiones utilizan la información ofrecida por los datos, para calcular ya sea el modelo, la normal o la curvatura representativa de cada región. Generalmente, los datos de rango registrados en una imagen presentan ruido, lo cual produce márgenes de error en los modelos de superficies calculados y en la obtención de normales o curvaturas promedio representativas. Sin embargo, muchos de los métodos propuestos aparentemente trabajan bajo el supuesto de homogeneidad de los grupos de puntos que se van formando. Esta afirmación se fundamenta en el hecho de que en el momento de tomar la decisión de unir dos regiones, los criterios de similitud no consideran todos los elementos contenidos en las regiones, sino solamente sus representativos, lo cual hace que el error se incremente. De esta manera, se puede ver que la decisión de unir dos regiones, soportada directamente sobre el criterio de similitud, puede conducir en muchos casos a sobre-segmentaciones, sub-segmentaciones o bordes mal definidos.
En el estado del arte de los algoritmos de segmentación para imágenes de rango, algunos métodos proponen criterios de similitud con mecanismos para considerar el ruido presente en las imágenes. Por ejemplo, el método de segmentación de Köster, (Köster, 2000), trabaja con un valor de error permitido para cada modelo ajustado, el cual es recalculado cada vez que se intenta unir un nuevo punto a la región, y sobre este se soporta la decisión. Para el caso de unir dos regiones, Köster compara las distribuciones de las regiones, utilizando el número de elementos que mutuamente pertenecerían a ellas, llamado Mutual Inlier Ratio (MIR); si las distribuciones son similares, entonces su MIR es más grande que un valor discriminante. Otros trabajos, como LaValle, 1995; Boulanger, 2005, plantean criterios de similitud basados en el ajuste de modelos polinomiales y en la teoría Bayesiana. Con este tipo de criterios, se calcula la probabilidad de que una región pueda pertenecer a otra. En la siguiente sección se puede apreciar cómo, con este tipo de criterios basados en la teoría bayesina, se tienen en cuenta las observaciones individuales y la dispersión de los datos de cada grupo.
TEORÍA BAYESIANA
El problema de agrupamiento de dos regiones, o un elemento a una región, se puede ver como un problema de clasificación. Si se tiene un elemento para agrupar, esto se puede expresar como el determinar a qué grupo de puntos pertenece, entre las regiones preestablecidas. En el caso de dos regiones se puede expresar como el determinar si los elementos de una de las regiones pueden ser clasificados como pertenecientes a la otra región.
La teoría de la decisión Bayesiana plantea que la tarea de predecir la clase a la que pertenece un elemento se puede tratar en términos probabilísticos, (Duda, 2001). Una manera simple de ver lo anterior es con el siguiente ejemplo: si se tiene una muestra, cuyos elementos pertenecen a una de dos clases, y se sabe por conocimiento del universo y de la muestra que la ocurrencia de la clase A es mayor que la clase B, entonces, se podría asignar a priori una mayor probabilidad de ocurrencia para A que para B. Partiendo del hecho de que lo anterior es correcto, al llegar un nuevo elemento X y clasificarlo como A se tendría menor riesgo de equivocación que si se dice que pertenece a B. Este sería un clasificador bastante simple, pero poco preciso. Para mejorarlo, se introduce en él, el concepto de probabilidades combinadas, que permite considerar características en la toma de decisiones. Suponiendo que la nueva observación X es un conjunto de valores de características, al igual que cada elemento de la muestra, la probabilidad a priori P (W), W = A o B, se puede convertir en la probabilidad a posteriori P (W X), esto es la probabilidad de W dado el valor observado X. La clase W para la cual P (W X) es más grande es más probable a ser la clase real.
La probabilidad combinada W, X es igual a:
La probabilidad a posteriori P(W X), de la clase W, dados los valores del nuevo elemento X, es igual a la probabilidad condicional de que se presenten los valores de X dada la clase W, por la probabilidad a priori de la clase W, sobre la probabilidad de ocurrencia de los valores de X. El cálculo de las probabilidades necesarias, es decir, de cada término de la ecuación 2 se realiza con base en las observaciones de la muestras, por tal motivo los clasificadores bayesianos están muy sujetos a lo que en el aprendizaje supervisado se denomina conjunto de entrenamiento.
La ecuación 2 es el teorema de Bayes, sobre el cual se basa la toma de decisión bayesiana. Para algunos casos particulares se puede observar la ventaja de utilizar probabilidades combinadas en el problema de clasificación, por ejemplo: retomando el caso anterior en que se tienen dos clases A y B, en el caso de que las probabilidades a priori sean: P(A) = P(B), el decidir a qué clase pertenece un nuevo elemento, basado en las solas probabilidades de las clases sería difícil, pero utilizando la ecuación 2, se tendría que el término determinante de la decisión sería P(X W). El término P(X) es un factor de normalización que podría ser descartado de la ecuación.
En el caso de un problema de clasificación con más de dos clases, la decisión se puede realizar utilizando la siguiente regla: una nueva observación X será asignada a la clase Wi, i = 1,....,c, donde c es el número de clases que se tienen, si gi (X) > gj (X), para todo j = 1,...,c, j ? i, y
En la ecuación 3 se puede observar que la estructura del clasificador bayesiano está determinada, tanto por la probabilidad a priori P(Wi), como por la densidad condicional P (X Wi). En los problemas de clasificación con varibles continuas, esta densidad condicional debe ser la función de densidad de los datos de la muestra que pertenecen a la clase Wi. En la mayoría de este tipo de problemas se asume que es una distribución normal. Si el problema de clasificación es un problema en el que cada observación o elemento X es un conjunto de valores de distintas variables, entonces usualmente se utiliza la función de la densidad normal multivariables, expresada en la ecuación 4.
EL CRITERIO DE SIMILITUD BASADO EN LA TEORÍA BAYESIANA
Como se había mencionado antes, el problemas de agrupamiento de dos regiones, o de un elemento a una región se puede ver como un problema de clasificación, en el que la muestra de datos y las nuevas observaciones son elementos multivariados y el número de clases es el número de grupos preestablecidos por el particionaminto inicial de la imagen, el cual irá variando a medida que los grupo se vayan uniendo. En este caso, se esperaría que los datos de cada una de las regiones se ajusten realmente a una distribución normal, en la que ì sería la normal promedio, la curvatura promedio, o el modelo que la representa.
Si se tiene un conjunto de particiones R = R1, .... Rn de una imagen y un elemento X, el problema de unir X a una de las regiones preestablecidas se puede expresar como:
Seleccionar Ri, para la cual su respectiva gi > gj para todo j = 1,...,n, j ? i y X adyacente a Rj.
Las ecuaciones 5 y 6 expresan la probabilidad de que X pertenezca a una región representada por ìi. ìi podría ser la normal promedio, la curvatura promedio o un vector de parámetros del modelo ajustado. La probabilidad de ìi, P(ìi) se puede calcular, también con base en el teorema de Bayes. Considerando que Ri, es conjunto de datos D = D1,...,Dm obtenidos independientemente a partir de una distribución normal con ì = ìi , se puede calcular la probabilidad de que ìi ocurra dado Di, de la siguiente manera:
En las ecuaciones 6, 7 y 8 se puede apreciar cómo todos los datos de la región que se esté analizando están involucrados en el cálculo de la probabilidad que va a soportar la decisión de unir a ella o no el nuevo elemento X. En estas ecuaciones el cálculo de la matriz de covarianza se puede ver, además, como una medida del error de los datos con respecto a la ìi que en el problema de segmentación se está tomando como representativa de cada región.
Para el caso de la unión de dos regiones, el problema se puede plantear de manera similar al anterior, tomando una de las regiones como si fuera un único elemento sin agrupar, representado por su valor ì, de tal manera que en este caso se tomaría ìx como si fuera X y las ecuaciones utilizadas serían las mismas.
Otra ventaja de utilizar un criterio de similitud basado en la teoría bayesiana es que para relacionar diferentes características en la toma de la decisión de unir dos elementos, no se necesita diseñar funciones complicadas. Esta situación se ilustra por ejemplo en el trabajo de Garland, (Garland, 2001), en el que la función criterio propuesta involucra tres características distintas de las regiones, como una combinación lineal, en la que cada componente tiene asociado un peso que debe ser introducido por el usuario. Los clasificadores bayesianos establecen la probabilidad de ocurrencia de los valores de las características involucradas en el problema, y las clases, basándose en observaciones de los datos suministrados.
CONCLUSIÓN
En este artículo se ha realizado un análisis sobre los criterios de similitud utilizados en la segmentación de imágenes de rango, para dar soporte a la decisión de unir dos regiones, o un elemento a una región. Muchos de los resultados no deseados en una imagen de rango están directamente relacionados con el desempeño de este criterio. Entre los resultados no deseados en una imagen segmentada, se encuentran: la sobre-segmentación, la sub-segmentación y la mala definición de los bordes.
En la literatura se pueden encontrar dos tipos de criterios de similitud empleados por los algoritmos de segmentación, estos son: los basados en el ajuste de modelos paramétricos a cada región, y los basados en el cálculo de una característica promedio representativa de la región como la normal o la curvatura. Una de las principales debilidades de ambos tipos de criterios es que al tomar el elemento representativo de cada grupo, ya sea un modelo paramétrico o la característica promedio, se asume una homogeneidad de cada región y no se tiene en cuenta el error de la aproximación debido al ruido presente en los datos de rango.
Solo algunos pocos trabajos utilizan funciones criterios, basados en la estadística, implicando las observaciones de cada grupo en la medida o cálculo de la probabilidad de unión. Una de las razones de lo anterior es el alto costo computacional que ello implica.
BIBLIOGRAFÍA
1. BESL, P. and JAIN, R. (1988). Segmentation through variable-order surface fitting. In: IEEE Transactions on Pattern Analysis and Machine Intelligence. Vol. 10, No. 2, pp. 167 - 192 [ Links ]
2. BOULANGER, P., OSORIO, G., and PRIETO, F. (2005). Hierarchical segmentation of range images with contour constraints. In: The 5th International Conference on 3-D Digital Imaging and Modeling, pp. 278 - 284, Ottawa, Canada. [ Links ]
3. DÍAZ, I., BRANCH, J. and BOULANGER, P. (2005). A genetic algorithm to segment range image by edge detection. In: Conference on Industrial Electronics and Control Applications, ICIECA 2005, pp. 7, Quito, Ecuador. [ Links ]
4. DUDA, O., HART, P., STORK, D. (2001). Pattern classification, Ed. Wiley-Interscience, Second edition, pp. 20-159, United State. [ Links ]
5. HOOVER, A. (1996). An experimental comparison of range image segmentation algorithms. In: IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 18, pp. 673 - 689. [ Links ]
6. JIANG, X. and BUNKE, H. (1994). Fast segmentation of range images into planar regions by scan line grouping. In: Machine Vision and Applications. Vol. 7, No. 2, pp. 115 - 122. [ Links ]
7. KATZ, S. and TAL, A. (2003). Hierarchical mesh decomposition using fuzzy clustering and cuts. In: ACM Transactions on Graphics (Proceedings SIGGRAPH 2003). Vol. 22, No. 3, pp. 954-961. [ Links ]
8. KÖSTER, K. and SPANN, M. (2000). MIR: An approach to robust clustering - application to range image segmentation. In: IEEE Transaction on Pattern Analysis and Machine Intelligence, Vol. 22, No. 5, pp. 430-444. [ Links ]
9. LAVALLE, S. and HUTCHINSON, S. (1995). A bayesian segmentation methodology for parametric image models. In: IEEE Transactions on Pattern Analysis and Machine Intelligence. Vol. 17, No. 2, pp. 211-217. [ Links ]
10. LEE, K., MEER, P. and PARK, R. (1998). Robust adaptive segmentation of range images. In: IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 20, No. 2, pp. 200-205. [ Links ]
11. SANDER, P., WOOD, Z., GORTLER, SNYDER, and HOPPE, H. (2003). Multi-chart geometry images. In: Proceedings of the Eurographics Symposium on Geometry Processing, pp. 146-155. [ Links ]
12. SHAMIR, A. (2004). A formalization of boundary mesh segmentation. In: Proceedings of the 2nd International Symposium on 3DPVT. [ Links ]
13. SHLAFMAN, S., TAL, A. and KATZ, S. (2002) Metamorphosis of polyhedral surfaces using decomposition. In: Proceedings of Eurographics, pp. 219-228. [ Links ]
14. VIEIRA, M., SHIMADA, K. (2005). Surface mesh segmentation and smooth surface extraction through region growing. In: Computer Aided Geometric Design, Vol. 22 No. 8, pp. 771-792. [ Links ]
15. YAMAUCHI H., LEE, S., LEE, Y., OHTAKE, Y., BELYAEV, A. and SEIDEL, H. (2005). Feature sensitive mesh segmentation with mean shift. In: International Conference on Shape Modeling and Applications, pp. 238-245. [ Links ]
16. ZUCKERBERGER, E., TAL, A. and SHLAFMAN, S. (2002). Polyhedral surface decomposition with applications. Computers & Graphics, Vol. 26, No. 5, pp. 733-743. [ Links ]
Recibido: 22/08/2007
Aceptado: 26/08/2007