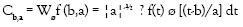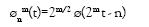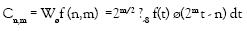Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Ingenierías Universidad de Medellín
Print version ISSN 1692-3324On-line version ISSN 2248-4094
Rev. ing. univ. Medellin vol.6 no.11 Medellín July/Dec. 2007
PREVISIÓN DE CRISIS EPILÉPTICAS USANDO TRANSFORMADA WAVELET Y CORRELACIÓN CRUZADA
PREVENTION OF EPILEPTICAL CRISIS USING WAVELET TRANSFORM AND CROSS-CORRELATION
Claudia C. Botero Suárez*; Erich Talamoni Fonoff**; Gerson Ballester, PhD***; Francisco Javier Ramírez-Fernández****
* Magíster en Ingeniería Eléctrica; profesora de Ingeniería de Telecomunicaciones, Universidad de Medellín. ccbotero@udem.edu.co
** Laboratorio de Neurocirugía Funcional
*** Laboratorio de Neurocirugía Funcional
**** Doctor en Microelectrónica; Coordinador del programa de postgrado de Ingeniería Eléctrica de la Escuela Politécnica de la Universidad de Sao Paulo. javier.ramirez@poli.usp.br
Resumen
Este artículo describe la detección de actividad precrisis mediante la aplicación de la correlación cruzada junto con la transformada Wavelet. La transformada Wavelet es aplicada a los datos EEG puros para la reducción y pre-procesamiento de las señales. Esta técnica de extracción de características provee las señales simplificadas para ser procesadas por medio de la técnica de correlación cruzada. El análisis ha sido realizado con un grupo de datos tanto precrisis como intercrisis, (incluyendo crisis agudas inducidas y crisis espontáneas recurrentes), con el fin de determinar su sensitividad y especificidad (tasa de falsas predicciones). Son determinados, adicionalmente, el período de ocurrencia de crisis y el horizonte de previsión de crisis.
Palabras clave
Datos epileptogénicos, previsión de crisis, transformada wavelet, correlación cruzada.
Abstract
This paper describes the detection of a pre-crisis activity through the application of Cross-Correlation together with the Wavelet Transform. The Wavelet Transform is applied in the data reduction and pre-processing of signals. This feature extract technique provides the simplified signals to process by means of the Cross-Correlation technique. The analysis with a group of pre-crisis and inter-crisis data (including both induced acute crises and recurrent spontaneous crises), to determinate its sensitivity and its specificity (False Prediction Rate) has been done. The seizure occurrence period and the seizure prediction horizon are calculated additionally.
Key Words:
Epileptogenic data, crisis prevention, Wavelet transform cross-correlation.
INTRODUCCIÓN
La teoría que explica la generación de las señales de EEG está lejos de ser totalmente aclarada. Sin embargo, hay una variedad de métodos que se puedan utilizar para cuantificar los cambios presentes en esas señales. Varias de las técnicas son complementarias y proporcionan diferentes puntos de vista del mismo fenómeno. Algunos de esos métodos cuantifican los precursores de las crisis mediante el estudio de los patrones de disparo de la actividad epileptiforme compleja y de la interrupción de las formas de onda normales de fondo. Dentro de estas técnicas se encuentran, por ejemplo, la detección y cuantificación del número de disparos subclínicos pseudocrisis [2] y métodos de detección de ocurrencia de crisis [1].
Una vez que estos métodos están disponibles para detectar precursores de crisis, todavía resta la pregunta sobre cómo aplicarlas de la mejor manera sobre pacientes específicos. Esteller [1] ha demostrado que para un paciente dado, los métodos que usan las características cuantitativas complementarias múltiples permiten detectar las crisis epilépticas más exactamente que aquellos que usan características cuantitativas simples. De esa manera, cuando se encuentra la combinación de mejor desempeño para un paciente dado, el vector de características resultante es usado para configurar el método o entrenar la red neural para evaluar los datos de chequeo y para una potencial implementación online.
El análisis realizado en este trabajo, y cuyo detalle se describe en las secciones posteriores, busca determinar la confiabilidad de un método de previsión de crisis basado en técnicas matemáticas que han sido usadas separadamente para el estudio de este tipo de señales [4,8,3], y que se estima que en una adecuada combinación puedan ayudar a la localización más exacta de patrones. Con esta finalidad se hace en este trabajo una descomposición inicial de las señales electroencefalográficas usando la Transformada Wavelet Discreta, con el objeto de separar la información que esté contenida en los rangos de frecuencias determinados por los estudios clínicos: alfa, beta, delta, theta, gama y súper gama. Estas señales simplificadas son procesadas matemáticamente por medio de la correlación cruzada, la cual permite determinar la existencia de patrones en una señal o conjunto de señales.
La estructura de este artículo es entonces la siguiente: en la próxima sección se describe brevemente el método para computar los coeficientes Wavelet, y su interpretación en una señal dada. A continuación, son usados los coeficientes Wavelet como características que permiten anticipar crisis mediante el análisis de correlación cruzada. Esos resultados son evaluados para determinar la sensitividad, tasa de Falsas predicciones y tiempo de previsión.
MATERIALES Y MÉTODOS
A. Datos EEG
Los datos EEG fueron obtenidos de ratas Wistar adultas con arreglos de 8 electrodos bipolares de Ni-Cr implantados en los lóbulos frontal y parietal. Las ratas son sometidas al status epilepticus mediante inyección de Pilocarpina, siguiendo el modelo animal de epilepsia crónica [5,6].
Después de 7 días, son captados registros continuos a una frecuencia de muestreo de 256 Hz. La mitad de los datos fue usada para configurar el método y la otra mitad fue usada para chequearlo.
B. Transformada Wavelet
La Transformada Wavelet Continua (TWC) de una señal análoga f(t) es expresada como [4]:
La función ø [(t-b)/a] es obtenida mediante la translación b y la dilatación a (el factor de escala) de la 'Wavelet Básica' (o 'Wavelet Madre') ø(t). El resultado de la TWC son muchos coeficientes Wavelet Cb,a. Con el fin de construir algoritmos eficientes para calcular la Transformada Wavelet Wøf (b,a), son usualmente elegidos valores diádicos b=m/2n y a=1/2n. Esta forma de la Trasformada Wavelet es llamada la Transformada Wavelet Diádica o Trasformada Wavelet Discreta (TWD). En la TWD, la Wavelet madre se expresa como:
Y los coeficientes Wavelet de la ecuación (1) están dados por:
En las ecuaciones (2) y (3), n es ahora el factor de traslación y m el factor de escala. Entre mayores sean los valores de m, menores son los componentes de frecuencia.
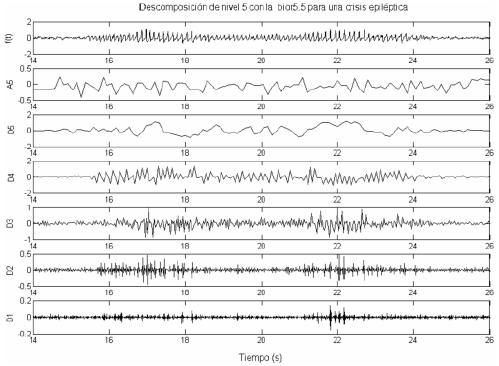
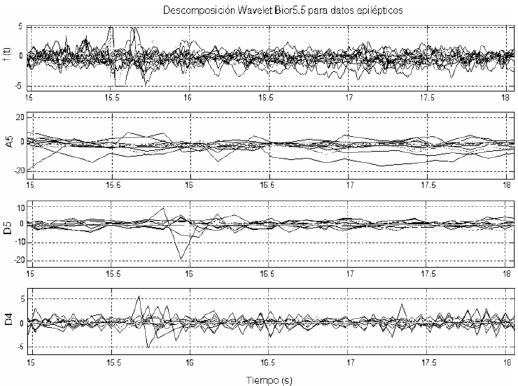
La biortogonal es una Wavelet madre, que ha presentado buenos resultados en la clasificación de señales EEG [8,3]. En particular, mediante el uso de la descomposición de quinto nivel de señales EEG crudas muestreadas a 256 Hz por canal, los rangos de frecuencia de los niveles (figura 1) se sitúan cerca de las bandas de frecuencias definidas como estándares clínicos: súper-gama (64-128 Hz), gama (32-64 Hz), beta (16-32 Hz), alfa (8-16 Hz), teta (4-8 Hz) y delta (2-4 Hz). Esto se ve más claramente en la figura 1 que muestra los resultados de aplicar la Wavelet Biortogonal de orden 5 para señales EEG epilépticas de un electrodo cortical.
Figura 1. Transformada Wavelet con la descomposición de la señal EEG f(t) en varias bandas de frecuencias.
A5 muestra los componentes de frecuencia en el nivel 5, mientras que las partes detalladas (D1-D5) muestran los componentes de frecuencia más altos en cada nivel de descomposición. La señal original f(t) es reconstruida por medio de la suma de todos los componentes.
El análisis de la señal inicia con la creación de una ventana de procesamiento de 7692 muestras, representando aproximadamente 30 segundos de datos por cada canal. El pre-procesamiento por medio de la transformada Wavelet es aplicado a las señales EEG crudas dentro de la ventana para determinar los coeficientes que serán usados como características que describen la señal.
C. Procesamiento mediante correlación cruzada
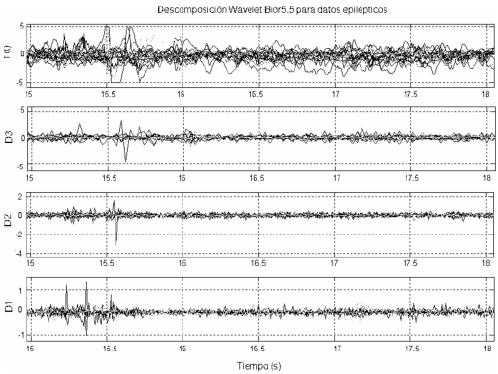
Los coeficientes obtenidos con la transformada Wavelet son separados en 6 arreglos representando cada banda de frecuencia y conteniendo los coeficientes Wavelet de los 8 canales en el dominio del tiempo (figuras 2 y 3). Esta separación en bandas de frecuencias permite encontrar características que se manifiestan más en algunas frecuencias que en otras. Y el complemento con la correlación permite determinar patrones que no son perceptibles a simple vista.
Figura 2. Coeficientes Wavelet agrupados por bandas de frecuencias. Niveles A5 (ä), D5 (è) y D4 (á) para todos los canales en un intervalo de tiempo.
Figura 3. Coeficientes Wavelet agrupados por bandas de frecuencias. Niveles D3 (â), D2 (ã) y D1 (Sã) para todos los canales en un intervalo de tiempo.
En cada arreglo, los 8 canales fueron correlacionados cruzadamente por pares, creando 8 vectores de correlación cruzada. Los M vectores fueron promediados y la desviación estándar fue usada como una medida de sincronía. La correlación cruzada fue recalculada para cada nuevo segundo de datos EEG adquiridos, y la sincronía medida en cada banda de frecuencia fue usada para determinar si estaba próxima a ocurrir una crisis.
Con los datos de configuración, el valor crítico de la medida de sincronía se seleccionó de manera que el 100% de las crisis tenía una desviación estándar menor que este valor, y el 1% de los datos sin crisis tenían una desviación estándar menor que este valor crítico.
D. Evaluación del método
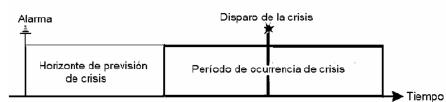
Los actuales métodos de previsión están aún lejos de la perfección, entonces Winterhalder [7] sugirió considerar la incertidumbre para indicar el punto exacto en el tiempo cuando iba a ocurrir una crisis. Esa incertidumbre puede ser considerada por medio del período de ocurrencia de crisis (POC), que está definido como el período durante el cual es esperado que ocurra una crisis. Adicionalmente, se denota el horizonte de previsión de crisis (HPC) como la ventana mínima de tiempo entre la activación de la alarma por parte del método de previsión y el comienzo del POC (Figura 4).
Figura 4. Períodos estimados para considerar la incertidumbre al indicar el momento exacto en que va a ocurrir una crisis.
Los dos períodos deben ser tenidos en cuenta para juzgar una previsión como correcta. Para una correcta previsión, no debe ocurrir ninguna crisis durante el horizonte de previsión, pero sí durante el período de ocurrencia. Por lo tanto se debe definir un valor mínimo para el horizonte de previsión de crisis y un valor máximo para el período de ocurrencia de crisis, según el sistema de intervención elegido. Mientras los dispositivos implantados pueden requerir sólo de unos pocos segundos para controlar una crisis en proceso, un sistema de alarma tiene que predecir la crisis por lo menos unas decenas de segundos antes de ocurrir para que se puedan tomar medidas de prevención o por lo menos colocar al paciente en una situación segura. De forma similar, el período de ocurrencia debe estar limitado por el riesgo de los efectos colaterales producidos por una intervención prolongada, sea electro-estimulación o aplicación de medicamento anticonvulsivos. En el caso de sistemas de alarma, se debe considerar el estado de ansiedad a que se somete el paciente.
RESULTADOS
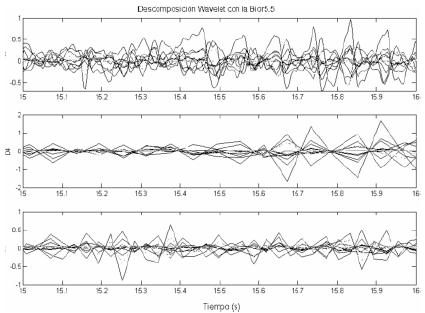
El uso de los coeficientes Wavelet permite un análisis más rápido y representa un soporte para confirmar con mayor certeza los eventos que están ocurriendo y que algunas veces no son identificados claramente en los datos crudos. Las figuras 2 y 3 muestran que en casi todas las bandas de frecuencias se pueden identificar cambios significativos en algunos canales en el intervalo de tiempo entre 15,5 y 16 segundos, demarcando una crisis epiléptica. La figura 5 presenta el detalle de una sola banda de frecuencias, la wavelet D4, que en este caso representa los ritmos alfa. Esta banda muestra una amplitud y sincronía mayores a partir de los 15.6 segundos.
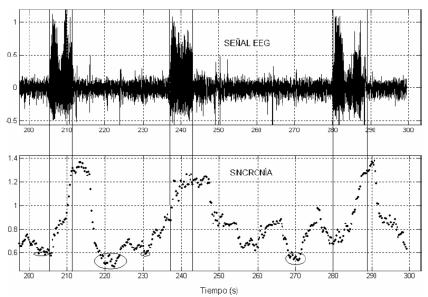
Pero el propósito va más allá de la detección de crisis, tratando de anticipar su ocurrencia. Para este objetivo se hace necesaria entonces la correlación cruzada. Como se describió anteriormente, cuando se hace el análisis de correlación entre los coeficientes de todos los canales en cada banda de frecuencias, se obtiene un valor de sincronía a partir de la desviación estándar. La figura 6 muestra la sincronía obtenida en la banda delta (Wavelet D5) que representa las frecuencias entre 4 y 8 Hz.
Este ejemplo muestra que los valores de sincronía mayores se encuentran en el período poscrisis, anticipados por una inclinación máxima positiva durante la crisis. Pero existen algunos valores mínimos que se encuentra por debajo de los 0.6 para esta banda de frecuencias. Esos valores menores a un límite obtenido en el período precrisis (indicado con circunferencias en la figura 6 permiten activar una alarma indicando que una crisis está próxima a ocurrir.
Figura 5. Detalle de los coeficientes wavelet en los niveles D4 y D3, en el segundo donde comienza una crisis epiléptica.
Figura 6. Análisis de sincronía obtenido a partir de la desviación estándar de la correlación cruzada.
DISCUSIÓN
La sensitividad (S) de un método de previsión se calcula como la fracción de las predicciones correctas respecto a todas las crisis ocurridas, mientras que la tasa de falsas predicciones (TFP) cuantifica el número de falsas predicciones por unidad de tiempo.
El método de detección de actividad precrisis fue evaluado con un conjunto de datos EEG independientes de los usados en la configuración. El método identificó 19 de las 31 crisis marcadas por los expertos, representando una sensitividad de 61,29% .
Debido a que las consideraciones clínicas no han determinado aún los valores aceptables para la TFPmax, HPCmin y POCmax, Winterhalder [7] propuso la comparación con las condiciones mínimas que un método estadístico puede ofrecer, usando algunas suposiciones 'razonables' independientemente de cualquier aplicación clínica particular. Por ejemplo, la ocurrencia media de las crisis puede indicar un rango razonable para la TFPmax:
Bajo monitoreo prequirúrgico, los pacientes dejan de tomar medicamentos de control y pueden alcanzar una frecuencia de ocurrencia de 3,6 crisis por día, significando 0,15 crisis por hora [7]. De esa manera, unos valores razonables para la TFPmax serían menores a la frecuencia de crisis representando el peor de los casos con una tasa máxima de 50% de falsas alarmas.
Es este estudio hecho con ratas a las cuales se les aplicó Pilocarpina, los registros son captados durante el período agudo similar al de monitoreo prequirúrgico en humanos, lo cual puede representar aproximadamente 0,15 FP/h. El método de previsión identificó falsamente 2 crisis que no habían sido marcadas por los especialistas en un conjunto de datos que suman 4 horas de registro, representando una TFP de 0,5 FP/h. Este valor es bajo pero no se encuentra dentro de los valores máximos esperados, debido posiblemente a que son necesarios registros continuos aún más largos (en lo posible alrededor de 24 horas) para lograr TFP mucho menores que 1 FP por día.
Por otro lado, este estudio consiguió tiempos de 13 segundos para el horizonte de previsión, y 137 segundos para el período de ocurrencia, correspondiendo a los valores mínimos para sistemas de intervención rápidos.
CONCLUSIONES
La posibilidad de lograr métodos de previsión de crisis puede mejorar la calidad de vida y la seguridad de los pacientes con epilepsia, brindando una ventana de tiempo durante la cual se podría dar un aviso o aplicar intervención terapéutica automatizada, logrando con eso minimizar el riesgo de accidentes y hasta posiblemente evitar la ocurrencia de la crisis. También pueden ser disminuidos los efectos secundarios de un tratamiento farmacológico de largo plazo.
Un método de previsión orientado a aplicaciones clínicas debe presentar una alta sensitividad para reducir la incertidumbre de los pacientes acerca de la ocurrencia inminente de una crisis, o mejor aún, activar un sistema de intervención para evitar que la crisis ocurra. Simultáneamente, se deben calcular las falsas predicciones del sistema porque en el caso de valores altos, se puede causar que los pacientes ignoren el sistema de alarma, o se estaría llevando a posibles efectos colaterales por las intervenciones innecesarias.
El horizonte mínimo de previsión de crisis y el período máximo de ocurrencia de crisis tienen que estar basados en consideraciones clínicas, porque un POC largo estaría incrementado el estrés psicológico del paciente, mientras que un HPC corto no brindaría suficiente tiempo para evitar daños en el paciente.
En este trabajo se evaluaron las características de un método para la detección automática de actividad precrisis, usando las técnicas de la transformada Wavelet y la correlación cruzada. El estudio preliminar mostró la viabilidad de usar estas técnicas para la previsión de la epilepsia, mas se requieren mejoras en el método para ajustar los valores de sensitividad, falsas predic ciones y tiempos de aviso orientados a una aplicación clínica.
RECONOCIMIENTO
Este trabajo está soportado por fondos del PNM del Consejo Nacional de Desarrollo Científico e Tecnológico -CNPq-, Brasil.
BIBLIOGRAFÍA
1. R. ESTELLER, J. ECHAUZ, M. D'ALESSANDRO, G. VACHTSEVANOS, B. LITT, 'Feature parameter optimization for seizure detection / prediction', Proceedings of the 23rd Annual EMBS International Conference, pp. 1711-1714, October 25-28, 2001. [ Links ]
2. J. J. NIEDERHAUSER, R. ESTELLER, J. ECHAUZ, G. VACHTSEVANOS, B. LITT. 'Detection of Seizure Precursors From Depth-EEG Using a Sign Periodogram Transform'. IEEE Trans. on Biom. Eng., vol. 51, No. 4, pp. 449-458, April 2003. [ Links ]
3. J. S. PAUL, C. B. PATEL, H. AL-NASHASH, N. ZHANG, W. C. ZIAI, M. A. MIRSKI, D. L. SHERMAN. 'Prediction of PTZ-Induced Seizures Using Wavelet-Based Residual Entropy of Cortical and Subcortical Field Potentials'. IEEE Trans. on Biom. Eng., vol. 50, No 5, May 2003. [ Links ]
4. N. V. THAKOR, S. TONG. 'Advances in Quantitative Electroencephalogram Analysis Methods'. Annu. Rev. Biomed. Eng., v. 6, pp 453-95, April 2004. [ Links ]
5. W.A. TURSKI, E.A. CAVALHEIRO, M. SCHWARZ, S.J. CZUCZWAR, Z. KLEINRONK, L. TURSKI. 'Limbic seizures produced by pilocarpine in rats: behavioral, electroencephalographic and neurophatological study'. Behav. Brain Res., 1983, 9:315-336. [ Links ]
6. L. TURSKI, C. IKONOMIDOU, W.A. TURSKI, Z.A. BORTOLOTTO, E.A. CAVALHEIRO. 'Cholinergic mechanisms and epileptogenesis. The seizures induced by pilocarpine: a novel experimental model of intractable epilepsy'. Synapse, 1989, 3(2):154-71. [ Links ]
7. M. WINTERHALDER, T. MAIWALD, H.U. VOSS, R. SCHENBRENNER-SCHEIBE, J. TIMMER, A. SCHULZE-BONHAGE, 'The seizure prediction characteristic: a general framework to assess and compare seizure prediction methods', Epilepsy & Behavior, 4, pp. 318-325, 2003. [ Links ]
8. C. YAMAGUCHI. 'Fourier and Wavelet Analyses of Normal and Epileptic Electroencephalogram (EEG)'. Proceedings of the 1st International IEEE EMBS Conference on Neural Engineering, pp. 406-409, March 2003. [ Links ]
Recibido: 07/08/2007
Aceptado: 12/08/2007