Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Ingenierías Universidad de Medellín
Print version ISSN 1692-3324On-line version ISSN 2248-4094
Rev. ing. univ. Medellin vol.7 no.12 Medellín Jan./June 2008
Dos aproximaciones a la metodología de diseño a momento flexionante de secciones T en concreto reforzado que se comportan como rectangulares y constituyen la sección recta de la viguetería de losas aligeradas
Two approaches to design methodology at T sections bending moment in reinforced concrete which behave as rectangular sections and constitute the straight sections of beams of light slabs
José Christian Chanchí Golondrino1; Luz Ángela Marín Torres2
1 Ingeniero Civil Universidad del Cauca - Magíster en Ingeniería Civil (Área Estructuras). Universidad de los Andes - Profesor Asistente adscrito al Departamento de Ingeniería Civil - Jefe de Laboratorio de Estructuras - Director del Grupo de Investigación ESTRUCTUNAL - Universidad Nacional de Colombia - Sede Manizales. Consultor asociado a la Compañía CAPE (Colombian Association of Professional Engineers). Dirección: Universidad Nacional de Colombia- Sede Manizales, Departamento de Ingeniería Civil, Campus la Nubia, Oficina V224, Manizales (Caldas) – Colombia. Teléfono: + (57) 6-8745409 Ext. 55799 Fax + (57) 6- 8879300 Ext. 50313. E-mail: jcchanchigo@unal.edu.co
2 Ingeniero Civil - Universidad Nacional de Colombia - Sede Manizales. Dirección: Armetales S.A.- Manizales, Cra 19 No 24-58. Teléfono: + (57) 6- 8842227 Ext. 160 Fax + (57) 6- 8800284. E-mail: angela.marin@armetales.com
RESUMEN
El presente artículo esboza dos aproximaciones sobre la ecuación de diseño a momento flexionante de secciones T en concreto reforzado que se comportan como secciones rectangulares y que trabajan como viguetería de losas aligeradas. La primera aproximación discute la viabilidad de usar el ancho del nervio de la vigueta en lugar de usar el ancho efectivo de la aleta, dentro del proceso de la obtención del acero, requerida para asumir un momento flexionante; la segunda aproximación discute la viabilidad de aproximar la ecuación cuadrática que rige la obtención del área del acero requerida para obtener un momento flexionante en una ecuación lineal, cuyas únicas variables son el área del acero y la altura efectiva de la sección T. Se ha dimensionado geométricamente un conjunto de secciones de losas aligeradas siguiendo los requisitos del título C13 de la norma sismo resistente colombiana NSR98, los cuales se obtuvieron para un modelo simplemente apoyado, cuya luz varía entre [2 - 7] m y el ancho del casetón ente [0.30 – 1] m. El dimensionamiento antes mencionado fue utilizado para sensibilizar la efectividad de cada una de las aproximaciones propuestas respecto a la solución general para la obtención del área del acero de la sección T que se comporta como rectangular.
Palabras clave: losas aligeradas, sección T, diseño a momento flexionante, viguetas simplemente apoyadas.
ABSTRACT
This article presents two approaches on the moment design equation of T shaped beams. Particularly the beam's T cross section analyzed behaves like a rectangular cross section when the beam works like a component of a slab system built from a set of T shaped beams. The first approach discusses the feasibility to use the web width instead of effective flange width to obtain the steel area associated to the moment solicitation of T shaped beam. The second approach discusses the feasibility to approach the quadratic equation used to obtain the steel required to take the bending moment into linear equation related to variables such as steel area and the effective depth of the T shaped cross section. It has designed geometrically a set of slabs (built from T shaped beams) according to the regulations presented in the chapter C13 of the Seismic Constructions Colombian Code. The other hand the reinforcement associated to the slabs was obtained for single supported T shaped beams with spans in the range [2 – 7] m and separations between them in the range [0.30 – 1.00] m. The design process described above was used to check the reliability of the discussed approaches with respect to the general solution (quadratic equation) used to obtain the reinforcement of a T shaped beam when the behaviour of its section is close to a rectangular equivalent cross section.
Keywords: T shaped slab system, T shaped section, Bending moment design, T shaped singled supported beam.
INTRODUCCIÓN
Con el fin de presentar el desarrollo matemático y la sensibilidad que soporta cada una de las aproximaciones sobre la metodología de diseño a momento flexionante de secciones T que trabajan como viguetería de losas aligeradas, este artículo se ha dividido en cuatro partes. En la primera parte se deduce la ecuación cuadrática que gobierna el diseño a momento flexionante de secciones rectangulares, la cual es aplicada a secciones T que trabajan como tal. En la segunda parte se esboza la primera aproximación realizada sobre la ecuación cuadrática, la cual está relacionada con el ancho de la sección a considerar durante el proceso de diseño; para tal consideración se efectúan los respectivos ajustes sobre la ecuación; a la ecuación resultante se le efectúa una sensibilidad en aras de demostrar la efectividad de esta aproximación. En la tercera parte, se propone realizar una nueva aproximación sobre la ecuación cuadrática la cual consiste en prescindir del término cuadrático; en este sentido, la ecuación ajustada se convertirá en una ecuación lineal, para la cual se efectúa la sensibilidad respectiva con el fin de demostrar la efectividad de la nueva aproximación. Finalmente, se comentan los resultados asociados a cada una de las sensibilidades correspondientes a las aproximaciones objeto de este artículo, a partir de las cuales se realizan las conclusiones pertinentes.
METODOLOGÍA Y RESULTADOS
Para el diseño a momento flexionante de la sección de una vigueta de una losa aligerada se pueden seguir dos procedimientos:
a) Diseñar la sección siguiendo la teoría de diseño de secciones T según el caso, si la sección se comporta como rectangular o como una sección T (Park y Paulay, 1975).
b) Diseñar la sección realizando una aproximación, la cual consiste en despreciar el aporte de compresión que suministran las aletas, es decir, la sección de forma T se diseña como una sección rectangular de ancho igual al ancho del nervio y de altura igual a la altura de la losa (Rochel, 1999).
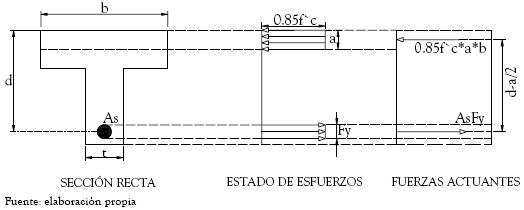
A continuación se expone un desarrollo matemático enfocado a demostrar la validez del procedimiento establecido en el literal b presentado anteriormente; para tal fin se supondrá el caso en el cual la sección T se comporta como una sección rectangular debido a que el bloque equivalente de compresión tiene una altura inferior a la de la aleta de la sección T. Se ha adoptado este caso debido a que corresponde a la totalidad de los diseños realizados como soporte de este artículo. La figura 1 representa el estado de esfuerzos y fuerzas actuantes en la sección bajo las consideraciones antes descritas.
Figura 1. Estado de esfuerzos y fuerzas actuantes sobre una sección T
Debido a que la filosofía de funcionamiento de la sección de una viga está basada en la generación de un par resistente conformado por la fuerza de compresión en el concreto y la de tensión en el acero, es inminente la igualdad de estas fuerzas debido a las características mecánicas de un par (Park y Paulay, 1975); mencionada igualdad se puede expresar a través de la siguiente expresión
A partir de la ecuación (1) es posible expresar la altura del bloque equivalente de compresión en función de las propiedades mecánicas de los materiales que constituyen la sección y las propiedades geométricas de la misma como se aprecia en la ecuación (2)
Uno de los objetivos de obtener la altura del bloque equivalente es posicionar la fuerza resultante de compresión respecto a la fuerza de tensión; en ese sentido la distancia entre las fuerzas que constituyen el par queda definida como se presentó en la figura 1 (fuerzas actuantes), y la capacidad nominal de la sección podrá obtenerse como el producto de una de las fuerzas por la distancia; particularmente se usará la fuerza asumida por el acero, lo cual conduce a la expresión para la capacidad nominal (momento nominal Mn) para la sección T comportándose como sección rectangular, como se muestra en la ecuación (3)
La sustitución de la ecuación (2) en la ecuación (3) permite obtener la capacidad nominal a momento de la sección en función de las características mecánicas de los materiales que la constituyen y sus propiedades geométricas.
Para efectos de diseño, la ecuación (4) debe ser factorada por un coeficiente de reducción f cuyo valor es establecido por la norma sismo-resistente colombiana NSR98 en el numeral C 9.3.2. (Coeficientes de reducción de resistencia), una vez factorada la ecuación se obtiene la capacidad nominal a momento (fMn) de la sección T comportándose como rectangular, la cual es expresada a través de la ecuación (5).
La filosofía de diseño de la sección consiste en igualar la capacidad nominal (fMn) con la solicitación correspondiente a momento (Mu) proveniente del análisis estructural de la estructura cuando está sometida a cargas mayoradas; mencionada filosofía es establecida por la Norma Sismorresistente Colombiana NSR98, capítulo C10 (Flexión y Fuerza Axial) y puede expresarse a través de la ecuación
La asociación de las ecuaciones (5) y (6) permite obtener la expresión general de diseño para la sección T comportándose como rectangular, la cual se presenta a través de la ecuación (7)
Al revisar la expresión (7) se puede observar que está constituida por las propiedades mecánicas de los materiales, dimensiones geométricas, la acción externa mayorada, el factor de reducción, todos estos como datos, y como única variable aparece el área de acero; en ese sentido, es posible expandir la ecuación y darle la forma de una ecuación cuadrática en el área de acero; al realizar la operación algebraica mencionada se obtiene la siguiente expresión:
La expresión (8) es la ecuación general para el dimensionamiento a nivel del área de acero para una sección T que se comporta como rectangular. Esta ecuación fue sensibilizada para el caso de diseño de vigueteria simplemente apoyada con luces entre 2 m y 7 m con las limitaciones de material y requisitos aplicables provenientes de la norma sismo-resistente colombiana, NSR98, condiciones bajo las cuales se desarrollaron la totalidad de diseños que soportan este artículo. A continuación se describe la sensibilidad matemática sobre la ecuación de diseño (8) tendiente a demostrar la validez del proceso de diseño esbozado en el literal b de esta sección.
I. SENSIBILIDAD DE LA ECUACIÓN DE DISEÑO (8)
Para el desarrollo de la sensibilidad bajo las condiciones anteriormente establecidas se siguió la siguiente mecánica:
a) Definición de parámetros básicos de sensibilidad.
b) Desarrollo de sensibilidad.
A continuación se describen los procesos establecidos en los literales a y b
a) Definición de parámetros básicos de sensibilidad
Se consideraron dos tipos de parámetros básicos:
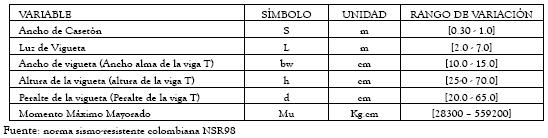
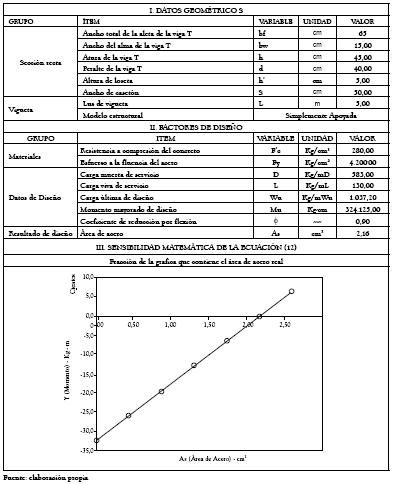
• Datos: Se consideran en esta categoría las limitaciones o constantes de material y de restricciones de diseño, establecidas por la norma sismo-resistente colombiana NSR98. La tabla 1 presenta el listado de parámetros contenidos en este subgrupo.
• Variables: Se consideran en esta categoría los valores cambiantes con las dimensiones de la luz en la geometría de la sección y cuantía de material. La tabla 2 presenta el listado de parámetros contenidos en este subgrupo.
Tabla 1 - Parámetros considerados como datos en la sensibilidad
Tabla 2 - Parámetros considerados como variables en la sensibilidad
El rango de variación del momento máximo mayorado fue extraído de la sensibilidad correspondiente al diseño de las viguetas simplemente apoyadas, realizado como soporte de este artículo.
b) Desarrollo de sensibilidad
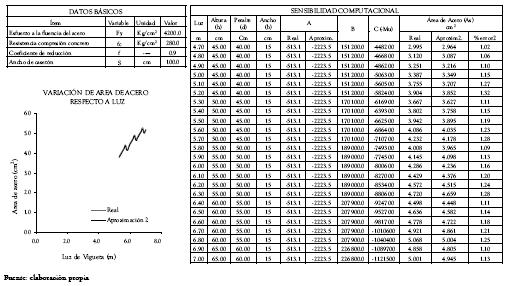
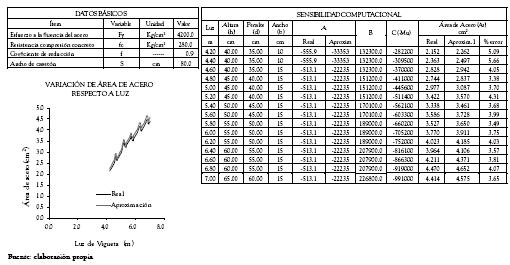
Para efectuar la sensibilidad en consideración se ha desarrollado una hoja electrónica en la cual a los datos y a las variables se les asignaron los valores o los rangos establecidos en las tablas 1 y 2, respectivamente. A partir de esta información base, se sensibilizaron las constantes de la ecuación cuadrática (8), las cuales se nombraran en forma análoga a las constantes de la expresión general de una ecuación cuadrática como se presenta a continuación
A partir de la ecuación (9) es posible observar que la aproximación objeto de esta sensibilidad está relacionada únicamente con la constante A, dado que el ancho de la sección está incluido en esta expresión; en este sentido, el valor de la constante A se ha obtenido para los casos mencionados a continuación:
CASO 1: Valor real de A
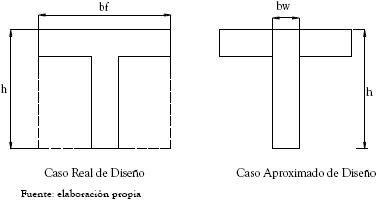
Se obtuvo el valor de la constante usando como ancho de sección (b) el ancho total de aleta de la viga T (bf), caso en el cual las sección a diseñar es de dimensiones bf x h como se muestra en la figura 2.
CASO 2: Valor aproximado de A
Se obtuvo el valor de la constante usando como ancho de sección (b) el ancho del alma de la viga T (bw), caso en el cual la sección a diseñar es de dimensiones bw x h como se muestra en la figura 2.
Figura 2. Consideraciones real y aproximada sobre el diseño de una sección T
Dada las anteriores consideraciones, al resolver la ecuación cuadrática correspondiente a cada luz, se obtuvieron dos áreas de acero cada una de ellas correspondiente a los casos 1 y 2 antes mencionados (área de acero real y área de acero aproximado). A partir de las dos áreas de acero en consideración se obtuvo un factor de error que permitió conceptuar la eficiencia de la metodología aproximada de diseño. La sensibilidad antes descrita fue desarrollada para 15 anchos de casetón pertenecientes al rango de variación establecido en la tabla 2, particularmente realizando variaciones cada 0.05m. Un conjunto de ejemplos de sensibilidad típica se presentan desde la tabla 3 a la tabla 6.
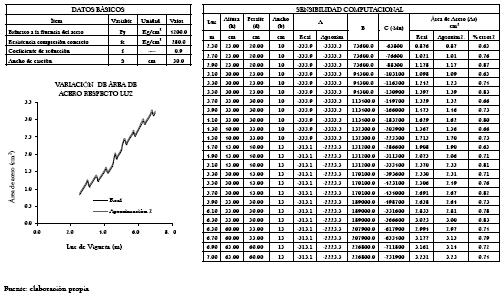
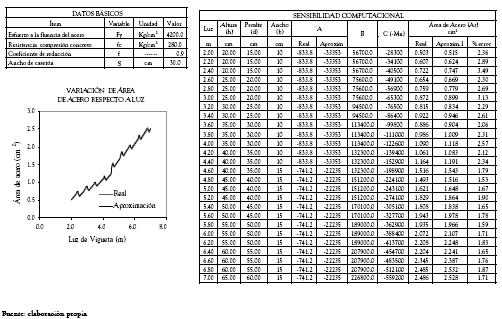
Tabla 3. Variación de Áreas de acero real y aproximada asociadas al diseño de una sección T que se comporta como rectangular para un ancho de casetón de 0.30 m.
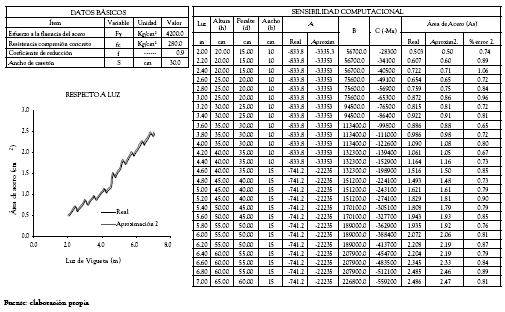
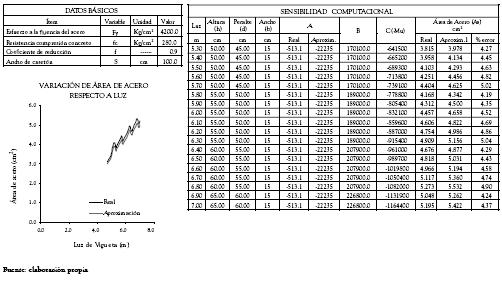
Tabla 4. Variación de Áreas de acero real y aproximada asociadas al diseño de una sección T que se comporta como rectangular para un ancho de casetón de 0.50 m.
Tabla 5. Variación de Áreas de acero real y aproximada asociadas al diseño de una sección T que se comporta como rectangular para un ancho de casetón de 0.80 m.
Tabla 6. Variación de Áreas de acero real y aproximada asociadas al diseño de una sección T que se comporta como rectangular para un ancho de casetón de 1.00 m.
II. RESULTADOS DE LA SENSIBILIDAD DE LA ECUACIÓN (8)
Al observar las áreas de acero real y aproximado obtenidas a partir de las sensibilidades presentadas en el numeral anterior se pueden realizar las siguientes precisiones:
1. Para el rango de ancho de casetones analizado [0.30 – 1.00] m la metodología de diseño expuesta para secciones T que se comportan como rectangulares genera áreas de acero superiores a las realmente requeridas, como se puede verificar en la columna denominada 'Porcentaje de Error', en las tablas 3, 4 y 5 presentadas anteriormente, las cuales hacen parte de un grupo total de 15 tablas asociadas al rango de casetones en el cual se realizó la sensibilidad. Particularmente el porcentaje de error al que se hace referencia fue calculado a través de la expresión:
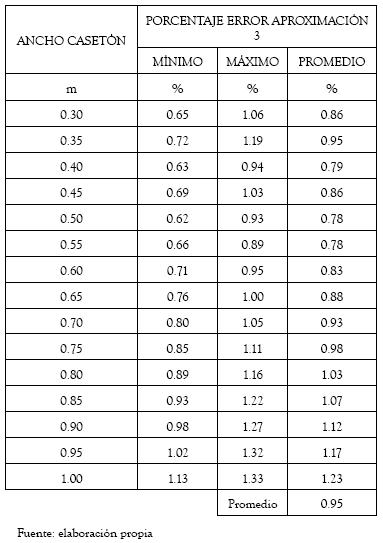
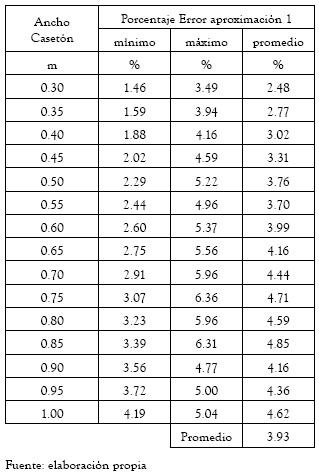
Desde esta ecuación, se puede afirmar que la metodología de diseño expuesta genera resultados conservativos. Particularmente un rango de errores para cada dimensión de casetón analizada en el rango de luces de 2 m a 7 m es presentado en la tabla 7.
Desde la tabla anterior se puede observar que el máximo porcentaje de error en el que se puede incurrir al usar la metodología de diseño aproximada es del 7% por encima de la solución real, condición que implica que el uso de la metodología aproximada no genera sobredimensionamientos que puedan afectar la economía dentro del proceso de diseño. De otro lado, al observar el error del valor promedio de la sensibilidad (3.93%) se puede establecer que la metodología aproximada es totalmente válida y segura para el diseño de vigueteria de sistema de losas aligeradas en el rango de casetones, objeto de esta publicación.
Tabla 7. Rango de errores de la comparación entre el área de acero real y el área de acero aproximada
III. APROXIMACIÓN SOBRE LA ECUACIÓN (8)
Desde el resultado establecido en la sección anterior, se puede afirmar que la ecuación cuadrática (8) es poco sensible al ancho (b) de la sección, parámetro que solo afecta el término cuadrático de la expresión en consideración, como se puede apreciar en la expresión matemática
Bajo estas consideraciones se puede establecer que el término cuadrático presenta una baja sensibilidad en la ecuación (8); por tal razón, mencionada ecuación podría aproximarse a una ecuación lineal (cuando se suprime su término cuadrático) cuya expresión matemática es:
Esta aproximación traería como ventaja un dimensionamiento rápido y simplista en el área de acero de una sección rectangular o de una vigueta que constituya un sistema de losa aligerado bajo las limitaciones geométricas establecidas en este artículo.
En esta sección se presentará un desarrollo matemático tendiente a demostrar la validez de la ecuación lineal (11) frente a la ecuación cuadrática (8) desde el punto de vista matemático y de dimensionamiento de área de acero en las secciones antes descritas.
IV. VALIDEZ MATEMÁTICA DE LA ECUACIÓN LINEAL (11)
- Descripción matemática de la ecuación (8)
Con el fin de verificar la validez matemática de la ecuación lineal (11) respecto a la ecuación cuadrática (8), se iniciará por describir matemáticamente la ecuación (8) usando la teoría básica de cálculo diferencial.
La ecuación básica a describir es una ecuación cuadrática expresada a través de la expresión (12) donde el área de acero (As) es la variable independiente y 'y' es la variable dependiente cuyo significado estructural es un momento flector
La descripción matemática de esta se realizará obteniendo los siguientes puntos característicos de la curva: intersección con el eje y, intersecciones con el eje x y vértice. La obtención de cada uno de estos puntos se presenta a continuación.
• Intersección con el eje y Para obtener la intersección con el eje y, basta reemplazar el área de acero (As) por cero, con lo cual se encuentra que la ordenada de este punto corresponde al momento solicitante (Mu), para el cual se desea obtener el área de acero. El respectivo reemplazo se presenta a continuación.
Así la abscisa y la ordenada de la intersección con el eje y están dadas por el punto coordenado:
• Intersecciones con el eje x Las intersecciones de la ecuación con el eje x corresponden a las raíces de la ecuación, que para este caso serán dos, dado el grado de ecuación en consideración; mencionadas raíces serán obtenidas usando la solución general de una ecuación cuadrática dada a través de la expresión (15) la cual fue adoptada a la expresión (9) de este articulo.
Por comparación directa entre la ecuación (9) y la ecuación (12), se puede establecer que las expresiones para las constantes A, B y C serán:
Al sustituir apropiadamente los valores de las constantes A, B y C en la solución general de la ecuación dada por la expresión (15) se encuentra que:
Al efectuar las reducciones apropiadas sobre la expresión (19) se encuentra una expresión general para las raíces de la ecuación la cual está dada por:
Finalmente las intersecciones de la ecuación con el eje x estarán dadas por dos puntos coordenados, donde las abscisas corresponden a la expansión de la expresión (20) y las ordenadas a un valor nulo en la variable dependiente.
Matemáticamente, las dos raíces siempre serán positivas para valores consistentes de los parámetros mecánicos y geométricos asociados al dimensionamiento del acero de una viga sometida a flexión. En cuanto al significado estructural solo debe tenerse en cuenta la expresión (21), la cual arroja la menorá rea de acero, condición que se puede verificar en las sensibilidades de diseño presentadas en las tablas 3, 4, 5 y 6, respectivamente.
• Vértice
El vértice puede ser obtenido como el único punto crítico de la ecuación; para tal fin la ecuación en estudio (12) debe ser derivada respecto al área de acero (As) e igualada a cero en aras de obtener la abscisa del vértice; la expresión que satisface esta condición está dada por:
Resolviendo para el área de acero se encuentra que la abscisa de punto crítico asociada al vértice es:
A partir de la abscisa del punto critico, es posible conocer matemáticamente si el punto corresponde a un máximo o un minino, sustituyendo este en la segunda derivada de la ecuación en estudio (12); mencionada derivada está dada por la expresión (25), la cual está constituida por una constante menor que cero, condición que puede ser interpretada matemáticamente como la presencia de un máximo; por tal razón, la parábola definida por la expresión (12) es cóncava hacia abajo.
La ordenada del vértice puede ser encontrada sustituyendo la expresión de la abscisa (24) en la ecuación de estudio (12); la respectiva sustitución se muestra en la siguiente expresión:
Al efectuar las reducciones sobre la expresión (26) se encuentra que la ordenada del vértice está dada por la ecuación:
En este contexto el punto coordenado que define el vértice será:
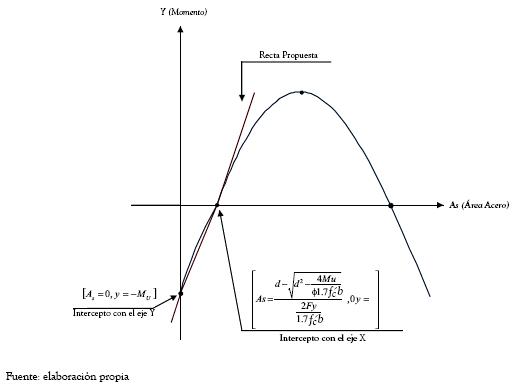
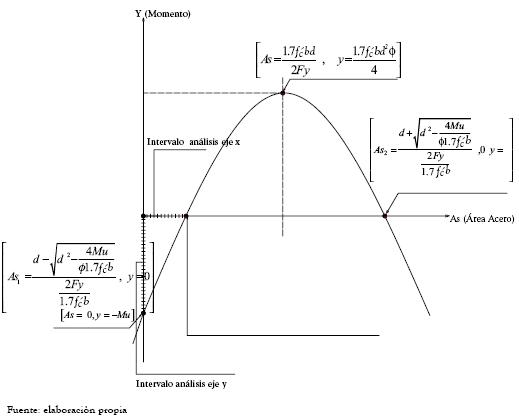
A partir de los puntos coordenados obtenidos que definen la intersección con el eje y, la intersección con el eje x y el vértice es posible realizar un esbozo de la ecuación en estudio (12); una grafica general de esta ecuación es presentada en la figura 3.
Figura 3. Descripción matemática de la ecuación cuadrática (12) Con el fin de ilustrar el comportamiento gráfico de la ecuación (12) se ha realizado una sensibilidad de la misma para lo cual se ha seleccionado uno de los ejemplos de diseño (vigueta) que forma parte de la sensibilidad de diseño, soporte de este artículo.
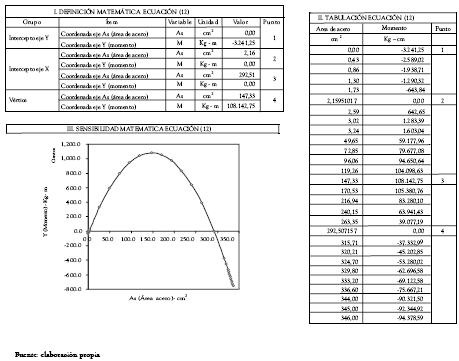
Para la vigueta en consideración, las características geométricas y de los materiales se han considerado constantes, mientras que el área de acero se ha variado, encontrando para cada área de acero el momento respectivo. Un sumario de este proceso es presentado en la tabla 8. Una comparación directa entre la figura 3 y la tabla 8, permiten verificar cualitativa y numéricamente la validez de la figura 3 y de las ecuaciones de los puntos característicos que definen la misma.
Tabla 8. Sensibilidad de la ecuación (12) sobre una vigueta particular
Tabla 8. Sensibilidad de la ecuación (12) sobre una vigueta particular
- Demostración de la validez matemática de la aproximación lineal
Una vez descrita matemáticamente la ecuación (8) se demostrara matemáticamente la validez de la aproximación (11) sobre la ecuación cuadrática (8); para tal fin se aplicarán algunos conceptos de cálculo diferencial sobre las ecuaciones que gobiernan la figura Nº 3.
Inicialmente se obtendrá la expresión general para obtener la pendiente en cualquier punto de la ecuación (8); la obtención de esta expresión pretende evaluar la pendiente en la fracción en la figura Nº 3 que contiene la solución real del área de acero de la sección de la viga (expresión As1); la comparación entre la pendiente de la fracción de la figura 3 y la pendiente de la ecuación aproximada 11 definirá la validez de la aproximación en consideración.
La expresión general que define la pendiente en cualquier punto de la ecuación (8) está dada por la primera derivada de la misma, la cual puede expresarse a través de la ecuación (29)
La fracción de la figura 3 a considerar corresponde a la definida en el eje x por el intervalo (0, As1) y en el eje y por el intervalo (0, -Mu). Se ha establecido usar esta fracción debido a que esta contiene la solución real del área de acero (As1), y su tendencia es aproximada a la de una función lineal; en aras de verificar la validez de la ecuación lineal se obtendrá la pendiente de la curva en los puntos extremos de la gráfica en la fracción considerada (intercepto con el eje y e intercepto con el eje x o raíz As1); de ser estas pendientes iguales o aproximadamente iguales se podrá calificar la validez de la aproximación lineal. A continuación se presenta el desarrollo de la idea anteriormente expuesta.
Pendiente en el intercepto con el eje y
Para la ecuación de la pendiente en el punto en consideración se debe sustituir la coordenada x del punto en la expresión (29); el proceso respectivo es presentado en la ecuación (30).
Pendiente en el intercepto con el eje x
Para la evaluación de la pendiente en el punto en consideración se debe sustituir la coordenada x del punto en la expresión (29); el proceso respectivo es presentado a continuación:
La coordenada x en el intercepto con el eje x está dada por la expresión del área real de acero
La sustitución de la ecuación (31) en la ecuación (29) y las respectivas reducciones permiten obtener una expresión de la pendiente de la figura 3, la cual está dada por la expresión (32).
La ecuación (32) puede ser transformada sustituyendo el momento externo mayorado (Mu) por el momento desarrollado por la sección (Mn), dadas las condiciones de igualdad que deben existir en el diseño entre la solicitación externa y la capacidad nominal; la expresión asociada a la capacidad nominal será obtenida a partir de la figura 4.
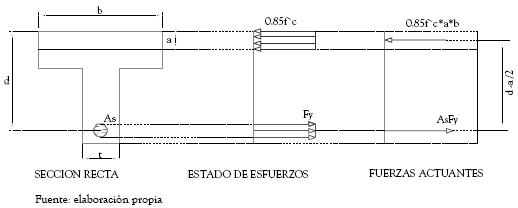
Debido a que la fuerza de compresión en el concreto es igual a la fuerza de tensión del acero, el momento asociado al par resistente podrá calcularse desde cualquiera de estas dos fuerzas (Winter, 1958); en este caso particular se usará la fuerza de compresión del concreto con el fin de poder efectuar reducciones en el interior de la raíz de la ecuación (32); la expresión que define el momento nominal está dada por la ecuación
Figura 4. Estado de Esfuerzos y Fuerzas actuantes sobre una sección T
Al sustituir la ecuación (33) en la ecuación (32) y realizar las respectivas reducciones se encuentra que la expresión que define la pendiente en el punto de intersección con el eje x está dada por la expresión (34).
Se puede observar que las expresiones de las pendientes en el intercepto con el eje y y el intercepto con el eje x ecuaciones (30) y (34), respectivamente, tienen la misma forma, salvo por la presencia del radical en la ecuación (34); en ese sentido es conveniente analizar la expresión dada por la ecuación (35).
En las secciones rectas de viguetas de losas aligeradas que se comportan como rectangulares, el valor de la altura del bloque equivalente es muy bajo respecto a la altura efectiva para cuantías de acero cercanas a la mínima, como típicamente son diseñados este tipo de elementos; bajo estas consideraciones, la expresión (35) tiende a cero (0) y la expresión de la pendiente en el intercepto con el eje x podría expresarse aproximadamente a través de la ecuación (36).
Debido a que las pendientes en el intercepto con el eje y y en el intercepto con el eje x son aproximadamente iguales se puede definir una recta entre estos puntos como se muestra en la figura No 5; mencionada recta modelará el comportamiento de la relación entre el área de acero (As) y el momento (M) en la fracción de estudio definida previamente.
La ecuación de la recta propuesta puede obtenerse a partir de la pendiente y la coordenada de un punto; en este caso particular la pendiente a usar será la pendiente común a los puntos de intersección con los ejes y y x, la cual está dada por las ecuaciones (30) y (36); el punto a usar es el de intersección con el eje y, cuya coordenada está dada por la ecuación (14); al ensamblar estas ecuaciones en la ecuación básica de una recta se podrá obtener la ecuación de la recta a través de la expresión (37).
Figura 5. Aproximación lineal propuesta sobre la ecuación cuadrática (8)
Al comparar la ecuación (37) con la ecuación (11) se encuentra que la ecuación (37) es la forma general de la ecuación (11) o que la ecuación (11) es la ecuación evaluada en el área de acero real de una sección de viga T que se comporta como rectangular. Bajo estas condiciones queda probada la aproximación lineal sobre la ecuación cuadrática de diseño (8).
V. SENSIBILIDAD MATEMÁTICA COMPARATIVA ENTRE LA ECUACIÓN (8) Y LA APROXIMACIÓN LINEAL
Con el fin de verificar prácticamente la validez del diseño a momento de secciones T que se comportan como rectangulares usando la aproximación lineal (Ecuación (11)) sobre la ecuación cuadrática (8), se ha utilizado la sensibilidad de diseño, base de este documento; en esta sensibilidad se ha efectuado el diseño de la totalidad de secciones contenidas en la misma usando la aproximación lineal; bajo estas consideraciones en la sensibilidad se obtuvieron dos áreas de acero correspondientes a los casos 1 y 3 (área de acero real y área de acero aproximado). A partir de las áreas de acero en consideración se obtuvo un factor de error que permitió conceptuar la eficiencia de la metodología aproximada de diseño. A continuación se presentan 4 ejemplos de sensibilidad típica desde la tabla 9. hasta la tabla 12.
VI. RESULTADOS DE LA SENSIBILIDAD DE LA APROXIMACIÓN LINEAL
Al observar las áreas de acero real (Real) y la aproximada (Aproxim2.) obtenidas a partir de la sensibilidad presentada en el numeral anterior se pueden realizar las siguientes precisiones:
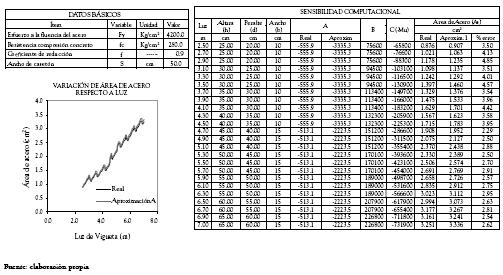
1. Para el rango de ancho de casetones analizado (0.30 - 1.00m) la metodología de diseño para secciones T que se comportan como rectangulares basada en la aproximación lineal antes expuesta, genera áreas de acero inferiores a las realmente requeridas, como se puede verificar en la columna denominada 'porcentaje de error' en las tabla 9, 10, 11 y 12, presentadas anteriormente; particularmente el porcentaje de error al que se hace referencia fue calculado a través de la expresión :
Desde esta ecuación, se puede afirmar que la metodología de diseño basada en la aproximación lineal genera resultados inferiores a los reales; sin embargo, los porcentajes de error encontrados son despreciables, condición que justifica la validez del uso de la ecuación lineal en el caso de diseño considerado en este artículo. Particularmente, un rango de errores para cada dimensión de casetón analizada en el rango de luces de 2m a 7m es presentado en la tabla 13.
2. Desde la tabla anterior se puede observar que el máximo porcentaje de error en que se puede incurrir al usar la aproximación lineal en el proceso de diseño es del 1.5 % por debajo de la solución real, condición que implica que el uso de la aproximación lineal no genera errores apreciables en el dimensionamiento del área de acero de una sección T que se comporta como rectangular. De otro lado, al observar el error promedio de la sensibilidad (0.95%) se pude establecer que la aproximación lineal es válida, segura y rápida para el diseño de vigueteria de sistemas de losas aligeradas en el rango de casetones y luces, objeto de esta publicación.
Tabla 9. Variación de áreas de acero real y aproximada asociadas al diseño de una sección T que se comporta como rectangular para un ancho de casetón de 0.30 m.
Tabla 10. Variación de áreas de acero real y aproximada asociadas al diseño de una sección T que se comporta como rectangular para un ancho de casetón de 0.50 m.
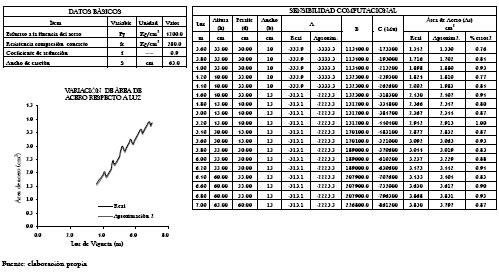
Tabla 11. Variación de áreas de acero real y aproximada asociadas al diseño de una sección Tque se comporta como rectangular para un ancho de casetón de 0.65 m.
Tabla 12. Variación de áreas de acero, real y aproximada, asociadas al diseño de una sección T que se comporta como rectangular para un ancho de casetón de1.00 m.
Tabla 13. Rango de errores de la comparación entre el área de acero real y el área de acero aproximada
CONCLUSIONES
Desde los resultados obtenidos en cada una de las sensibilidades asociadas a las aproximaciones discutidas en este artículo se pueden efectuar las siguientes conclusiones:
1. Para la obtención del área de acero de secciones T en concreto reforzado que se comportan como rectangulares y que trabajen como viguetería de losas aligeradas cuya sección cumpla con los requisitos del Título C13 de la norma sismo-resistente colombiana NSR 98, la sección T puede ser diseñada como una sección rectangular cuyo ancho corresponde al ancho del alma y la altura efectiva a la de la viga T. Bajo estas consideraciones, el área de acero obtenida usando la aproximación en consideración presenta un porcentaje máximo de error del 7% por encima del área de acero obtenida realizando un diseño exhaustivo en donde se tenga en cuenta el aporte de las aletas a compresión; de otro lado, el error promedio(por encima) de la metodología aproximada sobre la exhaustiva es aproximadamente 3.93%. Bajo estas condiciones se puede establecer que la aproximación es totalmente válida, segura y no genera sobredimensionamientos que puedan afectar la economía dentro del proceso de diseño. Es importante resaltar que los porcentajes de error a los que se hace referencia son válidos para sistemas de losas aligeradas cuya luz varía entre (2 – 7) m y el ancho de casetón entre (0.30 – 1.00) m.
2. La ecuación cuadrática que gobierna el dimensionamiento del área de acero asociado al momento flexionante al que están sometidas secciones rectangulares de vigas y que es extensible a secciones T que se comportan como rectangulares puede aproximarse a una ecuación lineal compuesta por una única variable correspondiente al área de acero y tres constantes correspondientes al momento mayorado, al esfuerzo a la fluencia del acero y la altura efectiva de la sección. Mencionada aproximación sobre la ecuación cuadrática es factible, por cuanto esta última es poco sensible al ancho de la sección; particularmente se pudo verificar que el área de acero obtenida usando la aproximación presenta un porcentaje máximo de error del 1.5% por debajo del área de acero obtenida realizando un diseño exhaustivo en donde se tenga en cuenta el ancho de la sección a través de la ecuación cuadrática; de otro lado, el error promedio (por debajo) de la metodología aproximada sobre la exhaustiva es aproximadamente 0.95%. Bajo estas consideraciones se puede establecer que la aproximación lineal es totalmente válida, rápida y segura, pues los errores de dimensionamiento pueden considerarse despreciables. Es importante destacar que los porcentajes de error a los que se hace referencia son válidos para sistemas de losas aligeradas cuya luz varía entre (2 – 7) m, y el ancho de casetón entre (0.30 – 1.00) m.
REFERENCIAS
1. Normas Colombianas de Diseño y Construcción Sismo Resistente. NSR-98. Asociación Colombiana de Ingeniería Sísmica. [ Links ]
2. WINTER, G., 1958. Design of Concrete Structures, United States of America. [ Links ]
3. ROCHEL, R., 1999. Hormigón reforzado. Primera parte, Medellín, Antioquia. [ Links ]
4. PARK, R., and PAULAY, T., 1975. Reinforced Concrete Structures. United States of America. [ Links ]
Recibido: 29/02/2008
Aceptado: 23/04/2008













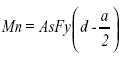 (3)
(3)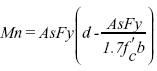 (4)
(4)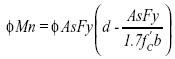 (5)
(5)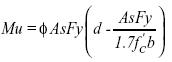 (7)
(7)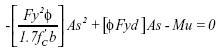 (8)
(8)
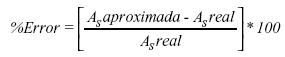 (10)
(10)
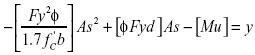 (12)
(12)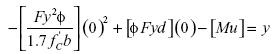 (13)
(13)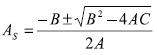 (15)
(15)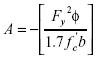 (16)
(16)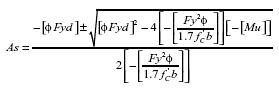 (19)
(19)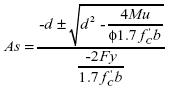 (20)
(20)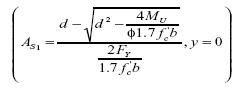 (21)
(21)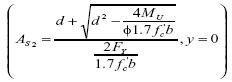 (22)
(22)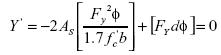 (23)
(23)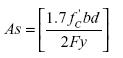 (24)
(24)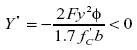 (25)
(25)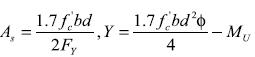 (28)
(28)
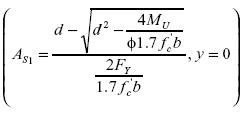 (31)
(31)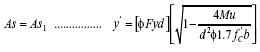 (32)
(32)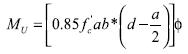 (33)
(33)
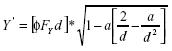 (34)
(34)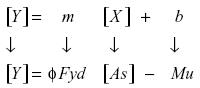 (37)
(37)