Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Ingenierías Universidad de Medellín
Print version ISSN 1692-3324On-line version ISSN 2248-4094
Rev. ing. univ. Medellin vol.7 no.12 Medellín Jan./June 2008
Modelación de la volatilidad de los precios de la energía eléctrica en Colombia
Volatility modeling of electric power prices in Colombia
Martha María Gil Zapata1; Cecilia Maya Ochoa2
1 Martha María Gil Zapata. Universidad de Medellín. mmgil@udem.edu.co Tel: 057 4 3405223
2 Cecilia Maya Ochoa. Universidad EAFIT. cmaya@eafit.edu.co Tel: 057 4 2619500
RESUMEN
Se explora en este trabajo un adecuado procedimiento para modelar el precio de la energía eléctrica y su volatilidad, para con ello aportar al desarrollo del mercado de contado y de derivados sobre este, subyacente en Colombia, en términos de su valoración, de un cálculo más acertado de los márgenes de operación del sistema y de un manejo adecuado del riesgo asociado.
Palabras clave: modelación de precios de energía eléctrica, modelos de series de tiempo, volatilidad, mercado de energía, modelos GARCH
ABSTRACT
This article analyzes an appropriate procedure to model electric power price and its volatility with the purpose of making some contributions to the development of cash market and its by-products, underlying in Colombia, in terms of its valuation, of a more precise calculation of system operation margins and an appropriate management of associated risk.
Keywords: Electric powers price modelling, time series modelling, volatility, energy market, GARCH energy models
INTRODUCCIÓN
Los mercados de energía eléctrica son relativamente nuevos si se comparan con los mercados financieros. A diferencia de éstos, se caracterizan por ser de bajo impacto con respecto a los ciclos económicos y, en cambio, de alto impacto con respecto a las condiciones de almacenamiento y entrega, así como por presentar una baja correlación entre precios de corto y largo plazo y una compleja estacionalidad. La mayoría de estos mercados están sometidos a condiciones de regulación y se caracterizan por una mediana o baja liquidez. Los mercados más desarrollados son el sistema Noruego (Nordpool), la Bolsa de España, el Mercado de Electricidad de Australia, el England-Wales Pool y el Sistema PJM. En Latinoamérica se destacan el mercado eléctrico chileno y el colombiano.
En aquellos mercados de energía eléctrica competitivos, a diferencia de los regulados, las series de precios horarios se caracterizan por presentar:
1. Alta frecuencia de negociación
2. Media y varianza no constante
3. Estacionalidad múltiple (correspondiente a periodicidad diaria y semanal)
4. Efecto calendario (fines de semana y días de fiesta)
5. Alta volatilidad
6. Alto porcentaje de precios no usuales (principalmente en períodos de alta demanda)
7. Dependencia de variables explicatorias como la hidrología y la demanda.
En Colombia, el Mercado de Energía Mayorista (MEM) se constituyó en el año 1995, permitiendo la libre competencia y la participación privada; este mercado puede definirse como 'el conjunto de sistemas de intercambio de información entre generadores y comercializadores de grandes bloques de energía eléctrica en el sistema interconectado nacional para realizar contratos de energía a largo plazo y en bolsa sobre cantidades y precios definidos con sujeción a los reglamentos y normas establecidas'. (Véase Comisión de regulación de energía y gas. www.creg. gov.co). El MEM es operado por un administrador (Expertos en Mercados XM S.A.) bajo un marco regulatorio establecido por la Comisión de Regulación de Energía y Gas, CREG, de carácter estatal. En este mercado participan, además del agente operador y el administrador, los agentes generadores, los transmisores, los comercializadores y sus clientes.
El funcionamiento del MEM está soportado en una bolsa de energía (pool de generadores) en la cual se realizan intercambios comerciales definidos en el contexto de un mercado spot con resolución horaria y soportado por un operador del sistema interconectado nacional (Centro Nacional de Despacho). Este estudio se enfoca en la modelación de la volatilidad de los precios del mercado spot dentro de un esquema competitivo.
Una adecuada modelación de la volatilidad permite una estimación más exacta de los márgenes o garantías necesarios para la negociación de instrumentos derivados de energía eléctrica que se espera ofrecer en el futuro en el país. El análisis de volatilidad que se presenta a continuación se basa en modelos de series de tiempo, ampliamente utilizados, tales como la metodología de Box-Jenkins también conocida como ARIMA y los procesos tipo GARCH de varianza condicional auto-regresiva heterocedástica.
1. Modelos para la media y la varianza de precios de energía eléctrica
Los precios de la energía pueden ser modelados a partir de modelos auto-regresivos integrados con medias móviles. Este modelo es representado por un proceso ARIMA(,
,
), donde
es el orden del modelo auto-regresivo,
denota el orden de integración de la serie, y
es el orden del modelo de media móvil, tal como se describe en la ecuación (1):
donde es el operador de rezago y
es el término de error.
De otra parte, podemos definir la volatilidad como una medida de los cambios aleatorios e impredecibles en el precio de un bien, los cuales, aunque no pueden ser observados directamente, pueden ser estimados a partir de los datos históricos disponibles. En particular, en el caso de los precios de la energía eléctrica, las series de variaciones logarítmicas de precios se caracterizan por presentar exceso de curtosis, conglomerados de volatilidad y convergencia o regresión a la media como queda expresado en la Resolución CREG-039-94.
El modelo de volatilidad condicional autorregresivogeneralizado GARCH (,
) (Bollerslev, 1986) permite modelar la varianza de un proceso que presenta las características señaladas anteriormente. El modelo GARCH tiene la siguiente especificación:
El orden está asociado a la dependencia temporal de la varianza de la serie con choques aleatorios al cuadrado ocurridos
períodos hacia atrás. El orden
está asociado a la dependencia temporal de la misma en el período
al valor que haya tomado en
períodos anteriores. Los errores deben ser independientes y presentar una distribución con media cero y varianza constante.
Diferentes autores han propuesto derivaciones del modelo GARCH. A continuación se presenta una síntesis de los más utilizados para precios de energía eléctrica:
Modelo Threshold GARCH o T-GARCH (Glosten, Jagannathan y Runkle, 1993):
Donde
en otros casos.
Este modelo es considerado asimétrico, toda vez que las variaciones positivas y las variaciones negativas
, tienen efectos diferentes en la varianza condicional. Las variaciones positivas tienen un impacto
, mientras que las variaciones negativas tienen un impacto
con un efecto de apalancamiento de orden
.
Exponential GARCH o EGARCH (Nelson, 1991):
Este modelo trata de capturar la asimetría existente entre los retornos positivos y negativos, así como la mayor volatilidad de los retornos negativos conocida como efecto 'leverage', el cual puede expresarse de la siguiente manera:
El efecto leverage o de apalancamiento es exponencial, por tanto, los pronósticos de la varianza condicional siempre serán no negativos.
Power GARCH o P-GARCH (Ding, Granger y Engel, 1993).
En este modelo, la potencia a la cual está elevada la desviación estándar es un parámetro más a estimar, sin asumir que se trata de la varianza :
2. EVIDENCIA EMPÍRICA NACIONAL E INTERNACIONAL
Los modelos auto-regresivos ARIMA ya han sido aplicados a pronósticos de precios de commoditie. (Weiss, 2000) tales como el aceite (Morana, 2001) o gas natural (Buchananan, 2001). Para energía eléctrica, la metodología ARIMA ha sido usada para pronóstico con buenos resultados (Gross, 1987; Hagan, 1987). Los modelos simples auto-regresivos AR han sido usados para predecir precios semanales, por ejemplo en el sistema noruego (Fosso, 1999).
Igualmente, Contreras y otros (2003), presentan un método para predecir precios de electricidad diario basado en la metodología ARIMA, usando técnicas para analizar series de tiempo a partir de información histórica aplicada a los mercados de España y California. Fruto de estos estudios se ha encontrado que las series de precios del mercado de electricidad presentan alta frecuencia, media y varianza no constante, y múltiple estacionalidad, correspondiente a estacionalidad diaria y semanal, efecto calendario, alta volatilidad y un alto porcentaje de precios inusuales, principalmente en períodos de alta demanda. Asimismo, se ha encontrado cómo la predicción del modelo horario arroja como resultado que en el caso español se necesitan 5 horas para predecir, en tanto en el de California sólo se necesitan dos. Por otra parte, el promedio de los errores del modelo del mercado español es alrededor del 10% y alrededor del 5% en el mercado de California con variables explicatorias adicionales. En el mercado español las variables explicatorias son sólo necesarias mensualmente, destacándose entre ellas la disponibilidad hídrica.
Nogales y otros en el año 2002 emplearon dos eficientes modelos de pronósticos basados en el análisis de series de tiempo, regresión dinámica y modelos de funciones de transferencia. El caso d enuevamente en los mercados de electricidad de España y California y los errores promedio del modelo encontrados son 5% para el mercado español y 3% para el mercado de California.
García, y otro (2005), emplearon modelos de pronóstico GARCH para predecir los precios de la electricidad en los mercados de España y California, encontrando que los errores promedio en el mercado español están alrededor del 7% y alrededor del 4% en el mercado de California. Concluyen que es posible mejorar el modelo considerando efectos calendario y la inclusión de variables exógenas tales como demanda y almacenamiento de agua.
Otros estudios sobre la volatilidad de los precios de energía eléctrica son M. Benini, M. Marracci, P. Pelachi y A. Venturini, (2000) con aplicaciones en diversos mercados como el de España, California, Inglaterra y Gales; T. Mount, (2001) y sobre valor en riesgo en el mercado de California (Dahlgren, y otros 2001).
Schwartz y Lucia (2002) argumentan la importancia de los patrones regulares en el comportamiento de los precios de la electricidad y sus implicaciones para los propósitos de valoración de derivados. Su estudio se enfoca en el mercado de energía nórdico (NordPool), tanto en el mercado spot, como el de forwards y futuros. En el estudio se encuentra que los precios spot pueden ser altamente dependientes de las condiciones temporales y locales de oferta y demanda tales como las condiciones del clima, hábitos de la población, entre otras, debido a la imposibilidad de almacenamiento y a las limitaciones de transporte; por otra parte, la no almacenabilidad de la electricidad afecta el precio de los derivados significativamente, lo cual influencia la forma de la curva Forward.
Para ello se aplican modelos de uno y dos factores, capturando patrones estacionales de la curva de Forward y futuros directamente implicada por el comportamiento estacional de los precios spot de la electricidad, los cuales describen el comportamiento de los precios en términos de dos tipos de componentes: el determinístico y el estocástico. El primer componente es totalmente predecible y contiene las características de la evolución de los precios, tales como la tendencia determinística y algún genuino comportamiento periódico. El segundo componente es estocástico y puede ser asumido como un proceso de difusión continuo.
Pilipovic (1997) coincide con Schwartz y Lucia (2002) en el comportamiento estacional periódico de los precios de la electricidad y su reversión a la media (posiblemente no estacionaria). En su trabajo sobre Energy Risk presenta un completo estudio sobre series financieras asociadas a energéticos, en el cual analiza el comportamiento de la serie spot, la volatilidad, la valoración de derivados y medidas y políticas de riesgo. El autor analiza varias series de energéticos entre las que se destaca el Mid Columbia (MC) precio spot de electricidad, sobre el cual aplica modelos de reversión a la media en función de precios y del logaritmo natural de los precios, y encuentra que el mejor ajuste es el del modelo de reversión a la media en el precio.
Finalmente, Martínez, et al (2006) en 'Opciones de cubrimiento del riesgo por subidas fuertes en los precios del mercado en bolsa de energía y su relación con el cargo por capacidad' analizan la volatilidad del mercado de energía eléctrico en Colombia, tomando precios diarios constantes a enero de 2005. En el estudio se describe cómo las volatilidades antes de mayo de 2001 son superiores a las observadas después de esa fecha, lo cual se interpreta debido a la inmadurez del mercado en el período inicial de funcionamiento, a la presencia del evento Niño en el período 1997-1998, así como a la recesión económica experimentada en Colombia en la década pasada y al uso de gas natural que ejercieron una presión hacia abajo en los precios. En este estudio se modela la serie de precios mensuales deflactada por la inflación, para lo cual se ajusta un modelo GARCH (1,1).
3. Análisis de la serie de precios de energía eléctrica en Colombia
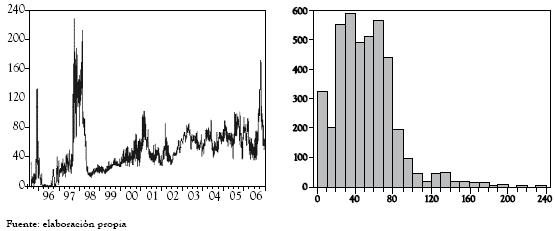
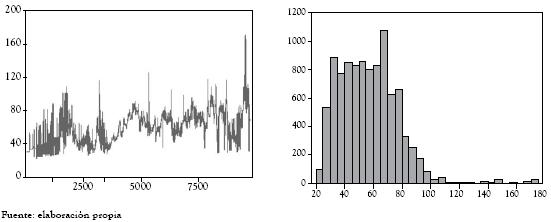
Para el desarrollo del trabajo se contó con información disponible de precios de bolsa horarios (100,365 registros suministrados por XM Compañía de expertos en Mercadeo S.A) desde el inicio del mercado de energía mayorista, el 20 de julio de 1995 hasta el 31 de diciembre de 2006. Un primer análisis parte del estudio de los promedios diarios formados a partir de la serie horaria y su correspondiente histograma de frecuencia, así como los retornos asociados, los cuales se presentan a continuación en las figuras 1 y 2.
En la figura 1 se observan las fluctuaciones del precio de bolsa a lo largo del período de operación energía mayorista; igualmente se destacan dos picos importantes antes del año 2000, asociados a períodos macroclimáticos denominados El Niño, y a la inmadurez del mercado para afrontar estos eventos. Igualmente se observa cómo en el histograma de frecuencias no es posible asociarlo con una distribución conocida, lo cual fue corroborado por los contrastes de bondad de ajuste de Kolmogorov-Smirnov y Anderson-Darling.
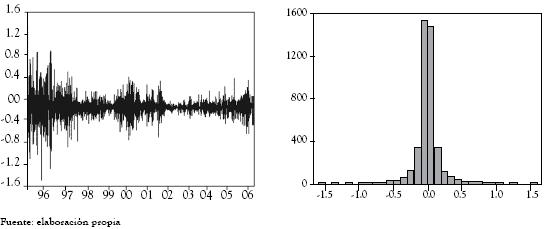
La figura 2 presenta la serie de retornos diarios, calculados como variaciones logarítmicas, la cual evidencia estacionariedad en media y la existencia de clusters de volatilidad de diferente intensidad, más notorios antes del año 2000. En el histograma de frecuencia se observa una alta frecuencia alrededor de la media, sin embargo, el contraste de Jarque Bera rechaza la normalidad de la serie.
Figura 1 Precios promedio diarios
Figura.2 Retornos de la serie de precios promedio diario
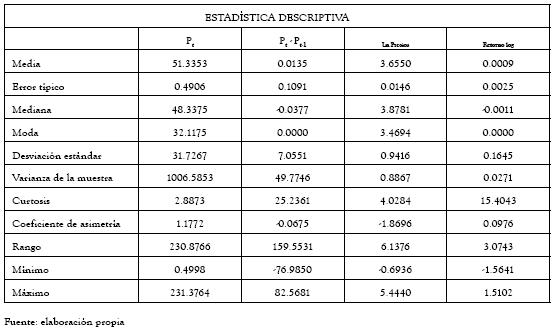
En la tabla No 1 se presenta el cuadro con la estadística descriptiva correspondiente a la serie de precios promedio diarios, así como la serie de las diferencias, del logaritmo natural de la misma y de las variaciones logarítmicas.
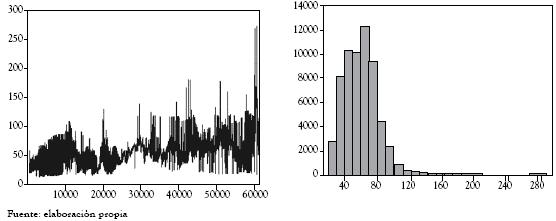
Al aplicar pruebas de raíz unitaria, en particular los contrastes de Dickey-Fuller, Phillips Perron y KPSS, puede concluirse que la serie de precios no es estacionaria, contrario a lo obtenido para la serie de retornos logarítmicos. Este resultado permite modelar esta última serie mediante procesos auto-regresivos; sin embargo, se evaluaron diferentes modelos, sin que ninguno de ellos se ajuste de manera adecuada a las series diarias, probablemente porque se trata de precios promedio. Es por ello que este estudio se concentra en adelante en la modelación de los precios horario en el período comprendido entre diciembre de 1999 y noviembre de 2006, que se representa en las figuras 3 y 4.
Tabla 1 Estadística descriptiva de la serie de precios diarios
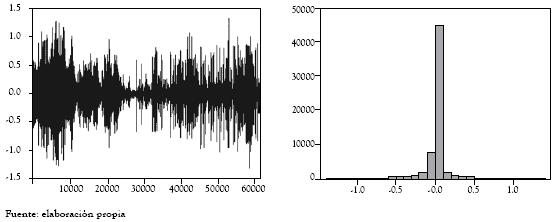
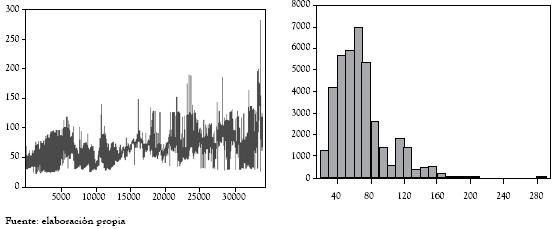
Figura 3 Serie de precios horarios e histograma
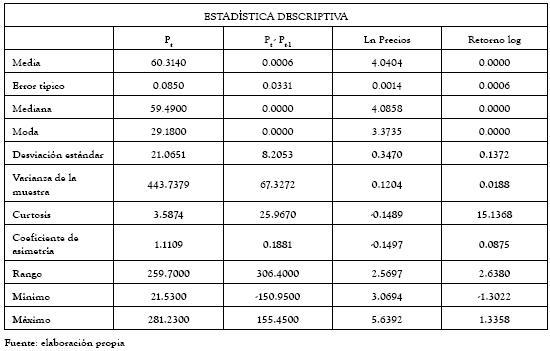
En las figuras 3 y 4, se destaca cómo los histogramas de la serie de precios horario, y de sus variaciones logarítmicas, rechazan la normalidad de la serie, lo cual fue corroborado por el contraste de Jarque Bera. A continuación se presenta una selección de estadísticos para la serie de precios horario, sus diferencias, el logaritmo natural de los precios y sus respectivos retornos.
Figura 4 Serie de retornos logarítmicos horarios e histograma
Tabla 2. Estadística descriptiva de la serie de precios horarios
4. Modelación de la media y la varianza de los precios de la energía el éctrica en Colombia
Se parte del modelo de un factor para el precio spot propuesto por Schwartz y Lucia (2002), el cual puede ser representado de la siguiente forma:
En donde representa una función determinística de tiempo y
representa un proceso estocástico de difusión de la forma:
representa un movimiento Browniano y
sigue un proceso estocástico de reversión a la media o proceso Ornestein-Uhlenbeck con media de largo plazo igual a cero y velocidad de ajuste
. Las dos ecuaciones anteriores pueden re-escribirse de la siguiente forma:
El proceso seguido por puede expresarse como la solución de la siguiente ecuación diferencial estocástica (versión particular del modelo de Vasicek (Hull y White, 1990)):
En donde la distribución condicional de puede considerarse normal con media condicional y varianza dada usando
como:
El componente determinístico es representado por Schwartz y Lucia (2002), con la siguiente expresión:
En donde es una variable tipo dummy que está asociada a si el día es laboral o de fin de semana, y
corresponde al mes
. Es importante resaltar que en este trabajo, se incluyen en el componente determinístico otras variables adicionales a las consideradas por Schwartz y Lucía que resultan significativas para explicar el comportamiento de los precios de la energía eléctrica en Colombia, tal como se detalla más adelante.
El componente estocástico del modelo de un factor para el modelo de precios sigue un proceso auto-regresivo tal como muestra la ecuación (17):
Y para el logaritmo natural de los precios:
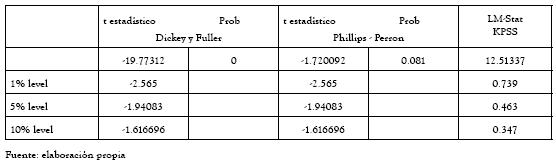
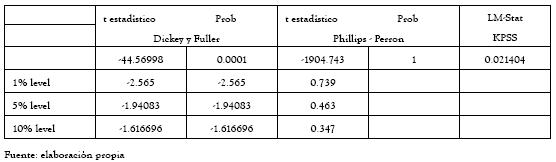
Adicionalmente, luego de modelar la media, se modeló la volatilidad de la serie, con base en los modelos de volatilidad condicional heteroscedástica descritos en la sección 1. Para proceder a la modelación de la serie de precios horarios, se verificó la estacionariedad de la misma. Tanto las pruebas de Dickey Fuller y Phillips Perrón como la prueba KPSS rechazan la estacionariedad, tal como se observa en la tabla 3:
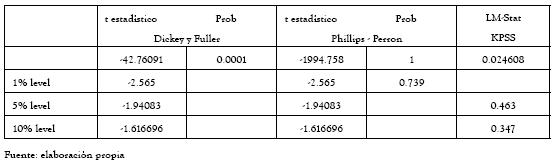
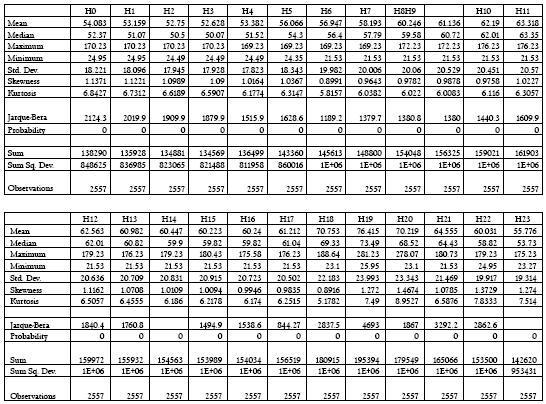
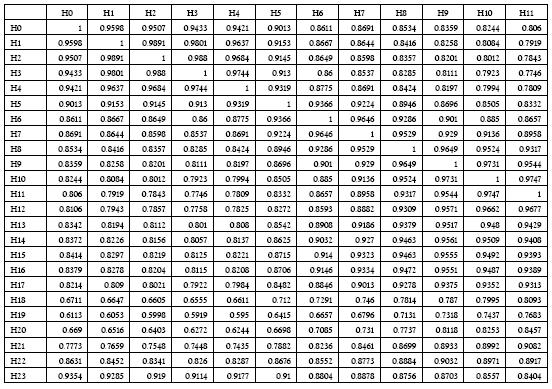
Por el contrario, para las series de diferencias de precio y retornos logarítmicos se verifica la estacionariedad, tal como se presenta en las tablas 4 y 5, lo cual permite modelar la media de estas series con procesos ARMA, los cuales deberán complementarse con variables exógenas relacionadas con la estacionalidad propia de las series de energía eléctrica. Para identificar cuáles de estos factores son significativos, la serie fue clasificada en cada una de las horas correspondientes con el fin de establecer sus patrones. En las tablas A1 y A2 del apéndice se presentan los estadísticos y la matriz de correlación asociadas a cada hora:
Tabla.3 Análisis de estacionariedad de la serie de precios horarios
Tabla 4 Análisis de estacionariedad de la serie de logaritmos de precios horarios
Tabla 5 Análisis de estacionariedad de la serie diferenciada de precios horarios
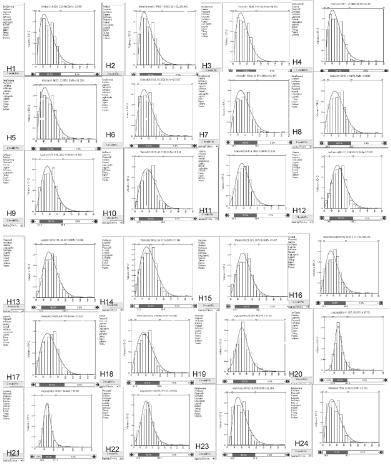
Continuando con el análisis, se aplican pruebas de bondad de ajuste (Contraste de Kolmogorov- Smirnov, Anderson Darling y Chi-Square. El software empleado es Best Fit.) a cada serie, cuyos resultados se observan en la figura A1 del apéndice
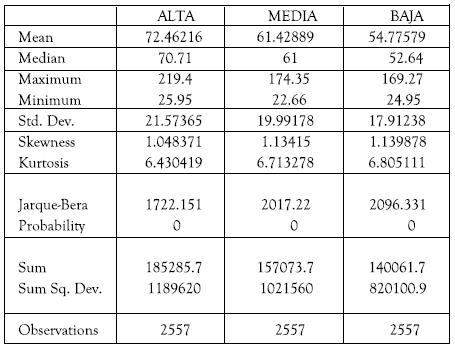
Los análisis anteriores permiten establecer un patrón de comportamiento de los precios horario, clasificándolos en tres categorías asociadas a la curva de demanda intradiaria. Existe un patrón asociado a la demanda alta, correspondiente a las horas 19:00, 20:00 y 21:00, otro asociado a la demanda media entre las horas 8:00 a las 18:00, incluyendo la hora 22:00 y, por último, uno asociado a la demanda baja, correspondiente a las horas entre las 1:00 a las 7:00 y las horas 23:00 y 24:00. Los estadísticos asociados a cada uno de los períodos de demanda establecidos se presentan en la tabla A3 del apéndice:
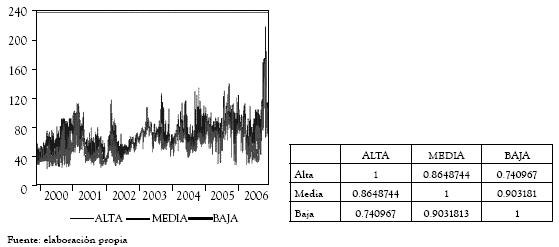
En la figura 5 se presenta el comportamiento de los precios de bolsa asociado a cada uno de los períodos de demanda, así como la matriz de de correlaciones asociadas.
Figura 5 Demanda de intrahorario de precios de bolsa
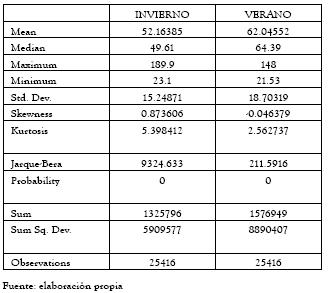
Otro de los patrones analizado corresponde a los períodos de invierno y verano y su efecto en los precios de bolsa en Colombia. Para ello la serie de precios de bolsa se clasificó en los períodos de invierno y verano establecidos por la CREG, el verano correspondiente a los meses de diciembre a abril e invierno asociado a los demás. A continuación se presentan los estadísticos asociados.
Como es de esperarse, dada la alta componente hídrica del sistema, los períodos de verano se relacionan con altos precios de bolsa.
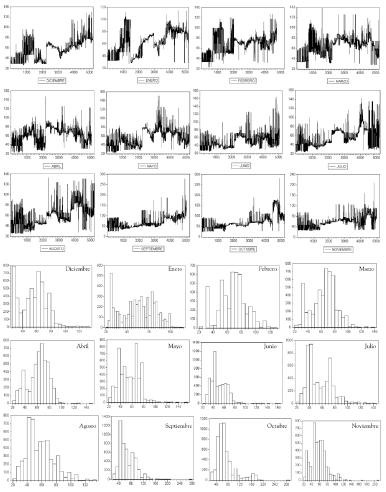
De otro lado, se analizan los patrones de comportamiento de los precios horarios asociados al ciclo anual en Colombia, representado por los diferentes meses. En la figura A2 del apéndice se presenta el comportamiento de los precios horarios en cada uno de los meses del año, así como el histograma de frecuencia asociado
Asimismo, se presentan en la tabla No A4 del apéndice los estadísticos correspondientes y la matriz de correlaciones dentro del ciclo anual.
Adicionalmente, se evaluó el comportamiento estacional en los precios de la energía asociado a efectos macroclimáticos, dentro del cual se analizó el Índice de Oscilación del Sur como uno de los indicadores que representa de mejor manera el comportamiento macroclimático reflejados en los fenómenos El Niño y La Niña:
Tabla 6. Patrones del comportamiento de los precios de bolsa asociados a períodos de invierno y verano
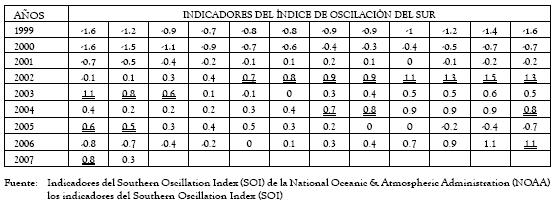
Tabla 7. Variables macroclimáticas
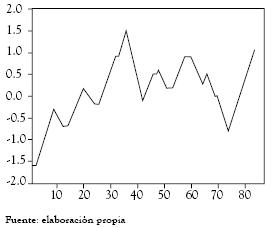
Los episodios cálidos – El Niño (doble subrayado en la tabla 7) y fríos - La Niña (negrita en la tabla 7) están asociados a variaciones positivas y negativas por encima de +/- 0.5 en el SOI. La siguiente figura describe el Indice de Oscilación del Sur y las estadísticas que representan las temporadas Niño y Niña:
Figura 6. Índice macroclimático (IOS)
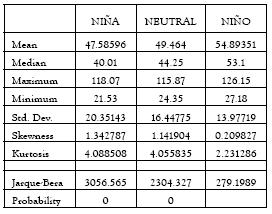
Tabla 8. Patrones de los precios de bolsa asociados a varibles macroclimáticas
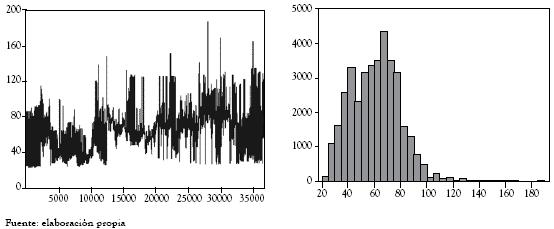
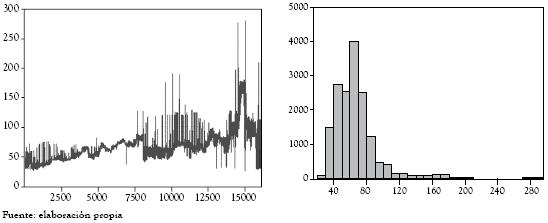
La alta componente hídrica del sistema eléctrico colombiano, influye en que los más altos precios de bolsa están asociados a períodos de Niño en Colombia o períodos de escasez hídrica. A continuación se detallan los diferentes períodos asociados a las condiciones macroclimáticas.
Figura 7 Comportamiento de los precios de bolsa asociado al período neutral
Figura 8 Comportamiento de los precios de bolsa, asociados a períodos El niño
Figura 9 Comportamiento de los precios de bolsa, asociados a períodos La niña
Otro de los patrones considerados en el análisis de los precios de bolsa en Colombia se relaciona con el efecto calendario. Para ello, a continuación se presentan los estadísticos que reflejan este efecto en los precios de bolsa.
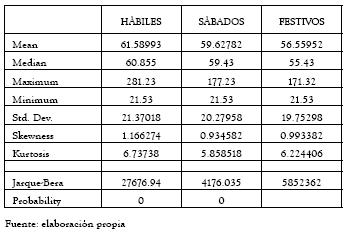
De la información siguiente se observa cómo en los días sábados y festivos, los precios de bolsa sufren un decaimiento tanto en su precio como en su volatilidad.
Tabla 9 Patrones de comportamiento del precio de bolsa, asociados a efecto día calendario
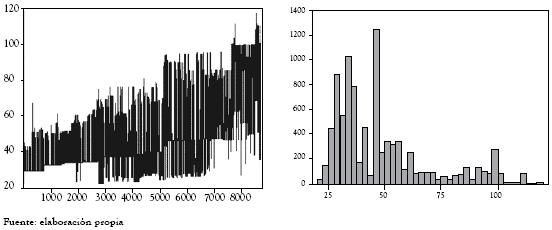
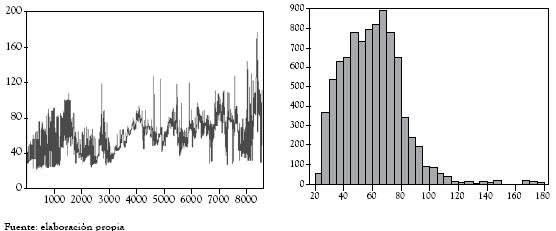
Igualmente, a continuación, se presenta el comportamiento gráfico de los precios de bolsa horarios en Colombia asociados a días hábiles, sábado y festivos, así como el histograma asociado.
Figura 10 Comportamiento del precio de bolsa horario en los días hábiles
Figura 11 Comportamiento del precio de bolsa horario en los días sábados
Figura 12 Comportamiento del precio de bolsa horario en los días festivos
A partir del análisis de la estacionariedad de las series y de los patrones asociados al comportamiento de los precios de bolsa de la energía eléctrica en Colombia (demanda, ciclo anual, macroclimáticas y efecto calendario), se procedió a evaluar el modelo que representa de la mejor manera los precios y la volatilidad de los precios de la energía eléctrica en Colombia.
Para realizar la modelación, se empleó el software E-Views 5.0, en el cual los regresores exógenos corresponden a variables dummy que representan las características de estacionalidad de los precios presentadas anteriormente. Posteriormente, se estimó el modelo GARCH de mejor ajuste, en el cual se logra con base en la distribución generalizada de los errores (Generalized Error Distribution, GED).
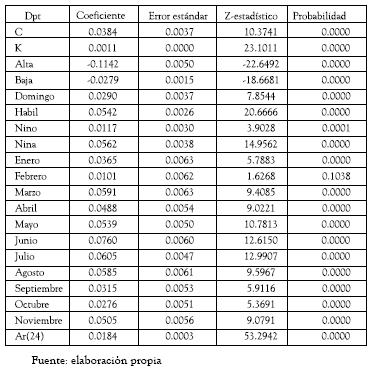
Se encuentra que el precio sigue un proceso de reversión a la media, y un proceso auto-regresivo del día anterior, en el cual son significativas las variables demanda alta y baja, los días de la semana domingo y hábil, las variables macroclimáticas niño y niña y cada uno de los meses del año. Del ajuste de modelos tipo GARCH, EGARCH, T-GARCH, P-GARCH, se encontró que el modelo de mejor ajuste para la varianza es el EGARCH (1,1). En el modelo ajustado, los residuales no presentan autocorrelación e igualmente se presenta un buen comportamiento de los residuales al cuadrado. El siguiente es el resultado de la estimación, específicamente para la serie de diferencial de los precios :
Tabla.10. Variables estimadas en el modelo
CONCLUSIONES:
El trabajo presentado busca ajustar un modelo al precio y a la volatilidad de los precios de la energía en Colombia, serie caracterizada por curtosis, aglomeraciones de volatilidad, ocurrencia de eventos extremos y reversión a la media. Para ello se parte del modelo sugerido por Schwartz y Lucia (2004) donde se identifica un componente estocástico de reversión a la media y uno determinístico relacionado directamente con factores de estacionalidad. Efectivamente se encuentra en el caso colombiano evidencia de un proceso de reversión a la media, un proceso auto-regresivo del día anterior y patrones de estacionalidad en mayor número que los identificados por estos autores, tales como los meses de año, la demanda intrahoraria, la influencia de variables macroclimáticas (períodos niño y niña) y el efecto día calendario.
En cuanto a la volatilidad, el mejor ajuste se logra con un proceso EGARCH(1,1) asumiendo una distribución generalizada del error (GED). Se recomienda en un futuro explorar modelos de volatilidad estocástica en tiempo continua conocidos como SV o modelos de salto difusión, así como incluir variables exógenas como la hidrología y la demanda ofertable en embalse, entre otras.
REFERENCIAS
1. BENINI M., MARRACCI P., PELACHI P., VENTURINI, 2002. 'Day-ahead Market Price Volatility Analysis in Deregulated Electricity Markets', IEEE Power Engineering Society Summer Meeting, Vol. 3, pp 1354-1359, July 2002 [ Links ]
2. BOLLERSLEV, TIM, 1986. 'Generalized Autoregressive Conditional Heteroskedasticity'. Journal of Econometrics, 31, 307-28. [ Links ]
3. BOX, JENKINS, 1976. Time series analysis forecasting and control, Holden-Day. [ Links ]
4. BUCHANANAN, HODGES, 2001. Theis, Which way the natural gas price: an attempt to predict the direction of natural gas spot price movements using trader position, Energy economics. [ Links ]
5. CONTRERAS, J.; ESPINOLA, R.; CONEJO, A., 2003. 'ARIMA models to predict next-day electricity prices'. En: IEEE Transactions on Power Systems. Vol. 18, No. 3, p1014. [ Links ]
6. DAHLGREN, R.W., LIU C, LAWARREE, 2001. Volatility in the California power market: source, methodology and recommendations, Generation, Transmission and Distribution, IEE Proceedings-Mar 2001 Vol: 148, pag(s): 189-193 [ Links ]
7. DING Z., GRANGER C.W.J, ENGLE R.F, 1993, A Long Memory Property of Stock market returns and a new model, Journal Empirical Finance 1 83-106 [ Links ]
8. FOSSO, O.B., GJELSVIK A., HAUGSTAD A., MO B., WANGENSTEEN I., 1999. Generation scheduling in a deregulated system. The Norwegian case, Power Systems, IEEE Transactions on, Feb 1999, Vol 14 pag 75-81 [ Links ]
9. GARCÍA, R., CONTRERAS, J., VAN AKKEREN, M., 2005. 'A GARCH forecasting model to predict day-ahead electricity prices'. En: IEEE Transactions on Power Systems. Vol. 20, No. 2, p867, 8p. [ Links ]
10. GLOSTEN, L.; JAGANNATHAN, R.; RUNKLE, D, 1993. On the Relation Between the Expected Value and the Volatility of the Nominal Excess Return on Stocks. Journal of Finance, 48 (5), 1779–1801. [ Links ]
11. GROSS, G., 1987. Short-term load forecasting, Proc, IEEE, vol 75, pp 1558-1573, Dec 1987. [ Links ]
12. HAGAN, BEHR, 1987. The time series approach to short term load forecasting, IEEE, Trans, Power Syst. [ Links ]
13. HULL, J., WHITE A., 1990. Pricing interest-rate-derivative securities - Review of Financial Studies. [ Links ]
14. MARTÍNEZ, et al, 2006. Opciones de cubrimiento del riesgo por subidas fuertes en los precios del mercado en bolsa de energía y su relación con el cargo por capacidad. Colciencias-ISA-Escuela Colombiana de Ingenieria [ Links ]
15. MORANA, 2001. A semiparametric approach to short-term oil prince forecasting, Energy economics, vol 23. [ Links ]
16. MOUNT T., 2001. Market power and price volatility in restructured markets for electricity, Decision Support Systems Volume 30, Issue 3, January 2001, Pages 311-325 [ Links ]
17. NELSON, D., 1991. 'Conditional Heteroskedasticity in Asset Returns: A New Approach'. En: Econométrica, 59, 347– 370. [ Links ]
18. NOGALES, FJ, CONTRERAS, J., CONEJO AJ, ESPINOLA, R., 2002. 'Forecasting next-day electricity prices by time series models'. En: IEEE Transactions on Power Systems. Vol. 17, No. 2, p342, 7p. [ Links ]
19. SCHWARTZ, E. S y LUCÍA, J. J., 2002. 'Electricity prices and power derivatives: evidence from the Nordic Power Exhange'. En: Review of Derivatives Research. 5 (1), pp. 5-50. [ Links ]
20. WEISS, 2000. Forecasting commodity prices using ARIMA, Technical analysisi of stocks & commodities, vol 18. [ Links ]
APÉNDICE
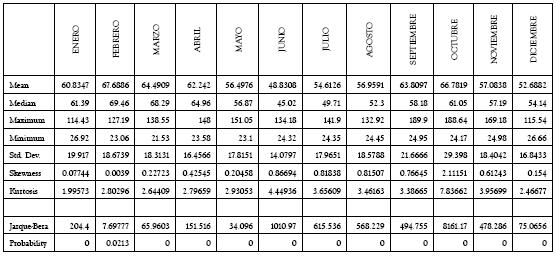
Tabla A1 Estadísticos de la serie horaria de precios de bolsa en Colombia
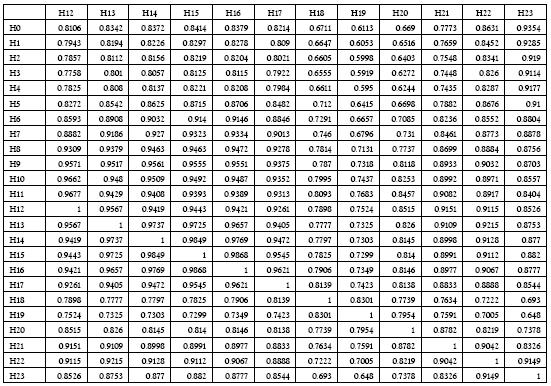
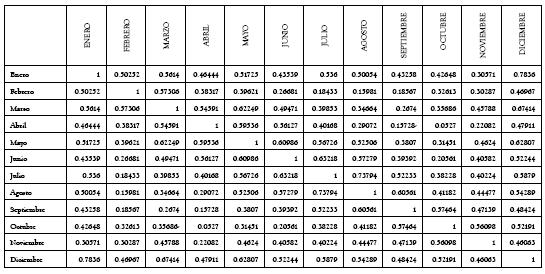
Tabla A2 Covarianzas de la serie horaria de precios de bolsa en Colombia
Tabla A2 Covarianzas de la serie horaria de precios de bolsa en Colombia (Continuación)
Figura A1 Pruebas de Bondad de Ajuste para las series intradiarias
Tabla A3 Patrones de comportamiento horario asociado a la demanda
Figura A2 Patrones del comportamiento de precios de bolsa asociados al ciclo anual
Tabla A4 Estadísticas correspondientes a los patrones de comportamiento de los precios de bolsa, asociados al ciclo anual
Recibido: 15/03/2008
Aceptado: 15/04/2008













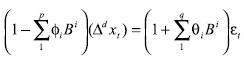 (1)
(1)