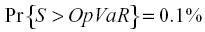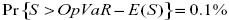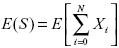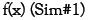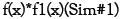Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Ingenierías Universidad de Medellín
Print version ISSN 1692-3324On-line version ISSN 2248-4094
Rev. ing. univ. Medellin vol.7 no.13 Medellín July/Dec. 2008
Loss Distribution Approach (LDA): metodología actuarial aplicada al riesgo operacional
Loss Distribution Approach (LDA): actuarial methodology apply to operational risk
Luis Ceferino Franco Arbeláez1; Juan Guillermo Murillo Gómez2
1 Docente-investigador en el programa de Ingeniería Financiera de la Universidad de Medellín. Medellín-Colombia. lfranco@udem.edu.co
2 Docente-investigador en el programa de Ingeniería Financiera de la Universidad de Medellín. Medellín-Colombia. jgmurillo@udem.edu.co
Resumen
Este artículo es resultado de un proyecto de investigación sobre la gestión integral del riesgo operacional promovido por la Vicerrectoria de Investigaciones de la Universidad de Medellín, y cofinanciado por una firma comisionista.
Se presenta una aplicación del modelo LDA, el cual se basa en la recopilación de los datos de pérdidas históricas (frecuencia y severidad), que se registran internamente en las organizaciones. Dichos datos pueden ser complementados con datos externos. Estas pérdidas son clasificadas en una matriz que relaciona las líneas de negocio de la organización y los eventos operacionales de pérdida, a partir de la cual se calcula la carga de capital. La aplicación se desarrolló para una entidad financiera. El artículo está organizado de la siguiente forma: la primera sección es introductoria al tema. En la segunda parte se presenta formalmente el modelo LDA; luego se realiza una aplicación, y en la cuarta sección se presentan algunas conclusiones.
Palabras Clave: Riesgo, riesgo operacional, LDA, carga de capital.
Abstract
This paper is the result of a research project on integrated management of operational risk, promoted by Universidad de Medellin Research Vice-Principal's Office and co-financed by a financial company.
It presents an application of the LDA model, which is based on data collection of historical losses (frequency and severity), which are recorded internally in organizations. Such data can be supplemented with external data. These losses are classified in a matrix that relates business lines of the organization and operational loss events, from which capital charge is estimated. The application was developed for a financial institution. The paper is organized as follows: The first section is introductory to the subject. The second part formally presents a LDA model; then an application is made, and in the fourth part some conclusions are presented.
Key words: Risk, operational risk, LDA, capital charge.
INTRODUCCIÓN
En el contexto de las finanzas, cuando se habla de riesgo, se hace referencia a la posibilidad de pérdidas causadas por variaciones en los factores que afectan el valor de un activo. Por esa razón, es importante que se identifiquen, se cuantifiquen, se controlen, y se haga un monitoreo continuo de los diversos tipos de riesgo a los que están expuestas las entidades en el devenir cotidiano de sus actividades.
La cuantificación del riesgo financiero siempre ha sido una de las preocupaciones centrales de los investigadores y operadores en finanzas, no sólo por la necesidad cada vez más creciente de responder a la normativa emanada de las entidades reguladoras nacionales e internacionales, como es el caso de la Superintendencia Financiera Colombiana y el Banco de Pagos Internacionales (Bank for Internacional Settlements-BIS) del Comité de Basilea, sino también, y primordialmente, para mejorar continuamente los procesos de toma de decisiones y generación de valor.
No obstante la gran cantidad de riesgos conocidos en finanzas, desde la perspectiva de los acuerdos de Basilea, todos los riesgos financieros pueden clasificarse en una de tres categorías básicas: riesgo de mercado, riesgo crediticio o riesgo operacional.
Según el Comité de Supervisión Bancaria de Basilea, en sus documentos sobre Convergencia Internacional de Medidas y Normas de Capital, 'El riesgo operacional se define como el riesgo de pérdida debido a la inadecuación o a fallos de los procesos, el personal y los sistemas internos o bien a causa de acontecimientos externos'.
Este riesgo se presenta debido a fallos en el núcleo operacional, errores humanos o de capacidad de procesamiento. Cada una de las empresas que generan valor con base en sus actividades de manufactura, servicios o aquellas actividades que en diferentes grados se vean afectadas por procesos, se encuentran expuestas al riesgo operacional: fallos en el sistema de control de calidad, negligencias en procesos de mantenimiento, entregas perdidas a clientes, fallos en las transacciones procesadas, o cualquier error operacional que dificulte el flujo de una alta calidad de productos y servicios, expuestos de manera potencial a pérdidas y negligencia de la firma. En general, el riesgo operacional corresponde a fallas en los sistemas, en los procesos y en las personas.
Es necesario que toda firma cuente con un sistema para identificar, cuantificar y gestionar el riesgo operacional, que le permita proveer el capital necesario para cubrir las pérdidas potenciales.
En términos generales, para la clasificación del riesgo operacional, se consideran ocho líneas de negocio (finanzas corporativas, negociación y ventas, banca minorista, banca comercial, liquidación y pagos, servicios de agencia, administración de activos e intermediación minorista) y siete categorías de riesgo operacional que potencialmente impactan negativamente a cada una de esas líneas (fraude interno, fraude externo, daños en activos físicos, prácticas de los empleados, prácticas del negocio, interrupción del negocio, gestión del proceso). Cada entidad debe hacer una adaptación del anterior esquema general, acorde con sus actividades específicas.
En los últimos años, pero fundamentalmente desde el surgimiento del Nuevo Acuerdo de Basilea (2004-2006), también conocido como Basilea II, que incorporó el riesgo operacional para el cálculo de los requerimientos de capital, los procesos de identificación de ese riesgo, su medición y gestión se han convertido en un desafío no sólo para los operadores de las finanzas, sino también para los académicos e investigadores, que han propuesto múltiples modelos para su cuantificación.
Los modelos propuestos varían en requerimientos de datos, complejidad, completez, exactitud, y en satisfacción de los estándares generales, cualitativos y cuantitativos, planteados por ese acuerdo.
Dentro del enfoque de los modelos AMA (Advanced Measurement Approach), el Comité de Basilea propone: cuadros de mando (Scorecards), El modelo de medición interna (IMA), y el modelo de distribución de pérdidas (Loss Distribution Approach, LDA).
Aunque inicialmente, el Comité de Basilea parecía inclinarse hacia los modelos de medición interna (IMA) para el cálculo del capital económico por riesgo operacional, el enfoque que ha tomado mayor fuerza y tiene un mayor posicionamiento en la práctica es el modelo de distribución de pérdidas (LDA).
Los orígenes del LDA se ubican en las aplicaciones actuariales, desarrolladas por la industria de seguros durante muchos años (Bühlmann, 1970). Es una de las ideas más naturales importadas de técnicas actuariales, para ser aplicadas en situaciones específicas que caracterizan el riesgo operacional, y en particular cuando hay escasez de datos. Diversos estudios que se han hecho acerca de datos empíricos convergen en que esa escasez de datos tiene un impacto dramático en la carga de capital, por lo que, en metodologías diferentes al LDA, se impone la necesidad de usar, para el tratamiento de ellos, procedimientos muy sofisticados.
El principal objetivo del modelo LDA es proveer un estimado del riesgo operacional para una entidad y sus unidades de negocio, basado en una distribución de pérdida que refleja los datos de pérdidas subyacentes. El LDA se basa en la recopilación de los datos de pérdidas históricas (frecuencia y severidad), que se registran internamente en las organizaciones, los cuales son complementados con datos externos. Estas pérdidas son clasificadas en una matriz que relaciona las líneas de negocio de la organización y los eventos operacionales de pérdida. Aunque Basilea propone ocho líneas de negocio y siete tipos de eventos estándar para la construcción de esa matriz, cada firma tiene la libertad de considerar sus propias líneas y eventos, de tal forma que se adecuen a la estructura y necesidades de la organización, como es el caso particular de una firma comisionista. Esta asignación debe hacerse en un número pequeño pero suficiente, de tal forma que la matriz resultante se pueda manejar adecuadamente.
El modelo LDA proporciona estimaciones para la pérdida, tanto por línea de negocio como por evento. Dicha distribución de pérdida es producto de la convolución entre un proceso estocástico discreto asociado a la frecuencia, y un proceso continuo asociado a la severidad de los eventos de riesgo. Esta técnica ha sido utilizada en los trabajos de Frachot et al, 2001; Lee, 2001; Cruz, 2002; Frachot et al, 2003; Frachot et al, 2004; Shevchenko,2005; Nešlehová et al, 2006; Akkizidis y Bouchereau, 2006; Böcker, 2006; Dutta y Perry, 2006; Degen et al, 2006; Aue y Kalkbrener, 2007; Chernobai y Rachevt, 2006, con gran éxito en la modelación de la distribución de pérdidas, la cual es fundamental para el cálculo de la matriz de capital propuesta por Basilea.
En este artículo se presenta una aplicación del LDA desarrollada para una entidad financiera. Está organizado de la siguiente forma: la presente sección que es introductoria. En la segunda parte se presenta formalmente el modelo LDA; luego se realiza la aplicación, y en la cuarta sección se presentan algunas conclusiones
MODELO DE DISTRIBUCIÓN DE PÉRDIDAS (LDA)
Principales supuestos del LDA
En el LDA la pérdida total se define como una suma aleatoria de las distintas pérdidas:
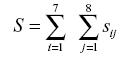
donde 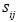
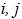
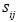
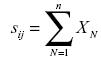
Con 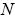
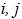
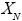
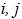
En esencia el modelo LDA tal como se utiliza en el riesgo operativo o en ciencias actuariales asume los siguientes supuestos dentro de cada clase de riesgo:
a) 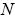
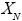
b) 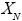
c) 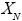
El primer supuesto admite que la frecuencia y la severidad son dos fuentes independientes de aleatoriedad. Los supuestos 2 y 3 significan que dos diferentes pérdidas dentro de la misma clase son homogéneas, independientes e idénticamente distribuidas (Frachot et al., 2004).
Modelación de la severidad
La primera etapa consiste en ajustar distintos modelos de distribución probabilística a una serie datos históricos de pérdidas operacionales desglosadas por su tipología para una determinada línea de negocio y evento de pérdida. En definitiva, se trata de encontrar la distribución de probabilidad que mejor se ajuste a los datos observados y estimar sus parámetros. Lee, 2001; Cruz, 2002; González, 2004; Shevchenko y Donnelly, 2005 y Carrillo y Suárez, 2006, proponen la distribución Lognormal o la de Weibull como las más recomendables a la hora de modelar la severidad, aunque en la práctica ninguna distribución simple se ajusta a los datos satisfactoriamente; de ahí la necesidad de recurrir a una mixtura de distribuciones para variables aleatorias continuas.
Sea 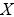
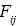
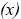
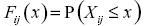
Modelación de la frecuencia
La frecuencia es una variable aleatoria discreta que representa el número de eventos observados durante un período de tiempo establecido, con una determinada probabilidad de ocurrencia. Lee, 2001; Cruz, 2002; González, 2004 y Shevchenko, 2005, proponen la distribución de Poisson como una candidata con muchas ventajas a la hora de modelar dicha variable; también recomiendan contemplar otras alternativas como la binomial o la binomial negativa.
Sea 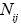
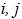
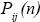
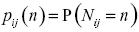
Pruebas de bondad de ajuste para severidad y frecuencia
Hasta ahora la comunidad científica alrededor del riesgo operacional viene tomando un número limitado de distribuciones de probabilidad tanto para las variables discretas (eventos), como para las variables continuas (severidad), y es importante resaltar las diferentes pruebas de bondad de ajuste tales como Chi-cuadrado, A-D, K-S, necesarias para cada distribución.
Dentro de estas pruebas tenemos:
a) Prueba de la Chi-cuadrado 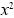
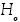
Decisión: Se rechaza
Se utiliza para determinar si una distribución de probabilidad específica se ajusta a los datos históricos. En riesgo operacional se aplica a la variable aleatoria discreta frecuencia.
b) Test de Anderson-Darling:
El test Anderson-Darling determina si los datos vienen de una distribución específica. La fórmula para el estadístico 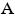
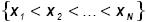
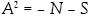
Donde
Decisión: Se rechaza
Este test se caracteriza por su mayor sensibilidad a la presencia de datos extremos, lo cual es una característica de las distribuciones de pérdidas en riesgo operacional.
El estadístico de la prueba se puede entonces comparar contra las distribuciones del estadístico de prueba (dependiendo de cuál 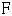
c) Test de Kolmogorov –Smirnov:
Se basa en una comparación entre las funciones de distribución acumulativa que se observan en la muestra ordenada y la distribución propuesta bajo la hipótesis nula.
En este caso:
Decisión: si esta comparación revela una diferencia suficientemente grande entre las funciones de distribución muestral y propuesta, entonces la hipótesis nula de la distribución se rechaza.
Adicionalmente, se pueden aplicar diagnósticos gráficos como las pruebas P-P y Q-Q.
Obtención de la distribución de pérdidas agregada
Una vez caracterizadas las distribuciones de severidad y frecuencia, el último paso del proceso consiste en obtener la distribución de pérdidas agregada (LDA), para lo cual tenemos que proceder a la combinación de ambas. A dicho proceso estadístico se le denomina convolución*.
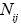
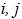
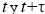
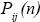
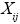
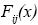
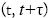
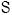
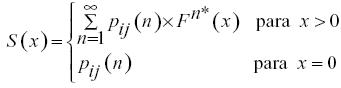
Donde, 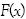
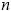
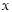
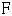
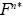
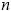
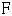
Para obtener 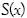
a) Algoritmo de Panjer
Se trata de un procedimiento recursivo, que exige, como paso previo, la discretización de la severidad.
Si la función de masa de la frecuencia puede ser escrita como:
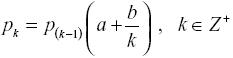
donde 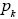
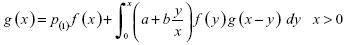
donde, 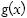
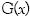
La limitación de este algoritmo radica en que sólo es válido para distribuciones de probabilidad discretas. Ello implica que la severidad, al ser una variable continua, debe ser discretizada antes de aplicar dicho procedimiento. Sin embargo, el principal inconveniente, en la práctica, radica en la complejidad al realizar las convoluciones.
b) Enfoque de simulación por Montecarlo
Después de ajustar ambos modelos (frecuencia y severidad) el siguiente paso es realizar la convolución entre ellos para obtener la distribución de pérdidas agregadas. Una forma simple y flexible para encontrar esa distribución consiste en utilizar simulación Montecarlo. Al utilizar este enfoque se estima la distribución de pérdidas agregadas utilizando un número suficiente de escenarios hipotéticos, generados aleatoriamente, a partir de las distribuciones de severidad y frecuencia.
Cálculo de la carga de capital
Después de calibrar las distribuciones de probabilidad de la frecuencia y de la severidad, el cálculo de la carga de capital es simple. Para ello es necesario precisar algunos conceptos sobre la carga de capital y la forma de calcularla.
Entonces se tienen las siguientes definiciones:
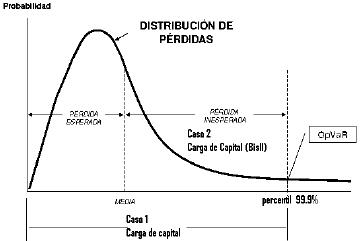
Definición 1 (Op-VaR): La carga de capital es el percentil 99.9% de la distribución de probabilidad de pérdida 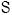
Definición 2: Si se opta por considerar sólo las pérdidas inesperadas se tiene:
donde 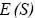
Basilea acepta esta definición siempre y cuando la entidad haya provisionado las perdidas esperadas. En la siguiente gráfica se ilustran los dos casos correspondientes a estas definiciones.
Fuente: elaboración propia
Definición 3 (OpVaR sobre un umbral): La carga de capital es el percentil 99.9% de la distribución de pérdida total, donde solamente se consideran las pérdidas por encima de un umbral mínimo 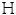
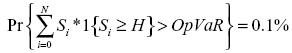
donde 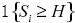
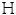

El umbral puede afectar la precisión de la carga de capital debido a que la precisión de los parámetros de frecuencia y severidad depende del umbral. La exactitud se deteriora cuando el umbral se fija en un nivel alto, porque para la calibración de la distribución de la severidad se utilizan pocos datos.
Es decir, la parte extrapolada de la distribución de la severidad llega a ser demasiado importante. Por lo tanto, en las definiciones 1 y 2, la compensación que resulta en un umbral óptimo está más relacionada con el equilibrio entre costos de recolección y precisión de la carga de capital que con el nivel de la carga de capital en sí mismo.
APLICACIÓN
Uno de los objetivos desarrollados en la investigación fue la implementación del modelo LDA para una entidad financiera. La principal dificultad encontrada en una exploración inicial de la información disponible fue la carencia de datos, ya que éstos en su momento debieron haber sido producto del registro de unos eventos de frecuencia y severidad de pérdidas. Pero tal escasez ha sido una característica muy generalizada en las entidades financieras, inclusive a escala mundial, cuando se ha intentado implementar la cuantificación del riesgo operacional. Para superar ese inconveniente se recurrió a un panel de expertos, a partir de los cuales se generó información acerca de la frecuencia y severidad de eventos de pérdida, haciendo é nfasis en lo relacionado con una línea específica de negocios. Esa etapa inicial fue desarrollada en el año 2005. Aunque posteriormente se ha avanzado significativamente tanto en la modelación, como en la estructuración de bases de datos, también se ha complicado la obtención de ese tipo de información, dado que esto se ha convertido en ventaja competitiva para las entidades financieras.
Estimación de la distribución de probabilidad para la severidad
Como ocurre en muchas aplicaciones de riesgo operacional, para estimar la distribución de probabilidad para la severidad, se tienen dos posibilidades básicas:
a. Dados 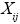
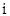

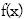
b. A partir de la información obtenida de los expertos, asumir que dichos datos siguen un modelo probabilístico 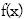
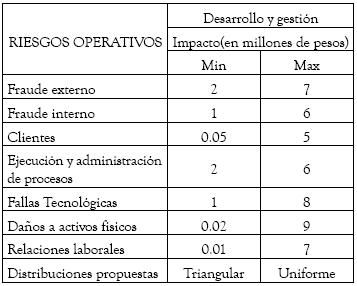
Dada las características de los datos obtenidos, que se presentan en la tabla 1, se decidió implementar la segunda opción planteada. En la tabla se observa que los expertos determinaron mínimos y máximos para la severidad, lo cual conduce a establecer rangos para cada evento de riesgo en la línea considerada. Para estos datos, y siguiendo las recomendaciones de autores como Lee, 2001; Cruz, 2002; González, 2004; Shevchenko y Donnelly, 2005 y Carrillo y Suárez, 2006, se asumen las distribuciones uniforme y triangular como potenciales distribuciones para la severidad del siguiente período.
Tabla 1. Fuente: Elaboración de los autores
Fuente: elaboración propia
En la tabla 2, se presentan los valores esperados para cada una de las distribuciones que se definieron en @Risk. Dichas esperanzas corresponden a la severidad promedio.
Tabla 2.
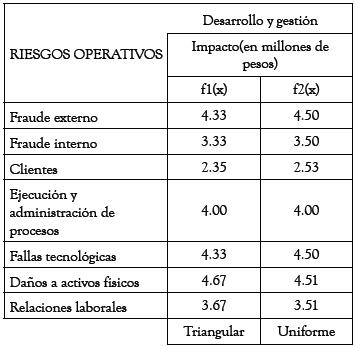
Fuente: elaboración propia
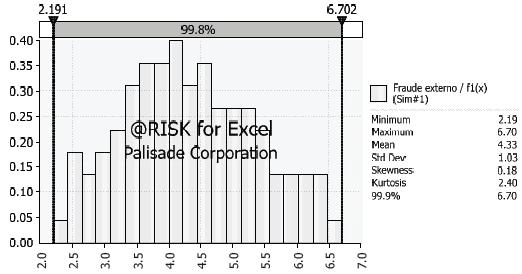
Utilizando @Risk se generó una simulación con 1000 iteraciones. A partir de los datos obtenidos se obtuvo la distribución de probabilidad que representa el perfil de riesgo para la severidad del siguiente año. Esta distribución se muestra en la gráfica 1.
Estimación de la distribución de probabilidad para la frecuencia
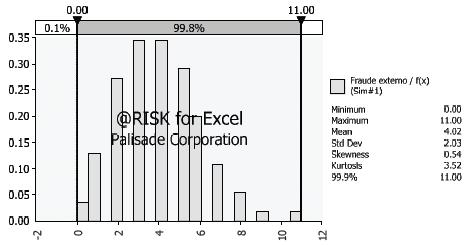
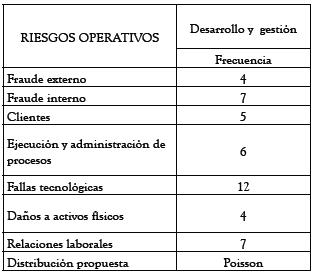
Para la distribución de probabilidad para la frecuencia se tiene una situación análoga a la presentada en la tabla 1, para la severidad. Pero a diferencia de lo anterior, en este caso, la gama de distribuciones potenciales, que deben ser discretas, es mucho más reducida. Específicamente, y según la experiencia en el campo actuarial, y en concordancia con los autores citados en el apartado anterior, se ha encontrado que la distribución de Poisson es la que mejor explica el fenómeno en la línea bajo estudio. En la tabla 3 se tienen las frecuencias promedio planteadas por los expertos. A partir de esos datos se obtuvo la distribución de probabilidad que representa el perfil de riesgo para la frecuencia del siguiente año. Esta distribución se muestra en la gráfica 2.
Fuente: elaboración propia
Gráfica 1. Fraude externo /
Fuente: elaboración propia
Gráfica 2. Fraude externo /
Tabla 3.
Fuente: elaboración propia
Estimación de la distribución de pérdidas
A diferencia de los modelos utilizados para evaluar riesgo de mercado y riesgo de crédito, los modelos para la estimación del riesgo operacional tienen unas características muy específicas: Se deben combinar variables aleatorias continuas y discretas; la pérdida agregada es una variable incierta, y la relación entre variables es no lineal. Estas características complican la estimación de la distribución de pérdidas por métodos analíticos, y por lo tanto se recurre a simulación Montecarlo, porque se considera, entre los métodos no analíticos, como el más simple y flexible, cuando se dispone de una plataforma adecuada. Dicha metodología implica la convolución de las distribuciones de frecuencia y severidad para luego generara la distribución de pérdidas.
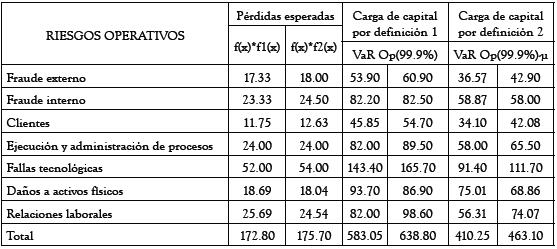
Los resultados obtenidos aplicando SMC se muestran en la tabla 4. En ella se tienen, respectivamente, los valores esperados de 1000 iteraciones de las convoluciones entre las distribuciones de frecuencia y severidad, inicialmente tomando una combinación Poisson-Triangular; y luego una combinación Poisson-Uniforme, para cada evento de riesgo.
Por ejemplo, el 18. Significa que para el siguiente año, la pérdida esperada por fraude externo es 18.000.000 de pesos. En forma análoga se interpretan los otros datos.
Esta información sería esencial para la entidad, no sólo porque las provisiones requeridas por la normativa, expresadas en términos de activos ponderados por riesgo, están en función de esas pérdidas, sino también para tener menor incertidumbre en su capital de trabajo.
Tabla 4.
Fuente: elaboración propia
Fuente: elaboración propia
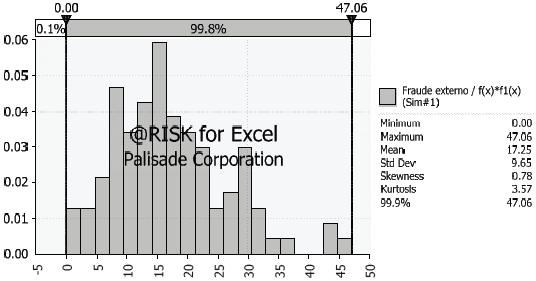
Gráfica 3. Fraude externo /
Los totales en las columnas de la tabla anterior indican, respectivamente, la pérdida operacional total esperada para el siguiente año en la línea de negocio, según cada modelo.
En la figura 3. Se muestra la correspondiente función de distribución de pérdidas para el evento fraude externo.
Cálculo de la carga de capital
Después de estimar las distribuciones de probabilidad de la frecuencia y de la severidad, el proceso de la carga de capital se hace con una de las dos definiciones planteadas anteriormente. Los resultados respectivos se muestran en la tabla 4. En las columnas cinco y seis se muestra la carga de capital aplicando la definición dos. Siempre será preferible para cada entidad disponer del modelo que genere la mínima pérdida operacional total, ya que los supervisores aceptarán este cálculo siempre que la entidad demuestre claramente que su modelo de cálculo satisface los criterios de solidez para modelos de medición avanzada, establecidos por Basilea II.
Intervalos de confianza
El procedimiento anterior proporciona una cuantificación de la carga de capital que por naturaleza es incierta. Se puede conjeturar que los reguladores esperarán que la estimación no esté lejos de su valor real. Esto es un punto crucial en la modelación del riesgo operacional debido a que la falta de datos normalmente puede traducirse en cierta inexactitud en la cuantificación de la carga de capital. Como consecuencia de lo anterior, el intervalo de confianza es la herramienta básica para justificar la estimación de la carga de capital, dado que se deben hacer numerosas simulaciones cuando se carece de datos.
La inexactitud de la carga de capital se asocia directamente a la inexactitud de los estimadores de los tres parámetros subyacentes de las distribuciones de probabilidad. Esto implica que para la construcción de un intervalo de confianza para la carga de capital se puede realizar de la siguiente forma:
Primero, obtener (en algunos casos, aproximada) la distribución de los estimadores subyacentes; luego, correr un número suficientemente de simulaciones de estas distribuciones y finalmente, para cada simulación, obtener su distribución empírica para calcular la carga de capital.
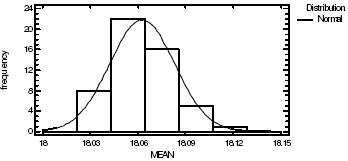
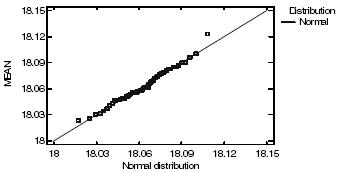
En las tablas cuatro y cinco se presenta la normalización para la pérdida esperada en el evento y línea considerados; y en la tabla cinco se muestra las correspondientes pruebas de normalidad.
Fuente: elaboración propia
Gráfica 4. Histogramfor MEAN
Fuente: elaboración propia
Gráfico 5. Quantile-Quantile Plot
Tabla 5. Tests for Normality for MEAN
Fuente: Resultados de @Risk
CONCLUSIONES
• La ausencia de información es un fenómeno recurrente en la cuantificación del riesgo operacional. Cuando esto se presenta, una estrategia a seguir es la consulta a expertos, a partir de los cuales se obtendrá información que permite construir una solución inicial aproximada al problema.
• La frecuencia se debe modelar a partir de datos internos, ya que esa variable está en función directa de los controles internos que son específicos a cada entidad. Con respecto a la severidad, los datos internos pueden ser combinados con datos externos mediante un adecuado proceso de escalamiento; aunque se debe poner especial atención para no heredar errores de otras entidades.
• Los modelos para la estimación del riesgo operacional tienen algunas características muy específicas: deben combinar variables aleatorias continuas y discretas; la distribución de pérdida agregada no corresponde a ningún modelo aleatorio predeterminado; y la relación entre variables del modelo es no lineal. De estas características se concluye la dificultad de estimación del riesgo operacional por métodos analíticos, lo que obliga a recurrir a métodos numéricos, entre los cuales el más flexible es la simulación Montecarlo.
• Recientemente, se están planteando metodologías para estimar el riesgo operacional incorporando correlaciones potenciales entre eventos y entre líneas de negocios, lo cual podría conducir a un positivo efecto de diversificación.
• Un mayor conocimiento de los riesgos de la entidad permitirá mejor calidad en el modelo de cuantificación, lo cual se debe traducir en una menor carga de capital, lo que dará una ventaja competitiva y una mejor administración del capital de trabajo.
REFERENCIAS
1. Akkizidis , L. y Bouchereau , V., (2006). Guide To Optimal Operational Risk & Basel II, Boca Raton, FL, Auerbach Publications. [ Links ]
2. AUE, F., KALKBRENER, M., (2007). Lda At Work. [ Links ]
3. BÖCKER, K., 2006. Closed-form approximation for OpVaR when high frequency losses are parameterized by a generalized Pareto distribution (GPD). [ Links ]
4. BÜHLMANN, H., (1970). Mathematical Methods in Risk Theory. Heidelberg. Springer-Verlag. [ Links ]
5. CARRILLO, S., SUÁREZ, A., (2006). Medición Efectiva Del Riesgo Operacional. [ Links ]
6. Comité de Supervisión Bancaria de Basilea. (2001). Operational Risk, Basilea. [ Links ]
7. Comité de Supervisión Bancaria de Basilea. (2003, julio). Supervisory Guidance on Operational Risk Advanced Measurement Approaches for Regulatory Capital, Basilea. [ Links ]
8. CONVERGENCIA INTERNACIONAL DE MEDIDAS Y NORMAS DE CAPITAL. (2006). Basilea. [ Links ]
9. CRUZ, M., (2002). Modeling, Measuring And Hedging Operational Risk. [ Links ]
10. CHERNOBAI, A., RACHEV, S., (2006). Applying robust methods to operational risk modeling. [ Links ]
11. DUTTA, K. Y PERRY, J., (2006). A tale of tails: an empirical analysis of loss distribution models for estimating operational risk capital. [ Links ]
12. DEGEN, M. EMBRECHTS, P. DOMINIK D., (2006). The Quantitative Modeling of Operational Risk: Between g-and-h and EVT. [ Links ]
13. Feria, J. & Jimenez, e., (2005). El OpVaR como medida del Riesgo Operacional, Documento de trabajo, [ Links ]
14. Frachot , A., Georges , P. y RONCALLI, T., (2001). Loss Distribution Approach for Operational Risk, Documento de trabajo, Credit Lyonnais. [ Links ]
15. Frachot , A., Georges , P. &, BAUD, N. (2003). How to Avoid Over-Estimating Capital Charge for Operational Risk? [ Links ]
16. FRACHOT, A. Moudoulaud, O. RONCALLI, T., (2004). Loss Distribution Approach in Practice [ Links ]
17. FRANCO, LUIS C., MURILLO JUAN G. et al. (2006) Riesgo Operacional: Reto actual de las entidades financieras. REVISTA INGENIERÍAS UNIVERSIDAD DE MEDELLÍN. [ Links ]
18. JOBST, A. A. (2007). Operational Risk – The Sting is Still in the Tail But the Poison Depends on the Dose. Journal of Operational Risk 2, (2). [ Links ]
19. Lee , Christopher M, (2001). Measuring and Managing Operational Risk in Financial Institutions, Singapore, John Wiley & Sons. [ Links ]
20. M. H. TRIPP, H. L. BRADLEY, R. DEVITT, G. C. ORROS, G. L. OVERTON, L. M. PRYOR & R. A. SHAW. (2004, march). Quantifying operational Risk in General Insurance Companies. [ Links ]
21. MARIANO GONZÁLEZ SÁNCHEZ. (2004, julio). Análisis del Nuevo Acuerdo de Capitales de Basilea (BIS-II): Pyme- Risk, Country-Risk y Operational-Risk. [ Links ]
22. NEŠLEHOVÁ, J.,EMBRECHTS, P., DEMOULIN, V., (2006). Infinite-mean models and the LDA for operational Risk. [ Links ]
23. PATRICK DE FONTNOUVELLE, JOHN JORDAN, ERIC ROSENGREN. (2005, febrero). Implication of Alternative Operational Risk Modeling Techniques. February. [ Links ]
24. Shevchenko , P. & Donely , J. (2005). Validation of the Operational Risk LDA Model for Capital Allocation and AMA Accreditation under Basel II. CMIS Confidential report prepared for Basel II programmed ANZ bank. CMIS report number 05/132. [ Links ]
25. THE FOREIGN EXCHANGE COMMITTEE. (2003, march).Management of Risk Operational in Foreign Exchange. [ Links ]
Recibido: 26/09/2008
Aceptado: 31/10/2008
* Una convolución es un operador matemático que transforma dos funciones f y g en una tercera función que en cierto sentido representa la magnitud en la que se superponen, f y una versión trasladada e invertida de g.