Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Ingenierías Universidad de Medellín
Print version ISSN 1692-3324On-line version ISSN 2248-4094
Rev. ing. univ. Medellin vol.8 no.14 Medellín Jan./June 2009
Control de velocidad del motor de indución empleando linealización por realimentación de estados
Speed control of induction motor using state feedback linearization
Eduardo Giraldo Suárez1; Santiago Sánchez Acevedo2
1 Ingeniero Electricista, M. Sc. Profesor Auxiliar, Universidad Tecnológica de Pereira, La Julita. Pereira, Colombia. Tel 3137122 ext. 107; correo egiraldos@ohm.utp.edu.co. Grupo control automático (UTP)
2 Ingeniero Electricista, M. Sc. Docente investigador, Instituto Tecnológico Metropolitano, Calle 54A No. 30-01, Medellin, Colombia. Tel 4600727 ext:5546; correo santiagosanchez@itm.edu.co. Grupo MIRP (ITM)
RESUMEN
Este documento presenta la aplicación de la técnica de control no lineal clásica llamada linealización por realimentación de variables de estado. Se hace una aplicación en el motor de inducción, la variable a controlar es la velocidad del eje del motor, el sistema emplea el esquema de control vectorial para máquinas de corriente alterna desarrollado en las últimas décadas; este método es análogo a la técnica de control del motor de corriente directa. El modelo del motor de inducción se describe en el sistema de coordenadas de campo orientado del flujo de rotor y se muestra una introducción al producto y la derivada de Lie, empleados en el diseño del controlador no lineal.
Palabras clave: motor de inducción, linealización por realimentación, control de velocidadABSTRACT
This articles shows the application of a classic non-linear control technique called “linearization by feedback of status variables.” An application on the induction engine is made. Variable to be controlled is speed of the engine shaft. The system employs a vectorial control scheme for AC engines developed during the last decades. This is a method analogous to the DC engine control technique. Induction engine model is described in the guided field coordinate system of rotor flow. Introduction to the product and Lie derivative used for designing the non-linear controller are shown.
Key words: Induction engine; feedback linearization; speed control.
INTRODUCCIÓN
El motor de inducción se ha presentado en la industria como el caballo de batalla, debido a su potencia, robustez y buen rendimiento en ambientes de alta exigencia; esto lo hace la máquina ideal. Sin embargo, son significativamente más difíciles de controlar que los motores de corriente continua. Un gran número de aplicaciones requiere de un control exacto de par y flujo de magnetización para lograr el control de velocidad. Los parámetros del motor de inducción varían con la temperatura, y algunos de ellos tienen que ser estimados por medio de técnicas como el filtro de Kalman. Para algunas variables del modelo se pueden realizar mediciones directas o diseñar sistemas basados en la teoría de observadores para obtener un valor estimado (Astrom, 2002).
Leonhard (2005) presenta el modelado básico de la máquina de corriente alterna y analiza los controladores que utilizan el concepto de vector de campo. El concepto es presentado también en los trabajados de otros autores como Bose (2002), quien resume las técnicas más utilizadas de control de velocidad. Las técnicas de control lineal y que emplean sistemas de estimación los cuales tienen en cuenta las variaciones de la resistencia se han aplicado sobre la máquina de inducción (Duval et al., 2006). Estas técnicas hacen una aproximación alrededor de un punto de operación del modelo no lineal del motor. El control no lineal de la velocidad del motor de inducción ha sido abordado por Chiasson (1998, 2005), las técnicas de control no lineal han sido tratadas por Isidori (2001), Sastry (1999) y Slotine (1991), otros trabajos utilizan el control no lineal adaptativo (Ko, 1998). En los ú ltimos años Mohanti y De (2006) han trabajado el control del motor de inducción por linealización, considerando el acople entre el par eléctrico y el flujo del rotor, y presentando en su trabajo el desacople para llegar a un modelo lineal reducido. En Yazdanpanah et al., (2007) se emplea el control no lineal del motor de inducción acoplado a un sistema robusto, pero empleando el concepto de control del par eléctrico.
A la hora de resolver la tarea de seguimiento de trayectorias sobre rangos de operación amplios, los métodos lineales reducen su desempeño. Por esta razón es preferible implementar técnicas no lineales las cuales consideran un control global. El artículo está formado por las secciones que describen el modelo de la máquina, el diseño del controlador y los resultados de las pruebas; en la siguiente sección se muestra una descripción del campo orientado empleado como punto de referencia para el control del motor de inducción, a continuación se realiza una presentación del modelo de la máquina en un sistema de dos ejes, llamado coordenadas de campo orientado de flujo del rotor. Luego se realiza un estudio de la estrategia de control y se hace una simplificación del modelo del sistema; después se emplea la derivada y producto de Lie en el diseño del controlador con linealización por realimentación de variables de estado. Por último se presentan los resultados de simulación del sistema en lazo abierto y lazo cerrado empleando linealización por realimentación de variables de estado.
Concepto de campo orientado
El empleo del lazo de regulación para las corrientes de estátor de la máquina da como resultado una simplificación del modelo, donde los voltajes de estátor pueden ser omitidos. El par eléctrico inicialmente es función de las corrientes de estátor y rotor, pero las corrientes de rotor no pueden ser medidas de forma directa en un motor de jaula, es más conveniente presentarlo en función del flujo del rotor o su equivalente de corriente de magnetización que están definidos en las coordenadas del estátor (Leonhard, 2005). La solución a esta idea lleva a la transformación del vector de corrientes de estátor en las coordenadas de campo, esquema clave para el control de máquinas de corriente alterna (Bose, 2002).
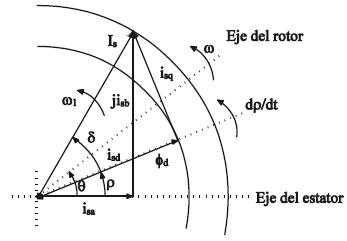
En la figura 1 se describe la transformación empleada. Is es el fasor de corriente de estátor y gira a la velocidad angular ω1, la corriente de estátor se puede descomponer en dos corrientes isa e isb, δ es un ángulo relacionado con la carga; en condiciones de carga cero este tiende a desaparecer. El flujo del rotor Φd es controlado y se encuentra alineado con la corriente isd. La componente ortogonal en el sistema de coordenadas de flujo de rotor es isq.
Figura 1. Relación de las corrientes
Fuente: elaboración propia.
MODELO EN EL SISTEMA DE COORDENADAS DE CAMPO DE FLUJO DEL ROTOR
El modelo transformado a las coordenadas de campo, el cual equivale al modelo trifásico del motor de inducción y que representa el sistema en dos fases se presenta en el conjunto de ecuaciones (1) a (6), donde las cantidades son de corriente directa.
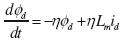 (2)
(2)
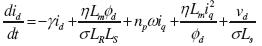 (3)
(3)
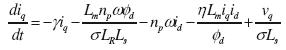 (4)
(4)
donde los voltajes de estátor para los ejes directo y de cuadratura son υd, υq la magnitud del flujo del rotor es descrita como Φd, ρ el ángulo del flujo del rotor, id, iq son las corrientes de estátor para simplificar el análisis, ω es la velocidad del rotor. Las constantes η, µ, γ y σ se presentan en las ecuaciones y son función de los parámetros del sistema. σ se denomina el factor de fuga, η el inverso multiplicativo de la constante de tiempo (Chiasson, 2005).
 (7)
(7)
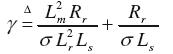 (8)
(8)
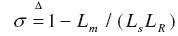 (9)
(9)
Rr, Rs son las resistencias del rotor y estátor, respectivamente, Ls, Lr y Lm son las inductancias de estátor, rotor y mutua, J es el coeficiente de amortiguamiento, np el número de polos y TL es el par de carga.
ESTRATEGIA DE CONTROL
Para desarrollar las técnicas de control en una forma simple, con lo cual se reduzca el problema de diseño, se utiliza una simplificación del sistema con un lazo de control interno proporcional integral (PI). Para alcanzar el comando de corriente, se escogen las entradas de las ecuaciones (10) y (11).
idr e iqr son las corrientes de referencia del regulador, kpd, kpq, kid y kiq son las ganancias proporcionales e integrales de los ejes directo y cuadratura, respectivamente, Una adecuada selección de las ganancias hace que las corrientes del motor tiendan al valor deseado. La dinámica de las corrientes se puede ignorar, de modo tal que el modelo puede ser reemplazado por un sistema de ecuaciones diferenciales no lineal reducido; el sistema se representa por las ecuaciones (12), (13) y (14).
ahora idr e iqr son las entradas. Para realizar control vectorial de forma análoga a la realizada en un motor de corriente continua, se debe mantener la corriente del eje directo constante, y la de cuadratura puede realizar el control de la velocidad como se muestra en las ecuaciones (12) y (13). Esto debido a que el par eléctrico desarrollado es proporcional al flujo y la corriente del eje q; además, el flujo está alineado con el eje directo lo que produce un control mediante la corriente de estátor id.
LINEALIZACIÓN POR REALIMENTACIÓN DINÁMICA
Para las ecuaciones que describen el modelo del motor de inducción (1)-(6) y por medio del análisis no lineal y los conceptos definidos en (Isidori, 2001, Sastry, 1999) este sistema no es linealizable por realimentación. El modelo reducido de (12), (13) y (14) con entradas idr e iqr y las variables de estado ω, Φ y ρ también es no linealizable por realimentación. El concepto de linealización por realimentación dinámica ha sido propuesto para un sistema dinámico el cual no es linealizable por realimentación; la adición de integradores en las entradas puede resultar en el sistema de orden mayor el cual puede ser linealizable por realimentación, si y sólo si este es (estáticamente) linealizable por realimentación (Chiasson, 1998), (Sastry, 1999), (Mohanti y De, 2006).
Se asume que todas las variables de estado son medibles y que los parámetros del motor, incluyendo el par de carga, son constantes y conocidos.
Sea 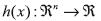 una función escalar, entonces el gradiente es definido como
una función escalar, entonces el gradiente es definido como  Sean
Sean  funciones vectoriales. Se define el producto Lie como
funciones vectoriales. Se define el producto Lie como La derivada de Lie de una función escalar h con respecto al campo vectorial f es escrita como
La derivada de Lie de una función escalar h con respecto al campo vectorial f es escrita como  , donde
, donde  es el producto punto de dh y f. (Slotine, 1991), (Isidori, 2001), (Chiasson, 1998, 2005), (Yazdanpanah et al., 2007).
es el producto punto de dh y f. (Slotine, 1991), (Isidori, 2001), (Chiasson, 1998, 2005), (Yazdanpanah et al., 2007).
Integrador en el eje q
Se hace la adición de un integrador en el eje q con el fin de hacer linealizable por realimentación el modelo de (12) a (14); se selecciona el eje q a partir del concepto de control vectorial explicado con anterioridad. Se asume que:
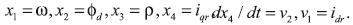
El sistema se convierte en el conjunto de ecuaciones de (15) a (18).
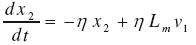 (16)
(16)
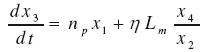 (17)
(17)
Las ecuaciones de (15) a (18) pueden escribirse como en (19).
Para este sistema el conjunto solución está definido por (20) y (21).
La aplicación de la realimentación es presentada en (22).
donde los productos de la matriz se definen por las ecuaciones (23) a 28).
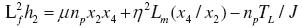 (24)
(24)
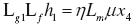 (25)
(25)
 (26)
(26)
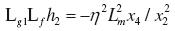 (27)
(27)
RESULTADOS
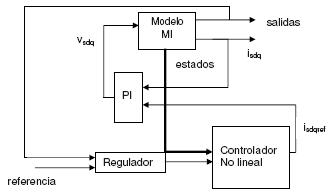
La figura 2 presenta el modelo implementado para simulación en el software Matlab®, donde se tienen como salidas el ángulo y la velocidad del eje; la señal de control del sistema es el voltaje en los ejes d y q. Los resultados de simulación del modelo se presentan en las figuras 3 y 4. Para la condición inicial donde los valores de las variables de estado del sistema descrito por (1)-(5), tienen el valor de la ecuación (29) y las señales de entrada al sistema vq = 90.0V, vd = 0.9V, y TL = 5Nm.
Figura 2. Modelo del controlador no lineal para el MI
Fuente: elaboración propia.
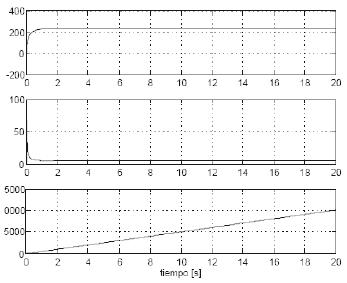
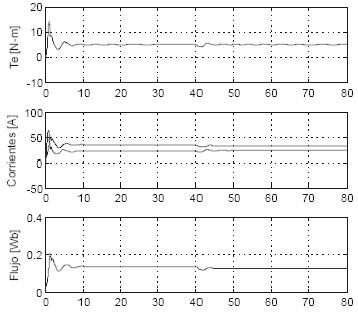
Figura 3. Comportamiento modelo motor de inducción
Fuente: elaboración propia.
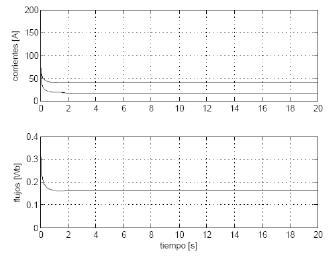
Figura 4. Comportamiento de las corrientes y el flujo
Fuente: elaboración propia.
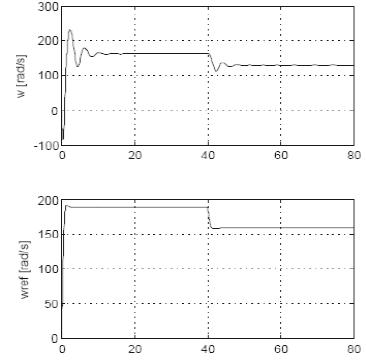
donde se observa que el motor tiende al punto de equilibrio 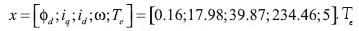 . Te es el par eléctrico desarrollado por la máquina. Al aplicar el sistema de control sobre el motor de inducción se obtiene el comportamiento presentado en las figuras 5, 6 y 7; la figura 5 presenta la variación de la velocidad en lazo cerrado (w) y la señal de referencia (wref); a los 40 segundos se realiza un cambio en la referencia de la velocidad del eje del motor; de esta se puede observar cómo la velocidad presenta una leve oscilación. La figura 6 presenta la variación del torque ante el cambio de velocidad; se aprecia el establecimiento del torque eléctrico en el valor del torque de carga (5Nm); las corrientes de estátor y el flujo de rotor se mantienen dentro de los rangos observados en lazo abierto, y la figura 7 muestra la señal de control del sistema que en este caso es el voltaje de estátor para los ejes directo y cuadratura.
. Te es el par eléctrico desarrollado por la máquina. Al aplicar el sistema de control sobre el motor de inducción se obtiene el comportamiento presentado en las figuras 5, 6 y 7; la figura 5 presenta la variación de la velocidad en lazo cerrado (w) y la señal de referencia (wref); a los 40 segundos se realiza un cambio en la referencia de la velocidad del eje del motor; de esta se puede observar cómo la velocidad presenta una leve oscilación. La figura 6 presenta la variación del torque ante el cambio de velocidad; se aprecia el establecimiento del torque eléctrico en el valor del torque de carga (5Nm); las corrientes de estátor y el flujo de rotor se mantienen dentro de los rangos observados en lazo abierto, y la figura 7 muestra la señal de control del sistema que en este caso es el voltaje de estátor para los ejes directo y cuadratura.
Figura 5. Comportamiento del motor en lazo cerrado
Fuente: elaboración propia.
Figura 6. Comportamiento de las variables del sistema en lazo cerrado
Fuente: elaboración propia.
Figura 7. Comportamiento voltajes de control
Fuente: elaboración propia.
CONCLUSIONES
Se presenta el desempeño del motor de inducción en lazo abierto, el cual tiene un transitorio significativo en el arranque.
La técnica de linealización por realimentación de las variables de estado para el modelo completo del motor de inducción es bastante difícil y extensa para la implementación; la reducción del modelo disminuye la complejidad del sistema para ser controlado usando linealización por realimentación de variables de estado.
La adecuada selección de las ganancias del PI interno permite que las corrientes alcancen de forma rápida las referencias que son las salidas del sistema de control y se lleve la velocidad al valor deseado.
Se ha logrado implementar un control de velocidad del motor de inducción usando técnicas de control no lineal clásico.
REFERENCIAS
1. Astrom , K. J., 2002, Control Systems Design, Lecture notes for ME 155A, Department of Mechanical and Environmental Engineering, University of California Santa Barbara, California. [ Links ]
2. Bose , B. K., 2002, Modern power electronics and ac drivers, Prentice-Hall Inc., U.S.A. [ Links ]
3. Chiason, J., (1998), A new approach feedback linearizaton control of an induction motor. IEEE Transactions on Automatic Control: 43 (3). [ Links ]
4. Chiasson , J., 2005. Modeling and High Performance Control of Electric Machines. IEEE Press Series on Power Engineering, Wiley-Interscience. [ Links ]
5. Duval , C.; Clerc , G. y Le Gorrec , (2006), Induction machine control using robust eigenstructure assignment, Control Engineering Practice: 14 (February), 29–43. [ Links ]
6. Isidori , A., 2001, Nonlinear control system. Springer, 3rd edition. [ Links ]
7. Ko, Jeonghwan , 1998. Adaptive feedback linearization for the control of a typical wing section with structural nonlinearity. [ Links ]
8. Mohanti , K.B. y De, N.K., 2006. Linearizing control of an induction motor. Industrial technology, ITIT 2006, IEEE international conference on industrial technology, pages 45–50, December. [ Links ]
9. Sastry , S., 1999, Nonlinear systems, analysis, stability and control. Springer, United States. [ Links ]
10. Slotine , J. E. y Li, W., 1991. Applied Nonlinear Control, Prentice-Hall Inc., U.S.A. [ Links ]
11. Yazdanpanah , R.; Soltani , J., y Markadeh , G.R., 2007. Nonlinear torque and stator flux controller for induction motor drive based on adaptive input-output feedback linearization and sliding mode control. Energy conversion management. [ Links ]
Recibido: 25/09/2008
Aceptado: 15/05/2009













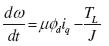 (1)
(1)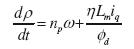 (5)
(5)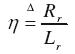 (6)
(6)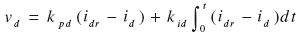 (10)
(10)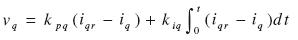 (11)
(11)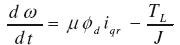 (12)
(12)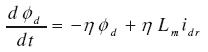 (13)
(13)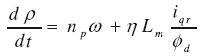 (14)
(14)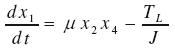 (15)
(15)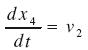 (18)
(18)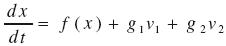 (19)
(19) (20)
(20)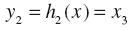 (21)
(21)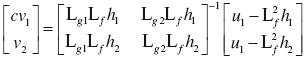 (22)
(22)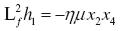 (23)
(23) (28)
(28)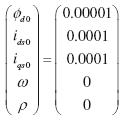 (29)
(29)