Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Ingenierías Universidad de Medellín
Print version ISSN 1692-3324On-line version ISSN 2248-4094
Rev. ing. univ. Medellín vol.8 no.15 suppl.1 Medellín July 2009
Marco histórico y estado del arte de los modelos de evolución del paisaje y de erosión
Historical framework and state of art of landscape evolution and erosion models
Juan José Montoya Monsalve*
* Ingeniero Geólogo, Universidad Nacional de Colombia, Sede Medellín. Doctor en Ingeniería Hidráulica y Medio Ambiente, Universidad Politécnica de Valencia, España. Profesor de tiempo completo e integrante del grupo GICI, Ingeniería Civil, Universidad de Medellín. Carrera 37 A Sur No. 1–41. Medellín. e–mail:jjmontoya@udem.edu.co. Tel: (574) 3138183.
Resumen
Se presenta un análisis del marco histórico de modelos de evolución del paisaje y de erosión, además se expone el estado del arte de cuyo análisis se derivan los aspectos fundamentales que deben ser tenidos en cuenta en la formulación de un modelo de erosión a escala de cuenca. Se introduce el tema con un breve recuento de la evolución del conocimiento de modelos geomorfológicos, los cuales constituyen el marco general de los modelos de erosión. De dicho análisis surgen las preguntas básicas que debe abordar un modelo de erosión. Posteriormente se efectúa un análisis del desarrollo histórico de modelos de erosión, se reseñan las características principales de los modelos de erosión actuales y se enumeran las potencialidades y limitaciones de estos. Este artículo corresponde a una revisión bibliográfica tendente a la definición del marco teórico del proyecto de investigación titulado "Desarrollo de un modelo conceptual de producción, transporte y depósito de sedimentos".
Palabras clave: modelos de erosión, modelos geomorfológicos, modelos de evolución del paisaje, geomorfología.Abstract
This articles presents an analysis of the historical framework of landscape evolution models, specifically erosion models: it also refers to the current state of the art from which critical analysis derive the fundamental aspects which should be taken into account in the formulation of an erosion model in catchment scale. The theme is introduced with a brief review of the evolution of knowledge of landscape evolution models, which provide the overall framework of erosion models. From this analysis, basic questions to be addressed by an erosion model arise. Later, analysis of the historical development of erosion models is made; It also summarizes the main characteristics of the current erosion models and lists potentialities and limitations of erosion models. This paper corresponds to a literature review aimed at defining the theoretical framework of a research project entitled "Development of an Erosion, Transport and Sedimentation Conceptual Model."
Key words: erosion models, geomorphic models, landscape evolution models, geomorphology.
INTRODUCCIÓN
Las ciencias actuales están regidas, en mayor o menor medida, por necesidades prácticas. En las ciencias naturales, los requerimientos se centran en la simulación y predicción del comportamiento del sistema natural por medio de la modelación. Los sistemas naturales son complejos y para acercarse a dicha complejidad se parte de ideas e impresiones, las cuales constituyen un conocimiento científico sólo cuando se establecen relaciones entre ellas [1].
Según Wagensberg [1] los pasos para comprender un sistema complejo se pueden resumir en a) Ver: quiere decir captar información de lo que visita nuestra área de percepción en un lugar y momento; b) Mirar: significa seleccionar la información que resulta de dirigir la visión cazada por cierta curiosidad; c) Observar: consiste en acumular la información que resulta de mantener la mirada según sea nuestra perplejidad; y d) Experimentar: equivale a enriquecer la información como consecuencia de provocar observaciones próximas según sea nuestro ingenio para intervenir en el resto del mundo. El progreso de cualquier rama de la ciencia se debe a la capacidad de observar y experimentar. Pero esta capacidad es limitada en sistemas complejos naturales, por ejemplo, en una cuenca hidrográfica.
Wagensberg [1] sugiere que estas limitaciones se pueden eludir acudiendo a una nueva forma de generar conocimiento: la simulación, esto es, la obtención de información que se genera en experimentos inventados. Dicho autor propone que la simulación no es teoría ni experiencia ni un mero útil de cálculo, sino una genuina tercera forma de aproximación a la realidad que acaso esté revolucionando el método científico. La simulación se nutre indistintamente de la teoría y la experiencia, puesto que cuando se modela un sistema se utilizan conceptos y, a la vez, se hace uso de datos y observaciones, aunque sean parciales, del sistema.
1. LOS MODELOS DE EVOLUCIÓN DEL PAISAJE
El análisis del paisaje como sistema dinámico comenzó con la teoría del ciclo geográfico, propuesta por el geógrafo norteamericano William Morris Davis (1850–1934) a finales del siglo XIX. Davis desarrolló su teoría apoyándose en los paradigmas de las ciencias naturales de la época, esto es, la teoría de la evolución de Charles Darwin (1809–1882) y el principio de uniformismo (el presente es la clave del pasado) del físico escocés James Hutton (1726–1797). Davis recopiló y sintetizó en su teoría los trabajos precedentes efectuados en el suroeste árido de Estados Unidos, de John Wesley Powell (1834–1902), que presentaba una línea fisiográfica; y de Grove Karl Gilbert (1843–1918), que se centraba en la génesis del paisaje. Con estos enfoques, Davis creó las bases de la geomorfología moderna. Su formulación es clara y concisa y justo al comenzar la disertación del ciclo geográfico señala lo siguiente: "Toda la variedad de formas del terreno dependen de —o, como dirían los matemáticos, son función de— tres variables, que pueden ser denominadas estructura, proceso, y tiempo" [2].
La teoría del ciclo de Davis fue la base para los tratados geomorfológicos durante la primera mitad del siglo XX. Se pueden diferenciar dos escuelas de pensamiento: una, basada en las relaciones ambientales y la distribución de procesos según contextos climáticos, se conoce comúnmente como la Geomorfología Climática y sus aportes dieron un impulso a la cartografía geomorfológica y a un método de carácter descriptivo; algunos autores la denominan la escuela francesa debido al protagonismo que tuvieron autores franceses (por ejemplo [3–5]). La otra escuela surgió de forma dispersa en varios países y autores (por ejemplo [6–13]), con elementos en común: el análisis, la parametrización y la cuantificación de procesos geomorfológicos según la configuración geométrica de las formas producidas y las relaciones dinámicas de los procesos. Dicha escuela se denomina la Geomorfología Dinámica.
1.1 Los principios de evolución del paisaje
Un paisaje es la expresión de procesos continuos de acreción o levantamiento tectónico (procesos endógenos), y de incisión o erosión por agentes meteóricos (procesos exógenos), actuando simultáneamente en el tiempo. Scheidegger [14] ha propuesto el principio del antagonismo señalando que si bien la evolución del paisaje no es cíclica en todo su sentido, el paisaje representa el estado instantáneo de la interacción entre los procesos exógenos y endógenos, los cuales son antagónicos.
Scheidegger [14] propone el principio de inestabilidad según el cual el equilibrio dinámico de un paisaje es inestable. Este principio ya ha sido tratado por Schumm [12] en su teoría del umbral geomorfológico.
Otro principio relacionado con el principio de inestabilidad es el principio de la catena, que según Blöschl y Sivapalan [15] fue definido inicialmente por Milne en el año de 1935 y se originó a partir de la observación de la física de los suelos al notar que ciertas secuencias de tipos de suelos se repiten a lo largo de una ladera en particular, estrechamente conectadas con la posición topográfica relativa en la ladera. El principio de la catena plantea uno de los aspectos fundamentales en los procesos geomorfológicos: su variabilidad espacial.
Otro principio fundamental en la evolución del paisaje se relaciona con la predominancia de geoformas en una región en particular, aun teniendo en cuenta la naturaleza estocástica de los procesos formadores. Según Scheidegger [14], el principio de selección fue introducido inicialmente por Gerber en el año de 1969, estableciendo que los procesos de erosión ocurren de tal manera que las geoformas estáticamente estables, con referencia a los esfuerzos actuantes, son seleccionadas preferentemente. Además de los principios descritos anteriormente, Scheidegger [14] establece el principio de control estructural, por el cual las características de un paisaje están prediseñadas de acuerdo con la configuración tectónica. Este principio se evidencia en la configuración de la red de drenaje y en la ocurrencia de procesos erosivos y de movimientos en masa.
Es necesario considerar la variabilidad espacial, tanto de los parámetros como de los procesos, en la aplicación práctica de modelos geomorfológicos e hidrológicos. Al respecto, Bloschl y Sivapalan [15] luego de efectuar un análisis de los problemas de escala, la heterogeneidad y la variabilidad espacial y temporal en la modelación hidrológica y geomorfológica, se decantan por la organización, más que por la aleatoriedad, al tratar el paisaje como un sistema. Ponen, entre otros ejemplos, el análisis de redes de drenajes a partir de los conceptos de Horton [7] y Strahler [8]; el estudio de la geometría hidráulica basada en las relaciones de Leopold y Maddock [16]; y la estimación de la variabilidad de parámetros hidrológicos del suelo a partir de conceptos tales como la catena de suelos en una ladera y el Índice Topográfico de Beven y Kirkby [17].
1.2 Modelos de evolución del paisaje actuales
Los modelos analíticos de evolución del paisaje tienen una historia relativamente larga, cuyos inicios se pueden ubicar a partir de la teoría de Davis. Según Willgoose [18] los modelos computacionales que tratan la dinámica de la evolución del paisaje a escala de cuenca comienzan con el trabajo de Ahnert en el año de 1976. Los avances recientes en técnicas computacionales han permitido el desarrollo de herramientas para representar la superficie del terreno. La capacidad de trabajar con Modelos de Elevación Digital (DEM) y con Redes de Triángulos Irregulares (TIN), a principios de la década de los ochenta del siglo pasado, generó un gran interés en la comunidad científica y técnica, en el desarrollo de modelos distribuidos en el espacio, tanto hidrológico como geomorfológico.
Esto permitió una adecuada representación de los procesos fluviales y de ladera, algunos ejemplos son los trabajos de Kirkby [19], Willgoose et al. [20, 21] y Howard [22]. Se desarrollaron modelos distribuidos en Hidrología de cuencas, por ejemplo los trabajos de Abbott et al. [23], Garrote y Bras [24], y Julien et al. [25], entre otros. En evolución del paisaje, donde se pueden destacar los trabajos de Willgoose et al. [26], Johnson y Beaumont [27], Tucker y Slingerland [28], y Tucker y Bras [29]. En erosión de suelos, por ejemplo, los trabajos de Laflen et al. [30], y Mitas y Mitasova [31]; y en estabilidad de laderas, como el trabajo de Montgomery y Dietrich [32]. Estos acercamientos han ayudado a entender las interrelaciones entre la hidrología, la erosión fluvial, los procesos en la ladera, la tectónica, el clima, la litología y su influencia en la génesis y evolución de las geoformas y la red de drenaje [33].
Los modelos referenciados tienen tres puntos en común, derivados de la necesidad de modelar flujos sobre la superficie del terreno [34]: a) La división de la superficie del terreno en una serie de elementos discretos y conectados; b) La aplicación de leyes de conservación de masa para cada elemento del terreno; y c) La definición de la dirección de flujo y la red de drenaje entre cada discretización de la superficie del terreno.
1.3 Los principios de evolución del paisaje y los modelos de erosión
Para el diseño de un modelo de erosión es necesario tener en cuenta los fundamentos y principios de un modelo de evolución del paisaje repasados hasta ahora. Las preguntas básicas que se deben abordar son: a) ¿Dónde y cuándo se presenta la erosión?; b) ¿Hasta dónde se transportan estos sedimentos?; c) ¿Dónde y cuándo se depositan los sedimentos?; d) ¿Cuál es el tiempo de residencia de los sedimentos en una localización específica de la cuenca?
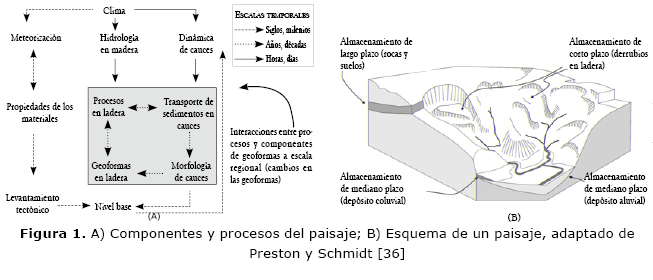
Para acercarse a estas cuestiones se define el sistema físico (el paisaje), los procesos que actúan en el sistema y la escala espacial y temporal de dichos procesos. En la figura 1–A se esquematiza la representación del sistema físico con sus diversas escalas espacio–temporales. Dependiendo de la escala de análisis (espacial y temporal) varios de los componentes pueden considerarse como elementos dinámicos del sistema, sujetos a presentar variaciones, y otros pueden considerarse como condiciones de frontera externas [35]. Además, el sistema físico está sujeto a entradas de energía y a la aplicación de fuerzas de acuerdo con los procesos geomorfológicos que estén actuando. Los flujos de sedimentos, en un contexto sistémico, están concebidos como una serie de geoformas en el paisaje en las cuales los sedimentos se almacenan en diversidad de longitudes de tiempo (figura 1–B).
2. LOS MODELSO DE EROSIÓN
Los primeros intentos para desarrollar métodos de estimación de la erosión se realizaron en Estados Unidos, en la década de los años veinte del siglo pasado, como una respuesta a las elevadas tasas de erosión y pérdida de suelo debido a la modernización de la agricultura. Según Hagen y Foster [37] la primera ecuación propuesta para el uso en planes de conservación fue asignada por Zingg en el año de 1940, quien relaciona la pérdida de suelo con la erosión laminar y concentrada, las cuales, a su vez, dependen de la longitud y grado de la pendiente.
Luego de un análisis empírico a partir de una gran cantidad de datos tomados en parcelas de erosión en más de 40 localidades de los Estados Unidos de América, se desarrolló la Ecuación Universal de Pérdida de Suelo (USLE) por un grupo de trabajo de investigadores dirigidos por W.H. Wischmeier [38]. Con esta perspectiva, se masificó el uso de la USLE en el territorio norteamericano, durante las décadas de los sesenta y los setenta del pasado siglo. Alternativamente, se implementó la USLE en otras partes del mundo y se realizaron numerosas investigaciones para adecuar los factores de la ecuación en zonas con características diferentes de las que se dedujeron inicialmente.
Posteriormente se efectuaron investigaciones tendentes a revisar y actualizar los factores de la USLE y se obtuvo la Ecuación Universal de Pérdida de Suelos Revisada (RUSLE) [39]. Esta modificación se limitó a la transformación de los factores de la anterior USLE, pero no cambió su estructura. La agregación temporal de la ecuación se basa en condiciones medias anuales, así el resultado de la aplicación de la USLE y la RUSLE en una zona es la masa total de sedimentos producidos por superficie de terreno por año. Como un intento por utilizar la estructura de la USLE en eventos de lluvias generadores de erosión se desarrolló la Ecuación Universal de Pérdida de Suelos Modificada (MUSLE) [40], que analiza eventos en vez de condiciones medias anuales.
La masificación y modernización de la agricultura se presenta unas décadas más tarde en Europa, y consecuentemente, la necesidad de desarrollar modelos de erosión se da posteriormente que en Estados Unidos [41]. Es justo cuando comienza la aplicación de modelos de erosión en Europa que los investigadores se preguntan por la aplicación de modelos basados en la USLE en condiciones diferentes a aquellas zonas en donde se implementó. A partir de la evaluación de los modelos existentes (basados en la USLE) con datos reales de pérdida de suelos, se observa el pobre desempeño particularmente en zonas de Europa y la necesidad de desarrollar una nueva generación de modelos.
De una revisión de los antecedentes y el posterior desarrollo de estos modelos, se observa que estos han surgido de la colaboración conjunta de investigadores (centros de investigación y universidades) y agencias gubernamentales facultadas de la planificación del territorio. El relativo éxito de los modelos de erosión existentes se debe en gran parte a la retroalimentación entre los planificadores (usuarios) y los investigadores (desarrolladores) y a la continuidad en el uso y la mejora del modelo. Si esta comunicación no es fluida y constante, lo que comúnmente ocurre es que el modelo termine siendo utilizado sólo por sus desarrolladores y en el mejor de los casos como herramienta didáctica en las universidades.
2.1 Tipos de modelos de erosión
Son varias las formas de clasificar los modelos de erosión. Se pueden clasificar de acuerdo con la escala de análisis, que en el caso de la escala espacial varía desde la escala de parcela experimental hasta modelos de escala continental; en el caso de la escala temporal, se encuentran modelos de eventos con intervalos de simulación del orden de minutos o segundos hasta modelos de evolución de paisajes en donde es necesario considerar varios miles de años.
Otra forma de clasificación es de acuerdo con la forma en que el modelo representa el sistema físico (por ejemplo, la representación de la topografía). Además, es posible clasificar los modelos de acuerdo con la forma de encontrar las relaciones que explican los procesos de erosión: los métodos de evaluación empíricos y los que tienen base física. La mayoría de los modelos de erosión son de tipo híbrido incluyendo tanto componentes empíricos como teóricos [42].
Modelos de erosión empíricos. La totalidad de modelos de erosión empíricos que se encuentran en la literatura o que se utilizan actualmente en programas computacionales disponibles, se derivan de la USLE. La USLE se diseñó para parcelas dedicadas a la agricultura, es válida para áreas de una hectárea. La USLE toma en cuenta la longitud de la pendiente (factor L), la inclinación (factor S), el clima (factor R), los suelos (factor K), el cultivo (factor C) y el manejo del suelo (factor P). El uso de la USLE y sus derivados están limitados a la estimación de la erosión bruta y carecen del cálculo de la sedimentación a lo largo de la ladera, en depresiones, valles o canales. Según Piest et al. [43], evidencias empíricas demuestran que alrededor del 80% de los sedimentos producidos en una cuenca de drenaje se depositan dentro de ella, ya sea en laderas cóncavas, en microbarreras producidas por la vegetación y en remansos ubicados en el sistema fluvial, hecho que no está presente en la formulación de la USLE.
Modelos de erosión basados en procesos. Las técnicas y métodos de estimación de la erosión hídrica basadas en procesos se caracterizan por utilizar relaciones matemáticas para describir los procesos fundamentales que actúan, esto es, el arranque, el transporte y la sedimentación, tanto de partículas individuales del suelo como de agregados. Otra característica de los modelos de erosión basados en procesos es la integración espacial de áreas en las cuales los procesos se pueden diferenciar. Hagen y Foster [37] señalan que la mayoría de modelos de erosión basados en procesos dividen el paisaje en las siguientes áreas fuente: áreas entre surcos, surcos y cárcavas efímeras, mientras que las zonas de acumulación se encuentran en las depresiones del terreno. Estas áreas representan elementos hidrológicos que pueden interrelacionarse de acuerdo con los patrones de flujo del paisaje. Los modelos de erosión basados en procesos tratan cada uno de los procesos de forma independiente, basados en relaciones matemáticas empíricas y/o con base física que relacionan propiedades del suelo con factores de erosionabilidad y con esfuerzos tangenciales producidos por los flujos de agua debido a las acumulaciones de flujo, ya sea en zonas entre surcos, en surcos o en cárcavas.
2.2 Posibilidades de los modelos de erosión
Para redondear los conceptos analizados hasta el momento se plantea esta pregunta: ¿Es posible un modelo universal de erosión? Es posible en la medida en que se base en la física de los procesos y que las simplificaciones que haga, que provienen en gran medida de la discretización del espacio–tiempo, permitan que las ecuaciones conceptuales de los procesos que ocurren sean representativas de la escala temporal (intervalo temporal de simulación) y la escala espacial (discretización del espacio).
Los cambios en las escalas temporales y espaciales generalmente se presentan interrelacionados. Por ejemplo, para modelar la erosión a escala de parcela o de una ladera particular, el tiempo, el volumen y la distribución espacial y temporal del flujo superficial son los factores críticos. Si la escala de análisis es regional o de cuenca, los parámetros determinantes son la topografía, los suelos y la vegetación, mientras que el intervalo temporal debe comprender no solamente eventos de tormenta sino varias décadas o centenas de años, en las cuales dichos parámetros pueden variar. En análisis globales, de escala nacional o continental, las variables críticas son el clima y la litología, con intervalos temporales que van desde decenas de años a cientos o miles de años, en los cuales ocurren cambios climáticos naturales [44].
Además es imperativo un conocimiento exhaustivo de las condiciones físicas de la zona de estudio (que normalmente es una cuenca hidrográfica), esto es, las características de los suelos, el régimen climático, la vegetación, los usos del suelo, etc.; e integrar este conocimiento en el modelo, que en términos reales se traduce en una adecuada parametrización y en la determinación a priori de los procesos relevantes según sean la escala y el objetivo del análisis.
Otra de las posibilidades de los modelos de erosión es que al tratar aspectos relacionados con la evolución del paisaje, necesariamente mejoran el conocimiento de la Hidrología. Al respecto, Dunne [45] señala la importancia de considerar el paisaje y su dinámica en la Hidrología. Para enfatizar esta relación menciona cómo la topografía condiciona las líneas de flujo (de agua y sedimentos), tanto en la superficie como en los primeros niveles del suelo; cómo los efectos gravitatorios (relacionados directamente con la topografía) tienen relevancia en parámetros del suelo tales como la profundidad y la concentración de macroporos; recalca la importancia de entender el umbral de la transición entre laderas y canales; y cómo la densidad de canales por unidad de área tiene implicaciones tanto en las características del paisaje como en el comportamiento hidrológico.
2.3 Limitaciones de los modelos de erosión
Los procesos básicos de la erosión hídrica están regidos por variables hidrológicas. Consecuentemente, los modelos de erosión están subordinados a modelos hidrológicos, cuyos resultados son variables de entrada para el modelo de erosión. Así, el modelo de erosión hereda las mismas capacidades y limitaciones que el modelo hidrológico en el que se basa.
Un modelo de erosión debe tener en cuenta las variaciones estacionales de las condiciones ambientales naturales, por ejemplo, los ciclos anuales de congelación–deshielo en las zonas climáticas templadas. Además, es necesario que tenga en cuenta las perturbaciones de las condiciones de la superficie del suelo por las labores de labranza, que normalmente se efectúan de acuerdo con los cambios estacionales. Estas labores agrícolas afectan la estructura del suelo, la porosidad, la densidad y la distribución de tamaños; propiedades que perturban las características hidráulicas del suelo [46]. Los modelos normalmente ignoran estos cambios temporales.
Otra limitación de los modelos de erosión es la dificultad para calibrar y validar los resultados arrojados por el modelo, debido a la imposibilidad de obtener medidas directas de campo de una forma lógica, sistemática e instrumental. Generalmente los modelos de erosión se validan usando datos de caudal líquido y carga de sedimentos tomados en la salida de la cuenca. Esto implica que no se puede examinar uno de los aspectos más importantes del modelo: la predicción de la variación espacial de los procesos de erosión y sedimentación en la cuenca. Una validación de este tipo puede enmascarar variaciones espaciales importantes dentro de la cuenca.
La falta de conocimiento de la distribución espacial de procesos hidrológicos y sedimentológicos, y de los parámetros asociados, da como resultado una calibración del modelo en la cual se supone una homogeneidad mayor que la que en realidad se presenta. El resultado puede ser una calibración correcta, esto es hidrogramas y sedimentogramas simulados cercanos a los observados, partiendo de razones incorrectas [47]. Estas cuestiones son un campo abierto a la investigación, que se resumen como el principio de la equifinalidad [48–50]. Dicho principio, originario de la teoría de sistemas, dice que en sistemas abiertos un estado final se puede alcanzar a partir de muchas formas posibles.
3. CONCLUSIONES
En la formulación de un modelo de producción, transporte y depósito de sedimentos es necesario considerar la variabilidad espacial y temporal de los parámetros. De esta forma hay que definir una discretización en el tiempo y en el espacio que represente de manera lo más cercana a la realidad la interrelación entre procesos, parámetros y variables de estado.
Un aspecto fundamental que se deriva de la revisión de los modelos de evolución del paisaje encontrados en la literatura es la visión holística (Todas las propiedades de un sistema no pueden ser determinadas como la suma de sus componentes. La holística enfatiza en la interdependencia de las partes de un sistema) que tienen de los procesos que ocurren en una cuenca hidrográfica. Al respecto, Willgoose et al. [21] apuntan que así como la hidrología puede determinar la forma de una cuenca, dicha forma condiciona a su vez a la hidrología. Esta retroalimentación hace que los modelos de evolución del paisaje sean especialmente difíciles de implementar debido a la gran cantidad de procesos actuantes con diferentes escalas espaciales y temporales.
REFERENCIAS
1. J. Wagensberg, "La simulación de la complejidad (ver, mirar, observar, experimentar y simular)", en Ideas sobre la complejidad del mundo, J. Wagensberg, Ed., Serie Metatemas 9, Barcelona: Tusquets Editores S.A., 1985, pp. 89–104. [ Links ]
2. W. Davis, "The Geographical Cycle", The Geograph. J., Vol. 14, pp. 481–504, 1899. [ Links ]
3. P. Birot, Morphologie Structurale, Vol. 2, Paris: Press. Universit. France, 1958. [ Links ]
4. J. Tricart y A. Cailleux, Traité de Géomorphologie, I, Introduction à la Géomorphologie Climatique, Paris: SEDES Ed., 1965. [ Links ]
5. M. Derrau, Geomorfología, Barcelona: Ariel Ed., 1978. [ Links ]
6. R. Horton, "Drainage basin characteristics", Trans. Am. Geophys. Un., Vol. 13, pp. 350–361, 1932. [ Links ]
7. R. Horton, "Erosional development of streams and their drainage basins: hydrophysical approach to quantitative morphology", Bull. Geolog. Soc. Am., vol. 56, pp. 275–370, 1945. [ Links ]
8. A. Strahler, "Quantitative analysis of watershed geomorphology", Trans. Am. Geophys. Un., vol. 38, pp. 913–920, 1957. [ Links ]
9. A. Young, "Deductive model of slope evolution", Slope Commun. Rep., vol. 3, pp. 45–65, 1963. [ Links ]
10. L. Leopold, M. Wolman, J. Miller, Fluvial Processes in Geomorphology, San Francisco: V. H. Freeman Ed., 1964. [ Links ]
11. R. Chorley, Spatial Analysis in Geomorphology, Londres: Methuen Ed., 1972. [ Links ]
12. S. Schumm, "Geomorphic thresholds: the concepts and its applications", Trans. Inst. British Geogr., vol. 4, pp. 485–515, 1979. [ Links ]
13. M. Selby, Earth's Changing Surface, New York: Oxford University. Press, 1985. [ Links ]
14. A. Scheidegger, "The fundamental principles of landscape evolution", Geomorphological Models. Catena Supplement, vol. 10, pp. 193–197. 1987. [ Links ]
15. G. Blösch y M. Sivapalan, "Scale issues in hydrological modeling: a review" en Scale Issues in Hydrological Modelling, UK: Wiley Ed., 1995, pp. 9–48. [ Links ]
16. L. Leopold y T. Maddock, "The hydraulic geometric of stream channel and some physiographic implications", Prof. Paper USGS, vol. 252, pp. 1–57, 1953. [ Links ]
17. K. Beven y M. Kirkby, "A physically – based contributing area model of basin hydrology", Bull. Hydrol. Sci., vol. 24, pp. 43–69, 1979. [ Links ]
18. G. Willgoose, "Mathematical modeling of whole landscape evolution", Ann. Rev. Earth Planetary Sci., vol. 33, pp. 443–459, 2005. [ Links ]
19. M. Kirkby, "Modelling some influence of soil erosion, landslide and valley gradient on drainage density and hollow development", Geomorphological Models. Catena Supplement, vol. 10, pp. 1–10. 1987. [ Links ]
20. G. Willgoose, I. Brass, I. Rodriguez–Iturbe, "Results from a new model of river basin evolution", Earth Surf. Processes and Landforms, vol. 16, pp. 237–254, 1991. [ Links ]
21. G. Willgoose, I. Brass, I. Rodriguez–Iturbe, "Hydrogeomorphology modeling with a physically based river basin evolution model" en Process Model and Theorethical Geomorphology, UK: Wiley, 1994, pp. 3–22. [ Links ]
22. A. Howard. "A detachment limited model of drainage basin evolution" Water Resources Research, vol. 30, pp. 2261–2285, 1994. [ Links ]
23. M. Abbott, J. Bathurst, J. Cunge, P. O'Connell, K. Rasmussen. "An Introduction to the European Hydrological System – Système Hydrologique Européen– SHE", Journal of Hydrology, vol. 87, pp. 45–77, 1986. [ Links ]
24. L. Garrote y R. Bras. "A distributed model for real–time flood forecasting using digital elevation model, Journal of Hydrology, vol. 167, pp. 279–306, 1995. [ Links ]
25. P. Julien, B. Saghafian, F. Ogden, "Raster – based hydrologic modelling of spatially – varied surface runoff", Water Resources Bull., vol. 31, pp. 523–536, 1995. [ Links ]
26. G. Willgoose, I. Brass, I. Rodriguez–Iturbe, "A physically based coupled network growth and hillslope evolution model", Water Resources Research, vol. 27, pp. 1671–1684, 1991. [ Links ]
27. D. Johnson y C. Beaumont, "Preliminary results from a planform kinematic model of orogen evolution, surface processes and the development of clastic foreland basin stratigraphy", en Stratigraphic Evolution of Foreland Basin, S. Dorobek y G. Ross Eds., 1995, pp. 3–24. [ Links ]
28. G. Tucker y R. Slingerland, "Drainage basin response to climate change", Water Resources Research, vol. 33, pp. 2031–2047, 1997. [ Links ]
29. G. Tucker, y R. Bras, "Hillslope processes, drainage density, and landscape morphology", Water Resources Research, vol. 34, pp. 2751–2764, 1998. [ Links ]
30. J. Laflen, W. Elliot, D. Flanagan, C. Meyer y M. Nearing, "WEPP–predicting water erosion using a process–based model". Journal of Soil and Water Conservation, vol. 52, pp. 96–102, 1997. [ Links ]
31. L. Mitas y H. Mitasova, "Distributed soil erosion simulation for effective erosion prevention", Water Resources Research, vol. 34, pp. 505–516, 1998. [ Links ]
32. D. Montgomery y W. Dietrich, "A physically–based model for the topographic control on shallow landslidining", Water Resources Research, vol. 30, pp. 1153–1171, 1994. [ Links ]
33. T. Coulthard, "Landscape evolution models: a software review", Hydrological Processes, vol. 15, pp. 165–173, 2001. [ Links ]
34. G. Tucker, S. Lancaster, N. Gasparini, R. Bras y S. Rybarczyk, "An object–oriented framework for distributed hydrologic and geomorphic modeling using triangulated irregular networks", Computers and Geosciences, vol. 27, pp. 959–973, 2001. [ Links ]
35. S. Schumm y R. Lichty, "Time, space, and causality in geomorphology", American Journal of Science, vol. 263, pp. 110–119, 1965. [ Links ]
36. N. Preston y J. Schmidt, "Modelling sediment fluxes at large spatial and temporal scales", en Long Term Hillslope and Fluvial System Modelling, Berlin: Springer, 2003. [ Links ]
37. L. Hagen y G. Foster, "Soil erosion prediction technology", Proceedings of Soil Erosion and Productivity Workshop, pp. 117–135, 1990. [ Links ]
38. W. Wischmeier y D. Smith, Predicting rainfall erosion – a guide to conservation planning. Agriculture Handbook 537, USA: USDA Ed., 1978. [ Links ]
39. K. Renard, G. Foster, G. Weesies, y J. Porter, "RUSLE – The Revised Universal Soil Loss Equation", Soil and Water Conservation Society Bull., 1989. [ Links ]
40. J. William, "Sediment yield prediction with Universal Equation using runoff energy factor", en Present and Prospective Technology for Predicting Sediment Yields and Sources. USA: USDA – Agricultural Research Service, 1975. [ Links ]
41. V. Jetten y D. Favis–Mortlock, "Modelling Soil Erosion in Europe", en Soil Erosion in Europe, UK: Wiley, 2006, pp. 695–716. [ Links ]
42. C. Haan, B. Barfield y J. Hayes, Design hydrology and sedimentology for small catchments. USA: Academic Press. 1994. [ Links ]
43. R. Piest, L. Kramer, H. Heineman, "Sediment movement from loessial watershed", en Present and Prospective Technology for Predicting Sediment Yields and Sources, Washington: U. Science y E. Administration Eds., 1975, pp. 130–141. [ Links ]
44. M. Kirkby, "Modelling across scales: the Medalus Family of models", en Modelling Soil Erosion by Water, NATO ASI Series I: Global Environmental Change. 1999 [ Links ]
45. T. Dunne, "Wolman Lecture: Hydrologic Science...in Landscapes...on a Planet...in the Future", en Hydrologic Sciences: Taking Stock and Looking Ahead, Washington: National Academy Press, 1998, pp. 10–43. [ Links ]
46. D. Regüés y F. Gallart, "Seasonal patterns of runoff and erosion responses to simulated rainfall in a badland area in mediterranean montain conditions (Vallcebre, Southeastern Pyrenees)", Earth Surface Process and Landforms, vol. 29, pp. 755–767, 2004. [ Links ]
47. D. Favis–Mortlock, J. Boardman y V. MacMillan, "The Limits of Erosion Modelling: Why We Should Proceed with Care", en Landscape Erosion and Evolution Modelling, New York: Kluwer Academic Plenum Publishing, 2001, pp. 477–516. [ Links ]
48. K. Beven, y A. Binley, "The future of distributed models: model calibration and uncertainty prediction", Hydrological Processes, vol. 6, pp. 279–298, 1992. [ Links ]
49. Q. Duan, S. Sorooshian y V. Gupta, "Effective and efficient global optimisation for conceptual rainfall–runoff models", Water Resources Research, vol. 28, pp. 1015–1031, 1992 [ Links ]
50. K. Beven, "Prophecy, reality and uncertainty in distributed hydrological modeling", Advances in Water Resources, vol. 16, pp. 41–51, 1993. [ Links ]
Recibido: 31/08/2009
Aceptado: 05/10/2009