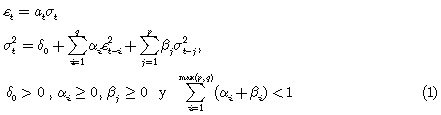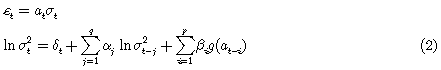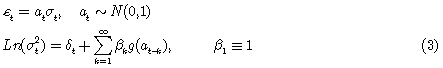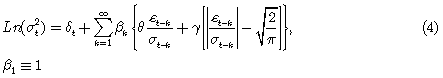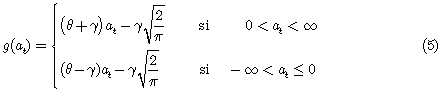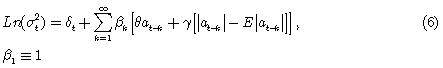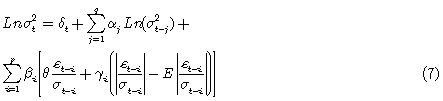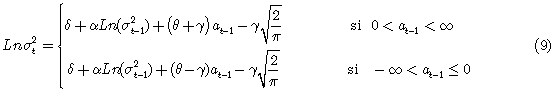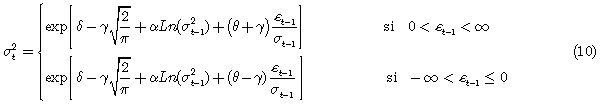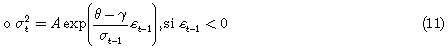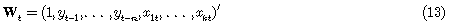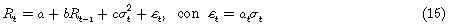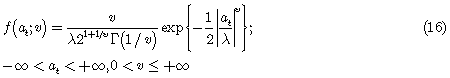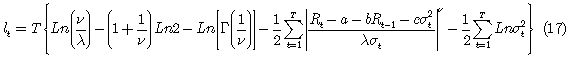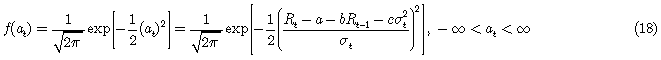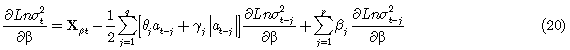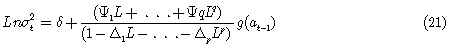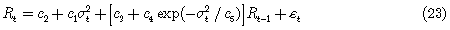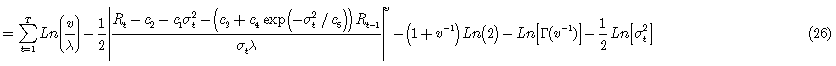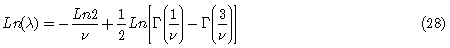Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Ingenierías Universidad de Medellín
Print version ISSN 1692-3324On-line version ISSN 2248-4094
Rev. ing. univ. Medellín vol.9 no.16 Medellín Jan./June 2010
EGARCH: un modelo asimétrico para estimar la volatilidad de series financieras
EGARCH: a model to estimate the asymmetric volatility of financial series
Horacio Fernández Castaño*
* Magíster en Matemáticas Aplicadas de la Universidad EAFIT, ingeniero civil de la Escuela de Ingeniería de Antioquia, especialista en Sistemas de Administración de la Calidad ISO 9000, especialista en Gerencia de Construcciones y licenciado en Matemáticas de la Universidad de Medellín. Profesor de tiempo completo, Facultad de Ingenierías. Programa de Ingeniería Financiera. Universidad de Medellín. E-mail: hfernandez@udem.edu.co; teléfono 4-3405495
Resumen
En la modelación de las volatilidades con cambios súbitos, es imperativo usar modelos que permitan describir y analizar el dinamismo de la volatilidad, ya que los inversionistas, entre otras cosas, pueden estar interesados en estimar la tasa de retorno y la volatilidad de un instrumento financiero u otros derivados, sólo durante el período de tenencia. En este artículo, que constituye la primera de dos entregas, se hace una evaluación del modelo asimétrico EGARCH que resulta ser muy útil para estudiar la dinámica del Índice General de la Bolsa de valores de Colombia (IGBC) y de su volatilidad, pues inicia haciendo una breve revisión del modelo GARCH, resaltando su importancia en la modelación de series de tiempo financieras, e identificando sus debilidades en cuanto a su propiedad de simetría para las distribuciones de colas gruesas y que pueden generar errores de pronóstico. Luego se muestra la importancia del modelo EGARCH para la modelación de algunos hechos que no se logran capturar con los modelos GARCH
Palabras clave: EGARCH, asimétrico, volatilidad, efecto de apalancamiento, IGBC.Abstract
In the modeling of volatility with rapid changes, it is imperative to use models to describe and analyze the dynamics of volatility, as investors, among other things, may be interested in estimating the rate of return and volatility of an instrument financial or other derivatives, only during the holding period. This article contains an evaluation of asymmetric EGARCH model that proves to be very useful to study the dynamics of the General Index of the Stock Exchange of Colombia (IGBC) and its volatility, since, as will be shown, the results suggest they could be more useful for capture the stylized facts of the Colombian market behavior. It is really significant to evidence the importance of asymmetric models to estimate the volatility of financial series is intended here as a model for identifying, in the best way to estimate the volatility of daily returns of the IGBC.
Key words: EGARCH, asymmetric, volatility, leverage effect, IGBC.
INTRODUCCIÓN
Es frecuente que en economía se condicionen los sucesos a movimientos que se produjeron en el pasado, y en la gran mayoría de las series de tipo económico el supuesto de homoscedasticidad resulte inadecuado, ya que a lo largo del tiempo su comportamiento no es estacionario ni en media ni en varianza, generando volatilidades altas para unos períodos y bajas para otros. Estos cambios sucesivos en tendencia al alza o a la baja son comunes en las series financieras, lo cual se ve claramente con la alta relación entre los mercados mundiales que es sustentada por numerosos estudios empíricos. Los numerosos períodos de inestabilidad y crisis financieras en el mundo, en los últimos treinta años, han generado fuertes requerimientos en cuanto a poner a prueba la gestión financiera mediante la puesta en marcha del estudio de los sistemas de administración del riesgo, y la necesidad de diseñar nuevos modelos y sistemas que permitan hacer una trazabilidad de lo ocurrido y un estudio exhaustivo del presente; la estimación de la volatilidad, en series financieras, es hoy uno de los retos en el campo económico.
Se han desarrollado varios modelos para investigar la volatilidad de series financieras, entre ellos los modelos ARCH (Autorregresive Conditional Heteroskedasticicity) y GARCH, (Generalized Autorregresive Conditional Heteroskedasticicity), que infortunadamente no capturan algunas características de los datos de una serie financiera, como los efectos asimétricos que pueden generar las buenas o malas noticias, como se muestra en [1]; Nelson [2] propuso un nuevo método como proceso de mejoramiento en los procesos de estimación. Se hace necesaria la modelación de series financieras, importantes en el mercado de capitales, que puedan analizar de forma exhaustiva y técnica el efecto que tienen las noticias sobre la heteroscedasticidad condicional. Este artículo evidencia la importancia del modelo EGARCH (Exponential Garch de Nelson [2]) y su valiosa utilidad en la modelación de algunos hechos que no pueden hacerlo de forma apropiada con los modelos GARCH. Los modelos anteriores al EGARCH recogen de manera adecuada las propiedades de distribuciones de colas gruesas, y de agrupamiento de volatilidades, pero la varianza condicional depende de la magnitud de las innovaciones retardadas, pero no de su signo, y esto motiva a la necesidad de capturar los efectos apalancamiento que se observan en series financieras. Para lograr el objetivo propuesto se exponen a continuación las características más notables de este artículo:
Se hace una breve revisión del modelo GARCH, resaltando su importancia en la modelación de series de tiempo financieras, e identificando sus debilidades en cuanto a su propiedad de simetría para las distribuciones de colas gruesas y que pueden generar errores de pronóstico.
Se muestra la importancia del modelo EGARCH para la modelación de de algunos hechos que no se logran capturar con los modelos GARCH.
En la aplicación, el rango muestral seleccionado son los datos del precio de cierre de Índice General de la Bolsa de valores de Colombia (IGBC) desde agosto 21 de 2003 hasta octubre 1 de 2008 incluyendo 1.248 observaciones. Es aquí donde se resalta la importancia del modelo EGARCH puesto que se exponen los resultados que evidencian la existencia del efecto ARCH y, además, se presenta la estimación y validación del modelo
Los resultados que se presentan se obtuvieron en el paquete informático, Econometric Views (EViews 6.0), y con los programas codificados para el EGARCH-M(p,q), con p = 1 , 2, 3, 4 y q = 1 , 2, 3, 4. La comparación de los distintos modelos estimados por máxima verosimilitud, se lleva a cabo atendiendo al criterio de información de Schwarz.
Finalmente se presentan unas conclusiones de los resultados encontrados.
1 HETEROCEDASTICIDAD CONDICIONAL AUTORREGRESIVA (ARCH)
Markowitz y Tobin [3, 4] trabajaron acerca de la forma como la evasión del riesgo era fundamental para evaluar la varianza del valor de una cartera, de lo cual se desprendió la teoría de cartera óptima. Sharpe [5] desarrolló la teoría del modelo de valoración de los precios de los activos (CAPM-Capital Asset Pricing Model- por sus siglas en inglés), y en la cual demostró que hay una alta relación entre la varianza y los rendimientos esperados. Black y Schloes y Merton [6, 7] propusieron un modelo que calcula el precio de una opción europea, manteniendo constante la volatilidad de la rentabilidad del activo subyacente.
Cuando se utilizan las propuestas de Black y Scholes y Merton, se requiere hacer estimaciones de las varianzas; lo que generalmente se usaba era el cálculo de la raíz cuadrada de la varianza, llamada volatilidad. Muy rápido se detectó que las volatilidades variaban cuando su análisis se hacía para diferentes horizontes de tiempo, y por lo tanto no tenía lógica financiera suponer que la varianza era constante. Era necesario entonces generar otras ideas acerca del dinamismo de la volatilidad. Fue entonces cuando Engle [8] desarrolló el modelo ARCH, tratando de validar la hipótesis de Friedman en [9], según la cual la incertidumbre con que se comporta la inflación era una de las principales causantes de los ciclos económicos. Así, el modelo ARCH describe la predicción de la varianza como una función de las variables observables actuales. En lugar de usar desviaciones típicas sobre muestras grandes o pequeñas, en el modelo se propuso usar medias ponderadas de los cuadrados de los errores de predicción del pasado. Estas ponderaciones pueden conceder mayor influencia a la información reciente y restarle peso al pasado no muy cercano. La fortaleza del modelo estaría en que permitía estimar las ponderaciones de manera empírica a pesar de que la volatilidad no se hubiera observado nunca. Luego surgió como una ampliación del modelo ARCH, el modelo GARCH (Generalized Autorregresive Conditional Heteroskedasticity) desarrollado por Bollerslev en [10], en el que se incluyen rezagos de la varianza condicional; en otras palabras, el modelo GARCH es un ARCH infinito.
2 PROCESO GARCH (Generalized Autorregresive Conditional Heteroskedasticity)
El modelo GARCH resulta ser una ampliación del ARCH. El mismo Engle [8] propuso algunas restricciones para los parámetros del modelo ARCH (1) que fueron insuficientes para múltiples aplicaciones; es por esto que Bollerslev [10] sugirió ampliar el modelo y planteó así el modelo GARCH(p,q) como un modelo simétrico que tiene en cuenta la varianza condicionada en cada etapa, y se expresa formalmente como:
De manera que, en particular cuando se toma βj = 0 para todo j, se obtiene el modelo ARCH(q). Se identifican dos ecuaciones:
En la primera,εt = atσt, se expresa explícitamente εt como proporcional a la desviación estándar, siendo la constante de proporcionalidad la variable aleatoria at, y que es, como ya se dijo, conocida como ruido blanco.
En la segunda se expresa a la varianza en el período t en términos de la constante δ0 y de los valores que se hayan tenido en el tiempo inmediatamente anterior. Es evidente que la predicción de la varianza, en el modelo GARCH, es una media ponderada de tres predicciones diferentes a ella. Se definen los términos: δ0: Valor medio de la varianza, a largo plazo, en torno al cual se produce la expectativa a ser modificada inmediatamente por los otros términos.
α1: Efecto de la observación del proceso en el tiempo t—1, sobre la varianza en el tiempot. β1: Efecto, de la varianza del tiempo t—1, sobre la varianza el tiempo t. α1 + β1: Medición porcentual de la persistencia de la volatilidad. Por lo tanto, si se tiene un valor muy cercano a uno (1), se concluye que hay una muy alta persistencia de los shocks de volatilidad.
De manera que el modelo GARCH nos es más que una mejor intención para modelar la volatilidad, y trata dos de las características más importantes que suceden en las series financieras: el exceso de curtosis y la volatilidad. Adicionalmente, se ha encontrado una variedad de aplicaciones en la administración del riesgo, en la colocación de activos, administración de portafolios, valoración de opciones, tasas de cambio y en la estructura de las tasas de interés, entre otros aspectos que son de alto interés en los estudios financieros.
2.1 Debilidades del pronóstico con modelos GARCH
Algunas críticas de Nelson [2] al modelo GARCH y que impulsaron la necesidad de otros desarrollos son: 1) El modelo contradice el comportamiento normal de las series temporales en el sentido de que la varianza condicional responde de igual forma ante residuales positivos y negativos, por lo que puede generar problemas de pronóstico, ya que no distingue entre noticias buenas y malas. 2) El supuesto de no negatividad de los parámetros restringe la dinámica misma de la varianza condicional. 3) Existe correlación negativa entre los retornos actuales y la volatilidad de los retornos futuros y, por su simetría, queda descartado el modelo. La elección de una forma cuadrática para la varianza condicional tiene consecuencias sobre el patrón del tiempo pasado: hace que el impacto de los valores pasados sobre la volatilidad actual sea solamente función de dicha magnitud pasada, lo cual no es cierto en la dinámica de los mercados financieros, en los que la volatilidad tiende a ser más alta cuando se presenta una caída, en comparación a cuando se presenta un alza. Ya Black [11] había sugerido la necesidad de plantear un contraste para detectar la presencia del efecto de apalancamiento en series temporales condicionales heteroscedásticas, ya que afirmaba que shocks negativos provocan mayores incrementos en la volatilidad que shocks positivos del mismo tamaño; por lo tanto, la respuesta de la volatilidad ante un shock positivo o negativo es asimétrica.
El efecto de apalancamiento se refiere al hecho de que los cambios en los precios de los activos tienden a correlacionarse negativamente con los cambios de volatilidad, de forma tal que esta es mayor después de que ocurre un choque negativo que después de uno positivo, incluso a pesar de que este sea de la misma magnitud relativa de aquél, es decir, el proceso dinámico de la volatilidad es asimétrico. 4). La forma en que el modelo GARCH mide la persistencia presenta dificultades al definir si un shock persiste o no.
Ante estas debilidades, como se muestra en Nelson [2], se propuso un novedoso método como proceso de mejoramiento y que permite capturar estos efectos.
3 PROCESO EGARCH
Es claro entonces, que los modelos ARCH y GARCH, antes descritos, además de ser simétricos, recogen adecuadamente las propiedades de distribuciones de colas gruesas, y de agrupamiento de volatilidades, y consideran la varianza condicional como dependiente de la magnitud de las innovaciones retardadas, pero no de su signo.
Como herramienta que permita recoger los apalancamientos observados en series financieras, fue propuesto el modelo EGARCH o GARCH exponencial por [2]. La misma fuente indica que la volatilidad puede responder de forma asimétrica a errores de predicción pasados. Propuso allí, entonces, una nueva forma funcional buscando resolver las deficiencias de los modelos GARCH que había observado en los trabajos empíricos desarrollados. Anunciaba el autor que los modelos GARCH tenían serias dificultades para medir los shocks pasados en los valores de la varianza condicional. En su artículo citado [2], Nelson resalta lo siguiente en cuanto a los modelos GARCH: a) No es posible, en la mayoría de los casos, que los parámetros sean no negativos, ya que es importante considerar los efectos que tiene la innovación en el período anterior, sobre la estimación de la varianza condicional, sea ésta negativa o positiva; b) el efecto de apalancamiento financiero no es detectable; c) pocas veces estos modelos se pueden llevar a la práctica.
Nelson [2] especificó la varianza condicional, de manera general, como:
El autor aduce, entonces, que si σ2t es la varianza condicional de εt, dada la información disponible hasta el tiempo t, siendo claro que debe ser positiva y con probabilidad uno; entonces, para asegurar que σ2t permanezca positiva, se asume que Ln(σ2t) es una función lineal del tiempo y de los rezagos, denotados at. Es decir para alguna función g, en [2] Nelson define su modelo EGARCH como
donde 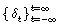 y
y 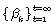 son secuencias no estocásticas de números reales.
son secuencias no estocásticas de números reales.
Para que la relación entre los retornos de los activos y los cambios en la volatilidad sea asimétrica, se requiere que el valor de g(.) sea función del signo y de la magnitud de εt. Se define entonces g(.) como una combinación lineal de at y |at| dada por, 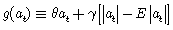 , donde los términos θat y γ[|at| — E| at|] tienen media cero, y por lo cual es evidente que E[g(at] = 0, y, además, θ y γ son constantes reales y no son ambos cero. De manera, que por construcción,
, donde los términos θat y γ[|at| — E| at|] tienen media cero, y por lo cual es evidente que E[g(at] = 0, y, además, θ y γ son constantes reales y no son ambos cero. De manera, que por construcción, 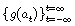 es una secuencia de variables aleatorias independientes e idénticamente distribuidas. Si la distribución de at es simétrica, las dos componentes son ortogonales, aunque, por supuesto, no son independientes. Generalmente se usa en esta formulación at como el error estandarizado, es decir, el error dividido por su desviación típica condicional. Es por esto que el modelo se puede escribir también como
es una secuencia de variables aleatorias independientes e idénticamente distribuidas. Si la distribución de at es simétrica, las dos componentes son ortogonales, aunque, por supuesto, no son independientes. Generalmente se usa en esta formulación at como el error estandarizado, es decir, el error dividido por su desviación típica condicional. Es por esto que el modelo se puede escribir también como 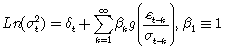 y además con at ~ N(0,1), se tiene
y además con at ~ N(0,1), se tiene 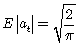 y por lo tanto se puede escribir el modelo de acuerdo con Nelson [2], como
y por lo tanto se puede escribir el modelo de acuerdo con Nelson [2], como
Ahora, como
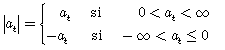 ,
,
entonces g(at) se puede expresar como,
Estos resultados muestran que, si 0 < at < ∞, entonces g(at) es lineal en at, con pendiente o tendencia θ + γ; y si —∞ < at∞ 0, entonces g(at) es lineal en at, con pendiente, o tendencia, θ — γ; por lo cual, g(at) permite al proceso de varianza condicional,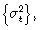 responder asimétricamente a las alzas y bajas en el precio de la acción. El causante de la asimetría es el segundo término de la función g(at), y esto porque está definida como la proporción de la diferencia entre el valor realizado de la innovación y su valor esperado. Esta diferencia, que puede ser positiva o negativa, incorpora mayor o menor volatilidad en función de su signo.
responder asimétricamente a las alzas y bajas en el precio de la acción. El causante de la asimetría es el segundo término de la función g(at), y esto porque está definida como la proporción de la diferencia entre el valor realizado de la innovación y su valor esperado. Esta diferencia, que puede ser positiva o negativa, incorpora mayor o menor volatilidad en función de su signo.
Para ver que el término 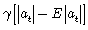 representa un efecto de magnitud en la esencia de los modelos EGARCH, se supone, por el momento que θ = 0 y γ > 0. La innovación en
representa un efecto de magnitud en la esencia de los modelos EGARCH, se supone, por el momento que θ = 0 y γ > 0. La innovación en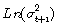 es, entonces: positiva cuando la magnitud de at es mayor que su valor esperado, y negativa cuando la magnitud de at es menor que su valor esperado.
es, entonces: positiva cuando la magnitud de at es mayor que su valor esperado, y negativa cuando la magnitud de at es menor que su valor esperado.
Si se asume que θ < 0 y γ = 0, se tiene que la innovación en la varianza condicional es: positiva cuando la innovación en los retornos son negativa, y negativa cuando la innovación en los retornos es positiva.
Es por esto que la forma exponencial
del modelo EGARCH encuentra la primera objeción hacia los modelos GARCH.
Las dinámicas de los modelos GARCH son indebidamente restrictivas (una conducta oscilatoria es excluida) e imponen unas restricciones desiguales que son frecuentemente violadas por los coeficientes estimados. Pero es claro que en la expresión (6) no hay restricciones desiguales; sin embargo, ese ciclo es permitido, ya que los términos de βk pueden ser negativos o positivos. La critica final, como se muestra en [2], respecto a los modelos GARCH es que resulta difícil evaluar si los sobresaltos a la varianza son persistentes o no. En el EGARCH, sin embargo, 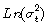 es un proceso con estructura lineal, y su estacionariedad (covarianza o absoluta confianza) y ergodicidad son fácilmente contrastadas. Vale agregar que la condición de estacionariedad para este proceso, aquí planteada, es la misma que aquella para un MA(+∞); y bastaría entonces, luego de estimar los parámetros, comprobar que la suma de ellos es menor que uno.
es un proceso con estructura lineal, y su estacionariedad (covarianza o absoluta confianza) y ergodicidad son fácilmente contrastadas. Vale agregar que la condición de estacionariedad para este proceso, aquí planteada, es la misma que aquella para un MA(+∞); y bastaría entonces, luego de estimar los parámetros, comprobar que la suma de ellos es menor que uno.
3.1 Modelo EGARCH(p,q)
Se tiene entonces que el modelo como el expresado en (2) es equivalente a tener:
Donde el lado izquierdo es el logaritmo natural de la varianza condicional. Esto implica que el leverage effect (efecto de apalancamiento) es exponencial. La elección de la forma funcional usando el logaritmo natural es la que facilita la estimación numérica de los parámetros, mediante métodos analíticos, puesto que de manera implícita restringe el valor de la varianza condicional a solo valores positivos, sin necesidad de imponer restricciones a parámetros del modelo, algo que era necesario en los modelos GARCH. El efecto de apalancamiento fue planteado como un efecto asimétrico cuando se presentan buenas o malas noticias. Este efecto de apalancamiento se puede capturar planteando la hipótesis γi < 0, y el impacto sería asimétrico si γi ≠ 0.
Un modelo EGARCH(1,1) queda especificado como
Ahora, reemplazando (2) en (8) queda que
O de igual manera
De lo anterior se tiene que en el modelo EGARCH(1,1), la curva del impacto de las noticias, cuando se evalúa la varianza condicional con base en los valores de la varianza condicional rezagada un período, se especifica como:
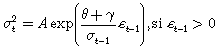
siendo 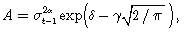
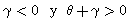
Por lo cual el modelo EGARCH permite que tanto las malas como las buenas noticias tengan efectos diferentes sobre la volatilidad, mientras que el GARCH, no.
4 PRUEBAS DE ESPECIFICACIÓN (O VALIDACIÓN)
Para probar el ajuste del modelo, se deben hacer varias pruebas del momento condicional usando condiciones ortogonales implicadas por especificaciones correctas sobre la función propuesta en [2]; de manera que, para contrastar las condiciones de ortogonalidad, se requiere que: (i) el valor esperado de at sea cero; (ii) la varianza marginal de at sea uno; (iii) la esperanza de la función g(at) sea nula; y, además, (iv) por simetría, de la función GED, se debe cumplir que E(at| at|) = 0. Es necesario también, en el modelo supuesto, que los valores de 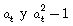 no estén correlacionados.
no estén correlacionados.
Una manera alternativa a la propuesta en [2] para evaluar la correcta especificación del modelo es utilizar el estadístico Q de Ljung y Box, el cual se usa realizando una prueba de significancia sobre un conjunto los coeficientes. Dicho estadístico está dado por 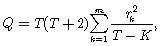 donde m, es un valor arbitrario, e indica el número de coeficientes de autocorrelación; k , el número de rezagos y el coeficiente de autocorrelación muestral está dado por
donde m, es un valor arbitrario, e indica el número de coeficientes de autocorrelación; k , el número de rezagos y el coeficiente de autocorrelación muestral está dado por 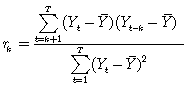
Se tiene que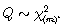 Si las
Si las 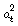 no están correlacionadas, rechazar la hipótesis nula es equivalente a rechazar como adecuada la estimación mediante el modelo EGARCH.
no están correlacionadas, rechazar la hipótesis nula es equivalente a rechazar como adecuada la estimación mediante el modelo EGARCH.
Se requiere, al hacer estimaciones con los modelos de la familia EGARCH, tener certeza acerca de las condiciones de existencia de los momentos y la clara definición de los parámetros, con el objeto de tener alta confiabilidad en los resultados que se obtendrían al hacer el estudio de las series financieras.
5 ESTIMACIÓN DE LOS PARÁMETROS
La estimación de los parámetros se efectúa generalmente por máxima verosimilitud, evaluando la función de densidad para los valores muestrales correspondientes a la muestra disponible, de manera que quede sólo en función de los parámetros del modelo que maximizan la función planteada. El valor de los parámetros que maximizan esta evaluación se conoce como estimaciones máximo verosímiles.
donde 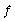 es una función doblemente diferenciable con respecto a
es una función doblemente diferenciable con respecto a 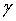 siendo
siendo
El proceso del error se parametriza como εt = atσt, t, . . ., T .
Donde {at} es una secuencia de variables aleatorias independientes e idénticamente distribuidas con media cero y varianza uno. El modelo EGARCH(p,q), como ya se dijo, queda definido como se expresa en (2)
La varianza condicional es restringida a valores positivos por el supuesto de que el logaritmo de 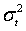
Si se cumplen los supuestos y asumiendo normalidad de at, la función de log verosimilitud de máxima verosimilitud del modelo EGARCH(p,q) es
Con 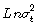 como se expresa en (7)
como se expresa en (7)
Nelson [2], en su documento Semilla del modelo EGARCH, propuso la estimación por máxima verosimilitud bajo el supuesto de que la distribución de los errores siguen una GED. El mismo autor, en un análisis de rentabilidades diarias del mercado de valores, especificó el modelo
Ahora, como la densidad generalizada está dada por la forma funcional
el logaritmo de la función de verosimilitud es
y para evaluar LnLt se requiere, a partir de valores iníciales de los parámetros δ,β, α, θ, γ, a, b y c generar datos para la varianza condicional, usando de manera reiterada, la expresión que define la varianza condicional del proceso expresado como en (9)
Para iniciar el procedimiento, hay varias opciones: una consiste en asignar valores a los parámetros con base en la constante obtenida para la varianza condicional del término de error, y otra forma es asignar valores arbitrarios adecuados y que cumplan con las restricciones propias del modelo. En este trabajo, con las macros elaboradas en Eviews 6.0, se usó la segunda opción.
Si se asume, para los errores una distribución normal entonces se tiene
y si 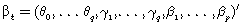 .
.
La primera derivada parcial, con respecto al vector de los parámetros, es
Donde
Con 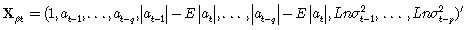
Los parámetros de (15) con los errores del EGARCH, dados en (17) y (18) pueden ser estimados conjuntamente por máxima verosimilitud. Vale agregar que en la estimación se usa, generalmente, derivación numérica, ya que las derivadas analíticas resultan algo complejas. La hipótesis de normalidad garantiza que la matriz de información es diagonal a bloques, de tal manera que los bloques que contienen las derivadas parciales, con respecto a la media y a la varianza, son matrices nulas.
Teniendo en cuenta que el método de máxima verosimilitud permite hacer estimaciones secuenciales, los parámetros de la media condicional definida por la ecuación (15) pueden ser estimados por separado sin pérdida de eficiencia; esto implica que los estimadores de máxima verosimilitud de los parámetros en (17) y (18) pueden ser obtenidos numéricamente con las condiciones de primer orden, igualando a cero la ecuación (26).
Bajo estas condiciones de regularidad suficiente, se espera que los estimadores de máxima verosimilitud sean consistentes y con distribución asintótica normal; sin embargo, parece que estas condiciones aún no han sido verificadas en la situación actual. Verificar esto en el GARCH ha sido una tarea difícil, y las cosas no parecen ser más fáciles en el caso de los EGARCH. La expresión (27) es la que obliga a que la estimación de los parámetros se haga mediante métodos iterativos.
Se modela entonces el logaritmo de la varianza condicional como:
siendo L el operador de rezagos.
Para considerar los períodos no transados en la varianza del mercado, se asume que cada día no transado tiene una contribución igual a una fracción de los días transados. Si por ejemplo esta fracción es una décima mayor que 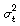 en un lunes típico, sería 20 por ciento más alto que en un martes típico. Como se muestra en [2], Nelson propuso entonces reemplazar el término constante δ por la expresión
en un lunes típico, sería 20 por ciento más alto que en un martes típico. Como se muestra en [2], Nelson propuso entonces reemplazar el término constante δ por la expresión
Donde Nt es el número de días no transados entre los días t — 1 y t, ρ1 y ρ2 son parámetros. Consideración que se debe hacer puesto que la información que se acumula cuando se cierran los mercados financieros se refleja en los precios después de la reapertura de los mercados. En [12, 13]Fama y Roll, encontraron que los períodos no transados tienen una contribución menor a la varianza del mercado, que los períodos transados, por lo que se espera que 0 < ρ2 = 1.
Los retornos se modelan, como se indica en [14] con la expresión
Donde la media y la varianza condicionales de ct, en el tiempo t son cero y 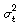 respectivamente, y además c1, c2, c3, c4, c5, son parámetros que deben determinarse. El término c3Rt–1 se refiere a la autocorrelación inducida por la discontinuidad transaccional en las acciones que componen el índice, y
respectivamente, y además c1, c2, c3, c4, c5, son parámetros que deben determinarse. El término c3Rt–1 se refiere a la autocorrelación inducida por la discontinuidad transaccional en las acciones que componen el índice, y 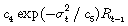 establece la relación inversa entre la correlación serial y la volatilidad de los retornos. Como resulta supremamente difícil estimar los parámetros c4, y c5, entonces, para facilitar los cálculos, de acuerdo con [15], se definió c5 como la varianza muestral de los retornos y queda expresada entonces como
establece la relación inversa entre la correlación serial y la volatilidad de los retornos. Como resulta supremamente difícil estimar los parámetros c4, y c5, entonces, para facilitar los cálculos, de acuerdo con [15], se definió c5 como la varianza muestral de los retornos y queda expresada entonces como
Las macros, realizadas en Eviews 6.0, maximizan la función de verosimilitud con la instrucción LogL y los parámetros estimados usando el algoritmo de Donald W. Marquardt [16], que es el algoritmo que utiliza Eviews 6.0 en sus librerías.
Para un ARMA (p,q) dado, las secuencias 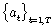 y
y 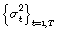 se pueden obtener fácilmente si se tiene la información
se pueden obtener fácilmente si se tiene la información 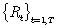 y los valores iníciales
y los valores iníciales 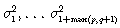
También, 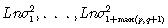 se establecen igual a sus esperanzas incondicionales
se establecen igual a sus esperanzas incondicionales 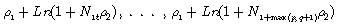 y esto permite escribir el logaritmo de verosimilitud como:
y esto permite escribir el logaritmo de verosimilitud como:
Donde
Lo que es equivalente a tener que 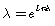 siendo
siendo
En la selección el orden adecuado del proceso ARMA para 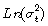 , se usa el criterio de Schwarz (SC) en [1], el cual se define por la expresión SC = (—2l + kLn(n))n-1, donde k es el número de parámetros estimados, n es el número de observaciones y l es el valor del logaritmo de la función de verosimilitud usando los k parámetros estimados. De manera que esta expresión evalúa la bondad de un determinado modelo mediante el grado de verosimilitud alcanzada, penalizándola por el número de parámetros utilizados para ello. Por tanto, los modelos con menor SIC serán los que mejor se ajusten a los datos. Hannan [14] demostró que el (SC) arroja estimaciones consistentes del orden en el contexto de modelos lineales ARMA. Las propiedades asintóticas del estimador (SC), en el contexto de modelos ARCH, aún no tienen muchos desarrollos. No se usa, en este trabajo, el criterio de información de Akaike ya que este tiende a escoger, en algunos casos, el modelo con el mayor número de parámetros.
, se usa el criterio de Schwarz (SC) en [1], el cual se define por la expresión SC = (—2l + kLn(n))n-1, donde k es el número de parámetros estimados, n es el número de observaciones y l es el valor del logaritmo de la función de verosimilitud usando los k parámetros estimados. De manera que esta expresión evalúa la bondad de un determinado modelo mediante el grado de verosimilitud alcanzada, penalizándola por el número de parámetros utilizados para ello. Por tanto, los modelos con menor SIC serán los que mejor se ajusten a los datos. Hannan [14] demostró que el (SC) arroja estimaciones consistentes del orden en el contexto de modelos lineales ARMA. Las propiedades asintóticas del estimador (SC), en el contexto de modelos ARCH, aún no tienen muchos desarrollos. No se usa, en este trabajo, el criterio de información de Akaike ya que este tiende a escoger, en algunos casos, el modelo con el mayor número de parámetros.
6 REFERENCIAS
1. R. S. Tsay, Analysis of Financial Time Series, 2 ed., New Jersey: John Wiley & Sons, Inc., Publication, 2005. [ Links ]
2. D. Nelson B, “Conditional Heteroskedasticity in Asset Returns: A New Approach,” Econometrica, vol. 59, no. 2, pp. 347-370, 1991. [ Links ]
3. H. Markowitz, “Portfolio selection,” Journal of finance, vol. 7, no. 1, pp. 77-91, 1952. [ Links ]
4. J. Tobin, “Liquidity preference as behavior toward risk,” Review of economic studies, vol. 25, no. 66, 67 y 68, pp. 65-86, 1957-1958. [ Links ]
5. W. F. Sharpe, “Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk,” Journal of Finance, vol. 19, no. 3, pp. 425-442, 1964. [ Links ]
6. F. Black, y M. Scholes, “The Pricing of Options and Corporate Liabilities,” Journal of Political Economy, vol. 81, pp. 637-654, 1972. [ Links ]
7. R. C. Merton, “Theory of Rational Option Pricing,” The Bell Journal of Economics and Mangement Science, vol. 4, pp. 141-183, 1973. [ Links ]
8. R. Engle, “Autoregresive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation,” Econometrica, vol. 50, no. 4, pp. 987-1007, 1982. [ Links ]
9. M. Friedman, “Nobel Lecture: Inflation and Unemployment ” Journal of Political Economy, vol. 85, no. 3, pp. 451-472, 1977. [ Links ]
10. T. Bollerslev, “Generalized autoregresive conditional heteroscedasticity,” Journal of Econometrics, vol. 31f, pp. 307-327, 1986. [ Links ]
11. F. Black, “The pricing of commodity contracts,” Journal of Financial Economics, vol. 3, no. 1-2, pp. 167-179, 1976. [ Links ]
12. E. F. Fama, “The Behavior of Stock-Market Prices,” Journal of Business, vol. 38, no. 1 pp. 34-105, 1965. [ Links ]
13. R. Roll, “Stock Return Variances, the Arrival of Information and the Reaction of Traders,” Journal of financial economics, vol. 17, no. 1, pp. 5-26, 1986. [ Links ]
14. E. J. Hannan, “The estimation of the order of an ARMA process,” Annals of Statistics, vol. 8, pp. 1071-1081, 1980. [ Links ]
15. B. LeBaron, “Some Relations Between Volatility and Serial Correlations in Stock Market Returns,” Journal of Business, vol. 65, no. 2, pp. 199-219, 1992. [ Links ]
16. D. W. Marquardt, “An Algorithm for Least-Squares Estimation of Nonlinear Parameters,” SIAM Journal on Applied Mathematics, vol. 11, pp. 431-441, 1963. [ Links ]
Recibido: 15/04/2009
Aceptado: 07/05/2009