Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Ingenierías Universidad de Medellín
Print version ISSN 1692-3324On-line version ISSN 2248-4094
Rev. ing. univ. Medellín vol.10 no.18 Medellín Jan./June 2011
Herramientas para análisis por confiabilidad en geotecnia: Aplicación
Tools for reliability analysis in geotechnical engineering: Application
César Augusto Hidalgo Montoya*; André Pacheco de Assis**
* Ingeniero civil, magíster en Geotecnia de la Universidad de Brasilia, profesor asociado de la Universidad de Medellín. teléfono 4344932, e-mail chidalgo@udem.edu.co
** Ingeniero civil de la Universidad de Brasilia, Brasil; doctor en Geotecnia de la Universidad de Alberta, Canadá. Profesor titular de la Universidad de Brasilia. Teléfono 55-61-3107-0965. e-mail: aassis@unb.br
Resumen
En este trabajoseaplicaron los métodos FOSM y de las estimativas puntuales (MEP) en la evaluación de la probabilidad de falla contra deslizamiento de una estructura de contención. Entre otras conclusiones, se resalta que es necesario definir valores de referencia para determinar la probabilidad de falla aceptable en obras geotécnicas, ya que existe un vacío en este tema.
Palabras clave: confiabilidad, incertidumbre, mecánica de suelos, mecánica de rocasAbstract
In this work, in order to calculate the failure probability against sliding of a contention structure, FOSM and point estimates methods (PEM) were used. As a conclusion, it is highlighted that it is necessary to define values of acceptable failure probability in geotechnical design, because there is a void in this aspect.
Key words: reliability, confidence, uncertainty, soil mechanics, rock mechanics.
INTRODUCCIÓN
El uso de técnicas probabilísticas, como el método de primer orden segundo momento FOSM, de las estimativas puntuales MEP y Montecarlo, para el análisis de confiabilidad permite que la incertidumbre pueda ser manejada de una forma más rigurosa en los procesos de diseño geotécnico. Como es de esperarse, el uso de métodos de confiabilidad no garantizan totalmente que no se produzcan fallas, pero su uso riguroso y metódico sí puede permitir que el ingeniero esté seguro de que los factores que se conocen y se pueden controlar no influirán sustancialmente en esas fallas [1]. En los últimos años se ha despertado un gran interés por introducir en los estudios geotécnicos metodologías que permitan una evaluación racional de la incertidumbre asociada con dichos procesos. Es así como han sido usados métodos estadísticos para evaluar el riesgo de movimientos de masa, como el método de Montecarlo que ha sido usado desde hace tiempo en la evaluación de la probabilidad de falla y de la amenaza [2-4], y se encuentra implementado en varios programas comerciales de análisis de estabilidad de taludes. Otros métodos probabilísticos que incluyen herramientas como los Análisis de Primer Orden Segundo Momento (FOSM), Método Avanzado de Primer Orden Segundo Momento (MFOSM) también han sido usados para determinar la confiabilidad de los taludes frente a la falla [3, 5, 6].
Aparte de estas aplicaciones ligadas a la estabilidad de taludes, en diferentes aplicaciones en la geotecnia se han usado métodos estadísticos como por ejemplo en la evaluación de confiabilidad e incertidumbre en mecánica de rocas [7] y desastres naturales [8], entre otras. Además, han sido usados para la obtención de índices para la evaluación del riesgo [9].
En este trabajo se presentan criterios para establecer valores límite, para ser usados en las evaluaciones de confiabilidad y para aplicar los métodos FOSM y MEP en la evaluación de la estabilidad por deslizamiento de una estructura de contención. Este trabajo es complementado por el artículo "Herramientas para análisis por confiabilidad en geotecnia: La teoría" en el cual se presentan las bases teóricas de estos métodos y tiene por objeto difundir el uso práctico de estas técnicas.
1 CONFIABILIDAD Y PROBABILIDAD DE FALLA ACEPTABLES
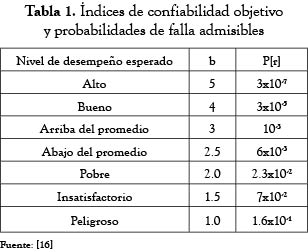
Para la determinación de la confiabilidad, en este trabajo se usará el índice de confiabilidad, β, del coeficiente o factor de seguridad (FS), definido por la siguiente expresión [10, 11] (ecuación 1), una vez que el FS crítico es igual a 1,0:
Donde E[FS] es el valor esperado del factor de seguridad, es decir, el factor de seguridad calculado con los parámetros medios de las variables independientes, y s[FS] es la desviación estándar del factor de seguridad.
Es claro que para que la ecuación 2 sea usada considerando una distribución de probabilidad normal para el factor de seguridad, las distribuciones de la resistencia del suelo o de la roca y de las cargas aplicadas también deben serlo. Para conocer más detalles de este índice y sobre el uso de otras distribuciones como la lognormal pueden ser consultadas referencias como Baecher y Christian [11], Wu [12] o Nadim [13].
La probabilidad de falla está dada por la porción del área bajo curva unitaria de distribución de frecuencia (función densidad de probabilidad) del FS correspondiente a los valores de FS inferiores a 1.0. Esta se puede determinar de cualquier tabla de función de distribución de probabilidades normal con media 0 y desviación estándar 1 o utilizando herramientas computacionales como Excel®.
Una de las principales dificultades a la hora de hacer análisis de confiabilidad está en definir los niveles de seguridad aceptables, es decir, cuál es la probabilidad de falla máxima que se puede tolerar para una estructura. Actualmente no existe un consenso sobre cuál es este valor de referencia, y son pocas las propuestas presentadas en las cuales se definan límites de decisión. En este sentido, la propuesta más conocida es la presentada por USACE [14] para niveles del índice de confiabilidad β y la probabilidad de ruptura (P[r]) o de falla asociada, como se muestra en la tabla 1.
Como se observa en la tabla 1, con este criterio la probabilidad de falla crítica es del orden de 6x10-3, que equivale a un índice de confiabilidad de 2.5, por lo cual se espera que estructuras con índices de confiabilidad superiores a 2.5 presenten un desempeño por encima del promedio de las estructuras.
En las aplicaciones subsecuentes, los valores del valor esperado y de la desviación estándar del factor de seguridad serán determinados usando los métodos FOSM y MEP, presentados en detalle en el artículo complementario "Herramientas para análisis por confiabilidad en geotecnia: La teoría", y los criterios de la tabla 1 son usados como referencia en el análisis de los resultados obtenidos.
2 APLICACIÓN DEL ANÁLISIS DE CONFIABILIDAD
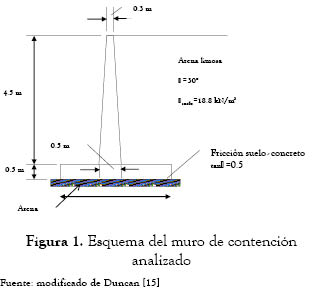
En este ejemplo se usaron el método FOSM y el de las estimativas puntuales para evaluar la probabilidad de falla por deslizamiento de la estructura de contención mostrada en la figura 1, adaptado de Duncan [15]. En esta estructura se consideran materiales de uso normal en obras de este tipo como son el hormigón y suelos de lleno compuestos por arenas limosas compactadas.
Por definición, el factor de seguridad contra deslizamiento es
Donde: FV: sumatoria de las fuerzas verticales; δ: ángulo de fricción entre el suelo y la base del muro; Ea: Componente horizontal del empuje activo.
Considerando que el suelo de lleno se comporta como un fluido equivalente de peso unitario geq, y que el empuje activo actúa solo en la dirección horizontal según la teoría de Rankine, las fuerzas verticales actuantes corresponden solo al peso del muro y al peso propio del suelo del lleno; la ecuación 2 se puede escribir como
Donde: gconc: peso unitario del hormigón (kN/m3); gsue: peso unitario del suelo de relleno (kN/m3); ø ángulo de fricción del suelo atrás del muro.
2.1 Método FOSM
Reemplazando los valores medios de cada parámetro en la ecuación 3 se obtiene el valor esperado del factor de seguridad por deslizamiento.
E(FS)=1.73
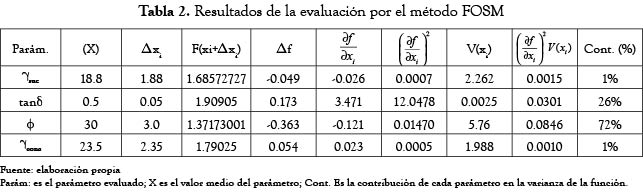
A partir de esta última ecuación, haciendo f=FSD y tomando incrementos de cada una de las variables definidas se efectuaron los cálculos presentados en la tabla 2. Los incrementos adoptados fueron de 10% de la media, ya que según resultados de Farías y Assis [16], valores menores no mejoran sustancialmente la precisión de los cálculos.
A partir de los resultados de la tabla 2 se obtuvieron los siguientes valores de varianza y desviación estándar del factor de seguridad.
(σ(FS))2=0.11
σ(FS)=0.34
Con los valores de la desviación estándar y del valor esperado se obtiene un índice de confiabilidad de 2.14 con el cual, y considerando una distribución normal, se obtiene una probabilidad de falla de 1.5x10 -2 para este muro de contención. Esto se puede interpretar como que para cada 150 estructuras de este tipo que se construyan, una presentará comportamientos por fuera de lo deseado o que de cada 150 m de muro que se construyan, 1 m presentará este comportamiento. Es decir, la falla en este caso no necesariamente implica una ruptura.
Esto significa que con la variabilidad que presentan los parámetros involucrados, existe una probabilidad de 1.5x10-2 de que el factor de seguridad por deslizamiento sea inferior a 1.0. De acuerdo con el valor de esta probabilidad de falla se puede decir que la estabilidad del muro está por debajo de lo que sería deseable, como se muestra en la tabla 1 (USACE [14], Sayed et al. [17]).
A partir de los resultados de contribución de cada parámetro en la varianza, se puede ver que los que presentan mayor influencia en la estabilidad de esta estructura de contención son la fricción entre el muro y la cimentación y la fricción del suelo atrás del muro 26% y 72%, respectivamente. Esto significa que la probabilidad de falla presenta poca influencia de la variación del peso de los materiales que ejercen la función estabilizadora, por lo cual el análisis se debe concentrar fundamentalmente en la variación del ángulo de fricción que influye tanto en el coeficiente de fricción entre el muro y el suelo como en los empujes.
En la práctica, es normal que para este tipo de estructura se estipule un factor de seguridad al deslizamiento de 1.5. Con el propósito de optimizar este diseño y de evaluar la conveniencia de este valor, se procedió a disminuir en 0.30 m la longitud de la base del muro y a calcular de nuevo la confiabilidad. Se obtuvo un valor esperado del factor de seguridad de 1.55, una desviación estándar de 0.30 un índice de confiabilidad de 1.79 y una probabilidad de falla de 3.6x10-2. De acuerdo con el valor de esta probabilidad de falla se puede decir que la estabilidad del muro está por debajo del desempeño deseable, USACE [14], Sayed et al. [17]
Se observa que con el factor de seguridad de 1.5 que habitualmente es definido para las estructuras de contención, no sería posible garantizar el comportamiento deseado. Existe pues la necesidad de evaluar cuál es el criterio adecuado para determinar la probabilidad de falla aceptable, ya que en esto no hay aún un consenso, pero de acuerdo con las referencias disponibles, este factor de seguridad es discutible. Por otro lado, deben ser determinados valores de desviación estándar o de coeficiente de variación para los materiales de cada obra, ya que con los parámetros recomendados por la literatura técnica y con materiales normales este criterio no sería aplicable. En este caso sólo se logra una probabilidad de falla arriba del valor considerado por encima del promedio para una longitud de la base de 3.9 m y un factor de seguridad de 1,85.
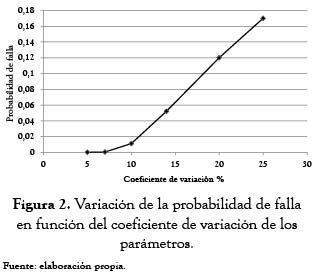
Otro aspecto importante es la sensibilidad de la probabilidad de falla con la dispersión de los datos. En la figura 2 se muestra cómo varía la probabilidad de falla de este muro para diferentes valores del coeficiente de variabilidad. Por simplicidad en estos cálculos se ha considerado que todos los parámetros tienen un coeficiente de variación igual. Esto se verifica también al comparar estos resultados con los reportados por Ribeiro [18] quien usó valores de desviación estándar diferentes y encontró probabilidades de falla más altas para el mismo problema.
2.2 Método de estimativas puntuales
En el numeral 2.1, se comprobó mediante el método FOSM que el 98% de la variabilidad del factor de seguridad se debe al ángulo de fricción del suelo en la parte posterior del muro y a la fricción entre la base del muro y el suelo de cimentación. Aprovechando esta situación, la evaluación por el método de las estimativas puntuales se hizo considerando que el factor de seguridad depende solo de estas dos variables. Así, al reemplazar los valores medios del peso unitario del lleno y del hormigón en la ecuación 3, esta se transforma en la siguiente ecuación.
Considerando las posibles combinaciones de la tabla 3 se obtuvo un valor esperado del factor de seguridad de 1.74 y una desviación estándar de 0.24. Estos dos valores se usaron para determinar el índice de confiabilidad; se obtuvo un índice de confiabilidad de 3.0 que corresponde a una probabilidad de falla de 1x10-3. Aunque se aprecian algunas diferencias numéricas, en general los valores determinados para el factor de seguridad, desviación estándar, índice de confiabilidad y probabilidad de falla son comparables con los del método FOSM. Para verificar esto, se procedió a aplicar el método de estimativas puntuales con las variables que no fueron considerables analizando para 3 y 4 variables.
Cuando se incluyó una variable adicional, peso unitario del lleno, se obtuvieron valores iguales a los determinados con las dos variables. Posteriormente se incluyó el peso unitario del hormigón como variable y se obtuvo un valor esperado de 1.98 y una desviación estándar de 0.45, con lo cual se obtuvo un índice de confiabilidad de 2.14 y una probabilidad de falla de de1.5x10-2. Los resultados de estos cálculos no se presentan por cuestión de espacio.
En general se observa que con el método de las estimativas puntuales se obtienen resultados comparables con los resultados del método FOSM, considerando las variables de mayor peso en la variabilidad, pero con la inclusión de todas las variables los resultados pueden cambiar sustancialmente.
3 CONCLUSIONES Y COMENTARIOS FINALES
El método FOSM permite determinar cuáles variables presentan mayor o menor influencia en la variación de las variables dependientes. En el caso del ejemplo estudiando en el numeral 2, la fricción entre el suelo y la cimentación, y el peso unitario del fluido equivalente representan el 98% del peso total de la variabilidad; estos se pueden considerar como los parámetros clave en un análisis de estabilidad por deslizamiento de un muro de contención.
El método de las estimativas puntuales, aunque puede requerir más cálculos, permite obtener resultados comparables con los que se obtienen en el método FOSM.
La probabilidad de falla de una estructura, muro de contención en este caso, presenta una relación inversa con el índice de confiabilidad, β. Cuanto mayor es el índice de confiabilidad, menor es la probabilidad de que se presente la falla.
Es necesario determinar valores de referencia para la probabilidad de falla aceptable, y parámetros de coeficientes de variabilidad para los suelos de cada localidad, para que los análisis de confiabilidad puedan conducir a conclusiones definitivas respecto al comportamiento de las estructuras.
Es necesario determinar los rangos de variación de los parámetros geotécnicos con una mejor aproximación, ya que la probabilidad de falla resulta ser bastante sensible a ésta.
Las evaluaciones de confiabilidad y la determinación de la probabilidad de falla no garantizan que las estructuras así diseñadas van a ser inmunes a posibles fallas, principalmente si se consideran los altos niveles de incertidumbre en los modelos. Sin embargo, evaluar los diferentes escenarios del proyecto sí puede dar mejores herramientas para la toma de decisiones.
REFERENCIAS
[1] R. V. Whitman, "Evaluating calculated risk in geotechnical engineering," J. of Geot. Eng, vol. 110, no. 2, 1984. pp. 144-188. [ Links ]
[2] G. Zhoua et al., "Spatial probabilistic modeling of slope failure using an integrated GIS Monte Carlo simulation approach," Eng. Geology, vol. 68, no. 3-4, 2003. pp. 373-386, [ Links ]
[3] C. Giasi et al., "Probabilistic and fuzzy reliability analysis of a sample slope near Aliano," Eng. Geology, vol. 67, no. 3-4, 2003. pp. 391-402. [ Links ]
[4] S. E. Cho, "Effects of spatial variability of soil properties on slope stability," Eng. Geology, vol. 92, no. 3-4, 2007. pp. 97-109. [ Links ]
[5] A. M. Hassan, y T. F. Wolff, "Effect of Deterministic and Probabilistic Models on Slope Reliability." en Slope Stability 2000 (GSP 101), Proceedings of Sessions of Geo-Denver 2000, Denver: 2000. pp. 194-208. [ Links ]
[6] M. Uzielli et al., "A First-Order Second-Moment Framework for Probabilistic Estimation of Vulnerability to Landslides," presentado a ECI Conference: Geohazards - Technical, Economical and Social Risk Evaluation, Lillehammer, Norway, 2006. [ Links ]
[7] H. Einstein, "Uncertainty in Rock Mechanics and Rock Engineering-Then and Now." presentado a International Society for Rock Mechanics 10th Congress Technology roadmap for Rock Mechanics, Pretoria: SAIMM, 2003. pp. 281-293. [ Links ]
[8] H. Einstein, y R. Sousa, "Warning System for Natural Threats," en ECI Conference on Geohazards, Lillehammer, Norway, 2006. [ Links ]
[9] J. Bonachea, "Desarrollo, Aplicación y Validación de Procedimientos y Modelos para la Evaluación de Amenazas, Vulnerabilidad y Riesgo Debidos a Procesos Geomorfológicos," Tesis doctoral, Universidad de Cantabria, 2006. [ Links ]
[10] J. T. Christian et al., "Reliability Applied to Slope Stability Analysis," J. of Geot. Eng, vol. 120, no. 12, 1994. pp. 2180-2207. [ Links ]
[11] G. Baecher, B, y J. T. Christian, Reliability and Statistics in Geotechnical Engineering, Chichester: John Wiley & Sons, 2003, 605 p. [ Links ]
[12] T. H. Wu, "Reliability analysis of slopes," en Reliability-Based Design in Geotechnical Engineering-Computations and Applications, K. K. Phoon, ed., Londres: Taylor-Francis, 2008. pp. 385-412. [ Links ]
[13] F. Nadim, "Tools and Strategies for Dealing with Uncertainty in Geotechnics," en Probabilistic Methods in Geotechnical Engineering, D. V. Griffths y G. A. Fenton, eds., Nueva York: Springer, 2007. pp. 71-96. [ Links ]
[14] USACE, "Risk-Based Analysis in Geotechnical Engineering for Support of Planning Studies", ETL 1110-2-556, U. S. Army Corps of Engineers, 1999. [ Links ]
[15] J. M. Duncan, "Factors of safety and reliability in geotechnical engineering," J. of Geot. and Geoenv. Eng, vol. 126, no. 4, 2000. pp. 307-316. [ Links ]
[16] M. Farias, y A. Assis, "Uma Comparação entre métodos probabilísticos aplicados à estabilidade de taludes." en Anais do XI Congreso Brasilero de Mecánica de Suelos e Ingeniería Geotécnica-COBRAMSEG, Brasilia: 1998. pp. 1305-1313. [ Links ]
[17] S. Sayed et al., "Reliability analysis of reinforced soil walls under static and seismic forces," Geosynth. Intern, vol. 15, no. 4, 2008. pp. 246-257. [ Links ]
[18] R. H. C. Ribeiro, "Aplicações de probabilidade e estatística em análises geotécnicas," Tesis de doctorado en ingeniería civil, Pontifícia Universidade Católica do Rio de Janeiro, Río de Janeiro, 2008. [ Links ]
Recibido: 09/04/2010
Aceptado: 06/04/2011













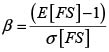 (1)
(1) 
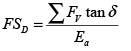 (2)
(2) 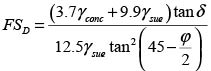 (3)
(3) 
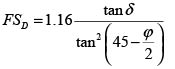 (4)
(4)