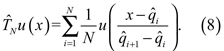Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Ingenierías Universidad de Medellín
Print version ISSN 1692-3324On-line version ISSN 2248-4094
Rev. ing. univ. Medellín vol.10 no.18 Medellín Jan./June 2011
Cuantificación del riesgo operacional utilizando sistemas de funciones iteradas
Operational risk quantification using iterated functions systems
Luis Ceferino Franco Arbeláez*; Hermilson Velásquez Ceballos**
* Universidad ITM. Correo electrónico luisfranco4146@itm.edu.co. Medellín, Colombia
** Universidad EAFIT. Correo electrónico evelas@eafit.edu.co. Medellín, Colombia.
Resumen
El presente artículo es uno de los resultados obtenidos en proyectos de investigación financiados por la Universidad EAFIT para el año 2011 y se basa en un estudio de Iacus y La Torre [1].Se presenta la estimación fractal, mediante sistemas de funciones iteradas (IFS), como una alternativa para estimar la función de distribución de las pérdidas agregadas, la cual es necesaria para la cuantificación del riesgo operacional. Como se muestra en el análisis, esta técnica puede superar algunas de las dificultades presentadas con las metodologías actuariales clásicas. Además, se presenta una aplicación, y se obtienen conclusiones.
Palabras clave: riesgo operacional, Basilea, método de distribución de pérdidas, sistema de funciones iteradas.Abstract
This article is one of the results obtain in a research project funded by the University EAFIT in 2011, This paper is based upon a study carried out by Iacus and La Torre [1], it is presented the fractal estimation, through Iterated Function Systems (IFS), as an alternative to estimate the distribution function of added losses which is necessary to quantify the operational risk. As it is shown in the analysis, this technique can deal with some of the difficulties presented with some of the classic actuarial methodologies. Furthermore, an application is presented and conclusions are obtained from it.
Key words:Operational risk, Basel, loss distribution approach, iterated function systems.
INTRODUCCIÓN
Aunque ha sido una preocupación histórica, la cuantificación del riesgo operacional se ha convertido en una actividad obligada en las instituciones financieras, desde el surgimiento de la Convergencia Internacional de Medidas y Estándares de Capital, o Nuevo Acuerdo de Basilea [2], emitido por el Banco de Pagos Internacionales (Bank for International Settlements-BIS) en el año 2006, que incorporó ese riesgo en el cálculo de la relación de solvencia, para estimar los requerimientos de capital.
Se debe cuantificar el riesgo para satisfacer los estándares regulatorios; pero el objetivo fundamental debe ser robustecer los procesos de control y lograr una disminución de pérdidas potenciales, y en general, fortalecer la toma de decisiones tendentes a la generación de valor. Según ese acuerdo, se define el riesgo operacional como la pérdida potencial de una entidad por fallas o deficiencias en los sistemas internos, en los procesos, en las personas o en factores externos. Se incluye el riesgo legal, pero se excluye el riesgo de reputación. La norma colombiana de la Superintendencia Financiera incluye, además, el riesgo de reputación. El riesgo legal es la pérdida posible por sanciones o indemnizaciones como consecuencia del incumplimiento de normas, regulaciones u obligaciones contractuales o por fallas en los contratos o en las transacciones. El riesgo de reputación corresponde a pérdidas posibles por desprestigio, mala imagen o publicidad negativa.
El procesamiento sistemático de cualquier tipo de riesgo en finanzas debe cubrir tres etapas esenciales: identificación, cuantificación y gestión. Entre los retos relativos al riesgo operacional se incluyen desde la falta de una estandarización conceptual y la prevalencia de una cultura reactiva, hasta la ausencia de una metodología unificada para la cuantificación.
En la gama de alternativas de medición avanzada, el método de distribución de pérdidas (Loss Distribution Approach-LDA), que involucra herramientas del cálculo actuarial, ha sido el más generalmente utilizado en este campo.
El método LDA está construido con los siguientes elementos, que se aplican inicialmente para cada combinación línea de negocio-evento de pérdida:
i) La distribución de frecuencia Pij(n) de la variable aleatoria de conteo Nij que representa el número de ocurrencias del evento j en la línea i.
ii) La distribución de severidad o impacto FXij(x) de la variable aleatoria Xij que representa el monto de la pérdida generada en la línea i por el evento j.
iii) La distribución de pérdidas agregadas: la agregación o convolución del proceso discreto asociado a la frecuencia, y el proceso continuo asociado a la severidad, procesos que por sus características específicas no son directamente aditivos ni multiplicativos.
A partir de la distribución de pérdidas agregadas, obtenida generalmente a través de métodos numéricos, se calcula la carga de capital, o el llamado Valor en Riesgo Operacional, mediante el cuantil correspondiente al nivel de confianza determinado, que para el caso de riesgo operacional ha sido establecido por Basilea en el 99.9%.
Al aplicar diversos métodos de cuantificación, y en particular el LDA, la carencia de bases de datos suficientes sobre eventos de pérdidas operacionales, con frecuencia, se ha convertido en el principal obstáculo, ya que surgen distorsiones en la estimación de la distribución.
En consecuencia, el método LDA ha demostrado diferentes fallas que podrían afectar realmente la bondad de la estimación del VaR operacional, Embrechts et al. [3] y Chavez-Demoulin et al. [4]. El principal problema es la falta de datos sobre pérdidas operacionales. Aunque el riesgo operacional no es nuevo, el problema de su cuantificación sí es relativamente reciente, y puede ocurrir que las colecciones disponibles de pérdidas relativas a ese riesgo no sean suficientes. Además, el LDA puede subestimar el riesgo de una pérdida extrema en líneas de negocio con alta frecuencia y bajo impacto (HFLI) y sobreestimar ampliamente el valor de la pérdida total en una línea de negocio con baja frecuencia y alto impacto (LFHI), La Torre et al. [5].
En este artículo se presenta la estimación fractal, mediante sistemas de funciones iteradas (IFS), como una alternativa para la cuantificación del riesgo operacional, que puede superar algunas de las dificultades presentadas con las metodologías actuariales clásicas.
Después de esta introducción, el artículo está organizado en la siguiente forma: se presenta una sección sobre los sistemas de funciones iteradas y su aplicación en el contexto del riesgo operacional. Luego se tiene una aplicación con datos obtenidos de una entidad financiera colombiana y, finalmente, algunas conclusiones sobre su eficiencia potencial y análisis del desempeño en comparación con la metodología LDA.
1 SISTEMAS DE FUNCIONES ITERADAS (IFS) EN RIESGO OPERACIONAL
Los sistemas de funciones iteradas (IFS) surgieron a mediados de los ochenta [6, 7], como aplicaciones de la teoría de sistemas dinámicos discretos y como herramientas útiles para construir fractales y otros conjuntos similares.
La iteración de funciones ha sido aplicada en economía [8, 9], en la teoría de procesamiento de imágenes [10], en modelos de crecimiento [11, 12], así como en sistemas dinámicos aleatorios [12-14].
Un sistema de funciones iteradas (IFS) es una familia finita ø de funciones contractivas en un espacio métrico completo (X,d).
El conjunto ø = {f1, f2, ... fk} de aplicaciones induce una aplicación F:P(X) →kP(X) entre las partes de X, definida por 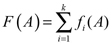 . Si consideramos en P(X) la distancia de Hausdorff y nos restringimos a los subconjuntos compactos, F será a su vez una aplicación contractiva sobre un espacio métrico que a su vez es completo, y por tanto tendrá un punto fijo K. Este punto fijo será también el límite de la sucesión {A, F(A), F(F(A)), ...}.
. Si consideramos en P(X) la distancia de Hausdorff y nos restringimos a los subconjuntos compactos, F será a su vez una aplicación contractiva sobre un espacio métrico que a su vez es completo, y por tanto tendrá un punto fijo K. Este punto fijo será también el límite de la sucesión {A, F(A), F(F(A)), ...}.
Con las siglas IFS se denota la aplicación de ø con factor de contracción dado por r = max{ri,i = 1,2, ..., k}, donde ri es el factor de contracción de la correspondiente fi .
El resultado fundamental sobre el cual están basados los IFS es el teorema del punto fijo de Banach.
En aplicaciones prácticas un problema crucial es el llamado problema inverso, que se formula de la siguiente manera: dado f en un espacio métrico (S,d), encontrar una contracción T:S → S que admita un único punto fijo 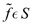 tal que
tal que 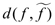 sea lo suficientemente pequeño. Si se resuelve el problema inverso con precisión adecuada, se puede identificar f con el operador T que tiene a f como punto fijo.
sea lo suficientemente pequeño. Si se resuelve el problema inverso con precisión adecuada, se puede identificar f con el operador T que tiene a f como punto fijo.
Una solución aproximada del problema inverso es la solución del siguiente problema de optimización restringida:
donde 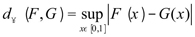 , para F,G pertenecientes al espacio de funciones acotadas en [0,1].
, para F,G pertenecientes al espacio de funciones acotadas en [0,1].
1.1 Contracciones en el espacio de funciones de distribución
El espacio de funciones de distribución se denota F([0,1]) y dotado con la métrica d∞ es un espacio métrico completo.
Sea N ∈ N fijo y sea:
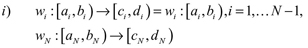
con
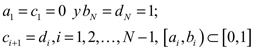 .
.
ii) wi, i = 1,2, ... N, son funciones crecientes y continuas.
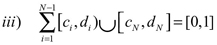
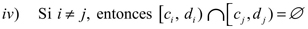
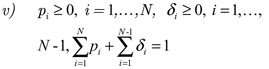
En F[0,1], d ∞) se define un operador en la siguiente forma:
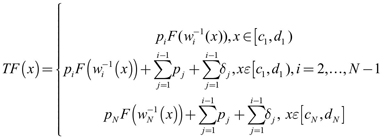
donde F ∈ F([0,1]).
En muchos casos prácticos se asume que los wi son mapeos afines. Suponemos en lo sucesivo que los mapeos wi y los parámetros δi son fijos mientras que los pi deben ser seleccionados. Como el operador T depende del vector p = (p1, ..., pN) se denota Tp.
Para generar funcionales más genéricos, en las hipótesis anteriores para definir Tp, se considera
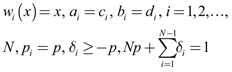 .
.
En estas condiciones, se tienen los siguientes resultados, cuyas demostraciones están en Iacus y La Torre [1]:
i) El operador Tp es contractivo de F([0,1]) en sí mismo, con constante de contracción 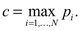
ii) Para ε > 0, y 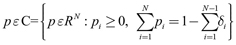 , si
, si 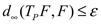 , entonces
, entonces 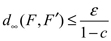 donde F' es el punto fijo de Tp .
donde F' es el punto fijo de Tp .
Para una función de distribución F ε F([0,1]) se trata de encontrar un mapeo contractivo T de F([0,1]) en sí mismo, que tenga un punto fijo "cercano" a F.
En el contexto del riesgo operacional esa F que se quiere estimar será la función de distribución de las pérdidas agregadas en una línea específica de negocio, o en toda la entidad.
La estimación fractal, mediante sistemas de funciones iteradas para la cuantificación del riesgo operacional, ha surgido como una alternativa cuya especificación difiere significativamente del clásico modelo LDA, y que puede superar algunas de sus limitaciones. La Torre et al. [5] permiten una estimación no paramétrica, que hace viable interpretar los datos de pérdida en la mejor forma posible y simular una población potencial de la cual provienen nuestras observaciones, especialmente cuando se tienen pocos datos, o hay datos faltantes, como ocurre en algunas líneas de negocios, caracterizadas por datos de pérdida de baja frecuencia y alta severidad.
Otra ventaja de este método consiste en excluir la necesidad de un análisis sobre distribuciones de frecuencia y severidad, y sobre la convolución entre esas distribuciones, ya que se estima directamente la función de distribución de pérdidas operacionales agregadas de la línea de negocio o entidad, sin considerar el tipo de evento, y luego se estima directamente la carga de capital requerida para la cobertura del riesgo operacional. El procedimiento se ilustra en la siguiente sección.
1.2 Estimación de la función de distribución de las pérdidas
Para estimar una función de distribución, en lugar de tratar de resolver el problema de optimización (P), usamos las propiedades de tales funciones para obtener, inicialmente, una "buena" aproximación de F, que luego es utilizada directamente en la estimación de la función de distribución de las pérdidas agregadas.
Consideremos x1, x2, ... xn una sucesión de variable aleatorias independientes e idénticamente distribuidas, que tienen función de distribución acumulativa continua común desconocida F ∈ F([0,1]), de una variable aleatoria X con valores en [0,1].
Así que F(x) = P(X < x), F(x) = 0 para x < 0 y F(x) = 1 para x > 1. Entonces la función de distribución empírica (EDF) está dada por:
donde 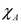 es la función indicadora del conjunto A.
es la función indicadora del conjunto A.
La EDF es un estimador de la función de distribución desconocida F, y para 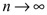 tiene propiedades de optimalidad asintótica, como se muestra en Millar [15].
tiene propiedades de optimalidad asintótica, como se muestra en Millar [15].
Esta función tiene una representación IFS que es exacta y puede ser encontrada sin resolver ningún problema de optimización. Se puede asumir que los xi en la muestra son todos diferentes, por ser F una función de distribución continua. Sea 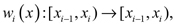 donde i = 0, 1, ... n y
donde i = 0, 1, ... n y 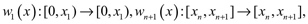 con x0 = 0 y xn + 1 = 1. Además se supone, en particular, que cada mapeo es de la forma wi(x) = x.
con x0 = 0 y xn + 1 = 1. Además se supone, en particular, que cada mapeo es de la forma wi(x) = x.
Si se escogen 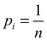 , i = 2, ... n + 1, p1 = 0, y
, i = 2, ... n + 1, p1 = 0, y 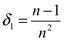 "
"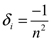 , entonces se tiene:
, entonces se tiene:
Para xε [xi-1, i). Es claro que cualquier función de distribución discreta se puede representar exactamente con un IFS con argumentos similares.
A partir de ahora suponemos δi = 0, para toda i. Para producir un estimador, primero debemos proporcionar una buena aproximación de F. Así que se fija una F ε F([0,1]) y se escogen N + 1 puntos ordenados (x1, ... xN + 1) de tal manera que x1 = 0 y xN + 1 =1. Define los mapas wi y los coeficientes pi de la siguiente manera: para i = 1, ..., N,
El funcional Tp puede ser denotado como TN con este determinado conjunto de mapas y de coeficientes, ya que depende del número de puntos y sus valores. Para cualquier uεF([0,1]), TN puede ser escrito para xòR como:
TN es una contracción sobre (F[0,1], dsup) y TNu(xi), para todo i.
Como este funcional es una función de F, no puede ser usado directamente en aplicaciones estadísticas cuando F es desconocida. Pero para este fin, se toman los puntos xi como los cuantiles qi de F; es decir, escoger N+1 puntos u1 = 0 u2 < ... < un < uN + 1 = 1 igualmente espaciados en [0,1] y sea qi = F-1(ui). En este caso la función TN se convierte en:
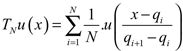 ,
,
TN depende de F sólo a través de los cuantiles qi.
En esta forma se asegura que el perfil de F se sigue suavemente. De hecho, si dos cuantiles qi y el qi + 1 son relativamente distantes uno del otro, entonces F está aumentando lentamente en el intervalo (qi, qi + 1), y viceversa. Como los cuantiles pueden ser fácilmente estimados a partir de una muestra, ahora tenemos un candidato para un estimador IFS de la función de distribución.
Por lo tanto, sea x1, ... xn una muestra de F y sean 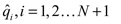 los cuantiles empíricos de orden 1 / N tal que
los cuantiles empíricos de orden 1 / N tal que 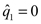 y
y 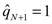 . Entonces para uòF([0,1]), se tiene el siguiente estimador IFS de la función de distribución:
. Entonces para uòF([0,1]), se tiene el siguiente estimador IFS de la función de distribución:
Este IFS sólo será una aproximación de la función de distribución objetivo F, ya que depende de los valores de los cuantiles de la muestra, que a su vez son funciones de los valores observados x1, ... xn. Además, es claro que la calidad de esta aproximación mejorará a medida que n crece, ya que los cuantiles muestrales convergen en probabilidad a los verdaderos cuantiles.
Iacus y La torre [1] muestran que el número de cuantiles necesarios para lograr una precisión ε es el menor entero N tal que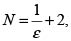 , y que como regla general es aplicable utilizar un N entre
, y que como regla general es aplicable utilizar un N entre 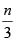 y
y 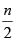 , siendo n el tamaño muestral.
, siendo n el tamaño muestral.
Para estimar a partir de una muestra, la función de distribución F de las pérdidas agregadas, el procedimiento sería el siguiente:
Los datos muestrales y1, y2, ... yn se convierten en datos x1, ... yn en [0,1] mediante una transformación adecuada, para aplicar los IFS, que funcionan sobre un soporte finito, y para el caso de funciones de distribución sobre [0,1].
i) Para i = 1, ..., N + 1, se utilizan los datos x1, ... x1, ... xn para hacer estimaciones 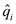 " de los cuantiles de orden
" de los cuantiles de orden 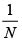 , con
, con 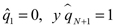
ii) Utilizando una función de distribución u∈F ([0,1]), calcular el estimador IFS "v10n18a09e36", de la función de distribución F.
2 APLICACIÓN Y RESULTADOS
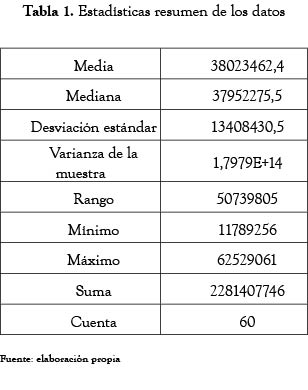
Las bases de datos relativas a riesgo operacional son escasas, y las entidades son muy reservadas para permitir acceso a ellas. Por esa razón, para elaborar una muestra de datos de pérdidas se recurrió a un grupo de expertos de una entidad financiera local, que proporcionaron estimativos de las pérdidas mensuales generadas desde enero de 2002 hasta diciembre de 2006. Cada observación es la suma mensual estimada de las pérdidas generadas en la entidad conjuntamente por los siete eventos de riesgo operacional considerados en la norma. En la tabla 1, se tiene un resumen de las estadísticas relevantes de los datos.
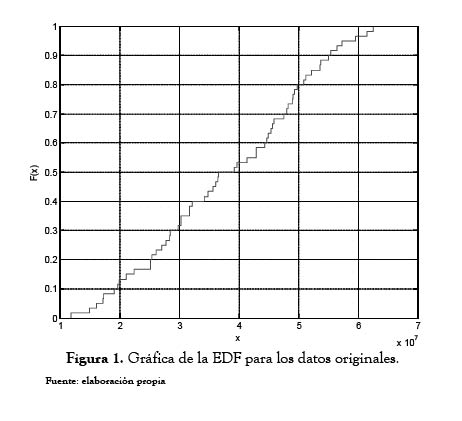
Utilizando el software Matlab, a partir de la muestra se obtuvo la distribución empírica (EDF), que se muestra en la figura 1, para efectos de comparación.
En la figura se tienen, en el eje horizontal, los valores originales de pérdidas mensuales, y en el eje vertical, la probabilidad acumulada, según la EDF planteada en la ecuación (3).
También se desarrolló todo el proceso para determinar la estimación IFS de la distribución de pérdidas totales mensuales, aplicando la técnica esbozada en este artículo.
En la etapa inicial del procedimiento IFS, cuando se debe aplicar una transformación de los datos muestrales para convertirlos a datos en el intervalo [0,1]; entre las múltiples alternativas se escogió como función de transformación 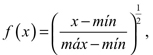 donde min y máx, son respectivamente, el mínimo y el máximo de la muestra. Esta f, así definida, es una función unívoca que transforma todos los datos del intervalo [m + in, máx] a datos en el intervalo [0,1]. En los datos de la muestra, el dato mínimo es 11.789.256, y el máximo es 62.529.061. Siguiendo la regla general, se seleccionaron 25 cuantiles para el proceso de estimación del IFS. Finalmente, con respecto a la función de distribución μ aplicable en la ecuación (8), para la cual no hay ninguna restricción específica, se seleccionó la distribución uniforme en [0,1].
donde min y máx, son respectivamente, el mínimo y el máximo de la muestra. Esta f, así definida, es una función unívoca que transforma todos los datos del intervalo [m + in, máx] a datos en el intervalo [0,1]. En los datos de la muestra, el dato mínimo es 11.789.256, y el máximo es 62.529.061. Siguiendo la regla general, se seleccionaron 25 cuantiles para el proceso de estimación del IFS. Finalmente, con respecto a la función de distribución μ aplicable en la ecuación (8), para la cual no hay ninguna restricción específica, se seleccionó la distribución uniforme en [0,1].
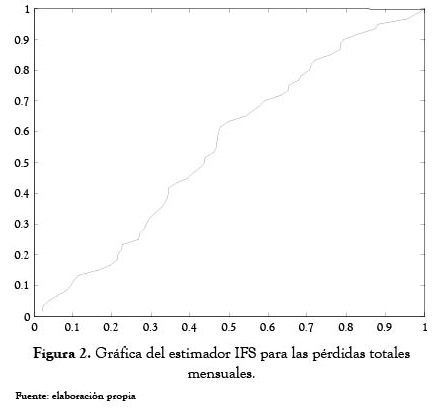
Con las hipótesis de la técnica y los supuestos planteados para cada paso, se desarrolló todo el procedimiento y se obtuvo la figura 2, correspondiente al estimador IFS para la función de distribución de la pérdida mensual total.
Con respecto a resultados numéricos de interés, a partir de los datos procesados en Matlab para esta distribución, se encontró que su percentil 99.9%, que es el exigido para riesgo operacional, es 0.9974010. Este resultado conduce, según las transformaciones utilizadas, a que el percentil 99.9 estimado para la distribución de pérdidas totales mensuales es de 62397186.
Esto indicaría que para la entidad analizada el VaR-Operacional mensual estimado por esta metodología, bajo el supuesto de que no se provisionen las pérdidas esperadas, estaría dado por: VaR - Op = $62.397186.
3 CONCLUSIONES
En los últimos años, fundamentalmente desde el surgimiento del Nuevo Acuerdo de Basilea, que planteó el requerimiento de incorporar el riesgo operacional en la relación de solvencia, han surgido diversas alternativas metodológicas para su cuantificación. En este artículo se ha presentado la llamada estimación fractal, basada en sistemas de funciones iteradas, como posible alternativa para la medición de ese riesgo. Como no se ha hecho una comparación especifica con otras metodologías, lo que será resultado de un estudio en proceso, algunas de las conclusiones siguientes están soportadas en los resultados de los autores referenciados.
Esta técnica no requiere el análisis sobre distribuciones de frecuencia y severidad, y sobre la convolución entre esas distribuciones; estima directamente la función de distribución de pérdidas operacionales agregadas de la línea de negocio o entidad, sin considerar el tipo de evento, y luego se estima directamente la carga de capital requerida para la cobertura del riesgo operacional.
En Iacus y La torre [1] se concluye que mediante el método IFS resulta un requerimiento de capital, más acorde con el perfil de riesgo de la institución financiera que permite capturar eventos de pérdidas extremas e inesperados.Además, se muestra que el LDA puede subestimar el riesgo de una pérdida extrema en líneas de negocio con alta frecuencia y bajo impacto (HFLI) y sobrestimar ampliamente el valor de la pérdida total en una línea de negocio con baja frecuencia y alto impacto (LFHI).
El método IFS captura perfectamente la posibilidad de cualquier riesgo extremo asignando un monto de capital consistente con el perfil de riesgo de la entidad.
El mejor desempeño del método IFS en la estimación se debe a su capacidad para superar la escasez de datos que afecta a otras metodologías.
Finalmente, se puede concluir que el método IFS podría brindar a las entidades financieras una estimación de riesgo más coherente que la del modelo LDA, a partir de bases de datos de pérdidas operacionales deficientes o incompletas, mejorando la eficiencia de la asignación de capital y, probablemente, generando ahorro de capital.
REFERENCIAS
[1] S. M. Iacus, y D. La Torre, "Approximating distribution functions by iterated function systems," Journal of Applied Mathematics and Decision Sciences, [En línea], vol. 2005, no. 1, Disponible: http://downloads.hindawi.com/journals/ads/2005/210719.pdf, 2005. [ Links ]
[2] B. d. P. Internacionales. "Comité de Supervisión Bancaria de Basilea," [En línea]; Disponible: http://www.bis.org/publ/bcbs128_es.pdf, 2006. [ Links ]
[3] P. Embrechts et al., "Correlation and dependence in risk management: properties and pitfalls," en Risk Management: Value at Risk and Beyond, M. A. H. Dempster, ed., pp. 176-223, Cambridge: Cambrigde University Press 2002. [ Links ]
[4] V. Chavez-Demoulin et al., "Quantitative Models for Operational Risk: Extremes, Dependence and Aggregation," presentado a Reunión Implementing an AMA for Operational Risk, Boston, 2005, pp. 34. [ Links ]
[5] D. La Torre et al., "Fractal Estimations and Simulations in Operational Risk Analysis," presentado a International Conference MAF 2008, Venecia, 2008, pp. 17. [ Links ]
[6] J. E. Hutchinson, "Fractals and self similarity," Indiana University Mathematics Journal, vol. 30, pp. 713-747, 1981. [ Links ]
[7] M. F. Barnsley, y S. Demko, "Iterated Functions Systems and the Global Construction of Fractals," Proceedings of the Royal Society of London, vol. 399, no. 1817, pp. 243-275, 1985. [ Links ]
[8] R. M. Solow, "A Contribution to the theory of economic growth," The Quarterly Journal of Economics, vol. 70, no. 1, pp. 65-94, 1956. [ Links ]
[9] R. H. Day, "Irregular growth cycles," The American Economic Review, vol. 72, no. 3, pp. 406-414, 1982. [ Links ]
[10] B. Forte, y E. R. Vrscay, "Solving the inverse problem for function and image approximation using iterated function systems," Dynamic of continuous, discrete and impulsive systems, vol. 1, no. 2, pp. 1-46, 1995. [ Links ]
[11] L. Montrucchio, y F. Privileggi, "On Fragility of Bubbles in Equilibrium Asset Pricing Models of Lucas-Type," Journal of Economic Theory, vol. 101, no. 1, pp. 158-188, 2001. [ Links ]
[12] L. Arnold, y H. Crauel, "Iterated function systems and multiplicative ergodic theory," en Diffusion Processes and Related Problems in Analysis, Vol. II, Stochastic Flows, Progress in Probability 27, M. A. Pinsky y V. Vihstutz, eds., pp. 283-305, Boston: Birkhäuser, 1992. [ Links ]
[13] J. H. Elton, y M. Piccioni, "Iterated Function Systems arising from recursive estimation problems," Probability Theory and Related Fields, vol. 91, no. 1, pp. 103-114, 1992. [ Links ]
[14] A. A. Kwiecinska, y W. Slomczynski, "Random dynamical systems arising from iterated function systems with place-dependent probabilities," Stat. and Prob. Letters, vol. 50, no. 4, pp. 401-407, 2000. [ Links ]
[15] P. W. Millar, "Asymptotic minimax theorems for the sample distribution function," Probability Theory and Related Fields, vol. 48, no. 3, pp. 233-252, 1979. [ Links ]
Recibido: 01/09/2010
Aceptado: 04/03/2011













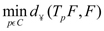 (P) (1)
(P) (1) 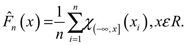 (3)
(3) 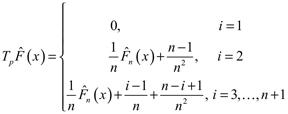 (4)
(4) 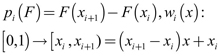 (5)
(5) 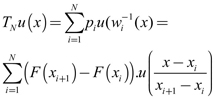 (6)
(6)