Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Ingenierías Universidad de Medellín
Print version ISSN 1692-3324On-line version ISSN 2248-4094
Rev. ing. univ. Medellín vol.10 no.19 Medellín July/Dec. 2011
ARTÍCULOS
VALORACIÓN DEL RIESGO FINANCIERO (CFAR) EN LAS EPS A TRAVÉS DE OPCIONES REALES: UNA APLICACIÓN AL NIVEL DE ATENCIÓN IV*
Financial Risk Valuation (CFAR)in EPS's through Real Options: An Application at the IV Assistance Level
Mónica A. Arango Arango**; Elizabeth T. Arroyave Cataño***; Juan D. Hernández****
** M. Sc., Profesora del Programa de Ingeniería Financiera, Universidad de Medellín. Carrera 87 N° 30 - 65 Medellín - Colombia. Teléfono: 3405420. Correo: moarango@udem.edu.co
*** M. Sc., Profesora del Programa de Ingeniería Financiera, Universidad de Medellín. Carrera 87 N° 30 - 65 Medellín - Colombia. Teléfono: 3405420. Correo: etarroyave@udem.edu.co
**** M. Sc., Profesor del Programa de Administración de Empresas, Universidad de Medellín. Carrera 87 N° 30 - 65 Medellín - Colombia. Teléfono: 3405420. Correo: jdhernandez@udem.edu.co
Recibido: 22/11/2010
Aceptado: 04/10/201
RESUMEN
El número de pacientes tratados por insuficiencia renal en Colombia es cada vez mayor; por esta razón conocer los costos asociados a esta enfermedad es una necesidad manifiesta de las Entidades Promotoras de Salud con el fin de garantizar la estabilidad del Sistema de Seguridad Social en Salud. Este trabajo evalúa financieramente, mediante opciones reales, la posibilidad de hacer un trasplante de riñón en un paciente bajo tratamiento de insuficiencia renal y el Flujo de Caja en Riesgo al tener en cuenta esta opción. Se encontró que al hacer un análisis periódico de los costos asociados a continuar con el tratamiento, existen casos en los que es más eficiente hacer el trasplante, disminuyendo el valor presente de las erogaciones del paciente, mejorando el flujo de caja en riesgo y controlando los gastos futuros de la entidad que lo atiende.
Palabras clave: opciones reales, flujo de caja en riesgo, simulación Montecarlo, insuficiencia renal.
Abstract
Number of patients treated for renal failure in Colombia is increasingly high; for this reason, knowing the costs associated to this disease is a clear need for Health Promoting Entities with the purpose of assuring stability of the Health Social Security System. Through real options, this article is a financial evaluation of the possibility of conducting a kidney transplant in a patient being under a renal failure treatment and the cash flow at risk when having this as an option. It was found that when a periodical analysis of costs associated to continuation of treatment is made, there are cases where transplant is a more efficient option to be executed since the present value of the patient's expenses is decreased, thus improving the cash flow at risk and controlling future expenses of the entity treating the patient.
Key words: real options; cash flow at risk; Montecarlo Simulation; renal failure.
INTRODUCCIÓN
El Ministerio de Protección Social, con el fin de reglamentar la administración del riesgo de salud, dicta la Resolución 1740 del 20 de mayo de 2008, en la cual se crea el Sistema de Administración del Riesgo (SAR), para las Entidades Promotoras de Salud (EPS) del régimen contributivo. En esta se establece la gradualidad del sistema de administración de riesgos, con cuatro fases de implementación anual por parte de las EPS: plan de implementación, despliegue del sistema, ampliación del sistema y consolidación del sistema, antes de diciembre de 2011. Esto ha generado el interés de las EPS por buscar metodologías que permitan gestionar y cuantificar el riesgo operativo, de negocio, mercado y crédito; y el riesgo en salud, de acuerdo con el Marco General del Sistema de Administración de Riesgos.
Según la Resolución 5261 de 1994 los servicios en salud de acuerdo con la complejidad de las actividades, procedimientos e intervenciones, cuentan con cuatro niveles de atención. Esta investigación se concentra en el estudio del nivel IV, específicamente en los procedimientos asociados a la insuficiencia renal (IR). Dicha enfermedad es considerada una patología catastrófica (artículo 117 de la Resolución 5261 de 1994), por lo que presenta una alta complejidad técnica en su manejo, alto costo, baja ocurrencia y bajo costo efectividad en su tratamiento. En este sentido, este artículo expone un análisis desde un punto de vista estrictamente económico y valora financieramente, a través de opciones reales (OR), uno de los procedimientos contemplados en el nivel IV: el trasplante renal en pacientes con IR.
El Ministerio de Protección Social en su informe sobre el modelo de prevención y control de la enfermedad renal crónica en Colombia presenta la ruta crítica para la atención del usuario con dicha patología, a partir de la cual se evalúa, de acuerdo con el estadio de la enfermedad, la viabilidad de los tratamientos asociados a esta enfermedad: la hemodiálisis, la diálisis peritoneal y el trasplante. Esta enfermedad genera el mayor impacto financiero y desviación del perfil epidemiológico en el Sistema de Seguridad Social en Colombia [1].
Ante la necesidad manifiesta de las EPS por medir el riesgo, este artículo presenta la valoración de los costos de atención en los pacientes con IR, por concepto de tratamiento o trasplante. Para ello, se utiliza como herramienta metodológica el análisis de las opciones reales y el Flujo de Caja en Riesgo (CFaR).
El artículo se divide en dos secciones; una primera presenta el marco teórico en el cual se hace una revisión de las metodologías de valoración de OR y una breve descripción del CFaR. La segunda sección muestra los resultados y la metodología implementada para valorar la opción, así como la significancia de las variables que alimentan el modelo. En la misma sección se exponen los resultados financieros, al considerarse la posibilidad de realizar un trasplante de riñón en un paciente bajo tratamiento de IR y el flujo de caja en riesgo al tener en cuenta esta opción.
1. ASPECTOS TEÓRICOS EN OPCIONES REALES
1.1. Valoración mediante opciones reales
La teoría de opciones se ha constituido en una base fundamental para la valoración de activos financieros en un ambiente de incertidumbre. Esta teoría ha sido extendida a la valoración de activos no financieros, como las inversiones productivas. Su análisis se fundamenta en que las decisiones, tanto en los proyectos de inversión como en las estrategias de negocios, requieren de una valoración que sea acorde a la flexibilidad que estos tengan hacia el futuro. Esta flexibilidad es posible valorarla con el uso de la teoría de opciones, lo cual ha pasado a llamarse OR [2].
El modelo desarrollado por Fischer Black, Myron Scholes y Robert Merton (BSM) ofrece una solución analítica para la valoración de opciones sobre activos financieros, con una fecha de ejercicio única, conocidas como opciones europeas. El modelo se basa en la condición de no arbitraje para garantizar dinámicamente que el valor de la opción es equivalente al valor de la cartera a medida que va evolucionando el precio del subyacente [3]. Esto es posible dado que se podría invertir simultáneamente en el subyacente y en la opción.
En algunos casos donde el precio del activo subyacente sigue un proceso difícil de solucionar analíticamente se utiliza el método Monte Carlo. En este caso la función de distribución del precio futuro del subyacente se establece a partir de los movimientos esperados en dicha variable; dicho proceso determinará la distribución del valor de la opción. Para obtener una estimación del valor de la opción en el tiempo t, una muestra de valores es generada aleatoriamente a partir de la distribución descrita. Este método utiliza la simulación para determinar las posibles trayectorias hacia adelante de los movimientos futuros del precio del subyacente. Algunas implementaciones de la simulación Monte Carlo en la valoración de opciones americanas han sido presentadas por Bossaerts [4], Fu [5], Fu y Hu [6], Carriere [7], Ibanez y Zapatero; y Raymar y Zwecher [8, 9].
Los modelos anteriores permiten el análisis de los proyectos a través de las opciones reales, las cuales consisten en obtener el derecho mas no la obligación de emprender, postergar, expandir, contraer o abandonar un proyecto a un costo de inversión (precio de ejercicio) predeterminado, durante un período específico (fecha de vencimiento de la opción), esperando obtener un valor presente de los flujos de caja superiores a los costos ejecutados [10]. De acuerdo con esta definición, el valor de un proyecto está determinado por la estimación conjunta de los Flujos de Caja Descontados (FCD) y el valor de sus OR.
VPN_A = VPN + VOR (1)
Donde:
VPN_A: Valor Presente Neto Ajustado del proyecto.
VPN: Valor Presente Neto de los Flujos de Caja del proyecto.
VOR: Valor de la Opción Real.
Bajo el análisis de opciones reales es posible aceptar proyectos con VPN < 0, siempre que al incluir VOR, VPN_A > 0.
1.2. CFaR como medida de riesgo de default de un proyecto
El flujo de caja en riesgo (CFaR) es una herramienta de control que busca simular el valor en riesgo (VaR) del flujo de caja futuro de un proyecto dentro de un intervalo de confianza predefinido y permite determinar el riesgo de default para proyectos de inversión [11]. A diferencia del cálculo tradicional del VaR que estima el menor valor del portafolio, el CFaR calcula la peor ganancia a obtener con un X% de probabilidad en un periodo de t días durante la vida del proyecto [12]. En este sentido, dicha estimación da una medida que indica el riesgo de no alcanzar las utilidades esperadas, definiendo el punto de default para un período durante la vida del proyecto.
La evidencia empírica indica que el CFaR se puede estimar de manera endógena, o exógena a la firma. La primera aplicación ha sido implementada por académicos y empresarios. Entre los académicos que han estudiado el CFaR de manera endógena, se encuentran [13-17], entre otros.
2. RESULTADOS
En esta sección se evalúa financieramente la opción real de trasplante de riñón para una persona que sufre IR. Adicionalmente, se calcula el CFaR de los costos de tratamiento de IR considerando dicha opción. Evaluar la opción consiste en comparar en un momento del tiempo el valor presente de los costos de tratamiento de la IR frente a los desembolsos necesarios para hacer el trasplante de riñón. En este orden de ideas, el valor del tratamiento es el valor presente de la sumatoria de todos los flujos de caja de los costos que tendrá el tratamiento bajo IR en todas las etapas por las que pasará el paciente (Ver tabla 1).
Por otro lado, el valor asociado al trasplante es el valor presente neto de la suma de todos los desembolsos en los que se incurre por un paciente al que se le puede practicar esta intervención, incluyendo tanto el costo del trasplante como los costos del tratamiento posterior a este.
Al evaluar el valor presente de los desembolsos de un paciente en tratamiento de IR y el valor presente de los costos del paciente trasplantado, se valora la opción asumiendo que la esperanza de vida es una variable aleatoria independiente en las dos posibilidades planteadas. Dicha característica es la principal fuente de volatilidad en el modelo.
2.1. Modelo de evaluación financiera del trasplante
Para valorar la opción de trasplante se consideraron las metodologías de valoración de opciones: Black, Scholes y Merton (BSM), árboles binomiales y simulación Monte Carlo. Al analizar la aplicación de cada una de estas encontramos que no es posible implementar algunos de estos modelos, por diversas razones que se presentan a continuación.
El modelo BSM tiene algunos supuestos que difícilmente se cumplen para este estudio. En primer lugar, esta metodología asume que el activo subyacente sigue una distribución normal, lo que para este caso es difícil que se dé. En segundo lugar, la tasa libre de riesgo utilizada como tasa de descuento, asume riesgo neutral y se utiliza siempre que sea posible invertir en la opción y en el subyacente simultáneamente; sin embargo, para la evaluación de una opción de trasplante de riñón en un paciente no es posible realizar esta doble inversión. Otro inconveniente para aplicar esta metodología es el precio de ejercicio, ya que este se asume constante y determinístico en el tiempo y que la opción se ejerce sólo hasta el final de la vida de la opción (opción tipo europea); no obstante, este no es el caso de la opción de trasplante, donde el ejercicio es posible desde el momento en que la persona sufre IR hasta el final de la vida; adicionalmente el tiempo de ejercicio, el comportamiento del subyacente –tratamiento IR–, y el precio de ejercicio son estocásticos.
La metodología de árboles binomiales, aunque se considera un poco más flexible que BSM, para la valoración de la opción del trasplante de riñón, también presenta algunas limitaciones. Con esta herramienta no es posible determinar una tasa libre de riesgo como tasa de descuento, como tampoco es posible calcular la volatilidad, porque no se posee un portafolio réplica, un factor predominante o un indicador de rentabilidad.
Por las razones expuestas, se opta por evaluar la opción utilizando simulación Monte Carlo. Consecuente con esta metodología para la evaluación de la opción de trasplante de riñón, se siguen los siguientes pasos: en primer lugar, se construye un modelo de los costos del tratamiento de IR en un paciente (activo subyacente); en segundo lugar, se construye un modelo estocástico, para la valoración de los costos asociados al trasplante de riñón. Por último, se compara en cada momento del tiempo el valor presente del tratamiento de IR con el valor presente del trasplante de riñón, y se evalúa si es eficiente o no el ejercicio de la opción de trasplante.
La simulación Montecarlo da como resultado una distribución de probabilidad empírica del valor de la opción como consecuencia de todas las iteraciones, evaluando para cada trayectoria del subyacente el ejercicio de la opción de trasplante, así:
Payoff = Min (CIR, CTR)
De esta forma para cada ruta estocástica y en cada momento del tiempo se compara el valor presente de los costos de seguir haciendo el tratamiento de IR con el valor presente neto de hacer el trasplante de riñón y se escoge el mínimo de los dos.
2.2. Resultados del modelo de valoración
Definidas las variables de entrada, y después de crear un modelo de simulación Monte Carlo para los costos de tratamiento de un paciente que se mantiene bajo tratamiento IR y los costos de un paciente con trasplante de riñón, se determinan las variables de salida para el análisis del valor de la opción de trasplante y se corren 100.000 iteraciones de simulación Monte Carlo bajo el programa @RISK. Los resultados obtenidos se presentan a continuación.
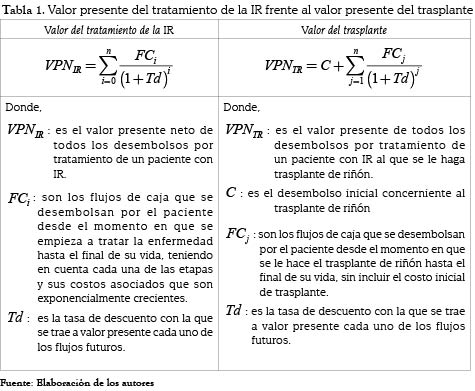
En primer lugar, se consideró el comportamiento del valor presente de los costos de un paciente con IR que se mantiene solo bajo tratamiento. Para cada una de las iteraciones simuladas se halla el valor presente (VP) de todos los desembolsos que se hacen por tratamiento de un paciente con IR en cada una de sus etapas, lo que da como resultado la distribución de probabilidad empírica presentada en la figura 1(a).
Los resultados muestran que el valor presente de los desembolsos de dinero (salidas de efectivo con signo negativo) en un paciente bajo tratamiento de IR oscilan entre $COP 0 y $COP 71'918.636 con un valor medio de $COP 17'805.114 y una desviación de $COP 10'792.450. Los valores que se acercan a cero corresponden al costo de los pacientes con esperanza de vida menor a un año. A medida que la esperanza de vida se incrementa, mayores son los costos asociados al tratamiento y, por ende, mayor el VPN, tal como se puede ver en la figura 1(b), donde se presenta el coeficiente de regresión de cada una de las variables de mayor significancia en el costo de un paciente en tratamiento de IR.
El tiempo en la etapa uno y la edad en la que se detecta la presencia de IR son las variables más significativas sobre el valor presente de los costos de un paciente con tratamiento por IR. Ambas, con un coeficiente de regresión positivo, lo que implica en el primer caso que a mayor tiempo en la etapa uno menor es el valor presente de los costos de tratamiento; esto, por tratarse de la etapa donde el tratamiento asociado es el menos costoso. Por otro lado, la tercera variable con mayor significancia, el tiempo que permanece el paciente en la etapa cuatro, presenta un signo negativo, por lo cual a mayor tiempo que permanezca el paciente en ella, mayor será el valor presente de los costos, esto porque es una etapa aproximadamente once veces más costosa que la primera.
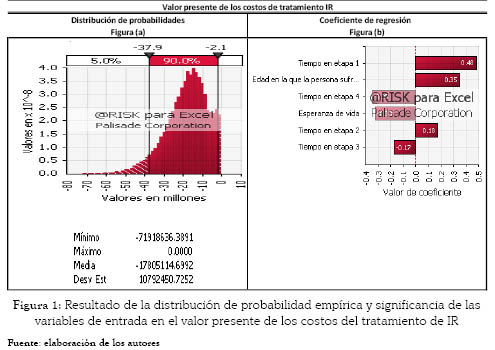
En segundo lugar, se consideróel comportamiento del valor presente de los costos de un paciente con insuficiencia renal trasplantado. Igual que para el caso anterior se simuló el valor presente de los desembolsos que se necesitarían por un paciente diagnosticado con IR, a quien se le practicó la cirugía de trasplante de riñón (ver figura 2 (a)). En este caso la única variable significativa e incidente en el valor presente de las erogaciones del trasplante son los años de vida postrasplante que tenga el paciente. Para este caso se asume que hay una independencia de esperanza de vida postrasplante y la esperanza de vida con tratamiento; en otras palabras, tanto el subyacente como el precio de ejercicio son variables estocásticas e independientes en su comportamiento. La relación que muestra la figura 2 (b) es que a mayor esperanza de vida, mayor es el valor presente de las erogaciones con trasplante; esta es la única variable estocástica incidente.
Conocido el comportamiento del valor presente de los desembolsos de dinero para un paciente bajo tratamiento de IR y el de los desembolsos de un paciente trasplantado es posible hacer el análisis del valor de la opción de practicar un trasplante a un individuo.
2.2.1. Valor sin flexibilidad Vs Valor con flexibilidad
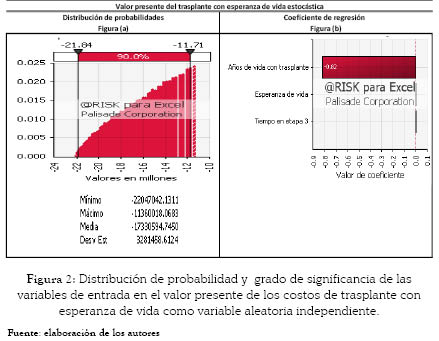
Hasta este momento se ha presentado la distribución de probabilidad empírica del valor presente de los costos de tratamiento de un paciente con IR, y del valor presente de los costos del trasplante de riñón. Por otro lado, es factible conocer la distribución del valor de la flexibilidad, es decir, considerando la posibilidad de realizar un trasplante de riñón cuando el valor presente de los costos de realizar este es menor que el valor presente de los costos del tratamiento, en un momento determinado, lo que significa, en términos de la teoría de OR que es viable el ejercicio de la opción.
El solo hecho de tener en cuenta la posibilidad de hacer el trasplante en cualquier momento (flexibilidad) indica que es posible disminuir y controlar los costos asociados a la enfermedad, gracias a la diferencia entre el valor presente de los costos de tratamiento y el valor presente de los costos postrasplante. De esta forma se reduce el costo máximo de $COP 71'918.636 a $COP 22'046.980 (figura 3).
En síntesis, al considerar la posibilidad de realizar un trasplante de riñón, se encuentra que los costos disminuyen significativamente, comparado con la continuación del tratamiento durante la vida del paciente.
Para conocer el valor de la opción se analiza la posibilidad de hacer o no el trasplante en cada momento del tiempo, de tal manera que se haga el trasplante siempre y cuando el valor presente de las erogaciones de este (CTR) sean menores al valor presente de los costos con tratamiento (CIR). De lo contrario, se continuará con el tratamiento.
Así, el valor que tendrá la opción de trasplantar un paciente estará dado por el ahorro en costos que se genera por el hecho de hacer el trasplante, en lugar de continuar con el tratamiento de IR, –en otras palabras, el valor de la opción a valor presente será el diferencial entre el valor con y sin flexibilidad–.
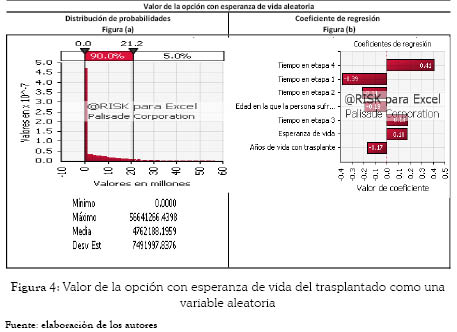
Los resultados presentados en la figura 4 (a) muestran que al considerar en cada uno de los períodos analizados la posibilidad de hacer un trasplante de riñón, la opción genera un ahorro promedio de $COP 4'762.188. Cuando no es viable realizar el trasplante la opción no tendrá valor, pero en el mejor de los casos se podría conseguir ahorros de hasta $COP 56'641.266.
En la figura 4 (b) se muestran las variables más significativas en el valor de la opción, donde el tiempo que un paciente podría pasar en la etapa cuatro bajo tratamiento de IR es la variable que más influye en el valor de la opción. Esto indica que mientras mayor sea el tiempo que permanece una persona en esta etapa, más alto es el valor de la opción, gracias a que los costos del tratamiento durante esta etapa son los más altos. Un comportamiento similar presentan el tiempo de permanencia en la etapa tres y la esperanza de vida.
Contrario es el efecto del tiempo que permanece una persona en la etapa uno, puesto que entre más tiempo pase en esta, menores serán los costos y no será viable ejercer la opción. La edad en la que la persona sufre insuficiencia renal y el tiempo que permanece en la etapa dos son variables que afectan el valor presente de los costos de la misma forma.
La esperanza de vida después del trasplante hace que el valor de la opción disminuya a medida que aumentan los años de vida postrasplante. Este resultado es muy lógico, pero puede ser contradictorio, puesto que es cierto que a mayor esperanza de vida, mayores serán los costos postrasplante, por lo tanto, menor el valor de la opción; no obstante, hay beneficios y costos ocultos, que no se tienen en cuenta en este modelo, como el valor de la vida misma o la productividad que puede tener un paciente trasplantado.
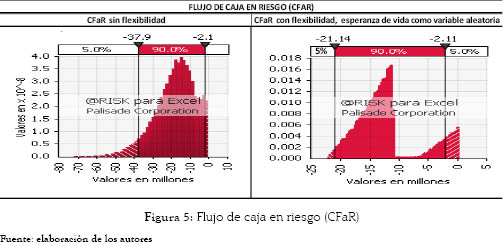
El valor presente del CFaR es el valor máximo de los costos a valor presente con un nivel de confianza del 95%. Para este caso tomamos la distribución de probabilidad empírica del valor presente de los costos de tratamiento del paciente con IR y lo comparamos con la distribución de probabilidad empírica del valor presente de los costos de tratamiento con flexibilidad, es decir, teniendo en cuenta el ejercicio de la opción, cuando sea eficiente hacerlo.
Al analizar el CFaR sin involucrar la flexibilidad se encuentra que representa un valor de $ COP 37,9 millones de pesos, lo que significa que, con un 95% de confianza, este es el costo máximo posible para mantener en tratamiento de IR a un paciente. El hecho de tener la posibilidad de ejercer la opción de trasplante disminuye considerablemente este valor presente de los costos en riesgo, como lo muestra la figura 5. Al tenerse en cuenta la flexibilidad, el CFaR baja a $COP 21'140.000, disminuyendo el costo máximo por paciente en un poco más de 16 millones de pesos.
3 CONCLUSIÓN
Considerando la Resolución 1740 del 20 de mayo de 2008 del Ministerio de Protección Social, las EPS se han visto abocadas a buscar metodologías que permitan gestionar y cuantificar el riesgo operativo, de negocio, mercado y crédito; y el riesgo en salud, de acuerdo con el Marco General del Sistema de Administración de Riesgos. Es así como en este trabajo se recomienda un análisis periódico de las personas a quienes se les detecta IR y la estimación de los costos asociados a continuar con el tratamiento o realizar un trasplante, de tal forma, que se puedan disminuir los riesgos en flujos de caja.
Tener en cuenta la flexibilidad de las decisiones en la valoración de proyectos reales afecta positivamente el resultado de los mismos. OR es una herramienta con aplicaciones al sector salud, que permite valorar las alternativas en los tratamientos médicos como es el caso de IR, donde el valor medio de un tratamiento puede bajar $COP 4'762.188 por paciente y en algunos casos lo beneficios pueden ser aún mayores.
Hacer un análisis detallado que contemple incluir una opción real en los flujos de caja asociados a enfermedades catastróficas, como es el caso de la IR, permite controlar el CFar de las erogaciones futuras obteniendo ahorros significativos como lo presentados en este artículo que ascienden aproximadamente a $COP 16'000.000 por paciente tratado.
REFERENCIAS
[1] L. Chicaíza, ''Valoración de primas de reaseguro para enfermedades catastróficas utilizando el modelo de Black-Scholes,'' Documentos de Trabajo Universidad Externado de Colombia 2005. [ Links ]
[2] M. A. Arango et al., ''Una aplicación de opciones reales a la valoración de contratos de leasing,'' Revista Ingenierías Universidad de Medellín, vol. 8, no. 15, pp. 93-103, 2009. [ Links ]
[3] M. Amram, y N. Kulatilaka, Opciones reales: evaluación de inversiones en un mundo incierto, Barcelona: Gestión 2000, 2000, 311 p. [ Links ]
[4] P. Bossaerts, ''Simulation Estimators of Optimal Early Exercise,'' Graduate School of Industrial Administration, 1989. [ Links ]
[5] M. C. Fu, ''Pricing of financial derivatives via simuation,'' presentado en Proceedings of the 1995 Winter Simulation Conference, 1995, pp. 126-132. [ Links ]
[6] M. C. Fu, y J. Q. Hu, ''Sensitivity analysis for Monte Carlo simulation of option pricing,'' Probability in the Engineering and Information Sciences, vol. 9, no. 3, pp. 417-446, 1995. [ Links ]
[7] J. F. Carriere, ''Valuation of the early-exercise price for derivative securities using simulations and splines,'' Insurance: Mathematics and Economics, vol. 19, no. 1, pp. 19-30, 1996. [ Links ]
[8] S. Raymar, y M. Zwecher, ''A Monte Carlo valuation of American call options on the maximum of several stocks,'' Journal of Derivatives, vol. 5, no. 1, pp. 7-23, 1997. [ Links ]
[9] A. Ibanez, y F. Zapatero, ''Monte Carlo valuation of American options through computation of the optimal exercise frontier,'' Journal of Financial and Quantitative Analysis, vol. 39, no. 2, pp. 253-275, 2004. [ Links ]
[10] T. E. Copeland, y V. Antikarov, Real options: a practitioner's guide, New York: Texere, 2001, 372 p. [ Links ]
[11] G. Alesii, ''Value at Risk (VaR) in Real Options Analysis,'' University of L'Aquila, 2005, p. 42. [ Links ]
[12] J. L. Arriagada, ''Aplicación de instrumentos financieros en el sector eléctrico,'' tesis de Magíster en Ciencias de la ingeniería, Pontificia Universidad Católica de Chile, 2001. [ Links ]
[13] G. Hayt, y S. Song, ''Handle with sensitivity,'' Risk, vol. 8, no. 9, pp. 94-99, 1995. [ Links ]
[14] C. Turner, ''Var as an industrial tool,'' Risk, vol. 9, no. 3, pp. 38-40, 1996. [ Links ]
[15] S. Godfrey, y R. Espinosa, ''Value at risk and corporate valuation,'' Journal of Applied Corporate Finance, vol. 10, no. 4, pp. 108-115, 1998. [ Links ]
[16] G. Dorris, y A. Dunn, ''Energy Risk Management: Making the shift to Earnings at Risk,'' Electric & Gas Trading Magazine, pp. 32, 2001. [ Links ]
[17] C. Blanco et al., ''Value at Risk: variations on a theme,'' Global Energy Business, no. mayo/junio 2001, pp. 12-19, 2001. [ Links ]
* Este artículo es producto de la Investigación, Análisis y Valoración del Riesgo Financiero (CFaR) en un Proyecto de Inversión a través de Opciones Reales, financiado por la Universidad de Medellín. Hace parte de los requisitos para optar al título de Magister en Administración Financiera en la Universidad EAFIT.