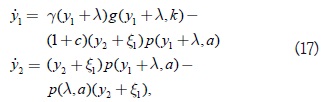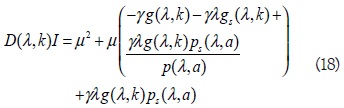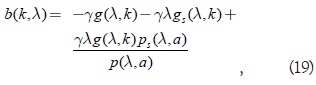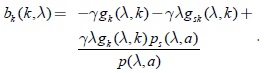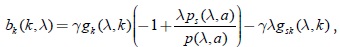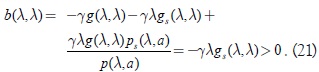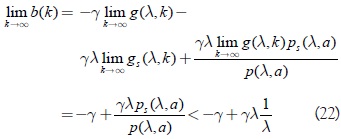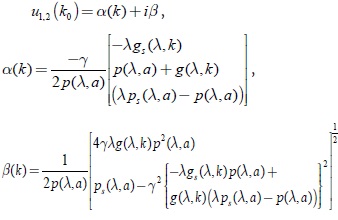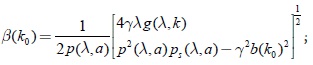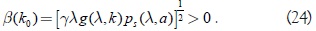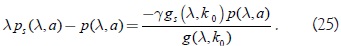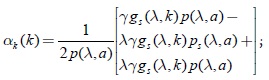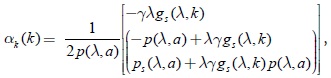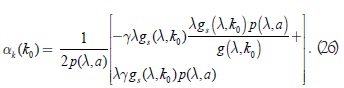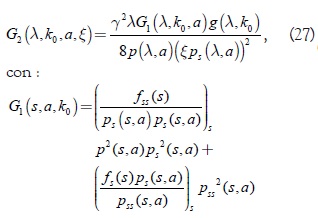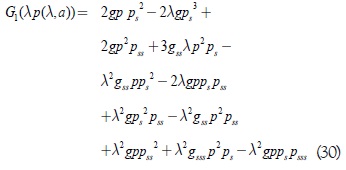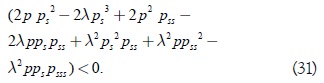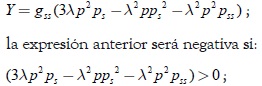Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Revista Ingenierías Universidad de Medellín
versão impressa ISSN 1692-3324versão On-line ISSN 2248-4094
Rev. ing. univ. Medellín v.10 n.19 Medellín jul./dez. 2011
ARTÍCULOS
DINÁMICA DE LA BIFURCACIÓN DE HOPF EN UNA CLASE DE MODELOS DE COMPETENCIA QUE EXHIBEN LA BIFURCACIÓN ZIP
Hopf Bifurcation Dynamic in a Class of Competence Model Exhibiting Zip Bifurcation
Carlos Mario Escobar Callejas*; José Rodrigo González Granada**
* M. Sc., Matemático, Universidad Tecnológica de Pereira, ccescobar@utp.edu.co, 3137300, FAX 3213206. Apartado Aéreo 097
** Ph. D., Matemático, Universidad Tecnológica de Pereira, jorodryy@utp.edu.co, 3137300, FAX 3213206. Apartado Aéreo 097
Recibido: 30/01/2010
Aceptado: 23/06/2011
RESUMEN
En el presente artículo de investigación se caracteriza el tipo de bifurcación de Hopf que se presenta en el fenómeno de la bifurcación de zip para un sistema tridimensional no lineal de ecuaciones diferenciales que satisface las condiciones planteadas por Butler y Farkas, las cuales modelan la competición de dos especies predadoras por una presa singular que se regenera. Se demuestra que en todas las variedades bidimensionales invariantes del sistema considerado se desarrolla una bifurcación de Hopf supercrítica lo cual es una extensión de algunos resultados sobre el tipo de bifurcación de Hopf que se forma en el fenómeno de la bifurcación de zip en sistema con respuesta funcional del predador del tipo Holling II, [1].
Palabras clave: bifurcación de Andrononov-Hopf, bifurcación de zip, exponente de Lyapunov.
Abstract
This research article characterizes the type of Hopf bifurcation occurring in the Zip bifurcation phenomenon for a non-linear 3D system of differential equations which meets the conditions stated by Butler and Farkas to model competition of two predators struggling for a prey. It is shown that a supercritical Hopf bifurcation is developed in all invariant two-dimensional varieties of the system considered, which is an extension of some results about the kind of Hopf bifurcation which is formed in the Zip bifurcation phenomenon in a system with functional response of the Holling-type predator.
Key words: Andrononov-Hopf bifurcation; Zip bifurcation; Lyapunov exponent.
INTRODUCCIÓN
En el estudio del problema concerniente a la validez del principio de la exclusión competitiva, para el caso de dos especies predadoras compitiendo por una presa que se regenera, el siguiente modelo ha sido considerado por varios autores [2]:
donde s(t) representa la población de especie de la presa y x1(t); x2(t) describen las poblaciones de las especies predadoras que compiten por la presa; (p=s,a1) (i = s,a1) representa la tasa de nacimiento o respuesta funcional Holling II del predador i; y g,(s,k) es la resistencia ambiental logística del medio al crecimiento de la presa. Las constantes γ; di > 0 son la tasa de crecimiento maximal de la presa y la tasa de muerte de la especie predadora i, respectivamente, y ai > 0 (i = 1,2) representa los parámetros de escala en la respuesta funcional del predador i. En este modelo se introducen las constantes:
que tienen teniendo el siguiente significado: x1 se incrementa si y sólo si s > λ; teniendo en cuenta que xi positivo (el lado derecho de la segunda o tercera ecuación de (1) es cero en (s = λi). En [2] se ha mostrado que las soluciones del sistema (1) correspondiente a valores iniciales positivos son acotadas y permanecen en el octante positivo y que la especie predadora i-ésima puede sobrevivir únicamente si 0 < λi < k; lo cual implica que mi > di. Además, los autores han estudiado el caso genérico con λ1 ≠ λ2, Farkas [3] ha tratado el caso λ2 = λ2 = k, donde ha establecido, en el caso a1 = a2 = a, que si k ≤ a + 2λ, entonces hay un segmento de línea de equilibrio estable para el sistema (1), mientras que si k > a + 2λ, entonces todas las tres especies sobreviven en un ciclo límite permanentemente, el cual surge, vía una bifurcación de Hopf, alrededor de cada punto de equilibrio del segmento Lk. En [1] se ha introducido el concepto de bifurcación zip para denotar el siguiente fenómeno. ''A bajos valores de la capacidad de carga k del ecosistema con respecto a la presa, una línea de equilibrio es un atractor del sistema, ella representa coexistencia estable de las tres especies. Si k es incrementado los equilibrios son continuamente desestabilizados, empezando por aquellos, que representan la dominancia del k-estratega sobre el r-estratega. Arriba de cierto valor de k, el sistema no tiene más equilibrios estables que representen coexistencia; sin embargo, un ciclo límite permanece representando la oscilación de coexistencia del r-estratega y la presa''. Además, Farkas [3] también ha establecido que la bifurcación de Hopf que se forma en los planos coordenados del sistema (1) es del tipo supercrítica. Recientemente en [3] se ha generalizado el fenómeno de zip a un sistema EDO cuatro dimensional con respuesta funcional generalizada Holling tipo III. En [4] se ha tratado la ocurrencia de la bifurcación de Hopf y zip en un sistema predador-presa (n+1)-dimensional con respuesta funcional Holling tipo II.
En [1, 5, 6] se ha mostrado que la mayoría de resultados concernientes al modelo (1) de Hsu y otros pueden ser investigados para toda clase de modelos del tipo dos-predadores-una-presa, modelo cuya característica común es que la tasa de desarrollo de la presa y la respuesta funcional del depredador son funciones arbitrarias que satisfacen ciertas condiciones naturales denominadas de Butler y Farkas y ellas son
A la función gs se le impone condiciones de uniformidad en [δ, S0] para cualquier δ, 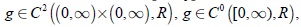 ,
, 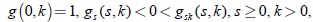 0 < δ < S0 y, la integral posiblemente impropia
0 < δ < S0 y, la integral posiblemente impropia 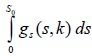 debe ser uniformemente convergente en [k0, ∞), para cualquier valor k0 > 0. Por último se impone la condición siguiente sobre p:
debe ser uniformemente convergente en [k0, ∞), para cualquier valor k0 > 0. Por último se impone la condición siguiente sobre p:
En este artículo se extienden algunos resultados de Farkas [1] sobre la caracterización del tipo de bifurcación de Hopf que se presenta en el fenómeno de la bifurcación de zip a la clase de sistemas dada por (1) satisfaciendo las condiciones planteadas en [1, 5, 6] con respuesta funcional del predador del tipo Rosenzweig dada por 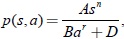 A > 0, B > 0, r > 0, D ≥ 0, 0 < n < 1; y tasa de desarrollo de la presa de forma exponencial algebraica
A > 0, B > 0, r > 0, D ≥ 0, 0 < n < 1; y tasa de desarrollo de la presa de forma exponencial algebraica 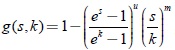 ; la cual es una generalización del modelo de Gilpin de resistencia ambiental del medio al crecimiento de la presa que incluye la rata de crecimiento logístico [6]. Finalmente, se elabora un ejemplo numérico, que corresponden a una clase del modelo degenerado no resoluble en forma algebraica, del tipo dos-predadores-una-presa, cuya característica es que la tasa de desarrollo de la presa y la respuesta funcional del depredador son funciones de forma exponencial algebraica del tipo Rosenzweig que satisfacen las condiciones de Butler y Farkas: También se hacen los retratos de fase de este sistema, los cuales muestran las distintas etapas de la bifurcación zip. Además, se evalúa la constante de Poincaré-Lyapunov mediante la generalización de la fórmula de Bautin-Farkas obtenida en [6]. Los resultados coinciden plenamente con la teoría existente.
; la cual es una generalización del modelo de Gilpin de resistencia ambiental del medio al crecimiento de la presa que incluye la rata de crecimiento logístico [6]. Finalmente, se elabora un ejemplo numérico, que corresponden a una clase del modelo degenerado no resoluble en forma algebraica, del tipo dos-predadores-una-presa, cuya característica es que la tasa de desarrollo de la presa y la respuesta funcional del depredador son funciones de forma exponencial algebraica del tipo Rosenzweig que satisfacen las condiciones de Butler y Farkas: También se hacen los retratos de fase de este sistema, los cuales muestran las distintas etapas de la bifurcación zip. Además, se evalúa la constante de Poincaré-Lyapunov mediante la generalización de la fórmula de Bautin-Farkas obtenida en [6]. Los resultados coinciden plenamente con la teoría existente.
2. RESULTADOS PRINCIPALES EN EL CASO λ1 = λ2 = λ1, A1 = A2 = A
2.1 Planteamiento del sistema
Se considera el sistema de ecuaciones diferencial tridimensional (1), bajo el supuesto de que existe una cantidad de presa común a ambos predadores, bajo la cual sus tasas de nacimiento y muerte llegan a ser iguales, es decir, existen un parámetro umbral λ, y un parámetro de escala a tales que a1 = a2 = a, y p(λ,a) = d1, = d2 = d. Tal es el caso de la competición de especies similares o también, de la competición intraespecífica entre la misma especie predadora. Las hipótesis adoptadas implican que el sistema (1) toma la forma siguiente
Es importante observar que el segmento Lk es no vacío, es decir, aparte de las soluciones triviales existirán soluciones de interés biológico cuando λ1 = λ2 = λes decir, se satisface la condición p(λ,a) = p(λ,a1) = p(λ,a2) = d.
2.2 Equilibrios del sistema
Los equilibrios del sistema (10) son Q1(0,0,0), Q2(k,0,0), y los puntos del segmento de línea recta Lk en el octante positivo del espacio R3 dado por
Los puntos que pertenecen a Lk se denotan con (λ ξ1, ξ2). Los puntos extremos del segmento de línea, es decir, los equilibrios en los planos x1 = 0 y x2 = 0, respectivamente, son:
Por linealización se observa que Q1 es inestable y que Q2 es asintóticamente estable para k < λ inestable para k < λ . Se conoce [5, 7] que k < λ, es una condición necesaria para la supervivencia de cada predador. Además, en lo que sigue se asume que el sistema (1) satisface las condiciones Butler y Farkas y que la siguiente desigualdad se satisface:
0 < λ = λ1 = λ2 < k (13)
Por la condición (5), si k es menor que λ, entonces Lk es vacío, y si k = λ, entonces Lk consta solo del origen Q1. Por lo tanto, nos restringimos al estudio de los puntos sobre el segmento de línea recta Lk.
Al dividir la tercera ecuación por la segunda ecuación del sistema (10) se obtienen las ecuaciones de las trayectorias que satisfacen la ecuación diferencial 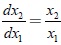 . Así se consigue que la función
. Así se consigue que la función 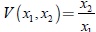 sea una integral primera del sistema (10). Como una consecuencia se tiene que los planos:
sea una integral primera del sistema (10). Como una consecuencia se tiene que los planos:
son superficies invariantes del sistema (10), donde c es una constante arbitraria no negativa; es claro que estas superficies particionan completamente el octante positivo es decir, a través de cada punto en este octante pasa una y sólo una superficie de la familia (14). Se fija el valor de c y se considera la restricción del sistema (10) a la variedad invariante (14) parametrizada por s y x1
Los equilibrios del sistema (15) son (s,x1) = (0,0), (s,x1) = (k, 0) y el punto singular en el cual la línea Lk intercepta (14). Así el punto de intersección se denota con (λ ξ1, ξ2) donde ξ2 = cξ1, y ξ1 dada por
Igualmente podemos ver que los equilibrios (0,0) y (k, 0) son inestables. Si se estudia la estabilidad del equilibrio P(k) = (λ, ξ1) del sistema (15), donde ξ1 es la solución positiva de (16), la capacidad de carga k puede ser considerada como un parámetro de bifurcación. Al variar k > λ, la línea de equilibrio Lk se mueve paralelamente y corta los planos (14) en diferentes puntos . (ξ1 = ξ1 (c,k), ξ2 = ξ2 (c,k)). Se usa la notación abreviada ξ1 = ξ1 (c,k) en algunas ocasiones. El siguiente teorema está relacionado con el sistema (15) sobre la variedad definida por (14).
Teorema 1. Existe un único k0 > k tal que si , λ < k < k0 el equilibrio (λ, ξ1 (c,k)) del sistema (15) es asintóticamente estable con región de atractividad Ls = {(s,x1): s > 0, x1 > 0}; en k0 el sistema está bajo una bifurcación de Hopf supercrítica o subcrítica, dependiendo del signo de la constante de Poincaré-Lyapunov. Si la bifurcación de Hopf es supercrítica (constante de Lyapunov negativa), existe un δ > 0 tal que para k0 < k < k0 + δ, en el sistema (15) tiene una única trayectoria cerrada dentro de una vecindad de (λ, ξ1 (c,k0)) rodeando este punto de equilibrio, la cual es orbital asintóticamente estable. En particular el sistema está bajo una bifurcación de Hopf supercrítica si la respuesta funcional del predador es del tipo Rosenzweig.
Prueba: Se mueve el origen al punto de equilibrio (s,x1) = (λ, x1) del sistema (15) por la transformación de coordenadas y1 = s – λ, y2 = x1 – λ1, por lo tanto:
donde ξ1 ha sido expresado en función de c, en la expresión (16). El sistema (17) tiene (0,0) como un punto de equilibrio para ξ1 ≥ 0 y k > λ; si se linealiza el sistema (17) en el origen, el polinomio característico del sistema linealizado será:
Aquí el término constante del polinomio característico (18) es positivo como consecuencia de la desigualdad (13), la propiedad (5) de la función g(λ, k) y la propiedad (7) de p(s,a), por lo tanto, la estabilidad depende básicamente del signo del coeficiente lineal en el polinomio característico. En lo que sigue, se muestra que existe un punto del parámetro k0 > λ, para el cual se cumple que el coeficiente de μ en (18) es positivo, si y sólo si k < k0. Así que el origen es asintóticamente estable para λ < k < k0, e inestable si k < k0: La actractividad global se sigue de [2, 7-9], además, k0 es independiente de c; por lo tanto, toda superficie de la familia (14) bifurca en el mismo punto k0; en particular en los planos coordenados xi = 0; i = 1,2.
El siguiente argumento muestra la existencia y unicidad de k0 para las funciones propuestas, g(s,k) y p(s,k) en el modelo:
Sea b(k) la función que define el coeficiente de μ en el polinomio característico, es decir:
se ve en primer lugar que b(k) es una función estrictamente decreciente, en efecto:
Agrupando términos:
como gi(λ,k) es positiva, por lo tanto el signo de b(k,λ) depende básicamente del signo del término 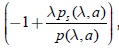 , ya que por la condición (3) γλgsk(λ,k) > 0. Pero
, ya que por la condición (3) γλgsk(λ,k) > 0. Pero 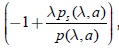 , por la condición (9) para p; por lo tanto, se puede concluir que:
, por la condición (9) para p; por lo tanto, se puede concluir que:
bk(k,λ) < 0 (20)
Adicionalmente a la desigualdad anterior, se muestra que b(k) cambia de signo por la condición (3) y (5) para la función g. Se tiene, en primer lugar, que b(λ) > 0:
En segundo lugar, aplicando la condición (4) para g y la condición (9) para p, se tiene que:
De las condiciones (20) - (22) se deduce la existencia y unicidad de k0 que satisface las condiciones del teorema 1. A continuación se verifican las condiciones para la existencia de la bifurcación de Hopf y se generaliza la fórmula de Bautin para el cálculo de la constante de Poincaré-Lyapunov, la cual sirve para la determinación del tipo de bifurcación crítica que se presenta en el origen del sistema (10). Además, para un subconjunto bastante general del espacio de parámetros del modelo, se demuestra que se presenta siempre un tipo de bifurcación de Hopf supercrítica.
Para la linealización del sistema (17) en P(0,0); los valores propios u1,2(k0) son de la forma:
Claramente de las propiedades (3), (7) y (8); se tiene que para λ < k < k0, α(k) < 0. En k = k0; se satisface la ecuación, 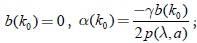 ; por lo tanto se tiene que
; por lo tanto se tiene que
α(k0) = 0, (23)
además β(k0) se puede escribir como
sustituyendo el valor de b(k0) = 0, en la expresión anterior se tiene:
Por otro lado la condición α(k0) = 0 implica que:
Diferenciando α(k) se obtiene:
factorizando algunos términos de la expresión anterior se concluye que:
sustituyendo la expresión (25) en la igualdad anterior:
Las condiciones (3), (4) y (6) implican que αk(k0) es mayor que cero; así, las condiciones (23), (24) y (26) del teorema de bifurcación de Andronov Hopf se cumplen según [6]. Para probar que la bifurcación es supercrítica nosotros usamos la expresión del exponente de Lyapunov ()
donde f(s) = sg(s,k0), s = λ.
La cual es obtenida mediante el procedimiento dado en [7, 8] el cual lleva el sistema (17) a la forma estándar sobre la variedad invariante determinada por ξ [6]:
En [6] también se demuestra que si se tiene una respuesta funcional del predador del tipo Rosenzweig p(s, a) y una tasa de desarrollo de la presa con forma exponencial algebraica 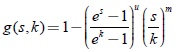 , entonces se tienen las siguientes condiciones monótonas, adicionales a las planteadas por Butler y Farkas para la tasa de desarrollo de la presa:
, entonces se tienen las siguientes condiciones monótonas, adicionales a las planteadas por Butler y Farkas para la tasa de desarrollo de la presa:
gss(λ,k0) < 0, gsss(λ,k0) < 0, (28)
y para la respuesta funcional del predador
pss(s,a) < 0, gsss(s,a) > 0. (29)
Si se tienen en cuenta adicionalmente las desigualdades (28) y (29) en las condiciones de Bultter Farkas es posible mostrar que G2 < 0; basta verificar que G1(λp(λ,a)) < 0, ya que tienen el mismo signo. Expandiendo G1(λp(λ,a)) se tiene la siguiente expresión:
Teniendo en cuenta la restricción sobre el dominio de parámetros con k > λ, se puede garantizar que cada uno de los términos de G1(λp(λ,a)) tendrán el mismo signo en el dominio considerado. Agrupando los términos que contienen la función g de G1(λp(λ,a)), se obtiene:
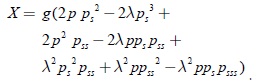
La expresión anterior será negativa si:
Al evaluar la desigualdad anterior para la respuesta funcional tipo Rosenzweig se tiene
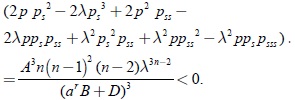
Por lo tanto, se concluye que los términos que contienen la función g en (30) son menores a cero. Agrupando los términos que contienen la función gss en (30), se obtiene:
evaluando la desigualdad anterior con respuesta funcional del tipo Rosenzweig se obtiene
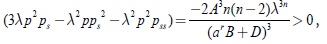
por lo tanto, se puede afirmar que la suma de los términos que contienen la función gss en G1(λp(λ,a)) es negativa. Finalmente considerando el último término, en G1(λp(λ,a)) se tiene que Z = gsss(λ2p2ps) < 0.
La expresión anterior es negativa si (λ2p2ps) > 0; evaluando la desigualdad anterior con respuesta funcional tipo Rosenzweig se tiene
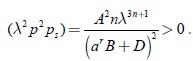
Por lo tanto, podemos afirmar que el último término en G1(λp(λp(λ,a)) es negativo con lo cual se termina la prueba del teorema 1.
La expresión (27) generaliza la fórmula G1(s,a,k0) obtenida por Butler y Farkas, la cual es válida en los planos coordenados del sistema (10); G2(λ,k0,a,ξ) y es válida en todas las variedades bidimensionales transversales del sistema al segmento Lk, en particular en los planos coordenados. Note que de la expresión (27) y (19) se deduce que todos los puntos de equilibrio del sistema (17) tienen el mismo signo para la constante de Poincaré-Lyapunov; significa que la línea de equilibrio está formada por puntos 3-atractores o por puntos 3-repulsores del sistema y que, además, todas las variedades bidimensionales del sistema presentan el mismo tipo de bifurcación de Hopf, supercrítica o subcrítica y oscilan con el mismo valor del parámetro de bifurcación k0 dependiendo del signo de la constante de Poincaré-Lyapunov. Cuando k < k0, cada equilibro sobre Lk es igualmente probable, incluyendo los que representan la ausencia de uno de los predadores. En k = k0 el sistema empieza a oscilar. Este fenómeno es llamado ''The paradox of enrichment''. Cada trayectoria cerrada sobre un cilindro que rodea a Lk es igualmente probable y su período aproximado de oscilación es 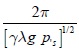 , a lo largo de todas órbitas cerradas sobre el cilindro que rodea a Lk. Finalmente se concluye que en este tipo de modelo bajo las restricciones planteadas, si la respuesta funcional del predador es del tipo Rosenzweig y la tasa de desarrollo de la presa es de forma exponencial algebraica, el exponente de Lyapunov es siempre negativo, lo cual significa que en todas las variedades bidimensionales invariantes del sistema se desarrolla una bifurcación de Hopf supercrítica.
, a lo largo de todas órbitas cerradas sobre el cilindro que rodea a Lk. Finalmente se concluye que en este tipo de modelo bajo las restricciones planteadas, si la respuesta funcional del predador es del tipo Rosenzweig y la tasa de desarrollo de la presa es de forma exponencial algebraica, el exponente de Lyapunov es siempre negativo, lo cual significa que en todas las variedades bidimensionales invariantes del sistema se desarrolla una bifurcación de Hopf supercrítica.
3. MODELO DEGENERADO
En esta sección presentamos un modelo degenerado con respuesta funcional tipo Rosenzweig. A continuación se presenta la respuesta funcional p(s,a) de los predadores y la resistencia ambiental g(s,k) de la presa, las cuales son dadas por
3.1 Sistema bidimensional
La expresión p(λ,a1) = d1 toma la forma:
Las condiciones b(k2) = 0, b(kp) = 0, determinan los parámetros de la bifurcación de Hopf para una de las variedades invariantes bidimensionales del sistema (10) en el plano coordenado s – x1, respectivamente
Resolviendo las ecuaciones b(k2) y bp(kp); para k se obtiene
k2 = kp = 12.8822.
La constante de Poincaré-Lyapunov G, en s = λ, a = a1, k0 = k2 = kp, definida por la fórmula (30), para el plano coordenado s – x1 está dada por G1(λ,k2,a1) = –0.145066, donde λ = 10, a1 = 0.581139, k2 = 12.8822.
Esta expresión muestra que el equilibrio es un punto espiral débil 3-atractor del sistema de orden uno, y la bifurcación de Hopf que se presenta es supercrítica. La localización del punto de equilibrio sobre esta superficie tiene coordenadas P1(k) = (λ,ξ1) y el parámetro ξ1 está dado por la siguiente expresión:
La constante de Poincaré-Lyapunov G2, por el método de Salvadori-Negrini, en la superficie invariante del sistema (10) caso a1 = a2 = a, y c = 1, está dada por
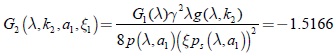
3.2 Sistema tridimensional
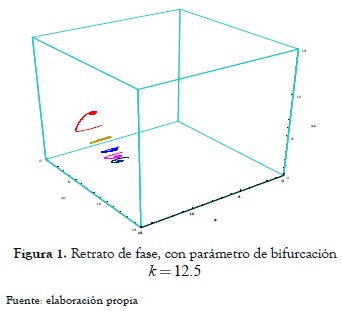
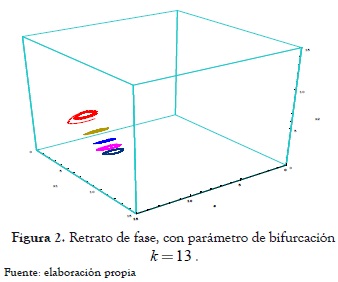
En las figura 1 y 2 se presentan los retratos de fase del sistema (10) para los distintos valores del parámetro de bifurcación seleccionados a propósito para mostrar cómo la bifurcación de Hopf que se presenta en los planos coordenados en este tipo de modelo es un caso límite de la bifurcación de Hopf que se desarrolla en todas las variedades bidimensionales del sistema en la bifurcación de zip (ver Escobar [6]).
Las ecuaciones paramétricas de los segmentos de línea Lk están dadas para los siguientes casos:
Para k = 12.5, se tiene
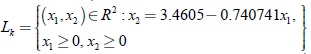
El segmento de línea de equilibrios Lk es asintóticamente estable y ellos representan coexistencia entre el predador uno y la presa. En la figura 1 se presenta el retrato de fase correspondiente al valor del parámetro de bifurcación k = 12.5. Se observa que los puntos alrededor de la línea de equilibrio Lk tienden asintóticamente hacia ella y por lo tanto el segmento Lk es un atractor del sistema.
Para k = 13, se tiene
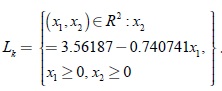
Ahora el segmento de línea Lk es un conjunto repulsor del sistema en el cuadrante positivo, lo cual indica inestabilidad del conjunto de equilibrios Lk ; sin embargo una familia de ciclos límite puede aparecer el cual es orbital asintóticamente estable, lo que significa coexistencia entre el r-estratega y el k-estratega y que, además, se desarrolla en las variedades invariantes del sistema una bifurcación de Hopf del tipo supercrítico como se muestra en las figuras 1 y 2.
4. CONCLUSIÓN
Se demuestra en este tipo de modelos bajo las restricciones planteadas, que si la respuesta funcional del predador es del tipo Rosenzweig y la tasa de desarrollo de la presa es de forma exponencial algebraica 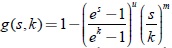 , la cual incluye la rata de crecimiento logístico del modelo de Gilpin, el exponente de Lyapunov es siempre negativo, lo que significa que en todas las variedades bidimensionales invariantes del sistema se desarrolla una bifurcación de Hopf supercrítca.
, la cual incluye la rata de crecimiento logístico del modelo de Gilpin, el exponente de Lyapunov es siempre negativo, lo que significa que en todas las variedades bidimensionales invariantes del sistema se desarrolla una bifurcación de Hopf supercrítca.
5. AGRADECIMIENTO
Agradecimiento al Profesor Miklós Farkas por su amable y acertada orientación en esta investigación.
REFERENCIAS
[1] M. Farkas, ''Zip bifurcation in a competition model,'' Nonlinear analysis, vol. 8, no. 11, pp. 1295-1309, 1984. [ Links ]
[2] B. Hassard et al., Theory and Applications of Hopf Bifurcation, Cambridge: Cambridge University Press, 1981, 313 p. [ Links ]
[3] M. Farkas, Periodic motions, New York: Springer-Verlag New York, 1994, 593 p. [ Links ]
[4] M. Farkas et al., ''Velcro Bifurcation in Competition Models with Generalized Holling Functional Response,'' Miskolc Mathematcal Notes, vol. 6, no. 2, pp. 165-168, 2005. [ Links ]
[5] G. Butler, ''Competitive predator-prey systems and coexistence,'' presentado en Population Biology Proceedings, Berlin: Springer-Verlag, 1983. [ Links ]
[6] C. Escobar, ''Modelo original de tipo exponencial algebraico que exhibe la bifurcación zip,'' tesis de Maestría, Universidad de Antioquia, Medellín, 2003. [ Links ]
[7] S. B. Hsu et al., ''Competing predators,'' SIAM J. appl. Math, vol. 35, no. 4, pp. 617-625, 1978. [ Links ]
[8] P. Negrini, y L. Salvadori, ''Atractivity and Hopf bifurcation,'' Nonlinear Analysis, vol. 3, pp. 87-100, 1979. [ Links ]
[9] A. L. Koch, ''Competitive coexistence of two predators utilizing the same prey under constant environmental conditions,'' Journal of Theoretical Biology, vol. 44, no. 2, pp. 387-395, 1974. [ Links ]