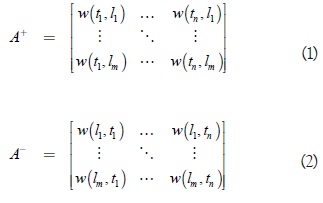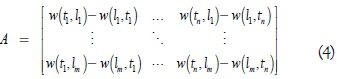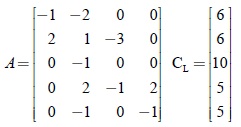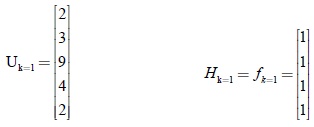Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Revista Ingenierías Universidad de Medellín
versão impressa ISSN 1692-3324versão On-line ISSN 2248-4094
Rev. ing. univ. Medellín v.10 n.19 Medellín jul./dez. 2011
ARTÍCULOS
UN MÉTODO COMPUTACIONAL PARA LA DETECCIÓN Y CARACTERIZACIÓN DE CONFLICTOS EN REDES DE PETRI
A Computational Method for Detection and Characterization of Conflicts on Petri Nets
Pedro Luis Ángel Restrepo*
* Ingeniero mecánico, magíster en Ingeniería Mecatrónica, Grupo de Desarrollo e Investigación en Sistemas Informáticos y Diseño Electrónico aplicado a las Nuevas Tecnologías En Salud, DISIDENTES, Universidad de Antioquia. E-mail: plangel@udea.edu.co. Bloque 20 oficina 405, Calle 67 Número 53-108. Ciudad Universitaria, Medellín, Colombia.
Recibido: 30/11/2010
Aceptado: 18/08/2011
RESUMEN
En este artículo se presenta un método que permite detectar la presencia de conflictos en modelos construidos con base en el formalismo matemático de las Redes de Petri. Se muestra cómo mediante la aplicación de un algoritmo que toma como datos de entrada la representación matricial de una red, es posible detectar la existencia de conflictos y caracterizar su tipo, identificando, además, el conjunto de elementos que los presentan. La utilización del método propuesto se ilustra usando una Red de Petri Ordinaria.
Palabras clave: redes de Petri, detección de conflictos, algoritmos.
Abstract
This article describes a method which allows detecting the presence of conflicts in models constructed based on the mathematical formalism of Petri Nets. The article shows how it is possible to detect the existence of conflicts and characterize their type through the application of an algorithm which takes the matricial representation as entry data, identifying also the number of elements which represent them. The use of the method proposed is shown using an ordinary Petri Net.
Key words: Petri nets; conflict detection; algorithms.
INTRODUCCIÓN
Las Redes de Petri (RdP) son una herramienta matemática de amplia utilización en la construcción de modelos; se han utilizado con éxito en áreas tan diversas como sistemas de control industrial, programación concurrente y en paralelo, sistemas de cómputo multiproceso, programación basada en lógica, redes de área local, filtros digitales, modelos de toma de decisiones, redes neuronales, etc. [1-3].
Las RdP permiten la simulación de sistemas concurrentes, paralelos y asíncronos; su gran aceptación tiene origen en su utilización como una herramienta gráfica de fácil empleo en la construcción de modelos, permitiendo su interpretación, comprensión y modificación de manera clara e intuitiva; dichos modelos gráficos son susceptibles de ser transformados a estructuras algebraicas, y permiten ser estudiados analíticamente [4].
La construcción, simulación, verificación y puesta a punto de los modelos construidos a partir de esta técnica formal se basa en el uso de herramientas informáticas denominadas bajo el término genérico de simuladores de Redes de Petri. Es de anotar que una revisión del estado del arte permite concluir que una tarea crítica que dichos simuladores no llevan a cabo de manera satisfactoria es la detección de los conflictos presentes a lo largo de la simulación del sistema representado por la red.
En este orden de ideas, este trabajo presenta un método computacional por el cual, mediante la representación matricial de una Red de Petri y la aplicación de un algoritmo propuesto por el autor, es posible detectar la presencia de conflictos, realizar la caracterización de los mismos e identificar los elementos de la red que los presentan.
El artículo está organizado como sigue: en la segunda parte se presentan los principios de la teoría de las RdP, en la tercera se deducen los principios matemáticos de la determinación de conflictos en RdP y se introduce un algoritmo para su detección, en la cuarta parte se aplica el mencionado algoritmo a una Red de Petri. Finalmente se exponen las conclusiones y recomendaciones.
1. REDES DE PETRI
Las Redes de Petri son una herramienta que permite la representación de sistemas a través de modelos en forma de estructuras matemáticas. Mediante el análisis de estas estructuras se puede obtener información importante acerca del comportamiento, propiedades, morfología y dinámica del sistema objeto de estudio [4, 5].
Las RdP tienen su inicio en la tesis doctoral de Carl Adam Petri, Comunicación con Autómata, presentada en la Universidad Técnica de Darmstadt en 1962. Desde entonces, se han desarrollado variaciones que han introducido nuevos elementos y técnicas que incrementan el poder de representación de los modelos construidos con dicha técnica formal. Estas variaciones son denominadas genéricamente como Redes de Petri Extendidas, las más comunes son: Redes con Arcos Habilitadores e Inhibidores, Redes con Tiempo y Redes Estocásticas. Igualmente, existen técnicas en las cuales durante la ejecución de la red se ven alterados algunos de sus componentes; estos tipos de red son conocidos como Redes de Alto Nivel e incluyen las Redes Coloridas, las Predicado/Transición y las Redes con Marcas Individuales [6].
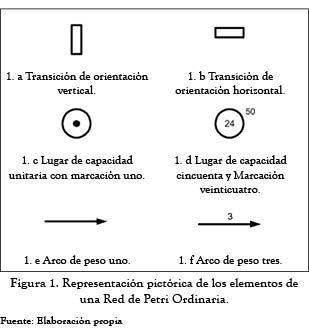
El método propuesto en este documento se restringe a la formulación fundamental de las Redes de Petri conocidas como Redes de Petri Ordinarias; por tanto, a lo largo de este texto el término RdP debe interpretarse como Red de Petri Ordinaria. Informalmente, una Red de Petri Ordinaria es una estructura matemática compuesta por tres tipos de elementos: lugares, transiciones y arcos. Por convención, los lugares simbolizan los aspectos pasivos del sistema, las transiciones se asocian a los aspectos dinámicos, y los arcos representan la relación de causalidad entre los elementos pasivos y los activos; la definición formal de una Red de Petri Ordinaria se presenta a continuación:
Definición 1: Red de Petri Ordinaria:
Una Red de Petri Ordinaria es una 5-Tupla, 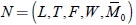 donde:
donde:
L = {l1, l2, ...,lm} es un conjunto finito de lugares.
T = {t1,t2,...,tn}es un conjunto finito de transiciones, de tal manera que L ∩ T = φ.
F ⊆ (L × T) ∪ (T × L) es un conjunto finito de arcos.
W:F →{1,2,...,f} es una función que asocia un peso a cada arco.
M0:L→{1,2,...,f} es la marcación inicial de los lugares.
Las RdP tienen una representación gráfica elaborada a partir de los elementos que la constituyen; esta representación consiste en un conjunto de círculos, rectángulos, marcas y arcos dirigidos. Por convención, los círculos representan a los lugares, y los rectángulos, a las transiciones; la función de los arcos es establecer las relaciones entre lugares y transiciones; por lo tanto, un arco solo puede ser trazado entre una transición y un lugar, o viceversa. Si el arco se traza a partir de un lugar a este lugar, se conoce como de entrada para la transición; si el arco parte de una transición, el lugar de destino se denomina lugar de salida. La figura 1 ilustra los elementos utilizados en la representación gráfica de una RdP.
2.1. Dinámica de las Redes de Petri
La dinámica del sistema representado por la red se simboliza mediante el movimiento de las marcas; este efecto se produce cuando una transición habilitada para disparar (firing) ejecuta un disparo modificando la marcación de sus lugares de entrada y de salida. Las condiciones de habilitación y disparo de las transiciones son: [1]
Definición 2: Condiciones de habilitación y disparo de las transiciones en una Red de Petri Ordinaria
1. Una transición está habilitada si cada lugar de entrada (l) está marcado con m(l) marcas y m(l) ≥ w(l,t) donde w(l,t) es el peso del arco entre l y t.
2. Una transición habilitada puede disparar o no, dependiendo de si el evento que representa ocurre o no. Una transición no habilitada no puede disparar.
3. El disparo de una transición t remueve w(l,t) marcas de cada lugar de entrada l y adiciona w(t,l) marcas a cada lugar de salida l de t.
Cuando en una RdP existen transiciones con lugares de salida de capacidad finita, la habilitación de dichas transiciones requiere como condición adicional que los lugares de salida tengan una capacidad libre para recibir las marcas. Esta limitación se conoce como condición de disparo estricto [1].
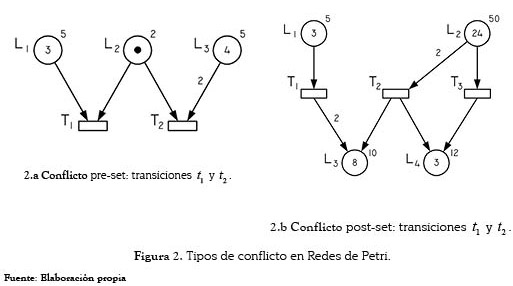
2.2. Conflictos en Redes de Petri
Una transición habilitada para disparar puede estar imposibilitada para hacerlo debido a la existencia de un conflicto. Un conflicto es una situación en la cual, dado un conjunto de transiciones habilitadas para disparar, el disparo de un subconjunto de dichas transiciones deshabilita otro subconjunto. Los conflictos en un modelo representado por RdP significan la necesidad de tomar decisiones sobre la realización de eventos que no pueden ocurrir de manera simultánea, es decir, los eventos representados por las transiciones en conflicto son mutuamente excluyentes.
Existen dos tipos de conflicto: el conflicto pre-set que se caracteriza porque los lugares de entrada de las transiciones que intentan disparar no contienen las marcas necesarias para poder llevar a cabo el disparo de la totalidad de dichas transiciones, y el conflicto post-set que ocurre cuando los lugares de salida de las transiciones no poseen la capacidad libre disponible para almacenar las marcas aportadas por el disparo de las transiciones; los conflictos Post-set sólo ocurren en RdP con lugares de capacidad finita. Las figuras 2.a y 2.b ilustran los conflictos pre-set y post-set, respectivamente.
En un modelo, la existencia de conflictos está determinada tanto por el nivel de abstracción como por las características del sistema modelado, por ejemplo, pueden presentarse conflictos entre los departamentos de producción y de marketing de una organización, así como en la asignación de recursos en una especificación del flujo de trabajo (workflow) en una planta, e inclusive en la asignación de camas en hospitales para los diferentes tipos de pacientes [7, 8].
La detección y resolución de conflictos es un aspecto de gran importancia en el estudio de modelos de sistemas basados en RdP, fundamentalmente porque si los conflictos no son gestionados de manera eficiente el rendimiento del sistema se verá comprometido. En presencia de conflictos, se requiere una política de solución de los mismos que depende tanto de las características del sistema modelado como del objetivo de la simulación que se esté llevando a cabo [9]. En la validación de un modelo, la estrategia de resolución de conflictos es tan importante como su detección [7], y la relación entre estos dos aspectos determina la consistencia y validez del modelo. [10].
Las aplicaciones de la detección y la resolución de los conflictos trasciende a las RdP ordinarias; por ejemplo, en [11] se utiliza la existencia de conflictos en Redes de Petri Jerárquicas para administrar la preeminencia en la aplicación de reglas heurísticas en un sistema de control inteligente para la detección de correo spam, mientras que en [12] se muestra cómo la resolución de conflictos en un sistema de manufactura flexible puede ser llevada a cabo con un modelo de RdP difusas y coloridas.
La presencia de conflictos es una propiedad dinámica de la red, por lo cual se hace necesario la utilización de un enfoque algorítmico para abordar el problema; es así como en [13] se presenta un método para la detección de conflictos basado en invariantes de lugar, y en [14] se plantea un algoritmo basado en matrices para la resolución de conflictos, con aplicación en la planificación en un flujo de trabajo. En este contexto, el algoritmo para la detección y caracterización de conflictos presentado en este trabajo se basa en la representación matricial de las RdP
2.3. Representación Matricial de las Redes de Petri
Una representación alternativa de las RdP se basa en su formulación matricial, en la cual se utilizan las relaciones existentes entre los componentes de la RdP para definirla por medio de matrices; este enfoque es equivalente a la forma tradicional. El estudio de las propiedades, dinámica y características de las RdP se basa en el enfoque matricial [4]; la definición matricial de una RdP se presenta a continuación:
Definición 3: Representación matricial de una Red de Petri Ordinaria:
Una Red de Petri Ordinaria se representa matricialmente por una 5-Tupla, N = (L, T, A+, A–, U) donde:
L = [l1, l2,...,lm]T es un vector que representa el conjunto de lugares.
T = [t1, t2,...,tn]T es un vector que representa el conjunto de transiciones.
A+: Es una matriz de orden |L |× |T | que registra el peso del arco de las transiciones a cada lugar de salida.
A–: Es una matriz de orden |L |× |T | que registra el peso del arco de las transiciones a cada lugar de entrada.
U = [u1, u2, ..., un]T es un vector que representa la marcación del conjunto de lugares.
De forma extendida las matrices A+ y A– se presentan en las ecuaciones (1) y (2) respectivamente.
Desde el enfoque matricial, la dinámica de una RdP se representa por la ecuación de disparo presentada en la ecuación 3, que describe la relación entre un estado dado de la red y el estado posterior a la realización de un disparo válido.
Uk+1 = A . fk + Uk (3)
La ecuación de disparo involucra una matriz de Incidencia A, que se obtiene de la resta algebraica de las matrices A+ y A–, como se presenta de forma extendida en la ecuación (4). El enfoque matricial no representa de manera precisa la existencia de ciclos entre elementos de la red, debido a que un ciclo implica una transición que retira y agrega simultáneamente marcas a un lugar, y la matriz A registra solo el aporte efectivo del disparo de la transición sobre cada lugar.
En la ecuación 3, los vectores Uk y Uk+1 registran, respectivamente, la marcación de los lugares antes y después de un disparo. Las transiciones que disparan se almacenan en el vector fk, en este vector una entrada de valor uno (l) representa una transición que dispara mientras que el valor cero (0) se asocia a aquellas que no disparan. En la medida que un evento puede estar habilitado para ocurrir pero no ocurrir realmente, se utiliza el vector Hk para registrar la totalidad de las transiciones habilitadas para disparar, y por tanto fk ≤ Hk.
3. DETECCIÓN Y CARACTERIZACIÓN DE CONFLICTOS EN REDES DE PETRI
Para detectar la existencia de conflictos es necesario realizar una simulación del disparo de las transiciones que se pretende disparar; el resultado de dicho disparo se obtiene al aplicar la ecuación 3 y llevar el resultado al vector Sk, tal como se presenta en la ecuación 5. Posteriormente se realiza el análisis de detección y caracterización de los conflictos. Las características de cada tipo de conflicto involucran un análisis diferente [15, 16].
Sk = A . fk + Uk (5)
3.1 Detección de conflictos post-set
Como en ningún momento la marcación de un lugar puede ser superior a su capacidad, un criterio válido para la detección de conflictos post-set es el hecho de que la marcación de un lugar, en el vector de simulación de disparo (Sk), no puede ser mayor que su capacidad. Por lo tanto, se requiere la comparación del vector Sk con un vector que registre las capacidades de los lugares: 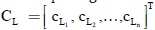 . De esta manera, la presencia de un conflicto post-set se determina utilizando la ecuación 6.
. De esta manera, la presencia de un conflicto post-set se determina utilizando la ecuación 6.
S+ = CL – SK (6)
Si si+ < 0 la totalidad de las transiciones que tienen como lugar de salida el i-ésimo lugar presentan conflicto post-set. Es posible utilizar la matriz A presentada en la ecuación 4, para detectar dichas transiciones, porque se corresponden a todas las entradas en la fila correspondiente al i-ésimo lugar cuyo valor es menor de cero.
3.2 Detección de conflictos pre-set
La cantidad de marcas removidas por el disparo de transiciones no puede ocasionar que la marcación de un lugar sea negativa; por tanto, aplicando la ecuación 5 el criterio de determinación de conflictos pre-set se basa en determinar si alguna entrada del vector Sk es negativa; en ese caso, todas las transiciones que tengan como lugar de inicio el correspondiente a dicha entrada presentaran conflicto pre-set. Dichas transiciones se detectan en la matriz A, observando las entradas correspondientes a la fila del lugar en conflicto que presentan valores mayores que cero.
3.3 Algoritmo para la detección de conflictos en Redes de Petri ordinarias
Teniendo en cuenta las consideraciones teóricas desarrolladas en los puntos 3.1 y 3.2, la figura 3 presenta un algoritmo para la detección y caracterización de conflictos en Redes de Petri Ordinarias con lugares de capacidad finita.
4. EJEMPLO DE APLICACIÓN DEL MÉTODO DE DETECCIÓN Y CARACTERIZACIÓN DE CONFLICTOS
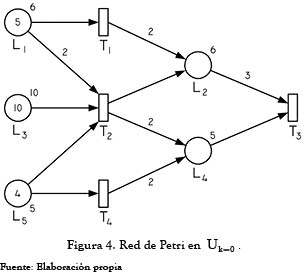
Los resultados de la aplicación del algoritmo ilustrado en la figura 3 a la RdP mostrada en la figura 4, suponiendo que todas las transiciones habilitadas para disparar lo intentan, se presentan a continuación.
Ninguna entrada negativa en S+, no existen conflictos post-set.
Análisis de Conflictos Pre-set
Ninguna entrada negativa en Sk=1, no existen conflictos pre-set.
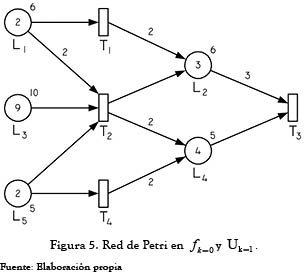
Al no existir conflictos post-set ni pre-set la totalidad de las transiciones que intentan disparar lo pueden hacer, por tanto: Uk=1 = Sk=1. La figura 5 ilustra gráficamente el resultado de efectuar este disparo. En este contexto, se procede a intentar el disparo fk=1, es decir a realizar una segunda iteración.
En tanto la cuarta entrada del vector S+ es un valor negativo, las transiciones relacionadas en la matriz A con el cuarto lugar (l4) por entradas mayores a cero, presentan conflicto post-set, es decir t2 y t4.
Análisis de conflictos pre-set
Teniendo en cuenta que:
SK=2 = [–1 3 8 7 0], al ser la primera entrada negativa se infiere que las transiciones relacionadas en la matriz A con el primer lugar (l1) por entradas menores de cero, presentan conflicto pre-set es decir t1 y t2.
De esta manera no es posible disparar todas las transiciones que se intentan disparar, y por tanto: Uk=2 ≠ Sk=2. Para lograr un disparo efectivo de la red, es decir, una simulación válida del modelo en fk=1, se requiere resolver los conflictos presentes mediante la selección de un conjunto de transiciones que al disparar no presenten conflictos.
La determinación de los subconjuntos de transiciones a disparar depende del significado y nivel de abstracción del modelo. Por ejemplo, se puede dar prioridad a las transiciones que en un modelo de una planta industrial representan las tareas de mayor eficiencia en el proceso productivo, dejando de disparar las que representan una menor. Se debe tener en cuenta que la solución de un conflicto afecta toda la red; por lo tanto, si se resuelve una sola situación de conflicto es necesario ejecutar de nuevo el algoritmo.
5. CONCLUSIONES Y TRABAJOS FUTUROS
El método computacional presentado en este trabajo se basa en un algoritmo que demuestra ser correcto desde el punto de vista computacional, y que permite determinar y caracterizar la presencia de conflictos en RdP, posibilitando el desarrollo de simuladores de un mayor nivel de rigor y exactitud, contribuyendo a incrementar la confiabilidad en la simulación y validación de sistemas basados en modelos de RdP.
La estructura de datos empleada en el algoritmo propuesto, toma como base la forma algebraica de las RdP que es equivalente a su definición por teoría de conjuntos; es una representación sencilla, compacta y funcional que posibilita su procesamiento computacional. Esta representación no puede ser utilizada en RdP que presenten bucles, por lo tanto, el algoritmo no es válido para redes que presenten dicha particularidad. En caso de RdP de capacidad infinita el algoritmo propuesto es válido, pero por eficiencia computacional se recomienda no realizar el análisis de conflictos post-set.
El algoritmo presentado se constituye en una herramienta útil para el análisis de modelos especificados con RdP, particularmente para situaciones en las cuales la presencia de conflictos deba ser resuelta buscando soluciones óptimas y/o rutas de disparo prioritarias.
El método presentado en este trabajo puede extenderse, previa implementación de las correspondientes modificaciones derivadas de las ecuaciones de disparo particulares, para ser aplicado a diversas extensiones de RdP tales como las redes Predicado transición, las orientadas a objetos y las coloridas. Igualmente, las características del mismo sugieren que puede ser utilizado en el análisis de otras situaciones propias de las RdP tales como la aparición de confusiones simétricas y/o asimétricas. [1]
REFERENCIAS
[1] T. Murata, ''Petri Nets: Properties, Analysis and Applications,'' Proceedings of the IEEE, vol. 77, no. 4, pp. 541-580, 1989. [ Links ]
[2] J. O. Moody, y P. J. Antsaklis, ''Petri net supervisors for DES with uncontrollable and unobservable transitions,'' IEEE Transactions on Automatic Control, vol. 45, no. 3, pp. 462-476, 2000. [ Links ]
[3] C. Girauld, y R. Valk, ed, ''Petri Net for System Engineering,'' Berlin: Springer, 2001, 621 p. [ Links ]
[4] J. L. Peterson, Petri Net Theory and the Modeling of Systems, New Jersey: Prentice-Hall Inc, 1981, 288 p. [ Links ]
[5] M. Silva et al., ''Petri Nets and Production Systems,'' presentado en Proceedings of Petri Nets (2) 1996: pp. 85-124, 1996. [ Links ]
[6] P. L. Ángel, ''Modelagem Orientada a Objetos de Sistemas a Eventos Discretos: Estudo de Caso na Síntese de Controle de Sistemas Prediais,'' tesis de Disertación de Maestría en Ing. Mecatrónica, Universidade Estadual de São Paulo, 2003. [ Links ]
[7] J. Blackhurst et al., ''A systematic approach for supply chain conflict detection with a hierarchical Petri Net extension,'' Omega, vol. 36, no. 5, pp. 680-696, 2008. [ Links ]
[8] Q. Zeng et al., ''Conflict Detection and Resolution for Workflows Constrained by Resources and Non-Determined Durations,'' Journal of Systems and Software, vol. 81, no. 9, pp. 1491-1504, 2008. [ Links ]
[9] C. G. Cassandras, Discret Event Systems: Modeling and Performance Analysis, Illinois: Aksen Associates Incorporated Publishers, 1993, 790 p. [ Links ]
[10] C. Lesire, y C. Tessier, ''Estimation and Conflict Detection in Human Controlled Systems. Hybrid Systems: Computation and Control,'' en J. Hespanha y A. Tiwari, eds., pp. 407-420: Springer Berlin / Heidelberg, 2006. [ Links ]
[11] Q. Liu et al., ''Application of Colored Petri Net in Spam-Filter Rules Property Detection,'' presentado en 2nd IEEE International Conference on Network Infrastructure and Digital Content, IC-NIDC 2010: pp. 62-65, 2010. [ Links ]
[12] E. R. R. Kato et al., ''A conflict Solution Manufacturing System Modeling Using Fuzzy Coloured Petri Net,'' presentado en Systems Man and Cybernetics (SMC), 2010 IEEE International Conference on, Istanbul: pp. 3983-3988, 2010. [ Links ]
[13] M. Zhou et al., ''Control of Batch Processes Based on Hierarchical Petri Nets,'' presentado en IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences: pp. 2895-2904, 2004. [ Links ]
[14] C. Popescu, y J. L. Martinez Lastra, ''Matrix-based Conflict Resolution Algorithm: Application to Path Selection in PN-based Scheduling Search,'' presentado en 15th IEEE International Conference on Emerging Technologies and Factory Automation, ETFA 2010, 2010. [ Links ]
[15] A. Giua, y F. DiCesare, ''Supervisory Design Using Petri Nets,'' presentado en 30th Conference on Decision and Control, Brighton: pp. 92-97, 1991. [ Links ]
[16] M. Zhou, y D. T. Wang, ''Design of Petri Net Objects and their Application in Command and Control systems,'' presentado en IEEE International Conference on Systems, Man, and Cybernetic, Vancouver: pp. 3463-3468, 1995. [ Links ]