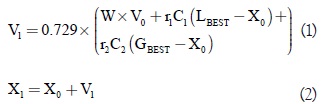ARTÍCULOS

 

EVALUACIÓN DE LA IMPLEMENTACIÓN EN UN DSP DEL ALGORITMO HÍBRIDO DE OPTIMIZACIÓN POR ENJAMBRES DE PARTÍCULAS Y EL SIMPLEX

 

Evaluation of a Digital Signal Processor (DSP) Implementation of Hybrid Particle Swarm Optimization (PSO) Algorithm and the Simplex

 

Julián Cote^*; Camilo Moncada^**; Rodrigo Correa^***

 

^* Ingeniero electrónico, Universidad Industrial de Santander, Bucaramanga, julian.cote@correo.uis.edu.co

^** Ingeniero electrónico, Universidad Industrial de Santander, Bucaramanga, camilo.moncada@correo.uis.edu.co

^*** Ph. D., profesor titular, Universidad Industrial de Santander, Bucaramanga, crcorrea@uis.edu.co

 

Recibido: 09/12/2010
Aceptado: 14/07/2011

 

---

RESUMEN

En este artículo se presentan los principales resultados de la evaluación que se llevó a cabo relacionada con la implementación del método de optimización PSO de convergencia garantizada en topología alternante con el método simplex, en un procesador digital de señales (DSP). Se comparó desempeño con funciones de prueba convencionalmente utilizadas en la evaluación de algoritmos de optimización. Se hizo la programación en el DSP confirmando la viabilidad de su implementación en este tipo de dispositivo caracterizado por ser transportable, de reducido tamaño, flexibilidad y bajo costo. No obstante este logro, se encontró que su mayor tiempo de cómputo sigue siendo aún su principal debilidad, al menos con el tipo de funciones probadas.

Palabras clave: PSO, simplex, DSP, optimización, algoritmo híbrido.

---

Abstract

This article shows the main results of an evaluation related to the implementation of the convergence PSO method assured in alternating topology with the simplex method, in a Digital Signal Processor (DSP). Comparisons on the performance of testing functions conventionally used for the evaluation of optimization algorithms were made. A programming was executed on the DSP confirming the feasibility of its implementation in this kind of device characterized by its small size, low cost, and portable feature. Despite this achievement, it was found that its longest computation time is still its main weakness, at least with the kind of functions tested.

Key words: PSO; simplex; DSP; optimization; algorithm; hybrid.

---

 

 

INTRODUCCIÓN

La optimización por enjambre de partículas (PSO) es una técnica de optimización aleatoria basada en poblaciones, desarrollada por Eberhart y Kennedy en 1995 [1], e inspirada en el comportamiento social de animales, como bandadas de aves o cardúmenes. Actualmente, el PSO se combina con otras técnicas de búsqueda para mejorar su rendimiento y velocidad [2, 4]. Los algoritmos evolutivos están siendo programados en diferentes plataformas de desarrollo y el único trabajo afín reportado en la literatura fue el realizado por Palangpour et al. [5], en el que se utilizó el algoritmo PSO original como estabilizador para un sistema de generación eléctrica, con el propósito de reducir la desviación de la velocidad en dos de los cuatro generadores de energía. Ellos lograron implementar satisfactoriamente el PSO en un DSP (Texas Instruments^®), reducir así las oscilaciones en la velocidad de los generadores y demostrar la viabilidad del PSO básico como controlador en un proceso real, aunque no detallan la características de la función objetivo. El presente artículo muestra los principales resultados obtenidos de la implementación del híbrido de optimización de enjambre de partículas y el simplex de topología alternante en un DSP (Motorola^®), evaluando su desempeño mediante funciones de prueba comúnmente utilizadas para ello. Se obtuvieron resultados favorables en cuanto a su precisión y convergencia, lo que indica la posibilidad de utilizarlo como un sistema de optimización portable y preciso mediante un DSP, en procesos donde el uso de un computador es complicado por su ubicación, disponibilidad, o aun, costo.

 

1 FUNDAMENTOS

A continuación se presentan algunos conceptos relacionados con el algoritmo híbrido que se implementó en el DSP. Este híbrido lo compone el tradicional método simplex desarrollado en los años 60, junto con el algoritmo de enjambre de partículas (PSO) creado a mediados de los años 90. Con relación al primero, se trata de una técnica de optimización determinística caracterizada por tener un proceso iterativo definido por varias reglas, que permite ir mejorando la solución en cada paso. Se utiliza ampliamente en la búsqueda de valores óptimos locales y se describe en detalle en [6]. El segundo, el PSO, se considera como una estrategia metaheurística reciente, en donde se define una población de posibles soluciones (partículas) que se desenvuelven dentro del espacio de búsqueda para encontrar la mejor solución a un problema. Cada partícula explora el dominio de la función objetivo teniendo presente su dirección anterior, la dirección de la mejor posición en que ella ha estado y la dirección de la partícula mejor ubicada [1, 7].

1.1 El híbrido

Existen al menos dos posibles formas de combinar estas dos estrategias numéricas, como son la topología secuencial y la alternate [8]. De análisis preliminares, y fundamentalmente por su alto porcentaje de efectividad para hallar la solución óptima global, se decidió utilizar el segundo tipo topología. Este híbrido entonces involucra el algoritmo PSO de convergencia garantizada dada por:

donde
V₁ → Velocidad de la partícula en la siguiente interación
V₂ → Velocidad de la partícula en la iteración actual
X₁ → Posición de la partícula en la siguiente iteración
X₀ → Posición de la partícula en la iteración actual
W → Factor de inercia
L_BEST → Mejor posición de la partícula
C₁ → Coeficiente de confianza relacionado al L_BEST; C₁ = C
C₂ → Coeficiente de confianza relacioando al G_BEST; C₂= Cr_1,2 → Números pseudoaleatorios entre 0 y 1

Combinado con el tradicional algoritmo del simplex, se caracteriza esta topología porque el espacio de búsqueda de cada uno de los algoritmos participantes es totalmente diferente e independiente el uno del otro. El espacio de búsqueda del PSO lo determina el problema de optimización que consta de las D dimensiones (variables) de la función objetivo; por otra parte, las dimensiones del espacio de búsqueda del simplex se definen a partir de los parámetros del método PSO y su labor es optimizarlos, para que, a su vez, este último mejore su desempeño. Posteriormente, hay un intercambio de información entre ambos algoritmos para la realimentación de cada uno de ellos [8].

1.2 Desarrollo del algoritmo y su implementación en el DSP

A diferencia del trabajo reportado por Palangpour et al. [5], en el que se implementa el PSO original en un DSP, en este trabajo se desarrolló un algoritmo híbrido combinado de forma alternante y que mostró consistentemente mejores resultados. Para elaborar el algoritmo, se definieron las matrices S (puntos G, B y W del simplex) y B (puntos en las reglas del simplex) para el método simplex. Para el PSO se emplearon las matrices X (X_i-coordenadas de las partículas del PSO junto con su respectivo valor en la función objetivo), L (L_Best-óptimo local de cada partícula con su valor evaluado por la función objetivo) y V (V₀-velocidad de cada partícula de la iteración anterior) y el vector G (G_Best -mejores coordenadas halladas por el PSO junto con su valor en la función objetivo). La matriz S tienes tres dimensiones ya que en ella están los parámetros relacionados con el número de partículas (Part), factor de inercia (W) y las constantes de confianza (C), que son valores requeridos por el PSO. En el momento en que se ordene la matriz S respecto a la columna descrita por el PSO, se deben aplicar las reglas del simplex, teniendo en cuenta que todas las compresiones son en un factor de 0.5 y las expansiones son en un factor de 2. Como criterio de parada del proceso de optimización implementado en el DSP se recurrió a determinar un número fijo de iteraciones, para que cuando el simplex realice la iteración final, automáticamente se termine el proceso. Otra forma consistió en definir que cada cinco iteraciones el método revisará si el valor de la posición S_0.3 (solución) es menor que la precisión buscada y si esto se cumple, se almacena en un vector de cinco posiciones y se calcula la varianza de los datos. Por otro lado, si esta es menor que un error definido elevado al cuadrado, el método se termina, ya que no evolucionó más en el tiempo y cumplió la precisión deseada. Al finalizar el método, la primera fila de la matriz S será la mejor solución encontrada.

1.3 El DSP

Un DSP es un procesador que se especializa en la ejecución de operaciones de manera digital. En comparación con los microprocesadores tiene un mejor desempeño de cómputo. El DSP utilizado para implementar el algoritmo híbrido se muestra como una herramienta eficiente ya que está diseñado para las operaciones matemáticas sencillas (acumulación y ponderación), repetitivas (lazos) y de acceso a memoria. El DSP tiene la ventaja de trabajar sobre señales reales y, además, de ejecutar instrucciones, logrando que estos dos procesos se realicen en un mismo dispositivo.

 

2 EXPERIMENTOS

Con el propósito de comparar resultados en cuanto a precisión y tiempo de procesamiento se refiere, se decidió realizar las mismas pruebas en un computador y en el DSP.

2.1 El computador

Se desarrolló el algoritmo en lenguaje C, con el fin de evaluar su desempeño en un computador personal, teniendo una RAM de 4 GB DDR2, un procesador INTEL CORE 2 DUO E8400 de 64 bits, trabaja con punto flotante a 24 GFLOPS, una memoria caché L1 de 64 KB, una L2 de 6 MB, una frecuencia del bus del sistema frontal de 1.333 MHz y una frecuencia de reloj de 3 GHz. Para la programación del algoritmo se utilizó el programa DEV CPP, que es un compilador de código C y C++. Para calcular el tiempo de ejecución del algoritmo se utilizó la función clock, que arroja el valor del reloj en ese instante. Se utilizó la función srand para generar los números aleatorios.

2.2 El DSP

Se utilizó un DSP 56F8357PY60 es de la familia de Freescale con una frecuencia de 60 MHz, 256 KB de memoria flash de programa, 4KB de RAM de programa, 8 KB de flash de datos, 16 KB de RAM de datos, 16 KB de flash de arranque, el formato de manejo de datos es de punto fijo de 16 bits y ejecuta hasta 60 millones de instrucciones por segundo. Además, posee periféricos internos para funciones de tiempo, conversión análogo-digital, pines para propósito general y otros módulos de comunicación. La tarjeta DSP se programó con Codewarrior Development Studio^® para la serie 56800E. Para medir el tiempo de ejecución del programa, se implementó un anexo al código original que no modifica significativamente el tiempo de ejecución. Mediante la herramienta de Processor Expert^®, se aplicó el método de ''TimeDate'', que configura los Timers para obtener un reloj en tiempo real con una resolución de centésimas de segundo.

 

3 RESULTADOS Y ANÁLISIS

Inicialmente se definieron los rangos para los experimentos realizados con las funciones de prueba, ver tabla 1.

 

 

De la amplia gama de funciones disponibles para probar la eficiencia de un algoritmo de optimización se seleccionaron seis de ellas. En la tabla 2 se recopilan algunos de los resultados obtenidos. Para todos los casos, tanto el computador como el DSP, lograron los resultados correctos en el 100% de los experimentos. La diferencia radicó en el tiempo de cómputo. Consistentemente, el computador lo hizo en menor tiempo. También se notó que a mayor dimensión de la función, mayor es el tiempo de cómputo.

 

 

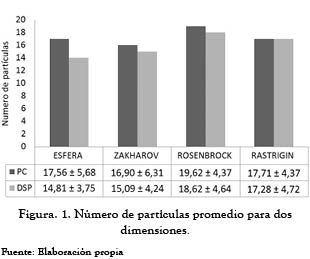
En la figura 1 se ilustra el número de partículas utilizadas por cada uno de los dos dispositivos. La tabla que acompaña la figura muestra el valor promedio de todas las pruebas realizadas.

 

 

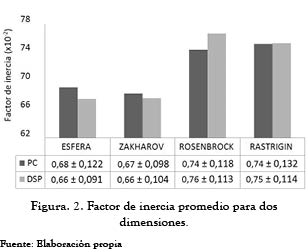
Se puede apreciar que el DSP en general utiliza una cantidad de partículas similar a las requeridas por el computador para hallar el óptimo en las funciones de prueba. Con el objeto de dilucidar igualmente el efecto del factor de inercia sobre la solución, se realizaron varias pruebas como se muestra en la figura 2. Al igual que en el número de partículas, no hay una diferencia apreciable para los dos dispositivos. Sin embargo, a medida que el problema se torna más complejo (mayor número de dimensiones y complejidad de la función), el valor de W se incrementa ligeramente.

 

 

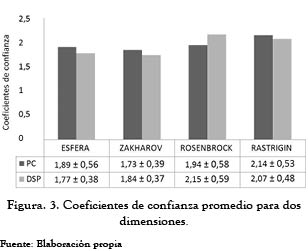
La figura 3 resalta el comportamiento de los coeficientes de confianza (C) para algunas de las funciones objetivo, seleccionadas. Se definió desde un inicio el rango para este coeficiente entre 1.5 y 3.5. Se observó que su valor se mantiene cercano a 2.0; se puede con ello reducir aún más el rango y lograr una búsqueda más directa.

 

 

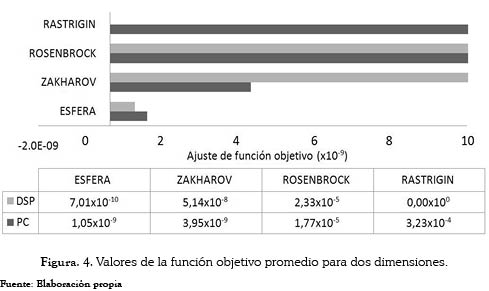
El siguiente factor que se consideró para cualificar el desempeño del híbrido, operando en el DSP frente al computador, fue la precisión. De la figura 4 se puede apreciar que la precisión entre estos dos dispositivos se mantuvo en un valor cercano para las funciones esfera, Zakharov y Rosenbrock, pero al momento de evaluarla para la función Rastrigin, se nota una diferencia considerable, ya que el DSP tuvo valores muy cercanos a los teóricos.

 

 

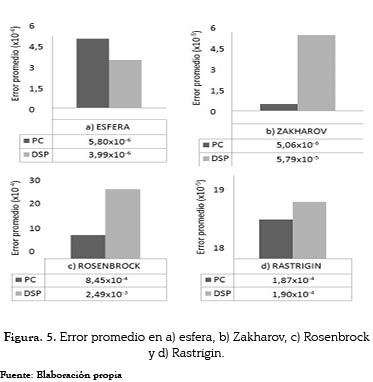
Si se observan los datos obtenidos para esta prueba, ninguno de ellos se ajusta a los resultados teóricos en forma exacta. Cuando se ejecutó el algoritmo en el DSP y éste generaba una respuesta inferior a 1x10^-4, automáticamente se aproximaba a cero. Para las funciones de prueba esfera, Zakharov y Rastrigin, en los dos dispositivos se calcularon los errores tal y como se observa en la figura 5. A diferencia de lo anterior, para la función Rosenbrock (figura 5-c), la implementación en el computador arroja resultados más cercanos al error establecido que el DSP.

 

 

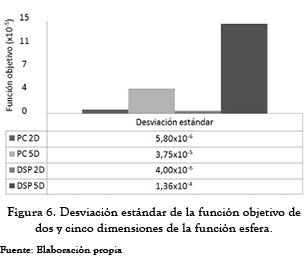
Se observó igualmente que cuando se incrementan las dimensiones, el proceso de optimización requiere más iteraciones con el propósito de cumplir la precisión exigida. Para 2D, el número de iteraciones promedio que realizó fue de 22 en el DSP y 28 en el computador, mientras que para 5D, en el DSP se elevaron a 42 y a 30 en el computador. En la figura 6, se evidencia que en el computador, la respuesta se encuentra más cercana al óptimo global que en el DSP. En cinco dimensiones, a pesar de que la función objetivo está más alejada comparada con la de dos dimensiones, el valor de sus coordenadas demuestra estar en un rango aceptable. También se aprecia que en el computador, la respuesta es más cercana con la precisión deseada que en el DSP para cinco dimensiones con iguales parámetros.

 

 

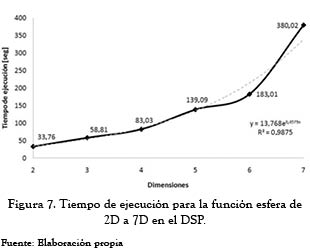
El incremento en el tiempo de ejecución del algoritmo en el DSP de acuerdo con el incremento del número de dimensiones para la función esfera se muestra en la figura 7. Para todos los experimentos, el error permitido fue de 1x10^-6, el rango de partículas estuvo entre 15 y 40 y el número máximo de iteraciones para el PSO fue de 50 mientras que para el simplex fue de 60. A medida que se incrementa el número de dimensiones, el tiempo de procesamiento del DSP aumentó de forma exponencial, tal y como lo demuestra la interpolación mostrada en esa figura por la línea punteada.

 

 

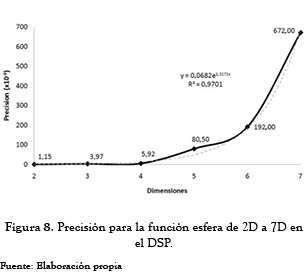
De un análisis global, se observó una pérdida de precisión del híbrido conforme se incrementaba el número de dimensiones del problema. Sin embargo, los resultados arrojados permanecieron dentro del error permitido (1x10^-6), (ver figura 8). Nuevamente, el comportamiento de los resultados describe una tendencia exponencial (línea punteada).

 

 

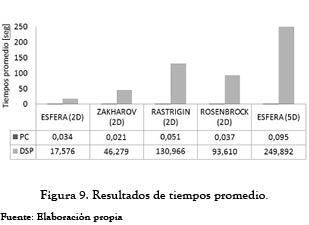
Los comportamientos descritos en las últimas dos figuras sirven como una ayuda inicial para estimar si la implementación del algoritmo híbrido en el DSP seleccionado es viable para una aplicación en particular. No obstante, no se puede generalizar, ya que no debe olvidarse que el tiempo de cómputo depende no solamente del hardware, del algoritmo utilizado, de los parámetros de este último, sino de la misma naturaleza (forma y dimensiones) de la función objetivo. Para el presente caso, se observó que el tiempo de operación del DSP fue consistentemente mayor que el utilizado por el computador, como se observa en la figura 9.

 

 

5 CONCLUSIONES

Se logró implementar el algoritmo híbrido de optimización enjambre de partículas con el simplex en un DSP, y se obtuvieron resultados con una precisión aceptable. Sin embargo, los tiempos de ejecución del algoritmo en el DSP disponible resultaron elevados, debido posiblemente, entre otras razones, a la diferencia del formato de manejo de datos entre ambos dispositivos, a su velocidad de lectura y escritura de datos entre los procesadores. Con las pruebas realizadas, se verificó con base en comparaciones con un computador, que en el DSP seleccionado los datos obtenidos cumplieron con la precisión establecida para la mayoría de las funciones de prueba. Ya que el DSP utilizado obtiene respuestas precisas y dentro del error permitido, se puede aprovechar el tamaño del mismo como un dispositivo portable, para situaciones que requieran, por ejemplo, de una gran capacidad de cómputo y alta precisión.

Es claro también que no es viable, por ahora, en aplicaciones de tiempo real donde la velocidad de respuesta sea una importante limitante de diseño, aunque este parámetro depende también de otros factores como la naturaleza misma (forma y dimensiones) de la función objetivo. Para un trabajo siguiente se está en la tarea de definir las mejores características técnicas del DSP, con el fin de lograr la disminución del tiempo de ejecución del híbrido y/o el uso de una alternativa más avanzada, como un FPGA, aunque mucho más costosa a nuestros días.

 

REFERENCIAS

[1] J. Kennedy, y R. Eberhart, ''Particle Swarm Optimization,'' presentado en Proceedings., IEEE International Conference on, Perth: pp. 1942-1948, 1995.         [ Links ]

[2] Y. Zhao et al., ''Hybrid Particle Swarm Optimization based on parallel Collaboration,'' presentado en Intelligent Computation Technology and Automation (ICICTA), 2008 International Conference on, Hunan: pp. 65-70, 2008.         [ Links ]

[3] J. Wen et al., ''Particle Swarm Algorithm based on normal cloud,'' presentado en Evolutionary Computation, 2008. CEC 2008. (IEEE World Congress on Computational Intelligence). IEEE Congress on Hong Kong: pp. 1492-1496, 2008.         [ Links ]

[4] X. Li et al., ''One immune Simplex Particle Swarm Optimization and its Application,'' presentado en Natural Computation, 2008. ICNC 08. Fourth International Conference on Jinan: pp. 331-335, 2008.         [ Links ]

[5] P. Palangpour et al., ''DSP-Based PSO Implementation for Online Optimization of Power System Stabilizers,'' presentado en Adaptive Hardware and Systems, 2008. AHS 08. NASA/ESA Conference on Noordwijk: pp. 379-384, 2008.         [ Links ]

[6] J. A. Nelder, y R. Mead, ''A simplex method for function minimization,'' The Computer Journal, vol. 7, no. 4, pp. 308-313, 1965.         [ Links ]

[7] M. Clerc, y J. Kennedy, ''The Particle Swarm-Explosion, Stability, and Convergence in a Multidimensional Complex Space,'' presentado en Evolutionary Computation, IEEE Transactions on: pp. 58-73, 2002.         [ Links ]

[8] M. Villareal, y J. Osma, ''Comparación del desempeño del algoritmo de Optimización PSOSX (PE) frente al PSOSX (S),'' tesis de Pregrado en Ingeniería, Universidad Industrial de Santander, 2009.         [ Links ]