Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Revista Ingenierías Universidad de Medellín
versão impressa ISSN 1692-3324versão On-line ISSN 2248-4094
Rev. ing. univ. Medellín v.11 n.20 Medellín jan./jun. 2012
ARTÍCULOS
EL MÉTODO DE ENJAMBRE DE PARTÍCULAS Y EL CRITERIO DE MÍNIMA ENTROPÍA EN EL DISEÑO ÓPTIMO DE UN DISIPADOR DE CALOR
PARTICLE SWARM OPTIMIZATION AND THE MINIMUM ENTROPY CRITERION IN THE OPTIMUM DESIGN OF A HEAT SINK
Alberto Hinojosa*; Katherine Espinosa**; Rodrigo Correa***
* Estudiante de Ingeniería Electrónica, Universidad Industrial de Santander. E-mail: alberto.hinojosa@correo.uis.edu.co.
** Estudiante de Ingeniería Electrónica, Universidad Industrial de Santander. E-mail: july.espinosa@correo.uis.edu.co.
*** Ph. D., Profesor titular, Universidad Industrial de Santander, Bucaramanga. E-mail: crcorrea@uis.edu.co.
Recibido: 09/12/2010
Aceptado:: 25/05/2012
RESUMEN
Este artículo de investigación presenta los resultados de simulación del diseño térmico de un disipador de calor tipo micro-canal, comúnmente utilizado en electrónica. Se utilizó el criterio de mínima entropía para generar el modelo matemático, posteriormente resuelto mediante multiplicadores de Lagrange y mediante la optimización con enjambre de partículas (PSO). Se encontró que, debido al gran número de parámetros del modelo, la solución mediante el primer método es altamente demandante, dado que requiere solucionar un sistema de ecuaciones no lineales. Este sistema fue resuelto mediante el método de Newton-Raphson multidimensional que, a su vez, requiere ''proponer'' un conjunto de soluciones iniciales sin tener mayor criterio técnico para hacerlo. De otro lado, la solución con PSO fue muy sencilla y requirió poco esfuerzo y tiempo computacional. Se contrastan los resultados de ambos métodos.
PALABRAS CLAVE
Minimización de entropía, transferencia de calor, circuitos integrados.
ABSTRACT
This research paper shows the simulation results of the thermal design of a micro channel heath sink. A minimum entropy generation criterion was used to generate the mathematical model, which was then solved by Lagrange multipliers and by particle swarm optimization (PSO). It was found that due to the extensive number of variables, traditional techniques demand elevated computational resources since it requires solving a system of non-linear equations. This system was solved using the multidimensional Newton-Raphson method, which needs a set of proposed initial solutions, without having technical criteria for choosing it. On the other hand, particle swarm optimization provides a rather simple solution to the problem. Results achieved with both methods are compared.
KEY WORDS
Minimization, heat transfer, integrated circuits.

INTRODUCCIÓN
En situaciones reales, muchos problemas de ingeniería se basan en resolver modelos con una gran cantidad de variables, además de funciones complejas y extensas. La eficacia, precisión y rapidez con que hoy en día se puedan resolver de manera simple estos modelos representan una parte importante en su solución.
Un problema evidente en la electrónica moderna está relacionado con el enfriamiento de circuitos integrados utilizando disipadores de calor, que están definidos por una cantidad considerable de parámetros físicos, por lo que se hace necesario disponer de un modelo matemático que los relacione. Se seleccionó un modelo que también considera la entropía generada por el disipador [1]. Su solución generalmente implica la implementación de algoritmos robustos con un costo computacional asociado elevado, por lo que se requiere un método de optimización que permita resolver este tipo de modelos de forma simple, precisa, exacta, rápida y con bajo costo computacional.
Este artículo se enfoca principalmente en el análisis de los métodos utilizados en la solución de la función objetivo. Igualmente, se presenta brevemente el modelo matemático que describe el comportamiento térmico de un micro-canal, que constituyó la función objetivo, minimizada con el método tradicional de los multiplicadores de Lagrange (implicando la solución de un sistema de 17 ecuaciones no lineales) y PSO. Seguidamente se discuten los aspectos más relevantes del modelo matemático así como una corta descripción de los métodos de optimización empleados. Al final se incluyen algunos de los resultados de la simulación obtenidos con ambos métodos.
1 FUNDAMENTACIÓN
Para el diseño óptimo del micro-canal se utiliza el concepto de ''minimización de la generación de entropía'', propuesto originalmente por Bejan [1]. Este método se utilizó posteriormente por Culham [2, 3] y Khan [4-6] para el diseño de disipadores de calor. Estudios realizados por Knight [7], Perret [8, 9], Kim [10], y Kandlikar [11] muestran cómo la resistencia térmica es un parámetro de gran importancia para el diseño y operación de un micro-canal. Para que un disipador de calor sea el adecuado, se debe optimizar su diseño, incluyendo tanto sus dimensiones como las propiedades físicas y térmicas del material de fabricación y del fluido de enfriamiento que utilizará. La solución de este problema se puede realizar, ya sea con la ayuda de técnicas de optimización metaheurísticas de reciente desarrollo, como lo es PSO, propuesto por Kennedy y Eberhat [12], o mediante métodos clásicos, como por ejemplo con los multiplicadores de Lagrange, entre muchos otros.
PSO es una técnica estocástica de optimización basada en poblaciones donde los individuos, llamados partículas (Npart), se mueven en el espacio solución de una función objetivo n-dimensional. Hay tres vectores asociados a una partícula: el vector posición (xi), el cual representa la solución candidata, el vector velocidad (vi), el cual representa la dirección de búsqueda de las partículas y el vector de los mejores personales (pi), el cual denota la mejor solución hasta ahora encontrada. Los puntos buenos en el espacio de búsqueda son comunicados y usados por otras partículas para guiar su búsqueda, de tal forma que al encontrar el óptimo global, este se comunica y todas convergen al punto (solución) [13].
1.1 Planteamiento del modelo
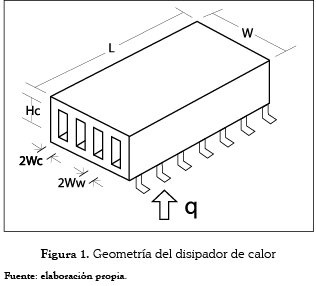
Para el desarrollo del modelo, se hace uso de la figura 1, donde se indican las tres variables físicas que se optimizarán. Esto es, Hc, Wc, y Ww. Las dimensiones del disipador de calor tipo micro-canal se observan en la misma figura. W y L son el ancho y largo, respectivamente.
Se asume que la superficie superior está aislada, mientras la superficie inferior se calienta uniformemente debido a la disipación de calor del dispositivo electrónico. Un fluido refrigerante (aire para este caso) se hace pasar a través de los micro-canales, retirando calor continuamente. Hay N canales y cada uno tiene una altura Hc y ancho 2Wc. El ancho de cada aleta es 2Ww. En la pared del canal, la velocidad de deslizamiento de flujo y la temperatura en la frontera fueron utilizadas para calcular los coeficientes de fricción y transferencia de calor. Para el análisis se tiene en cuenta que en la superficie inferior el flujo de calor es uniforme, que las superficies en el canal son lisas, que la pared superior es adiabática, que el material es isotrópico, que el flujo de calor y del fluido están completamente desarrollados, que el flujo de aire es estable y laminar, que hay flujo de transición (es decir, 0,1 < Kn < 10) o deslizamiento de flujo (es decir, 0,001 < Kn < 0,1) [14], que las propiedades del fluido son constantes, que la conducción axial en la aleta es despreciable y que los cambios en la energía cinética y potencial son despreciables. Si bien el modelo fue inicialmente propuesto por Khan [4], hay algunas diferencias con el modelo matemático propuesto en este artículo. La entropía, en un sistema térmico real se relaciona con la cantidad de energía generada, no utilizable, producida en el desarrollo natural de un proceso irreversible. El modelo de generación de entropía asociado al disipador de calor se puede definir mediante la siguiente expresión:

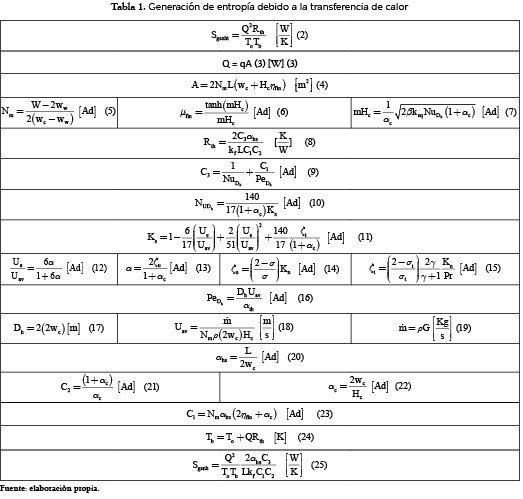
La definición de los términos globales Sgen,ht y Sgen,ff se desglosa en las tablas 1 y 2, respectivamente.
Por facilidad, se condensaron todas las ecuaciones necesarias en las tablas 1 y 2, ya que las ecuaciones (2)-(18) y (20)-(31) dependen de las variables Hc, Wc y Ww. Luego de una serie de reemplazos, se llega a la ecuación (32), donde aparecen los parámetros definidos para el diseño óptimo del micro-canal y que constituye la función objetivo del problema de optimización:
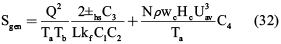
1.2 Optimización clásica
La expresión general de los multiplicadores de Lagrange se encuentra en la ecuación (33), donde f(x) es la función objetivo que se va a minimizar, χj los multiplicadores de Lagrange, hj(x) las restricciones de igualdad y εj las variables de deslizamiento de las restricciones de desigualdad.
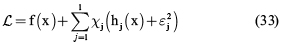
El esquema de solución consiste en derivar parcialmente (analítica o simbólicamente) la ecuación (33) en función de las variables de diseño y de cada uno de los coeficientes de Lagrange. Como resultado se obtiene un sistema de ecuaciones no lineales, que puede ser solucionado por técnicas tradicionales como Newton-Raphson multidimensional. La gran desventaja de este método radica en requerir el cálculo del Jacobiano y en tener que asumir valores iniciales cercanos a la solución, que obviamente es desconocida. Así, este problema puede llegar a ser de una alta laboriosidad, incluso para sistemas de 17 ecuaciones con 17 incógnitas. Para profundizar más en el método, el lector puede remitirse a Rao [15].
1.2.1 Optimización metaheurística
Se seleccionó como algoritmo meta-heurístico la optimización por enjambre de partículas (PSO), que ofrece una forma simple, sencilla y precisa de resolver modelos complejos con un algoritmo básico de fácil implementación y alta robustez. En la actualidad existen múltiples variantes, como se puede ver en De Freitas [16], Montes [13], Van der Bergh [17], Yang [18] y Zhan et al. [19]. El método basa su eficacia en las ecuaciones (34) y (35), que representan el comportamiento de una población de partículas, donde cada una de ellas cambia su posición de manera continua, actualizando estos valores en búsqueda de una ubicación óptima.
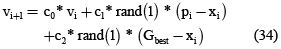

En el desarrollo del algoritmo se tienen en cuenta las restricciones asociadas al modelo de generación de entropía propuesto, al igual que en la optimización clásica, con las respectivas variaciones de la velocidad de flujo volumétrico y el número de Knudsen.
2 RESULTADOS Y ANÁLISIS
Para las primeras simulaciones se procedió a verificar el efecto que tienen los parámetros Hc, Wc y Ww en la generación de entropía.
2.1 Modelo matemático
La ecuación que representa el modelo del disipador de calor asociado a la tasa de generación de entropía está dada por (33) que se repite por comodidad y se convierte en la función objetivo del algoritmo de optimización, sujeto a las restricciones (36)-(39):
Optimizar:
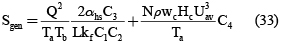
Sujeto a:
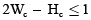 (36)
(36)
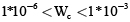 (37)
(37)
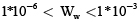 (38)
(38)
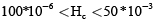 (39)
(39)
A cada una de las restricciones se le asocia tanto un multiplicador de Lagrange, como una variable de deslizamiento (generando 17 variables, incluidas las tres de diseño).
2.2 Efecto de la variación de los parámetros de diseño
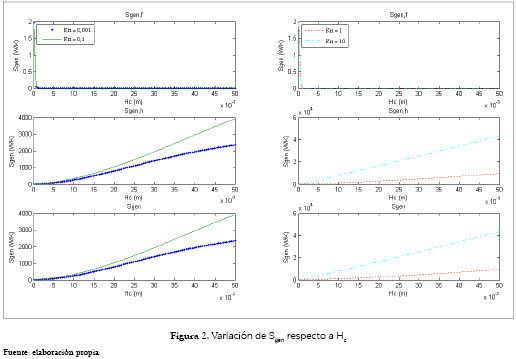
El comportamiento de la generación de entropía respecto a la variación de cada una de las variables a optimizar es diferente, ya que dependiendo de cada una, Sgen crece, decrece o tiende a estabilizarse en un valor aproximadamente constante, correspondiente a cada valor de Kn. La figura 2 muestra la variación de Sgen con respecto a Hc. Se puede observar que para todos los valores de Kn el comportamiento es semejante, mostrando inicialmente una disminución para luego establecerse en un valor aproximadamente constante. Es importante resaltar que en este caso, Sgen,h es el aporte dominante, representado en un crecimiento significativo a medida que aumenta el valor de Hc.
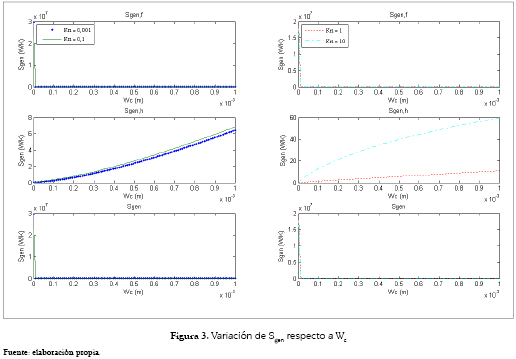
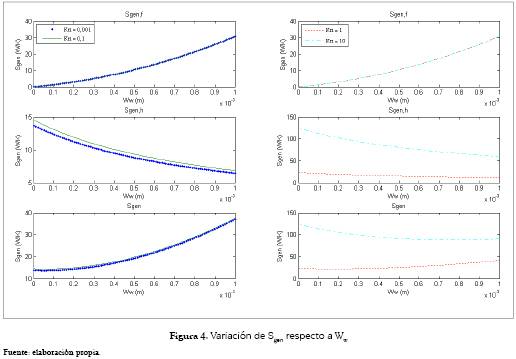
Al variar Wc, como se muestra en la figura 3, la incidencia de la tasa de generación de entropía por fricción del fluido es más significativa, con un comportamiento similar al de la variación de Hc, pero en intervalos diferentes. La variación sujeta a Sgen,h es creciente para cada valor de Kn, con un aporte superior para 1 y 10. Por otra parte, la figura 4 muestra la variación de Sgen, donde se puede observar que el comportamiento de Sgen,f toma mayor importancia, mientras que el de Sgen,h se invierte.
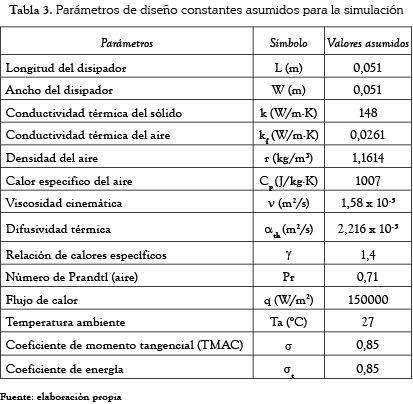
2.3 Definición de los parámetros del modelo
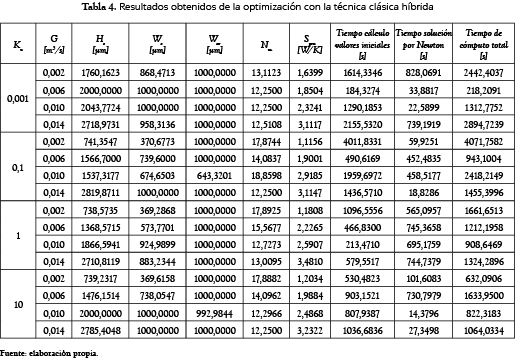
La tabla 3 muestra las constantes utilizadas durante la simulación. La tabla 4 muestra los resultados de la optimización, donde se tomaron los valores de la tabla 3, un número de Knudsen (Kn) con valores de 0,01, 0,1, 1 y 10, así como un flujo volumétrico (G) con valores de 0,002, 0,006, 0,010 y 0,014, (m3/s). Se utilizó un método híbrido entre los multiplicadores de Lagrange y PSO, ya que el sistema de ecuaciones fue resuelto por Newton-Raphson, con valores iniciales encontrados por PSO. Para el cálculo de los valores iniciales se realizaron simulaciones con un número determinado de partículas e iteraciones, 50 y 100, respectivamente. La columna 8 muestra el tiempo utilizado por PSO para el cálculo de los valores iniciales, mientras que la columna 9 muestra el tiempo requerido por el método Newton-Raphson. La suma de ambos (tiempo total) puede verse en la última columna de esta tabla.
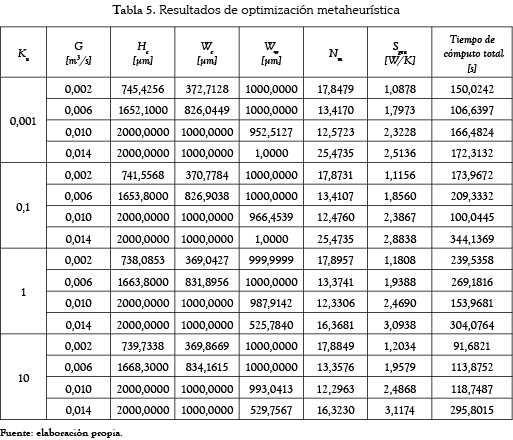
Para el caso en el que se utilizó solamente el algoritmo PSO, se logró obtener los parámetros de diseño óptimos, como se muestra en la tabla 5.
Al aumentar el valor de G se obtiene un incremento en la tasa de generación de entropía. También se puede observar que el comportamiento de Hc y Wc tiende a ser constante en términos de Kn. Por el contrario, Ww es aproximadamente constante en función de G.
La combinación de parámetros (Hc, Wc y Ww) que resulta en el mínimo valor de generación de entropía para un flujo de aire determinado y un valor del número de Knudsen corresponderá al micro-canal óptimo. Por ejemplo, para el caso en que las condiciones de operación corresponden a un flujo de aire (G) de 0,002 (m3/s) y un número de Knudsen (Kn) de 0,1, el micro-canal óptimo deberá tener una altura de 741,5 µm, un ancho de canal de 2*(370,78) µm y un espesor de pared de canal de 2*(1000) µm, con 18 canales en total (ver tabla 5).
3 CONCLUSIONES
Al comparar los resultados de los dos métodos, se puede concluir que PSO entrega soluciones (tasas de generación de entropía) similares a las presentadas por el método de los multiplicadores de Lagrange. El PSO ofrece una alternativa mucho más eficiente y sencilla que el método de Newton-Raphson, considerando el requerimiento de este último, de tener como valores iniciales, aproximaciones a las soluciones del sistema de ecuaciones, por lo que requeriría entonces métodos alternativos para encontrarlos, o una muy buena intuición por parte del usuario. Para el presente caso, fue un trabajo de considerable laboriosidad al pretender encontrar 17 valores iniciales apropiados para garantizar la convergencia del método de solución del sistema de ecuaciones no lineales, con el agravante de no disponer de criterios técnicos certeros. Se propuso entonces como estrategia de solución alterna, utilizar el algoritmo PSO para encontrar estos valores iniciales, lográndose resultados muy satisfactorios que fueron utilizados en la solución del sistema mediante Newton-Raphson. La diferencia de los tiempos de cómputo de ambos métodos es bastante notable, ya que los de PSO son aproximadamente 11 a 12 veces menores, considerando el peor de los casos, que los presentados por Newton-Raphson, demostrando que el algoritmo PSO tiene un desempeño superior en lo que a tiempos de cómputo se refiere. En cuanto a simplicidad de los algoritmos, basta con recordar la necesidad del método de Lagrange de resolver el sistema de ecuaciones no lineales generado, utilizando generalmente Newton-Raphson multidimensional en donde se requiere calcular el Jacobiano de la función objetivo ampliada (incluyendo restricciones) en cada iteración. Caso contrario ocurre con el PSO, que además de no requerir derivadas, no fue necesario un método auxiliar para la inclusión de las restricciones. Por las razones presentadas, es posible concluir que el PSO es una herramienta de optimización para el diseño de micro-canales que posee ventajas bastante notables ante métodos tradicionales como los multiplicadores de Lagrange, que aunque entrega resultados apropiados, requiere esfuerzos computacionales adicionales para hacerlo.
REFERENCIAS
[1] A. Bejan, ''Entropy generation in heat transfer,'' en Entropy Generation Minimization, J. Wiley, Boca Raton, FL: CRCPress, 1996, pp. 71-104. [ Links ]
[2] J. Culham y Y. Muzychka, ''Optimization of plate fin heat sinks using entropy generation minimization,'' IEEE Trans. Compon. Packag. Technol., vol. 24, n.° 2, pp. 159-165, jun. 2001. [ Links ]
[3] J. Culham et al., ''The influence of material properties and spreading resistance in the thermal design of plate fin heat sinks,'' presentado al Proc. 35th Nat. Heat Transfer Conf, Anaheim, CA, jun. 2001. [ Links ]
[4] W. Khan, et al., ''Optimization of microchannel heat sinks using entropy generation minimization method,'' IEEE Trans. Compon. Packag. Technol., vol. 32, n.° 2, pp. 243-251, jun. 2009. [ Links ]
[5] W. Khan, et al., ''Optimal design of tube banks in cross flow using entropy generation minimization method,'' AIAA J. Thermophys. Heat Transfer., vol. 21, n.° 2, pp. 372-378, enero, 2007. [ Links ]
[6] W. Khan, et al., ''Optimization of pin-fin heat sinks using entropy generation minimization,'' IEEE Trans. Compon. Packag. Technol., vol. 28, n.° 2, pp. 247-254, jun. 2005. [ Links ]
[7] R. Knight et al., ''Heat sink optimization with application to microchannels,'' IEEE Trans. Compon. Hybrids Manuf. Technol., vol. 15, n.° 5, pp. 832-842, octubre 1992. [ Links ]
[8] C. Perret, et al., ''Microchannel integrated heat sinks in silicon technology,'' Applied Physics., vol. 18, n.° 2, pp. 115-123, octubre 1998. [ Links ]
[9] C. Perret et al., ''Analytic modeling, optimization, and realization of cooling devices in silicon technology,'' IEEE Trans. Compon. Packag. Technol., vol. 23, n.° 4, pp. 665–672, diciembre 2000. [ Links ]
[10] S. Kim, ''Methods for thermal optimization of microchannels heat sinks,'' Heat Transfer Eng., vol. 25, n.° 1, pp. 37–49, enero 2004. [ Links ]
[11] S. Kandlikar y W. Grande, ''Evaluation of single phase flow in microchannels for high flux chip cooling-thermohydraulic performance evaluation and fabrication technology,'' Heat Transfer Eng., vol. 25, n.° 8, pp. 5–16, junio 2004. [ Links ]
[12] J. Kennedy y R. Eberhat, ''Particle swarm optimization,'' presentado al Proc. Of the IEEE Int. Conf. on Neural Networks IV., Pistakaway, NJ, 1995. [ Links ]
[13] M. Montes et al., ''Heterogeneous particle swarm optimizers,'' presentado al IEEE. Congress on Evolutionary Computation.University Libre de Bruxelles, Brussels, mayo 2009. [ Links ]
[14] M. Fichman, y G. Hetsroni, ''Viscosity and slip velocity in gas flow in microchannels,'' Physics of fluids., vol. 17, no.12, pp.123102-123102-5, dic. 2005. [ Links ]
[15] S. Rao, ''Classical optimization techniques,'' en Engineering Optimization: Theory and Practice, J. Wiley, Ed. 4a ed. New Jersey: J. Wiley & Sons, 2009, pp. 85-93. [ Links ]
[16] A. De Freitas y E. Pinto, ''Optimization of nonlinear constrained particle swarm,'' Ilumina., vol. 12, n.° 1, pp. 30-36, enero 2006. [ Links ]
[17] F. Van Den Bergh y A. Engelbrecht, ''A cooperative approach to particle swarm optimization,'' IEEE transactions on evolutionary computation, vol. 8, n.° 3, pp. 225-239, junio 2004. [ Links ]
[18] X. Yang y W. Zhang, ''A new strategy for improving particle swarm optimization,'' presentado al IEEE. Second international conference on intelligent computation technology and automation, Changsha, China, octubre 2009. [ Links ]
[19] Z. Zhan et al., ''Adaptive particle swarm optimization,'' IEEE Transactions on systems, Man and Cybernetics., vol. 39, n.° 6, pp. 1362-1381, enero 2009. [ Links ]