Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Ingenierías Universidad de Medellín
Print version ISSN 1692-3324
Rev. ing. univ. Medellín vol.11 no.21 Medellín July/Dec. 2012
ARTÍCULO ORIGINAL
INFERENCIA DIFUSA APLICADA A LA INGENIERÍA CONCURRENTE PARA EL DISEÑO DE PRODUCTOS DE MANUFACTURA EN CONDICIONES DE INCERTIDUMBRE*
FUZZY INFERENCE APPLIED TO CONCURRENT ENGINEERING FOR MANUFACTURING PRODUCT DESIGN UNDER CONDITIONS OF UNCERTAINTY
Martín Darío Arango Serna**; Conrado Augusto Serna Urán***; Ana Carolina Gómez Builes****
** I.I, PhD., Profesor titular Universidad Nacional de Colombia. Escuela Ingeniería de la Organización. Facultad de Minas. mdarango@unal.edu.co.
*** I,I, MSc, profesor asistente Universidad de San Buenaventura. casernau@unal.edu.co.
**** I.A MSc. Universidad Nacional de Colombia. acgomez@unal.edu.co.
Recibido: 04/02/2011
Aceptado: 05/10/2012
RESUMEN
En este artículo se desarrolla un modelo de inferencia difusa para la toma de decisiones en condiciones de incertidumbre aplicado al diseño de productos bajo un esquema de ingeniería concurrente. Los requisitos del cliente y los criterios de los diferentes equipos interdisciplinarios para evaluar un diseño en particular son presentados como variables difusas. El modelo aquí desarrollado es aplicado a una empresa de confecciones.
PALABRAS CLAVE
diseño concurrente, conjuntos difusos, diseño de productos.
ABSTRACT
In this article a fuzzy inference model is developed for decision making under uncertainty conditions, applied to the design of products under a scheme of concurrent engineering. Customer requirements and criteria of different interdisciplinary teams to evaluate a particular design are presented as fuzzy variables. The model developed is applied to a garment company.
KEY WORDS
concurrent design; fuzzy sets; product design.
INTRODUCCIÓN
Actualmente el mercadeo se fundamenta en tendencias de diversificación cultural, estilos de vida individuales, globalización y consideraciones ambientales cada vez más complejas y significativas que obligan a las empresas a tener sistemas de manufactura ágiles que respondan a los continuos cambios en las condiciones de mercado y de manufactura. Es así como para enfrentar los nuevos requerimientos, han sido propuestas nuevas herramientas para una nueva generación de sistemas de manufactura, tales como: sistemas de manufactura basados en agentes, sistemas de manufactura fractal [1]. Igualmente, la gestión de la incertidumbre a través de las aplicaciones de los conjuntos difusos hacen que las anteriores herramientas puedan ser consideradas para desarrollar sistemas inteligentes en ambientes abiertos y dinámicos que faciliten el diseño y desarrollo de productos de una forma más ágil y rápida.
La ingeniería concurrente ha demostrado su efectividad al considerar grupos interdisciplinarios que actúan en pro de diseños más ajustados a los requerimientos del cliente y a las capacidades de manufactura que pueden tenerse.
La ingeniería concurrente (IC) cuenta con una definición para cada uno de los acercamientos teóricos o prácticos que sobre ella se han realizado; existe una variedad de nombres con los cuales se designan principios o procesos básicos de la ingeniería concurrente tales como ingeniería simultánea, ingeniería cooperativa, diseño integrado de procesos y productos, diseño concurrente, entre otros [2]. La primera definición dada en 1986 por el Instituto para Análisis de Sistemas de Defensa de los EE. UU. fue: ''La ingeniería concurrente es una aproximación al diseño concurrente, integrado de productos y a sus procesos relacionados, incluyendo fabricación y soporte. Esta aproximación pretende que quienes desarrollan el producto consideren todos los elementos del ciclo de vida del producto desde su concepción hasta su desaparición, incluyendo calidad, costo, tiempo y necesidades del usuario'' [3]. Otra definición general es: ''La ingeniería concurrente es un enfoque sistemático para el desarrollo de productos integrados que hace énfasis en la respuesta a las expectativas del cliente. Involucra valores de equipo, como la cooperación, la confianza y el intercambio, de tal manera que la toma de decisiones sea por consenso, con la participación de todas las perspectivas en paralelo, desde el comienzo del ciclo de vida del producto'' [4].
La ingeniería concurrente en el diseño y desarrollo sirve como mecanismo para sincronizar la información tomada en el mercado con las posibilidades para el desarrollo de productos que tenga la empresa, tratando de acortar el tiempo necesario para colocar los productos a disposición de los clientes, reducir los costos asociados y evitar los reprocesos a lo largo de la cadena de valor.
La ingeniería concurrente remplaza el enfoque tradicional secuencial de diseño y fabricación de producto por un enfoque simultáneo en paralelo con menos procesos vinculados en serie. Por lo tanto, se pretende reducir el esfuerzo total que se invierte en llevar un producto desde su concepto hasta el momento de la entrega, teniendo en cuenta las necesidades tanto de los consumidores como de los clientes industriales.
El problema de diseño de productos abordado con lógica difusa permite de forma efectiva acortar el período de desarrollo y puede reducir los costes de fabricación, a pesar del aumento de las necesidades en los diferentes departamentos. Los modelos difusos facilitan la introducción de una variedad de familias de productos que satisfacen las necesidades de diversos usuarios. El método de diseño mediante un conjunto difuso es uno de los métodos para resolver problemas relacionados con la flexibilidad. Es así como el modelo de diseño y desarrollo de productos, bajo un esquema de ingeniería concurrente como el que se presenta en este articulo, tiene como objetivo satisfacer las necesidades del cliente y reducir los costos de desarrollo y producción, utilizando los conjuntos difusos para desarrollar una metodología que responda a una amplia gama de necesidades de los clientes y simultáneamente minimizar los costos en producción.
Este artículo está organizado de la siguiente manera: En la sección 2 se presenta el estado del arte relacionado con el diseño de productos en contexto de incertidumbre. En la sección 3 se describe el concepto de la inferencia difusa. En la sección 4 se desarrolla la metodología del modelo propuesto en una empresa del sector de la confección de prendas intimas. En la sección 5 se analizan los resultados arrojados por el modelo propuesto y finalmente en la sección 6 se dan a conocer las conclusiones.
1. DISEÑO DE PRODUCTOS EN CONTEXTO DE INCERTIDUMBRE, UN ESTADO DEL ARTE
A partir de los trabajos de Thunnissen [5], Wynn et al. [6] y Hastings y McManus [7], se puede destacar que frente a la incertidumbre son dos los caminos que se han adoptado. Por un lado, una parte importante de los estudios ha pretendido desarrollar estrategias que permitan erradicar o al menos mitigar su injerencia en el diseño y desarrollo de productos y, por otro, una buena parte de la bibliografía sobre la incertidumbre se ha concentrado en generar alternativas que les permitan a las empresas adaptarse de mejor manera a todos aquellos factores que necesariamente permanecerán como desconocidos, y diseñar modos de respuesta ágil para cuando los imprevistos alteren o modifiquen el curso regular de un proceso de manufactura. Hastings y McManus [7] ilustran las variables que componen la incertidumbre y presentan los modos de acuerdo con los cuales puede ser valorada como 'riesgo' o como 'oportunidad', y explican las acciones que conducirían a mitigar la incertidumbre o, bien, a explotarla a favor de los rendimientos de la empresa.
Hastings y McManus [7] y Wynn et al. [6] presentan trabajos en los cuales, aunque la intención pareciera ser la de aquellos que pretenden eliminar o disminuir los impactos de la incertidumbre en los procesos de diseño y producción, lo que realmente logran es dar forma a una estrategia que reconoce a la incertidumbre como una realidad incuestionable dentro de la dinámica empresarial. En consecuencia, diseñan una serie de pasos que basados en los 'dominios', que facilitan incrementar los márgenes de fiabilidad de los sistemas y de los procesos que se puedan ver afectados por la ocurrencia de distintos tipos de eventos (desde pequeñas demoras en la corrección de un plan de diseño, hasta la crisis total generada por una situación inesperada que haga inviable la culminación del proyecto).
El aumento de la fiabilidad en los procesos internos de la empresa (administración, diseño, fabricación) hace que estos se deban orientar a robustecer la capacidad general de cada uno de los equipos de trabajo, de modo que la capacidad general de la empresa en cada proceso se vea fortalecida [7]. Este fortalecimiento debe verse reflejado en una mayor flexibilidad de los equipos de trabajo y de los procesos, así como en la versatilidad para desarrollar las actividades de forma más efictiva, generando una mayor capacidad de adaptación para responder de modo eficiente a los constantes e imponderables ataques de la incertidumbre, cuya presencia será siempre un hecho para los procesos empresariales.
Fujita et al. [8] propusieron un método de diseño que permite la optimización simultánea, centrándose en las necesidades difusas de los clientes en consideración de la combinación estructural de módulos y atributos. Con este método y la importancia de mejorar la independencia de la estructura modular, Koga, et al. [9] proponen una metodología de diseño de productos que considera la falta de claridad con respecto a los requisitos del cliente y el desempeño productivo; dicho método usa una clasificación difusa para maximizar la variedad de ofertas y minimizar los costos.
Otras aplicaciones de la lógica difusa en los sistemas de producción en el ámbito local se pueden encontrar en los trabajos de Arango et al. [10, 11], quienes desarrollan modelos matemáticos difusos aplicados a la planificación de la producción en contextos de incertidumbre en la industria automotriz. Por otro lado, Gómez [12] presenta un modelo de inferencia difusa aplicado al diseño y desarrollo de productos en la industria de las confecciones, bajo un esquema de ingeniería concurrente en el que se define seis factores de análisis para seleccionar la muestra que mejor se ajuste a las condiciones de entrada de los clientes externos e internos.
2. INFERENCIA DIFUSA
Un sistema lógico difuso es un mapeo no lineal de un vector de datos de entrada con una salida escalar [13]. La lógica difusa y los conjuntos difusos definen las especificaciones para realizar un mapeo no lineal, ya que se pueden utilizar datos numéricos y conceptos lingüísticos de forma simultánea. Los tipos más populares de sistemas de inferencia difusa son: sistemas difusos de tipo Mamdani y sistemas difusos de tipo Sugeno [13]; se definen ambos sistemas de la siguiente manera:
2.1 Sistemas de tipo Mamdani
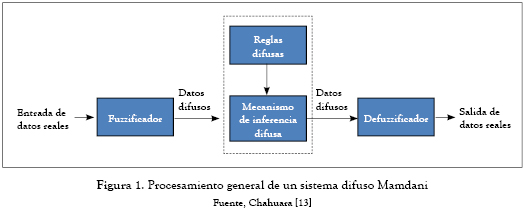
Este modelo fue propuesto por Ebrahim Mamdani en 1974; en este sistema difuso las reglas están dadas por expresiones lingüísticas. La figura 1 muestra la estructura general que posee un modelo tipo Mamdami
Los componentes principales de este sistema se explican a continuación:
• Fuzzficador: la entrada para este tipo de sistemas es un valor numérico y es necesario convertir este valor numérico en un valor difuso para que pueda ser interpretado por el mecanismo de inferencia.
• Mecanismo de inferencia difusa: una vez que el fuzzificador arroja los valores difusos, el mecanismo de inferencia los procesa para obtener el grado de pertenencia a un determinado subconjunto difuso. Posteriormente, utilizando dicho grado de pertenencia se realiza la búsqueda de la regla más adecuada con la base de reglas difusas para obtener la salida difusa más apropiada.
• Base de reglas difusas (base de conocimiento): es la manera que tiene el sistema difuso de guardar el conocimiento lingüístico que le permite resolver el problema para el cual está diseñado. Estas reglas son del tipo SI-ENTONCES, el cual está formado por dos partes: el antecedente y el consecuente. Un ejemplo de regla difusa es el siguiente:
Si el servicio es bueno, entonces la propina es alta
Antecedente Consecuente
El consecuente de una regla fuzzy asigna un conjunto difuso a la salida, los cuales sufren el proceso de agregación que se hace según el método ''MAX'' que elige en cada valor posible de salida el máximo valor de pertenencia obtenido en todas las reglas. Así, el conjunto difuso agregado de salida será la respuesta difusa del sistema de decisión.
• Defuzzificador: la salida que genera el mecanismo de inferencia es una salida difusa, la cual no puede ser interpretada por una entidad externa que solo manipula información numérica. Para lograr que la salida del sistema difuso pueda ser interpretada, es necesario convertirla al tipo de salida que entienda la entidad externa. Existen varias opciones para realizar dicha conversión, las cuales se presentan a continuación:
Centro de Gravedad:

Centros Promediados:

2.2 Sistemas de tipo Sugeno
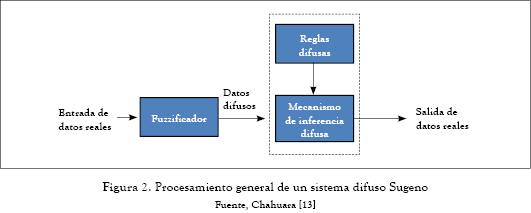
De acuerdo con el trabajo de Chahuara [13], este modelo difiere del de Mamdani en que no cuenta con un desfuzzificador; su estructura está compuesta por:
• Fuzzificador: realiza la misma función que el fuzzificador de Mamdani.
• Mecanismo de inferencia difusa: es igual a la descripción del mecanismo de inferencia difusa de Mamdani.
• Base de reglas difusas: son diferentes de las reglas de un sistema Mamdani y el consecuente de estas reglas no es una etiqueta lingüística, sino una función de la entrada del sistema en un momento dado.
El resultado arrojado por la regla difusa activa es un valor numérico real que puede ser utilizado por la entidad externa adecuada. Por tal motivo, ya no se requiere de una etapa de defuzzificación. Ver figura 2:
La principal diferencia entre los modelos Mamdani y Sugeno es la forma en que son determinadas las salidas del sistema. De acuerdo con el trabajo de León [14], el tipo Mamdani es muy utilizado y tiene como principal característica que las funciones de pertenencia de salida corresponden a conjuntos difusos, los cuales necesitan ser desfuzzificados utilizando para ello alguna técnica particular.
3. APLICACIÓN DEL MODELO PROPUESTO
El sistema de inferencia difusa elegido para desarrollar el modelo es de tipo Mamdani; este será aplicado al desarrollo de brasieres femeninos para mujeres adultas. El modelo propuesto define las variables de entrada que pueden condicionar el proceso de decisión. Por lo tanto, es necesario decidir los valores que pueden llegar a tomar dichas variables (universos de discurso) así como las etiquetas y sus funciones de pertenencia asociadas.
En una primera instancia es necesario contar con una base de datos de conocimiento, que puede provenir de las opiniones de expertos o por entrevistas al personal involucrado. A continuación, se debe llevar a cabo el proceso decisorio, para lo cual se define la base de reglas que combina los factores de entrada en el modo preciso para obtener la salida correspondiente. Para resolver el modelo tipo Mamdani resultante, se emplea el método del centroide, para calcular la abscisa correspondiente al centro de gravedad de dicho número difuso, y a partir de allí se puede seleccionar la alternativa que mejor se adapte según los requisitos.
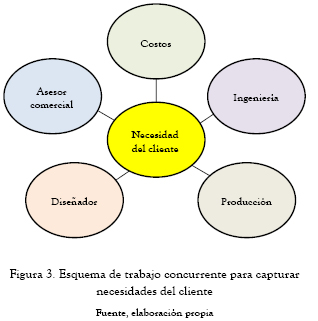
El modelo propuesto parte de considerar una estructura de trabajo concurrente para la captura e interpretación de las necesidades del cliente y su integración con características funcionales de la compañía, considerando así desde actividades tempranas los principales procesos de la compañía que intervienen en el desarrollo de nuevos productos (figura 3).
A partir del modelo propuesto se presentan mecanismos particulares para la detección, interpretación y desarrollo de las necesidades del cliente desde dos enfoques básicos: requerimientos objetivos y requerimientos subjetivos para combinarlos con factores técnicos de la empresa que intervienen el desarrollo del producto. El modelo pretende ser una herramienta para la toma de decisiones, dirigidas a tener en cuenta no solamente las cualidades funcionales de un producto, sino también las restricciones técnicas de la empresa en etapas tempranas de su desarrollo.
A continuación se presentan las actividades que se proponen para el desarrollo de productos especiales:
• Actividad 1. Establecer requisitos del cliente: esta primera actividad está orientada en recopilar todos los requisitos y necesidades que el cliente tiene con respecto al producto.
• Actividad 2. Seleccionar posibles diseños base: se eligen cinco posibles diseños que pueden servir de base para elaborar el producto que el cliente necesita. En la medida que se tenga diseños similares a lo requerido por el cliente y se realice una selección apropiada de estos, el proceso de desarrollo será más efectivo.
• Actividad 3. Seleccionar mejor diseño. De los cinco modelos seleccionados en la actividad anterior y usando el modelo difuso aquí explicado, se selecciona el modelo que tenga una mejor combinación de las calificaciones dadas por el cliente y los procesos de costos, ingeniería, comercial y diseño.
• Actividad 4. Elaborar muestra física. Se califica el grado de dificultad de la muestra seleccionada y se informa a los demás procesos los cambios surgidos en la referencia base para iniciar con la elaboración de la muestra física.
• Actividad 5. Aprobación de muestra por el cliente: se presenta la muestra física al cliente, se realizan otros posibles cambios que puede sugerir o se aprueba el diseño para iniciar con su producción.
3.1 Factores de evaluación y variables de entrada
A continuación se presenta la aplicación práctica en la que se basa el modelo difuso propuesto, con el fin de ilustrar el funcionamiento del mismo.
En primer lugar, se definen los siguientes factores, para el diseño solicitado:
• Costo: está conformado por los costos de los materiales y el tiempo de producción. Esta información está registrada en el aplicativo de costos, donde se relaciona el consumo de cada material y se multiplica por el costo unitario del mismo, más el tiempo de operación total. La responsabilidad de dicha información está a cargo del proceso de costos.
• Tiempo de entrega: se determina a partir de la complejidad y el tiempo de producción. Esta información surge a partir de la secuencia de actividades definida y del estudio de tiempos. La responsabilidad de dicha información está a cargo del proceso de ingeniería.
• Textura: es definida como la propiedad que tienen las superficies externas de los objetos, así como las sensaciones que causan, que son captadas por el sentido del tacto. En los brasieres, esta propiedad depende principalmente de las características de los materiales y los acabados de la prenda.
• Diferenciación: se refiere al grado de innovación del producto, ya sea por sus materiales, por los beneficios que ofrece u otra característica.
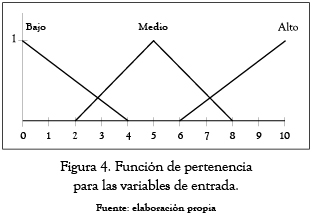
En segundo lugar, se establece el nivel de importancia con la que los clientes califican los factores anteriormente mencionados; el equipo de ingeniería también da una valoración sobre la facilidad técnica con la que se elaboraría el producto. De esta manera se tienen dos variables de entrada por cada factor mencionado. Estas variables pueden tomar valores continuos en una escala de 0 a 10 y definirse con la siguiente función de pertenencia de tipo triangular (ver figura 4).
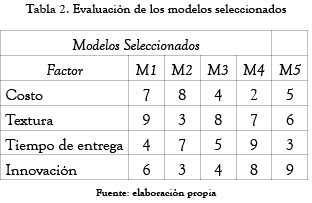
Para el ejemplo que se quiere ilustrar, en la tabla 1 se presentan las siguientes variables de entrada.
Una vez definidos los requisitos del cliente, se seleccionan cinco diseños base (M1, M2, M3, M4 y M5) los cuales son evaluados por un equipo interdisciplinario conformado por personas de ingeniería, costos, comercial y diseño. Los resultados obtenidos para cada uno de los cinco modelos seleccionados con respecto a los tres factores de evaluación son presentados en la tabla 2.
3.2 Restricciones
Para elegir cuál de estos modelos se ajusta más a los requerimientos definidos anteriormente, se definen a partir de la tabla 2, las siguientes restricciones de acuerdo con la arquitectura de un modelo de inferencia difusa de tipo Mamdani:
En total fueron formuladas 180 restricciones, las cuales surgen a partir del total de combinaciones de las variables de entrada con los diseños, es decir:
4 factores x 3 niveles de valoración del cliente x 3 niveles de valoración de ingeniería x 5 diseños de brasier = 180
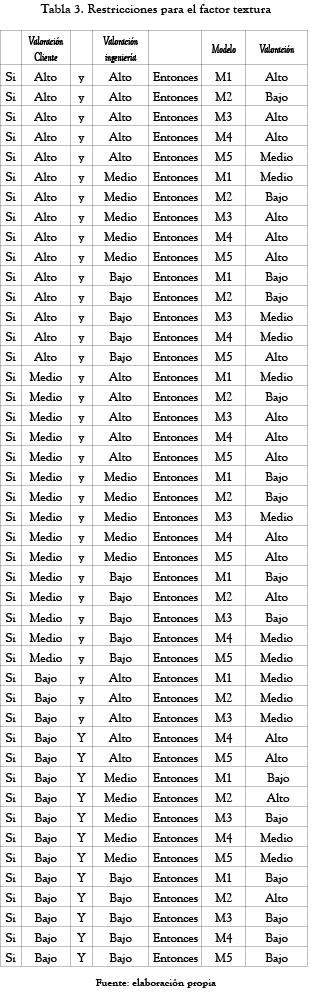
En la tabla 3 se muestran las restricciones formuladas para el factor textura.
3.3 Variables de salida
El modelo posee cinco variables de salida (M1, M2, M3, M4, M5) las cuales indican la valoración obtenida por cada modelo de brasier ante una combinación específica de las dos variables de entrada (valoración cliente y valoración ingeniería) en los cuatro niveles formulados. Al igual que las variables de entrada, las funciones de pertenencias para las variables de salida también se formulan como funciones de distribución triangular con niveles bajo, medio, alto. Estos valores se generan por medio del método del centro de gravedad, posteriormente son comparados entre sí, para seleccionar el modelo de brasier que resulta más adecuado ante una combinación particular de parámetros de entrada.
4. ANÁLISIS DE RESULTADOS
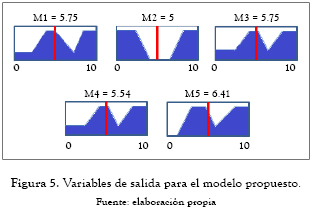
La herramienta informática utilizada para resolver este problema es MATLAB 7.0 a través del toolbox Fuzzy, que permite modelar sistemas de tipo Sugeno o Mamdani. Los resultados obtenidos para cada uno de las variables de salida definidas, en este caso los cinco modelos de brasier preseleccionados, se presentan a continuación (figura 5):
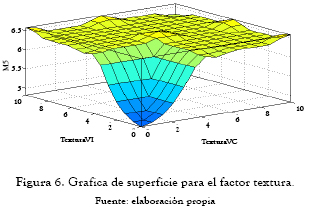
De acuerdo a estos resultados, se determina que el diseño que más se ajusta al conjunto de necesidades del cliente y de factibilidad considerado por los diferentes departamentos de la empresa es el modelo M5, el cual tiene una valoración de 6.41. En la figura 6, se observa la relación entre las variables de entrada para el factor textura y su correspondiente nivel de ajuste de acuerdo con las restricciones formuladas para dicho factor.
El resultado obtenido puede variar considerablemente en caso que se asignen diferentes niveles de importancia a los factores, como puede suceder cuando se quiere dar un mayor nivel de importancia a los factores asociados directamente a los clientes como tiempo de entrega, innovación, entre otros.
5. CONCLUSIONES
En este artículo se ha propuesto un modelo difuso de tipo Mamdani para la evaluación de alternativas existentes a partir de la combinación de diversos factores de entrada, que en este caso corresponden a la integración entre las necesidades del cliente y algunas especificaciones técnicas de la empresa; este modelo permite incluir cualquier cantidad de factores que afecten al proceso decisorio, sin importar su número y naturaleza (cuantitativa o cualitativa). Además, permite que se incluya el lenguaje natural apropiado, asociado a las variables relevantes en el proceso de diseño y desarrollo de productos.
El modelo de inferencia difusa planteado permite integrar la incertidumbre asociada al diseño y desarrollo de productos, ya que permite incluir variables de diversa naturaleza. Se ha comprobado que es posible contar con un mecanismo para identificar, interpretar y materializar de una manera eficiente y acertada las necesidades del cliente respecto a un tipo de producto, todo esto a partir del análisis y selección entre alternativas de diseño que se ajusten a los intereses del cliente y de la compañía.
REFERENCIAS
[1] W. Gu, D. Tanga and L, Wanga. ''A novel bio-inspired approach for adaptive manufacturing system control. New world situation: New Directions in Concurrent Engineering,'' presentado al the 17th ISPE International Conference on Concurrent Engineering. New York. 2010 [ Links ]
[2] S. C. Skalak. Implementing Concurrent Engineering in Small Companies. Marcel Dekker, New York, 2002, pp. 5-10. [ Links ]
[3] R. I. Winner, J.P. Pennell, H. E. Bertrand y M. G. Slusarczuk. ''The role of concurrent engineering in weapons system acquisition'', IDA Report R-338, Institute for Defense Analyses, Alexandria, 1988. [ Links ]
[4] K. J. Cleetus. ''Definition of concurrent engineering,'' en: Cerc Technical Report Series, Reseach Notes, CERC-TR-RN-92-003, West Virginia University. Morgantow. 1992. [ Links ]
[5] D. P. Thunnissen. Propagating and mitigating uncertainty in the design of complex multidisciplinary systems. Tesis doctoral, California Institute of Technology, Pasadena, California. 2005, pp.23-35. [ Links ]
[6] D. Wynn, M. Marek and J. Clarkson. ''Approaches to mitigate the impact of uncertainty in development processes,'' presentado al International Conference on Engineering Design. Stanford University, Stanford, Ca, USA. 2009. [ Links ]
[7] D. Hastings y H. Mcmanus. ''A Framework for understanding uncertainty and its mitigation and exploitation in complex systems,'' presentado al MIT Engineering Systems Symposium, Cambridge, 2004. [ Links ]
[8] K. Fujita. ''Research on optimization in designing product family integration and on the method of optimization (1st report: structure and aspect of optimization problem)'', Collected papers of Japan Society of Mechanical Engineers, Collection C, Vol. 68, N.° 666, pp. 675–682. 2002 [ Links ]
[9] T. Koga y K. Aoyama. ''Module design based on interface integration to maximize product variety and minimize family cost'', presentado al the International Conference on Engineering Design, Paris, 2007 [ Links ]
[10] M. D. Arango, C. A. Serna, G. Pérez. ''Uso de la programación lineal paramétrica en la solución de un problema de planeación de requerimiento de materiales bajo condiciones de incertidumbre''. Rev. Ing. Univ. Nacional, vol. 30, n.° 3, pp. 96-105, dic. 2010. [ Links ]
[11] M. D. Arango, C. A. Serna, K. C. Álvarez. Modelos difusos aplicados a la planeación de la producción. Editorial Universidad Nacional de Colombia, Medellín. 2009, pp. 55-70. [ Links ]
[12] A. C. Gómez. Elaboración de un modelo de ingeniería concurrente para el diseño de productos en condiciones de incertidumbre. un caso aplicado a pequeñas y medianas industrias del sector de la confección en el valle de Aburrá. Tesis de maestría, Universidad Nacional de Colombia, Medellín, 2010, pp. 76-94. [ Links ]
[13] J. C. Chahuara. Control Neuro-difuso aplicado a una grúa torre. Tesis, Universidad Nacional Mayor de San Marcos, Lima (Perú), 2005, pp. 35-44 [ Links ]
[14] J. A. León. Metodología para la detección de requerimientos subjetivos en el diseño de producto. Tesis doctoral, Universitat Politécnica de Catalunya. España. 2005, pp. 18-106. [ Links ]
Notas:
* Artículo procedente del proyecto de investigación ''Elaboración de un modelo de ingeniería concurrente para el diseño de productos en condiciones de incertidumbre. un caso aplicado a pequeñas y medianas industrias del sector de la confección en el valle de Aburrá'', financiado por la DIME - Universidad Nacional de Colombia- Sede Medellín.