Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Revista Ingenierías Universidad de Medellín
versão impressa ISSN 1692-3324
Rev. ing. univ. Medellín vol.11 no.21 Medellín jul./dez. 2012
ARTÍCULO ORIGINAL
UN ALGORITMO METAHEURÍSTICO BASADO EN RECOCIDO SIMULADO CON ESPACIO DE BÚSQUEDA GRANULAR PARA EL PROBLEMA DE LOCALIZACIÓN Y RUTEO CON RESTRICCIONES DE CAPACIDAD*
A META-HEURISTIC ALGORITHM BASED ON THE SIMULATED ANNEALING WITH GRANULAR SEARCH SPACE FOR THE CAPACITATED LOCATION ROUTING PROBLEM
John Willmer Escobar**; Rodrigo Linfati***
** Corresponding Author. Researcher, University of Bologna. Profesor Tiempo Completo, Pontificia Universidad Javeriana Cali, Colombia. PhD(C) in Operations Research, University of Bologna, Italy. Magíster en Ingeniería Industrial, Universidad del Valle, Cali, Colombia. Especialista en Finanzas, Universidad del Valle, Cali, Colombia. Ingenierio Industrial, Universidad del Valle, Cali, Colombia. Departamento de Ingeniería Civil e Industrial, Pontificia Universidad Javeriana, Calle 18 No. 118-250, 26239 Cali, Colombia. Department of Electronics, Computer Sciences and Systems (DEIS), University of Bologna, Viale Risorgimento 2, 40136 Bologna, Italy. Email: johnwillmer.escobar2@unibo.it. Fax: +572 3218266.
*** Profesor Tiempo Completo, Universidad del Bío-Bío, Chile. PhD in Operations Research, University of Bologna, Italy. Magíster en Ingeniería Industrial, Universidad de Concepcion, Concepcion, Chile. Ingeniero Civil Industrial, Universidad de Concepcion, Concepcion, Chile. Department of Electronics, Computer Sciences and Systems (DEIS), University of Bologna, Viale Risorgimento 2, 40136 Bologna, Italy. Email: rlinfati@ubiobio.cl.
Recibido: 09/08/2012
Aceptado: 05/11/2012
RESUMEN
Consideramos el problema de localización y ruteo con restricciones de capacidad (CLRP), en el cual la meta es determinar los depósitos a ser abiertos, los clientes a ser asignados a cada depósito abierto, y las rutas a ser construidas para satisfacer las demandas de los clientes. El objetivo es minimizar la suma de los costos de abrir depósitos, de los costos de los vehículos usados, y de los costos variables asociados con la distancia recorrida por las rutas. En este paper, proponemos una metaheurística basada en simulado y recocido con espacio de búsqueda granular para resolver el problema CLRP. Experimentos computacionales en instancias de benchmarking tomadas de la literatura muestran que el algoritmo propuesto es capaz de obtener, dentro de tiempos computacionales razonables, soluciones de alta calidad mostrando su eficacia.
PALABRAS CLAVE
problema de localización y ruteo; simulado y recocido; búsqueda granular: algoritmos metaheurísticos.
ABSTRACT
The article deals with the Capacitated Location Routing Problem (CLRP) where the goal is to determine the depots to be opened, the customers to be assigned to each deposit opened, and the routes to be constructed for fulfilling customers' demands. The objective is to minimize the sum of costs resulting from opening depots, costs resulting from used vehicles, and variable costs associated to the distance across the routes. In this paper, a metaheuristic based on simulated annealing with granular search space for solving the CLRP is proposed. Computational experiments on benchmarking instances taken from literature show that the proposed algorithm is able to obtain high-quality solutions within reasonable computational times, thus showing its efficiency.
KEY WORDS
location routing problem; simulated annealing; granular search; metaheuristic algorithms.
INTRODUCCIÓN
El estudio de los problemas de localización y ruteo es un área relativamente nueva de investigación en el campo de la logística dentro de la ingeniería industrial e ingeniería de sistemas (específicamente en el campo de ciencias de la computación). Este tipo de problemas incluye dos decisiones fundamentales de la cadena de abastecimiento: la localización de instalaciones y el ruteo de vehículos. Un gran número de trabajos se ha dedicado a estudiar cada una de estas decisiones de manera independiente. Este hecho se puede explicar debido a que la localización es una decisión estratégica, la cual es tomada por un horizonte largo de tiempo. Por su parte, el ruteo es un aspecto operacional modificado varias veces en un tiempo corto. Sin embargo, según Rand [1], las decisiones de localizar depósitos frecuentemente son influenciadas por los costos de transporte, y viceversa. De igual forma, Salhi y Nagy [2] han encontrado que el costo logístico puede ser reducido a lo largo del tiempo, cuando se consideran decisiones de localización y ruteo simultáneamente.
Este artículo considera el problema de localización y ruteo con restricciones de capacidad en depósitos y vehículos (CLRP). El CLRP puede ser descrito como un problema de grafos de la siguiente manera. Sea G = (V,A) un grafo completo no dirigido, en el cual V = {1, …, m + n} es el conjunto de vértices y A es el conjunto de arcos. El conjunto de vértices es dividido en dos subconjuntos. Vértices i = 1, …, m corresponden a los depósitos potenciales, cada uno con capacidad Wi y costo fijo de apertura Oi. Vértices j = m + 1, m + n corresponden a los clientes, cada uno con valor de demanda Dj. Una flota homogénea de vehículos k, cada uno con capacidad Q, es disponible en cada depósito i ∈ V. Cada vehículo cuando es utilizado para realizar una ruta genera un costo fijo F. Un costo no negativo cij es asociado con cada arco (i,j) ∈ A.
El objetivo del CLRP es determinar los depósitos a abrir, los clientes a asignar a cada depósito abierto y las rutas a construir para satisfacer la demanda de los clientes con el mínimo costo global. Este costo incluye los costos fijos de apertura de los depósitos, los costos fijos asociados a los vehículos usados por las rutas y los costos de los arcos visitados por cada ruta. En el CLRP las siguientes restricciones son consideradas: i) cada ruta debe comenzar y terminar en el mismo depósito; ii) cada cliente debe ser visitado por una ruta exactamente una vez; iii) la suma de las demandas de los clientes visitados en una ruta no debe exceder la capacidad del vehículo Q; iv) la suma de las demandas de los clientes asignados a un depósito no debe exceder su capacidad Wi; v) los flujos entre depósitos no son permitidos.
Prins et al. [3] han propuesto una formulación de tres índices para el CLRP. Dicha formulación utiliza las variables binarias yi = 1 si el depósito i es abierto, fij = 1 si el cliente j es asignado al depósito i y xjlk = 1 si el arco (j,l) es visitado desde j a l en la ruta desarrollada por el vehículo k. El problema entonces es formulado mediante el siguiente modelo:
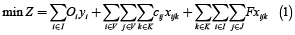
Sujeto a

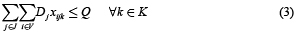
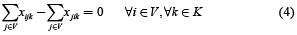
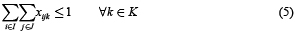
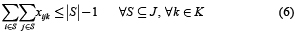
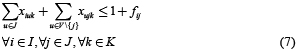
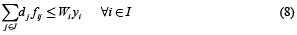
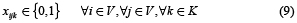

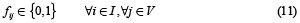
La función objetivo (1) suma los costos de los depósitos abiertos, los costos de los arcos visitados por las rutas y los costos fijos asociados con el uso de los vehículos. El grupo de restricciones (2) garantiza que cada cliente sea visitado exactamente por una ruta y que solamente tenga un predecesor en la secuencia de la ruta. El grupo de restricciones (3) y (8) son asociadas con las capacidades del depósito y vehículo, respectivamente. Restricciones (4) y (5) aseguran la continuidad de cada ruta y determina que cada una de ellas comience y termine en el mismo depósito. La eliminación de los subtours es satisfecha a través de las restricciones (6). Restricciones (7) especifica que un cliente puede ser asignado a un depósito solamente si existe una ruta que lo une. Finalmente restricciones (9), (10) y (11) representan las variables binarias usadas en el modelo.
El CLRP es considerado un problema NP-hard debido a que es la generalización de dos problemas NP-hard: el problema de localización de instalaciones con restricciones de capacidad (CFLP) y el problema de ruteo de vehículos con múltiples depósitos (MDVRP). En este artículo se propone un algoritmo metaheurístico basado en simulado y reconocido con espacio de búsqueda granular para resolver el CLRP. La literatura existente para el problema de CLRP es descrita en la Sección 1. La Sección 2 detalla el algoritmo propuesto. Los resultados computacionales son presentados en la Sección 3. Finalmente, conclusiones e investigación futura se detallan en la Sección 4.
1. REVISIÓN DE LA LITERATURA
La literatura relacionada con problemas de localización y ruteo ha sido condensada en Min et al. [4] y Nagy y Salhi [5]. En [4] se propone una clasificación para los problemas de localización y ruteo basada en el método de solución y las perspectivas del problema. Por su parte, en [5] se propone una clasificación más amplia basada en diferentes aspectos tales como el método de solución, la estructura jerárquica, el tipo de información, el período de planeación, etc.
De acuerdo con el método de solución, el problema CLRP ha sido resuelto mediante algoritmos exactos y heurísticos. Métodos exactos están basados en formulaciones de dos y tres índices. Formulaciones de tres índices han sido propuestas en [3]. Por otro lado, formulaciones de dos índices han sido propuestas por Laporte et al. [6] y Belenguer et al. [7]. Elementos comunes de estos trabajos son técnicas de relajación, desigualdades válidas y algoritmos de separación. En términos generales, estos trabajos han sido capaces de probar optimalidad solo en instancias que contienen menos de 100 clientes. Debido a lo anterior, algoritmos heurísticos han sido propuestos como alternativa para la solución de problemas de localización y ruteo de mediana y gran escala (problemas con más de 100 clientes).
En la literatura existente, varios trabajos han considerado métodos heurísticos para resolver el CLRP. Usualmente, métodos heurísticos determinan buenas soluciones con razonables tiempos de ejecución. Estas técnicas emplean diferentes métodos de solución para modelar la relación entre los dos subproblemas (problema de localización y problema de ruteo).
En [5] se ha realizado una clasificación de los algoritmos heurísticos en cuatro categorías: métodos secuenciales, métodos basados en clústeres, métodos iterativos, métodos jerárquicos. Métodos secuenciales resuelven el problema de localización y luego el problema de ruteo. Estos algoritmos, según Salhi y Rand [8], no permiten una retroalimentación entre los dos subproblemas. Métodos iterativos resuelven ambos subproblemas en un modo iterativo, retroalimentando la solución entre dos subproblemas. Estos métodos pueden resolver el CLRP de dos maneras: resolviendo el problema de ruteo de vehículos y asignando un depósito a cada ruta o resolviendo el problema de localización de depósitos y construyendo al menos una ruta para cada depósito. Métodos iterativos han sido estudiados recientemente por [3] y Tuzun y Burke [9].
En [5] se propone un algoritmo de dos fases que intercambia información entre ellas. En la primera fase, los clientes son agregados en ''súper clientes'', y el correspondiente problema de localización de instalaciones con restricciones de capacidad es resuelto por medio de la técnica de relajación Langragiana. En la segunda fase, un procedimiento metaheurístico basado en una búsqueda granular tabú (ver Toth y Vigo [10]) con un solo vecindario fue usado para resolver el resultante problema de ruteo con múltiples depósitos. Al final de cada iteración, información sobre los arcos predominantes es transmitida durante la siguiente fase. En [9] se ha propuesto un algoritmo tabú de dos fases: ruteo y localización. Este algoritmo itera entre la localización y ruteo para encontrar mejores soluciones para instancias medianas y grandes. En este trabajo, resultados para instancias de hasta 200 clientes han sido reportados.
Métodos basados en clústeres han sido propuestos por Barreto et al. [11]. En esta metodología, los clientes son agrupados en clústeres de acuerdo con la capacidad del vehículo. Luego, el problema de viajero de negocios (TSP) es resuelto para cada grupo de clientes. Finalmente, los grupos de clientes son asignados a cada depósito abierto. Métodos jerárquicos resuelven el CLRP usando una estructura jerárquica. El problema de localización es solucionado como problema principal, y luego el subsecuente problema de ruteo es resuelto como problema subordinado. En particular, estos métodos resuelven el problema de localización en un modo aproximado aplicando una subrutina que resuelve el correspondiente problema de ruteo.
Otras metaheurísticas para el CLRP han sido propuestas por Prins et al. [12]. En este trabajo, un algoritmo basado en un procedimiento aleatorio de búsqueda adaptativa goloso (GRASP) con estrategia de path-relinking ha sido propuesto. Los mismos autores han propuesto un algoritmo memético con administración de la población (MA|PM). Para mayores detalles, los lectores son referidos a Prins et al. [13].
Recientes metaheurísticas han sido propuestas por Duhamel et al. [14], Yu et al. [15] y Escobar et al. [16]. En [14] se propone un método basado en un hibrido GRASP con una búsqueda local evolucionada (ELS). En [15] se propone un procedimiento aleatorio basado en la heurística de recocido simulado con tres vecindades. Finalmente, en [16] se propone un algoritmo heurístico de dos fases para la solución del problema CLRP.
2. DESCRIPCIÓN DEL ALGORITMO PROPUESTO
En esta sección, se explica el algoritmo propuesto para resolver el CLRP. El algoritmo propuesto está basado en la metaheurística de recocido simulado con búsqueda de espacio granular propuesta en [10]. Recocido simulado es una metaheurística popular usada para resolver problemas discretos y continuos. La metaheurística recocido simulado adopta su nombre gracias a la analogía con el proceso físico de recocido con sólidos. En Eglese [17] se puede observar una buena visión general sobre el desarrollo teórico y la aplicación de la metaheurística de recocido simulado.
La principal característica de la metaheurística de recocido simulado es que proporciona una alternativa eficiente para escapar de óptimos locales al permitir movimientos ''peores'' respecto a la función objetivo (hill-climbing moves) en aras de encontrar un óptimo global. A medida que la temperatura se reduce a cero, los movimientos ''peores'' se producen con menos frecuencia convergiendo a óptimos globales. El procedimiento de recocido simulado comienza desde una solución aleatoria inicial. En cada iteración, una nueva solución es tomada del vecindario predefinido de la actual solución. El valor de la función objetivo de la nueva solución es comparado con la actual para determinar si un mejoramiento ha sido alcanzado.
En el algoritmo propuesto, se construye una solución inicial factible mediante un procedimiento híbrido introducido en [16]. Para mejorar dicha solución, un procedimiento basado en recocido simulado con espacio de búsqueda granular es aplicado. El procedimiento híbrido inicial permite obtener una solución factible con un tiempo de cómputo reducido. Una de las ventajas de usar este procedimiento es que permite localizar correctamente los depósitos, lo cual reduce el espacio de búsqueda del procedimiento de mejoramiento de un CLRP a un MDVRP. En otras palabras, el procedimiento de recocido simulado propuesto no considera decisiones de cierre y apertura de centros de distribución. Los procedimientos descritos con anterioridad son detallados en las siguientes Secciones.
2.1 Solución inicial
El procedimiento híbrido inicial introducido por [16] es capaz de encontrar soluciones de alta calidad con tiempos computacionales reducidos. Este procedimiento combina métodos exactos y heurísticos. A continuación se menciona cada uno de los pasos para la construcción de la solución inicial:
Paso 1: Un TSP tour gigante es construido considerando todos los clientes, mediante el conocido procedimiento heurístico Lin-Kernighan (LKH). Para mayores detalles ver Helsgaun [18].
Paso 2: El TSP tour gigante es divido en varios grupos de clientes llamados clústeres. El criterio para obtención de los grupos de clientes es la capacidad de los vehículos.
Paso 3: Para cada depósito i y cada clúster g, el procedimiento LKH es aplicado para encontrar el correspondiente TSP tour. De esta manera, es posible obtener la longitud de la ruta lig asignando el depósito i al clúster g.
Paso 4: Los depósitos son asignados a los clústeres resolviendo el correspondiente problema de localización de planta con restricciones de una sola fuente de abastecimiento (''Single Source Capacitated Plant Location Problem''). De esta manera se determina qué depósitos serán abiertos y cuáles TSP tours serán asignados a cada depósito.
Paso 5: Finalmente un procedimiento de división es aplicado a la solución actual. Este procedimiento busca reducir la distancia recorrida, adicionando nuevas rutas y asignándolas a depósitos diferentes. Este procedimiento es efectivo solamente cuando el costo por el uso de un vehículo F es reducido. Para las tres combinaciones de dos arcos, arcos (r,s) y (t,u), los siguientes pasos son repetidos:
– Arcos (r,s) y (t,u) son removidos de la ruta actual;
– El arco (r,u) es insertado en la nueva ruta;
– El conjunto de clientes que pertenecen a la cadena que conecta vértice s con vértice t en la ruta considerada es seleccionado como un nuevo clúster;
– Para cada depósito para el cual la asignación de los clientes satisface las restricciones de capacidad, el procedimiento LKH es aplicado para encontrar el correspondiente TSP tour de cada depósito abierto i al nuevo clúster;
– El clúster es asignado al depósito para el cual el costo de la ruta es mínimo;
– Finalmente un procedimiento de mejoramiento para el problema de ruteo de vehículos (VRP) propuesto en [16] es aplicado para el depósito asignado.
2.2 Fase de mejora de la solución inicial
En la segunda fase del procedimiento, el algoritmo trata de mejorar la solución inicial (x0) obtenida por el procedimiento heurístico anteriormente descrito, mediante la aplicación de la metaheurística de recocido simulado con un espacio de búsqueda granular. Este procedimiento trata de mejorar la solución mediante movimientos que involucran mover clientes dentro y entre rutas.
2.2.1 Espacio de búsqueda granular
En un procedimiento de búsqueda local, el número de vecindades que se puede alcanzar con un movimiento simple crece directamente con las dimensiones del problema. Para reducir considerablemente el tiempo de cálculo requerido en la evaluación de vecindades, en [10] se ha propuesto el uso de espacios de ''búsqueda granular'' para el problema de ruteo de vehículos con restricciones de capacidad. La metodología de búsqueda granular usa una lista de ''buenos vecindarios'', llamada Lista de Candidatos a ser evaluados para obtener una nueva solución.
El espacio de búsqueda granular, determinado por la Lista de Candidatos, es obtenido por la unión de los arcos ''cortos'', los arcos incidentes a los depósitos y los arcos que pertenecen a las mejores soluciones encontrados durante la búsqueda. Los arcos ''cortos'' son los que su distancia es menor que el valor de granularidad (ν), definido este como el producto entre un factor de esparsificación (β) y el costo promedio de los arcos que componen una ''buena'' solución. El costo promedio de estos arcos está definido como el valor objetivo de una ''buena'' solución (z) dividido por el número de clientes (n) más el número de depósitos (K), como se observa en la ecuación (12). El factor de esparcificación β sirve para controlar el número de arcos que pertenecen a la Lista de Candidatos. En [10] se aconseja el uso de un valor de β entre 1.0 y 2.5, lo cual permite seleccionar entre el 10% y el 20% de los arcos de un grafo completo. En este caso, se evalúan algunas vecindades reduciendo notablemente el tiempo de cálculo.

El cambio en el valor del factor de esparcificación β permite considerar simultáneamente estrategias de diversificación e intensificación. El valor de β es alterado a medida que va evolucionando la búsqueda. Al inicio de la búsqueda el valor de β es ajustado a un valor pequeño β0. Si la solución actual no mejora después de Ns iteraciones, el valor de β es incrementado hasta βd, permitiendo al algoritmo explorar nuevas áreas de búsqueda (estrategia de diversificación). Cuando se desea intensificar la búsqueda, el valor de β después de Nr iteraciones es reducido nuevamente al valor β0.
2.2.2 Vecindades
El algoritmo propuesto utiliza cinco vecindades, las cuales son evaluadas hasta que se cumpla la condición de término (número de iteraciones Nstop).
• Shift: un cliente es transferido desde su ubicación actual a otra posición en la misma ruta o en una ruta diferente (perteneciente al mismo depósito o a otro diferente).
• Swap: dos clientes intercambian su posición, es decir, el cliente u toma el lugar del cliente v o viceversa. Los clientes pueden pertenecer a la misma ruta o a diferentes rutas (perteneciente al mismo depósito o a otro diferente).
• Two-Opt: Dos arcos no consecutivos son eliminados de la solución actual y las rutas son reconectadas de forma diferente para obtener una nueva solución. Si los arcos pertenecen a la misma ruta, el movimiento es considerado como el método tradicional Two-Opt para TSP. Si ambos arcos pertenecen a rutas diferentes que están abastecidas por el mismo depósito, se obtiene el método tradicional Two-Opt para VRP. Finalmente, si las dos rutas pertenecen a diferentes depósitos, para reconectar las rutas es necesario realizar movimientos adicionales con los arcos incidentes al depósito.
• Exchange: dos clientes consecutivos son transferidos de su ubicación actual, a una nueva ubicación en la misma ruta o en una ruta diferente (perteneciendo al mismo depósito o a otro depósito diferente).
• Inter-tour Exchange: es una extensión del movimiento de Swap considerando dos pares de clientes consecutivos que pertenecen a diferentes rutas. El arco que conecta a los clientes consecutivos se conserva en la solución actual.
2.2.3 Algoritmo de recocido simulado
El algoritmo de recocido simulado es un procedimiento iterativo que permite movimientos de ''no mejora'' de forma probabilística. Este método fue introducido por Kirkpatrick et al. [19], quienes fueron los primeros en usarlo para resolver problemas de optimización combinatoria. El algoritmo de recocido simulado imita la evolución de un sistema físico inestable hacia un equilibrio termodinámico a una temperatura fija. En cada iteración de dicho procedimiento, una nueva solución (x') es seleccionada de forma aleatoria de las vecindades de la solución actual (x).
El algoritmo de recocido simulado acepta nuevas soluciones de acuerdo con dos criterios: i) si el valor de la función objetivo de la nueva solución es mejor, ii) si el valor de la función objetivo de la nueva solución es peor, y un valor aleatorio generado entre cero y uno es menor que la diferencia entre la solución actual y la nueva solución divido por la temperatura del sistema T. Al inicio del algoritmo, la temperatura del sistema es ajustada en un valor T0. Este valor disminuye cada Ncool iteraciones de manera proporcional a un factor de enfriamiento ∞, donde ∞ < 1. El Algoritmo 1 resume el procedimiento de Recocido y Simulado propuesto.

3. EXPERIENCIA COMPUTACIONAL
El algoritmo propuesto (GSA) ha sido implementado en C++ y los experimentos fueron ejecutados en una CPU Intel Core Duo (2.00 Ghz) bajo Linux Ubuntu 11.04 con 2 GB de memoria. El desarrollo del algoritmo propuesto ha sido probado en 2 sets de instancias de benchmarking de la literatura propuestas en [9] y Barreto [20]. En ambos set de datos, los clientes y depósitos potenciales son representados por puntos en el plano cartesiano. De esta forma, el costo de transporte de un arco es la distancia euclidiana calculada como un número real de doble precisión. El primer set de datos (propuesto por Tuzun y Burke [9]) considera 36 instancias con depósitos sin restricciones de capacidad. El número de clientes es determinado en el intervalo [100, 200], y el número de depósitos potenciales es 10 o 20. La capacidad del vehículo es determinada como 150. El set de datos propuesto en [20] considera 13 instancias obtenidas de problemas clásicos de ruteo de vehículos con restricciones de capacidad adicionando nuevos depósitos con sus correspondientes capacidades y costos fijos. El número de clientes varía entre 21 y 150, y el número de depósitos potenciales de 5 a 10.
3.1 Ajuste de parámetros
En particular, para cada instancia, cinco corridas independientes del algoritmo han sido ejecutadas con cinco semillas diferentes. Los resultados reportados corresponden a los mejores valores encontrados durante las ejecuciones y el tiempo de cómputo corresponde al tiempo total de las cinco ejecuciones.
Los mejores resultados de la heurística son reportados en las tablas 1 y 2. El siguiente set de parámetros ha sido obtenido después de varias corridas en los dos sets de instancias: β0 = 1.50, βd = 2.50, Ns = 2000, Nr = 1000, T0 = 1000, ∞ = 0.97, Ncool = 1200, MaxIter = 6000. Estos valores han sido utilizados para la solución de todas las instancias consideradas.
3.2 Estudio comparativo
El algoritmo propuesto ha sido comparado con las siguientes heurísticas publicadas para el CLRP: GRASP en [12], MA|PM en [13], LRGTS en [3], GRASP+ELS en [14], SALRP en [15] y 2-Phase HGTS en [16]. Los resultados reportados para GRASP, MA|PM, LRGTS, SALRP, y 2-Phase HGTS corresponden a una sola corrida del algoritmo asociado. Finalmente, GRASP+ELS ha sido ejecutado cinco veces considerando cinco semillas randómicas, y el costo reportado es el mejor resultado sobre las corridas con el tiempo computacional requerido para alcanzar la mejor solución dentro de la correspondiente ejecución.
En las tablas 1-2, la siguiente notación es usada:
Instancia nombre de la instancia;
Costo costo de solución obtenida por cada método (en una sola corrida o la mejor corrida);
BR costo del mejor resultado encontrado por los algoritmos considerados;
Gap BR variación porcentual del costo encontrado por cada algoritmo con respecto al valor de BR;
CPU time tiempo de ejecución en segundos en la CPU usada por cada algoritmo;
Average promedio de los valores de la columna;
CPU CPU usado por cada algoritmo;
CPU index Passmark performance test para cada CPU.
En las tablas 1 y 2, para cada instancia, los valores para los cuales el costo de cada algoritmo es igual al valor de BR son resaltados en negrilla. Cuando el algoritmo propuesto (GSA) mejora el valor del BR, su resultado es subrayado. Finalmente, el CPU índex es obtenido por el Passmark Performance Test. Este bien conocido test está relacionado con el CPU y el desarrollo de memoria. Una CPU es rápida cuando el valor del CPU índex es alto.
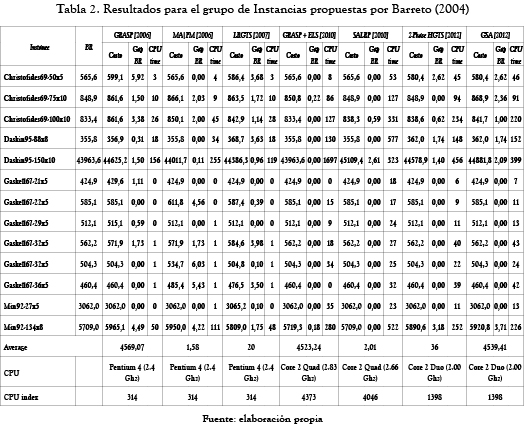
En las tablas 1 y 2, nosotros reportamos resultados para el set de instancias propuestos por Tuzun y Burke (1999) y Barreto (2004), respectivamente. En particular, valores promedios de Gap BR, CPU time y CPU índex son reportados. La tabla 1 muestra que el algoritmo propuesto provee un valor promedio global de Gap BR menor que GRASP, MA|PM, LRGTS, GRASP+ELS, SALRP. Solamente 2-Phase HGTS obtiene, con mayores tiempos de computación, valores ligeramente superiores para el valor promedio de Gap BR. En cuanto al tiempo computacional, el algoritmo GSA es más veloz que GRASP+ELS, SALRP y 2-Phase HGTS, los cuales obtuvieron los mejores resultados previos en término de Gap BR. Sin embargo, el CPU time usado por GASP+ELS no representa el tiempo global requerido para encontrar las mejores soluciones, desde que este corresponde al CPU time para cada instancia para obtener las mejores soluciones en su respectiva ejecución. Algoritmos GRASP, MA|PM, LRGTS toman menos tiempo computacional, pero ellos parecen ser menos robustos en términos de la calidad de la solución.
Finalmente, en la tabla 2 se muestran los resultados para el set de datos propuestos por Barreto (2004). Los resultados remarcan que nuestro algoritmo es competitivo en términos de calidad de la solución. El algoritmo GSA es capaz de obtener mejores resultados que GRASP, MA|PM y LRGTS pero superado por GRASP+ELS, SALRP y 2-Phase HGTS.
4. CONCLUSIONES Y FUTURAS INVESTIGACIONES
Nosotros proponemos un algoritmo efectivo basado en la metaheurística recocido con un espacio de búsqueda granular para el problema de localización y ruteo con restricciones de capacidad (CLRP). El algoritmo propuesto ha sido evaluado considerando instancias de benchmarking tomadas de la literatura. Los experimentos computacionales muestran que el algoritmo propuesto es capaz de obtener, dentro de razonables tiempo de computación, varias soluciones obtenidas por los métodos anteriormente publicados y nuevas mejores soluciones. Los resultados obtenidos sugieren que el algoritmo propuesto es competitivo con los algoritmos anteriormente publicados. El algoritmo GSA podría ser aplicado a otros problemas de logística similares como el problema de ruteo con múltiples depósitos (MDVRP), el problema de localización y ruteo con restricciones de periodicidad (PLRP), etc.
5. AGRADECIMIENTOS
El trabajo del primer autor ha sido parcialmente financiado por el MIUR (Ministero Istruzione, Università e Ricerca) Italia, y la Pontificia Universidad Javeriana, Cali, Colombia. Este soporte es altamente agradecido.
REFERENCIAS
[1] G. Rand, ''Methodological choices in depot location studies'', Operational Research Quarterly, vol. 27, n.° 1, pp. 241-249, 2003. [ Links ]
[2] S. Salhi, y G. Nagy, ''Consistency and robustness in location – routing'', Studies in Locational Analysis, vol. 13, pp. 3-19, 1999. [ Links ]
[3] C. Prins et al., ''Solving the capacitated location routing problem by a cooperative Lagrangean relaxation-granular tabu search heuristic'', Transportation Science, vol. 41, pp. 470-483, 2007. [ Links ]
[4] H. Min et al., ''Combined location-routing problems: A synthesis and future research directions'', European Journal of Operational Research, vol. 108, n.° 1, pp. 1-15, 1998. [ Links ]
[5] G. Nagy, y S. Salhi, ''Location – routing: issues, models and methods'', European Journal of Operational Research, vol. 177, n.° 2, pp. 649-672, 2007. [ Links ]
[6] G. Laporte et al., ''An exact algorithm for solving a capacitated location-routing problem'', Annals of Operations Research, vol. 6, n.° 9, pp. 291-310, 1986. [ Links ]
[7] J. Belenguer et al., ''A Branch and Cut method for the Capacitated Location-Routing Problem'', Computers and Operations Research, vol. 38, n.° 6, pp. 931-941, 2011. [ Links ]
[8] S. Salhi, y G.K. Rand, ''The effect of ignoring routes when location depots'', European Journal of Operational Research, vol. 39, pp. 150-156, 1989. [ Links ]
[9] D. Tuzun, y LI. Burke, ''A two–phase tabu search approach to the location routing problem'', European Journal of Operational Research, vol. 116, pp. 87-99, 1999. [ Links ]
[10] P. Toth, y D. Vigo, ''The granular tabu search and its application to the vehicle routing problem'', INFORMS Journal on Computing, vol. 15, n.° 4, pp. 333-346, 2003. [ Links ]
[11] S. Barreto et al., ''Using cluster analysis in capacitated location routing problem'', European Journal of Operational Research, vol. 179, n.° 3, pp. 968-977, 2007. [ Links ]
[12] C. Prins et al., ''Solving the capacitated location routing problem by a GRASP complemented by a learning process and path relinking'', 4OR – A Quarterly Journal of Operations Research, vol. 4, n.° 3, pp. 221-238, 2006. [ Links ]
[13] C. Prins et al., ''A memetic algorithm with population management (MA|PM) for the capacitated location – routing problem'', Lecture notes in computer science, vol. 3906, pp. 183-194, 2006. [ Links ]
[14] C. Duhamel et al., ''A GRASP x ELS approach for the capacitated location-routing problem'', Computer and Operations Research, vol. 37, n.° 1, pp. 1912-1923, 2010. [ Links ]
[15] V.F. Yu et al., ''A simulated annealing heuristic for the capacitated location routing problem''. Computer and Industrial Engineering, vol. 58, pp. 288-299, 2010. [ Links ]
[16] J.W. Escobar et al., ''A two-phase hybrid heuristic algorithm for the capacitated location-routing problem'', Computers and Operations Research, vol. 40, n.° 1, pp. 70-79, 2013. [ Links ]
[17] R.W. Eglese, ''Simulated annealing: a tool for operational research'', European Journal of Operational Research, vol. 46, pp. 271-281, 1990. [ Links ]
[18] K. Helsgaun, ''An effective implementation of the Lin-Kernighan traveling salesman heuristic'', European Journal of Operational Research, vol. 126, n.° 1, pp. 106-130, 2000. [ Links ]
[19] S. Kirkpatrick et al., ''Optimization by Simulated Annealing'', Science, vol. 220, pp. 671-680, 1983. [ Links ]
[20] S. Barreto, Analise e modalização de problemas de localização – distribuição, PhD thesis, University of Aveiro, Portugal, October 2004. [ Links ]
Notas:
* Artículo resultado de una investigación parcialmente financiada por el MIUR (Ministero Istruzione, Università e Ricerca) Italia, y la Pontificia Universidad Javeriana, Cali, Colombia