Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Ingenierías Universidad de Medellín
Print version ISSN 1692-3324
Rev. ing. univ. Medellín vol.12 no.22 Medellín Jan./June 2013
ARTÍCULO ORIGINAL
UN MODELO DE GESTIÓN DE LA CALIDAD Y CANTIDAD DE AGUA CON LÓGICA DIFUSA GRIS PARA EL RÍO ABURRÁ
A MODEL FOR WATER AND QUALITY MANAGEMENT USING GREY FUZZY LOGIC FOR ABURRÁ RIVER
Luis Fernando Carvajal Serna*
* MSc., Profesor asociado, Universidad Nacional de Colombia, Sede Medellín, e-mail: lfcarvaj@unal.edu.co
Recibido: 09/03/2012
Aceptado:: 07/05/2013
RESUMEN
Este artículo presenta un modelo de lógica difusa gris para la gestión de la calidad y cantidad del agua en el río Aburrá, el cual permite tener en cuenta la incertidumbre de los parámetros ambientales, que por lo general hacen que la toma de decisiones para las autoridades ambientales presente conflictos con los descargadores o contaminadores de los cuerpos de agua. La aplicación del modelo se hizo a una campaña del río Aburrá tomando como datos el caudal, el oxígeno disuelto y la demanda bioquímica de oxígeno. El modelo toma los aportes de las quebradas como los puntos de contaminación de los descargadores. Este modelo implica una optimización de acuerdo con los objetivos de la autoridad ambiental y los descargadores. El modelo se desarrolló en Matlab. Como conclusión se muestra el potencial del modelo para la gestión del agua del río y para alcanzar las metas planteadas por la autoridad ambiental.
PALABRAS CLAVE
Inteligencia artificial, lógica difusa gris, optimización, gestión del agua, calidad del agua, río Aburrá (Colombia).
ABSTRACT
This paper shows a model of grey fuzzy logic for water and quality management in the Aburrá river (Colombia). Grey fuzzy logic considers the uncertainty of the environmental parameters. This uncertainty produces a lot of conflicts between environmental agencies and polluters of water bodies. The application of this model was done in the Aburrá river, the campaing data includes discharges, dissolved oxygen and biochemical oxygen demand. The model takes the tributaries to Aburrá river like polluter points. Also, this model implies an optimization, in accordance with the goals and objectives of both polluters and environmental agencies.The model was developed using Matlab. The general conclusion is that the model has a great potential for water quality management in the river and for achieving the environmental agencies goals.
KEY WORDS
Artificial intelligent, Grey fuzzy logic, Optimization, Water management, Water quality, Aburrá river (Colombia).
INTRODUCCIÓN
Se presenta un modelo de gestión de calidad de agua para el río Medellín en la jurisdicción del Área Metropolitana del Valle de Aburrá (AMVA) basado en el modelo gris difuso de asignación de carga de residuos MGDACR [1]. El modelo se enfoca sobre el río y sus afluentes como transportadores de la carga de contaminantes con dos objetivos principales: uno relacionado a la calidad de agua del río, que es el objetivo de la autoridad ambiental que gestiona el río, y el segundo es el objetivo de los descargadores o fuentes de contaminación (industrial, residencial, comercial). El modelo utiliza el oxígeno disuelto y la demanda bioquímica de oxígeno asociados a cada uno de los objetivos. Además, implica una optimización que se realiza con ayuda del software Matlab.
El modelo permite identificar las fuentes de contaminación puntuales que ingresan al rio y sus cantidades, para establecer parámetros de calidad de agua en el río y la cantidad de contaminación máxima permisible. Además, el modelo optimiza los costos económicos del tratamiento previo de los residuos antes de ser vertidos y de este modo los ''contaminadores'' podrían estar cumpliendo plenamente la reglamentación y hacer un mejor uso de los recursos.
1. MARCO TEÓRICO
En general la lógica difusa es un sistema lógico de inteligencia artificial (IA) que usa variables cuyos valores son palabras en lugar de números (variables lingüísticas-lenguaje natural). Aunque las palabras son inherentemente menos precisas que los números, el uso de la lógica difusa está más cerca de la intuición y del razonamiento humano. También se considera una disciplina de las matemáticas que utiliza expresiones que no son totalmente ciertas ni completamente falsas. Se le considera la ciencia del razonamiento preciso. Para el pensamiento científico tradicional y para la cultura occidental, la comprensión de un fenómeno se mide por la capacidad de analizarlo cuantitativamente. Sin embargo, a medida que la complejidad de un sistema crece, disminuye la posibilidad de dar simultáneamente afirmaciones precisas y significativas sobre su comportamiento, es decir, a partir de un determinado límite estas dos características se excluyen mutuamente [2].
La teoría de sistemas grises fue propuesta por Deng [3]. Un sistema gris es un sistema que no es blanco (sistema de información completamente conocido) ni tampoco un sistema negro (sistema de información completamente desconocido). En realidad, la mayoría de procesos de interés en la gestión ambiental están en etapa gris debido a la información insuficiente y confusa. Un ''número gris'' es un número cuyo valor exacto se desconoce, pero una serie o rango de números en la que el valor se encuentra es conocida. Sea x un conjunto cerrado y acotado de números reales. Un número gris (x+) se define como un intervalo con límite menor conocido (x–) y límite superior conocido (x+). La distribución de información desconocida para x:
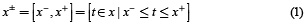
x+ se convierte en un ''número determinista'' o ''número blanco'' cuando, x+ = x– = x+. Cuando x+ = [x–, x+] = [–∞, +∞] , se llama un ''número negro''. Un ''número de intervalo'' o ''número de intervalo gris'' (x+ = [x–, x+]) es uno entre varias clases de números grises. El ''grado gris'' es una medida útil para evaluar cuantitativamente la calidad de la incertidumbre de la información de entrada o salida para los modelos matemáticos. El ''grado gris'' de un número de intervalo gris se define como el ancho del intervalo [xω = (x+ – x–)] dividido por su valor medio blanqueado (VBM) (WMV: whitened mid value) [xm = 1/2 (x– – x+)], y es expresado en porcentaje (%), de la siguiente manera:

Donde: Gd(x+) es el grado gris de x+. Soluciones (o productos) con grado considerablemente alto de ancho gris (xω) de las variables de salida, son consideradas menos útiles y de mala calidad para la toma de decisiones. A medida que el grado de gris de la función objetivo de un modelo de optimización se reduce, lo que implica la disminución de las incertidumbres del sistema, la eficacia del modelo gris se incrementa. Por lo tanto, un menor valor del grado gris de la función objetivo óptima implica la consecución de soluciones grises más aplicables y confiables.
Debe tenerse en cuenta la aclaración de que el concepto de modelado de sistemas grises es diferente de la noción de análisis de sensibilidad. El análisis de sensibilidad se considera como un análisis posóptimo, mientras que la modelación de los sistemas grises se dirige directamente a las incertidumbres de todos los parámetros inciertos del modelo en un marco matemático simple y da las soluciones como los números grises de intervalo, que puede ser utilizado directamente para la generación de alternativas de decisión. En el presente estudio se maneja un modelo de optimización difusa [4], donde las variables de decisión son números grises de intervalo y se demuestra una aplicación realista de la incertidumbre de las funciones de pertenencia en la gestión de la calidad del agua del río. La incertidumbre en los parámetros de pertenencia y en las funciones de pertenencia difusa también puede ser abordada mediante el conjunto de intervalos difusos valorados (CISV) (IVFS: interval valued fuzzy sets), si las variables de decisión que participan en el modelo de optimización, son números determinísticos. En el problema actual, donde las funciones de pertenencia mismas son inciertas y las variables de decisión son en términos de números grises de intervalo, puede que no sea posible formular y resolver el problema mediante el uso de números difusos [5, 6].
2. DATOS Y METODOLOGÍA
2.1 Descripción de la zona de estudio
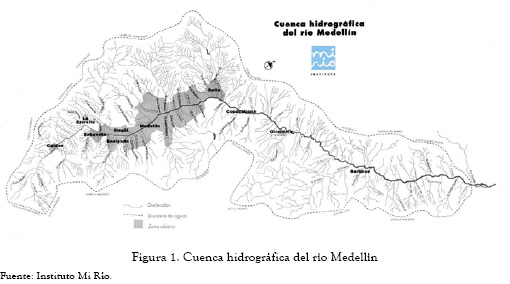
La subregión del Área Metropolitana del Valle de Aburrá (AMVA) está localizada en el centro del departamento de Antioquia, y limita con las subregiones Norte, Nordeste, Oriente, Suroeste y Occidente. La ciudad de Medellín se encuentra dividida en dos por el río Aburrá o Medellín; este río tiene una extensión de 100 kilómetros desde su nacimiento en el alto de San Miguel a unos 2700 m. s. n. m., hasta el sitio denominado Puente Gabino, punto en el cual se convierte en el río Porce. En su trayecto recibe las aguas de cerca de 200 afluentes directos. El río ha tenido gran significancia tanto en la vida económica como en la vida cultural de Medellín, y en las últimas décadas, en el urbanismo de nuestra ciudad. El área total de la cuenca es de 1.152 km2. Del área total de la cuenca un 15.2 % es urbana y alberga un 75 % de la población del departamento de Antioquia; por lo tanto, el impacto sobre el río Aburrá como eje de desarrollo y referencia espacial es relevante para las futuras generaciones. La cuenca aparece hoy como un ecosistema altamente intervenido donde su recuperación y protección no obedecen solamente a factores ecológicos, sino que también se imponen aspectos económicos, sociales, culturales, etc. (ver figura 1) [7].
A lo largo de la historia de la ciudad, el río cumplió el papel de vertedero o receptor de aguas servidas, por lo cual se encuentra aún hoy en día contaminado con toneladas de materia orgánica y desechos tóxicos como cianuros, fenoles, sulfuros, mercurio y plomo. Además de la contaminación que le es inherente, el río ha sufrido otros problemas simultáneos como son la deforestación, las basuras sólidas, el vertedero de escombros, etc. En la actualidad Empresas Públicas de Medellín –EPM–, está adelantando el plan de saneamiento del río Medellín y el Área Metropolitana del Valle de Aburrá en con convenio con la U. de A., UNAL, U. de M. y UPB ha desarrollado el estudio de diagnóstico y puesta en marcha de una red de monitoreo ambiental para la cantidad y calidad del agua del río Aburrá en tres fases [8, 9].
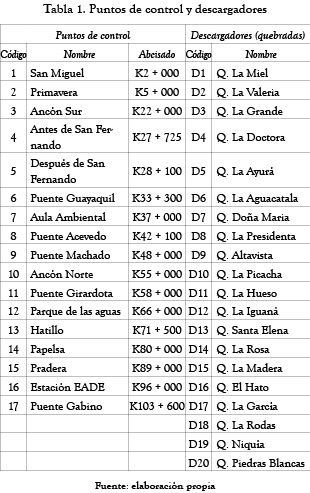
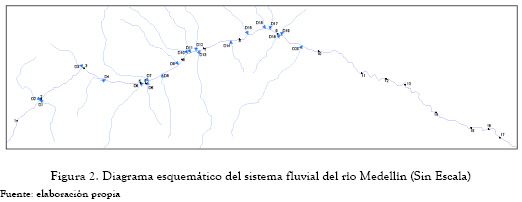
La descripción del sistema del río se presenta en la tabla 1. Para la red fluvial se asumen todos los supuestos mencionados en la sección 2.2.4. Veinte puntos de vertimientos son considerados como las fuentes puntuales de contaminantes. El contaminante considerado en el sistema es la carga de residuos de demanda bioquímica de oxígeno (DBO) a las fuentes puntuales y el indicador de la calidad del agua de interés es el déficit de oxígeno disuelto (OD). Diecisiete puntos de control se consideran como se muestra en la figura 2. La notación de las diferentes variables se ha simplificado y se usan solo dos sufijos, l (puntos de control) y m (descargadores). Por ejemplo, cl+ denota un intervalo de déficit de OD en el puesto de control l, y xm+ denota un rango de niveles de extracción fraccionada de DBO para el descargador m. Del mismo modo, los objetivos de la Autoridad de Control de la Calidad del Agua se denotan por El, y los objetivos de los descargadores se denotan por Fm. Para el modelo no se trabajará con todos los descargadores y todos los puntos de control, ya que el modelo exige que los datos de entrada tengan simultaneidad temporal. Los datos de caudales e indicadores en los descargadores y en los puntos de control fueron obtenidos de la base de datos del proyecto del AMVA, ''Red de monitoreo ambiental red rio-Fase III'' ejecutado por la UdeA, UNAL, UdeM y UPB [9]. La tabla 1 y la figura 2 muestran los puntos de control y las quebradas analizadas como descargadores.
2.2 Parámetros y metodología de la lógica gris difusa
2.2.1 Autoridad ambiental
La autoridad ambiental que gestiona la calidad de agua en el río Medellín es el AMVA. El AMVA, en virtud de la Ley 99 de 1993, artículo 66, ejerce dentro del perímetro urbano las mismas funciones atribuidas a las Corporaciones Autónomas Regionales: otorgamiento de licencias ambientales, concesiones, permisos y autorizaciones para el ejercicio de actividades o ejecución de obras. Además, efectúa el control de vertimientos y emisiones contaminantes, disposición de desechos sólidos y de residuos tóxicos y peligrosos, dicta medidas de corrección o mitigación de daños ambientales y adelanta proyectos de saneamiento y descontaminación. Según lo anterior, se puede definir un objetivo, dentro del modelo difuso a desarrollar para la autoridad ambiental, pero este es un objetivo hipotético, puesto que se desconocen las proyecciones reales del AMVA; además, por facilidad y para tener también presente un caso general, a la autoridad que gestiona la calidad del agua la denotaremos ACCA (Autoridad de Control de la Calidad del Agua). Para el caso de estudio el objetivo que se define es mantener el nivel de un indicador de calidad de agua, en este caso el déficit de OD, lo más cercano posible a un nivel deseable y por debajo de un nivel máximo permisible.
2.2.2 Descargadores
El modelo usado plantea que al río ingresan contaminantes de fuentes puntuales llamados descargadores; en este caso los descargadores serán las quebradas afluentes al río. En general en un descargador como fuente de contaminación las autoridades exigen una extracción fraccionada de los contaminantes a verter. El objetivo para los descargadores es tener un nivel aceptable de extracción de contaminantes para cumplir con la parte ambiental y un nivel máximo de extracción fraccionada de contaminantes para que los costos de tratamiento no sean excesivos.
2.2.3 Déficit de oxígeno disuelto y demanda bioquímica de oxígeno
El déficit de oxígeno disuelto es el indicador que se usará como parámetro de los objetivos de la ACCA en los puntos de control determinados sobre el río. El déficit de oxígeno disuelto hace referencia, como su nombre lo indica, a la falta del oxígeno disuelto en el agua para mantener calidades aceptables. Aunque el indicador es el déficit, el dato de entrada del modelo es el oxígeno disuelto; con este parámetro el modelo integra los objetivos de la ACCA y los descargadores, y entrega los requerimientos de OD, para mantener el nivel de calidad de agua deseado. Los niveles de oxígeno disuelto típicamente pueden variar de 0 a 18 ppm, aunque la mayoría de los ríos y riachuelos requieren un mínimo de 5 a 6 ppm para soportar una diversidad de vida acuática.
La DBO será el indicador usado para los objetivos de los descargadores, en términos de la cantidad de DBO como contaminante tratado por extracción fraccionada y el restante vertido al río. Este parámetro define los objetivos de los descargadores en el sentido de cuánto se aspira a extraer y el máximo a extraer por cuestiones económicas. La demanda bioquímica de oxígeno es una prueba que mide la cantidad de oxígeno consumido en la degradación bioquímica de la materia orgánica mediante procesos biológicos aerobios. La más frecuente determinación de la DBO es la DBO5. Las aguas subterráneas suelen contener menos de 1 ppm; contenidos superiores son indicativos de contaminación. En las aguas residuales domésticas se sitúa entre 100 y 350 ppm, y en las industriales, depende del proceso de fabricación, pudiendo alcanzar varios miles de ppm.
2.2.4 Descripción del sistema fluvial
Un sistema fluvial es considerado para el desarrollo del modelo de gestión de la calidad del agua. Los componentes relevantes del sistema se identifican como conjuntos. Fuentes incontrolables de contaminantes (por ejemplo, los contaminantes debido a la escorrentía y la erosión), grupo de vertidos (por ejemplo, industriales o municipales), los contaminantes liberados por los vertidos después de la eliminación de algunas fracciones de los contaminantes (por ejemplo la DBO, la concentración de contaminantes tóxicos, etc.) todos son considerados como conjuntos. Una práctica común de las ACC para garantizar condiciones aceptables de calidad del agua es comprobar la calidad del agua en un número finito de puntos de control de calidad del agua. La calidad del agua en un puesto de control se describe por medio de algunos indicadores de calidad, por ejemplo: OD, déficit de OD, la dureza, la concentración de nitrato de nitrógeno, etc. La calidad de agua del modelo de gestión propuesto se desarrolla con base en los siguientes supuestos:
1. Un estado de flujo constante de agua en el río y se considera la mezcla instantánea de los contaminantes en el punto de descarga.
2. Las características del río se suponen homogéneas y los parámetros del río no cambian en un tramo.
3. Para los indicadores de calidad del agua se considera conveniente que el nivel sea inferior al nivel permitido (por ejemplo, el déficit de OD, cualquier concentración de contaminantes tóxicos.)
4. Un contaminante se supone que afecta a uno o más de un indicador de la calidad del agua, pero se supone que los contaminantes no son reactivos químicamente entre sí.
5. Los residuos industriales y municipales son tratadas previamente en el sitio antes de la descarga de este en el río. La influencia de un contaminante en un indicador de la calidad del agua en un lugar intermedio se da por un modelo de simulación de calidad de agua adecuado, que define un conjunto de restricciones en el modelo de gestión de la calidad del agua.
2.2.5 Formulación MGDACR
El modelo de optimización MDACR se describe como [10 - 13]:

Sujeto a:
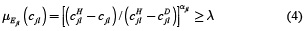
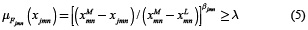



Las restricciones 4 y 5 se construyen a partir de funciones de pertenencia para los objetivos de la ACCA y los contaminadores, respectivamente. Estas restricciones definen el nivel de cumplimiento mínimo del objetivo (λ). Las restricciones 6 y 7 se basan en los requerimientos de calidad de agua fijados para la ACCA, y los posibles niveles de extracción fraccionada fijados por los descargadores, respectivamente. La restricción 8 representa los límites del parámetro λ. En el presente estudio MDACR se expresa como MGDACR, teniendo en cuenta la incertidumbre en los parámetros de pertenencia, que se tratan como números de intervalo gris. El MGDACR se representa como:

Sujeto a:
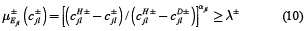
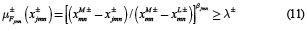



Donde

Las restricciones 10 y 11 representan las funciones de pertenencia imprecisa de los objetivos de la ACCA y de los contaminadores, respectivamente. El modelo de gestión de la calidad de agua se formula como un problema de optimización gris difuso, utilizando los conceptos de la programación gris y la programación inexacta. La organización del modelo gris difuso de asignación de carga para la gestión de la calidad del agua del sistema fluvial se muestra en la figura 2. Se trata de un modelo de optimización, que considera el conflicto de los objetivos imprecisos de la ACCA y de los descargadores. Dos niveles de incertidumbre se abordan en el modelo: uno asociado a la imprecisión en las metas de gestión de la ACCA y de los descargadores, que se modela usando funciones de pertenencia de la matemática difusa, y el otro relacionado con la incertidumbre en la asignación de estas funciones de pertenencia, modelado usando números de intervalo gris de la teoría de sistemas grises. En la expresión de los objetivos de la ACCA (restricción 10), el nivel de concentración cjl+, del indicador de la calidad del agua j en el puesto de control l, puede ser expresada matemáticamente como:

Donde la función de transferencia f es una función monótona, e indica el efecto acumulado de todos los contaminantes y descargadores (que se encuentran aguas arriba del punto de control l) en el indicador de la calidad del agua j. La función de transferencia puede ser evaluada utilizando modelos matemáticos apropiados que determinan la distribución espacial del indicador de la calidad del agua debido a la descarga de contaminantes en el río por fuentes puntuales. Los niveles de extracción fraccionada de distintos contaminantes por diferentes descargadores (x+jmn) y el nivel de cumplimiento del objetivo (λ+) son las variables de decisión en este modelo. El valor óptimo de λ+ (es decir, 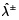 ) se obtiene como un número de intervalo gris de dos formulaciones separadas de dos submodelos; el submodelo 1 maximiza el límite superior, λ+, y el submodelo 2 maximiza el límite inferior, λ–. Los límites inferior y superior de las variables de decisión son (x–jmn y x+jmn) y se obtienen de estos dos submodelos. Usando la relación en la ecuación (16) el indicador de la calidad del agua (c+jl) se puede expresar en términos de x+jmn. Para la mayoría de los indicadores de calidad del agua, un alto grado de extracción fraccionada de contaminantes (por ejemplo, la carga de DBO, concentración de contaminantes tóxicos) resulta en un bajo nivel de indicador de la calidad del agua (por ejemplo, déficit OD, concentración de nitrato-nitrógeno). Por tanto, el límite inferior del indicador de calidad de agua (c–jl) es expresado en términos de límite superior del nivel de extracción fraccionada ( x+jmn, mediante el uso de la ecuación. (16):
) se obtiene como un número de intervalo gris de dos formulaciones separadas de dos submodelos; el submodelo 1 maximiza el límite superior, λ+, y el submodelo 2 maximiza el límite inferior, λ–. Los límites inferior y superior de las variables de decisión son (x–jmn y x+jmn) y se obtienen de estos dos submodelos. Usando la relación en la ecuación (16) el indicador de la calidad del agua (c+jl) se puede expresar en términos de x+jmn. Para la mayoría de los indicadores de calidad del agua, un alto grado de extracción fraccionada de contaminantes (por ejemplo, la carga de DBO, concentración de contaminantes tóxicos) resulta en un bajo nivel de indicador de la calidad del agua (por ejemplo, déficit OD, concentración de nitrato-nitrógeno). Por tanto, el límite inferior del indicador de calidad de agua (c–jl) es expresado en términos de límite superior del nivel de extracción fraccionada ( x+jmn, mediante el uso de la ecuación. (16):

Del mismo modo, el límite superior de c+jl se puede expresar como:

Como las variables de decisión que participan en este modelo de optimización son x+jmn y λ+, las ecuaciones (18) y (19) se pueden utilizar en la restricción 16 para expresar la variable dependiente 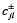 en términos de la variable independiente x+jmn, tal que ambas expresiones de los objetivos de gestión (restricciones 10 y 11) quedan en términos de x+jmn. Como todas las variables son números de intervalo gris, los límites, inferior y superior, de cada variable de decisión ([x–jmn, x+jmn] y [λ–, λ+]) se tratan como variables de decisión independientes en el modelo. El modelo de optimización se formula teniendo en cuenta las restricciones 10 y 11 de forma secuencial. El orden de consideración de las restricciones 10 y 11, junto con la selección de los límites de las variables de decisión (x–jmn, x+jmn, λ– y λ+) crea dos diferentes casos de formulación del modelo, que se llaman caso 1 y caso 2. En el caso 1, la restricción basada sobre la función de pertenencia imprecisa de los objetivos de la ACCA (restricción 10) se considera en primer lugar, lo que obliga a incluir x+jmn en el submodelo 1 y x–jmn en el submodelo 2, respectivamente, como variables de decisión, mientras que en el caso 2, la restricción basada sobre la función de pertenencia imprecisa de los objetivos de los descargadores (restricción 11) se considera en primer lugar, lo que obliga a incluir x+jmn en el submodelo 1 y x–jmn en el submodelo 2, respectivamente, como variables de decisión. Estos dos casos son considerados como dos problemas separados. Cada problema se divide en dos submodelos para obtener dos valores extremos de los niveles óptimos de cumplimiento de los objetivos
en términos de la variable independiente x+jmn, tal que ambas expresiones de los objetivos de gestión (restricciones 10 y 11) quedan en términos de x+jmn. Como todas las variables son números de intervalo gris, los límites, inferior y superior, de cada variable de decisión ([x–jmn, x+jmn] y [λ–, λ+]) se tratan como variables de decisión independientes en el modelo. El modelo de optimización se formula teniendo en cuenta las restricciones 10 y 11 de forma secuencial. El orden de consideración de las restricciones 10 y 11, junto con la selección de los límites de las variables de decisión (x–jmn, x+jmn, λ– y λ+) crea dos diferentes casos de formulación del modelo, que se llaman caso 1 y caso 2. En el caso 1, la restricción basada sobre la función de pertenencia imprecisa de los objetivos de la ACCA (restricción 10) se considera en primer lugar, lo que obliga a incluir x+jmn en el submodelo 1 y x–jmn en el submodelo 2, respectivamente, como variables de decisión, mientras que en el caso 2, la restricción basada sobre la función de pertenencia imprecisa de los objetivos de los descargadores (restricción 11) se considera en primer lugar, lo que obliga a incluir x+jmn en el submodelo 1 y x–jmn en el submodelo 2, respectivamente, como variables de decisión. Estos dos casos son considerados como dos problemas separados. Cada problema se divide en dos submodelos para obtener dos valores extremos de los niveles óptimos de cumplimiento de los objetivos 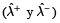 , que dan las soluciones para los dos casos extremos que abarcan todas las posibilidades intermedias.
, que dan las soluciones para los dos casos extremos que abarcan todas las posibilidades intermedias.
La figura 2 muestra el diagrama de flujo del modelo de optimización implementado MGDACR.
3. APLICACIÓN DEL MODELO MGDACR AL RÍO ABURRÁ
El GFWLAM para la gestión de la calidad del agua del sistema fluvial se presenta ahora como sigue:

Sujeto a:
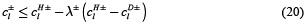
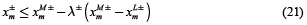




Donde:

Las restricciones lineales 20 y 21 hacen del modelo difuso de optimización (19 - 26) un problema de programación lineal para obtener la relación lineal c+l =f (x+m). Estas relaciones lineales, junto con las funciones lineales de pertenencia, facilitan el uso de la técnica de programación lineal para resolver el problema de gestión de la calidad de agua de los ríos. El problema resultante de programación lineal se ha resuelto mediante el toolbox ''Global optimization'' de Matlab 7.11.0.
Los resultados de los parámetros de pertenencia en las expresiones de los objetivos de la ACCA y de los descargadores 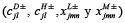 son números de intervalo gris. En el caso de estudio un conjunto de límites inferiores y superiores de los parámetros de pertenencia son fijados inicialmente de forma arbitraria para obtener un conjunto de soluciones óptimas. Esto provee un conjunto de niveles óptimos de extracción fraccionada (como números de intervalo gris) para los diferentes descargadores, lo que maximiza el nivel de cumplimiento de objetivos (λ+). Además de este conjunto de soluciones óptimas para un determinado conjunto de parámetros de pertenencia
son números de intervalo gris. En el caso de estudio un conjunto de límites inferiores y superiores de los parámetros de pertenencia son fijados inicialmente de forma arbitraria para obtener un conjunto de soluciones óptimas. Esto provee un conjunto de niveles óptimos de extracción fraccionada (como números de intervalo gris) para los diferentes descargadores, lo que maximiza el nivel de cumplimiento de objetivos (λ+). Además de este conjunto de soluciones óptimas para un determinado conjunto de parámetros de pertenencia 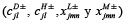 , un análisis de sensibilidad del modelo se puede realizar cambiando los valores de los parámetros de pertenencia , que evalúa el rendimiento del modelo en diferentes escenarios de entrada de intervalos grises.
, un análisis de sensibilidad del modelo se puede realizar cambiando los valores de los parámetros de pertenencia , que evalúa el rendimiento del modelo en diferentes escenarios de entrada de intervalos grises.
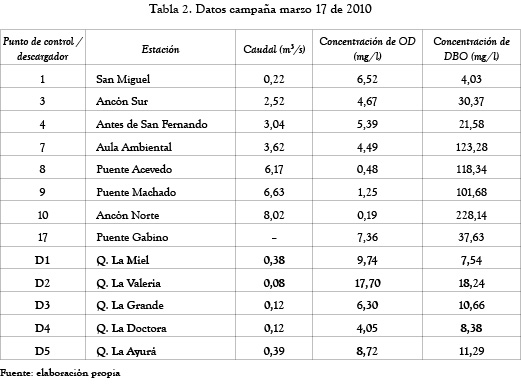
La aplicación del modelo se hizo a los datos de la campaña del día 17 de marzo de 2010 [9]. En esta campaña los puntos de control sobre los que se conocen datos son (1, 3, 4, 7, 8, 9, 10,17) y los descargadores (quebradas) (D1, D2, D3, D4, D5). Los datos obtenidos para esta campaña se muestran en la tabla 2.
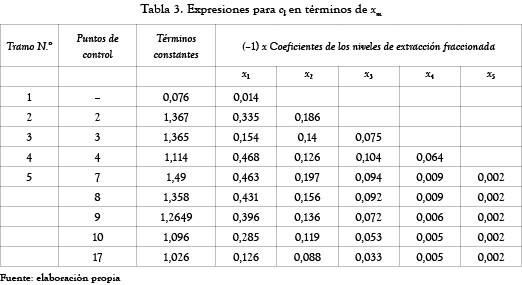
Para esta campaña el río se divide en 5 tramos, según los descargadores (desde un descargador a otro se define un tramo), y en cada uno de estos tramos se cumplen todos los supuestos mencionados en la sección 2.2.4. Los resultados del modelo se presentan en las tablas 3 a 6.
4. RESULTADOS Y DISCUSIÓN
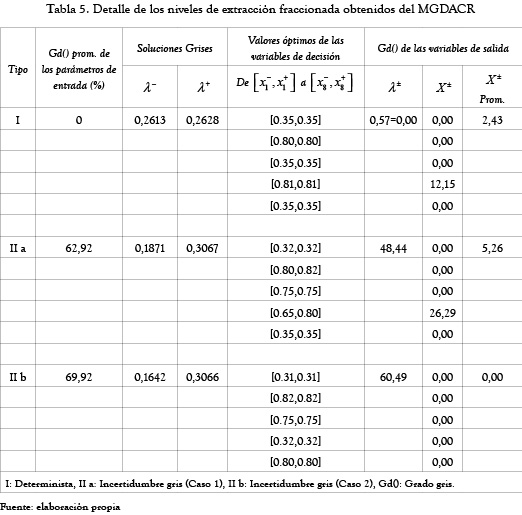
Los resultados obtenidos del modelo facilitan una comparación entre el caso determinista, donde los parámetros de pertenencia son números determinísticos, y el caso gris difuso, donde los parámetros de pertenencia son inciertos y se representan como números de intervalo gris. Los resultados del análisis se resumen en las tablas 5 y 6. El modelo ofrece un conjunto de políticas flexibles (los niveles de extracción fraccionada, 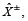 de diversos contaminantes para diferentes descargadores) en forma de números de intervalo gris para los valores óptimos de λ+, que es también un número gris de intervalo. Además, una política óptima se obtiene cuando los valores de todas las variables de decisión caen dentro de sus intervalos de gris por tomador de decisiones en el marco de la decisión final de acuerdo con la necesidad y la viabilidad práctica. La tabla 5 muestra los niveles óptimos de extracción fraccionada de los contaminantes vertidos por diferentes descargadores para cada caso determinista y la caja gris difuso. Para un determinado conjunto de parámetros de pertenencia
de diversos contaminantes para diferentes descargadores) en forma de números de intervalo gris para los valores óptimos de λ+, que es también un número gris de intervalo. Además, una política óptima se obtiene cuando los valores de todas las variables de decisión caen dentro de sus intervalos de gris por tomador de decisiones en el marco de la decisión final de acuerdo con la necesidad y la viabilidad práctica. La tabla 5 muestra los niveles óptimos de extracción fraccionada de los contaminantes vertidos por diferentes descargadores para cada caso determinista y la caja gris difuso. Para un determinado conjunto de parámetros de pertenencia 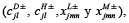 con grado gris promedio de 62,92%, un conjunto de valores óptimos de
con grado gris promedio de 62,92%, un conjunto de valores óptimos de 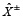 y
y 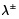 se deriva tanto para el caso 1 y el caso 2. El valor de
se deriva tanto para el caso 1 y el caso 2. El valor de 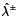 se puede considerar como una medida del conflicto existente en el sistema. Un valor de 0 para
se puede considerar como una medida del conflicto existente en el sistema. Un valor de 0 para 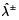 indica un escenario de fuerte conflicto, mientras que el valor de 1 corresponde a un escenario sin conflictos. Para evaluar la calidad de la información incierta de entrada o de salida, se usa la medida del ''grado gris''. Como el grado gris de valor óptimo de la función objetivo decrece, la eficacia del modelo gris se incrementa con el decrecimiento de los argumentos de las incertidumbres del sistema. Por lo tanto, un valor más bajo del grado gris de la función objetivo implica el logro de soluciones grises más aplicables y realizables. Por ejemplo, en el caso 1, la tabla 5.
indica un escenario de fuerte conflicto, mientras que el valor de 1 corresponde a un escenario sin conflictos. Para evaluar la calidad de la información incierta de entrada o de salida, se usa la medida del ''grado gris''. Como el grado gris de valor óptimo de la función objetivo decrece, la eficacia del modelo gris se incrementa con el decrecimiento de los argumentos de las incertidumbres del sistema. Por lo tanto, un valor más bajo del grado gris de la función objetivo implica el logro de soluciones grises más aplicables y realizables. Por ejemplo, en el caso 1, la tabla 5. 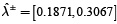 ; donde
; donde 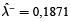 y
y 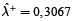 ; valor blanqueado medio,
; valor blanqueado medio, 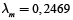 ; y ancho, λm = 0,1196, lo que da lugar a un grado gris de
; y ancho, λm = 0,1196, lo que da lugar a un grado gris de 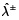 ,
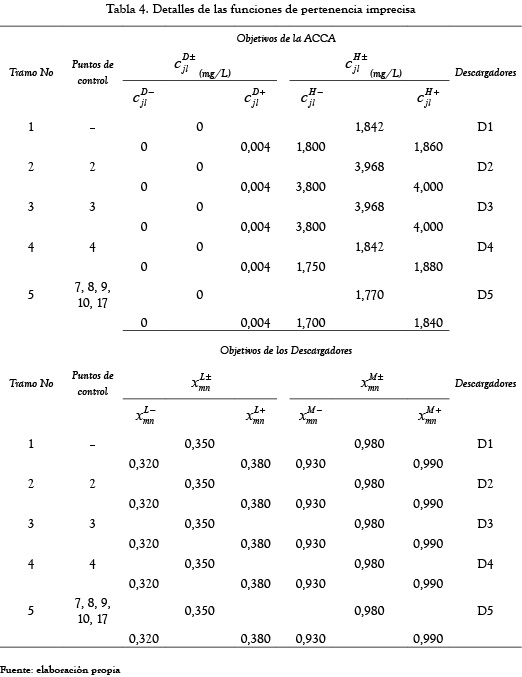
, 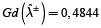 es decir 48,44%. En la tabla 5 (fila de tipo I), se presenta en primer lugar un caso determinista, para el cual el valor promedio de grado gris de los parámetros de entrada (parámetros de pertenencia para las funciones de pertenencia imprecisa de diferentes objetivos grises difusos (los valores entre paréntesis en la tabla 4) es cero. El grado gris de 12,5 % resultante para
es decir 48,44%. En la tabla 5 (fila de tipo I), se presenta en primer lugar un caso determinista, para el cual el valor promedio de grado gris de los parámetros de entrada (parámetros de pertenencia para las funciones de pertenencia imprecisa de diferentes objetivos grises difusos (los valores entre paréntesis en la tabla 4) es cero. El grado gris de 12,5 % resultante para 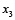 (que en teoría debería ser cero), se debe a las limitaciones interactivas. La razón de estos resultados inciertos para las entradas deterministas es la incorporación de las restricciones interactivas entre los dos submodelos. Ambos casos (casos 1 y 2) de la formulación del MGDACR se consideran en el caso gris incierto de la tabla 5. En el caso 1 el grado gris de
(que en teoría debería ser cero), se debe a las limitaciones interactivas. La razón de estos resultados inciertos para las entradas deterministas es la incorporación de las restricciones interactivas entre los dos submodelos. Ambos casos (casos 1 y 2) de la formulación del MGDACR se consideran en el caso gris incierto de la tabla 5. En el caso 1 el grado gris de 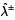 es menor que el grado gris
es menor que el grado gris 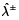 en el caso 2. Esto indica que el ancho del intervalo del número de intervalo gris
en el caso 2. Esto indica que el ancho del intervalo del número de intervalo gris 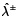 es más alto en el caso 2 y también implica que la incertidumbre en es menor en el caso 1. Por lo tanto, el caso 1 describe la decisión imprecisa difusa apropiada en esa situación particular, que da soluciones más fiables y aplicables que soluciones obtenidas a partir de caso 2. En el caso 1 (tipo II a)
es más alto en el caso 2 y también implica que la incertidumbre en es menor en el caso 1. Por lo tanto, el caso 1 describe la decisión imprecisa difusa apropiada en esa situación particular, que da soluciones más fiables y aplicables que soluciones obtenidas a partir de caso 2. En el caso 1 (tipo II a) 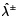 se obtiene como un número de intervalo gris, viene dada por [0.1871,0.3067]. El valor de
se obtiene como un número de intervalo gris, viene dada por [0.1871,0.3067]. El valor de 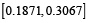 en el caso determinista [0.2613, 0.2628] se encuentra en este intervalo cerrado, es decir, [0.1871, 0.3067]. Los niveles óptimos de extracción fraccionada de la carga de residuos de DBO por diferentes descargadores, que se menciona en la columna 5 (tipo II a de la tabla 5) también se encuentran como números de intervalo gris. Al comparar los intervalos óptimos de los niveles de extracción fraccionada con las soluciones obtenidas del MGDACR (tipo I de la tabla 5), se observa que, para el segundo y cuarto descargadores los niveles de extracción fraccionada son más flexibles (es decir,
en el caso determinista [0.2613, 0.2628] se encuentra en este intervalo cerrado, es decir, [0.1871, 0.3067]. Los niveles óptimos de extracción fraccionada de la carga de residuos de DBO por diferentes descargadores, que se menciona en la columna 5 (tipo II a de la tabla 5) también se encuentran como números de intervalo gris. Al comparar los intervalos óptimos de los niveles de extracción fraccionada con las soluciones obtenidas del MGDACR (tipo I de la tabla 5), se observa que, para el segundo y cuarto descargadores los niveles de extracción fraccionada son más flexibles (es decir, 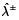 y
y 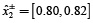 ) que en los deterministas (tipo I tabla 5) (es decir,
) que en los deterministas (tipo I tabla 5) (es decir, 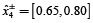 y
y 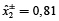 ). Estos intervalos óptimos de los niveles de extracción fraccionada resultan de los valores de los parámetros de pertenencia imprecisa en la tabla 3. El ancho gris de los elementos
). Estos intervalos óptimos de los niveles de extracción fraccionada resultan de los valores de los parámetros de pertenencia imprecisa en la tabla 3. El ancho gris de los elementos 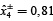 y
y 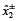 del vector gris
del vector gris 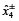 (es decir, la columna 7, tipo II a de la Tabla 5) no es considerablemente alto. Esto implica una menor flexibilidad de los descargadores 2 y 4 en la elección del régimen de la decisión final respecto de los valores óptimos de los niveles de extracción fraccionada, que se dan en términos de números de intervalo gris. Los otros elementos del vector gris
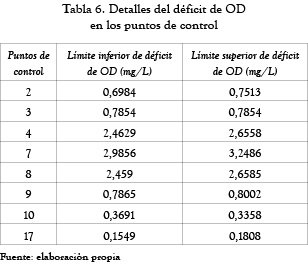
(es decir, la columna 7, tipo II a de la Tabla 5) no es considerablemente alto. Esto implica una menor flexibilidad de los descargadores 2 y 4 en la elección del régimen de la decisión final respecto de los valores óptimos de los niveles de extracción fraccionada, que se dan en términos de números de intervalo gris. Los otros elementos del vector gris 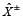 tienen ancho cero en esta situación particular (para los valores particulares de los parámetros de pertenencia, tabla 4), lo que implica la no flexibilidad de los otros descargadores diferentes a 2 y 4, y en la elección del régimen de la decisión final para los niveles de extracción fraccionada. La flexibilidad en la toma de decisiones de los descargadores para la fijaci&o acute;n de los niveles de extracción fraccionada se puede aumentar al incrementar el ancho de los parámetros de composición de entrada. La tabla 6 recoge la lista de los valores de déficit de OD en los 8 puestos de control que se usaron en el modelo, después de aplicar los niveles de extracción fraccionada de DBO mencionada en el caso 1 (tipo II a, tabla 5). Las relaciones de las ecuaciones (17) y (18) se utilizan para determinar los límites inferior y superior de concentración del indicador de calidad del agua (c–l y c+l) desde los límites superior e inferior del nivel de extracción fraccionada de contaminantes (c–m y c+m), respectivamente. Esto demuestra que los valores óptimos del intervalo gris del déficit de OD en la tabla 6 se encuentran dentro del intervalo de valores grises estándares del déficit de OD fijados por la ACCA en la tabla 4. Los resultados dados en la tabla 5 se obtienen de un conjunto determinado de valores de los parámetros de pertenencia mencionados en la tabla 4.
tienen ancho cero en esta situación particular (para los valores particulares de los parámetros de pertenencia, tabla 4), lo que implica la no flexibilidad de los otros descargadores diferentes a 2 y 4, y en la elección del régimen de la decisión final para los niveles de extracción fraccionada. La flexibilidad en la toma de decisiones de los descargadores para la fijaci&o acute;n de los niveles de extracción fraccionada se puede aumentar al incrementar el ancho de los parámetros de composición de entrada. La tabla 6 recoge la lista de los valores de déficit de OD en los 8 puestos de control que se usaron en el modelo, después de aplicar los niveles de extracción fraccionada de DBO mencionada en el caso 1 (tipo II a, tabla 5). Las relaciones de las ecuaciones (17) y (18) se utilizan para determinar los límites inferior y superior de concentración del indicador de calidad del agua (c–l y c+l) desde los límites superior e inferior del nivel de extracción fraccionada de contaminantes (c–m y c+m), respectivamente. Esto demuestra que los valores óptimos del intervalo gris del déficit de OD en la tabla 6 se encuentran dentro del intervalo de valores grises estándares del déficit de OD fijados por la ACCA en la tabla 4. Los resultados dados en la tabla 5 se obtienen de un conjunto determinado de valores de los parámetros de pertenencia mencionados en la tabla 4.
Por lo tanto, dos problemas diferentes para casos diferentes se resuelven en este modelo, y se derivan dos conjuntos de soluciones en términos de números de intervalo gris. Las soluciones con un menor grado gris son seleccionadas como soluciones de aplicación entre las distintas problemáticas de los distintos casos. El conjunto de intervalos de niveles óptimos de extracción fraccionada de DBO 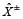 (tipo II a, tabla 5) es utilizado por los tomadores de decisiones para llegar a una decisión más comprometida, realista y aceptable para la ACCA y los descargadores.
(tipo II a, tabla 5) es utilizado por los tomadores de decisiones para llegar a una decisión más comprometida, realista y aceptable para la ACCA y los descargadores.
5. CONCLUSIONES
El modelo gris difuso de asignación de carga de residuos (MGDACR) se aplica como un modelo para hacer frente a la incertidumbre en las funciones de pertenencia. Las funciones de pertenencia de los diferentes objetivos de gestión son subjetivas, y los límites inferior y superior de las funciones de pertenencia se fijan de manera arbitraria.
La incertidumbre en los valores de los parámetros de pertenencia se cuantifican y se comunican directamente al modelo de gestión de la calidad del agua al tratarlos como números de intervalo gris.
La solución óptima no es un valor particular de color blanco o determinista, es un número gris de intervalo. Esto da flexibilidad en la toma de decisiones e indica que las preferencias de los tomadores de decisiones ''tienen una influencia importante'' en la decisión final aplicada al caso realista.
Una limitación del modelo presentado es que en situaciones en las que existen varias soluciones, la solución del modelo no puede presentar los intervalos óptimos de los niveles de extracción de contaminantes que cubren todas las posibilidades de las soluciones óptimas alternativas.
Teniendo en cuenta la función de transferencia apropiada para la distribución espacial y temporal de los contaminantes en el cuerpo de agua, el MGDACR se puede utilizar para la gestión de la calidad del agua de cualquier sistema de agua en general. En un sentido general, GFWLAM es adaptable a diversos sistemas ambientales para un uso sostenible y eficiente del medioambiente.
El modelo permite tomar decisiones pertinentes y realistas en cuanto a las restricciones y/o permisos de descarga de contaminantes por parte de una fuente de contaminación específica, y facilita a las mismas fuentes a partir de la extracción de contaminantes gestionar el recurso hídrico con parámetros de optimización económica.
Se presenta un ejemplo de aplicación al río Aburrá. Lo ideal es que se hubieran dispuesto más puntos de control y mejorar la confiabilidad del modelo. Esto genera que no se describan de manera más detallada los indicadores de calidad de agua, y la gestión se vea reducida a una gama cerrada de parámetros e intervalos de soluciones para implementar las decisiones.
AGRADECIMIENTOS
El autor agradece al Área Metropolitana del Valle de Aburrá por el apoyo para llevar a cabo el trabajo de grado del estudiante de Ingeniería Civil de la Facultad de Minas Juan Camilo Medina dentro del proyecto ''Implementación de la red de monitoreo ambiental en la cuenca hidrográfica del río Aburrá, fase III'', realizado por la UdeA, UNAL, UPB, UdeM durante el período 2010-2011.
REFERENCIAS
[1] Karmakar, S. and Mujumdar, P. P. An inexact optimization approach for river water-quality management. 2005. [ Links ]
[2] Wang, L. X. A course in fuzzy systems and control, Prentice Hall Inc., 1997. [ Links ]
[3] Deng J. L. Control problems of grey systems. Syst Control Lett 1982; 1(5):211–5. [ Links ]
[4] Bellman RE, Zadeh LA. Decision-making in a fuzzy environment. Manage Sci 1970; 17(4): B141–64. [ Links ]
[5] Bender MJ, Simonovic SP. A fuzzy compromise approach to water resources planning under uncertainty. Fuzzy Sets Syst 2000; 115(1):35–44. [ Links ]
[6] Chang NB, Wang SF. A grey nonlinear programming approach for planning coastal wastewater treatment and disposal systems. Water Sci Technol 1995; 32(2):19–29. [ Links ]
[7] Medina, J. C. Modelo de optimización gris difuso para la gestión de la calidad del agua, en el río Medellín, jurisdicción del Área Metropolitana del Valle de Aburrá. Trabajo de Grado, Universidad Nacional, Sede Medellín, 2011, 50 p. [ Links ]
[8] UDEA, UNAL, UPB, UdeM-AMVA. Diseño y Puesta en Marcha de la Red de Monitoreo Ambiental en la Cuenca Hidrográfica del Río Medellín en Jurisdicción del Área Metropolitana'' Fase 1. Convenio 366/2003 Calidad de las aguas del río Medellín y sus principales afluentes. Diciembre de 2004. [ Links ]
[9] UDEA, UNAL, UPB, U. de M.-AMVA. Implementación de la red de monitoreo ambiental en la cuenca hidrográfica del río Aburrá, en revisión. 2010-2011. [ Links ]
[10] Sasikumar K, Mujumdar P.P. Application of fuzzy probability in water quality management of a river system. Int J Syst Sci. 2000;31(5):575–91. [ Links ]
[11] Sasikumar K, Mujumdar PP. Fuzzy optimization model for water quality management of a river system. J Water Resour Plann Manage, ASCE 1998;124:79–88. [ Links ]
[12] Sasikumar K, Mujumdar PP. Fuzzy optimization model for water quality management of a river system. J Water Resour Plann Manage, ASCE 1998; 124:79–88. [ Links ]
[13] Fugiwara O, Puangmaha W, Hanaki K. River basin water quality management in stochastic environment. J Environ Eng, ASCE 1988; 114(4):864–77. [ Links ]