Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Ingenierías Universidad de Medellín
Print version ISSN 1692-3324
Rev. ing. univ. Medellín vol.12 no.23 Medellín July/Dec. 2013
ARTÍCULOS
MODELO AUTORREGRESIVO BILINEAL APLICADO A LA PREDICCIÓN MENSUAL DE CAUDALES EN COLOMBIA
STREAM FLOWS IN COLOMBIA
Juan David Cadavid*; Luis Fernando Carvajal**
Estudiante Posgrado en Ingeniería de Recursos Hidráulicos, Universidad Nacional de Colombia, Sede Medellin, Cra 80 x Calle 65, Bloque M2 – 303, Medellín, Colombia, e-mail: jdcadavia@unal.edu.co
** Profesor Asociado, Universidad Nacional de Colombia, Sede Medellín, Cra 80 x Calle 65, Bloque M2 – 323, Tel: (574) 425 51 09, Fax: (574) 425 51 03, Medellín, Colombia, e-mail: lfcarvaj@unal.edu.co
Recibido: 03/11/2011
Aceptado: 25/10/2013
RESUMEN
Se aplica un modelo estocástico bilineal, el cual inicialmente es propuesto para análisis de retornos financieros y otros sistemas complejos combinando la alta no linealidad y multiplicidad del ruido. Este modelo, por su carácter aleatorio, no tiene componente determinística que permita considerar la persistencia de los caudales en una aplicación a la Hidrología. Por lo tanto, se propone el acoplamiento entre la parte determinística de un modelo autorregresivo de orden 2 y el modelo estocástico bilineal como componente aleatorio, y se obtiene un modelo autorregresivo bilineal (MAB). El MAB se empleó para la predicción de caudales en ventanas de 3, 6 y 12 meses en 12 ríos de Colombia de diferentes regiones del país. El MAB tiene una estructura simple y muestra una mejora sustancial en la disminución de los errores para los caudales máximos y mínimos en el período de validación respecto de los modelos estocásticos tradicionales.
PALABRAS CLAVE
Modelación estocástica, modelo autorregresivo bilineal, predicción de caudales.
ABSTRACT
A bilinear stochastic model is applied, which is initially proposed for analyzing financial returns and other complex systems by combining high non-linearity and multiplicity of noise. Due to its random character, this model does not have a deterministic component which allows considering persistence of stream flows in a hydrology application. Therefore, the combination of a deterministic segment of an order 2 auto-regressive model and the bilinear stochastic model as the random component, and a bilinear auto-regressive model (BAM) is obtained. The BAM was employed to predict stream flows in windows of 3, 6, and 12 months in 12 rivers from several regions of Colombia. The BAM exhibits a simple structure and shows a substantial improvement in error reduction for maximum and minimum flows during the validation period compared to traditional stochastic models.
KEY WORDS
Stochastic modeling; bilinear auto-regressive model; stream flow prediction.
INTRODUCCIÓN
Actualmente existen muchos modelos para la simulación de caudales, entre los que están: redes neuronales artificiales, análisis espectral singular, modelos de ajuste no lineal por partes, modelos de onditas, modelos adaptativos de regresión múltiple, modelos estocásticos (AR(p), MA(q), ARMA(p,q), ARIMA(p,i,q)) [1, 2, 3, 4], además de modelos derivados de estos. Estos modelos van desde consideraciones lineales hasta no lineales para la predicción de caudales. La alta no linealidad de los procesos físicos en una cuenca y que generan los caudales requiere de nuevos enfoques tanto en los modelos físicos como en los matemáticos. Además, se requiere que los modelos predigan mejor los caudales en condiciones de fenómeno ENSO (El Niño-Oscilación del Sur), el cual modula fuertemente el clima en Colombia [5].
En este artículo se hace el desarrollo de un modelo autorregresivo bilineal (MAB) el cual consta de una parte autorregresiva [1] que aporta la componente lineal y de persistencia hidrológica, y una parte bilineal [6, 7], que aporta la componente no lineal y de carácter estocástico. Este último modelo es propuesto inicialmente para sistemas complejos de multiplicidad del ruido y para retornos financieros.
La motivación para proponer el MAB responde a la búsqueda dentro del campo de los modelos estocásticos del desarrollo de modelos que mejoren el desempeño en la predicción de caudales. Los modelos estocásticos, por ser lineales, se han quedado rezagados en su desempeño con respecto a otros modelos de inteligencia artificial, análisis espectral, modelos paramétricos, etc. El modelo que se presenta ofrece muy buenas expectativas ya que los resultados obtenidos son prometedores en un primer ejercicio de calibración y validación para 12 ríos en Colombia.
1. MARCO TEÓRICO
1.1 Modelo autorregresivo bilineal
El modelo autorregresivo bilineal (MAB) es una combinación de la componente autorregresiva de un AR(p) y un modelo bilineal. La fundamentación del MAB no es diferente a la de los dos modelos mencionados. La aplicación del MAB requiere que las series de tiempo cumplan con estacionariedad y ergodicidad, y la generación de una componente estocástica con distribución normal, N (0, s2).
La metodología para la estimación de los parámetros del modelo MAB es simple, se basa en la estimación de los parámetros del modelo autorregresivo [1, 7] y bilineal [6]. En el modelo bilineal los parámetros son b y la varianza s2 y la estandarización de la serie para su cálculo está determinada por la relación:

Donde:
r(t): Serie estandarizada para el cálculo de los parámetros del modelo bilineal.
Para los parámetros b y s2 del modelo bilineal se emplearon las ecuaciones (2) y (3) [6].
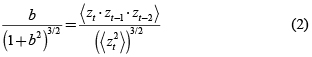

Donde:
zt–i: Estimadores del valor esperado en el instante t, con i = 0, 1, 2.
E[r(t)]: Valor esperado de la serie estandarizada.
El cálculo de los parámetros del modelo autorregresivo de orden p queda determinado por las ecuaciones de Yule-Walter [1]. Para el caso del modelo MAB de orden 2 el sistema de ecuaciones que determinan los parámetros de la componente autorregresiva son:


Donde:
ρi: Coeficiente de correlación, con i = 1, 2.
Φi: Parámetros del Modelo Autorregresivo, con i = 1, 2.
Así la ecuación que rige el MAB de orden p es:
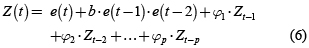
Donde:
Z(t): Valor de la variable estandarizada en el instante t.
e(t): Proceso de ruido blanco con distribución normal, N (0, s2).
b: Parámetro de la componente bilineal.
Φp: Parámetros del modelo autorregresivo.
1.2 Independencia de las componentes del MAB
La componente determinística o la autorregresiva del MAB deben ser independientes para asegurar que no exista correlación entre los caudales y el ruido blanco, y poder establecer un modelo como el que se plantea y estimar los parámetros tal como se hace para un AR(p), en este caso un AR(2). Para esto se presenta a continuación la independencia de la parte autorregresiva respecto de la estocástica.
El análisis de la independencia de la componente autorregresiva para un AR(2) parte de la premultiplicación de la ecuación 6 por Zt–1 y se toman valores esperados a ambos lados de la ecuación.
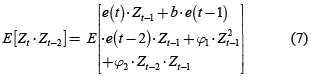
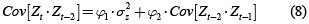
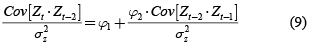

De igual forma obtenemos para Zt–2:

Las expresiones 10 y 11 son la mismas que se usan para la estimación de los parámetros de la componente determinística de un AR(2).
1.3 Media y varianza del MAB
Es importante mostrar la media y la varianza del modelo planteado. Para el caso de la media se toma el valor esperado en cada miembro de la ecuación para un MAB de orden 2.
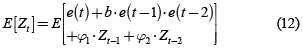
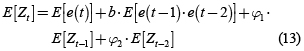
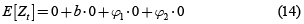
Es decir, E[Zt ] = 0, el ruido de carácter bilineal no afecta la media del proceso.
Para la varianza del proceso se multiplica a ambos lados del MAB de orden 2 por Zt y se toma el valor esperado:
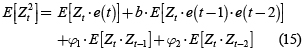

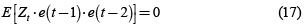
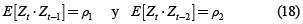
Por lo tanto, la varianza del proceso Zt queda de la siguiente forma:

La ecuación 19 corresponde a la varianza de un proceso AR(2) en su parte determinística. La componente aleatoria e(t) tiene distribución normal con media cero y varianza s2, N(0,s2). De aquí se deduce que la varianza del proceso no está afectada por el ruido bilineal.
2. DESCRIPCIÓN DE LA INFORMACIÓN
2.1 Características del régimen de caudales en Colombia
Colombia se encuentra ubicada en la esquina noroccidental de América del Sur, sobre la línea ecuatorial, en plena zona tórrida. No obstante, la mayor parte de su extensión se encuentra en el hemisferio norte.
Las fronteras y áreas de influencia climática son el Atlántico tropical y el mar Caribe por el norte, el Pacífico ecuatorial por el oeste, la zona andina del Ecuador y la vertiente del Amazonas por el sur, y los Andes y los llanos venezolanos con el norte brasileño por el este. Ocasionalmente hay influencia de frentes de latitud media, tanto del hemisferio sur como del norte; la posición de las respectivas corrientes de chorro en ambos hemisferios es otro factor extratropicale a considerar. Hacia el este se tienen las perturbaciones tropicales del este que se originan en África. Y del oeste se tiene la influencia del Pacifico que alcanza hasta el Índico y la zona de monzones en el subcontinente Índico y el sureste asiático [5].
Regionalmente, Colombia tiene una gran variabilidad de climas, debido a los factores generales de circulación global y del cambio en la posición aparente del Sol durante el año, la topografía, la convección profunda, la cercanía de las costas y la vegetación. Estos factores y su interrelación generan el clima colombiano, dado que la circulación es débil en lo que se refiere a la presión, temperatura, humedad y velocidad del viento [5].
2.2 Ubicación y registro de caudales medios mensuales
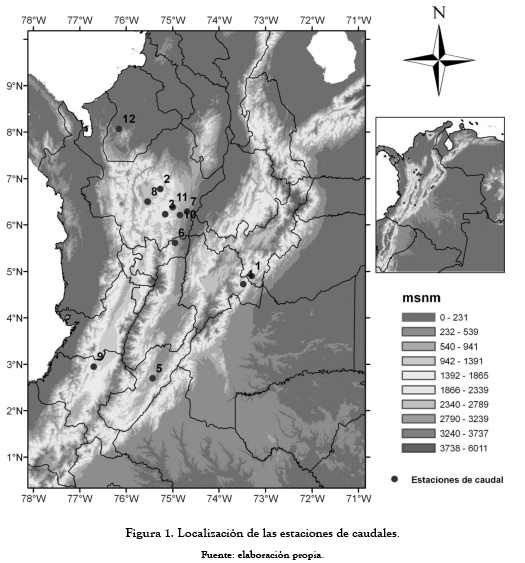
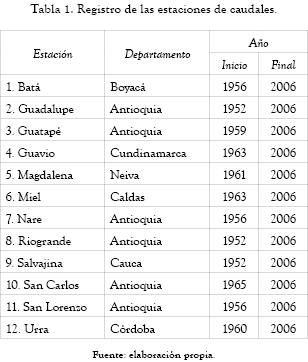
El estudio de las series de caudales medios mensuales se centra en la región Andina, parte de la región del Caribe y la Orinoquia. Las series de caudales de estas regiones presentan ciclos unimodales para Batá y Guavio, y ciclos bimodales para Guadalupe, Guatapé, Magdalena, Miel, Nare, Riogrande, Salvajina, San Carlos, San Lorenzo y Urrá, esto debido a los aspectos climatológicos y orográficos del territorio colombiano (ver figura 1). El comportamiento de la ZCIT genera en la zona andina un régimen de caudales bimodal. En la zona oriental la topografía de piedemonte y el régimen de los vientos alisios generan un régimen de caudales unimodal. Las estaciones de caudales consideradas se muestran en la tabla 1.
3. APLICACIÓN DEL MODELO
El MAB fue empleado para la predicción de series de caudales mensuales sobre 12 ríos en diferentes regiones de Colombia. En la sección 3.1 se presenta la calibración del modelo y los resultados de la validación. Para la validación se hicieron 20 ejercicios de predicción para cada ventana y río, obteniéndose los errores mínimo, y se obtuvieron los errores mínimo, medio y máximo así como el promedio de las 20 predicciones (ver tablas 2 y 3).
3.1 Calibración y validación del modelo autorregresivo bilineal
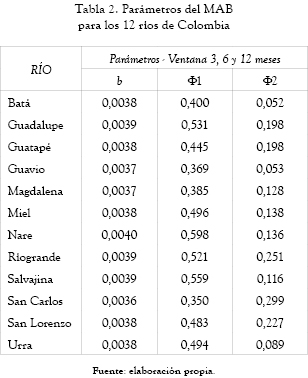
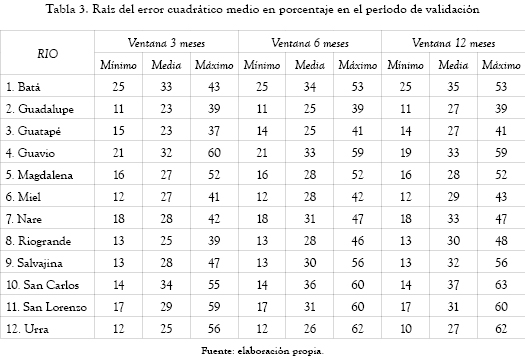
La estimación de los parámetros del MAB para cada río se hizo de acuerdo con el numeral 2.1, (ver tabla 2). La validación del modelo se trabajó con los registros de las series descritas en la tabla 1. Se tomó % del total de la serie de caudales medios mensuales un 70 % para realizar la calibración del modelo y un 30 % para el proceso de validación del mismo. La validación se hizo para las ventanas de predicción de 3, 6 y 12 meses sobre las estaciones mencionadas, y se calculó la raíz del error cuadrático promedio (ver tabla 3).
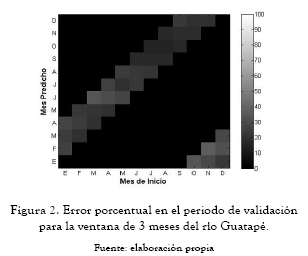
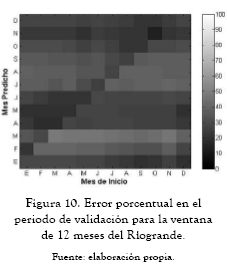
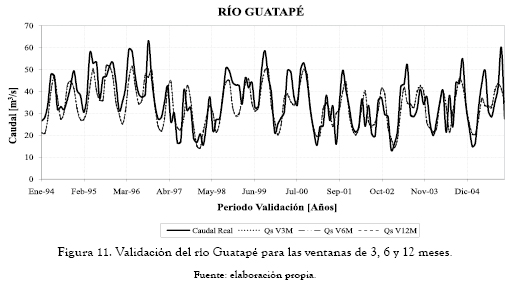
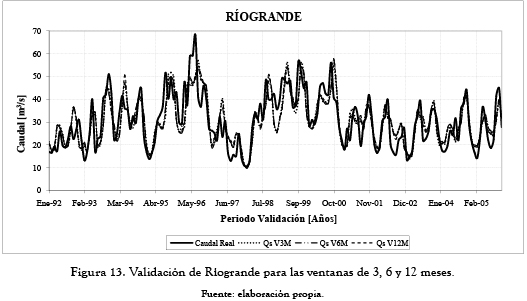
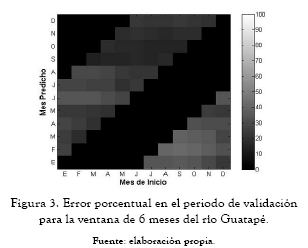
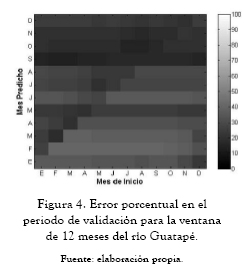
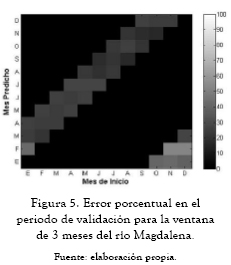
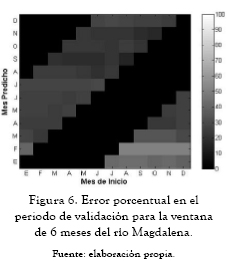
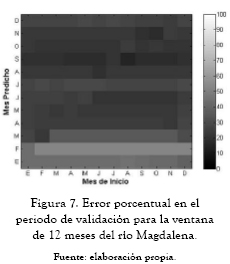
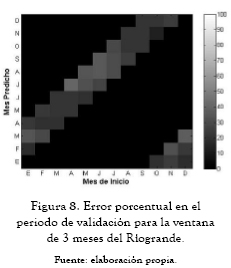
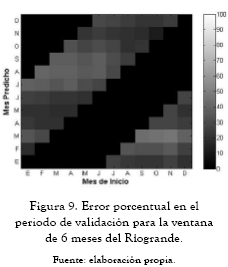
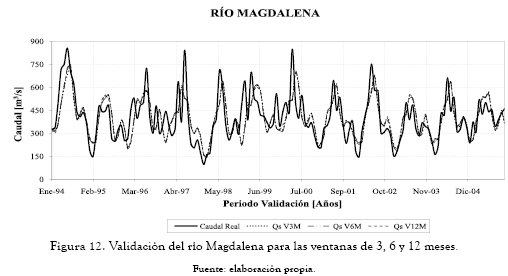
A continuación se presentan los ajedreces de predicción que significan el error porcentual del período de validación (figuras 2 a 10). En las abscisas se da el mes de inicio de la predicción, y en las ordenadas encontramos la ventana de predicción. Estos ajedreces permiten observar cómo cambia el error en el período de validación para cada mes predicho según el mes de inicio de la predicción. Las figuras 11 a 13 muestran las predicciones obtenidas para los ríos Guatapé, Magdalena y Riogrande en las tres ventanas de predicción de 3, 6 y 12 meses.
4. ANÁLISIS DE RESULTADOS Y CONCLUSIONES
La aplicación del MAB a la predicción mensual de series de caudales en Colombia superó las expectativas dentro de los modelos de carácter estocástico, ya que siendo un modelo simple es capaz de capturar la dinámica de los caudales con una buena aproximación para ventanas de 3, 6 y 12 meses. Además, este modelo es parsimonioso respecto a otros modelos más estructurados y empleados para los mismos fines.
Los parámetros estimados del MAB a cada uno de los ríos en su componente determinística muestran la persistencia hidrológica de los caudales. Solo se calibró el modelo para un AR(2), ya que para los ejercicios de predicción en Colombia este rezago ha mostrado ser adecuado. Respecto al parámetro b de la componente bilineal todos los ajustes muestran un valor similar alrededor de 0,0039. Es un valor bajo pero la componente bilineal, e(t-1)e(t-2), es no lineal y le introduce al modelo MAB un peso importante, lo que hace que la respuesta sea mejor que un AR(2) tradicional.
Regionalmente, las estaciones presentan errores similares dentro de la aplicación de los modelos: los ríos Batá, Magdalena y Guavio tienes errores medios de alrededor del 30 %; Nare y San Lorenzo de un 29 %, y Guadalupe y Riogrande alrededor de 26 % en el error medio.
En cuanto a los errores mínimos y máximos, los valores mínimos se obtienen para los ríos de Antioquia, es decir, Riogrande, Guatapé, Nare, San Carlos, San Lorenzo y Guadalupe. Igualmente para el río Miel en Caldas.
Como era de esperarse, el comportamiento de los errores medios y máximos aumenta a medida que lo hace la ventana de predicción, no superando en el mayor caso una diferencia del 5 % para el error medio y del 8 % para el error máximo. En cuanto a la variación del error mínimo se observa que prácticamente se puede considerar un comportamiento constante, es decir, este error es independiente de la longitud de la ventana de predicción. Se puede concluir que el modelo se muestra bastante robusto para un río en sus tres diferentes ventanas de predicción.
Los ajedreces de error en el período de validación, figuras 2 a 10, muestran un patrón general. Los períodos de menores errores de predicción se obtienen para los meses de mitad de año. También se presenta una banda de errores máximos que se desplaza en forma constante a lo largo del año y una concentración de los errores máximos para los primeros meses de predicción al final de año calendario.
El modelo autorregresivo bilineal incluye una componente no lineal que genera que la componente aleatoria, cuya distribución queda determinada completamente por la formulación del modelo, sea capaz de representar de forma parcial los eventos extremos en la serie y así los máximos y mínimos se acercan más a los valores reales. Este hecho hace que la magnitud de los errores se reduzca considerablemente.
En conclusión este artículo presenta un modelo (MAB) que tiene como componente determinística la parte autorregresiva de un AR(2) y como componente estocástica una bilineal que depende de una distribución normal, característico de los modelos estocásticos. La característica fundamental del MAB es que introduce la no linealidad a través de la parte bilineal. Este modelo mostró su bondad en el ejercicio de validación obteniendo errores muy por debajo a los obtenidos con los modelos estocásticos tradicionales, cuya característica fundamental es la linealidad del proceso.
REFERENCIAS
[1] G. E. P. Box, G.M. Jenkins and G.C. Reinsel. Time Series Analysis: Forecasting and Control. New Jersey, John Wyley and Sons, Fourth Edition, 2008, 746 p. [ Links ]
[2] N. Matalas. Mathematical assessment of synthetic hydrology. Water Resources Research 3(4), 1967, pp. 937-945. [ Links ]
[3] J. Moreno y J. E. Salazar. Generación de series sintéticas de caudales usando un modelo Matalas con medias condicionadas. Universidad Nacional de Colombia. Avances en Recursos Hidráulicos – Número 17, Medellín, pp. 17-24, mayo de 2008. [ Links ]
[4] Coulibaly P. and C. K. Baldwin. Nonstationary hydrological time series forecasting using nonlinear dynamic methods. Journal of Hydrology 3007, pp. 164-174, 2005. [ Links ]
[5] Mesa, O, Poveda, G. y L. F. Carvajal, 1997. Introducción al Clima de Colombia, Universidad Nacional de Colombia, 1997, 390 p. [ Links ]
[6] Sornette, D. and V. F. Pisarenko. Properties of a simple bilinear stochastic model: Estimation and predictability. Physica D: Nonlinear Phenomena, Vol 37, issue 4, pp. 429-445, April 2008. [ Links ]
[7] J. E. Salazar y O. Mesa. Aplicación de dos modelos no lineales al estudio de series temporales en hidrológica. Tesis de Maestría en Ingeniería-Recursos Hidráulicos. Universidad Nacional de Colombia, 1994, 114 p. [ Links ]