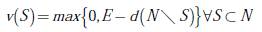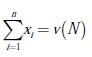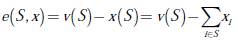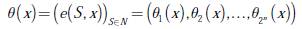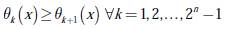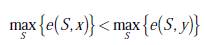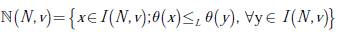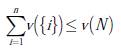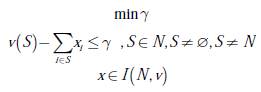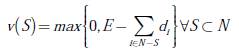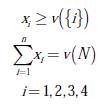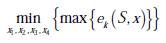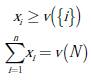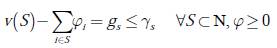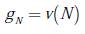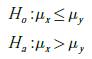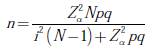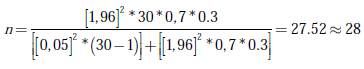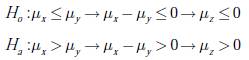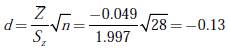INTRODUCCIÓN
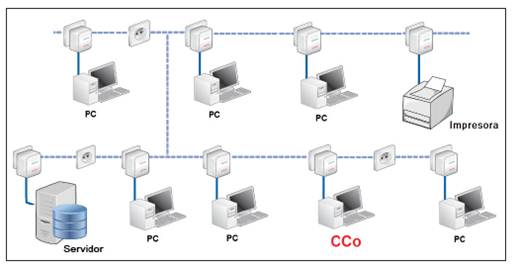
Una red de datos, y en particular una red BPL (ver figura 1) en ambientes de baja tensión, se presenta como un escenario donde los nodos tienen una permanente necesidad de transmitir [1-4], lo que genera una disputa por acceder al medio y usar los recursos del canal de acuerdo con las necesidades de ancho de banda [5,6] . Esto puede ocasionar situaciones de inequidad y de satisfacción particular de cada nodo. De acuerdo a lo planteado surge el siguiente interrogante: ¿Cómo distribuir de manera equitativa la capacidad de un canal BPL entre todos los nodos que forman parte de la red, para optimizar la asignación de recursos de acuerdo con los requerimientos establecidos por cada nodo, ofreciendo adecuados niveles de QoS y sin afectar el rendimiento de otro servicio e, incluso, superar la capacidad máxima permitida por el canal? Ante la situación planteada, se propone como estrategia de solución el uso de un área matemática denominada teoría de juegos.
El concepto de teoría de juegos fue propuesto por John Von Neumann en 1928, y está orientado a evaluar las decisiones que puede tomar un individuo en un contexto competitivo de ganancia o pérdida, frente a las decisiones que adopten los demás competidores. A este escenario competitivo se le denomina juego y a los individuos que forman parte de este escenario se les denomina jugadores [7]. El uso de la teoría de juegos establece tres formas para realizar el modelamiento de un escenario real: extensiva, estratégica y de coalición. Las dos primeras solamente son aplicables a juegos no cooperativos, en los que únicamente prima el interés de cada jugador por obtener el beneficio propio, sin importar el resultado de los demás jugadores. La tercera forma (coalición), es aplicable exclusivamente a juegos de tipo cooperativo, y corresponde a un juego en el cual dos o más jugadores no compiten entre sí sino que, por el contrario, trabajan de manera conjunta para conseguir el mismo objetivo y, por lo tanto, ganan o pierden como un grupo, aumentando la probabilidad de obtener una ganancia superior frente a la obtenida de actuar individualmente [8]. En un juego cooperativo no es necesario analizar las estrategias de los jugadores como ocurre en los juegos no cooperativos, basta únicamente con conocer la utilidad que puede obtener cada coalición y el vector pagos asociado a los resultados del juego [9].
El presente artículo propone el uso de dos técnicas para la asignación equitativa de recursos en una red BPL: nucleolus y max-min fairness, que forman parte integral de la teoría de juegos cooperativos y teniendo en cuenta que una red de datos puede ser representada como un juego cooperativo de utilidad transferible.
1. METODOLOGÍA
1.1 Juegos cooperativos de utilidad transferible (UT)
Un juego cooperativo UT (con utilidad transferible) es un par(N , v)donde N = {1, 2,3…n} es el conjunto de jugadores y v: 2 N →ℝ se denomina función característica del juego, con v(∅)= 0. Se denomina coalición a cualquier subconjunto no vacío de N. Para cada coalición S ⊂ N está asociado un número v(S) el cual representa el pago que se puede asegurar a los jugadores que forman parte de S, independientemente de lo que hagan los demás jugadores [9]. El valor de una coalición se puede considerar como la cantidad mínima que puede obtener una coalición si todos los jugadores que forman parte de ella se asocian y juegan en equipo.
En la teoría de juegos cooperativos, en diversas ocasiones, es necesario dividir el valor neto de un bien o de un recurso entre un conjunto de jugadores de manera equitativa, teniendo en cuenta que en muchos casos la cantidad a dividir es insuficiente para satisfacer las demandas de cada jugador. En este punto es donde surge el problema conocido como bancarrota.
Juego de bancarrota: un juego de bancarrota está definido como una terna (N, d, E) donde N = {1, 2,…, n} es el conjunto acreedores, d = {d 1 ,d 2 ,…,d n } con d i ≥ 0,∀i∈N es el vector de demandas de los acreedores y E corresponde al valor neto que se debe repartir entre los elementos de N [10]. Para cada problema de bancarrota (N, d, E) se puede definir un juego cooperativo (N, v). El conjunto de jugadores N será el mismo conjunto de acreedores o demandantes del problema de bancarrota. El valor de la coalición S en el juego se define como la propiedad a repartir entre los jugadores que no fue reclamada por los demandantes que no pertenecen a la coalición S.
Sea 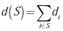 la suma de las demandas de todos los acreedores que forman parte de la coalición S; y sea
la suma de las demandas de todos los acreedores que forman parte de la coalición S; y sea 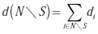 la suma de las demandas de todos los acreedores que no forman parte de la coalición S [11].
la suma de las demandas de todos los acreedores que no forman parte de la coalición S [11].
Juego cooperativo: un juego cooperativo (N , v) es un juego de bancarrota si existe un problema de bancarrota tal como el que se describe por la ecuación (1):
El valor de cada coalición v(S ) obedece a una valoración pesimista de lo que esta puede lograr y después de realizar un proceso de repartir entre los demandantes que no están en la coalición, el saldo es asignado a la coalición S [9]. Uno de los principales problemas para un juego cooperativo UT es cómo repartir la ganancia total v(N ) entre todos los jugadores de manera equitativa y de acuerdo con la participación individual de cada jugador. Para dar solución al problema de optimización representado como un juego de utilidad transferible se propone el uso de dos técnicas: nucleolus y max-min fairness. Además, se realizará un análisis de tratamientos para identificar cuál de las técnicas presenta un mejor desempeño, tanto en optimización como en complejidad computacional, teniendo en cuenta que la técnica seleccionada está proyectada para ser implementada en dispositivos embebidos de bajo costo.
1.2. El nucleolus
El núcleo es un concepto de solución que tiene una dificultad importante debido a que, en algunas ocasiones, puede tratarse de un conjunto muy grande y en otras de un conjunto vacío. Por lo anterior, surge el concepto de nucleolus, el cual propone una solución siempre que el conjunto de imputaciones sea no vacío. El nucleolus es capaz de superar las falencias que presenta el núcleo, y entrega como resultado un conjunto no vacío y único. Además, el nucleolus forma parte del núcleo cuando este no es vacío.
Procedimiento para estimar el nucleolus: sea un juego (N , v) con una distribución de pagos x = (x1,x2,…,xn) ∈ℝn eficiente entre los jugadores, como se presenta en la ecuación (2):
Entonces, el exceso de una coalición S con respecto a la distribución de pagos x, es la diferencia entre el valor de la coalición S y lo que recibe la coalición por la distribución x, es decir (ecuación (3)):
Aquí e(S, x), obedece a la medida del grado de insatisfacción de la coalición S con la distribución x. Cuanto mayor es e(S, x), mayor es el grado de insatisfacción. Para cada vector de distribución de pagos se construye un vector θ(x), de forma que los excesos estén ordenados de mayor a menor, en relación con el orden de las coaliciones.
Vector de excesos: para cada componente x ∈ I (N,v), se define el vector de excesos como el vector θ(x), con 2n componentes, como se describe en la ecuación (4):
Dados dos vectores excesos: x, y; se comparan en orden lexicográfico, elemento por elemento con el fin de identificar cuál de ellos presenta una menor diferencia o menor grado de insatisfacción. El proceso de comparación comienza evaluando la condición de desigualdad entre los primeros elementos de cada vector de excesos (θ1 (x)< θ1 ( y)). Si la condición se cumple, se puede decir que θ(x)<Lθ( y), de lo contrario se repite el proceso pero con el segundo elemento de cada vector y así sucesivamente hasta encontrar alguna diferencia entre sus elementos. Lo anterior se puede expresar con la ecuación (5):
Nucleolus: el nucleolus de un juego (N,v), se define como el conjunto ℕ(N, v) el cual puede ser expresado con la ecuación (6):
Por tanto, se puede decir que el nucleolus contiene aquellas distribuciones de pagos que son imputaciones y para las cuales se minimiza el mayor de los grados de insatisfacción. Una condición suficiente para que el nucleolus exista y sea único, es la ecuación (7):
Para calcular el nucleolus x = (x1,x2,…,xn) ∈ℝn de un juego (N , v), es necesario resolver el siguiente problema de programación lineal presentado en la ecuación (8):
Dondeγ es el mínimo valor posible para el problema planteado, el cual es alcanzado en un punto x. Entonces se puede decir que x es el nucleolus.
La metodología propuesta para calcular el nucleolus x = (x1,x2,…,xn) ∈ℝn procede de la siguiente forma:
Paso 1: establecer los valores de v(S). Teniendo en cuenta que la demanda total de ancho de banda (AB) es superior al ancho de banda total disponible, el escenario propuesto por la red BPL se puede considerar como un juego de bancarrota. El valor para v(S )puede ser calculado usando la ecuación (9):
Paso 2: el nucleolus x = (x1, x2, x3, x4), por tratarse de una imputación, debe cumplir con las restricciones presentadas en la ecuación (10):
Paso 3: finalmente, para calcular el nucleolus se puede plantear como un problema minimax de la siguiente forma que se muestra en la ecuación (11):
Sujeto a:
Paso 4: para dar solución al problema de optimización se utilizó el toolbox de optimización [12], incluido en Matlab, el cual permite hacer uso de diversos métodos de optimización. Los valores para cada uno de los parámetros (función objetivo, las restricciones y el punto inicial de iteración de forma matricial) para el problema propuesto.
Donde F: vector de coeficientes de la función objetivo; A,b: corresponden a las restricciones de desigualdad, en donde A es la matriz de coeficientes y b el vector de resultados para cada una de las inecuaciones (Ax ≤ b); Aeq ,beq : corresponden a las restricciones de igualdad, en donde Aeq es la matríz de coeficientes y beq es el vector de resultados para cada una de las ecuaciones (Aeq x = beq); x0: punto inicial para la iteración.
Los autores desarrollaron un algoritmo en MATLAB que integra cada uno de los pasos mencionados anteriormente, para facilitar los procesos de asignación de recursos mediante el uso del nucleolus, y que puede ser utilizada en futuros trabajos de investigación descritos en la sección 1.3.
1.3. Algoritmo de equidad max-min fairness (MMF)
Uno de los algoritmos que ha sido utilizado en diversos trabajos de investigación relacionados con la asignación de recursos de forma justa, es el algoritmo denominado max-min fairness (MMF), el cual proviene de la teoría de juegos cooperativos. En [13] y [14] se encuentran algunos de los trabajos que hacen uso de este algoritmo como estrategia de optimización. Los de [15-17] forman parte de los primeros trabajos de investigación soportados en la teoría de juegos que hacen de procesos de ordenamiento lexicográfico y, particularmente, el trabajo de Schmeidler [18] quien introdujo la noción de ordenamiento lexicográfico cuando estableció el nucleolus de una función característica de un juego, el cual puede definirse de la siguiente forma:
En un juego UT (N , v), con una función característica v : 2 N → ℝ+ que asocia un valor v(S)≥ 0 para cada coalición S ⊆ N ; se desea encontrar una distribución justa o equitativa de la ganancia total v(N ) entre todos los jugadores i = 1, 2,…, n. Un vector de pago φ ∈ℝn esta definido de forma que φi ≥ 0. Por cada coalición S ⊆ N , se establece un 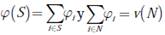 [19]. Por último, para cualquier vector de pago φ, existe un vector γ cuyos componentes toman los valores v(S)− φ(S), para todo S ⊆ N. De esta manera, el vector φ se define como el nucleolus del juego y γ es la max-min fairness que puede ser calculada de acuerdo con las ecuaciones (12) y (13):
[19]. Por último, para cualquier vector de pago φ, existe un vector γ cuyos componentes toman los valores v(S)− φ(S), para todo S ⊆ N. De esta manera, el vector φ se define como el nucleolus del juego y γ es la max-min fairness que puede ser calculada de acuerdo con las ecuaciones (12) y (13):
MMF es una técnica iterativa que permite distribuir de forma óptima los recursos entre todos los elementos que formen parte del sistema [20] y puede ser utilizada en diversos escenarios de red, incluida una red BPL en la que cada nodo puede establecer varias sesiones producto de diversas fuentes de tráfico y cada enlace puede ser compartido con otras sesiones existentes.
El algoritmo MMF es el siguiente:
Se genera un vector V , en el cual se registran los valores de AB solicitados por cada nodo i y clase (AB' ir ) de acuerdo con la necesidad del servicio (AB' ir ≥ 0) y se determina el número de fuentes de tráfico o número de jugadores (N j ) presentes en la red BPL.
Se procede a ordenar de manera ascendente el vector V
Se calcula un valor de referencia inicial (AB ref ), mediante el uso de la expresión:
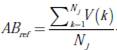 . En la primera iteración (i = 1), si V (i |i=1)> ABref → V (1)= ABref de lo contrario se mantiene el valor que presenta antes de realizar el proceso de comparación, en donde se asignaría el valor de AB solicitado por el nodo.
. En la primera iteración (i = 1), si V (i |i=1)> ABref → V (1)= ABref de lo contrario se mantiene el valor que presenta antes de realizar el proceso de comparación, en donde se asignaría el valor de AB solicitado por el nodo.Se realiza un nuevo proceso de estimación de ABref teniendo en cuenta la cantidad de elementos que forman parte del vector V y que aún no se les ha realizado el proceso de comparación. Es decir:
En la siguiente iteración (i = i +1), si V (i)> ABref → V (i)= ABref , de lo contrario V (i) conserva el valor que presenta antes de realizar el proceso de comparación y repite el ítem (d). Este proceso se repite hasta que todos los elementos del vector V sean valorados.
Se asigna el ancho de banda para cada nodo i y clase (ABir) de acuerdo con los valores registrados en el vector V resultante.
2. RESULTADOS Y ANÁLISIS
2.1. Descripción del escenario propuesto
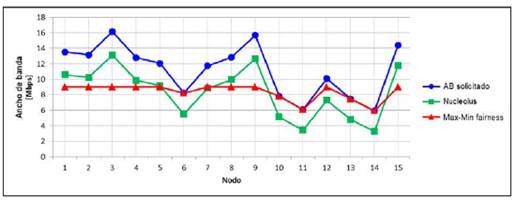
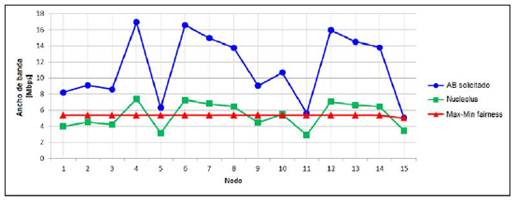
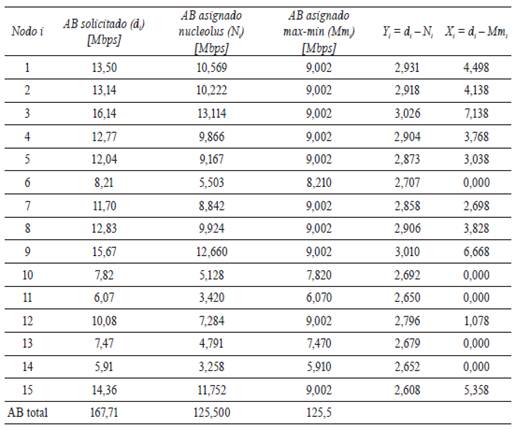
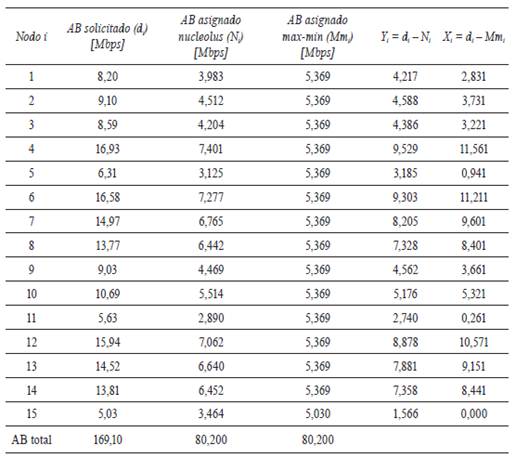
Con el fin de evaluar el comportamiento del nucleolus y de la max-min fairness al momento de realizar procesos de asignación de recursos en una red LAN operando con tecnología BPL, se han propuesto dos escenarios conformados por 15 nodos cada uno, a través de los cuales solamente circulará tráfico de datos. En cada escenario el nodo 15 actúa como coordinador central (CCo) ‒ver figura 1‒ y los requerimientos de canal por cada uno de los nodos (AB solicitado) se encuentran establecidos en la tabla 1, en ella se observa que el AB total (ABT) requerido es mayor que el AB total disponible, estableciendo un estado de saturación del canal BPL en ambos escenarios. Para calcular el valor de ABT se hace uso de la herramienta denominada “generador de canal PLC (GC_PLC)”, escrita en Matlab [21]. El GC_PLC permite estimar el comportamiento de un canal BPL de acuerdo con los parámetros asociados a la topología de una red BPL, en un ambiente residencial típico. Adicionalmente, la herramienta realiza un proceso de evaluación del canal por debajo de la banda de los 30MHz, considerando que los adaptadores de red BPL bajo el estándar HPAV operan en esta banda de frecuencia [22]. En [21] se presenta la información necesaria para el uso de la herramienta GC_PLC. El resultado obtenido bajo condiciones de canal típica y deficiente, arrojó valores de ABT para las condiciones de canal establecidas en los escenarios 1 y 2 de 125.5 Mbps y 80,2 Mbps respectivamente.
Tabla 1 Requerimientos de AB para cada escenario propuesto
| Nodo i | Escenario 1: AB solicitado [Mbps] | Escenario 2: AB solicitado [Mbps] |
|---|---|---|
| 1 | 13,50 | 8,20 |
| 2 | 13,14 | 9,10 |
| 3 | 16,14 | 8,59 |
| 4 | 12,77 | 16,93 |
| 5 | 12,04 | 6,31 |
| 6 | 8,21 | 16,58 |
| 7 | 11,70 | 14,97 |
| 8 | 12,83 | 13,77 |
| 9 | 15,67 | 9,03 |
| 10 | 7,82 | 10,69 |
| 11 | 6,07 | 5,63 |
| 12 | 10,08 | 15,94 |
| 13 | 7,47 | 14,52 |
| 14 | 5,91 | 13,81 |
| 15 | 14,36 | 5,03 |
| AB total requerido | 167,71 | 169,10 |
| AB total disponible | 125,50 | 80,20 |
Fuente: elaboración propia.
2.2. Comparación de tratamientos AB max-min fairness vs. AB-nucleolus
En las tablas 2 y 3 se registran los valores correspondientes al AB max-min fairness, AB-nucleolus, Xi y Yi que corresponden a la diferencia entre el AB solicitado por cada nodo (di ) y el AB asignado a través de los métodos max-min fairness y nucleolus respectivamente, los cuales se encuentran asociados y acordes con cada uno de los escenarios propuestos (ver figuras 2 y 3). Adicionalmente, se observa que la suma total del AB asignado en cada método es igual al AB total disponible para cada escenario propuesto. Con el fin de evaluar, si el uso de la max-min fairness como estrategia de optimización en una red BPL realiza un mejor proceso de asignación de recursos que el método del nucleolus, se plantean las siguientes hipótesis:
Donde μx y μy son las medias correspondientes a la diferencia existente entre el AB solicitado y el AB asignado, a través de los métodos de max-min fairness y nucleolus respectivamente. La hipótesis Ho, plantea que el método max-min fairness realiza un mejor ajuste que el método del nucleolus acorde a los requerimientos de cada nodo al presentar una diferencia promedio inferior y la Ha establece la condición contraria. Para aceptar o rechazar las hipótesis planteadas es necesario realizar un contraste de hipótesis sobre diferencia de medias con muestreo apareado, mediante la prueba denominada t-pareada. Para ello, se establecen los siguientes pasos:
Paso 1: realizar un proceso de muestreo aleatorio simple tomando como población los resultados que se encuentran registrados en las tablas 2 y 3. Para estimar el tamaño de la muestra en una población finita se hace uso de la siguiente ecuación [23]:
Donde n: tamaño de la muestra; Zα: valor correspondiente a la distribución de Gauss con un error α. El valor de Zα para α =0,05 es de 1,96; p : prevalencia esperada del parámetro evaluador; q :1− p; i : error estimado durante el proceso de muestreo. Los valores asignados para cada uno de los parámetros son los de la tabla 4.
Mediante el uso de la expresión anterior, el número de muestras que se deberán escoger aleatoriamente es presentado en la ecuación (16):
Paso 2: se define una nueva variable aleatoria Z = X −Y y se procede a calcular el valor medio y la desviación estándar para la variable Z. El resultado de este proceso arrojó los valores de −0.049 y 1.997 para 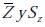 respectivamente. Por otro lado, al definirse una nueva variable Z, es necesario realizar un ajuste en las hipótesis planteadas en la ecuación (17)
respectivamente. Por otro lado, al definirse una nueva variable Z, es necesario realizar un ajuste en las hipótesis planteadas en la ecuación (17)
Paso 3: se procede a calcular el valor del estadístico establecido para la prueba mediante el uso de la ecuación (18):
Donde d es el valor del estadístico y n obedece al número de muestras para los dos escenarios propuestos.
Paso 4: establecer el rango de aceptación de la H
o
para 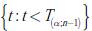 al 5 % de significancia (α = 0.05) y n −1 grados de libertad. Para el caso particular, el valor de T (0.05; 27) = 1.7033, definiendo el rango de aceptación de la H
o
entre (−∞,1.7033). Al evaluar el valor del estadístico d se observa que se encuentra dentro del intervalo de aceptación, razón por la cual la H
o
no es rechazada. De acuerdo a lo anterior, se concluye que la técnica max-min fairness logra una mejor asignación de recursos en redes LAN sobre BPL que el nucleolus, teniendo en cuenta que, para los escenarios propuestos, la max-min fairness realizó una mejor asignación de AB en comparación con el método del nucleolus al minimizar la diferencia entre el AB valor solicitado y el AB valor asignado para cada nodo, con un 95 % de confianza. Adicionalmente, la max-min fairness requiere de una complejidad computacional y temporal mucho menor que el nucleolus, teniendo en cuenta que, a la hora de realizar el procesamiento de los cálculos para la asignación de recursos en cada uno de los escenarios propuestos, el tiempo promedio que tardaron el nucleolus y la metodología max-min fairness en arrojar el resultado fue de 63,23 segundos y 0,043 segundos respectivamente. Es importante resaltar, que entre los factores que pueden influir en el máximo ancho de banda disponible se destacan las condiciones eléctricas del medio, la atenuación, el tipo de cableado y la calidad de la energía, así como las interferencias, las impedancias y el número de usuarios conectados, entre otros.
al 5 % de significancia (α = 0.05) y n −1 grados de libertad. Para el caso particular, el valor de T (0.05; 27) = 1.7033, definiendo el rango de aceptación de la H
o
entre (−∞,1.7033). Al evaluar el valor del estadístico d se observa que se encuentra dentro del intervalo de aceptación, razón por la cual la H
o
no es rechazada. De acuerdo a lo anterior, se concluye que la técnica max-min fairness logra una mejor asignación de recursos en redes LAN sobre BPL que el nucleolus, teniendo en cuenta que, para los escenarios propuestos, la max-min fairness realizó una mejor asignación de AB en comparación con el método del nucleolus al minimizar la diferencia entre el AB valor solicitado y el AB valor asignado para cada nodo, con un 95 % de confianza. Adicionalmente, la max-min fairness requiere de una complejidad computacional y temporal mucho menor que el nucleolus, teniendo en cuenta que, a la hora de realizar el procesamiento de los cálculos para la asignación de recursos en cada uno de los escenarios propuestos, el tiempo promedio que tardaron el nucleolus y la metodología max-min fairness en arrojar el resultado fue de 63,23 segundos y 0,043 segundos respectivamente. Es importante resaltar, que entre los factores que pueden influir en el máximo ancho de banda disponible se destacan las condiciones eléctricas del medio, la atenuación, el tipo de cableado y la calidad de la energía, así como las interferencias, las impedancias y el número de usuarios conectados, entre otros.
3. CONCLUSIONES
Ante la necesidad de realizar una distribución equitativa de recursos, de acuerdo con la demanda del servicio, entre los nodos que forman parte de una red BPL, se propuso el uso de la teoría de juegos cooperativos de utilidad transferible como estrategia de optimización y para ofrecer adecuados niveles de QoS en cada uno de los nodos. Dos técnicas fueron consideradas: nucleolus y max-min fairness. Con base en los resultados obtenidos se pudo evidenciar que la teoría de juegos puede ser considerada como una estrategia para la optimización de recursos en una red LAN sobre BPL, teniendo en cuenta que las dos técnicas propuestas generaron valores adecuados para la asignación de recursos en cada nodo. No obstante, para los escenarios propuestos, la max-min fairness fue la técnica que realizó una mejor asignación de AB, al minimizar la diferencia entre el AB valor solicitado y el AB valor asignado para cada nodo, con un 95 % de confianza. Adicionalmente, max-min fairness requiere de una complejidad computacional y temporal mucho menor que el nucleolus, teniendo en cuenta que, al realizar el procesamiento de los cálculos para la asignación de recursos en cada uno de los escenarios propuestos, los tiempos promedio que tardaron el nucleolus y la max-min fairness para generar el resultado fueron de 63,23 seg y 0,043 seg respectivamente, con lo cual es posible considerar el uso de max-min fairness como estrategia para la asignación de recursos, soportada en el uso de dispositivos embebidos de bajo costo.