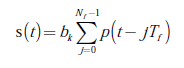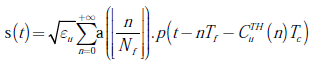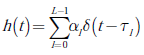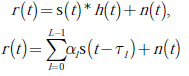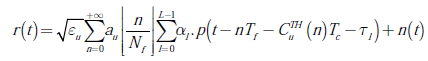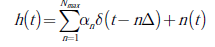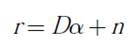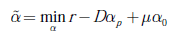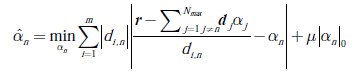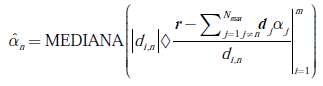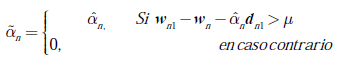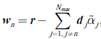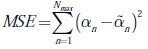INTRODUCCIÓN
Los sistemas de comunicaciones de ultra banda ancha de tipo radio impulsiva (IR-UWB, impulse radio ultra wide-band) se han conformado como una tecnología de transmisión de datos para ambientes cerrados y distancias cortas, que utiliza el concepto de espectro ensanchado para la gestión de amplios anchos de banda y para la transmisión de señales a muy baja potencia. Según las regulaciones de la Comisión Federal de Comunicaciones de los Estados Unidos [1], los sistemas UWB utilizan de toda la banda disponible de 7.5 GHz, en la banda espectral desde 3.1 a 10.6 GHz, con un consumo de potencia máxima no mayor a 0,5 mW, lo que permite así la coexistencia de la tecnología UWB con otros sistemas de comunicaciones, tales como redes wifi o sistemas de localización satelital tipo GPS. En este sentido, debido al amplio ancho de banda utilizado por los sistemas UWB y a las características de refracción propias de los ambientes cerrados, cada pulso transmitido generalmente se propaga a través de múltiples trayectorias, obteniéndose, en el lado del receptor, múltiples versiones del pulso transmitido desplazadas en el tiempo. Además, la transmisión de un pulso UWB es afectada por la contaminación inherente al medio de comunicación, así como también por la interferencia causada por la presencia de múltiples usuarios, que comúnmente se reúnen en una fuente única de ruido aditivo caracterizada, en general, por una distribución estadística particular [2]. No obstante, bajo estas condiciones de propagación, se han incorporado estrategias de detección de los símbolos transmitidos, asistidas por técnicas de estimación del canal en las que la poca densidad de la respuesta impulsiva de los canales UWB es aprovechada para el desarrollo de métodos basados en la teoría de representación de señales poco densas en diccionarios redundantes [3-5].
En general, los métodos tradicionales de estimación del canal consideran que la contaminación es de tipo gaussiana. Sin embargo, debido a los niveles de potencia propios de los sistemas UWB, las señales transmitidas son afectadas por perturbaciones de naturaleza impulsiva. Por tanto, el ruido que contamina las señales transmitidas puede aproximarse mejor usando modelos estadísticos con colas más pesadas que las exhibidas por la distribución gaussiana. Es más, estos modelos de ruido impulsivo también pueden usarse en la caracterización de la interferencia multiusuario (MUI, Multi-user Interference) comúnmente presente en los sistemas de comunicaciones UWB. Según [6] este tipo de interferencia es caracterizada con cierta precisión con la clase de distribuciones alfa-estable simétricas (SαS, symmetric alpha stable), estos modelos de interferencia y contaminación deben tomarse en cuenta para una adecuada estimación de los parámetros que modelan el canal de comunicaciones.
En este trabajo, se propone un método robusto para la estimación del canal de comunicaciones UWB, que explota la característica poco densa de la respuesta impulsiva del canal. Específicamente, el método propuesto representa la señal recibida como una combinación lineal de señales prototipo que conforman un diccionario parametrizado, donde cada señal del diccionario consiste en una versión desplazada en el tiempo de pulso transmitido. Además, el método propuesto describe el ruido que contamina la señal recibida usando el modelo estadístico laplaciano, que es una distribución de colas más pesadas que las mostradas por el modelo gaussiano, lo que conlleva a la determinación de la ganancia de cada trayectoria relevante del canal aplicando la mediana ponderada sobre una versión desplazada y escalada de la señal recibida. El rendimiento de la técnica de estimación propuesta se compara con el desempeño exhibido por el algoritmo de búsqueda voraz basado en la media ponderada [5] usando extensas simulaciones para diversas condiciones de ruido aditivo, donde, el método propuesto muestra un rendimiento superior bajo diversas condiciones del canal y de la señal transmitida.
La organización del presente artículo es como sigue: la sección 1 presenta el modelo matemático simplificado del sistema de comunicaciones UWB. En la misma sección, se describe la señal recibida en el marco de la representación de señales poco densas en diccionarios parametrizados. En la sección 2, se desarrolla el método propuesto de estimación de los parámetros del canal UWB basado en la mediana ponderada. El desempeño del método propuesto se evalúa en la sección 3 y las conclusiones del trabajo son expuestas brevemente en la última sección.
1. MÉTODOS
1.1. Modelo de la señal transmitida en un sistema UWB
Los sistemas de comunicaciones UWB radio impulsivo (IR-UWB, impulsive radio ultra wide band) se fundamentan en la transmisión de pulsos de muy corta duración que abarcan un amplio espectro de frecuencias. Estos sistemas no requieren de señales portadoras, lo que convierte a este esquema de transmisión en una tecnología de modulación en banda base. En particular, la transmisión de un símbolo de duración T s , que equivale una velocidad de transmisión de 1 / T s baudios, consta de N f pulsos de corta duración, donde cada pulso de esta secuencia se transmite cada T f = T s / N f . En este sentido, la señal transmitida al enviarse el k − ésimo símbolo b k puede modelarse como se expresa en la ecuación (1):
Donde T f se denomina tiempo de trama y p(t) describe la función del pulso usada en la transmisión cuya duración, denotada como T p , está en el orden de los nanosegundos. Como puede observarse en la ecuación (1), la señal transmitida s(t) está compuesta por N f pulsos p(t), donde N f y T f se seleccionan de acuerdo a la velocidad de transmisión de los símbolos. Es importante mencionar que el intervalo de duración de cada pulso T p generalmente es mucho menor que el tiempo de trama, esto es T p << T f , por consiguiente, cada símbolo de información se reduce a la transmisión de N f pulsos no solapados.
La ecuación (1) representa el modelo de la señal transmitida para un símbolo b
k
transmitido por un único usuario. Sin embargo, si se considera que el canal es compartido por múltiples usuarios, deben usarse técnicas de acceso múltiple al medio de comunicación, como por ejemplo, saltos de tiempo (TH, Time Hopping) mediante los cuales a cada usuario se le asigna una secuencia única 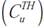 , que lo caracteriza y diferencia de los demás usuarios. Considerando la presencia de múltiples usuarios, la señal transmitida puede modelarse de acuerdo a la ecuación (2):
, que lo caracteriza y diferencia de los demás usuarios. Considerando la presencia de múltiples usuarios, la señal transmitida puede modelarse de acuerdo a la ecuación (2):
Donde 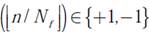 a determina la polaridad del símbolo transmitido, si se considera en este caso modulación BPSK; [n/ N
f
] denota el número entero más grande menor o igual a n / N
f
; ε
u
es la energía del pulso transmitido; p(t) representa el pulso transmitido y
a determina la polaridad del símbolo transmitido, si se considera en este caso modulación BPSK; [n/ N
f
] denota el número entero más grande menor o igual a n / N
f
; ε
u
es la energía del pulso transmitido; p(t) representa el pulso transmitido y 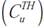 es una secuencia de saltos de tiempo en la que cada elemento de la secuencia se encuentra en el subconjunto {0,1,2,.. Nc}, siendo Nc = Tf / Tc el número de intervalos en que se divide el tiempo de trama Tf , cada intervalo con duración Tc [7].
es una secuencia de saltos de tiempo en la que cada elemento de la secuencia se encuentra en el subconjunto {0,1,2,.. Nc}, siendo Nc = Tf / Tc el número de intervalos en que se divide el tiempo de trama Tf , cada intervalo con duración Tc [7].
1.2. Modelo del canal UWB
El estándar IEEE 802.15.3a propone un modelo estocástico para el canal de comunicación UWB [1]. En dicho modelo, la respuesta impulsiva del canal se representa en la ecuación (3):
Donde δ(⋅) es la función delta dirac; α1 y τ1 son, respectivamente, la ganancia y el retardo asociada a la 1− ésima trayectoria del canal de comunicaciones que contiene un número de L de trayectorias [8]. El objetivo del proceso de estimación del canal UWB consiste en determinar los parámetros α1 y τ1 que caracterizan el canal de comunicaciones a partir de la señal recibida, cuyo modelo se describe a continuación.
1.3. Modelo de la señal recibida
La señal transmitida s(t), definida en la ecuación (2), al ser propagada a través de un canal UWB es afectada por el medio de comunicación caracterizado por la respuesta de impulso unitario definida en la ecuación (3). Además, la señal transmitida es contaminada por perturbaciones aleatorias inherentes al canal de comunicación cuyos efectos generalmente se reúnen en una fuente única de ruido aditivo n(t). De este modo, la señal recibida se modela como se presenta en la ecuación (4):
Donde * denota el operador convolución. En síntesis, al transmitir un pulso en distintos instantes de tiempo, con una forma de onda p(t) de duración Tp, este se difunde a través de las múltiples trayectorias de propagación y así se obtienen en el receptor múltiples réplicas del pulso transmitido. Dichas réplicas tienen una amplitud dada por α1 y su posición temporal depende de τ1 para 1 = 0,…, L−1. En consecuencia, antes del proceso de detección del símbolo transmitido, se requiere realizar la estimación de los parámetros que caracterizan el canal, en otras palabras, α1 y τ1, para 1 = 0, 2,…, L−1.
1.4. La señal UWB recibida en el contexto de representación poco densa de señales en diccionarios parametrizados
La señal base, comúnmente utilizada en los sistemas UWB, es el pulso gaussiano, que tiene una duración en el orden de los nanosegundos. Cuando el pulso es transmitido sobre un canal de múltiples trayectorias, la señal recibida es representada por múltiples versiones de p(t) retardadas y escaladas. Dado que p(t) tiene una duración muy corta y que el número de trayectorias con ganancia relevante es bajo, la señal recibida sin ruido se puede considerar como una señal poco densa, donde las componentes no nulas de la señal representan menos del 10 % del total de las muestras que componen la señal. Por consiguiente, la señal recibida puede describirse mediante el uso de la ecuación (5):
Donde α1 y τ1 son los parámetros del canal UWB, ganancia y retardo de la 1−ésima trayectoria de propagación, respectivamente. Si el número de múltiples trayectorias L es limitado y si muy pocos valores de α1 son diferentes de cero, se habla de un canal con respuesta impulsiva poco densa. En este trabajo se asume que la respuesta impulsiva del canal UWB es poco densa, tal suposición está en concordancia con trabajos publicados por terceros autores [4, 5; 9, 10].
Existen diversos métodos de estimación del canal UWB fundamentados en explotar la característica poco densa del canal de comunicación [5, 9, 11, 12]. Todos estos métodos coinciden en describir las perturbaciones que contaminan la señal recibida n(t) como ruido aditivo blanco gaussiano (AWGN, additive white Gaussian noise). Esta suposición se aleja de la realidad de los sistemas UWB reales en los que la presencia de ruido e interferencia interusuarios se modela usando distribuciones estadísticas de colas más pesadas que las exhibidas por el modelo gaussiano [13], lo que origina ruido de naturaleza impulsiva para el cual los métodos tradicionales de estimación del canal UWB tienen un desempeño pobre.
2. MÉTODO ROBUSTO PARA LA ESTIMACIÓN DE LOS PARÁMETROS DEL CANAL UWB
Como se sugiere en [14], un modelo apropiado para la descripción del efecto que producen los canales con múltiples trayectorias sobre las señales transmitidas, viene dado por un modelo discreto de respuesta impulsiva del canal. En este modelo, el retardo de propagación del canal es dividido en pequeños intervalos de tiempo llamados bins, y en cada uno de estos intervalos de tiempo se asume que está contenido uno o ningún camino perteneciente a las múltiples trayectorias del canal. Además, se descarta que en un bin exista más de un camino de propagación, reduciéndose el modelo del canal a una versión discreta que contiene el tiempo de ocurrencia de cada trayectoria, dado por la ecuación (6):
Donde Nmax es el número de bins máximo incluidos dentro del retardo de propagación del canal y Δ es el tiempo de duración de cada bin. Para simplificar el modelo, se asume además que el retardo de la n−ésima trayectoria es un múltiplo entero de ∆, de este modo, τn = n∆, con n = 1, 2,…, Nmax. Adicionalmente, se puede observar en la ecuación (6), que αn es la ganancia de la n−ésima trayectoria, y debido a la naturaleza poco densa del canal UWB se espera que solo unas pocas ganancias de trayectorias αn sean distintas de cero. Por tanto, el objetivo de la estimación del canal se reduce a determinar los índices n para los cuales αn ≠ 0 y en consecuencia la ubicación de las trayectorias relevantes del canal.
En este sentido, es común asumir que el retardo de propagación del canal es menor que el tiempo de trama, es decir Nmax∆ <Tf, evitando la interferencia intersímbolo entre símbolos adyacentes transmitidos. Bajo esta suposición, la señal recibida en una trama puede ser modelada por la ecuación (7):
Donde denota la matriz de diccionario de dimensiones mxNmax, con m=Tf / ∆ que contiene las bases de un dominio alternativo en el que la señal recibida r será representada. Específicamente, la matriz de diccionario D está conformada por Nmax vectores columnas, donde cada columna representa una versión desplazada del pulso p(t). En otras palabras, la n−ésima columna de D, denotada como dn es definida como p(t−(n−1)∆) para n= 1, 2,…, Nmax. Así mismo, 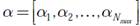 es el vector de ganancias de las múltiples trayectorias del canal UWB, donde un número reducido de elementos son no nulos. Por tanto, si α
n
≠ 0, es porque en el bin n∆, existe una trayectoria relevante cuya ganancia es α
n
.
es el vector de ganancias de las múltiples trayectorias del canal UWB, donde un número reducido de elementos son no nulos. Por tanto, si α
n
≠ 0, es porque en el bin n∆, existe una trayectoria relevante cuya ganancia es α
n
.
Como puede observarse en la ecuación (7), la señal recibida puede representarse como la expansión lineal de algunas pocas señales bases del diccionario D . Encontrar cuáles son esas señales y en qué magnitud contribuyen a la formación de la señal recibida, conduce favorablemente a la estimación de los parámetros del canal de comunicación UWB.
En el contexto de representación poco densa de señales en diccionarios, el objetivo es aproximar la señal recibida r (t) dada en la ecuación (5), por una combinación lineal de unas pocas señales prototipo del diccionario D , de forma tal que la norma del error de aproximación sea minimizada. En otras palabras, la estimación de los parámetros del canal se reduce a la solución del problema de la ecuación (8):
Donde µ es el parámetro de regularización que controla el número de elementos no nulos del vector resultante; α 0 es la seudonorma ℓ 0 del vector α, que cuenta el número de elementos no nulos de α; y r-Dα p denota la normaℓ p del error de aproximación, cuyo caso particular indica el grado de robustez requerido por el proceso de estimación. Así, si el ruido que contamina la señal obedece a un modelo estadístico gaussiano, la norma cuadrática (p = 2) es la óptima desde la perspectiva del principio de verosimilitud máxima, de forma tal que la estimación de los parámetros del canal puede obtenerse mediante la aplicación del algoritmo de búsqueda voraz tradicional [2,5]. Sin embargo, si la contaminación sigue un modelo de colas pesadas, como las exhibidas por una distribución laplaciana, el criterio a minimizar es el error medio absoluto (p = 1).
Resolver la ecuación (8) para p = 1 conduce a un proceso robusto de estimación de los parámetros del canal basado en el algoritmo de búsqueda voraz usando el operador de mediana ponderada recientemente propuesto en [15], donde el problema de optimización multidimensional (6), se reduce a resolver N max problemas de la forma de la ecuación (9):
Cuya solución viene dada por la ecuación (10):
Seguido de un proceso de umbralización que determina si la n−ésima trayectoria es significativa, esto es (ecuación (11))
Donde representa el vector residuo sin la contribución del n-ésima vector columna de la matriz de diccionario
D
. Obsérvese que en la ecuación (11) el parámetro de regularización actúa como un parámetro de umbralización que establece cuál trayectoria de propagación se considera relevante. Obsérvese que en la ecuación (10) no es más que la mediana ponderada de una versión desplazada y escalada de la señal recibida, donde las ponderaciones de este operador corresponden a los elementos del n−ésimo vector columna del diccionario, relacionado con el pulso retardado en el bin ∆n, esto es p(t-(n-1)∆). Nótese que si la ganancia no supera la operación de umbralización de la ecuación (11), esta se considera como una trayectoria irrelevante a la formación de la señal recibida, por tanto, su efecto se considera despreciable. Finalmente, al definir la ecuación (10) se asume que las magnitudes de las ganancias de las trayectorias restantes, esto es, 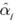 para i ≠ n, se conocen a priori o se considera que han sido previamente estimadas. Esto nos guía a definir un método iterativo de estimación de los parámetros del canal en el que, en principio, se asume que las ganancias asociadas a las múltiples trayectorias son nulas, definiendo un parámetro de regularización que disminuye a medida que el algoritmo progresa. Al encontrarse la primera trayectoria no nula cuyo valor de ganancia supere la prueba dada en la ecuación (11), esto se usa para definir la señal escalada y desplazada que permite la estimación de los subsiguientes parámetros.
para i ≠ n, se conocen a priori o se considera que han sido previamente estimadas. Esto nos guía a definir un método iterativo de estimación de los parámetros del canal en el que, en principio, se asume que las ganancias asociadas a las múltiples trayectorias son nulas, definiendo un parámetro de regularización que disminuye a medida que el algoritmo progresa. Al encontrarse la primera trayectoria no nula cuyo valor de ganancia supere la prueba dada en la ecuación (11), esto se usa para definir la señal escalada y desplazada que permite la estimación de los subsiguientes parámetros.
Este procedimiento se repite hasta que las L trayectorias más significativas son encontradas o hasta que un error de aproximación alcance un valor predefinido. Al finalizar el proceso iterativo, se tendrán las ganancias asociadas a las múltiples trayectorias más significativas, así como el instante τ n = n∆ de ocurrencia de dichas trayectorias. El algoritmo de estimación de los parámetros del canal UWB se resume en la tabla 1.
3. ANÁLISIS DE RESULTADOS
El escenario seleccionado para este conjunto de simulaciones corresponde al modelo de propagación de señales en un ambiente cerrado presentado en el estándar IEEE 802.15.3a. En concreto, se considera el modelo con línea de vista directa denotado como CM1, este modelo de canal se simula tomando los parámetros establecidos en el estándar IEEE 802.15.SG3a [16]. Además, el ruido aditivo de los canales de comunicaciones UWB es modelado usando una distribución alfa-estable simétrica (SαS, symetric α-stable) [6,14], aquí, el exponente característico 0 < α ≤ 2 define el nivel de impulsividad del ruido, con α → 0, lo que apunta a un modelo extremada- mente impulsivo y α = 2 que genera ruido gaussiano. Para efectos de estimación de los parámetros del canal, se considera que un número fijo de símbolos piloto (N pi ) conocidos por el receptor.
Los parámetros del sistema UWB a simular se seleccionan siguiendo las consideraciones sugeridas en [5]: el tiempo de trama T s = 100ns, el tiempo de chip T c = 25ns, número de pulsos por bits transmitidos
N s = 15, retardo de propagación T ds = 24,5ns, y el número de señales piloto N pi = 8.
3.1. Rendimiento de MSE para diferentes valores de GSNR
La relación geométrica señal a ruido (GSNR, geometric signal-to-noise ratio) es una métrica que relaciona la amplitud de la señal con respecto al ruido [17]. Este tipo de métrica se utiliza en los casos donde la distribución del ruido presenta momentos de segundo orden infinitos, y, en consecuencia, no se puede usar la definición de la relación señal a ruido (SNR, signal-to-noise ratio) tradicional. En esta primera simulación, se determina el error medio cuadrático (MSE, mean square error) entre las ganancias de las múltiples trayectorias del canal estimado α˜ y las ganancias del canal de comunicación verdadero α, es decir:
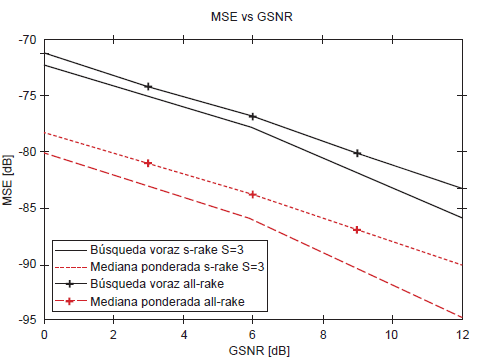
La figura 1 muestra el rendimiento del método propuesto para la estimación del canal UWB, así como el desempeño del algoritmo de búsqueda voraz clásico basado la media ponderada [5]. En concreto, la figura 1 muestra el MSE de las ganancias estimadas en función de la GSNR de la señal recibida, para un nivel de impulsividad establecido en α = 1,50. Además, en la figura 1 se muestra el MSE de las ganancias estimadas para todas las trayectorias de propagación (denotado como All Rake) y el MSE asociado solo a las tres trayectorias más relevantes (S-Rake), en el contexto de receptores tipo selectivo. Así mismo, cada punto de las curvas es obtiene al aplicar el promedio sobre los resultados de 1000 realizaciones del canal de comunicación y del ruido SαS.
Como puede observarse en la figura 1, el algoritmo propuesto tiene un rendimiento superior comparado con el desempeño exhibido por el algoritmo tradicional de búsqueda voraz [5] en el contexto de estimación de los parámetros del canal UWB. En particular, se observa una ganancia de desempeño de aproximadamente 9 dB entre los estimadores Rake selectivo aplicando el algoritmo propuesto basado en la mediana ponderada y Rake selectivo aplicando el algoritmo de búsqueda voraz tradicional, cuando la contaminación corresponde a un GSNR de 6 dB.
Además, se puede observar que el receptor tipo S-Rake de tres caminos ofrece resultados con valores menores del MSE que el receptor que estima todos los caminos de propagación denominado All Rake. Esto se observa, tanto en el método basado en media ponderada, como en el algoritmo propuesto, lo cual es consistente con lo reportado previamente en la literatura, siendo el S-Rake mucho más útil para una implementación de receptores UWB en aplicaciones de carácter práctico, debido a su simplicidad, bajo costo computacional y rendimiento. En este sentido, estimar los tres caminos de propagación más relevantes usando el algoritmo de mediana ponderada genera el mejor rendimiento en términos del MSE para el rango de ruido bajo estudio.
3.2. Rendimiento de los algoritmos de estimación en función del número de señales piloto
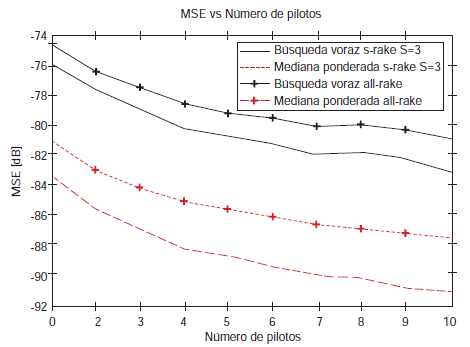
El proceso de estimación propuesto asume que los primeros símbolos son conocidos por el receptor. Este tipo de procedimiento se conoce como estimación del canal auxiliado por señales piloto de entrenamiento. Un número elevado de señales piloto conducen a un mejor estimado de los parámetros del canal, pero a su vez disminuye la velocidad efectiva de transmisión de los bits de información. Por otro lado, un número reducido de señales piloto puede conllevar a una estimación pobre del canal. En esta simulación se evalúa, para diferente número de símbolos pilotos, el desempeño de los dos algoritmos de estimación anteriormente mencionados. En particular, todos los parámetros se mantienen igual a los establecidos en la simulación anterior. La figura 2 presenta el error medio cuadrático versus el número de señales piloto, para un GSNR de 9 dB y α = 1,50.
El rendimiento de todos los estimadores del canal UWB presenta mejoras a medida que incrementa el número de señales piloto. El método propuesto basado la mediana ponderada presenta valores menores de MSE, en el rango bajo estudio, comparado con los valores de error generados por el algoritmo de búsqueda voraz clásico [5], demostrando de manera numérica, que el algoritmo robusto propuesto genera mejores resultados para la estimación de los parámetros del canal UWB ante la presencia de ruido SαS, donde el rendimiento de los algoritmos mejora a medida que el número de señales piloto se incrementa.
3.3. MSE para diferentes niveles de impulsividad del ruido
En esta simulación se desea observar el desempeño del método propuesto de búsqueda voraz basado en mediana ponderada ante distintos niveles de impulsividad del ruido aditivo. Para ello, se realizaron los experimentos usando tres valores del parámetro que controla la impulsividad del modelo de ruido SαS.
En la figura 3 se puede visualizar que para un nivel de impulsividad α = 1,50, el rendimiento del algoritmo robusto basado en mediana ponderada es mucho mejor que el algoritmo de búsqueda voraz clásico en la estimación del canal UWB. Por ejemplo, para un GSNR = 6 dB, la ganancia en desempeño es de aproximadamente 10 dB. Para un valor de α = 1, 75, la figura 3 muestra una mejora de desempeño de aproximadamente 3 dB del algoritmo propuesto basado en la mediana ponderada comparado con respecto al rendimiento del algoritmo clásico de búsqueda voraz.
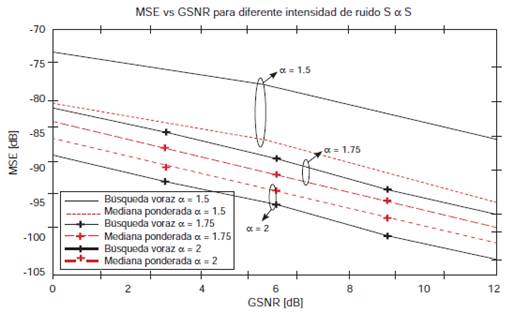
Fuente: elaboración propia.
Figura 3 MSE vs GSNR para distintos valores del exponente característico
Si la contaminación aditiva es modelada usando α = 2, que corresponde con el caso de ruido gaussiano, el rendimiento de ambos algoritmos es similar, con una leve ganancia de rendimiento por parte del algoritmo de búsqueda voraz tradicional. Esto se debe a que el algoritmo de búsqueda voraz clásico se fundamenta en la minimización de la norma ℓ2 del error de aproximación, la cual es óptima bajo el principio de verosimilitud máxima cuando la contaminación obedece a una distribución gaussiana.
3.4. Rendimiento de la BER para diferentes valores de GSNR
En esta simulación se evalúa el desempeño del algoritmo propuesto usando como medida de rendimiento la tasa de error binaria (BER, bit error rate). Este experimento permitirá mostrar la importancia de realizar una estimación robusta del canal de comunicaciones UWB para lograr una adecuada detección del símbolo transmitido. Para este fin, se generaron 350 realizaciones del canal UWB, transmitiendo 10000 bits en cada modelo del canal con un número de símbolos piloto igual a N pi = 8. La señal transmitida se contamina con ruido impulsivo siguiendo el modelo SαS, con un valor de α = 1,50.
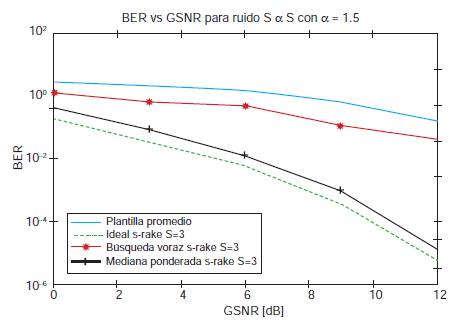
Las curvas comparativas de la BER se presentan para cuatro casos de receptores UWB. Primero, se considera el receptor promediador de plantilla piloto, es decir, las ocho señales piloto transmitidas se promedian, definiéndose una plantilla piloto, la cual se usa en el detector como un filtro acoplador en la etapa de detección de símbolos. Segundo, se presenta el receptor S-Rake con S = 3, basado en el algoritmo de búsqueda voraz clásico. Tercero, se propone el receptor S-Rake fundamentado en el algoritmo de búsqueda voraz de mediana ponderada y, finalmente, se presenta la comparación con el caso ideal donde se tiene conocimiento a priori de los parámetros del canal.
Como se puede observar en la figura 4, el receptor basado en el algoritmo de búsqueda voraz de mediana ponderada ofrece un rendimiento superior comparado con el desempeño de los receptores clásicos para todos los valores de GSNR simulados. Obsérvese, que el rendimiento del algoritmo propuesto es el que mejor se acerca al caso ideal, donde los parámetros del canal son conocidos por el receptor. Para un valor de GSNR igual a 6 dB, el algoritmo de búsqueda voraz de mediana ponderada presenta aproximadamente una BER = 0,01, y para el mismo valor de GSNR el algoritmo de búsqueda voraz clásico presenta aproximadamente una BER = 0, 09
4. CONCLUSIONES
Este artículo presenta un método robusto para la estimación de los parámetros del canal UWB usando un algoritmo de búsqueda voraz basado en la mediana ponderada. El método propuesto explota el hecho de que la señal recibida de un canal UWB exhibe una característica poco densa, por lo que se aprovechan los conceptos de representación de señales poco densas en diccionarios parametrizados. Más precisamente, la señal recibida se representa como la expansión lineal de unas pocas columnas de una matriz de diccionario que consiste en una colección de versiones desplazadas en el tiempo del pulso base usado en el proceso de transmisión UWB. Por tanto, la estimación del canal UWB se reduce a la implementación de un algoritmo de representación de señales poco densas, que, en este caso particular, determina la ganancia de cada trayectoria como la mediana ponderada de una versión desplazada y escalada de la señal recibida, donde el operador de mediana ponderada emerge naturalmente de la caracterización del ruido que contamina la señal de recibida usando una distribución la placiana.
El desempeño del algoritmo propuesto de búsqueda voraz basado en mediana ponderada se comparó con el desempeño exhibido por el algoritmo de búsqueda voraz clásico [5] usando extensas simulaciones. Específicamente, se muestran los resultados del error medio cuadrático (MSE) de los estimados de las ganancias de trayectorias múltiples en función de la relación geométrica señal a ruido (GSNR) de la señal recibida, para valores de GSNR (0-12 dB), donde el algoritmo de búsqueda voraz basado en la mediana ponderada ofrece un mejor rendimiento cuando el ruido que contamina la señal es impulsivo, lo cual simula un ambiente adaptado a las aplicaciones reales para las cuales fue diseñado el sistema UWB.