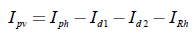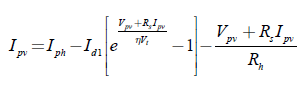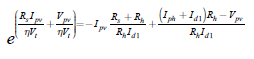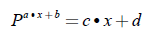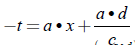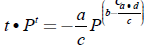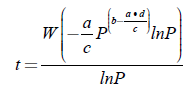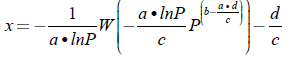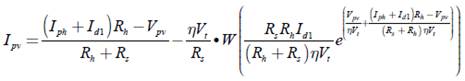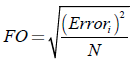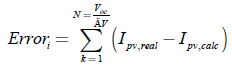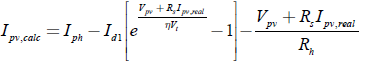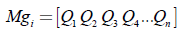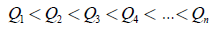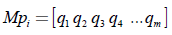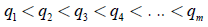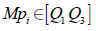Espanhol (pdf)
Artigo em XML
Referências do artigo
Tradução automática
Enviar este artigo por email
Citado por SciELO 
Citado por Google 
Similares em
SciELO 
Similares em Google 
Permalink
INTRODUCCIÓN
Ante la creciente demanda de energía y el deterioro ambiental, los gobiernos están promoviendo el uso de energías renovables no convencionales donde antes se empleaban combustibles fósiles [1]. La producción de energía a partir de la luz del sol es, en la actualidad, la fuente renovable de mayor uso a nivel mundial [2], de ahí la necesidad de desarrollar celdas solares más eficientes, confiables, de bajo costo y que permitan maximizar la transformación de energía bajo cualquier condición ambiental. La celda fotovoltaica (PV) es el dispositivo básico para la generación de energía eléctrica a partir de fotones. A pesar de los avances tecnológicos que se han tenido en su fabricación, la eficiencia de esta está limitada por factores como radiación solar, temperatura y sombreado [3-5].
Por múltiples propósitos [6-8], una celda PV puede ser modelada con diferentes niveles de exactitud y complejidad [9-13]. Los modelos circuitales de uno y dos diodos son los más utilizados en la literatura: el de un diodo por su simplicidad, ya que el número de parámetros por estimar es reducido; y el de dos diodos por su exactitud, ya que es una mejor representación del comportamiento de la celda en condiciones de baja radiación solar [14-15].
Con el objetivo de poder evaluar el desempeño de una celda PV, controlarla, conocer su eficiencia y establecer su punto de máxima potencia (Maximum Power Point Tracking (MPPT)), es necesario encontrar los parámetros del modelo de la celda. Se han realizado múltiples trabajos con diferentes enfoques para tratar de estimar los parámetros del modelo de la celda PV, los cuales pueden ser clasificados en tres categorías: métodos analíticos, métodos de optimización y métodos híbridos. Estos últimos utilizan enfoques analíticos en combinación con algoritmos de optimización metaheurísticos [16].
En [17-24] se emplean métodos analíticos para estimar los parámetros del modelo de un solo diodo de una celda PV; en algunos casos el modelo empleado solo considera pérdidas óhmicas y en otros se introducen, además, las corrientes de fuga en la juntura del semiconductor.
En [25-26] se han estimado los parámetros del modelo de la celda solar de uno y dos diodos empleando el algoritmo de optimización basado en un enjambre de abejas artificial. La función objetivo está basada en el error cuadrático medio del error de los datos experimentales y los estimados. Los algoritmos de evolución diferencial son empleados en [27-29] con el objetivo de estimar los parámetros de los modelos de la celda fotovoltaicas, tanto de un diodo como de dos diodos. En todos los casos, la función objetivo es reiterativa: el error cuadrático medio entre los datos experimentales y los estimados. PSO (Particle Swarm Optimization) es otro algoritmo de optimización metaheurístico empleado para estimar los parámetros del modelo de dos y tres diodos de la celda fotovoltaica [30], en el cual la función objetivo es el error absoluto promedio de la corriente del panel. En [31-32] la sumatoria del error absoluto individual de los cinco parámetros del modelo de un diodo de la celda fotovoltaica es considerada como la función objetivo para la estimación a partir del algoritmo de búsqueda de patrones. Las ventajas de este algoritmo con respecto a otros, como algoritmos no lineales basados en mínimos cuadrados, algoritmos basados en el método de Newton modificado y algoritmos genéticos, se evidencian en este artículo. Otros métodos de optimización se han empleado con el fin de estimar los parámetros del modelo de uno y dos diodos de la celda fotovoltaica, entre ellos están Biogeography-Based Optimization (BBO) [33], Innovative Global Harmony Search (IGHS) [34], Simulated Annealing (SA) [31], Bird Mating Optimization (BMO) [35], entre otros.
Este artículo está dividido en cinco partes. En primer lugar, se presenta el modelo de un diodo de la celda fotovoltaica y la solución explícita de la ecuación del modelo. En segundo lugar, se describe detalladamente del algoritmo de búsqueda de patrones mejorado (Improved Pattern Search Method [IPSM]). Posteriormente, se presenta el algoritmo de simulación de curvas V-1 de paneles comerciales. A continuación, se implementa el algoritmo IPSM y se compara con PSO. Finalmente, se presentan las conclusiones.
1. MODELO DE UN SOLO DIODO DE LA CELDA FOTOVOLTAICA
El modelado de PV tiene como uno de sus objetivos representar las curvas I-V de la celda o arreglo bajo diferentes condiciones de radiación solar o temperatura. Como se mencionó en la introducción, los modelos basados en un circuito eléctrico equivalente a uno y dos diodos son los más utilizados en la literatura; el primero por su simplicidad y el segundo por su exactitud.
En el modelo de dos diodos (descrito por la ecuación (1)] la corriente del panel fotovoltaico I pv es debida a la corriente fotoinducida I ph menos las pérdidas debidas a la absorción de la luz solar Id1, al mecanismo de recombinación en la juntura del diodo Id 2 y las pérdidas óhmicas que producen fugas de corriente I Rh [36].
(1)
Típicamente, el modelo de la celda fotovoltaica se ajusta para el caso de celdas de silicio cristalino, lo que implica despreciar las pérdidas debido a la recombinación, donde Id2 = 0 (véase Figura 1]. Por lo tanto, el modelo de la celda fotovoltaica se convierte en el modelo de un diodo, el cual está dado en la ecuación (2) [36].
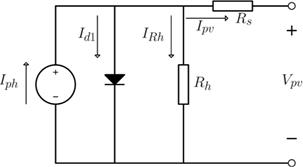
Fuente: elaboración propia.
Figura 1 Circuito equivalente del modelo de un diodo de una celda fotovoltaica
(2)
En este caso, Id1 es la corriente de saturación del diodo, η es el factor de idealidad del diodo, que para un diodo ideal es 1. Sin embargo, típicamente η∈ [1, 1, 5], Rs y Rh son parámetros desconocidos y representan las pérdidas de voltaje y corriente del panel, Vt = kT/q es el voltaje térmico de la juntura PN de la celda fotovoltaica, y se calcula a partir de la temperatura T, la constante de Boltzmann k y la carga del electrón q. Finalmente, Vpn es el voltaje de salida del panel.
Dependiendo de la precisión deseada en la simulación, el modelo de un diodo puede simplificarse aún más. Por ejemplo, se utilizan también modelos con Rs = 0, con Rh = 0 o bien con Rs = Rh = 0. Este circuito equivalente de un diodo para la celda fotovoltaica, es solo una simplificación de esta y no representa todas sus dinámicas.
1.1 Solución explícita de La ecuación del modelo
La ecuación (2) no admite una solución basada en funciones elementales, pero sí una solución explícita basada en la función Lambert W [37]. Reescribiendo la ecuación (2), obtenemos la ecuación (3).
(3)
Esta ecuación es de la forma dada en la ecuación (4).
(4)
Donde P es la base de los logaritmos naturales,
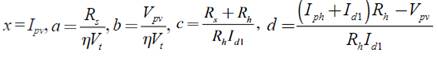. Con la sustitución dada en la ecuación (5), la ecuación (4) se convierte en la ecuación (6).
(5)
(6)
Por definición de la función trascendente Lambert’s W obtenemos la ecuación (7) cuya solución está dada en la ecuación (8).
(7)
(8)
Para el caso del modelo de un solo diodo de la celda fotovoltaica, la relación de Ipv en función de Vpv, según la ecuación (8), está dada en la ecuación (9).
(9)
2. ALGORITMO BÚSQUEDA DE PATRONES MEJORADO (IPSM)
El IPSM es un algoritmo que divide el campo de búsqueda en un número de mallas igual al número de variables a optimizar, las cuales están previamente acotadas. El rango de cada variable a optimizar se divide en n puntos equidistantes. El algoritmo (véase Figura 2] busca los valores de las variables que optimizan la función de costo definida en la ecuación (10), FO donde Errori de la ecuación (11) es el error entre la corriente real Ipv,real dada por la curva experimental V-I y la corriente calculada Ipv,calc de acuerdo con la ecuación (9) o la ecuación (12). Finalmente, N es el número de puntos de la curva experimental V-I.
(10)
(11)
(12)
Luego de determinar los valores de las variables que optimizaron la función de costo, se establecen nuevas mallas cuyo rango estará entre los dos puntos adyacente a los valores hallados (véase Figura 3]. A modo de ejemplo, si las mallas grandes (Mg) están conformada por n puntos equidistantes, entonces cada i-ésima variable está representada en la ecuación (13).
(13)
donde:
(14)
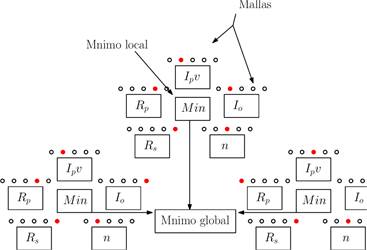
Figura 2 Procedimiento para la estimación de los parámetros del modelo matemático de un módulo fotovoltaico usando el algoritmo de optimización PSM
Las mallas pequeñas (Mp) estarán conformadas por m puntos alrededor del punto de la malla grande en donde se encuentre el mínimo local que se halló previamente en la ecuación (15). Como muestra la ecuación (16), los puntos tendrán un orden de menor a mayor.
(15)
donde:
(16)
Como ejemplo, si el mínimo local hallado en la malla grande fue Q2, entonces la malla pequeña debe cumplir lo establecido en la ecuación (17).
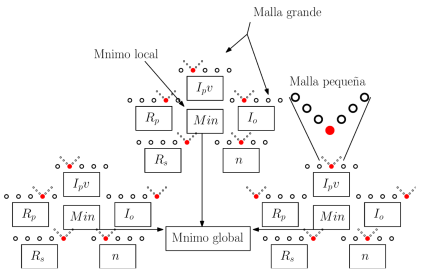
Fuente: elaboración propia.
Figura 3 Gráfico del procedimiento para la estimación de los parámetros de modelo matemático de un módulo fotovoltaico usando el algoritmo de optimización IPSM
(17)
Una vez que se definen las mallas grandes (Mg) y pequeñas (Mp) se procede a encuestar cada una de las variables de las mallas grandes y así obtener los valores que más se acercan al punto óptimo de la función de costo. Estos valores serán el centro de las mallas pequeñas. En este sentido, se realiza de nuevo una encuesta para lograr así una búsqueda exhaustiva (véase Figura 3].
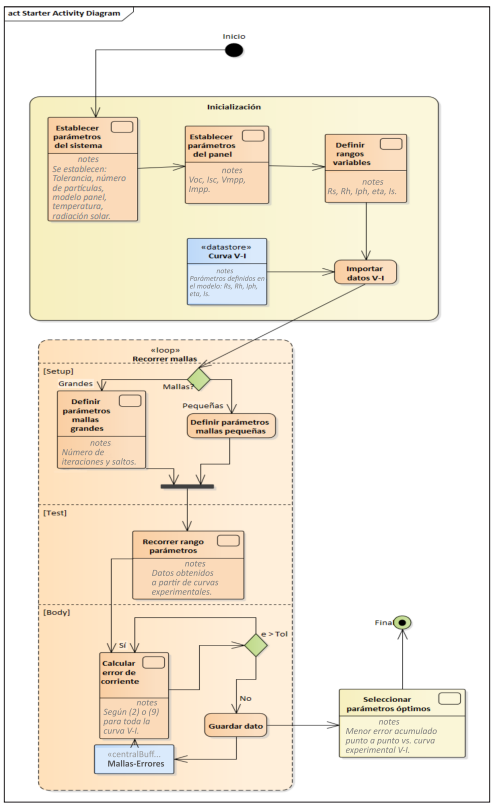
Figura 4 Diagrama de actividades de la optimización IPSM de los parámetros del modelo de la celda fotovoltaica
Si se encuentra un nuevo valor que esté aún más cerca del punto óptimo de la función de costo, este reemplazará al previamente hallado para dicha malla. Por cada iteración se reducen el rango de las nuevas mallas pequeñas, y el algoritmo finaliza después de determinado número de iteraciones o cuando el error acumulado sea menor que la tolerancia.
Para finalizar la búsqueda, se puede definir una tolerancia que garantice la exactitud deseada. Pero si esta exactitud no puede alcanzarse, el algoritmo quedará en un lazo infinito. Por lo tanto, se recomienda definir un número máximo de iteraciones que sacaría al algoritmo del posible bucle infinito, en caso de no alcanzar la exactitud esperada.
La Figura 4 muestra el diagrama de actividades del algoritmo implementado en Matlab® y su seudocódigo se presenta en la Figura 5. El algoritmo tiene una actividad de inicialización en la cual se establecen los parámetros del sistema (tolerancia, número de partículas, modelo del panel, temperatura, radiación solar, etc.), los parámetros del panel (voltaje de circuito abierto, corriente de corto circuito y punto de operación de máxima potencia), el rango de los parámetros a optimizar (resistencia serie y paralela, corriente fotovoltaica, corriente inversa y factor de idealidad del diodo) y finalmente se importan los datos de la curva experimental V-I del panel.
En la actividad estructurada del tipo loop se representan los ciclos anidados. Estos recorren los rangos previamente definidos en los cinco parámetros del modelo de un solo diodo de la celda fotovoltaica que se quieren optimizar en la ecuación 2, esto es, Rs , Rh , I ph , η, Id1. Además, para cada valor de los cinco parámetros se recorre la curva experimental V-I completa del panel, cuyo modelo se desea obtener. La actividad estructurada finaliza luego de recorrer el rango completo de los cinco parámetros del modelo, y la selección de los valores óptimos de dichos parámetros se da de acuerdo con una tolerancia definida establecida por la ecuación 11. Debe tenerse en cuenta que esta actividad estructurada sirve para modelar las consultas realizadas tanto a las mallas grandes como a las pequeñas.
Finalmente, luego de recorrer las mallas grandes y pequeñas, se obtienen los valores de los parámetros que optimizan el modelo de un diodo de la celda fotovoltaica con cuya curva experimental V-I se cuenta.
El método de búsqueda de patrones mejorado (IPSM) se puede representar por el pseudocódigo presentado en la Figura 5.
3. OBTENCIÓN DE LAS CURVAS EXPERIMENTALES DE LOS PANELES FOTOVOLTAICOS
Para poder validar los resultados obtenidos luego del proceso de optimización basado en IPSM se generan los datos de las curvas del panel utilizando el algoritmo propuesto por [38], en donde se encuentran los parámetros de un modelo matemático equivalente. De esta manera se generan, finalmente, las curvas características. Para las pruebas experimentales se generaron las curvas V-I de cuatro paneles con características diferentes, tal como puede verse en la Tabla 1.
Tabla 1 Paneles fotovoltaicos empleados para comparar la curva característica
| Panel | Celdas | P max (W) | (V mp , I mp ) | I sc (A) |
| MSX 60 | 60 | 60 | (17,1V,3,50A) | 3,80 |
| JS65 | 36 | 65 | (17,5V,3,71A) | 4,00 |
| KC200GT | 54 | 200 | (26,3V,7,61A) | 8,21 |
| STP245S | 60 | 245 | (30,5V,8,04A) | 8,52 |
Fuente: elaboración propia.
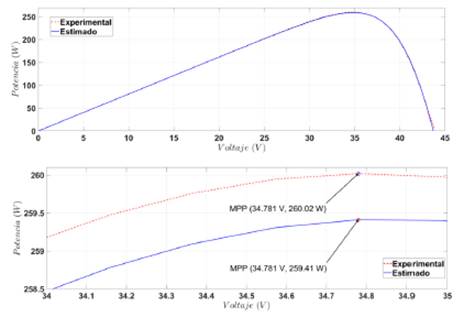
En las Figuras 6, 7, 8 y 9 pueden verse, en el lado izquierdo, la curva V-P estimada y la experimental de los paneles BP MSX-6, JS65 Series, KC200GT y STP245S respectivamente. El lado derecho de estas figuras muestra un acercamiento al punto de máxima potencia, el cual es el más importante debido a la exigencia de extraer siempre la máxima potencia del panel. Se puede observar que la pérdida de potencia más alta entre el modelo estimado y el experimental se da para el panel JS65 Series, donde la diferencia está por debajo del 1,1%. Para los demás paneles, la pérdida en potencia está por debajo del 1 %. En los demás sectores de la curva V-P el algoritmo alcanza una aproximación muy cercana a la ideal.
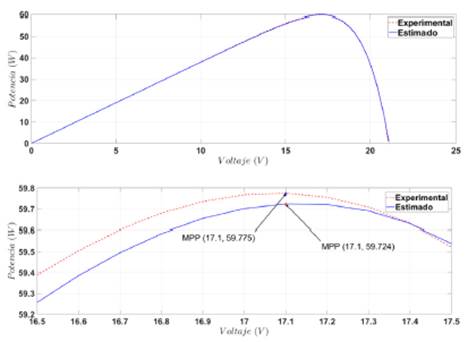
Fuente: elaboración propia.
Figura 6 Curva experimental del BP MSX-60 vs. modelo matemático estimado según IPSM
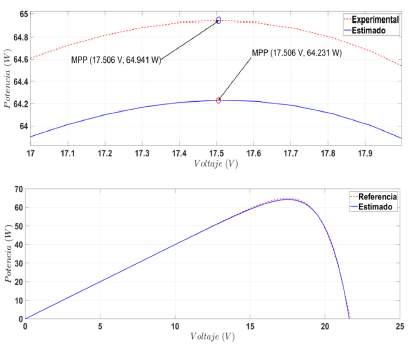
Fuente: elaboración propia.
Figura 7 Curva experimental del panel JS65 vs. Modelo matemático estimado según IPSM
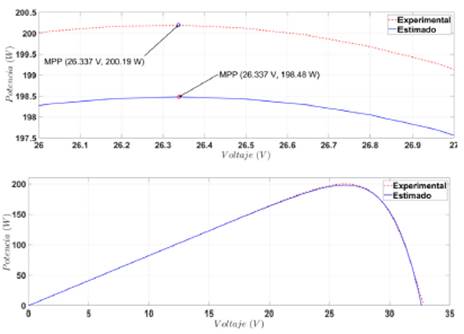
Fuente: elaboración propia
Figura 8 Curva experimental del panel KC200GT vs. modelo matemático estimado según IPSM
4. COMPARACIÓN DEL ALGORITMO IPSM CON EL ALGORITMO PSO
La validación del algoritmo de optimización IPSM para la estimación de los parámetros del modelo de un diodo del panel fotovoltaico se hizo bajo las mismas condiciones y la misma cantidad de partículas e iteraciones contra el algoritmo de optimización PSO [39].
Para la prueba se tomaron diez partículas con cincuenta iteraciones en ambos algoritmos de optimización (IPSM y PSO). También se aplicaron los algoritmos a la estimación de los cinco parámetros (Rh , Rs , η, Is , I ph ) sobre los paneles BP MSX-60, JS65 Series, KC200GT y STP245S de acuerdo con los rangos que se describen en la Tabla 2.
Tabla 2 Rangos para la estimación de las variables n, I d1, R s , R h , I ph [40]
| Variables | Límite inferior | Límite superior |
| R h (Ω) | 5 | 10.000 |
| R s (Ω) | 0 | 5 |
| | 0,5 | 2,5 |
| I d1 (A) | 1e-12 | 1e-5 |
| I ph (A) | 0 | 10 |
Fuente: elaboración propia.
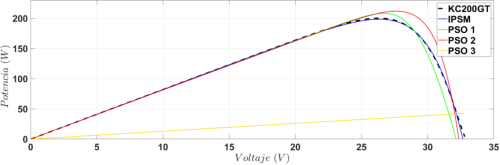
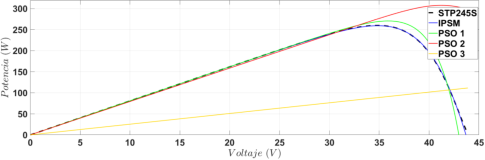
Los resultados se exponen en las Figuras 10, 11, 12 y 13 para los paneles BP MSX60, JS65 Series, KC200GT y STP245S respectivamente. Las figuras muestran la curva experimental de cada uno de los paneles (línea azul continua), la optimización obtenida con IPSM (línea punteada roja) y tres aproximaciones obtenidas con PSO de diez partículas.
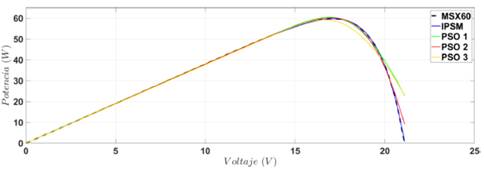
Fuente: elaboración propia.
Figura 10 Comparación entre los datos de referencia del panel BP MSX60, la estimación según IPSM y tres estimaciones según PSO
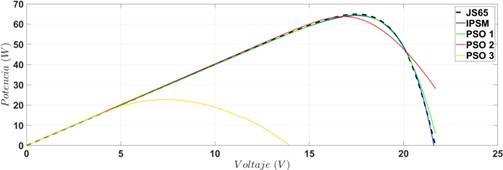
Fuente: elaboración propia.
Figura 11 Comparación entre los datos de referencia del panel JS65 series, la estimación según IPSM y tres estimaciones según PSO
Fuente: elaboración propia.
Figura 12 Comparación entre los datos de referencia del panel KC200GT, la estimación según IPSM y tres estimaciones según PSO
Fuente: elaboración propia.
Figura 13 Comparación entre los datos de referencia del panel STP45S, la estimación según IPSM y tres estimaciones según PSO
Como el algoritmo de optimización PSO depende de la aleatoriedad, se ejecutó tres veces para cada uno de los paneles. Por otro lado, el algoritmo de optimización IPSM solo se ejecutó una vez, ya que siempre arroja el mismo resultado. En la Tabla 3 se pueden observar los parámetros obtenidos usando IPSM y que hacen que el modelo de un solo diodo se asemeje más a la curva de referencia se pueden observar.
Tabla 3 Mínimo global encontrado para n, I 0, R s , R h , I ph de cuatro paneles diferentes
| Panel | R h (Ω) | R s (Ω) | | I d1 (A) | I ph (A) |
| MSX60 | 9.502,56 | 48,23 | 0,9915 | 3,7693 | 3,8002 |
| JS65 | 3.591,17 | 42,44 | 1,6744 | 5,0849 | 4,0046 |
| KC200GT | 7,836,73 | 48,23 | 1,0810 | 6,7323 | 8,2137 |
| SPT245S | 3.915,08 | 96,45 | 0,7608 | 2,4614 | 8,0941 |
Fuente: elaboración propia.
La Tabla 4 muestra el error absoluto de corriente, de acuerdo con la ecuación (11), para las estimaciones hechas para los cuatro paneles utilizando el algoritmo IPSM y el mejor caso del algoritmo PSO. Nótese que el error de la estimación realizada con el algoritmo IPSM siempre es menor que la obtenida en el mejor caso con el PSO. Por ejemplo, para el MSX60 el menor error obtenido con PSO es el 250,1 % más que el error obtenido con el algoritmo IPSM. El caso en el cual las dos estimaciones tuvieron el error de corriente más semejante fue para la estimación PSO 1 (trazo verde en la figura 11) del panel JS65, donde el error con el PSO fue el 77,1 % más del error obtenido con el algoritmo IPSM.
Sin embargo, cabe anotar que no todas las estimaciones con el algoritmo PSO convergen. Por ejemplo, la estimación PSO3 en los paneles JS65 series, KC200GT y STP245S muestran que el modelo no sigue a la referencia. Por ello, este algoritmo no garantiza, a diferencia del IPSM, la convergencia en todos los casos.
Finalmente, para obtener el modelo matemático de un diodo para cada uno de los cuatro paneles comerciales considerados en este trabajo, se debe reemplazar en la ecuación 2 los parámetros mostrados en la Tabla 3.
CONCLUSIONES
En este artículo se abordó la estimación de los parámetros del modelo matemático de un diodo para cuatro diferentes paneles fotovoltaicos de uso industrial: MSX60, JS65 Series, KC200GT y STP245S. Dicha estimación se realizó usando el algoritmo IPSM, el cual es una propuesta mejorada del conocido algoritmo PSM. Los parámetros del modelo que fueron estimados son: Rh , Rs , η, Id1 , I ph.
El modelo resultante obtenido a partir del algoritmo de optimización IPSM reproduce con buena exactitud la curva de referencia V-P para los cuatro paneles. Se hicieron estimaciones utilizando el algoritmo de optimización de enjambre de partículas, y en todas las estimaciones los resultados obtenidos con el algoritmo IPSM fueron mejores que los otros algoritmos expuestos. Asimismo, se puede determinar que los resultados son un 50 % mejores que los expuestos por PSM [41].
