Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Ciencias de la Salud
Print version ISSN 1692-7273On-line version ISSN 2145-4507
Rev. Cienc. Salud vol.6 no.3 Bogotá Sep./Dec. 2008
Caracterización geométrica de los glóbulos rojos. Diferenciación de muestras normales y patológicas
Geometric characterization of red blood cells. Differentiation of normal and pathologic samples
Javier Rodríguez,1 Catalina Correa,2 Signed Prieto,3 Benjamín Ospino,4 Pedro Bernal,5 Liliana Ortiz,6 Ángela Munévar7
1. MD, Director Grupo Insight. Profesor Universidad Militar Nueva Granada. Dirección. Cra 79 B No 51-16 Sur Int 5 Apto 102, Barrio Casablanca, Bogotá D.C., Cundinamarca, Colombia. Correo electrónico: grupoinsight2025@yahoo.es
2. Ps, investigadora del Grupo Insight.
3. Investigadora del Grupo Insight.
4. MD, Esp., Hospital Militar Central.
5. Estudiante de ingeniería de sistemas, investigador del Grupo Insight.
6. Delineante de arquitectura, investigadora del Grupo Insight.
7. Bact., Hospital Militar Central.
Recibido: 20 de julio de 2008 Aceptado: 28 de agosto de 2008
Resumen
Introducción. La geometría fractal mide la irregularidad de objetos abstractos y naturales con la dimensión fractal. Se han aplicado cálculos fractales a las estructuras del cuerpo humano y a cuantificaciones en fisiología desde la teoría de los sistemas dinámicos.
Material y métodos. Se calcularon las dimensiones fractales, el número de espacios de ocupación del borde en el espacio de box counting y la superficie ocupada por la imagen en píxeles de dos grupos de eritrocitos provenientes de pacientes y de bolsas para transfusión (7 normales, grupo A y 7 anormales, grupo B), utilizando el método de box counting y un software desarrollado para tal efecto. Se compararon las medidas obtenidas, buscando diferencias entre eritrocitos normales y anormales de manera individual y muestras de estos.
Resultados. La anormalidad se caracteriza por un número de espacios de ocupación del espacio fractal mayor o igual a 180 píxeles; valores de superficie en píxeles entre 25.117 y 33.548 corresponden a normalidad. En caso de que la evaluación sea de normalidad, de acuerdo con el número de espacios, debe confirmarse con el valor de la superficie en pixeles a eritrocitos adyacentes dentro de la muestra, la cual, en caso de tener valores por fuera de los establecidos y/o espacios mayores o iguales a 180 píxeles, sugieren anormalidad de la muestra.
Conclusiones. La metodología desarrollada es eficaz para diferenciar alteraciones eritrocitarias y probablemente útil en el análisis de bolsas de transfusión para uso clínico.
Palabras clave: fractal, transfusión, glóbulo rojo.
Summary
Introduction. Fractal geometry measures the irregularity of abstract and natural objects with the fractal dimension. Fractal calculations have been applied to the structures of the human body and to quantifications in physiology from the theory of dynamic systems.
Material and Methods. The fractal dimensions were calculated, the number of occupation spaces in the space border of box counting and the area of two red blood cells groups, 7 normal ones, group A, and 7 abnormal, group B, coming from patient and of bags for transfusion, were calculated using the method of box counting and a software developed for such effect. The obtained measures were compared, looking for differences between normal and abnormal red blood cells, with the purpose of differentiating samples.
Results. The abnormality characterizes by a number of squares of occupation of the fractal space greater or equal to 180; values of areas between 25.117 and 33.548 correspond to normality. In case that the evaluation according to the number of pictures is of normality, must be confirmed with the value of the area applied to adjacent red blood cells within the sample, that in case of having values by outside established and/or the greater or equal spaces to 180, they suggest abnormality of the sample.
Conclusions. The developed methodology is effective to differentiate the red globules alterations and probably useful in the analysis of bags of transfusion for clinical use.
Key words: fractal, transfusion, red blood cells.
INTRODUCCIÓN
A partir de la definición del concepto de dimensión fractal, la geometría fractal permite caracterizar la irregularidad de los objetos. El desarrollo de esta geometría se hizo necesario al encontrar paradojas en los resultados de la medición de objetos irregulares con las tradicionales medidas euclidianas. Mandelbrot mostró que si se mide el contorno de un objeto irregular, como una costa, superponiendo segmentos de rectas, al disminuir la longitud de las rectas, el contorno total del objeto tiende a infinito [1].
De manera general, existen tres tipos de fractales: los abstractos, en los cuales la parte es igual a la totalidad [2], los salvajes, en los que las partes se superponen entre sí [3], y los estadísticos con distribuciones hiperbólicas como en el lenguaje [4] y el sistema inmune [5-8]. Si el objeto es abstracto, como en el caso del conjunto de Cantor, el triángulo de Sierpinski o la curva de Koch, puede usarse la dimensión Hausdorff; en cambio, si los objetos son fractales salvajes, su dimensión puede calcularse con el método de box counting [9]. Este método se basa en el conteo de espacios ocupados por el contorno de la figura en rejillas bidimensionales, que pueden ser dos o más, de diferente escala y una linealización logarítmica de estos valores de ocupación.
La geometría fractal se ha aplicado a la geología, la economía, la morfología y el análisis de espacios de fase en sistemas dinámicos, entre otras áreas [9-12]. Ejemplo de sus aplicaciones en la medicina, son las caracterizaciones que pueden ser de utilidad en la detección de falsos positivos en mamografías [13,14], en la determinación de diferentes grados de lesión de cáncer de vejiga [15], en el análisis de alteraciones neoplásicas de la mucosa oral [16], o en diferencias en la vasculatura sana y tumoral en ratones andrógenodependientes [17]. Se han desarrollado múltiples aplicaciones de la geometría fractal a la caracterización de células y tejidos normales y enfermos [13-17, 20-21]. Sin embargo, la mayoría de los trabajos en geometría fractal se basan en la comparación de medidas fractales aisladas y en la búsqueda de rangos característicos de salud o enfermedad, lo cual no permite establecer diferencias en muchos casos. Rodríguez et al [22] midieron placas histológicas de arterias normales y reestenosadas con dimensiones fractales en un modelo experimental en porcinos, evidenciando que estas medidas no permiten establecer diferencias entre normalidad y enfermedad, mientras que el desarrollo de metodologías y conceptos ulteriores, como el de Armonía Matemática Intrínseca (AMI), permiten su diferenciación objetiva. Posteriormente, desarrollaron metodologías con base en geometría fractal para diferenciar Ramificación Coronaria Izquierda (RCI) con presencia y ausencia de enfermedad oclusiva arterial en angiografías [23] y ventriculogramas con fracción de eyección normal y <40% [24], además, para caracterizar células preneoplásicas [25] del epitelio escamoso cervical.
El éxito de las transfusiones de glóbulos rojos empaquetados (ERG) depende de la viabilidad de los eritrocitos, la cual está determinada por la morfología de los mismos al momento de la transfusión. Si bien los procedimientos de reemplazo de la volemia han avanzado en el mantenimiento de la integridad de los componentes sanguíneos posteriores al empaquetamiento –desarrollo de estabilizantes y anticoagulantes–, poco se ha podido avanzar en la determinación de métodos de tamización de la viabilidad eritrocitaria [18]. Por ello, tal tamización se hace sin claros criterios matemáticos o geométricos de diagnóstico, mediante observación microscópica basada en la pericia del evaluador [18,19]. De acuerdo con la observación experimental, la célula cambia de forma durante su almacenamiento; pasa de ser un discocito a ser un equinocito o esferoequinocito, con 10 a 30 espículas de longitud regular e igualmente distribuidas por la superficie [19]. Se ha establecido que la forma óptima del eritrocito para la circulación in Vitro, corresponde a la del discocito, pues al transformarse en estomatocito se altera el paso a través de la microcirculación, debido a la disminución de la filtrabilidad celular, mientras que al transformarse en equinocito puede alterarse el flujo en los grandes vasos [19]. Debido a lo anterior, es de vital importancia el desarrollo de nuevas metodologías de aplicación clínica que permitan caracterizar la viabilidad eritrocitaria de manera precisa y objetiva.
Para la descripción matemática de los hematíes, los trabajos se han centrado en la cinética de los glóbulos rojos. Reuben et al y Sharma et al centran la discusión en los problemas matemáticos de la interpretación actual de la velocidad de sedimentación globular (VSG), la cual obvia los procesos patológicos en los que la agregación eritrocitaria depende de concentraciones matemáticas relativamente desconocidas, que no pueden explicarse desde una sola variable lineal sino que necesitan interpretarse desde medidas de la geometría fractal [26,27]. Kuo et al encontraron que la VSG es una constante intrínseca, característica de la interacción entre los eritrocitos y las macromoléculas que, al introducirse en la función de la ley de la energía de la sedimentación, permite definir curvas simétricas de sedimentación que definen una dimensión fractal D y una nueva constante de la VSG, las cuales explican la tendencia para la acumulación de líquido dentro del coágulo de retracción [28]. Tang et al desarrollaron un modelo que predice la dimensión fractal de los agregados de sedimentación [29]. Ismailov et al relacionan la estructura interna con la VSG y el medio, desde ecuaciones diferenciales derivadas de las fundamentales [30]. Estos trabajos evidencian la pertinencia del desarrollo de nuevas metodologías para la evaluación del estado eritrocitario con base en medidas fractales.
La presente investigación tiene como propósito evaluar dimensiones fractales, superficie en pixeles y cantidad de espacios en el espacio de box counting de eritrocitos normales y anormales, buscando diferencias matemáticas de su morfología, relacionadas con enfermedades eritrocitarias que puedan ser de utilidad para evaluar la calidad de las muestras en transfusiones.
MATERIALES Y MÉTODOS
Definiciones
Dimensión fractal de box counting:
(Ecuación 1)

Superficie en píxeles del objeto
Número de píxeles que tocan el interior o el borde de la imagen medida.
Número de espacios pequeños en el espacio de box counting
La medición de la dimensión fractal de box counting, requiere la superposición de dos rejillas, como mínimo, a la imagen medida. Las rejillas utilizadas fueron de 5 y 50 píxeles. El número de espacios pequeños corresponde al número de espacios que tocan el borde de la imagen medida al superponer la rejilla de 5x5 píxeles.
Procedimiento
Se escogieron 14 muestras que se dividieron en dos grupos: el grupo A, conformado por 7 muestras de sangre normal procedentes de: 1) un individuo diagnosticado normal, según criterio médico convencional, 2) tres bolsas de sangre para transfusión, las cuales se mantuvieron en refrigeración a 4ºC hasta por 42 días para trasfundir los pacientes del mismo grupo sanguíneo y a las que se han hecho pruebas cruzadas según está indicado, y 3) tres pacientes cuyos cuadros hemáticos presentaron valores de hemoglobina menores a 9 g/dl, sin otras alteraciones en las características de los eritrocitos, por lo que les había sido ordenada una transfusión. El grupo B, compuesto por 7 muestras anormales provenientes de: 1) cinco pacientes con alteraciones eritrocitarias, y 2) dos bolsas descartadas por su no viabilidad para transfusión.
Los extendidos y las 14 células fueron seleccionados por Benjamín Ospino y Ángela Munévar, expertos en hematología del Hospital Militar Central. De acuerdo con su experiencia, se buscó incluir todas las características morfológicas de normalidad y las alteraciones morfológicas más importantes, con base en la observación cualitativa, de manera que la determinación de las características matemáticas comunes a cada uno de los grupos contribuyera a la caracterización que permita diferenciar ambos estados.
Dado que unas pocas células patológicas en una muestra son indicadoras de patología, y la aplicación de una caracterización matemática permite establecer objetivamente su estado, es innecesario un análisis muestral mayor, lo cual permite prescindir de la utilización de grandes volúmenes de sangre, tanto en el desarrollo de la metodología como en su aplicación. Igualmente, este procedimiento hace que no se requiera el uso de un método probabilístico de cálculo de tamaño de la muestra.
Los extendidos de sangre periférica, en lámina tratada con el colorante de Wright, se observaron a un aumento de 100X a través de microscopio (Axiostar Plus), posteriormente se fotografiaron con una cámara digital (Canon Power Shot65), finalmente fueron transferidas a través de interfase en serie al computador (ver figuras 1 y 2). Para el procesamiento de las imágenes se desarrolló un software mediante el cual se midió la dimensión fractal del eritrocito, con espacios de 5x5 y 50x50 píxeles, anotando el número de espacios de 5x5 píxeles que eran tocados por el borde del eritrocito en el espacio de box counting y la superficie ocupada por la totalidad del eritrocito en píxeles. Estas dos rejillas fueron escogidas porque sus escalas permiten evidenciar las diferencias entre normalidad y enfermedad, mientras que escalas más pequeñas o más grandes ignoran irregularidades con las que pueden diferenciarse los grupos, o bien evalúan demasiados detalles que resultan innecesarios para la diferenciación.
Figura 1. Eritrocito normal N4 seleccionado y delineado en la rejilla de 5x5 píxeles. La morfología espiculada del borde del eritrocito anormal en contraposición con el normal puede medirse matemáticamente en esta escala.

Figura 2. Eritrocito anormal A5 seleccionado y delineado en la rejilla de 50x50 píxeles. Esta rejilla es útil para la determinación de la dimensión fractal, pero no para establecer diferencias entre normalidad y enfermedad porque es una escala demasiado grande.

El software se desarrolló en una plataforma C++; el algoritmo usado se basa en un conteo de cuadros ocupados bajo una rejilla seleccionada por el usuario; luego, dicho conteo es enviado a una función que evalúa la dimensión fractal (ver ecuación 1). El valor resultante, tanto de la dimensión fractal como de los espacios ocupados por el borde, se muestra a través de una ventana emergente de la aplicación. Además, el programa cuenta con la utilidad de arrojar el número de píxeles ocupados por la superficie de la figura a evaluar. El tiempo de ejecución del conteo de cuadros y de la dimensión fractal es del orden de los microsegundos. Hasta ahora se ha usado en procesadores Pentium M con capacidad mínima de 1,6 Ghz, sin ninguna dificultad de procesamiento de datos. La velocidad del procesamiento de los datos no se ve afectada por la disminución de los espacios de 5x5 hasta 50x50, que se sigue manteniendo en el orden de los microsegundos.
Finalmente se estudiaron las características comunes a ambos grupos, con el fin de establecer los parámetros matemáticos que permitan diferenciarlos.
RESULTADOS
Los espacios de 5x5 tocados por el borde de la célula presentaron valores entre 135 y 184 píxeles, oscilando entre 135 y 177 píxeles en el grupo de eritrocitos normales, mientras que los anormales presentaron valores entre 138 y 184 píxeles (ver tabla 1).
Tabla 1. Dimensión fractal, superficie en píxeles y número de espacios ocupados por el borde en la rejilla de 5x5 píxeles
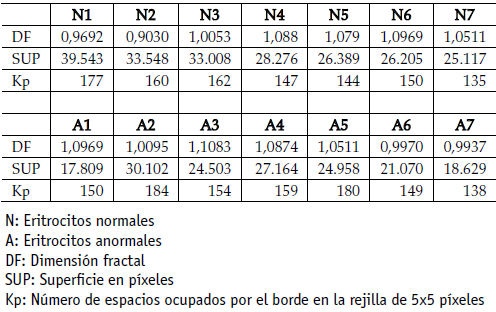
Las dimensiones fractales se encontraron entre 0,9030 y 1,1083. Para eritrocitos normales entre 0,9030 y 1,0969, y para eritrocitos anormales entre 0,9937 y 1,1083 (ver tabla 1). Los espacios de 50x50 sólo fueron utilizados para la evaluación de la dimensión fractal, pues es una escala tan grande que su observación resulta irrelevante para la diferenciación de los grupos.
Las superficies se encontraron entre 17.809 y 39.543 pixeles. Para eritrocitos normales entre 25.117 y 39.543 pixeles, y para eritrocitos anormales entre 17.809 y 30.102 pixeles (ver tabla 1).
Mediante el siguiente procedimiento es posible diferenciar normalidad de anormalidad en las muestras: se evalúa el número de espacios ocupados por el borde del eritrocito, el cual, en caso de ser mayor o igual a 180 píxeles es marcador de anormalidad de la muestra. Si el eritrocito presenta un número normal de espacios del borde, se evalúa la superficie en píxeles de los eritrocitos adyacentes, los cuales, para ser normales, deben encontrarse entre 25.117 y 33.548 píxeles. En caso de encontrar números de espacios del borde mayores a 180 píxeles o superficies por fuera de los valores de normalidad, la muestra se considera anormal.
DISCUSIÓN
Éste es el primer trabajo en el cual se realiza una caracterización geométrica de la morfología de los glóbulos rojos a partir del análisis de varios de éstos en una muestra, por medio de las geometrías fractal y euclidiana. Se encontraron órdenes matemáticos que caracterizan la forma y la funcionalidad del eritrocito, a partir de proporciones geométricas objetivas y reproducibles, basadas en parámetros matemáticos. De esta manera, se mejora el diagnóstico clínico convencional pues brinda información objetiva y reproducible que diferencia matemáticamente eritrocitos normales de enfermos. Se encontró que estos parámetros son aplicables a bolsas de transfusiones y evaluaciones pre y postransfusión.
Para el desarrollo de esta metodología sólo fueron necesarios 14 eritrocitos, los cuales se escogieron por ser característicos de normalidad y anormalidad, sin duda; por lo anterior, no se requieren grandes volúmenes de sangre, debido a las importantes diferencias morfológicas entre los eritrocitos seleccionados. El presente trabajo evidencia que fueron necesarias medidas tanto euclidianas como fractales para llegar al resultado diagnóstico, pues el espacio de box counting contiene un conteo euclidiano de los espacios ocupados por el borde de la figura irregular dentro de un espacio bidimensional finito, del mismo modo, se realiza un conteo euclidiano al evaluar la superficie evaluada en píxeles por el objeto medido en dos dimensiones. El análisis de dimensiones fractales aisladas no permite establecer diferencias entre normalidad y anormalidad, evidenciando que lo que permite establecer las diferencias es la observación de la forma en la cual es ocupado el espacio en la relación de la superficie y el perímetro.
Al comparar los valores entre grupos, se observa que éstos se encuentran superpuestos, lo cual hace necesario evaluar más de un eritrocito para establecer el diagnóstico de la muestra. El valor de 180 píxeles se consideró como límite de normalidad porque ninguno de los valores de normalidad es mayor a 177 píxeles, mientras que valores iguales o mayores a 180 están siempre asociados a eritrocitos anormales. Valores inferiores a 24.958 píxeles en la superficie están asociados a enfermedad en todos los casos, mientras que valores superiores pueden darse tanto en normalidad como en enfermedad, por lo cual el rango de normalidad se tomó entre 25.117y 33.548 píxeles en eritrocitos adyacentes. El valor de 39.543 píxeles no fue incluido como límite de normalidad porque, aunque se presenta en un eritrocito normal, todos los demás presentan valores por debajo de 33.548 píxeles mientras que el eritrocito que presenta el valor más alto, presenta además el valor más cercano al límite de anormalidad en el número de espacios del borde. Estos valores límite pueden tener rangos cercanos en nuevas medidas realizadas, manteniéndose la consistencia metodológica planteada.
Dado que los métodos de tamización utilizados en la actualidad utilizan observaciones microscópicas de las alteraciones morfológicas de las muestras, su diagnóstico está limitado a la experiencia del evaluador. Este trabajo contribuye al desarrollo de parámetros objetivos y reproducibles, los cuales mejorarán tanto la precisión como el tiempo de evaluación, pues el desarrollo de parámetros matemáticos claros constituye la base para el desarrollo de métodos automatizados de diagnóstico.
Es necesario llevar a cabo correlaciones a nivel clínico, aplicando esta metodología para evaluar su aplicabilidad en el mejoramiento de las transfusiones, así como desarrollar medidas en diferentes momentos durante el almacenamiento de las bolsas para establecer posibles alteraciones en el tiempo de almacenamiento y hacer una mejor escogencia con esta metodología para las transfusiones.
CONCLUSIONES
Se desarrolló una nueva metodología de evaluación del estado eritrocitario a partir de la caracterización matemática de la morfología el eritrocito con base en geometría fractal y euclidiana.
Las medidas euclidianas y fractales evaluadas aisladamente no permiten la diferenciación de los grupos, pero la observación de ambas permite la determinación del estado de la muestra mediante el siguiente procedimiento: primero se determina el número de espacios ocupados por el borde del eritrocito, el cual resultó ser menor a 180 píxeles en muestras normales. En caso de ser mayor o igual a 180 píxeles es marcador de anormalidad. Si el eritrocito presenta un número normal de espacios del borde, se evalúa la superficie en píxeles de los eritrocitos adyacentes, los cuales, para ser normales, se encuentran entre 25.117 y 33.548 píxeles. En caso de encontrar números de espacios del borde mayores a 180 píxeles o superficies por fuera de los valores de normalidad, la muestra se considera anormal.
La precisión de las medidas obtenidas permite una evaluación matemática general y objetiva de cualquier caso particular de los grupos evaluados, haciendo innecesario el uso de metodologías estadísticas.
AGRADECIMIENTOS
A la Unidad de Educación e Investigación Médica del Hospital Militar, en especial al Dr. Ricardo Rodríguez por su apoyo a nuestro grupo de investigación. Al decano de la Universidad Militar Nueva Granada, Coronel Estrada, y al Dr. Forero por apoyar nuestras investigaciones.
Agradecemos el apoyo del Servicio de Hematooncología del Hospital Militar, en especial a Santiago Ortiz, auxiliar del Laboratorio de Hematología y a Gineth Martínez y Katherine Martínez, secretarias, por su colaboración en esta investigación.
DESCARGOS DE RESPONSABILIDAD
Los autores de este artículo asumen la responsabilidad total por el contenido del presente manuscrito.
REFERENCIAS
1. Mandelbrot B. ¿Cuánto mide la costa de Bretaña?. En: Mandelbrot B. Los objetos Fractales. Barcelona: Tusquets Eds. S.A., 2000, p. 27-50. [ Links ]
2. Peitgen J, Jürgens H, Saupe D. Classical fractals and self-similarity. En: Jürgens H, Saupe D. Chaos and fractals: New Frontiers of Science. N.Y.: Springer-Verlag, 1992, p. 63-134. [ Links ]
3. Mandelbrot B. The fractal geometry of nature. Barcelona: Freeman Tusquets Eds S.A., 2000. [ Links ]
4. Mandelbrot, B. Structure formelle des textes et communication. World 1954;10:1-27. [ Links ]
5. Burgos J. Fractal representation of the immune B cell repertoire. Biosystems 1996;39:19-4. [ Links ]
6. Burgos J, Moreno-Tovar P. Zipf-scaling behavior in the immune system. Biosystems 1996;39:227-32. [ Links ]
7. Rodríguez J. Comportamiento fractal del repertorio T específico contra el alergeno Poa P9. Rev Fac Med Univ Nac Colomb 2005;53:72-8. [ Links ]
8. Naumov Y, Naumova E, Hogan K, Selin L, Gorski J. A fractal clonotype distribution in the CD8 memory T cell repertoire could optimize potencial immune responses. J Immunol 2003;170:3994-01. [ Links ]
9. Peitgen J, Jürgens H, Saupe D. Length area and dimension. Measuring complexity and scalling properties. En: Jürgens H, Saupe D. Chaos and fractals: New Frontiers of Science. N.Y.: Springer-Verlag, 1992, p. 183-28. [ Links ]
10. Goldberger A, Rigney D, West B. Chaos and fractals in human physiology. Sci Am 1990;262:42-9. [ Links ]
11. Goldberger A. Non-linear dynamics for clinicians: chaos theory, fractals, and complexity at the bedside. Lancet 1996;347:1312-14. [ Links ]
12. Goldberger A, Amaral L, Hausdorff J, Ivanov P, Peng C, Stanley H. Fractal dynamics in physiology: alterations with disease and aging. Proc Natl Acad Sci USA 2002;99:2466-72. [ Links ]
13. Pohlman S, Powell K, Obuchowski NA. Quantitative classification of breast tumors in digitized mammograms. Med Phys 1996;23:1337-45. [ Links ]
14. Lefebvre F, Benali H. A fractal approach to the segmentation of microcalcifications in digital mammograms. Med Phys 1995;22:381-90. [ Links ]
15. Luzi P, Bianciardi G, Miracco C, Desanti MM, Del Vecchio MT, Alia L, Tosi P. Fractal analysis in human pathology. Ann NY Acad Sci 1999;879:255-57. [ Links ]
16. Landini G, Rippin JW. Fractal dimensions of epithelial-connective tissue interfaces in premalignant and malignant ephitelial lesions of the floor of mouth. Anal Quant Cytol Histol 1993;15:144-49. [ Links ]
17. Gazit Y, Baish JW, Safabaksh N. Fractal characteristics of tumor vascular architecture during tumor growth and regression. Microcirculation 1997;4:395-02. [ Links ]
18. Naotaka, H, Masaaki, Y. Red blood cell function and blood storage. Vox Sanguinis 2000;79:191-97. [ Links ]
19. Peñuela OA, Urbina A, Palomino LF. Preservación de eritrocitos y cambios físicos ocurridos durante el almacenamiento. Revista Facultad de Medicina, Universidad Nacional de Colombia 2003;51:190-97. [ Links ]
20. Baish J, Jain R. Fractals and cancer. Cancer Res 2000;15;60:3683-88. [ Links ]
21. Gazit Y, Berk DA, Leunig M. Scale-invariant behavior and vascular network formation in normal and tumor tissue. Phys Rev Lett 1995;75:2428-31. [ Links ]
22. Rodríguez J, Mariño M, Avilán N, Echeverri D. Medidas fractales de arterias coronarias, un modelo experimental en reestenosis, armonía matemática intrínseca de la estructura arterial. Rev Col Cardiol 2002;10:65-2. [ Links ]
23. Rodríguez J, Álvarez L, Mariño M, Avilán N, Prieto S, Casadiego E, Correa C, Osorio E. Variabilidad de la dimensión fractal del árbol coronario izquierdo en pacientes con enfermedad arterial oclusiva severa. Dinámica fractal de la ramificación coronaria. Rev Col Cardiol 2004;11:185-2. [ Links ]
24. Rodríguez J, Prieto S, Ortiz L, Avilán N, Álvarez L, Correa C, Prieto I. Comportamiento fractal del ventrículo izquierdo durante la dinámica cardiaca. Rev Col Cardiol 2006;13:165-70. [ Links ]
25. Rodríguez J, Prieto S, Ortiz L, Wiesner C, Díaz M, Correa C. Descripción matemática con dimensiones fractales de células normales y con anormalidades citológicas de cuello uterino. Revista Ciencias de la Salud, Universidad del Rosario 2006;4:58-3. [ Links ]
26. Reuben AJ, Shannon AG. Some problems in the mathematical modelling of erythrocyte sedimentation. J Math Appl Med Biol 1990;7:145-56. [ Links ]
27. Sharma GC, Jain M, Saral RN. A mathematical model for concentration of blood affecting erythrocyte sedimentation. Comput Biol Med 1996;26:1-7. [ Links ]
28. Kuo CD, Bai JJ, Chien S. A fractal model for erythrocyte sedimentation. Biorheology 1994;31:77-89. [ Links ]
29. Tang P, Greenwood J, Raper JA. A model to describe the settling behavior of fractal aggregates. J Colloid Interface Sci 2002;247:210-9. [ Links ]
30. Ismailov RM, Shevchuk NA, Khusanov H. Mathematical model describing erythrocyte sedimentation rate. Implications for blood viscosity changes in traumatic shock and crush syndrome. Biomed Eng Online 2005;4:4-24. [ Links ]














