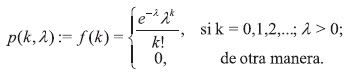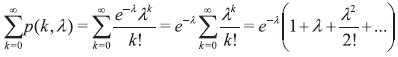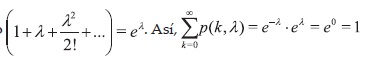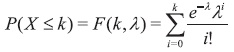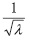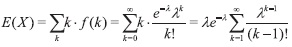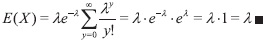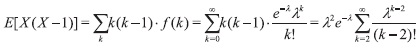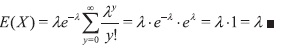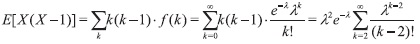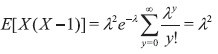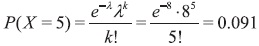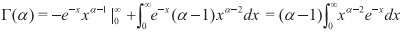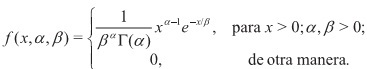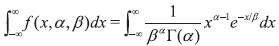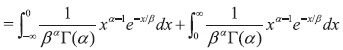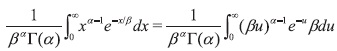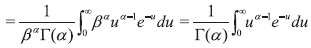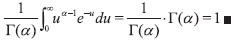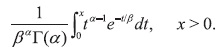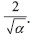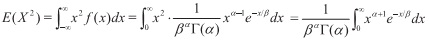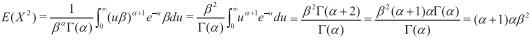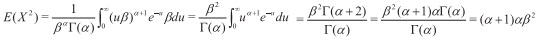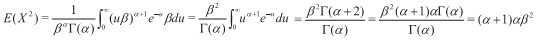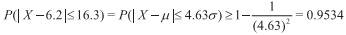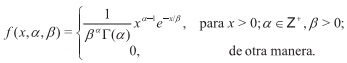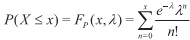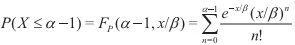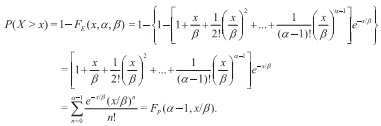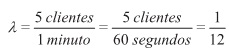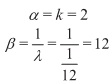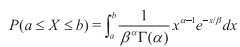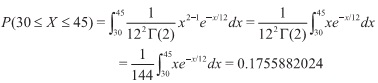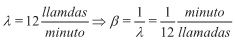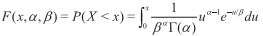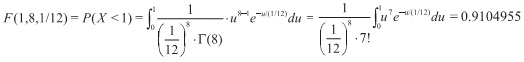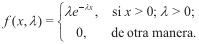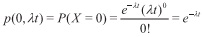Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Prospectiva
Print version ISSN 1692-8261
Prospect. vol.12 no.1 Barranquilla Jan./June 2014
https://doi.org/10.15665/rp.v12i1.156
http://dx.doi.org/10.15665/rp.v12i1.156
Distribuciones Poisson y Gamma: Una Discreta y Continua Relación
Poisson and Gamma Distributions: A Discrete and Continuous Relationship
Indira Arroyo1, Luis C. Bravo M.2, Dr. Ret. Nat. Humberto Llinás.3, Msc. Fabian L. Muñoz.4
1 Estudiante de Maestría en Estadística Aplicada. Universidad del Norte, Barranquilla, Colombia.
2 Estudiante de Maestría en Estadística Aplicada. Universidad del Norte, Barranquilla, Colombia.
3 Director de Maestría en Estadística Aplicada. Universidad del Norte, Barranquilla, Colombia.
4 Docente Investigador. Universidad del Norte, Barranquilla, Colombia. E-mail: flmunoz@uninorte.edu.co.
Recibido 18/12/13, aceptado 30/01/2014
Resumen
En el presente artículo se indica la relación que existe entre la distribución de Poisson y la distribución Gamma, de una manera concisa y elemental. Se inicia revisando los aspectos y/o propiedades básicas de cada distribución. Esto incluye las respectivas demostraciones de función de probabilidad y función de densidad, además de las pertinentes fórmulas de esperanza y varianza, junto con las demostraciones de cada una de éstas. Se exhiben algunas propiedades a tener en cuenta para cada distribución, y posteriormente se presenta la relación existente entre estas últimas. Se proponen también, algunos ejemplos que ilustren el empleo de cada distribución y su mencionada relación.
Palabras clave. Distribución de Poisson, Distribución Gamma, Función de Probabilidad, Función de Densidad, Distribución Acumulada, Esperanza, Varianza.
Abstract
This article shows the relationship between the Poisson distribution and the Gamma distribution, in a concise and elementary way. It starts by reviewing the aspects and/or basic properties of each distribution. This includes demonstrations respective probability function and density function, besides the pertinent formulas expectation and variance, together with demonstrations of each of these. It exhibits some properties to be considered for each distribution, and presents the relationship between the latter. It also proposes some examples that illustrate the use of each distribution and its relationship mentioned.
Keywords. Poisson Distribution, Gamma Distribution, Probability Function, Density Function, Cumulative Distribution, Expectation, Variance.
Introducción
La distribución de probabilidad de la variable aleatoria que representa el número de resultados que suceden durante un intervalo de tiempo dado, o una región específica, recibe el nombre de distribución de Poisson, con parámetro λ. Mientras que la distribución de probabilidad de la variable aleatoria que representa el tiempo, hasta que se produce a veces un determinado suceso, se llama distribución Gamma (ésta es una manera de describir a la distribución gamma), con parámetros α y β. A primera vista, no es tan inmediato presentar una relación entre las dos distribuciones. Pero ésta sí existe y es tratada brevemente en diversos textos especializados.
La relación esencial entre las distribuciones anteriormente mencionadas, sucede cuando el parámetro de la distribución gamma, α, es un entero positivo cuando esto sucede, la distribución gamma es también llamada distribución de Erlang y el número de eventos aleatorios independientes que suceden en un intervalo específico es una variable de Poisson, con una frecuencia constante de ocurrencia igual a λ = VJ3.
Además, recordemos que existe una distribución de probabilidad llamada distribución exponencial (llamada también exponencial negativa), la cual es un caso especial de la distribución gamma o distribución de Erlang, y que presenta una evidente conexión entre la distribuciones Poisson y gamma. La distribución exponencial describe el tiempo hasta la primera ocurrencia de un evento de Poisson. Así, las aplicaciones más importantes de esta distribución son aquellas situaciones en donde se aplica el proceso de Poisson. En la distribución de Poisson λ es el número promedio de eventos por unidad de tiempo, mientras que en la distribución exponencial l/λ es la tasa de ocurrencia de un evento por unidad de tiempo.
Es primordial informar que la importancia de este artículo no solo radica en presentar la relación final entre las distribuciones Poisson y gamma, la cual brinda un grano de arena en el proceso de observar y/o analizar de mejor manera el propósito y la estructura de la teoría de probabilidad, sino que también es relevante reconocer o recordar las propiedades, y demás aspectos, que tiene cada una, para efectuar un mejor estudio y uso de éstas.
Cabe señalar que textos como el de Probabilidad y Estadística de G. Canavos[1], Probabilidad y Estadística para Ingenieros de Walpole[1] y Probabilidad y Estadística de Alejandro D. Zylberberg[2] realizan, en algunos de sus apartados, un análisis similar en ciertos aspectos, al que se hace en este artículo. Obviamente, dichos textos no solo abordan las distribuciones de las que aquí se hablará, sino que, como su nombre lo indica, presentan una introducción a la teoría de la probabilidad y a la estadística, enfatizando en sus aplicaciones. Además, se informa que algunos aspectos estructurales de este trabajo se basaron en el artículo La Distribución Poisson-Beta: Aplicaciones y Propiedades En La Teoría Del Riesgo Colectivo [3].
Este artículo está estructurado como sigue: En la primera sección se presenta la distribución de Poisson; función de probabilidad, ejemplo práctico, función de distribución acumulada, propiedades, gráficas, y las demostraciones de las respectivas esperanza y varianza. En la segunda sección se aborda la distribución gamma; se inicia con un apartado de la función gamma y, posteriormente, se desarrolla el mismo proceso de presentación de la distribución de Poisson. En la tercera sección se exhiben la distribución de Erlang y la distribución exponencial como las distribuciones que evidencian la relación entre la distribución de Poisson y la distribución gamma, incluyendo algunos ejemplos. Finalmente en la última sección se da a conocer algunas conclusiones.
La distribución de Poisson es una distribución de probabilidad discreta que expresa, a partir de una frecuencia de ocurrencia media λ, la probabilidad que ocurra un determinado número de eventos k ∈ X durante un intervalo de tiempo dado o una región específica.
Definición 1.1 Sea X una variable aleatoria que representa el número de eventos aleatorios independientes que ocurren a una rapidez constante sobre el tiempo o el espacio. Se dice entonces que la variable aleatoria X tiene una distribución de Poisson con función de probabilidad
Teorema 1.1 La función ƒ es una función de probabilidad.
Demostración 1.1
Debemos probar que 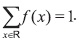 Para este caso
Para este caso 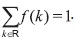
Debido a que si k ± 0,1,2,... entonces ƒ(k) = 0, solo debemos analizar
Por tanto ƒ es una función de probabilidad.
La función de distribución acumulativa de Poisson F(k), la cual permite determinar la probabilidad de que una variable aleatoria de Poisson X sea menor o igual a un valor específico k, tiene la siguiente forma:
1.2 Propiedades de la distribución de Poisson
La distribución de Poisson desempeña un papel importante, por derecho propio, como un modelo probabilístico apropiado para un gran número de fenómenos aleatorios.
Las características mas sobresalientes de esta distribución son:
-E{X) = λ
-Var(X) =λ
- Con lo anterior se puede observar que la distribución de poisson es leptocúrtica con un sesgo positivo.
- La función generadora de momentos de la variable aleatoria de Poisson X, con valor esperado λ es mx(t) = e (λ (et-1)).
- El espacio muestral en un modelo de Poisson se genera por un número muy grande (puede considerarse infinito) de repeticiones de un experimento cuyo modelo de probabilidad es el de Bernoulli, con probabilidad de éxito muy pequeña. Por esta razón, a la distribución de Poisson se le suele llamar de eventos raros. Las repeticiones del experimento de Bernoulli se realizan en cada uno de los puntos de un intervalo de tiempo o espacio. La probabilidad de que se tenga dos o más éxitos en el mismo punto del intervalo es cero. El número promedio de éxitos en un intervalo es una constante λ que no cambia de intervalo a intervalo.
- La distribución de Poisson se puede expresar de forma gráfica, ya que en realidad consiste en un diagrama de barras, con forma asimétrica positiva como sucede con la distribución binomial. Sin embargo, al ir aumentando los valores de λ, va adquiriendo la típica forma de la Campana de Gauss (esto se puede evidenciar analizando el coeficiente de asimetría -su objetivo es determinar, sin necesidad de dibujar, la deformación horizontal de la distribución con respecto a un valor central, generalmente la media [6]- mencionado anteriormente), pudiendo deducirse, que conforme aumenta λ, las variables de Poisson van a poder aproximarse a la distribución normal, por el Teorema Central del Limite. La aproximación se considera buena para valores de λ iguales o superiores a nueve.
1.3 Esperanza E (X) y Varianza Var (X)
Ya sabemos que los valores de la esperanza (o media) y de la varianza para la distribución de Poisson son respectivamente E (X) = λ y Var(X) = X. Observemos ahora la demostración de estas afirmaciones.
Teorema 1.3 La esperanza de la distribución de Poisson tiene valor E(X) = λ.
Demostración 1.3 Tenemos que
Ahora bien, sea y = k-1, con lo cual obtenemos
Teorema 1.4 La varianza de la distribución de Poisson tiene valor Var (X)= λ.
Demostración 1.4 Por propiedades de la varianza tenemos que Var(X)= E(X2)-[(X)]2. Además, E ( X2)=E [X (X-1) ]+ E (X). Entonces, sea
Ahora bien, sea y = k-l, con lo cual obtenemos
Teorema 1.4 La varianza de la distribución de Poisson tiene valor Var ( X )= α
Demostración 1.4 Pos propiedades de la varianza tenemos que Var (X) = E (X2)-[ E(X)]2. Además, E ( X2)= E [X(X-1)] + E(X). Entonces, sea
Ahora bien, sea y = k-2, por lo que obtenemos
Así, E{X2) = E[X(X-l)] + E(X) = λ2+λ. Con lo cual Var(X) = E(X2) - [E(X)f =λ2+λ-λ2 =λm
Observemos ahora, un ejemplo práctico en donde se aplica la distribución de Poisson.
Ejemplo 1. Los buses llegan a cierta terminal de transporte, y se sabe que siguen un proceso de Poisson, con tasa de 8 buses por hora, de modo que el número de llegadas por un período de horas es una variable de Poisson con parámetro λ = 8t [7].
- -¿Cuál es la probabilidad de que exactamente 5 buses lleguen durante un periodo de una hora?
-¿Cuantos buses se pueden esperar a que lleguen durante 90 minutos?
Solución
La llegada de los buses a la terminal de transporte se distribuyen según Poisson. Sea λ una variable que representa el número de buses que llegan a la terminal de transporte durante un periodo de tiempo t.
λ = 8 buses * tiempo = 8*1 = 8
- Se pide calcular la probabilidad de que lleguen exactamente 5 buses durante una hora.
Por tanto, existe una probabilidad del 9.1% de que lleguen exactamente 5 buses a la terminal durante una hora.
- Se pide calcular la cantidad de buses que podrían llegar en un tiempo de hora y media.
E(X) = λ = 8*1.5 = 12 buses
Ahora bien, por propiedad de la distribución de Poisson, Var(X) = 12. Con lo cual tendríamos que la desviación estándar, D.E., para este caso es D.E. = 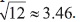
Se espera entonces, que en una hora y media lleguen, en promedio, 12 buses a la terminal de transporte, con una desviación estándar de 3 buses. Esto quiere decir que, en realidad, se espera que lleguen entre 9 y 15 buses.
2. Distribución gamma
Antes de estudiar la distribución gamma, es pertinente observar y/o examinar algunos detalles de la función a la que debe su nombre, la función gamma.
2.1 Función Gamma Γ(α)
Es una función que extiende el concepto de factorial a los números complejos. Fue presentada, en primera instancia, por Leonard Euler entre los anos 1730 y 1731. La función gamma Γ se define,
Definición 2.1 Sea Γ: (0, ∞)→ R, donde Γ(α)= ∫∞o xa-1 e-x dx, para α > 0
Con el fin de observar algunos resultados o propiedades de esta función, procederemos a integrar por partes. Tomando u = x"'1 y dv = e∼xdx, obtenemos
Para α>, lo cual ocasiona la fórmula Γ(α) = ( α-l ) Γ( α-l )
Al aplicar reiteradamente la fórmula anterior tendríamos, Γ(α) = (α -l) (α- 2)Γ(α- 2) = (α - l)(α- 2)(α-3) Γ(α- 3),
y así sucesivamente. Se evidencia que cuando α = n, donde n es un entero positivo,
Γ( n ) = ( n-l )( n-2 )...Γ( l ).
Sin embargo, por la definición de Γ( a ), Γ ( 1 )= ∫∞0 e -x dx= 1, y de aquí Γ (n )!
Algunas propiedades adicionales de Γ(α) son:
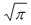
Estas propiedades serán de gran utilidad en las secciones 2.2 y 2.4.
2.2 Distribución gamma
Se le conoce, también, como una generalización de la distribución exponencial, además de la distribución de Erlang y la distribución Ji-cuadrada [8]. Es una distribución de probabilidad continua adecuada para modelizar el comportamiento de variables aleatorias con asimetría positiva y/o los experimentos en donde está involucrado el tiempo.
Definición 2.2 Una variable aleatoria X tiene una distribución gamma si su función de densidad está dada por:
Teorema 2.1 La función ƒ es una función de densidad.
Demostración 2.1
Debemos demostrar que 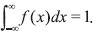 1. Para este caso
1. Para este caso 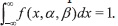
Pero según la definición de 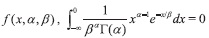 Asi,
Asi, 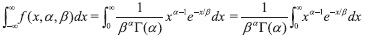
Realizamos el siguiente cambio de variable. Sea u = x/β, entonces x = βu, así dx = βdu. Por lo cual tendríamos
Ahora bien, recordemos que Γ: (0,∞) → R, donde Γ(α) := ∫∞0 ua-1e-udu, ∀β >0.
Por tanto ƒ es una función de densidad.
La función de distribución acumulativa de gamma F(x), la cual permite determinar la probabilidad de que una variable aleatoria de gamma X sea menor a un valor específico x, se determina de la siguiente expresión:
2.3 Propiedades de la distribución gamma
Como se mencionó anteriormente, es una distribución adecuada para modelizar el comportamiento de variables aleatorias continuas con asimetría positiva. Es decir, variables que presentan una mayor densidad de sucesos a la izquierda de la media que a la derecha. En su expresión se encuentran dos parámetros, siempre positivos, α y βde los que depende su forma y alcance por la derecha, y también la función gamma Γ (α), responsable de la convergencia de la distribución.
Podemos presentar las siguientes propiedades:
-E(X) = αβ
-Var(X) = αβ2
La verificación y/o demostración de estas fórmulas se presentan más adelante en esta sección.
- Con lo anterior se puede observar que la distribución gamma es leptocúrtica y tiene un sesgo positivo. También observamos que conforme el parámetro α crece, el sesgo se hace menos pronunciado y la curtosis relativa tiende a 3.
X: γ(α, β1) y Y: γ(α,β2)
Se cumplirá que la suma también sigue una distribución Gamma
X+Y : γ(α,β1+β2)
- Si se tiene un parámetro α de valores elevados y β pequeña, entonces la función gamma converge con la distribución normal. De media µ= αβ, y varianza σ2 = αβ2.
- Cuando la proporción entre parámetros es [Α = v/2:β=] entonces la variable aleatoria se distribuye como una Chi-cuadrado con v grados de libertad.
- Si α= 1, entonces se tiene la distribución exponencial de parámetro λ= 1/β.
De esta forma, la distribución gamma es una distribución flexible para modelizar las formas de la asimetría positiva, de las más concentradas y puntiagudas, a las más dispersas y achatadas.
Para valorar la evolución de la distribución al variar los parámetros se tienen los siguientes gráficos. Primero se comprueba que para α =1 la distribución tiene similitudes con la exponencial.
2.4 Esperanza E(X) y Varianza Var(X)
Sabemos que los valores de la esperanza (o media) y de la varianza para la distribución gamma son respectivamente E(X) = αβ y Var(X) = αβ2. Observemos ahora la demostración de estas afirmaciones.
Teorema 2.3 La esperanza de la distribución gamma está dada por E(X) = αβ.
Demostración 2.3 Tenemos
Ahora bien, sea u = x/β; x = uβ, con lo que dx =βdu así
Teorema 2.4 La varianza de la distribución gamma está dada por Var(X) = αβ2
Demostración 2.4 Al igual que para la distribución de Poisson tenemos que Var(X) = E(X2)- [E(X)]2. Encontremos entonces
Ahora bien, sea u = xβ; x = uβ, con lo que dx = βdu, así
Con esto,
Var(X) = E(X2) - [E(X)]2 = (α+l)αβ2-(αβ)2= α2β2+αβ2- α2β2 = αβ2
Observemos ahora, un ejemplo práctico en donde se aplica la distribución gamma.
Ejemplo 2. Supongamos que la experiencia demuestra que el tiempo X (en minutos) necesario para dar mantenimiento periódico a un dictáfono sigue una distribución gamma con α = 3.1 y β= 2.A un nuevo técnico en mantenimiento le toma 22.5 minutos revisar la máquina. ¿Concuerda este tiempo utilizado en el mantenimiento al dictáfono con el período anterior? [7]
Solución
La media y varianza de los tiempos de mantenimiento (con base en la experiencia anterior) son:
E(X) = αβ= (3.1)(2) = 6.2 y
Var(X) = αβ= (3.1)(22)= 12.4
Se deduce que 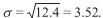 Advierta que x;= 22.5 supera a la esperanza E(X) = 6.2 por 16.3 minutos o, k= 16.3/3.52= 4.63. Así según la regla de Tchebychev.
Advierta que x;= 22.5 supera a la esperanza E(X) = 6.2 por 16.3 minutos o, k= 16.3/3.52= 4.63. Así según la regla de Tchebychev.
Por tanto,
P( X-6.2≥16.3)=P( X-6.2≥16.3)≥ 1-0.9534=0.0466
Esta probabilidad se basa en el supuesto de que la distribución de los tiempos de mantenimiento no es diferente de lo establecido. Por consiguiente, si observamos que P(X≥ 22.5) es pequeña, debemos concluir que nuestro nuevo técnico en mantenimiento generó por azar un período de mantenimiento prolongado, que tiene baja probabilidad de ocurrir, o que es más lento que los anteriores. Si tomamos en cuenta la baja probabilidad de P(X ≥22.5), optamos por la última probabilidad.
3. Una discreta y continua relación
La relación entre estas dos distribuciones (Poisson y gamma) se efectúa al incluir la distribución de Erlang, y su caso especial, la distribución exponencial.
3.1 Distribución de Erlang
Esta distribución fue desarrollada para examinar el número de las llamadas telefónicas que se pudieron efectuar, al mismo tiempo, a los operadores de las estaciones de conmutación. Recibe su nombre en honor al científico danés Agner Krarup Erlang, quien la introdujo por primera vez a principios del año 1900.
La distribución de Erlang sucede cuando el parámetroα en la distribución gamma, es un entero positivo. Es decir,
es la función de densidad de probabilidad para la variable aleatoria X que tienen una distribución de Erlang.
Ahora bien, si el número de eventos aleatorios independientes que ocurren en un lapso específico es una variable de Poisson, con una frecuencia constante de ocurrencia igual a 1&beta entonces para un α el tiempo de espera hasta que ocurre el α-ésimo evento de Poisson tiene una distribución de Erlang. Lo anterior se evidencia al comparar las funciones de distribución acumulativas de las distribuciones Poisson y Erlang. Así, siendo Fp la función de distribución acumulada para la distribución de Poisson, tenemos
Con lo cual, la probabilidad de que ocurran a lo más α-1 eventos de Poisson en un tiempo x,a una frecuencia constante 1/β, está dada por:
Por otro lado, si se supone que el tiempo de espera sigue el modelo de Erlang, la probabilidad de que el tiempo de espera hasta que ocurra el α-ésimo evento exceda un lapso x específico, está determinado por
En otras palabras, la probabilidad de que el tiempo que transcurre hasta el α-ésimo evento exceda el valor x es igual a la probabilidad de que el número de eventos de Poisson observados en x no sea mayor que α-1. De esta forma, la distribución de Erlang es el modelo para el tiempo de espera hasta que ocurre el or-ésimo evento de Poisson, y la distribución de Poisson es el modelo para el número de eventos independientes que ocurren en un tiempo x,encontrándose éste distribuido de acuerdo con el modelo de Erlang. En este contexto, λ= 1/β es la frecuencia constante de ocurrencia y β es el tiempo promedio entre dos ocurrencias sucesivas. Análisis basado en Canavos [9]
Ejemplo 3 El número de clientes, en promedio, que llegan por minuto a solicitar servicio a un banco es de 5. ¿Cuál es la probabilidad de que dos clientes tarden de 30 a 45 segundos en llegar al banco?
Solución.
Tener en cuenta que:
Ahora bien,
Sea X la variable aleatoria continua que representa el tiempo, en segundos, que tardan k clientes en llegar a un banco.
Así, X: y(α,β). Donde
Por tanto, X: y(2,12).
Con lo cual,
Para este caso,
De esta manera, la probabilidad de que dos clientes tarden de 30 a 45 segundos en llegar al banco es de aproximadamente 17.56%.
Ejemplo 4 A una centralista de teléfonos llegan 12 llamadas por minuto, siguiendo una distribución de Poisson. ¿Cuál es la probabilidad de que en menos de 1 minuto lleguen 8 llamadas? [10]
Solución.
Sea X la variable aleatoria que representa el tiempo que transcurre hasta un determinado número de llamadas. Se observa que
Además, α=8, por lo que X: Erl(x,α= 8,β= 1/12)
Para este caso,
Así, existe una probabilidad del 91.05%, aproximadamente, de recibir 8 llamadas en un lapso menor a un minuto.
3.2 Distribución Exponencial
Se ha observado que la distribución gamma, cuando el parámetro α toma un valor entero positivo, se conoce como distribución de Erlang. Ahora bien, cuando ese entero positivo es igual a uno, esto es α=1, la distribución de Erlang se reduce a la conocida distribución exponencial, siendo así la distribución exponencial un caso especial de la distribución gamma. Debido a lo mencionado anteriormente y al hecho de que ésta distribución se deriva de la distribución de Poisson, su descubrimiento se le atribuye a Agner Krarup Erlang y Siméon-Denis Poisson.
La distribución exponencial es utilizada para determinar la probabilidad de que en cierto tiempo suceda un determinado evento.
Definición 3.1 Una variable aleatoria X tiene una distribución exponencial si su función de densidad está dada por
Donde λ es igual a 1β.
De este modo, y gracias al análisis efectuado en la sección anterior (distribución de Erlang), se puede interpretar a la distribución exponencial como el lapso que transcurre hasta el primer evento de Poisson. De hecho, las aplicaciones más relevantes de la distribución exponencial son situaciones en donde se aplica el proceso de Poisson.
La relación entre la distribución exponencial y la distribución de Poisson la podemos observar de la siguiente manera. Recordemos que la distribución de Poisson es una distribución con un solo parámetro λ donde λ representa el número medio de eventos por unidad de tiempo.
Consideremos ahora la variable aleatoria X descrita por el tiempo que se requiere para que ocurra el primer evento. Haciendo uso de la distribución de Poisson, encontramos que la posibilidad de que no ocurra algún evento, en el periodo hasta el tiempo t está dada por
Podemos ahora utilizar lo anterior y hacer que X sea el tiempo para el primer evento de Poisson. La probabilidad de que la duración del tiempo hasta el primer evento exceda x es la misma que la probabilidad de que no ocurra algún evento de Poisson en x. Esto último, por supuesto, está dado por e-λx Como resultado,
P(X ≥ x)=e-λx
Así la función de distribución acumulada para X está dada por
P(0 ≤ X ≤ x)= 1-e-λx
Ahora bien, a fin de que reconozcamos la presencia de la distribución exponencial, podemos diferenciar la función de distribución acumulada anterior para obtener la función de densidad
ƒ(x)= λe-λx
que es la función de densidad de la distribución exponencial con λ= 1/β. Análisis basado en Walpole [1].
Ejemplo 5En promedio, por un parador de buses poco transitado, pasan 3 buses por hora, distribuidos según un proceso Poisson. ¿Cuál es la probabilidad de tener que esperar un bus más de 20 minutos?
Solución.
La llegada de los buses al parador se distribuye según Poisson. Sea X la variable aleatoria que representa el tiempo de espera hasta llegar un (o el primer) bus. Entonces,
Así, X: Exp (λ= 0.05),y
Por tanto, la probabilidad de esperar la llegada de un bus por más de 20 minutos es del 36.8% aproximadamente.
Ejemplo 6 En una tela, las fallas se distribuyen según un proceso Poisson, a razón de 1 falla cada 15 metros. ¿Cuál es la probabilidad de que la distancia entre la 4a y la 5a la falla sea mayor a un metro?
Solución
Este ejemplo muestra que, en un proceso Poisson, el intervalo entre dos eventos consecutivos es una variable exponencial. Entonces La distancia entre dos fallas consecutivas (sean éstas la 4a y 5a la u otras dos consecutivas cualesquiera) es una variable exponencial con λ= 1/15. Con lo cual,
Por tanto, hay una probabilidad del 93.55% de que la distancia entre la 4a y 5a la falla sea mayor a un metro.
4. Conclusiones
Generalmente conocemos el valor de λ (la cantidad esperada de eventos por unidad de tiempo), y entonces nos preguntamos cuántos eventos obtendremos en una determinada cantidad de tiempo, o cuánto tiempo tendremos que esperar hasta observar una determinada cantidad de eventos. De esta forma obtenemos 2 distribuciones:
- -Poisson: consiste en preguntar por la cantidad de eventos en el período T (la longitud de un intervalo del continuo que va a estudiarse). Es decir, dado T, calcular la distribución de k (la cantidad de eventos que hay en ese intervalo).
- -Gamma: consiste en preguntar por la cantidad de tiempo necesario hasta observar k eventos. Es decir, dado k, calcular la distribución de T.
Y además:
- Exponencial: caso particular de Gamma cuando k= 1, es decir, consiste en preguntar por la cantidad de tiempo necesaria hasta obtener el primer evento.
- La relación entre la distribución de Poisson y la distribución gamma se hace evidente al estudiar las distribuciones de Erlang y exponencial (derivadas de la distribución gamma). Así, mientras la distribución de Erlang es el modelo para el tiempo de espera hasta que ocurre el α-ésimo evento de Poisson, la distribución exponencial modela el lapso de tiempo que transcurre hasta el primer evento de Poisson. Además, al estudiar las gráficas de las distribuciones de Poisson y gamma (o sus factores de forma) nos damos cuenta que ambas son leptocúrticas con sesgos positivos, con características muy similares al variar sus parámetros.
Referencias
[1] Canavos G. C. Probabilidad y Estadística. Aplicaciones y Métodos. Traducción de Edmundo G. Urbina M. McGraw-Hill. México, 1988. [ Links ]
[2] Blanco L. Probabilidad. Universidad Nacional de Colombia. Bogotá, 2004. [ Links ]
[3] Llinás H., Rojas C. Estadística Descriptiva y Distribuciones de Probabilidad. Ediciones Uninorte. Barranquilla, Colombia 2009. [ Links ]
[4] Walpole R. E., Myers R. H., Myers S. L. Probabilidad y Estadística Para Ingenieros. Traducción de Ricardo Cruz. Prentice-Hall, Inc. México, 1999. [ Links ]
[5] Zylberberg A. D. Probabilidad y Estadística. Editorial Nueva Librería. Argentina, 2005. [ Links ]
[6] García H. A., Solarte C., Imuez M. Bio Estadística. Editorial Universitaria - Universidad de Nariño. Pasto, Colombia 2009. [ Links ]
[7] Goméz E., Sarabia J. M., Prieto F. La Distribución Poisson-Beta: Aplicaciones Y Propiedades En La Teoría Del Riesgo Colectivo. Tomado desde: http://www.actuarios.org/espa/anales/2009/Pag%20141-160.pdf, [Acceso el 5 de agosto de 2013] [ Links ].
[8] Ecos de la economía. Distribución Gamma. Tomado desde: http://ecosdelaeconomia.fles.wordpress.com/2011/05/distribucion-gamma.pdf, [Acceso el 5 de agosto de 2013] [ Links ].
[9] Armitage P., Berry G. Estadística Para La Investigación Biomédica. Edición en español. Harcourt Brace. Madrid, España. 1997. [ Links ]
[10] Montero J. Ma. Estadística Descriptiva. International Thomson Editores. España. 2007. [ Links ]