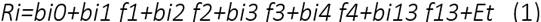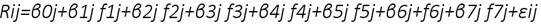INTRODUCCIÓN
Desde la década de los sesenta la teoría financiera se ha venido preocupando por postular un enfoque teórico alterno a los modelos de valoración de activos financieros CAPM, una de estas teorías es la teoría de fijación de precios de arbitraje (APT), la cual plantea que los retornos de los activos están influenciados por los fundamentales macroeconómicos, - denominados factores sistémicos de riesgo - y no solamente por el tamaño del mercado como lo argumenta los CAPM. De esta manera, este documento pretende identificar las variables macroeconómicas que explican estadísticamente los retornos de las carteras en los mercados bursátiles de los cuatro países que conforman la Alianza del Pacífico, para los años comprendidos entre 2009 y 2015.
La construcción de las carteras para todos y cada uno de los países se realizó siguiendo la metodología argumentada por Fama y French (1996), de tal forma, que se construyeron seis carteras para cada país, combinando las empresas grandes y pequeñas con los niveles de liquidez de cada una de ellas. De otro lado, siguiendo a (Türsoy, Günsel, & Rjoub, 2008) se procede a estimar los modelos econométricos a través de mínimos cuadrados ordinarios, en donde las variables macroeconómicas utilizadas fueron exportaciones, importaciones, PIB, tasa de desempleo, inflación por IPC, el agregado monetario M2, y la tasa de interés.
Este trabajo se presenta en la primera parte la revisión de la literatura, compuesta por las referencias teóricas y por estudios empíricos realizados alrededor del tema. Posteriormente, se muestra la metodología utilizada, la cual está conformada por la construcción de las carteras para cada país y por la estimación de los modelos econométricos planteados para Chile, Colombia, México y Perú; por último, se presentan las conclusiones.
REVISIÓN DE LITERATURA
La teoría financiera relacionada con los precios de los activos en los mercados de capitales es postulada inicialmente por (Sharpe, 1964), quien argumenta que el riesgo genera efectos en las transacciones financieras, lo cual ha permitido que se acojan modelos de comportamiento de precios, que van más allá de las mismas postulaciones teóricas. Una de las explicaciones más comunes en la determinación de los precios de los activos de capital se origina en el establecimiento de la tasa de interés pura de equilibrio, la cual surge de la relación entre las preferencias individuales y las mismas relaciones físicas.
El autor también afirma que hasta el momento no se ha generado una teoría que describa la manera en que el precio del riesgo es originado por las preferencias de los inversionistas, así como por los atributos de los activos de capital. Por lo que, en ausencia de este tipo de posturas teóricas, es complejo relacionar el precio de un solo activo con su respectivo riesgo, sin embargo, un porcentaje del riesgo se puede mitigar con la diversificación, lo cual permite argüir que el riesgo no influye significativamente en el precio del activo.
Lo anterior explicaría que la implicación de todas las combinaciones eficientes tendrá una correlación perfecta, siendo útil para analizar el retorno esperado de un activo individual y su respectivo riesgo. De esta manera la teoría implicaría solamente que existe una correlación perfecta entre las tasas de retorno de las combinaciones eficientes, lo cual se debería a su dependencia con el nivel de la actividad económica. Por consiguiente, para evaluar el riesgo solo se requiere la respuesta de la tasa de retorno del activo al ritmo de la actividad económica.
Siguiendo la línea de (Sharpe, 1964), (Lintner, 1965) plantea la lógica para establecer los precios de equilibrio explícitos de los activos de riesgos negociados en condiciones ideales en los mercados competitivos. El documento mide el alcance de las “incertidumbres residuales” que se tienen en cuenta en acciones individuales que lideran los portafolios diversificados, por lo que las regresiones de las tasas anuales de los rendimientos en más de 300 firmas grandes del sector industrial se estimaron sobre los retornos correspondientes del índice industrial de S&P 425. En este aspecto, el poder y las limitaciones de la diversificación para lograr la reducción del riesgo y optimizar el rendimiento de la inversión se explican a través de 70 fondos mutuos grandes sobre el índice, por lo que el 80% de los fondos tenían una tasa más alta del retorno medio al riesgo que el mismo índice.
Posteriormente, (Ross, 1976) postula la teoría de arbitraje de los precios de los activos de capital, afirmando que el modelo de arbitraje fue propuesto como una alternativa al modelo de varianza media de los precios de los activos de capital, el cual fue postulado por (Sharpe, 1964) y (Lintner, 1965) , dicho modelo se ha convertido en la principal herramienta de análisis para comprender y explicar los acontecimientos de los mercados de capitales para los activos riesgosos. El autor también argumenta que el supuesto acerca de que los inversionistas tienen expectativas idénticas cada vez se debilita más, mientras que la teoría de arbitraje supone aún expectativas idénticas, así es como, los resultados empíricos son robustos cuando se relacionan los coeficientes de expectativas ex antes con expectativas ex post. Por consiguiente, si este supuesto se debilita, se necesitaría una prueba más rigurosa de que las expectativas ex antes se transforman en expectativas ex post; por lo que esta investigación hace parte de la dinámica de desequilibrio general, centrándose en el efecto de la información en los mercados.
En su investigación (Roll & Ross, 1980), prueban empíricamente la teoría del arbitraje de la fijación de precios de los activos postulada por Ross en 1976, para los años comprendidos entre 1962 y 1972, con datos de acciones individuales en el mercado bursátil de Nueva York. Se postula que el APT tiene como base fundamental el proceso de generación de retornos lineales, en el cual la función de utilidad debe cumplir con los axiomas de concavidad y monotonicidad, por otra parte, el APT supone que existe por naturaleza unos componentes sistemáticos de riesgo, lo cual explica la existencia de carteras que tienen sustitutos cercanos, por lo tanto, deben tener el mismo valor. Dichos factores sistemáticos de riesgo están relacionados con los agregados económicos fundamentales como el producto nacional bruto, la tasa de interés o el clima, de esta manera, se debe explorar qué fuerzas económicas son las que influyen sistemáticamente en los rendimientos.
La estimación del modelo APT, se hace a través de la metodología de sección cruzada estimando mínimos cuadrados ordinarios generalizados. El estudio concluye que los datos empíricos apoyan el APT, en cuanto a que es una alternativa no especificada como también que es una prueba muy débil, sin embargo, los autores afirman que dichas pruebas son pruebas iniciales y que se deben ver desde ese punto de vista, recomendando que este trabajo debe incentivar a identificar estadísticamente los factores macroeconómicos subyacentes que expliquen los retornos de los activos.
Aportando al debate en términos empíricos de la fijación de los precios de los activos de capital, (Chen, Roll & Ross, 1986), establecen si las perturbaciones en las variables agregadas macroeconómicas generan riesgos que terminan siendo recompensados en el mercado accionario, por lo cual estiman econométricamente los retornos de las acciones en función de variables macroeconómicas, asumiendo endogeneidad en el mercado de valores en relación con otros mercados. Teniendo en cuenta la teoría del mercado de capitales, en la que uno de sus principales argumentos de base es la diversificación, se postula que solo las variables económicas de estado influirán en los precios de los grandes agregados bursátiles; de esta manera, se asume que cualquier variable sistemática que incida en el vector de precios de la economía, o en los dividendos, también incidirá en el retorno del mercado bursátil. Adicional a esto, cualquier variable que sea necesaria para completar la descripción del estado natural también será parte de la descripción de los factores de riesgo sistemáticos, es así como los precios de las acciones responden a las fuerzas de la economía. Por consiguiente, la inflación esperada y no esperada, el spread entre las tasas de interés de corto y largo plazo, el spread entre bonos de alto y bajo grado, y la producción industrial son las variables macroeconómicas que la teoría financiera postula para explicar sistemáticamente los retornos del mercado de valores.
A partir de la teoría financiera, los autores construyen los factores económicos proponiendo un conjunto de variables relevantes a saber: Producción industrial, inflación, prima de riesgo, tasa de interés que mide los imprevistos de los retornos de los bonos de largo plazo, índices de mercado, consumo y precios del petróleo; dichos factores son las variables explicativas de los retornos del mercado accionario, este modelo econométrico planteado se estima a través de regresiones de sección cruzada. El documento concluye que los rendimientos de los portafolios accionarios están expuestos a las noticias económicas, reflejando un precio con respecto a sus exposiciones, de otro lado, estas noticias se pueden medir como innovaciones en las variables de estado, las cuales se pueden identificar utilizando la teoría financiera.
Continuando con (Nieto, 2001), el objetivo principal de su investigación es comprobar empíricamente los modelos CAPM estándar, Fama y French, CAPM condicional, intertemporal sin consumo de Campbell y el APT postulado por (Ross, 1976); con el propósito de comparar y ordenar los resultados de los modelos en el mercado de valores de España.
Por su parte, la metodología econométrica se realiza a través de regresiones de sección cruzada, con periodicidad mensual desde 1982 a 1998, planteándose como variable dependiente el retorno de diez carteras las cuales están ordenadas por su valor del capital en el mercado bursátil. En lo que se refiere a la estimación del modelo APT, la regresión se estima en función de los tres primeros componentes principales asintóticos de la matriz de varianza - covarianza de los retornos de los activos. (Nieto, 2001) concluye que las variables independientes no son estadísticamente significativas en ninguno de los cinco modelos estimados, y la constante es la que explica los retornos de los portafolios en el CAPM estándar, en el modelo de Fama y French y en el APT.
Siguiendo a (López & Vázquez, 2002), realizan pruebas que conducen a explicar el retorno de 32 acciones que participan en la cotización de la bolsa de valores de México entre los años 1999 y 2000, utilizando el riesgo sistemático originado de algunas variables macroeconómicas argumentadas por el modelo APT. El estudio realiza el análisis de 1.400 portafolios generados de las 32 acciones, estimando inicialmente MCO, sin obtener resultados robustos, por lo que utilizaron el modelo EGARCH para estimar 32 regresiones por máxima verosimilitud. Los autores concluyen principalmente que el modelo no explica en su totalidad la relación entre el retorno esperado y el riesgo sistémico.
Luego del estudio empírico realizado por (Nieto, 2001) es España, para el año 2020 (Antonelo & Levy, 2002), relacionan el retorno de los activos financieros y los fundamentales macroeconómicos en el mercado de valores de España, usando variables como los índices más representativos de los mercados de valores de España y Estados Unidos, exportaciones e importaciones, el índice de producción industrial, las tasas de interés de corto y largo plazo en España, Estados Unidos y Alemania y finalmente, el riesgo crediticio, para 70 acciones del mercado accionario español. La comprobación empírica de los modelos se realiza por medio de metodología de estructuras de covarianzas, la cual analiza un conjunto simultáneo de relaciones lineales observables y no observables. El estudio concluye que el retorno del mercado es la única variable que explica las variaciones en su conjunto de las rentabilidades de las acciones.
En esta misma línea de investigación, (Gonzalez, 2004), prueba las diferentes posturas de la APT en cuanto a la aplicabilidad y regresión de los modelos multifactoriales de valoración de activos para el mercado continuo de España, pretendiendo responder cuál es el número de factores óptimo a estimar. La estimación de los modelos econométricos se realiza utilizando la metodología de los modelos de State-Space, haciendo en primer lugar el filtro de Kalman. En el estudio el autor presenta la literatura concerniente al modelo multifactorial y al modelo multifactor State-Space; y luego muestra de manera detallada el desarrollo metodológico, en el que elige el número de factores de riesgo y estima el modelo que mejor explique el comportamiento de la cartera, dicha cartera está compuesta por cinco activos del mercado continuo español con datos diarios de 1992 a 2001.
Continuando con la literatura española, (Gómez, 2004), también aporta a la temática de estudio, limitando el espacio de análisis a una ciudad española, realizando una aplicación de los modelos CAPM y APT a las 24 acciones más importantes que participan en la bolsa de valores de Bilbao, en los años comprendidos entre 1980 y 1987. Inicialmente calculan las rentabilidades semanales de cada una de las acciones elegidas, luego calculan las rentabilidades semanales del mercado; posteriormente, realizan un modelo factorial partiendo del método de componentes principales y finalmente muestran el modelo de mercado. El documento afirma que el modelo factorial explica mejor que el modelo de mercado, porque hace uso de una mayor cantidad de variables independientes.
Continuando con los estudios en México, (Saldaña, Palomo, & Blanco, 2007), aportan al estudio presentado en el 2002 por (López & Vázquez, 2002) presentando las principales características de los modelos CAMP (Capital Asset Pricing Model) y APT, realizando una prueba empírica de los dos modelos en el portafolio de nueve acciones del sector de las telecomunicaciones que cotizan en el mercado bursátil mexicano; se incluyen variables, financieras, operativas y macroeconómicas, en el periodo comprendido entre los años 2002 a 2005. La prueba empírica la realizan a través de modelos de regresión múltiple, estimando las betas del portafolio accionario para cada uno de los modelos. Finalmente, el artículo concluye que el factor riesgo de mercado, es decir, todas las betas de las variables explicativas fueron significativas; mientras que el modelo APT evidencia que no explica en su totalidad la variabilidad del retorno accionario, infiriéndose que no es un modelo confiable para realizar pronósticos de largo plazo.
Por su parte, (Türsoy, Günsel, & Rjoub, 2008), en su estudio prueban de manera empírica la teoría de fijación de precios de arbitraje (APT) para la bolsa de valores de Estambul, determinando las variables macroeconómicas que más explican el mercado de valores. Los autores construyen once portafolios pertenecientes al sector de la industria, ya que la participación de dichas acciones dentro del total negociadas representa cerca del 68%. El modelo econométrico de mínimos cuadrados ordinarios (MCO) que estiman es la siguiente ecuación 1:
Donde:
Ri es el retorno del portafolio
bi es el coeficiente que mide el cambio del retorno de la cartera cuando varían los factores de riesgo
fi representa cada uno de los factores macroeconómicos, a saber: Oferta de dinero (M2), producción industrial, precio del petróleo crudo, índice de precios al consumidor, importaciones, exportaciones, precio del oro, tipo de cambio, tasa de interés, producto interno bruto, reservas internacionales, tasa de desempleo e índice de presión del mercado.
El documento concluye que las variables macroeconómicas no explican de manera significativa a la rentabilidad de las acciones en Estambul, por lo cual pueden existir otros factores macroeconómicos que afectan el APT multifactorial.
Por su parte para el caso colombiano, (Londoño, Lopera, & Restrepo, 2010), relacionan el Índice General de la Bolsa de Valores de Colombia (IGBC) con variables financieras y con los fundamentales macroeconómicos, con el propósito de evaluar tanto los factores económicos nacionales como internacionales que pueden tener efectos en la valoración de activos colombianos. Utilizan metodológicamente la red neuronal multicapa, de tal manera que se propone un modelo APT tradicional y un modelo APT modificado, este modelo modificado conjuga los fundamentales macroeconómicos y el indicador de las bolsas del mundo. El documento concluye que el modelo APT tradicional predice mejor el mercado de acciones de Colombia que el modelo APT modificado. Por otra parte, los modelos de redes neuronales multicapa presentan resultados más explicativos y robustos que los mismos modelos econométricos tradicionales, ya que presentaron mayor nivel de precisión y explicación.
De manera seguida, el estudio de (Londoño & Cuan, 2011), establece si las rentabilidades promedio esperadas de los activos están determinadas por los factores de riesgo identificados por Fama y French o por los fundamentales macroeconómicos del modelo APT, para el mercado accionario de Colombia. Se construyeron dos portafolios, uno con capitalización bursátil de alto nivel de negociación y otro con bajo nivel de negociación. Posteriormente, el documento utiliza el modelo no lineal de redes neuronales artificiales, permitiendo capturar algunas irregularidades que se evidencian en los mercados financieros; estimando cuatro modelos: APT, APT aumentado (que reúne agregados macroeconómicos y variables financieras), CAMP y el modelo de Fama y French que usa variables tradicionales. Los autores concluyen que, de los cuatro modelos estimados, el de Fama y French es el que presenta el mayor nivel explicativo de los retornos esperados promedios en el mercado accionario de Colombia.
Para el mercado bursátil brasilero (De Sousa, 2013), realiza una evaluación de la aplicación empírica de los modelos CAMP y APT a las rentabilidades esperadas del mercado accionario del sector de energía eléctrica que componen el Índice de Energía Eléctrica en Brasil, para el periodo establecido entre diciembre de 2005 a diciembre de 2010. Los modelos fueron de regresión simple, estimados por medio MCO. El estudio concluye que las betas de los modelos (CAMP y APT), no explican los retornos esperados de las acciones del mercado analizado, es decir, que los fundamentales macroeconómicos no explican dichos retornos, infiriendo que el mercado accionario de la energía eléctrica está explicado por el exceso de control público que ha conducido a que este mercado les dé más relevancia a variables de la propia industria que a variables macro.
De acuerdo con (Leyva, 2014), el trabajo presenta los postulados teóricos fundamentales para plantear un modelo multifactorial macroeconómico basado en la estructura del modelo APT, con el fin de identificar la base de un modelo que explique el efecto de las variables de riesgo macroeconómicos en los retornos de diferentes tipos de activos financieros. El autor realiza una revisión de literatura exhaustiva, que permite establecer las características que debe tener el proceso de selección de los factores de riesgo macroeconómicos. El artículo concluye que teniendo en cuenta que el modelo APT no especifica los factores de riesgo macro que explican los retornos de los activos, entonces se proponen tres modelos multifactoriales para identificarlos: Modelos macroeconómicos, modelos estadísticos y modelos fundamentales, llegando a afirmar que los modelos macro tienen ventajas sobre los otros dos modelos, sin embargo, el autor afirma que este tema sigue en discusión.
Luego del estudio publicado por (Londoño & Cuan, 2011) para Colombia, (Carmona & Criollo, 2015), aportan al debate del mercado accionario de este país, al establecer los factores macroeconómicos que influyen en los retornos de los activos en el mercado bursátil colombiano en el periodo 2007 a 2012. Para ello, se estiman primero modelos unifactoriales de corto plazo utilizando el índice bancario de referencia para los años 2008 a 2012 y luego se estiman modelos multifactoriales de largo plazo tomando los TES de julio de 2020 como la tasa libre de riesgo. Los factores macroeconómicos están agrupados en cuatro conjuntos: Variables monetarias, índices, tasas de interés, tasas de cambio, e índices bursátiles. El documento concluye que para el modelo unifactorial, el mercado explica estadísticamente el índice bancario de referencia; mientras que para el modelo multifactorial de largo plazo las betas no son en su mayoría estadísticamente significativos, argumentando que tanto el tamaño del mercado como la información incompleta de los precios generan inconvenientes y desventajas para la estimación de dichos modelos multifactoriales.
METODOLOGÍA
Construcción de los portafolios para el grupo de la Alianza del Pacífico
Para estimar los modelos multifactoriales, es necesario construir las variables dependientes, las cuales representan las carteras de los retornos de las acciones de cada uno de los cuatros países que integran el grupo de la Alianza del Pacífico. Dichas carteras se conforman siguiendo la metodología de conformación de portafolios que postulan (Fama & French, 1996), quienes construyen dichas carteras combinándose y ponderándose por liquidez y tamaño en el mercado de valores. A su vez, la liquidez representando la ratio libro bolsa, se subdivide en alta, media y baja, y el tamaño se divide en pequeño y grande. De esta forma, se conforman seis carteras para cada país, constituidas por las siguientes acciones:
México:
Portafolio 1, firmas grandes con alta liquidez: AMXL MM Equity, WALMEX* MM Equity, LIVEPOLC MM Equity, KOFL MM Equity.
Portafolio 2, firmas grandes con mediana liquidez: FEMSAUBD MM Equity, GMEXICOB MM Equity, TLEVICPO MM Equity, BIMBOA MM Equity.
Portafolio 3, firmas grandes con baja liquidez: GFNORTEO MM Equity, GFINBURO MM Equity, SANMEXB MM Equity.
Portafolio 4, firmas pequeñas con alta liquidez: KIMBERA MM Equity, AC* MM Equity, LALAB MM Equity, PINFRA* MM Equity, PE&OLES* MM Equity, GENTERA* MM Equity, ALSEA* MM Equity, LABB MM Equity.
Portafolio 5, firmas pequeñas con mediana liquidez: GCARSOA1 MM Equity, GRUMAB MM Equity, GAPB MM Equity, ELEKTRA* MM Equity, MEXCHEM* MM Equity, ALFAA MM Equity, IENOVA* MM Equity, ASURB MM Equity, NEMAKA MM Equity, OMAB MM Equity.
Portafolio 6, firmas pequeñas con baja liquidez: CEMEXCPO MM Equity, SITESL MM Equity, OHLMEX* MM Equity, GFREGIO MM Equity, ICHB MM Equity, LACOMUBC MM Equity, SIMECB MM Equity, ICA* MM Equity.
Chile:
Portafolio 1, firmas grandes con alta liquidez: FALAB CC Equity, COPEC CC Equity, ENDESA CC Equity, CENCOSUD CC Equity.
Portafolio 2, firmas grandes con mediana liquidez: ENERSIS CC Equity, SQM/B CC Equity, CMPC CC Equity, COLBUN CC Equity.
Portafolio 3, firmas grandes con baja liquidez: CHILE CC Equity, ANTAR CC Equity, BSAN CC Equity, BCI CC Equity.
Portafolio 4, firmas pequeñas con alta liquidez: CCU CC Equity, AGUAS/A CC Equity, ANDINAB CC Equity, ENTEL CC Equity, SONDA CC Equity, BANMED CC Equity, CONCHA CC Equity, FORUS CC Equity, CAP CC Equity.
Portafolio 5, firmas pequeñas con mediana liquidez: AESGENER CC Equity, LAN CC Equity, PARAUCO CC Equity, SK CC Equity, ILC CC Equity, EMBONOB CC Equity, SMSAAM CC Equity, BUPACL CC Equity, SALFACOR CC Equity, BESALCO CC Equity.
Portafolio 6, firmas pequeñas con baja liquidez: SMCHILEB CC Equity, QUINENC CC Equity, CORPBANC CC Equity, ECL CC Equity, IAM CC Equity, GASCO CC Equity, SECUR CC Equity, RIPLEY CC Equity, VAPORES CC Equity.
Colombia:
Portafolio 1, firmas grandes con alta liquidez: ECOPETL CB Equity.
Portafolio 2, firmas grandes con mediana liquidez: BOGOTA CB Equity, PFAVAL CB Equity, PFBCOLO CB Equity, BCOLO CB Equity.
Portafolio 3, firmas grandes con baja liquidez: PFGRUPSU CB Equity, GRUPOSUR CB Equity.
Portafolio 4, firmas pequeñas con alta liquidez: ISAGEN CB Equity, CORFICOL CB Equity, CLH CB Equity, CNEC CB Equity, BVC CB Equity.
Portafolio 5, firmas pequeñas con mediana liquidez: EEB CB Equity, CEMARGOS CB Equity, PFCEMARG CB Equity, NUTRESA CB Equity, ISA CB Equity, EXITO CB Equity, PREC CB Equity.
Portafolio 6, firmas pequeñas con baja liquidez: GRUPOARG CB Equity, PFGRUPOA CB Equity, PFDAVVND CB Equity, CELSIA CB Equity, PFAVH CB Equity.
Perú:
Portafolio 1, firmas grandes con alta liquidez: SCCO PE Equity, BACKUSI1 PE Equity, CVERDEC1 PE Equity.
Portafolio 2, firmas grandes con mediana liquidez: EDEGELC1 PE Equity, ALICORC1 PE Equity, ENERSUC1 PE Equity, LUSURC1 PE Equity.
Portafolio 3, firmas grandes con baja liquidez: EDELNOC1 PE Equity, CONTINC1 PE Equity, BAP PE Equity.
Portafolio 4, firmas pequeñas con alta liquidez: VOLCABC1 PE Equity, MILPOC1 PE Equity, MINSURI1 PE Equity, GRAMONC1 PE Equity, BVN PE Equity, BROCALC1 PE Equity, ATACOBC1 PE Equity.
Portafolio 5, firmas pequeñas con mediana liquidez: CPACASC1 PE Equity, UNACEMC1 PE Equity, IFS PE Equity, INRETC1 PE Equity, FERREYC1 PE Equity, INVCENC1 PE Equity, TV PE Equity, PML PE Equity.
Portafolio 6, firmas pequeñas con baja liquidez: CORAREC1 PE Equity, RELAPAC1 PE Equity, AUSTRAC1 PE Equity, CASAGRC1 PE Equity, POMALCC1 PE Equity, MIRL PE Equity.
ESTIMACIONES DE LOS MODELOS ECONOMÉTRICOS
En el presente artículo se analiza la influencia que tienen las variables macroeconómicas sobre seis carteras diferentes construidas para cada país miembro de la Alianza del Pacífico, compuesta por diferentes títulos accionarios de Chile, Colombia, México y Perú. Las variables macroeconómicas tomadas para determinar el impacto sobre estas carteras fueron las exportaciones, importaciones, producto interno bruto, tasa de desempleo, inflación trimestral y la oferta monetaria ampliada, representada por M2.
El periodo de análisis está contemplado entre el 1 de enero de 20019 y el 1 de septiembre de 2015. Como se sabe, las carteras (conjuntos de acciones) poseen una periodicidad diaria, para convertir estas series a una periodicidad trimestral se utilizaron promedios geométricos, con el propósito de que las series analizadas en los distintos modelos contaran con el mismo espacio temporal.
Con base en la especificación del modelo planteado por (Türsoy, Günsel, & Rjoub, 2008), la estructura básica del modelo que se aplicó en esta investigación se relaciona en la ecuación 2: Dónde:
Rij: es el rendimiento real de la cartera i para el país j.
β0j: es el término independiente o constante para cada modelo en cada país, el cual evalúa el rendimiento de la cartera sin tener en cuenta las variables macroeconómicas tenidas en cuenta en el modelo;
βij: es el coeficiente de reacción, el cual mide el cambio en la rentabilidad de cada cartera en factores de riesgo, para cada país analizado;
fij: es el factor macroeconómico introducido en el modelo, el cual determina si este afecta de alguna manera la rentabilidad de las distintas carteras, para cada país de la Alianza del Pacífico.
En la tabla 1 se relacionan las distintas variables macroeconómicas introducidas en el modelo estimado.
Tabla 1 Variables introducidas en el modelo estimado
| Factor | Variable |
| F0 | (Constante) |
| F1 | Variación Exportaciones |
| F2 | Variación Importaciones |
| F3 | Variación PIB |
| F4 | Tasa de desempleo |
| F5 | Inflación Trimestral |
| F6 | Variación M2 |
| F7 | Tasa de Interés |
Fuente: Elaboración propia
Como se mencionó, este estudio busca determinar si las variables macroeconómicas relacionadas explican la rentabilidad de las distintas carteras generadas. Para cumplir este objetivo, se estimaron 24 modelos de regresión lineal múltiple, tomando como variables explicativas las mencionadas anteriormente, y como variable dependiente las distintas carteras (seis en total) para cada país. Para facilitar el análisis, los resultados se dividieron por país, para así al final poder realizar un análisis en conjunto de los distintos a partir de los resultados obtenidos de forma individual.
Resultados por país de la Alianza del Pacífico, con un nivel de significancia del 5% en todos los casos:
En la tabla 2 se presentan los resultados obtenidos para Chile para cada cartera y tomando como factores explicativos las variables macroeconómicas relacionadas en la tabla 1. Para el análisis, se tomarán en cuenta las significancias de los coeficientes estimados para cada modelo.
Tabla 2: Significancias de los coeficientes estimados para las distintas carteras para Chile
| País | Cartera | (Constante) | Variación Exportaciones | Variación Importaciones | Variación PIB | Tasa de desempleo | Inflación Trimestral | Variación M2 | Tasa de Interés |
| Chile | 1 | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo | Significativo |
| Chile | 2 | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo |
| Chile | 3 | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo |
| Chile | 4 | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo |
| Chile | 5 | Significativo | No significativo | Significativo | No significativo | Significativo | No significativo | Significativo | Significativo |
| Chile | 6 | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo | Significativo |
Fuente: Cálculos propios.
En el caso de Chile, se puede observar para la primera cartera la única variable significativa en su explicación es la tasa de interés. Por otra parte, para las carteras 2, 3 y 4, ninguna de las variables macroeconómicas introducidas en los modelos contribuye en la explicación de estas carteras. Al analizar la quinta cartera, se observó que tanto el termino de intercepto y la tasa de interés resultaron significativos. En el modelo 6, la única variable que explica el comportamiento de esta cartera es la tasa de interés, al igual que ocurrió en la primera cartera.
En la tabla 3 se presentan las significancias de las distintas variables macroeconómicas introducidas en los modelos, las cuales pretenden explicar las seis carteras construidas para Colombia.
Tabla 3: Significancias de los coeficientes estimados para las distintas carteras para Colombia
| País | Cartera | (Constante) | Variación Exportaciones | Variación Importaciones | Variación PIB | Tasa de desempleo | Inflación Trimestral | Variación M2 | Tasa de Interés |
| Colombia | 1 | Significativo | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo |
| Colombia | 2 | Significativo | No significativo | No significativo | No significativo | Significativo | No significativo | No significativo | No significativo |
| Colombia | 3 | Significativo | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo |
| Colombia | 4 | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo |
| Colombia | 5 | Significativo | No significativo | No significativo | No significativo | Significativo | No significativo | No significativo | No significativo |
| Colombia | 6 | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo |
Fuente: Cálculos propios.
Al analizar la significancia de los coeficientes estimados de las carteras construidas para Colombia, se puede determinar que la constante es significativa solamente en los modelos de las carteras uno y tres. Sin embargo, para los modelos dos y cinco, los coeficientes que resultaron significativos fueron la constante y el estimado para la tasa de desempleo. Por su parte, en los modelos cuatro y seis, ninguna de las variables macroeconómicas introducidas resultó significativa.
En la tabla 4 se presenta los resultados obtenidos para México, discriminados por cada cartera construida, tomando como factores explicativos las variables macroeconómicas relacionadas en la tabla 1. Para el análisis, se tomarán en cuenta las significancias a un nivel de confianza del 95%, para cada coeficiente estimado sobre las distintas carteras.
Tabla 4: Significancias de los coeficientes estimados para las distintas carteras para México
| País | Cartera | (Constante) | Variación Exportaciones | Variación Importaciones | Variación PIB | Tasa de desempleo | Inflación Trimestral | Variación M2 | Tasa de Interés |
| México | 1 | Significativo | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo |
| México | 2 | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo |
| México | 3 | Significativo | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo |
| México | 4 | Significativo | No significativo | Significativo | No significativo | No significativo | Significativo | No significativo | No significativo |
| México | 5 | Significativo | No significativo | No significativo | No significativo | No significativo | Significativo | No significativo | Significativo |
| México | 6 | Significativo | No significativo | No significativo | No significativo | No significativo | Significativo | No significativo | Significativo |
Fuente: Cálculos propios.
En la tabla 4 se pude determinar que para las carteras 1 y 3, el único estimador significativo es el intercepto. Para la cartera 2, ninguna de las variables macroeconómicas introducidas resultó significativa. El modelo 4, presentó significancia en el intercepto y las variables importaciones e inflación trimestral. Para los modelos 5 y 6, el intercepto resultó significativo, junto a las variables inflación y tasa de interés.
En la tabla 5, se presentan se presentan los resultados obtenidos para Perú, determinando la significancia de las variables macroeconómicas introducidas en los distintos modelos, las cuales pretenden explicar las seis carteras construidas para Perú.
Tabla 5: Significancias de los coeficientes estimados para las distintas carteras para Perú
| País | Cartera | (Constante) | Variación Exportaciones | Variación Importaciones | Variación PIB | Tasa de desempleo | Inflación Trimestral | Variación M2 | Tasa de Interés |
| Perú | 1 | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo | Significativo | No significativo |
| Perú | 2 | No significativo | No significativo | No significativo | No significativo | Significativo | No significativo | Significativo | No significativo |
| Perú | 3 | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo | Significativo | No significativo |
| Perú | 4 | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo |
| Perú | 5 | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo |
| Perú | 6 | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo | No significativo |
Fuente: Cálculos propios.
Al analizar los resultados, se puede observar que para las carteras 1 y 3, la única variable significativa es la variación de la base monetaria ampliada. Para la cartera 2, las variables que impactan de alguna manera en su rentabilidad son la tasa de desempleo y la variación de la base monetaria ampliada. En las carteras 4, 5 y 6, ninguna de las variables macroeconómicas introducidas resultó significativa, en la explicación de sus rentabilidades.
DISCUSIÓN
Teniendo en cuenta los resultados de los modelos econométricos estimados para cada país, se puede afirmar que para el mercado bursátil chileno la tasa de interés de intervención es la única variable macroeconómica que explica a los portafolios 1, 5 y 6, presentando una relación inversa entre las mismas; por su parte, en Colombia solamente la tasa de desempleo explica positivamente a las carteras 2 y 5; mientras que para México las carteras 4, 5 y 6 están influenciadas negativamente por la tasa de inflación, el portafolio 4 también es explicado positivamente por las importaciones, y a su vez las carteras 5 y 6 están afectadas negativamente por la tasa de interés; siguiendo con el mercado financiero peruano, la oferta monetaria ampliada M2 presenta una relación directa con las carteras 1, 2 y 3 registrando significancia estadística para las mismas, la tasa de desempleo explica también de manera positiva a la cartera 2.
Por lo anterior, se puede argumentar que en términos generales el modelo APT no se aplica a los países que integran la Alianza del Pacífico, ya que algunas de las carteras conformadas de acuerdo con la metodología expuesta por Fama & French, no son explicadas por ninguna variable macroeconómica o únicamente son explicadas por el término contante.