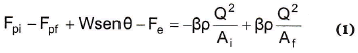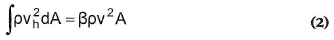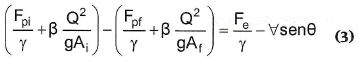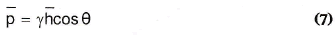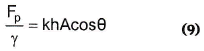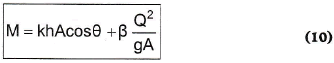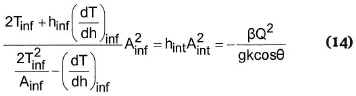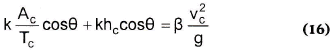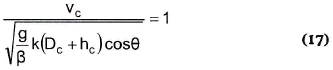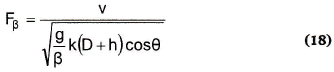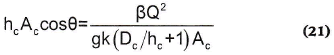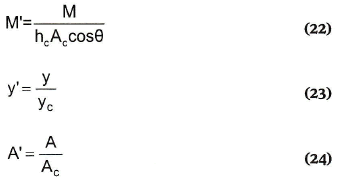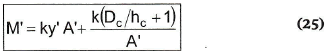Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Revista EIA
versão impressa ISSN 1794-1237
Rev.EIA.Esc.Ing.Antioq no.1 Envigado jan./jun. 2004
LA FUNCIÓN FUERZA ESPECÍFICA EN CANALES
Francisco Jaime Mejía*
* Ingeniero Civil. Profesor de Hidráulica, Escuela de Ingeniería de Antioquia. Grupo de Investigación Gabis. Gestión del Ambiente para el Bienestar Social., EIA. Envigado, Colombia. pffmejia@eia.edu.co.
Dibujos: Pedro Nel Orozco T. (Centro de Servicios y Apoyo Informático, EIA.)
Levantamiento de textos: Lina María Álvarez S. (alumna de ingeniería civil EIA; Grupo de Investigaciones Gabis)
Artículo recibido 23-IX-2003. Aprobado con revisión 19-I-2004
Discusión abierta hasta julio 2004
RESUMEN
Se presenta la función fuerza específica en flujo libre en canales de sección generalizada, se estudian sus características principales, un criterio de flujo crítico y su conversión a función adimensional o reducida.
PALABRAS CLAVE: Momentum; estado de flujo; fuerza específica; número de Froude.
ABSTRACT
This paper shows the momentum equation applied to open-channel flow and to study the specific force function in terms of its properties, the definition of a critical flow condition and its non-dimensional form.
KEY WORDS: Momentum; state of flow; specific force; Froude number.
INTRODUCCIÓN
El flujo libre de un líquido en un canal se explica y predice con la aplicación de un número reducido de principios físicos clásicos básicos: el teorema de transporte de Reynolds, la segunda ley de Newton sobre el movimiento, la ley de gravitación universal de Newton, la ley de viscosidad de Newton y las leyes de la termodinámica.
Aplicar las leyes de la termodinámica al flujo libre conduce a la ecuación de la energía; mientras que aplicar el conjunto de las leyes de movimiento a este flujo conduce a la ecuación que describe el delicado equilibrio del flujo uniforme en canales. De igual manera, puede decirse que aplicar el teorema del transporte de Reynolds al caso del flujo libre conduce a las expresiones de transporte de la masa, de la cantidad de movimiento lineal y de la cantidad de movimiento angular. A su vez, el conjunto de esas expresiones es la base para explicar y predecir el reposo y el movimiento de los fluidos en general y de los líquidos en particular.
Algunos fenómenos hidráulicos se explican o predicen con la aplicación de la ecuación de la energía, otros con la aplicación del principio del transporte de la cantidad de movimiento. En muchas situaciones ambos enfoques se complementan. Para la aplicación del transporte de la cantidad de movimiento en canales es necesario estudiar la función fuerza específica. Aquí se muestran las características de esa función, que posteriormente permitirá estudiar la ecuación de transporte de cantidad de movimiento lineal o momentum en flujo libre en canales.
LA FUNCIÓN FUERZA ESPECÍFICA
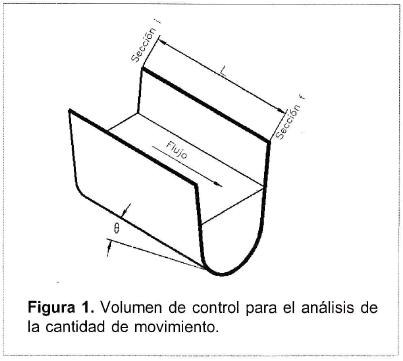
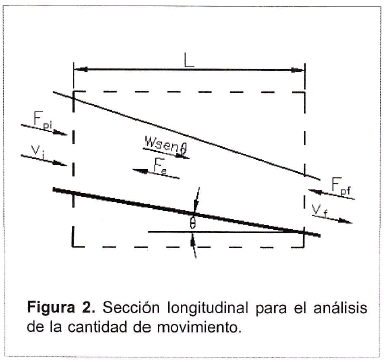
Para estudiar el transporte de cantidad de movimiento en la dirección paralela al fondo de un canal con flujo permanente e incompresible, se considera un volumen de control (figuras 1 y 2) y se obtiene1:
donde β es el coeficiente de corrección de cantidad de movimiento de Boussinesq, que aquí se considerará constante e independiente de la sección estudiada y de la altura del flujo. Si se requiere tener en cuenta esta variación, puede seguirse el procedimiento indicado por Naranjo (2000). Este coeficiente transforma el flujo de la cantidad de movimiento a través de la sección, donde existe una distribución de velocidad, vh, en términos de la velocidad media del flujo en la sección, v, que a su vez se obtiene con la continuidad del flujo volumétrico, v=Q/A:
Si se reordenan los términos de (1) y se divide por el peso específico2, se llega a la siguiente expresión:
A cada término entre paréntesis se le conoce como la fuerza específica en la sección, y se denota con la letra M:
Esta expresión reúne el empuje específico estático que ejerce el resto del flujo sobre el volumen de control y el empuje específico dinámico en la sección, que es el flujo de cantidad de movimiento a través de ésta.
La fuerza estática total en la sección es:
Ahora, si se puede ignorar la curvatura de las líneas de corriente (Naudascher, 2001) y se acepta la distribución uniforme de la velocidad, la fuerza estática sobre la sección se puede obtener con:
donde la presión en el centro de área es:
Además se tiene que la profundidad del centro de área es una fracción particular de la altura del flujo en la sección, que depende de la forma y tamaño de la sección transversal:
de manera que:
y con (4) se obtiene la función fuerza específica o ímpetu (Newton, 1687) en la sección:
CARACTERÍSTICAS GEOMÉTRICAS DE LA SECCIÓN TRANSVERSAL
La figura 3 ilustra los principales elementos geométricos en una sección transversal perpendicular al fondo del canal, a partir de los que se establecen las relaciones geométricas de interés que se muestran en la tabla 1:
En la tabla 1 se aprecia que las características geométricas de las secciones rectangular (zi=zd=0) y triangular (b=0) son casos particulares de la sección trapecial, que es aquella donde dos lados son paralelos entre sí, en este caso el fondo (b) y la superficie libre (T)3.
CARACTERÍSTICAS DE LA FUNCIÓN FUERZA ESPECÍFICA
La función fuerza específica (10) tiene dimensiones de longitud al cubo y está definida para todo valor no nulo de la profundidad (figura 4). La fuerza específica es asintótica a la profundidad cero, tiene concavidad positiva en el dominio positivo, tiene un punto de inflexión (d2M/dy2=0) en un valor negativo de la profundidad y un intercepto (M=0) en la profundidad negativa que cumplen lo expresado en (14):
En los casos particulares de secciones rectangular y triangular el punto de inflexión coincide con el intercepto. La función fuerza específica (10), en el rango de valores positivos de la profundidad, tiene un valor mínimo relativo a una profundidad que se conoce como profundidad crítica y a esa fuerza específica se le conoce como fuerza específica crítica o mínima. Para un valor dado de la fuerza específica existen tres profundidades que lo satisfacen. Si el tal valor dado es mayor que la fuerza específica mínima, existirán tres valores de profundidad que satisfacen la función, dos positivos diferentes entre sí y uno negativo. Si la fuerza específica es la mínima, habrá dos valores de profundidades positivas iguales entre sí, que corresponden precisamente a la profundidad crítica, y una profundidad negativa. Si la fuerza específica es menor que la mínima, la solución estará formada por una pareja de valores complejos conjugados entre sí y por un valor negativo de la profundidad. Para todo valor de M mayor que el mínimo, existen dos posibles profundidades positivas de flujo que se conocen como profundidades conjugadas: una de ellas, mayor que la profundidad crítica, es la profundidad secuente, que corresponde al estado subcrítico y la otra, menor que la profundidad crítica, está asociada al estado supercrítico del flujo.
La fuerza específica mínima es el ímpetu mínimo que se requiere en una sección de flujo para mantener el movimiento del flujo. Si el impulso en una sección es inferior a este valor mínimo, el flujo se remansa para acumular mayor cantidad de movimiento que a su vez permita transportar la masa fluida. Mientras se acumula esa cantidad de movimiento, el flujo deja de ser permanente y se conoce como flujo no permanente.
Si la ecuación que describe el comportamiento de la función fuerza específica (10) se deriva con respecto a la profundidad de flujo, se obtiene:
Combinar esta expresión con (11), (12) y la continuidad del flujo, permite obtener, en condiciones de fuerza específica mínima4 (dM/dy=0):
y por consiguiente:
que no es más que una forma del número de Froude para el estado crítico de flujo, en el sentido de la fuerza específica mínima, diferente del criterio crítico a partir del flujo de energía, o del flujo de masa (Naranjo, 2000)5.
De esta manera, puede definirse el número de Froude así:
y convertirlo a una expresión que contenga sólo elementos geométricos:
Con la expresión general para la fuerza específica (10) en la condición mínima, combinada con (19), también en estado crítico, se obtiene:
Las expresiones generales encontradas se pueden evaluar para algunas secciones transversales particulares y así obtener los resultados indicados en la tabla 2.
Tanto en la tabla 2 como en la tabla 1 y en las demás que se presentarán puede apreciarse que las secciones rectangular y triangular son casos particulares de la sección trapecial.
EFECTO DE LAS PEQUEÑAS PENDIENTES LONGITUDINALES
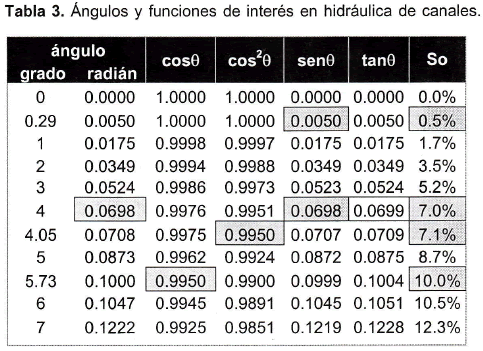
La tabla 3 muestra algunos valores de interés asociados a pequeños ángulos de inclinación longitudinal.
Los valores consignados en la tabla 3 muestran que para canales con pendientes tan altas, desde el punto de vista hidráulico, como 10%, se obtienen correcciones de altura de flujo insignificantes, representada por cos θ. El efecto de la corrección simultánea de la presión y la altura de flujo por pendiente, representada por cos2 θ, indica que, con pendientes inferiores a 7,1%, se refleja en magnitudes inferiores a la centésima. Así mismo, para pequeñas inclinaciones de los canales, inferiores al 7%, se observa la igualdad entre el ángulo, el seno, la tangente y la pendiente. También se observa que para pendientes inferiores a 0,5%, el efecto del peso del volumen de líquido en el volumen de control, representado por sen θ, empieza a ser insignificante. Por supuesto que si en algunas circunstancias los efectos de la corrección para algunas pendientes son insignificantes, no impide que esos valores puedan calcularse si se requiere mayor pulcritud en los cálculos.
Según lo anterior, se pueden transformar las expresiones reportadas en la tabla 2 para obtener las características de canales horizontales como se muestra en la tabla 4.
LA FUNCIÓN FUERZA ESPECÍFICA REDUCIDA EN CANALES (M')
La función fuerza específica (10) adopta valores diferentes de acuerdo con el caudal que transporta el canal. Se puede obtener una expresión adimensional e independiente del caudal a partir de una reducción de las variables respecto a las condiciones críticas.
Así, a partir del número de Froude (19), en estado crítico, se puede escribir:
Ahora, la relación (21) se adopta como factor para obtener las formas adimensionales de la función y las variables de flujo crítico se usan para definir otras variables adimensionales, así:
De manera que es posible obtener, mediante la combinación de (10) con (21), (22), (23) y (24):
Esta expresión es la función de fuerza específica reducida para cualquier sección transversal de canal.
Mediante procedimientos análogos puede obtenerse la expresión para la fuerza específica reducida en canales con otras secciones transversales, tal como se muestra en la tabla 5.
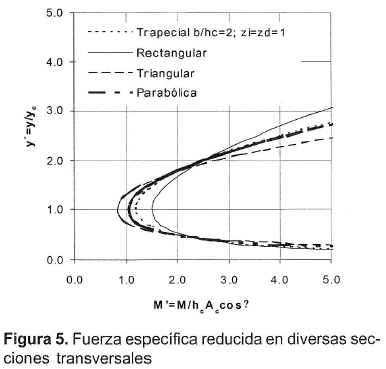
Finalmente, vale la pena resaltar que la ecuación para la fuerza específica reducida (25), es adimensional y representa una familia de curvas, independientemente del caudal que circule por el canal y de su pendiente, y está representada en la figura 5, para varias secciones transversales.
CONCLUSIONES
En la sección transversal de geometría generalizada en un canal con cualquier pendiente, se pueden obtener:
- La función fuerza específica (ecuación 10)
- El número de Froude a partir del criterio de fuerza específica (ecuación 19)
- La profundidad crítica a partir del criterio de fuerza específica mínima (ecuación 19 con el número de Froude unitario)
- La fuerza específica mínima (ecuación 20)
- La fuerza específica reducida (ecuación 25)
La combinación de las ecuaciones (3) y (4) permite estudiar el transporte de la cantidad de movimiento y, por tanto, el comportamiento de la altura del flujo gradual o rápidamente variado a lo largo de un canal sin estructuras o regulado por una compuerta o por un azud, o en una transición gradual, o en un resalto hidráulico si se conocen las condiciones de flujo en la sección inicial o en la sección secuente, para una sección generalizada o particular, pero todo ello se presentará en otro escrito y se publicará en otra oportunidad.
LISTA DE SÍMBOLOS
| A | área mojada de la sección transversal del canal. |
| a | inverso del latus rectum de la sección transversal parabólica. |
| A' | área mojada reducida de la sección transversal del canal. |
| Ac | área mojada crítica de la sección transversal del canal. |
| Af | área mojada de la sección transversal final. |
| Ai | área mojada de la sección inicial del volumen de control. |
| Ainf | área mojada de la sección para el punto de inflexión de la función fuerza específica. |
| Aint | área mojada del flujo en el intercepto de la función fuerza específica. |
| b | ancho del fondo en la sección transversal rectangular o trapecial. |
| D | profundidad hidráulica en la sección. |
| Dc | profundidad hidráulica crítica en la sección. |
| Fe | fuerza externa que actúa sobre el volumen de control. |
| Fp | fuerza estática total sobre la sección transversal. |
| Fpf | fuerza debida a la presión en la sección final del volumen de control. |
| Fpi | fuerza debida a la presión en la sección inicial del volumen de control. |
| Fβ | número de Froude para flujo de cantidad de movimiento (Boussinesq). |
| f | subíndice para la sección final del volumen de control. |
| g | aceleración gravitacional local. |
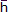 | profundidad hasta el centro de área. |
| h | profundidad de flujo en la sección, perpendicular al fondo del canal. Ordenada de la sección parabólica. |
| hinf | profundidad de flujo en la sección para el punto de inflexión de la función fuerza específica. |
| hint | profundidad de flujo en el intercepto de la función fuerza específica. |
| hc | profundidad crítica del flujo en la sección perpendicular al fondo del canal. |
| i | subíndice para la sección inicial del volumen de control. |
| k | fracción de profundidad del centro de área en la sección respecto a la profundidad del flujo. |
| L | longitud del volumen de control en la dirección del flujo. |
| M | fuerza específica. |
| M' | fuerza específica reducida para la sección del canal. |
| Mc | fuerza específica mínima. |
| M'c | fuerza específica mínima reducida. |
| n-n | sección transversal perpendicular al fondo del canal. |
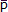 | presión en el centro de área. |
| p | función distribución de presión en la sección. |
| Q | caudal que circula a través de la sección. |
| So | pendiente del fondo del canal. |
| T | ancho de la superficie libre en la sección transversal. |
| Tc | ancho de la superficie libre crítico. |
| Tinf | ancho de la superficie libre en el punto de inflexión de la función fuerza específica. |
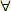 | volumen del líquido dentro del volumen de control. |
| v | velocidad media del flujo en la sección. |
| vc | velocidad crítica en la sección. |
| vf | velocidad media en la sección final del volumen de control. |
| vi | velocidad media en la sección inicial del volumen de control. |
| vh | función velocidad en términos de la distancia h desde el fondo. |
| x | abscisa de la sección parabólica en sentido perpendicular al flujo. |
| y | profundidad de flujo, paralela al eje vertical. |
| y' | profundidad reducida para la sección del canal. |
| yc | profundidad crítica. |
| yc,β | profundidad crítica obtenida con el criterio de fuerza específica mínima. |
| z | componente horizontal del talud (1V:zH), cuando son iguales en ambas márgenes. |
| zd | componente horizontal del talud (1V:zdH) correspondiente a la margen derecha del canal. |
| zi | componente horizontal del talud (1V:ziH) correspondiente a la margen izquierda del canal. |
| W | peso del líquido contenido en el volumen de control. |
| β | coeficiente de corrección de cantidad de movimiento o de Boussinesq. |
| γ | peso específico del líquido. |
| θ | ángulo de inclinación del canal medido con la horizontal. |
| ρ | densidad del líquido. |
BIBLIOGRAFÍA
CHOW, Ven Te (1959). Open-Channel Hydraulics. New York: McGraw-Hill, 667 p. [ Links ]
NARANJO MESA, Jorge Alberto (2000). La sección crítica son tres. XIV Seminario Nacional de Hidráulica e Hidrología. Villa de Leyva, Colombia, documento 41. [ Links ]
NAUDASCHER, Eduard (2001). Hidráulica de canales. México: Limusa, 381 p. [ Links ]
NEWTON, Isaac (1687). Philosophiae Naturales Principia Matemática. Barcelona, España: Altaza, 621 p. [ Links ]