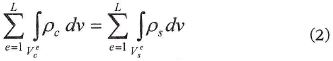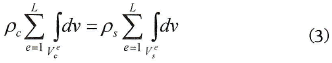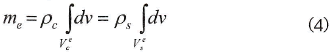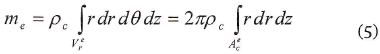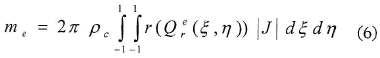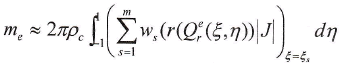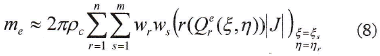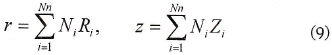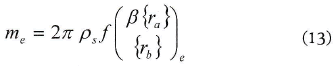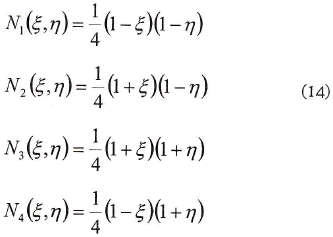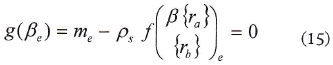Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista EIA
Print version ISSN 1794-1237
Rev.EIA.Esc.Ing.Antioq no.2 Envigado July/Dec. 2004
SINTERIZACIÓN CÉRAMICA POR ELEMENTOS FINITOS
Nolasco Arango*, Jorge Luis Restrepo**, Nelson de J. López***, Leonardo Carvajal****
* Matemático, Universidad Nacional de Colombia. Especialista en Análisis Avanzado y estudiante de la maestría en Matemáticas Aplicadas, Universidad EAFIT. Profesor Escuela de Ingeniería de Antioquia. Envigado, Colombia. pfnoara@eia.edu.co.
** Ingeniero Mecánico, Universidad Nacional de Colombia. Doctor en Ingeniería Industrial, Universidad Politécnica de Valencia. Profesor Universidad EAFIT. Medellín, Colombia. jrestrep@eafit.edu.co.
*** Ingeniero Químico, Universidad Nacional de Colombia. Estudiante de la maestría en Matemáticas Aplicadas, Universidad EAFIT. Locería Colombiana. Medellín, Colombia. nlopez@corona.com.
**** Matemático, Universidad Nacional de Colombia. Estudiante de la maestría en Matemáticas Aplicadas, Universidad EAFIT. Medellín, Colombia. lcarvajal@tutopia.com.
Artículo recibido 2-IV-2004. Aprobado con revisión 27-VII-2004
Discusión abierta hasta enero 2005
RESUMEN
Este artículo describe y establece la eficacia de utilizar el análisis de elementos finitos (discretización) para predecir los cambios de forma de un plato cerámico formado mediante la tecnología de prensado isostático (Prensa Sacmi PHO-600) durante el proceso de sinterización. El modelo desarrollado se basa en el principio de conservación de la masa y no incluye las deformaciones mecánicas del material. Para su implantación se requiere: i) la descripción de la malla de elementos finitos del cuerpo crudo prensado, ii) la densidad del plato compactado antes y después del proceso de sinterización. Las predicciones numéricas obtenidas se comparan con los resultados reales del proceso de cocción, mediante el contraste entre los diámetros y alturas de la pieza y el coeficiente de contracción. Los resultados muestran una diferencia de0,52% en diámetro y 0,48% en altura entre el valor numérico y el valor real; y una diferencia en contracción de 3,49%. Ésta es una muy buena predicción en términos prácticos.
PALABRAS CLAVE: Sinterización; elementos finitos (EF); cerámica.
ABSTRACT
This paper describes and demonstrates the effectiveness of a finite-element procedure to predict the compactation of a green ceramic isostatics pressed plate during sintering process. The approach is based on the conservation of mass principle and requires for its implementation: i) description of the finite element meshes of the green plate when ejected from the press, and ii) the density of the plate after compactation and sintering process. Numerical compactation predictions have been compared with experimental data. The comparisons reveal that the quantitative predictions regarding diameter and height range correlate closely with the measured values showing a difference of 0.52% in diameter and 0.48% in height and a variation on shrinkage of 3.49&. We consider this to be in good agreement, for most practical purposes.
KEY WORDS: Sintering; finite element; ceramic.
1. INTRODUCCIÓN
En cerámica tradicional, el diseño de productos se hace, en la mayoría de los casos, por tanteo, basado en la experiencia y heurística de un grupo de expertos. Este procedimiento puede tomar de 3 a 6 meses dependiendo de la cantidad de piezas que forman una familia y esto se traduce en pérdidas de competitividad de la empresa.
Es así como el desarrollo de la tecnología en la industria cerámica está llamado a encontrar procedimientos más eficientes en tiempo y en costos, que permitan tener productos más competitivos en el mercado. En la industria de la vajillería se requieren cadavez más productos de moda, de alta calidad y bajo precio, con un desarrollo rápido de formas y decoraciones.
El proceso estándar de manufactura de porcelana por vía seca se compone de varias etapas. Después de una preparación de la pasta, se seca en un atomizador y pasa al proceso de formación por prensado isostático, donde se compacta y queda la pieza con una densidad en crudo. Esta pieza pasa al proceso de cocción, donde ocurre la sinterización (densificación), con una contracción narural de la pieza y se presenta un cambio en su forma debido al comportamiento mecánico tipo "creep".
En el caso considerado, la densidad del material se supone uniforme en toda la pieza, tanto para el plato en crudo como para el plato sinterizado, pero el tratamiento matemático desarrollado es válido para el caso no uniforme, ajustando parámetros en la programación de la solución.
El método de los elementos finitos, entendido como un método para encontrar una solución aproximada de un modelo simplificado, entra a jugar un papel importante en el diseño cerámico. El tratamiento numérico reduce el modelo simplificado a una forma soluble mediante un número finito de operaciones numéricas. Esta solución tiene caracterizada por un número finito de parámetros, llamados grados de libertad, y al proceso se le conoce como discretización.
Se espera que, cuando el número de elementos sea grande, la solución por elementos finitos converja a la solución exacta, que es independiente de la selección de la discretización.
Hay estudios previos que tratan el tema, aplicados en su mayoría a compuestos cerámicos de alta tecnología, y algunos trabajos aplicados a la cerámica tradicional, como los presenta Navarro en el tratamiento de baldosas cerámicas. El modelo trabajado no requiere la solución de ecuaciones simultáneas, lo que optimiza la implementación, a diferencia de los modelos que requieren este tipo de soluciones como el caso presentado por A. Tsvelikh y otro. Los requisitos en datos de entrada son: (i) las densidades de la pieza cruda y sinterizada y (ii) la malla de la geometría de la pieza en crudo. Este artículo presenta la formulación teórica, el procedimiento de solución y los resultados globales usando el modelo del autor Kenan Y. Sanliturk.
2. FORMULACIÓN TEÓRICA
El procedimiento numérico propuesto para la determinación de la geometría final del plato sinterizado se basa en el método de los elementos finitos (FEM) (discretización) y en el principio de conservación de la masa (PCM) durante el proceso de sinterización y se expresará en coordenadas cilíndricas por tratarse de un problema axi-simétrico. Existen diferentes acercamientos para modelar el comportamiento cerámico durante la fase de sinterización. Algunos de ellos, como Kraft y Coube, utilizan modelos basados en leyes viscosas lineales con viscosidad aparente, Tsvelikh utiliza una función de las contracciones y hay propuestas que buscan eliminar la complejidad mediante un principio básico, como el propuesto por Aydin y otros en cerámica técnica, con resultados muy buenos. Este es el modelo que vamos a utilizar en este trabajo. El modelo consta de dos fases:
- Determinación de los elementos másicos individuales
- Determinación de la geometría final del plato sinterizado
A continuación describiremos cada una de estas fases.
2.1 Determinación de los elementos másicos individuales
El principio de conservación de la masa durante el proceso de sinterización puede escribirse en forma integral de la siguiente forma:
donde:
| ρc | Densidad del cuerpo en crudo |
| ρs | Densidad del cuerpo sinterizado |
| νc | Volumen del plato en crudo |
| νs | Volumen del plato sinterizado |
Cuando se divide el cuerpo en elementos finitos se cumple el PCM en cada elemento y así podremos escribir la masa total de la pieza como una suma de las contribuciones individuales, así:
donde: L es el número total de elementos en el proceso de discretización y e es el índice del elemento.
Debido a que la densidad es uniforme tanto para el plato crudo como sinterizado, la ecuación (2) se transforma en:
Como el PCM también se cumple en cada elemento
donde e = 1,2, ..., L y mc es la masa del elemento.
Expresando el diferencial de volumen dv en coordenadas cilíndricas r, θ, z y teniendo en cuenta la simetría axial del plato (ver figura 1) se obtiene:
donde Aec es el área, en la sección axi-simétrica del plato, del elemento e (con e = 1,2,3, ..., L).
Para calcular el valor de la masa expresada en la ecuación (5) se procede a realizar una transformación del sistema de coordenadas cilíndricas (r, z) a un sistema de coordenadas naturales (ξ, η) (ver figura 1).
Sean r = Qer(ξ, η) y z = Qer(ξ, η) las expresiones que representan la transformación de coordenadas (r, z) del sistema cilíndrico al sistema de coordenadas naturales (ξ, η). La integración en el elemento estándar se expresa como
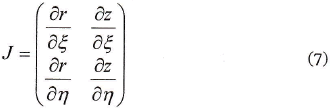
donde |J| es el determinante de la matriz jacobiana de la transformación definida por
La integral (6) se evalúa numéricamente por medio de una cuadratura, en este caso usaremos la cuadratura de Gauss-Legendre.
Para un punto fijo η podemos integrar numéricamente con respecto a ξ y obtenemos
donde ws y ξs son los pesos y valores de la coordenada ξ en los puntos de Gauss y m es el número de puntos de Gauss en la dirección de integración η.
Integrando numéricamente respecto a η se obtiene
donde n es la cantidad de puntos de Gauss en la dirección de integración η. Comúnmente m = n.
La transformación de r y z se hace mediante el uso de las funciones de forma Ni, y las coordenadas nodales (Ri, Zi) del elemento i, así:
donde Nn es el número total de nodos del elemento.
Finalmente, podemos expresar la ecuación (8) en forma compacta como una función del vector de coordenadas nodales de la pieza cruda {rc}.
Análogamente a la ecuación (10), podemos establecer que la masa de un elemento sinterizado es una función del vector {rc} de coordenadas nodales del elemento sinterizado.
2.2 Determinación de la geometría final del plato
Antes del proceso de sinterización, pueden producirse cambios en la masa del cuerpo, debido a la presencia de material orgánico proveniente de las materias primas o del uso de ligantes orgánicos necesarios para el proceso de formación por prensado con pasta granulada. Estos materiales se degradan antes de los 1.000 °C, aspecto que debe tenerse en cuenta en la aplicación del principio de conservación de la masa. En el caso de estudio, las pérdidas de masa por ignición son del 8%, debido al uso de los ligantes PVA (polivinil alcohol) y AC95. Esta pérdida de masa no afecta el proceso de sinterización como tal, porque las reacciones de descomposición se dan antes de los 1.000 °C y la sinterización ocurre entre los 1.000 y 1.200 °C.
Para determinar la geometría final del sinterizado, se puede obtener una solución aproximada contrayendo el volumen de cada elemento hasta que el producto de su volumen por su densidad nos dé la masa del elemento inicial afectada por sus pérdidas por ignición. En la práctica, la contracción del volumen es una función continua dentro del cuerpo, pero el modelo propuesto supone que es constante para cada elemento individual; sin embargo, puede variar de elemento a elemento de forma que al ir refinando la malla se tenderá a simular el continuo. Esta simplificación es necesaria para el problema y la solución. Basados en esta suposición, la contracción del elemento individual puede ser simulada multiplicando las coordenadas nodales del elemento en crudo por una constante de proporcionalidad y encontrando su nueva localización. Repitiendo este procedimiento para todos los elementos, uno a la vez, se puede obtener la geometría final del plato sinterizado.
Este proceso puede ser implementado numéricamente así: los elementos son ordenados secuencialmente tomando un punto de referencia (el centro radial del plato con coordenadas r = 0 y z = 0).
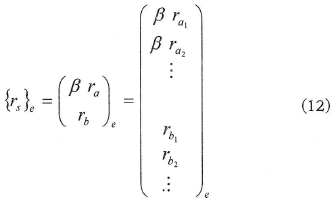
Los puntos nodales de cada elemento se mueven a su nueva posición sinterizada {rs}e por medio de la siguiente ecuación.
donde el vector {ra} contiene las coordenadas de los nodos que no se han movido en la sinterización y {rb} contiene las demás coordenadas que han sido procesadas; β es una constante de proporcionalidad para determinar durante la iteración. La constante de proporcionalidad se determina usando el principio de conservación de la masa para cada elemento, mediante la siguiente ecuación:
Es un valor conocido me, pues se calcula usando la densidad del plato crudo y la malla de elementos finitos, por tanto, sólo necesitamos calcular la constante β. Luego, el problema de encontrar la forma de la pieza sinterizada se convierte en calcular la constante β para los elementos individuales. Note, sin embargo, que en la ecuación (11), la función/denota el volumen de un elemento, conociendo el vector de las coordenadas nodales, y es una función no lineal de β, la cual requiere un algoritmo de solución no lineal (en esta implementación se utiliza el método de Newton-Raphson). Después que el valor de β se obtiene para el elemento e, los nodos del elemento adyacente son movidos a su posición sinterizada y el mismo procedimiento se repite para otros elementos. Por fin, cuando todos los elementos están procesados, la localización final de los nodos de la malla de EF proporciona la geometría sinterizada del plato cerámico completo.
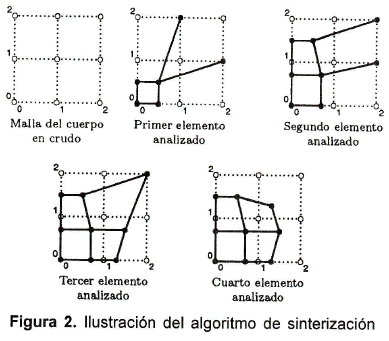
Para explicar el algoritmo se puede observar en la figura 2 una malla simple con 4 elementos en dos dimensiones y 9 nodos. Obsérvese que la posición sinterizada del elemento (1) se calcula y los nodos 1, 4, 5 y 2 se mueven a su nueva localización formando el vector {ra}. Para el segundo elemento las coordenadas de los nodos 5 y 2, que ya se han movido, forman el vector {rb} y no cambian; sin embargo; las coordenadas de los nodos 3 y 6 se multiplican por la constante de proporcionalidad, calculando su nueva posición sinterizada; el mismo procedimiento se sigue para los elementos 3 y 4 hasta obtener la forma final del plato. En la figura 2 se muestra la forma como opera este algoritmo.
3. PROCESO DE SOLUCIÓN
El diagrama de flujo que se muestra en la figura 3 describe el procedimiento general utilizado para la predicción de la geometría del sinterizado.
Para hallar los elementos másicos individuales en crudo y sinterizados se utiliza la integración numérica, basada en la cuadratura de Gauss-Legendre.
Las funciones de forma que usaremos para interpolar las coordenadas son las funciones jerárquicas para cuadriláteros de cuatro nodos, que son:
Como la ecuación (13) es una función no lineal de β, requiere una solución iterativa para cada elemento con el fin de encontrar las raíces de la ecuación
Estas raíces se pueden encontrar usando el método de Newton-Raphson, que requiere la evaluación de g(βe) y su derivada. Para más detalles ver Barna-Babuska y Zienkiewicz.
4. SIMULACIÓN NUMÉRICA
Para la simulación se diseñaron un programa principal y unas subrutinas en Matlab. El programa básicamente lee las coordenadas de los nodos y las conectividades de los elementos, los cuales se traen de un programa de generación de mallas (en nuestro caso se ha utilizado el programa Cosmos/M para generar la malla del plato que se desea analizar). El programa intemo posee un control del error que garantiza una tolerancia determinada para converger, en este caso fue de 0,0001 en la integración numérica y una tolerancia de 0,00001 para calcular β con una precisión de 0,001.
Adicionalmente el programa posee un control para el número máximo de iteraciones. En las pruebas realizadas se utilizaron elementos cuadriláteros de cuatro nodos con grado polinomial de 2 y los puntos de Gauss necesarios para dar la precisión requerida, dependiendo de los criterios de tolerancia establecidos por el usuario. Los tiempos de procesamientos son del orden de minutos, pero este aspecto puede mejorarse mucho elaborando una versión final del programa optimizada computacionalmente.
Las propiedades del material usado fueron:
- Densidad en crudo 1700 kg/m3
- Densidad sinterizada 2400 kg/m3
- Pérdidas por ignición 8%.
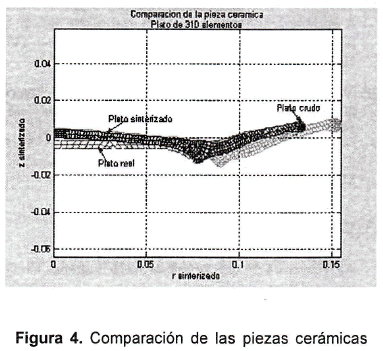
La prueba del proceso de sinterizado se realizó con un plato con 310 elementos. Se anexan los resultados y gráficas, donde se aprecia la pieza en crudo, sinterizada y real; ver figura 4. La pieza real incluye un comportamiento tipo "creep", más allá del alcance de este documento.
5. VALIDACIÓN DE LOS RESULTADOS
Se llevó a cabo una validación de la modelación numérica con la referencia 19.027, que se corresponde con un plato pando de porcelana de alúmina al 15%.
El procedimiento experimental consiste en tomar el plato crudo y someterlo al proceso de cocción; en este proceso se dan las reacciones de sinterización o densificación y ajuste de la geometría por el comportamiento tipo "creep" de la cerámica sometida a altas temperaturas.
El proceso de cocción se realizó en un horno túnel operado con carros refractarios de baja masa térmica, a un ciclo de 16 horas y una temperatura máxima de mesa de 1.200 °C. La formación de las piezas se realizó en una prensa Sacmi PHO-600, que opera en condiciones isostáticas, lo que lleva a tener una pieza con densidad en crudo muy homogénea. La cocción se lleva hasta tener una pieza con porosidad entre 0 y 0,6%.
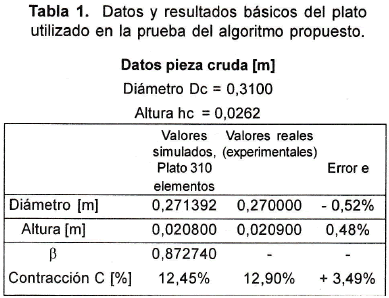
En la tabla 1 se comparan los resultados provenientes de la modelación numérica con los datos reales del proceso
Notas: Los valores de la contracción y el error presentados en esta tabla se calcularon con las siguientes relaciones:
6. CONCLUSIONES
El algoritmo propuesto con base en el principio de conservación de la masa, aplicado a la predicción de la geometría final de un plato cerámico durante el proceso de cocción y específicamente en la fase de sinterización, presenta un buen acercamiento. Los resultados obtenidos en términos del diámetro y altura de la pieza presentan diferencias de -0,52% equivalente a 1,4 mm para el caso del diámetro y de 0,48% equivalente a 0,1 mm para la altura final de plato; estas diferencias están dentro de la tolerancia permitida para un producto comercial, que acepta variaciones de ±2% en dimensiones.
El modelo es práctico y fácil de implementar en un computador convencional, con tiempos de procesamiento muy bajos, aunque se requiere disponer de un programa que genere previamente la malla de elementos finitos del plato.
Este algoritmo puede usarse como parte de un análisis más general en el que se incluya, por ejemplo, el efecto de "creep", que se presenta en el proceso de cocción de los platos de cerámica.
Es un algoritmo efectivo y sencillo, que permite realizar, con buena precisión y en un tiempo muy reducido, la predicción de la forrna final después de la sinterización de una pieza cerámica tradicional durante el proceso de cocción.
7. AGRADECIMIENTO
A la Universidad Eafit y al profesor Jorge Restrepo Ochoa, asesor del trabajo de grado "Aplicación de elementos finitos en la predicción de la geometría final de un plato cerámico", de la maestría en Matemáticas Aplicadas.
8. BIBLIOGRAFÍA
Aydin I. B.J. Briscoe and K. Y. Sanliturk. Dimensional variation of die-pressed ceramic green compacts, comparison of a finite element modelling with experiment. J. Eur. Ceramic. (1997). [ Links ]
Barna Szabo and Ivo Babuska. Finite element analysis. John Wiley and Sons. New York. 1991. [ Links ]
Becker A.A. Understanding no-linear finite element analysis though illustrative benchmark. Nafems. UK. 2001. [ Links ]
Kraft. T.; O. Coube and H. Riedel. Numerical simulation of pressing and sintering in the ceramic and hard metal industry. Fraunhofer Institute for Materials Mechanics. Freiburg, Germany. [ Links ]
Kenan Y. Sanliturk, Ismalil Aydin and Brian J. Briscoe. A finite element approach for the shape compacts during sintering. J. Am. Ceramic Soc. 1999. [ Links ]
Navano, J.E., V Cantavella, F. Negre and E. Sanchez. Model predicts tile deformation in firing. Bulletin of Am. Ceramics Society. 1999. [ Links ]
F. Taheri and G. P. Zhu. Simulation of processing and residual stresses in a ceramic composite. Finite element simulation and validation Part I y Part II. Interceram. 1997. [ Links ]
Tsvelikh A. W., Thompson, A. Easton and I. Freshwater. A geometrical finite element model of the sintering process of advanced ceramics. Comput. Mater. Sci. 1995. [ Links ]
W. Schulle and K. Shultz, Freiberg. FEM modeling of firing temperature and stress zones. Cfi/Ber. DKG 76. 1999. [ Links ]
Zienkiewicz. O. C. The finite element method. McGraw-Hill. London. 3 ed. 1997. [ Links ]