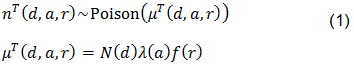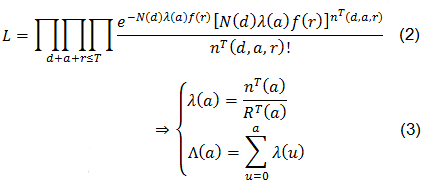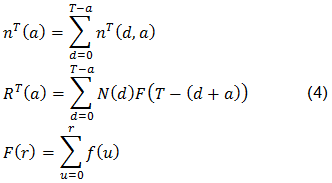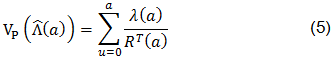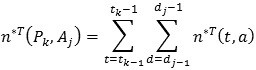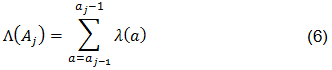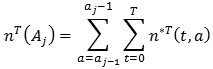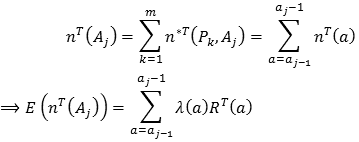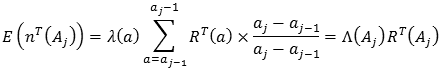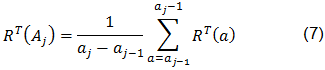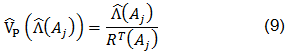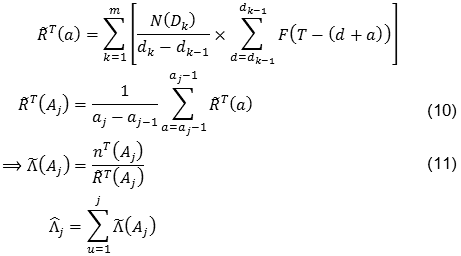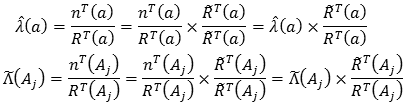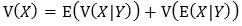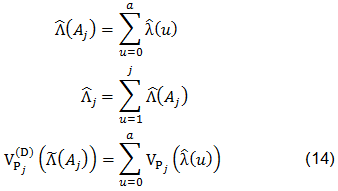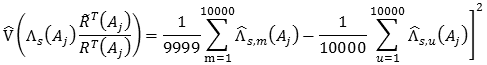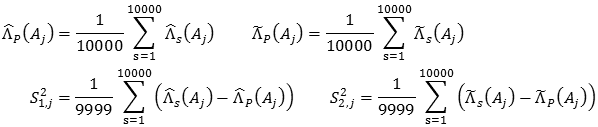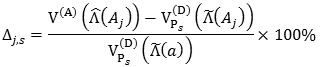Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista EIA
Print version ISSN 1794-1237
Rev.EIA.Esc.Ing.Antioq no.4 Envigado July/Dec. 2005
DATOS AGREGADOS Y DESAGREGADOS EN EL ANÁLISIS DE DATOS DE GARANTÍA
Jorge Mario Obando*, Sergio Yáñez**
* Ingeniero Administrador, EIA. Profesor Escuela de Ingeniería de Antioquia. Envigado, Colombia. pfjorgeo@eia.edu.co.
** Ingeniero Industrial. Magíster en Ciencias y Magíster en Estadística. Director Escuela de Estadística, Universidad Nacional de Colombia, Sede Medellín, Colombia. syanez@unalmed.edu.co.
Artículo recibido 27-V-2005. Aprobado con revisión 2-XI-2005
Discusión abierta hasta mayo 2006
RESUMEN
Los datos de garantía tratados estadísticamente son útiles para la predicción de reclamaciones futuras, para establecer comparaciones entre reclamaciones de productos y mejoras de ellos y estimación de la confiabilidad. Este análisis exige la disponibilidad de información diaria, que muchas veces sólo está disponible en forma agregada semanal o mensual debido a la logística de la empresa. En el presente trabajo se estudia el efecto que presenta la agregación de datos en los resultados del análisis.
PALABRAS CLAVE: Confiabilidad; análisis de datos de garantía; procesos de conteo; tasa de intensidad.
ABSTRACT
Warranty data, statistically well handled, is useful to predict future claims, to make comparisons between products claims, to estimate products field reliability, and to identify reliability improvements that can be made to the product. This analysis requires the availability of daily records that sometimes are only available in weekly or monthly total (grouped data) due to the nature of the operations of the organization. In this work the effect of the grouped data in the final results of the analysis is studied.
KEY WORDS: Reliability; warranty data analysis; counting processes; intensity rate.
1. INTRODUCCIÓN
Generalmente las empresas venden sus productos cubiertos con un período de tiempo (Ω) de garantía. Esto lo hacen por dos razones: la primera, la garantía hace parte del servicio posventa de la compañía; la segunda, la garantía hace parte de la calidad del producto. Así, un período de garantía ofrece un servicio posventa y un producto confiable.
Las empresas esperan que el número de unidades que fallen dentro del período de garantía sea mínimo, pues cada reclamación por garantía se convierte en un costo para la empresa, además de indicar que el producto falló antes de lo esperado. Si, por el contrario, el número de reclamaciones por garantía es alto, entonces existen problemas en el diseño o en alguna parte de la línea de producción, en otras palabras, la confiabilidad del producto es baja.
Es por esto por lo que el análisis estadístico de los datos de garantía se puede utilizar como un método de control estadístico de la calidad, como un medio para el estudio de la confiabilidad del producto y como herramienta para pronóstico de costos.
En la sección 2 se tratan los temas más importantes acerca del análisis de datos de garantía: el estimador de la tasa de reclamaciones por garantía y su varianza; además, se estudia el caso especial de agregación de los períodos de reclamación. La agregación de los registros de ventas lleva un supuesto acerca de las ventas diarias, esto se analiza en la sección 3. Finalmente, en la sección 4 se desarrolla el estudio de una simulación que compara los resultados de un análisis de datos de garantía a partir de datos de reclamaciones y ventas desagregados y agregados en un modelo de generación de reclamaciones específico.
2. ANTECEDENTES
El análisis de garantías consiste en el empleo del análisis estadístico para estimar la tasa de reclamaciones por unidad dentro del período de garantía (Kalbfleisch et al., 1991; Lawless y Kalbfleisch, 1992; Lawless y Nadeau, 1995; Lawless y Kalbfleisch, 1996), calcular intervalos de confianza para datos agregados y no agregados (Kalbfleisch et al., 1991; Lawless y Kalbfleisch, 1996; Lawless, 1998), determinar la influencia de variables explicatorias (Lawless y Nadeau, 1995), calcular el efecto sobre los costos y pronosticar el impacto futuro de las reclamaciones por garantía (Lawless, 1998; Blischke y Murthy, 2000), estimar la función de confiabilidad de los productos (Kalbfleisch et al., 1991; Lawless, 1998) y, más recientemente, realizar control de calidad sobre el proceso de producción (Wu y Meeker, 2002).
La estimación de la tasa de reclamaciones se basa en la edad de la unidad al realizar la reclamación, es decir, el tiempo transcurrido desde su venta hasta la reclamación; sin embargo, el cálculo de la varianza de dicho estimador depende de los supuestos con respecto al proceso de generación de reclamaciones. Lawless y Kalbfleisch (1996) establecen tres escenarios:
- Las reclamaciones por unidad en una edad específica son variables aleatorias independientes con distribución de Poisson (Kalbfleisch et al., 1991)
- Las reclamaciones por unidad en una edad específica son variables aleatorias independientes, pero se presenta un factor de sobredispersión debido a las condiciones de operación y de uso de cada unidad, y
- La presencia de correlación entre reclamaciones de distintas edades, debida a que las condiciones de operación y de uso generan un deterioro más rápido de las piezas dentro del período de garantía, lo que conduce a mayor número de reclamaciones.
Por otra parte, es común que los sistemas de registro se diseñen de acuerdo con las necesidades y limitaciones de la empresa, por lo tanto, se pueden presentar bases de datos, entre otros casos, con agregación de los registros (semanal, mensual o en otros intervalos de tiempo), tanto de ventas como de garantías; con retraso en el registro de las reclamaciones; con registros vacíos en algunos días del año por cierre. De ellos, los casos más comunes son la agregación de los datos y el retraso en los registros.
La agregación de los datos lleva a estimar las ventas diarias y a realizar supuestos acerca de la edad de las unidades, lo cual tiene impacto en el estimador de la tasa de reclamaciones y su correspondiente varianza, pues se introduce una variación extra debida al desconocimiento de las ventas diarias (Lawless, 1998). Asimismo, el retraso en los registros lleva a la subestimación de la tasa de reclamaciones, por tanto, se debe definir una función de probabilidad de retrasos para corregir este problema.
A continuación se introduce la notación y se expone el modelo de análisis estadístico de datos de garantías basado en la edad.
2.1 Notación
El análisis de datos de garantía se basa en la edad a del producto, medida como el número de días de servicio de la unidad i desde el día de su venta, di, hasta el día t en el que se presenta la reclamación. Para ello, suponga que las unidades i = 1, 2, ..., N se venden en los días d = 0, 1, 2, ..., τ; así, N(d) es el número de unidades vendidas el día d. Además, suponga que los registros incluyen todas las reclamaciones reportadas al productor hasta el día T, esto permite definir:
| nT(d,a) | → | Número de unidades vendidas el día d de edad a |
| λ(a) | → | Tasa de intensidad de reclamaciones por unidad de edad a (a = 1, 2, ...) |
| Λ(a) | → | Número esperado de reclamaciones por unidad hasta la edad a |
Por otra parte, es posible que las reclamaciones tarden algún tiempo en ser reportadas al productor, debido, entre otros, a la logística propia de las empresas; por esto, se define:
| f(r) | → | Probabilidades de que una reclamación se retrase r días en ser reportado (r = 0, 1, 2, ...) |
| RT(a) | → | Unidades de edad a en riesgo reportadas hasta T |
2.2 Análisis de reclamaciones por garantías
2.2.1 Estimador de la tasa de reclamaciones por garantía
Si nT(d,a,r) es el número de reclamaciones de unidades vendidas el día d, de edad a y que tuvieron un retraso de r días en ser reportadas al productor, de acuerdo con Kalbfleisch, Lawless y Robinson (1991):
Entonces, al contar con los registros de los nT(d,a,r) para d+a+r≤T, y suponer que f(r) (r = 0, 1, 2, ...) y N(d) (d = 0, 1, 2, ...) son conocidos, se tiene la ecuación de verosimilitud:
Donde:
No obstante, Kalbfleisch, Lawless y Robinson (1991) señalan que (1) realmente es una simplificación de modelos más generales, los cuales tienen en cuenta que:
- La distribución de las reclamaciones varía de unidad a unidad. Esto se debe a que las tasas y condiciones de uso de cada unidad son diferentes.
- Otra fuente de variación de los λ(a) es el efecto calendario: las reclamaciones por garantía son difíciles (o imposibles) de realizar en fines de semana (más aun los domingos y festivos en el caso colombiano). Así, para las unidades vendidas un lunes, por ejemplo, λ(7k - 1) = 0 (k = 1, 2, ...).
En estos casos, Kalbfleisch, Lawless y Robinson (1991) precisan que el modelo (1) es plausible si se tiene en cuenta que los conteos nT(d,a,r) obtenidos por la superposición de los procesos de muchas unidades son aproximadamente Poisson cuando la intensidad de las reclamaciones es pequeña; además, el parámetro λ(a) debe ser interpretado como el número marginal de reclamaciones por unidad de edad a.
Finalmente, el modelo (1) es válido porque los estimadores máximos verosímiles son también cuasiverosímiles (o ecuaciones de mínimos cuadrados generalizados) y llevan a estimadores concretos válidos con supuestos más generales.
2.2.2 Varianza del estimador de la tasa de reclamaciones por garantía
Es precisamente en este punto donde hay que tener en cuenta las variantes del modelo (1) mencionadas, pues la variabilidad de unidad a unidad en las distribuciones del número de reclamaciones y el efecto calendario no son tenidos en cuenta en el primer modelo, aunque, como ya se mencionó, esto no afecta el estimador de λ(a) propuesto en (3); por lo tanto, se tienen varios estimadores de la varianza de Λ(a), dependiendo de los supuestos del modelo que se esté trabajando:
- Si realmente (1) se cumple, es decir, los nT(d,a,r) son variables aleatorias Poisson independientes, entonces los nT(d,a) también son variables aleatorias independientes Poisson con media µT(d,a) = N(d)λ(a)F(r), y, en consecuencia (Lawless y Kalbfleisch, 1996), nT(a) = RT(a)λ(a) y la varianza de Λ(a) se estima con:
- Ahora, si se consideran supuestos más generales, como lo es la variabilidad en las distribuciones de reclamaciones de unidad a unidad, entonces se presentará variación adicional a la Poisson (Lawless y Kalbfleisch, 1996; Lindsey, 1997). Otra posibilidad, aun más general, es considerar que puede presentarse un grado de correlación entre los nT(d,a) (Lawless y Kalbfleisch, 1996; Lawless, 1998). Estos supuestos se discutirán en un trabajo futuro, ya que, por el momento, están por fuera de los objetivos de este artículo.
2.3 Datos agregados
Observe que hasta el momento, los estimadores propuestos suponen el conocimiento de las nT(d,a) y N(d), es decir, se cuenta con registros de reclamaciones, bien sea unidad por unidad o día a día; pero la organización logística de muchas empresas impide que se tenga esta clase de información tan detallada. En otras palabras, muchas empresas sólo tienen acceso a registros de reclamaciones y ventas totales semanales, quincenales, mensuales o en cualquier otro tipo de agregación temporal.
De acuerdo con Lawless y Kalbfleisch (1996), si los períodos de agregación de las reclamaciones y los reportes son del mismo tamaño, basta hacer las sustituciones necesarias en los estimadores propuestos y no habrá mayor diferencia, tal como lo muestran los autores en su artículo al comparar resultados con base en registros diarios y agregados mensualmente. Sin embargo, si los períodos de agregación de reclamaciones y reportes son de diferente tamaño (Lawless y Kalbfleisch, 1996), o, más aun, cuando los registros de ventas también están agregados en algún intervalo de tiempo (Lawless, 1998), es necesario hacer una extensión del análisis para realizar los ajustes necesarios.
Para ello se suponen los conjuntos de edad Aj = [aj-1,aj) y los intervalos de tiempo en los que ocurren las fallas Pk = [tk-1,tk).
Si se define n-T(t,a) = nT(t-a,a), se tiene su análogo agregado:
En el caso de datos agregados, se desea estimar:
Para ello, se define primero el número de reclamaciones reportadas de unidades con edad j:
Sin embargo, recuerde que no se tienen registros diarios; además, como todos los datos están agregados, T es el límite superior del último de los Pk. Así, si T ∈ Pm, entonces T = tm-1, por lo tanto:
Ahora bien, Lawless (1998) afirma que la suposición de λ(a) constante en Aj es válida; no obstante, esto en realidad depende de las características particulares del producto y de la amplitud de los intervalos de agregación y, por ello, otros supuestos serán necesarios en casos más especiales.
Tomando el supuesto de Lawless, se tiene que:
Donde:
De todo lo anterior se concluye que:
Ahora bien, (7) supone el manejo de registros diarios de ventas. Más adelante se analizará la expresión con el supuesto de agregación de los registros de ventas. Por el momento, se supondrá que los RT(Aj) son conocidos para la estimación de la varianza de (8). De acuerdo con Lawless y Kalbfleisch (1996) y Lawless (1998), se pueden calcular estimadores análogos a (5), pero teniendo en cuenta la agregación:
3. EXTENSIÓN DEL ANÁLISIS POR LA AGREGACIÓN DE LAS VENTAS
Note que las expresiones (7) a (9) suponen el conocimiento de las ventas diarias N(d), lo cual no es posible si los registros de ventas también están agregados en algún intervalo de tiempo. En este caso, Kalbfleisch, Lawless y Robinson (1991) proponen un estimador para RT(Aj), el cual está basado en aceptar que las N(d) son constantes en un intervalo [a,b]: Sean Dk = Pk - Aj y 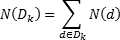 las ventas en el período Dk, y sea T ∈ Pm (así T = tm-1); entonces:
las ventas en el período Dk, y sea T ∈ Pm (así T = tm-1); entonces:
Ello resolvería el problema del desconocimiento de N(d) en (7) y (8). Además, (9) subestima la varianza del estimador, dado que también se tiene incertidumbre acerca de los N(d), es decir, el hecho de estimar N(d) introduce una nueva fuente de variación que debe tenerse en cuenta en el modelo.
Para ello, sea 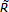 T = {
T = {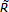 T(a); a = 0, 1, 2, ...}; además, suponga que los
T(a); a = 0, 1, 2, ...}; además, suponga que los 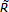 T(a) son insesgados e independientes del conteo de reclamaciones nT(d,a) y:
T(a) son insesgados e independientes del conteo de reclamaciones nT(d,a) y:
Entonces, recordando que:
y haciendo X = 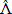 (a) y Y =
(a) y Y = 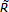 T, se tiene:
T, se tiene:
Ahora bien, (12) tiene dos términos. Según Lawless (1998), el primer término se calcula reemplazando 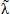 (a) y
(a) y 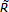 T(a) en (5); mientras que para el segundo término se hace necesario establecer una distribución para
T(a) en (5); mientras que para el segundo término se hace necesario establecer una distribución para 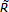 T(u)/RT(u) para, mediante simulación, poder reemplazar λ(a) por
T(u)/RT(u) para, mediante simulación, poder reemplazar λ(a) por 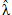 (a).
(a).
De la misma forma, se puede hacer la extensión para el caso agregado:
Ya en (13) se siguen los lineamientos propuestos por Lawless (1998), pero teniendo en cuenta la agregación.
4. SIMULACIÓN
Para generar las ventas diarias, se truncó y discretizó una distribución normal con parámetros µ=8 y σ=1 en el intervalo [5,12] (por simplicidad, esta distribución se denotará en adelante como NTD(µ,σ,a,b) , donde [a,b] es el intervalo de truncamiento); se generaron 240.000 números aleatorios de esta distribución y se agruparon en 8.000 conjuntos no traslapados de 30 números. Cada observación mensual correspondió a la suma de los 30 números aleatorios de cada conjunto; así se generó una serie de 8.000 observaciones de ventas mensuales, a la cual se le realizó una prueba de bondad de ajuste con una distribución discreta con un nivel de confianza del 95% y arrojó el resultado de la tabla 1.
donde KS es la abreviatura de Kolmogorov-Smirnov.
Luego se parametrizó la distribución binomial en términos del vector de parámetros θ'=[µ,σ2] y se supuso que, al desconocer las ventas diarias, se tendría una estimación de su distribución de probabilidad dada por Binomial (1/30θ). En este caso, el resultado es Binomial (9; 0,852956).
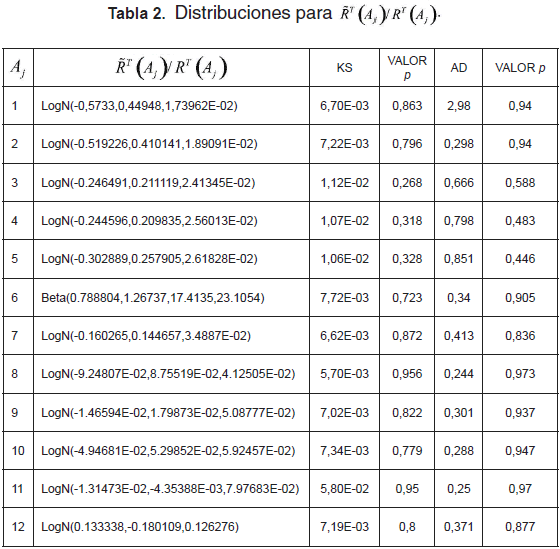
Conociendo las distribuciones de ventas mensuales y diarias, se generaron 7.620 observaciones de 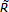 T(Aj)/RT(Aj), j = 1, 2, ..., 12, a las cuales se les realizó una prueba de bondad de ajuste, con los resultados que muestra la tabla 2.
T(Aj)/RT(Aj), j = 1, 2, ..., 12, a las cuales se les realizó una prueba de bondad de ajuste, con los resultados que muestra la tabla 2.
donde KS y AD son los estadísticos de las pruebas de Kolmogorov-Smirnov y Anderson-Darling, respectivamente. Además, la notación logN(µ,σ,x0) hace alusión a una distribución lognormal con parámetros µ y σ y punto de localización (inicio de la distribución) en x0.
Se realizaron entonces 100 simulaciones (indexadas s = 1, 2, ..., 100) de ventas y reclamaciones para d = 0, 1, 2, ..., 364, con los conteos siguiendo una distribución Poisson (λ = 0.002) y f(r) dada por:
Y para cada una de ellas se calcularon λi(a) y Vp(λ(a)) de acuerdo con (3) y (5), respectivamente; para luego calcular:
También se calcularon 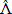 (Aj),
(Aj), 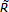 T(Aj), para después determinar el primer término de (13) reemplazándolos en (9).
T(Aj), para después determinar el primer término de (13) reemplazándolos en (9).
Finalmente, acudiendo a los resultados mostrados en la tabla 2 y a los 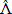 (Aj) obtenidos, se calculó el segundo término de (13) para j = 1, 2, ..., 12, siguiendo los pasos descritos a continuación:
(Aj) obtenidos, se calculó el segundo término de (13) para j = 1, 2, ..., 12, siguiendo los pasos descritos a continuación:
- Generar 10.000 valores de kx,m =
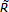 T(Aj)/RT(Aj), m = 1, 2, ..., 10.000.
T(Aj)/RT(Aj), m = 1, 2, ..., 10.000. - Calcular:
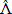 s,m(Aj) =
s,m(Aj) = 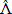 s(Aj)×ks,m
s(Aj)×ks,m - Calcular la varianza muestral para la s-ésima simulación:
5. ANÁLISIS DE RESULTADOS
La idea central del trabajo es realizar una comparación entre análisis de datos de garantía desagregados y agregados para determinar el efecto que tiene la agregación en los resultados finales. Por motivos de espacio y practicidad, aquí sólo se muestran las comparaciones y resultados para j = 3, 7; para los otros valores de j, los resultados son análogos.
En la figura 1 se muestran las comparaciones de 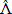 (Aj) con
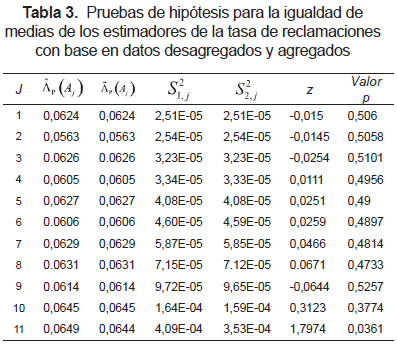
(Aj) con 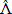 (Aj) para j = 3, 7. Note que prácticamente no hay diferencia entre ambos estimadores, esto se verifica en la tabla 3 donde se prueba la hipótesis nula E(
(Aj) para j = 3, 7. Note que prácticamente no hay diferencia entre ambos estimadores, esto se verifica en la tabla 3 donde se prueba la hipótesis nula E(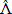 (Aj)) = E(
(Aj)) = E(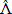 (Aj)) a partir de los estimadores muestrales
(Aj)) a partir de los estimadores muestrales
La hipótesis nula se acepta para j = 1, 2, ..., 10.
Con respecto a los estimadores de la varianza, la figura 2 muestra que existen diferencias entre V(D)(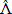 (Aj)) y V(A)(
(Aj)) y V(A)(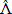 (Aj)). Para medir mejor el efecto de la agregación en la varianza del estimador, se calculó la diferencia porcentual Δj,s, j = 3, 7 (figura 3), entre las estimaciones dadas por (14) y (13)
(Aj)). Para medir mejor el efecto de la agregación en la varianza del estimador, se calculó la diferencia porcentual Δj,s, j = 3, 7 (figura 3), entre las estimaciones dadas por (14) y (13)
Esta diferencia porcentual fluctúa entre el 3,8% y el 8% para k = 3, y entre -0,5% y 9,2% para k = 7. No obstante, en la tabla 3 se observa la similitud entre los estimadores de la varianza de las muestras Monte Carlo, 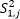 y
y 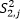 .
.
Por otra parte, en la tabla 4 se muestra que la amplitud de los intervalos de confianza para 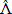 j y
j y 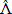 j, l y l*, respectivamente es muy similar y cercana a cero su diferencia porcentual
j, l y l*, respectivamente es muy similar y cercana a cero su diferencia porcentual
Con todo esto se comprueba que las distribuciones de 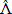 (Aj) y
(Aj) y 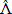 (Aj) son aproximadamente iguales y que la agregación de datos no tiene un efecto significativo en los resultados del análisis de datos de garantía.
(Aj) son aproximadamente iguales y que la agregación de datos no tiene un efecto significativo en los resultados del análisis de datos de garantía.
Como nota final, se aclara que no se incluyen resultados para j = 12, porque son atípicos, lo mismo ocurre para j = 11. Esto ocurre porque el tiempo de garantía (Ω) es igual al tiempo de observación de la base de datos, lo cual genera, para el caso de datos desagregados, que en algunas réplicas de la simulación se obtengan valores de RT(a) cercanos a cero para a ≥ 350 y, por lo tanto, valores de λ(a) altos, así se presente un solo reclamo.
4. CONCLUSIONES Y TRABAJO FUTURO
El presente artículo es sólo la parte inicial de un trabajo más amplio de comparación de análisis de datos de garantía desagregado y agregado que está en ejecución; en él se considerarán, además de otros escenarios de ventas diarias, variaciones en la naturaleza de generación de las reclamaciones; por ejemplo, un escenario para incluir consiste en suponer que las reclamaciones de distintas edades no son independientes.
Por el momento, se concluye que acudir al supuesto de Kalbfleisch et al., (1991) de suponer ventas constantes en un intervalo [a,b], cuando sólo se tiene información acerca de las ventas totales de dicho intervalo, no introduce sesgo en el estimador de la tasa de reclamaciones de garantía ni incrementa su variabilidad; de hecho, las distribuciones de los estimadores con base en datos desagregados y agregados son casi iguales; es decir, la agregación de datos no tiene un efecto significativo en los resultados del análisis de datos de garantías.
BIBLIOGRAFÍA
Blischke, W. R. and D. N. P. Murthy (2000). Reliability: modeling, prediction and optimization, John Wiley and Sons. [ Links ]
Kalbfleisch, J. D., Lawless, J. F. and Robinson, J. A. (1991). Methods for the analysis and prediction of warranty claims. Technometrics 33(3), 273-285. [ Links ]
Lawless, J. F. (1998). Statistical analysis of product warranty data. International Statistical Review 66 (1), 41-60. [ Links ]
Lawless, J. F. (2000). Statistics in reliability, Journal of American Statistical Association 95 (451), 989-992. [ Links ]
Lawless, J. F. and Kalbfleisch, J. D. (1996). Statistical analysis of warranty claims data, in: W. R. Blischke and D. N. P. Murthy, eds. Product Warranty Handbook, Marcel Dekker, chapter 9. [ Links ]
Lawless, J. F. and Kalbfleisch, J. D. (1992). Some issues in the collection and analysis of field reliability data, Survival analysis: state of the art, pp. 141-152. [ Links ]
Lawless, J. F. and Nadeau, C. (1995). Some simple robust methods for the analysis of recurrent events, Technometrics 37 (2), 158-168. [ Links ]
Lindsey, J. K. (1997). Applying generalized linear models, Springer. [ Links ]
Meeker, W. Q. and Escobar, L. A. (1998). Statistical methods for reliability data. John Wiley and Sons. [ Links ]
Wu, H. and Meeker, W. Q. (2002). Early detection of reliability problems using information from warranty databases. Technometrics 44 (2), 120-133. [ Links ]