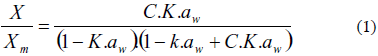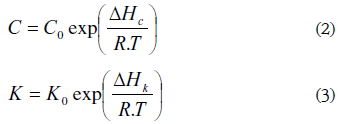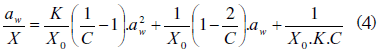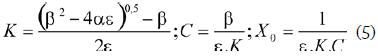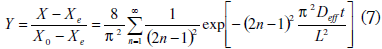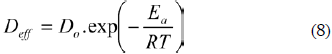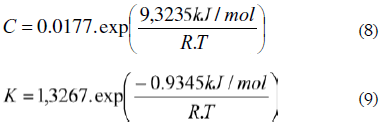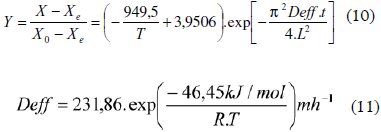Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista EIA
Print version ISSN 1794-1237
Rev.EIA.Esc.Ing.Antioq no.5 Envigado Jan./June 2006
MODELO CINÉTICO DEL SECADO DE LA PULPA DE MANGO
Aquiles Ocampo1
1 Ingeniero Químico Ph.D. Investigador EIA. Grupo de investigación GPC -Gestión de la Productividad hacia la Competitividad-, EIA. investigar@eia.edu.co.
Artículo recibido 26-V-2006. Aprobado 16-VI-2006
Discusión abierta hasta noviembre 2006
RESUMEN
El propósito de este trabajo fue encontrar un modelo que permitiera predecir el tiempo de secado de la pulpa de mango (Mangifera indica) con diferentes condiciones de temperatura. Se construyó un secador de laboratorio en el que se llevaron a cabo pruebas de secado a temperaturas de 55 °C, 60 °C y 65 °C, con una velocidad de aire constante de 2,0 m/s y una humedad relativa controlada de 50%. Se presenta un procedimiento sencillo que convierte el modelo de GAB en una ecuación polinomial de segundo orden. Igualmente, se muestra una manera simple aplicable a procesos similares de secado para establecer su cinética a partir de modelos simplificados de la ecuación clásica de Fick.
PALABRAS CLAVE: Secado; ecuación de GAB; modelos de secado; cinética de secado.
ABSTRACT
The aim of this work was to find a model which allows predicting the drying time of mango (Mangifera indica) pulp at different temperature conditions. A laboratory dryer was built in which several drying probes at 55 °C, 60 °C, and 65 °C took place, with a constant air velocity of 2,0 m/s and a 50% controlled relative humidity. A simple procedure to convert GAB model to a second order polynomial equation is shown. Also, it is shown a simple manner to establish process drying kinetics that could be applied to similar processes from simplified models of the classical Fick's equation.
KEY WORDS: Drying; GAB equation; drying models; drying kinetics.
INTRODUCCIÓN
El mango (Mangifera indica) es originario del sur de Asia y es una de las más conocidas frutas tropicales. Se conocen más de 500 variedades entre las que se encuentra la Tommy Atkins, una de las que más se cultivan comercialmente en Colombia. Se produce en tierras ubicadas entre los paralelos 25 N y 25 S y a alturas hasta de 1.000 metros sobre el nivel del mar, con una producción anual que oscila entre 28 y 67 toneladas por hectárea (Morton, 1987).
Esta fruta puede ser considerada como estratégica para la economía colombiana. Durante el año 2002, Colombia produjo 143.000 toneladas de mango que tenían en los mercados externos un valor aproximado de 150 millones de dólares, de los cuales exportó solamente 285.000 dólares, según CCI (2003). De acuerdo con la FAO, en el año 2002, la producción mundial de mango fue de 25,7 millones de toneladas, lo que representa el 36% de la producción de frutas tropicales. En el año 2004, Colombia realizó exportaciones por valor de 625.000 dólares, según datos presentados por el Ministerio de Agricultura y de Desarrollo Rural.
El secado es una operación que tiende a reducir el contenido de humedad de un producto y que se lleva a cabo por lo general mediante aire caliente. La deshidratación es una técnica adecuada para preservar los productos agrícolas y a la vez para reducir los costos de empaque, transporte y almacenamiento. Consiste en remover la humedad, lo cual impide el crecimiento de bacterias y hongos que deterioran la calidad del alimento (Holdsworth, 1986). Aunque el proceso de secado es más rápido a medida que sea mayor la temperatura, todos los materiales orgánicos son sensibles a la temperatura, más que todo en sus propiedades organolépticas y su valor nutricional.
La escogencia adecuada de un sistema de secado es importante para la productividad de una empresa procesadora de alimentos secos. El elevado costo de los combustibles, sumado a su elevado consumo por la ineficiencia de los procesos de secado, ha conducido no solamente a utilizar fuentes alternativas de energía, como la solar, sino al desarrollo de modelos que permitan alcanzar las mejores condiciones de proceso.
El establecimiento de modelos de secado permite no solo predecir el mejor proceso, sino que también ofrece herramientas para predecir las condiciones de almacenamiento y empaque. Además, ayudan a establecer el contenido final de humedad de los productos agrícolas y los requisitos energéticos del proceso de secado (Telis-Romero et al., 2005).
La mayoría de los modelos de secado se basan en las condiciones de equilibrio entre el material o adsorbente y el agua o adsorbato. Para ello se requiere definir las isotermas de desadsorción que dependen de su capacidad de retener la humedad, variable que se determina por medio de la actividad del agua. Las isotermas de desadsorción describen el comportamiento de la actividad del agua a una temperatura definida y a diferentes contenidos de humedad en condiciones de equilibrio.
Se define la actividad del agua (aw) como la relación entre la presión de vapor del agua, cuando el material alcanza el equilibrio a la temperatura indicada, y la presión de vapor del agua a la misma temperatura. Iglesias y Chriffe (1982) presentan una serie de isotermas de adsorción y desadsorción encontradas por vía experimental para algunos alimentos.
Este trabajo investigativo ofrece un modelo matemático que predice el comportamiento del secado del mango, basado ante todo en la aplicación de la ecuación clásica de Fick, pero simplificada a condiciones unidimensionales y con algunas otras simplificaciones matemáticas permitidas para el caso particular al que se aplica el modelo.
PRESENTACIÓN DE LOS MODELOS MATEMÁTICOS
La complejidad de los procesos de adsorción, sobre todo en materiales orgánicos, hace difícil el ajuste de las isotermas de desadsorción a un modelo definido. Según Bell y Labuza (2000), el modelo que más se ajusta en la simulación del secado de alimentos es el GAB, generado por los investigadores Guggenheim, Anderson y de Boer (1966) y presentado formalmente por Van der Berg (1981). Este modelo es una extensión de los modelos clásicos de Langmuir y el BET propuesto por Brunauer, Emmett y Teller (1938), aplicados para el efecto a la desadsorción en multicapa de materiales fibrosos.
La ecuación (1) presenta el modelo de GAB.
Donde X es el contenido de agua en base seca en kg de agua/kg de sólido seco del adsorbente; Xm es el contenido de agua en base seca correspondiente a una monocapa; C y K son constantes para una temperatura dada, pero a la vez son dependientes de la energía de enlace (calor de adsorción) resultante de las fuerzas de interacción entre la molécula de agua y la superficie adsorbente del material en estudio, por lo tanto, son dependientes de la temperatura; están relacionadas por las ecuaciones (2) y (3).
Donde ΔHc y ΔHk son funciones del calor de adsorción del agua; C0 y K0 son constantes que dependen del material adsorbente; R es la constante universal de los gases ideales y T es la temperatura absoluta.
Para la determinación de los valores de C, K y Xm la mayoría de los autores realizan una correlación no lineal; sin embargo, Labuza (2002) reorganizó la ecuación (1) como un polinomio de segundo orden y obtuvo la ecuación (4).
Un ajuste de los datos experimentales por medio de una correlación binomial permite obtener la solución que se muestra en la ecuación (5).
Donde α, β y ε son los coeficientes de la ecuación (4), cuyo valor numérico se encuentra a partir de la correlación respectiva.
El modelo de secado para la mayoría de los materiales se basa en la ecuación clásica de Fick, expresada en una dimensión por la ecuación (6).
Donde X es el contenido de humedad en base seca; t es el tiempo; x es la longitud y Deff es el coeficiente de difusión efectivo de la humedad en el sólido.
Esta ecuación se resuelve en forma analítica para la difusión del agua en un sólido en una dimensión y se obtiene la ecuación (7), (Crank, 1975).
Donde Y es un número adimensional que representa el contenido de humedad del sólido, X0 es el contenido de humedad inicial en base seca; Xe es la humedad de equilibrio en base seca; t es el tiempo de secado y Les el espesor del material que se seca.
MATERIALES Y MÉTODOS
Se utilizaron muestras de mango de la variedad Tommy Atkins proveniente de Conservas del Trópico, con un grado de maduración promedio correspondiente a un contenido de sólidos solubles de 8° Brix, azúcares totales de 17,5% y pH de 3. El mango fue pelado y cortado en trozos de más o menos 0,8 cm de espesor para todos los experimentos de desadsorción y de secado.
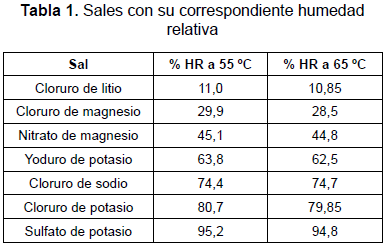
Las isotermas de desadsorción se realizaron a temperaturas de 55 °C y 65 °C. El desarrollo experimental se realizó acorde con la metodología propuesta por Bell y Labuza (2000), consistente en dejar equilibrar una muestra del mango con peso y humedad conocidos en un recipiente hermético que contiene un vaso con una solución saturada de una sal de humedad relativa conocida; la muestra se dejó durante unas siete semanas hasta llegar a peso constante. La tabla 1 presenta las sales utilizadas y su correspondiente humedad relativa reportada por los mismos autores Bell y Labuza.
Los experimentos de secado se realizaron en un secador de laboratorio construido localmente, y sometido a supervisión permanente durante el tiempo de secado para mantener constantes las condiciones establecidas en cada caso.
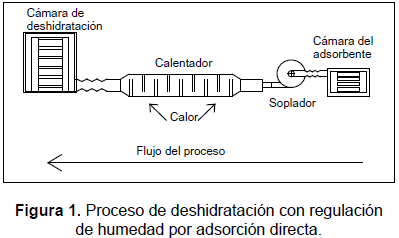
El sistema de secado está compuesto por una cámara de deshidratación, un calentador, un soplador industrial de velocidad regulable y una cámara de adsorción, tal como se muestra en la figura 1. La cámara de deshidratación es un recipiente de poliestireno, que contiene una serie de cinco bandejas enmalladas, en las cuales se deposita el mango. El aire es impulsado a un intercambiador donde se le aumenta la temperatura con un calentador de gas. El intercambiador contiene en su interior paletas o barreras que obligan al aire a recorrer un trayecto en zigzag. La cámara de adsorción contiene una serie de bandejas enmalladas en las cuales se deposita un adsorbente que regula la humedad del aire utilizado en el secado.
Las bandejas miden 38 cm x 36,5 cm y cada una tiene una capacidad aproximada de 550 g de pulpa fresca. Las cinco bandejas tienen una capacidad aproximada de deshidratación por lotes de 2,7 kg de mango fresco.
La cámara de deshidratación se observa en la figura 2.
La figura 3 presenta el montaje realizado para esta prueba.
RESULTADOS Y DISCUSIÓN
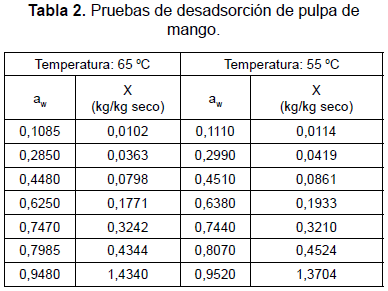
La tabla 2 muestra los resultados obtenidos en las pruebas de desadsorción para muestras representativas de pulpa de mango que se realizaron utilizando las siete sales referidas, con dos temperaturas.
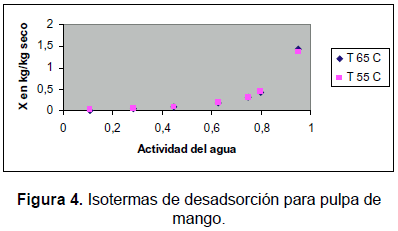
Estos valores son similares a los reportados por Telis-Romero et al. (2005), también obtenidos para pulpa de mango, pero de otra variedad. La figura 4 muestra las isotermas de desadsorción obtenidas a las dos temperaturas anteriores en donde puede observarse que prácticamente coinciden, al igual que sucede con las de Tellis-Romero et al.
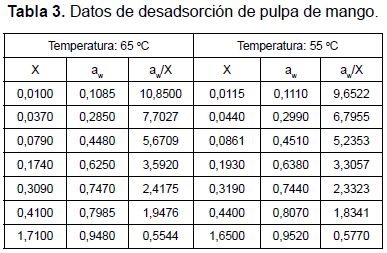
A estos resultados obtenidos en el proceso de desadsorción se les aplicó el procedimiento sugerido por el profesor Labuza (2002), que se mostrará en forma detallada a continuación para facilitar su comprensión. Los datos se presentan reorganizados en la tabla 3.
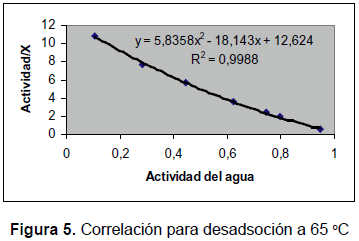
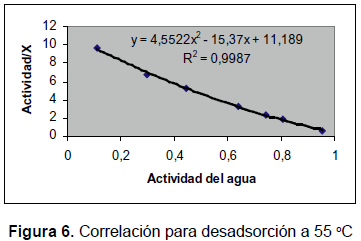
Las figuras 5 y 6 fueron obtenidas con los datos anteriores mediante la aplicación de una correlación polinomial de segundo orden disponible en Excel. Se le incluye la ecuación de segundo orden para facilitar el cálculo de los valores de C y K de la ecuación de GAB. Los coeficientes de correlación muestran el ajuste de estos datos con el modelo de GAB.
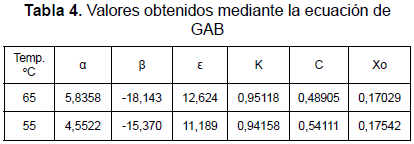
Para completar el estimativo del valor de los parámetros Co y Ko del modelo de GAB para la pulpa de mango, se aplicaron las ecuaciones 2 y 3 para llegar a los siguientes resultados: Xo = 0,1725; Co = 0,0177; ΔHc = 9,3233 kJ/mol; Ko = 1,3267 y ΔHK = - 0,9345 kJ/mol. Estos resultados difieren un poco de los reportados por Telis-Romero et al., pero esto es entendible por tratarse de una variedad diferente.
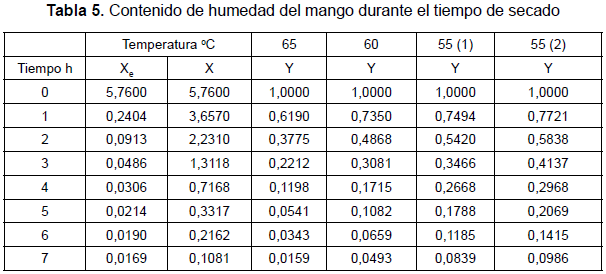
Para la obtención del modelo cinético del proceso de secado, se realizaron pruebas de secado a tres temperaturas diferentes (55, 60 y 65) °C, conservando constantes la humedad relativa del aire a 50% y su velocidad a 2,0 m/s. El mango tenía un contenido promedio de humedad inicial de 85,2%, y se realizaron mediciones de pérdida de peso a intervalos de una hora hasta completar un período de siete horas. La tabla 5 presenta los resultados de los valores calculados de X en kg de agua por kg de mango seco e incluye además los valores de equilibrio obtenidos mediante la aplicación de la ecuación de GAB con los parámetros encontrados en la tabla 4. El valor de Y corresponde a la expresión del lado izquierdo de la ecuación 4, y X0 al contenido de agua inicial, el cual fue de 5,76 kg de agua por kg de mango seco. Es de anotar que se presentan los resultados de dos pruebas independientes realizadas a 55 °C.
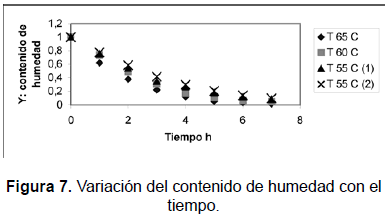
La figura 7 muestra la variación con el tiempo de la variable Y adimensional que está asociada al contenido de humedad de la pulpa de mango.
Los datos anteriores deben ajustarse a la ecuación (7) mediante la aplicación de una correlación no lineal. Sin embargo, otros autores (Vega et al., 2005) han realizado simplificaciones adicionales a dicha ecuación y han logrado modelar su proceso de secado.
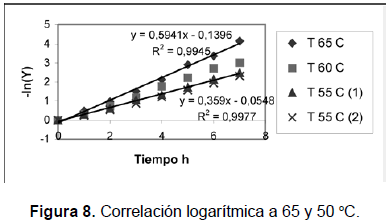
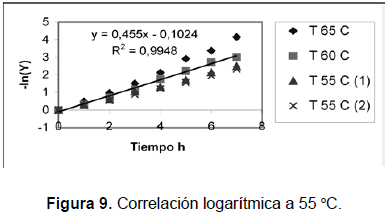
La primera aproximación que se hace acá, siguiendo la misma metodología, es suponer que el único término que tiene significación en el tiempo es el primer término de la sumatoria. De ser así, una gráfica logarítmica de Y contra el tiempo deberá dar una línea recta para cada una de las temperaturas tratadas. Esto se logra de manera satisfactoria, como puede observarse en las figuras 8 y 9.
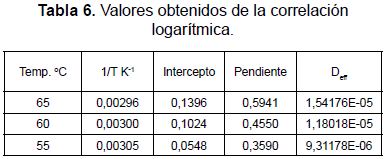
Las correlaciones encontradas se presentan en la tabla 6 para efectos de simplificación del modelo.
Tanto el intercepto como la pendiente varían con la temperatura. El primero corresponde a la simplificación que se hizo cuando se despreciaron los términos de la sumatoria; y el segundo, a la variación del coeficiente de difusión con la temperatura. La dependencia del intercepto podría ser polinómica, resultante del desarrollo en serie de los términos exponenciales. La dependencia de la pendiente, asociada a la energía, ha sido propuesta por Vega et al. (2005), y se ajusta a la ecuación (8).
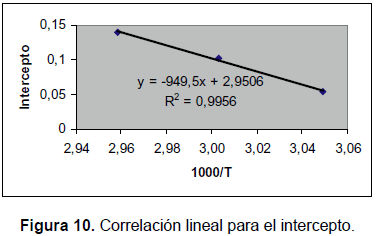
La figura 10 muestra que una correlación lineal es apropiada para el intercepto, indicando que solo se requieren dos términos del desarrollo en series de Taylor.
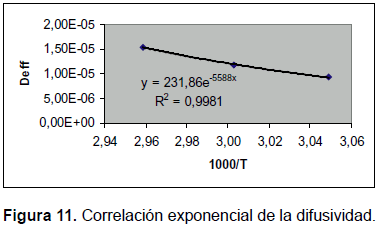
La pendiente de las gráficas anteriores o su correspondiente Deff se ajusta a una correlación exponencial tipo Arrhenius, como se muestra en la figura 11. De ahí se pueden encontrar los siguientes valores: Do = 231,86 m2h-1 y Ea = 46,459 kJ/mol.
El paso siguiente es demostrar que el modelo encontrado simula efectivamente el proceso de secado de la pulpa de mango. A continuación se presenta dicho modelo para la variedad de mango Tommy Atkins sometido a diferentes temperaturas de secado a una velocidad de aire de 2,0 m/s y una humedad relativa de 50%.
El modelo GAB presentó los resultados dados en las ecuaciones (8) y (9).
El modelo cinético de secado se resume en las ecuaciones (10) y (11) que equivalen a las ecuaciones (7) y (8), respectivamente.
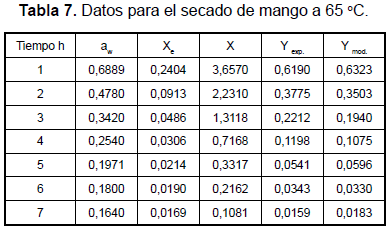
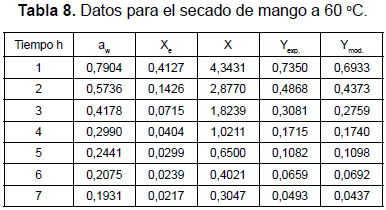
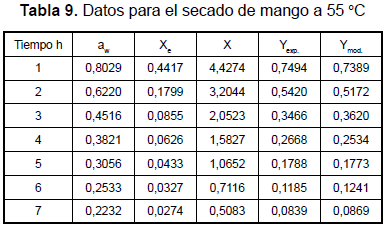
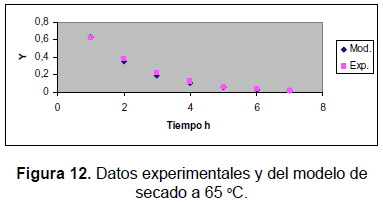
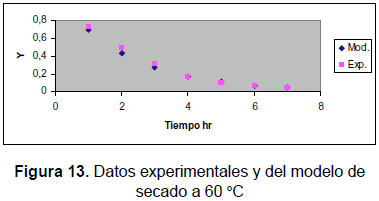
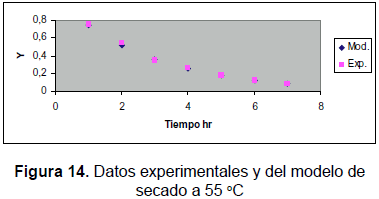
Las tablas 7, 8 y 9 muestran los valores obtenidos en el proceso experimental y los obtenidos con el modelo cinético desarrollado durante este trabajo. Se muestran también las figuras 12, 13 y 14, que permiten apreciar lo apropiado del modelo.
CONCLUSIÓN
Por medio de un desarrollo experimental se encontró que la desadsorción de la pulpa de mango se ajusta muy bien a la ecuación de GAB. El proceso cinético del secado de la pulpa de mango puede ser modelado a partir del modelo de Crank (1975), simplificado al considerar solamente el primer término de la sumatoria, más los dos primeros términos del desarrollo en serie de los primeros términos restantes. La construcción de modelos como el propuesto es importante para predecir el tiempo de secado con temperaturas diferentes a las usadas en este trabajo.
RECONOCIMIENTOS
El autor reconoce el apoyo brindado por Colciencias para la realización de este estudio mediante la cofinanciación del proyecto "Deshidratación de pulpa de mango por medio de una bomba calórica que utiliza energía solar". También agradece a las entidades Conservas del Trópico y Escuela de Ingeniería de Antioquia, participantes en este proyecto. Finalmente hace un reconocimiento del valioso aporte de Juan David Sánchez, Julián Esteban Castro y Y uliana María O sorio, estudiantes de Ingeniería Industrial en la Escuela de Ingeniería de Antioquia quienes participaron en la ejecución de parte de los experimentos realizados para este trabajo.
BIBLIOGRAFÍA
BELL, L. N. y LABUZA, T. P. (2000). Moisture sorption: practical aspects of isotherm measurement and use. 2 ed. Saint Paul, MN: Eagan Press, 122 p. [ Links ]
BRUNAUER, S.; EMMETT, P. H. y TELLER, E. (1938). Adsorption of gases on multilayer. J. Amer. Chem. Soc., vol. 60, pp. 309-319. [ Links ]
CORPORACIÓN COLOMBIA INTERNACIONAL (CCI). (2003). Perfiles del mercado No. 19. [ Links ]
CRANK, J. (1975). The mathematics of diffusion. Pergamon Press. Oxford. [ Links ]
FAO. (2003). http://www.fao.org/DOCREP/MEETING/004/Y1982S.html. [ Links ]
GUGGENHEIM, E. A. (1966). Application of statistical mechanics. Clarendon Press. Oxford. [ Links ]
HOLDSWORTH, S. D. (1986). Concentration and drying of food. Elsevier, London, pp. 293-303. [ Links ]
IGLESIAS, H. A. y CHRIFFE, J. (1982). Water sorption parameters for food and food components. En: Handbook of Food Isotherms. Academic Press, New York. [ Links ]
LABUZA, T. (2002). IFT Short course: Water activity and sorption isotherms. University of Minnesota. http://www.wateractivity.org/LabuzaIFT2002.pdf. [ Links ]
MINISTERIO DE AGRICULTURA Y DE DESARROLLO RURAL. COLOMBIA. (2005). http://www.agrocadenas.gov.co/frutales/reportes/exp_prd_16.pdf. [ Links ]
MORTON, Julia. (1987). Fruit of warm climates. Creative Resources Winterville, N.C. [ Links ]
TELIS-ROMERO, J.; KOHAYAKAWA, M. N.; SILVEIRA, V.; PEDRO, M. A. M. y GAVAS, A. L. (2005). Enthalpyentropy compensation based on isotherms of mango. Cienc. Tecnol. Aliment. V25, No. 2, Campinas, Brasil. [ Links ]
VAN DEN BERG, C. (1981). Vapor sorption equilibria and other water-starch interactions: a physico-chemical approach. Doctoral thesis. Wageningen, The Netherlands: Agricultural University. [ Links ]
VEGA, A.; ANDRÉS, A. y FITO, P. (2005). Modelado de la cinética de secado del pimiento rojo (Capsicum annuum L. cv Lamuyo). Inf. Tecnol. V. 16, n.6. La Serena, Chile. [ Links ]