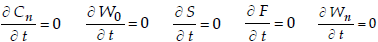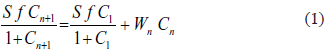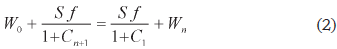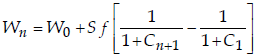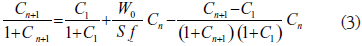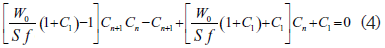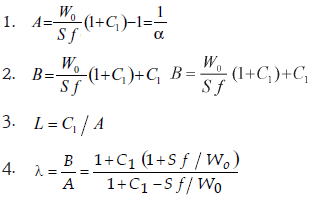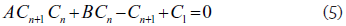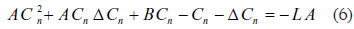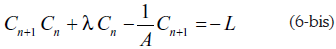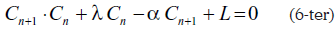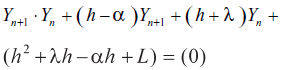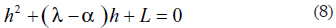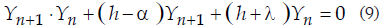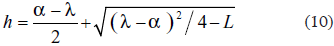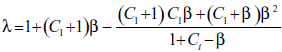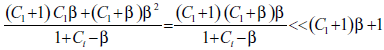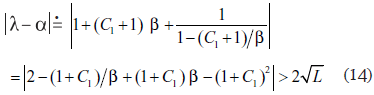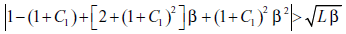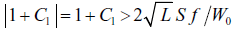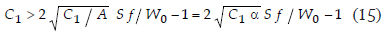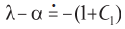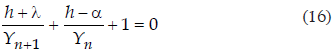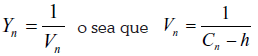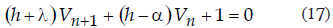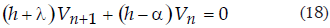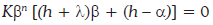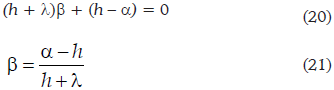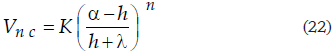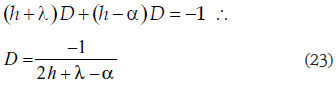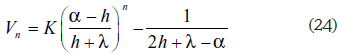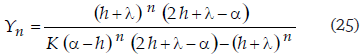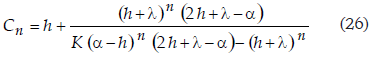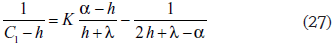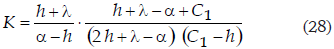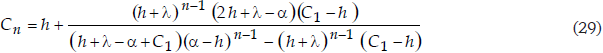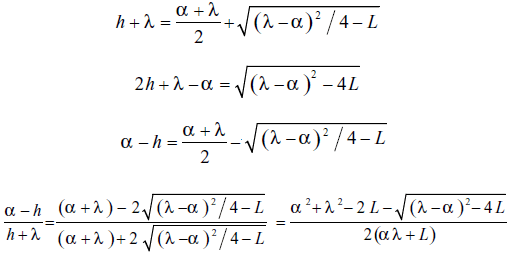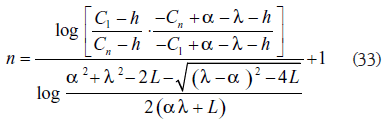LA ECUACIÓN EN DIFERENCIAS FINITAS DE RICCATI EN EL CÁLCULO DE BATERÍAS DE EXTRACTORES

Gabriel Poveda*

* Ingeniero Químico e Ingeniero Electricista, Doctor en Ingeniería (Honoris Causa) y Profesor Emérito, Universidad Pontificia Bolivariana. Profesor investigador, Escuela de Formación Avanzada, Universidad Pontificia Bolivariana. gabriel.poveda@upb.edu.co.

Artículo recibido 11-VIII-2006. Aprobado 22-XI-2006
Discusión abierta hasta junio de 2007

RESUMEN

Este trabajo presenta lo siguiente: 1) Un resumen del proceso de extracción de ácido fosfórico partiendo de roca fosfórica, por extracción con ácido sulfúrico diluido, en una batería de tanques en contracorriente; 2) un balance de masa para el P₂O₅ que lleva a una ecuación de Riccati en diferencias finitas, la que rige el incremento en concentración de ácido (Cn) en el enésimo tanque; 3) se resuelve la ecuación con las condiciones iniciales (técnicas) y las restricciones entre parámetros (económicas), y se obtiene la función explícita C_n = F(n); 4) tomando la inversa F^-1(C_n) = n se encuentra el número exacto de tanques necesarios, suficientes y de costo mínimo que se requieren. Se evitan los largos e imprecisos métodos que enseñan los textos usuales de Operaciones Unitarias.

PALABRAS CLAVE: Ecuaciones en diferencias finitas; Riccati, Jacobo Vicente; extracción; extractores; ácido fosfórico.

ABSTRACT

This document exposes: 1) A brief reminder of the process for the extraction of phosphoric acid from phosphoric rock by extraction with dilute sulfuric acid in a battery of Dorr thickeners in counter current; 2) a mass balance for P₂O₅ leads to a Riccati finite differences equation which governs the enrichment in acid concentration (C_n) in the tank number n; 3) the solution of the equation with technical initial conditions and economic restrictions gives the explicit function C_n = F(n); 4) the inverse function F^-1(C_n) = n gives the necessary, sufficient, and most economic number of tanks. No need of graphic, approximate methods neither of trial-and-error, as Unit Operations textbooks teach usually.

KEY WORDS: Finite differences equations; Riccati, Jacopo Francesco; extraction; extractors; phosphoric acid.

INTRODUCCIÓN

Este artículo resultó de un proyecto minero e industrial que se le pidió preparar al autor, ingeniero químico, cuando ejercía como consultor independiente, para producir ácido fosfórico (H₃PO₄) a partir de roca fosfórica (o fosforita o fosfato tricálcico natural) existente en un municipio del Tolima, en la cordillera Central de Colombia.

El autor sabe que algunos buenos ingenieros lectores conocen qué es la ecuación de Riccati. Pero sabe también que otros -quizás la mayoría- no la han estudiado u olvidaron cómo se resuelve¹. Por eso aquí se presenta dicha ecuación y se la resuelve con algún detalle, seguramente en beneficio de numerosos lectores.

Se propone con este trabajo cumplir los siguientes propósitos:

1. Mostrar un caso concreto y realista donde una herramienta matemática que no es muy conocida resulta ser un buen instrumento para proyectar procesos industriales y operaciones de ingeniería química.
2. Hacer ver a los "matemáticos puros" que su ciencia es más el producto de la realidad que lo que ellos piensan y que, por eso, es mucho más útil de lo que ellos imaginan para la humanidad del común.
3. Subrayar el hecho incontestable de que los profesores de matemáticas en las escuelas de Ingeniería no pueden ser totalmente desconocedores de todo lo que es la tecnología del mundo de hoy y que, por lo menos, deben entender bien el lenguaje técnico de los ingenieros.
4. Divulgar y propender por el uso más amplio de esta ecuación diferencial entre ingenieros en ejercicio y estudiantes de Ingeniería. Ella tiene numerosas aplicaciones en el estudio de circuitos eléctricos, operaciones unitarias (como destilación y evaporación), electroquímica, confiabilidad de máquinas y otras disciplinas muy útiles para ingenieros de varias denominaciones.
5. Enseñar cómo encontrarla donde no se le espera y cómo resolverla a los lectores que les interese, pero que no la conozcan.
6. Mostrar cómo usar métodos matemáticos rigurosos donde antes se usaban métodos de tanteo, reglas empíricas o decisiones intuitivas. Este trabajo permitió determinar muy exactamente el tamaño óptimo del proyecto y hacer economías apreciables en la inversión que requirió.

El proyecto minero-industrial mencionado se realizó y comenzó a producir ácido fosfórico como fertilizante agrícola y para elaborar superfosfatos (otros fertilizantes fosfóricos). Pero a los pocos años, la política oficial vigente desde 1990 de aranceles ínfimos y de tasa de cambio adversa a los productores y exportadores de los productos colombianos obligó a sus dueños a suspender la producción y a pasar a importar el ácido fosfórico.

EL PROCESO Y SUS VARIABLES TÉCNICAS

En la obtención de ácido fosfórico, (H₃PO₄) que es soluble en agua, a partir de roca fosfórica, la roca es triturada y sometida a lavados en una batería de extractores a contracorriente². El material entra a la batería como suspensión que se deja decantar en un espesador Dorr. El lodo que se retira del espesador contiene el ácido, el cual ha de extraerse por lavado a contracorriente con agua en una batería de extractores Dorr en cascada. Como primer paso en la determinación del proceso de la obtención óptima, se requiere una expresión matemática para la concentración de ácido en el lodo que se retira del último espesador. En este cálculo consideramos que el lodo que se retira del fondo de cada unidad Dorr contiene f kg de líquido por kg de sólidos inertes. Se supone que la concentración de ácido en el líquido embebido en los lodos es igual a la que tiene en la solución decantada de rebose en cada tanque, y que la batería opera en condiciones estacionarias.

Para determinar la variación de la concentración de ácido en la solución al pasar de un extractor a otro consecutivo y la concentración de ácido en el último extractor en función del número de los que componen la batería, adoptemos la siguiente nomenclatura:

C_n: kg de ácido/kg agua en el efluente del enésimo espesador, contado (numerado) a partir del que está en el extremo diluido de la batería (figura 1). En consecuencia, las concentraciones son números sin dimensiones físicas y son positivas. Además, por razones técnicas y económicas son menores que la unidad (1,00 ó 100%).

W₀: rata (caudal) de adición de agua pura al sistema, en el primer tanque, en kg/h.

S: rata (o caudal ponderal) de flujo de sólidos inertes, en kg/h.

f: kg de líquido que llevan los lodos/kg de sólidos inertes en ellos.

n: número natural de cada unidad: n=1 para el último espesador en el extremo diluido de la cascada.

W_n: rata de flujo de agua pura en la solución que rebosa del enésimo tanque, en kg/h.

Figura 1

La condición de operación estacionaria quiere decir que son nulas todas las siguientes derivadas parciales

El principio físico fundamental que interviene en esta operación unitaria, típica de las del conjunto llamado de transferencia de masa, es el de la conservación de la masa, que el ingeniero químico expresa en un balance de materiales. En ausencia de reacciones químicas, este balance puede hacerse para cada especie química de las que entran en la operación, que en este caso, evidentemente, son: el ácido fosfórico (soluto), el agua (solvente) y los sólidos inertes. Como en el problema los sólidos inertes no intervienen propiamente en la transferencia de masa, se establecen los balances de material sólo para el ácido y el agua, sobre el conjunto de unidades extractoras, desde la primera hasta la enésima. En la figura 1 el conjunto escogido se ha aislado del mundo exterior por una frontera imaginaria esquematizada por un rectángulo, a trazos discontinuos.

El detalle del balance del ácido es:

• Ácido que entra al sistema disuelto en el líquido que llevan los lodos procedentes de la unidad (n+1): S fC_n+1/(1+C_n+1).
• Ácido que sale del sistema con el líquido de los lodos retirados del primer tanque: S fC₁/(1+C₁).
• Soluto que sale del sistema en el efluente retornado del tanque n al (n+1): W_nC_n.

La ecuación que expresa este balance es:

El detalle del balance de agua es:

Agua suministrada al sistema: W₀

Agua que entra al sistema en el lodo del tanque (n+1): S f/(1+C_n+1)

Agua que sale del sistema en el lodo del primer tanque: S f/(1+C₁)

Agua que sale del sistema en el efluente retornado del tanque n al (n+1): W_n

y la ecuación que lo expresa es

Los balances se han hecho con las cantidades de materiales que fluyen por el sistema en unidad de tiempo, precisamente por la condición de operación estacionaria, condición que para nuestro propósito es necesaria y que en la práctica industrial es la usual.

DEDUCCIÓN DE LA ECUACIÓN

Eliminando W_n entre las ecuaciones (1) y (2) obtendremos una ecuación en C_n+1 y C_n. De la ecuación (2) se tiene

que, introducida en la ecuación (1) y por simplificación por S f da

Racionalizando esta ecuación, desarrollando los productos y reagrupando términos, se obtiene:

Esta ecuación relaciona las concentraciones de ácido en los extractos de dos unidades Dorr consecutivas. Llamando

la ecuación (4) puede escribirse brevemente

y haciendo C_n+1 - C_n = ΔC_n, como es usual en la teoría de funciones de variable discreta (n), la ecuación (5) se transforma en

Se reconoce inmediatamente que la ecuación (6) es una ecuación en diferencias finitas de segundo orden no lineal de la variable C_n como función de la variable discreta n.

La ecuación (5) en diferencias finitas y su equivalente, la (6), es una ecuación no homogénea y no lineal que corresponde al tipo de ecuaciones llamado de Riccati.

La solución de estas ecuaciones de Riccati se encuentra en algunos buenos textos de Ecuaciones Diferenciales. Conviene primero escribirla como

o como

para ponerla en la forma llamada canónica de Riccati.

Haciendo el cambio de variable

se logra anular en (6-ter) el término constante, porque se obtiene

y en esta última ecuación se puede imponer la condición de que

con lo cual la ecuación (7) se convierte en

y h vale

(La otra solución para h no se toma en cuenta, porque sería muy cercana a L o sería un número complejo del tipo k₁ + ik₂, siendo i=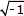, lo que para este problema no es utilizable).

Siendo h un número real, según la definición que ya se le dio, para que la solución que se busca sea real, es necesario que

En la realidad de un proceso como éste, el transporte de agua que acarrean los lodos es mucho menor que el suministro de agua pura al sistema en el primer tanque, lo cual se expresa en la desigualdad S f << W₀, o sea, S f/W₀ << 1 y además la solución que sale del primer espesador debe ser muy diluida: C₁ < 1, para recuperar lo máximo del ácido fosfórico, por consideraciones económicas.

Estas últimas son condiciones prácticas y obvias en el diseño de la planta y son necesarias para lograr una recuperación satisfactoria de ácido extraído de la roca.

Ahora bien, dado que C₁ es mucho menor que 1, puede aceptarse la aproximación de λ según la fórmula

en donde b designa la expresión S f/W₀ ≡ β y donde es β << 1. Usando el algoritmo de Euclides para dividir polinomios se obtiene

Pero, dado que β << 1:

Entonces

con aproximación muy cercana.

Ya se vio que

y, por lo tanto,

Multiplicando ambos lados de la desigualdad por b se tiene

y puesto que β - S f/W₀ << 1 (del orden de 0,1 o menos), se tiene que

de tal manera que la concentración de ácido fosfórico en el líquido desechado con los lodos del primer espesador tiene que cumplir la desigualdad

De lo contrario, el parámetro h no encontraría valores reales sino complejos o antitécnicos.

Según las ecuaciones (12-bis) y (13) se obtuvo ya que

por lo tanto, además de ser real, el parámetro h es negativo (observar la ecuación (10)).

Dividiendo la ecuación (9) por Y_n+1·Y_n, tenemos

en la cual efectuamos un nuevo cambio de variable

que da lugar a la ecuación

la cual ya es una ecuación en diferencias finitas lineal, no homogénea, de primer orden y con coeficientes constantes. Es bien sabido que este tipo de ecuaciones tiene una solución general que es la suma de dos partes: la solución de la ecuación reducida correspondiente

que se llama parte complementaria; y una función dependiente del término de inhomogeneidad, que se llama solución particular.

SOLUCIÓN DE LA ECUACIÓN

La solución de la ecuación reducida de primer orden, con coeficientes constantes (17), como se sabe, es de la forma

en donde K es una constante, por lo pronto arbitraria, y b es otra constante que, aunque indeterminada por ahora, debe satisfacer la ecuación (18). Sustituyendo la (19) en la (18), se tiene

de donde

Como h < 0 y a < 0, pero | a | > | h | y también | h | > | λ |, tal como puede comprobarse observando sus correspondientes expresiones, se deduce que (a - h) < 0 y que también (h + λ) < 0, razón por la cual β > 0. La solución complementaria de la ecuación (17) es, pues,

La búsqueda de la solución particular (V_n^*) se simplifica en este caso, porque el término de inhomogeneidad es constante: -1; y, como es sabido, la solución particular también será constante:

y su sustitución en la ecuación (17) nos permite calcularla

que es también positiva.

La solución general de la ecuación (17) es, entonces,

de la cual obtenemos Y_n:

y también se obtiene la concentración de ácido en el enésimo tanque de sedimentación

Aún es necesario evaluar la constante indeterminada K; y puede hacerse aplicando la ecuación (24) al tanque de la batería señalado con n = 1, cuyas condiciones de operación vienen a constituir algo así como lo que en la teoría de ecuaciones diferenciales se denomina una condición inicial: para n = 1, C_n = C₁ Y_n = C₁ - h V_n = 1/(C₁ - h). Basta esta única condición, porque la ecuación en diferencias finitas (17) es de primer orden. Se tiene así que

de donde

Finalmente, obtenemos que

siendo:

El significado de C₁ ya se definió.

La ecuación (29) obtenida es la que da la concentración en el enésimo tanque de la batería, en función del ordinal n y de la concentración C1 que se admite para el extracto residual efluente del 1° (en el extremo diluido):

y puede verse que esta función es positiva para todo n entero positivo, y creciente con el número n de extractores que ha recorrido el extracto (C_n+1 > C_n), tal como debe serlo de acuerdo con el fenómeno físico particular que interpreta. Es decir, la concentración de ácido fosfórico en el líquido que lo extrae va aumentando al pasar de un tanque Dorr al siguiente. El aumento de concentración en el enésimo tanque es ΔC_n; no debe perderse de vista que dicha función no es continua, pues la variable independiente n es variable discreta. La concentración aumenta discontinuamente de cada tanque espesador al siguiente.

Número de tanques

La obtención de las funciones inversas de (29), o sea

puede resultar laboriosa por la forma como aparece C₁ en las expresiones definidas por h y λ. Puesto que en el diseño general de la batería es importante el cálculo del número de unidades necesarias para reducir la concentración desde un cierto valor inicial (C_n) hasta un valor final prescrito (C₁), dados ambos por las condiciones de trabajo que se impongan al sistema, es interesante expresar el número de unidades de la batería en función de tales concentraciones, es decir, establecer la función explícita (32). Basta para ello despejar n de la ecuación (29) para obtener:

Utilizando las ecuaciones (29) y (33) y mediante cómputo tabular, puede trazarse una familia de curvas C_n contra C₁ con n como parámetro variable de la familia, que puede emplearse también como solución gráfica del sistema funcional formado por las ecuaciones (30), (31) y (32), solución que puede ser ampliamente utilizada para resolver otros problemas del diseño de la planta.

Este es un problema que se presenta, como ya se dijo, en la obtención de ácido fosfórico de los lodos resultantes del tratamiento de rocas fosfóricas trituradas con ácido sulfúrico y en muchas otras industrias con proceso de extracción.

Su estudio, además del interés teórico que por sí mismo presenta la cuestión, y tal como se ha hecho, permite calcular previamente algunos resultados importantes de esta operación.

CONCLUSIONES

1. El autor no ha visto ninguna aplicación, en Colombia o en América Latina, de este método de la ecuación de Riccati en diferencias finitas a ningún problema colombiano de Ingeniería (Química, Eléctrica, Civil, Mecánica, etc.).
2. Para calcular baterías de extractores sólido-líquido a contracorriente no son necesarios ni muy convenientes los métodos aproximados (gráficos o numéricos) que presentan nuestros textos usuales de Operaciones Unitarias de Ingeniería Química.
3. Es preciso enseñar, de modo sistemático, el tema de las ecuaciones en diferencias finitas, en general, y la de Riccati en especial, en las escuelas de Ingeniería Química. Actualmente, no se hace así en 10 de las 11 que hay en Colombia.
4. Por ser exacto, este método produce importantes economías de capital en la construcción de baterías de extractores.
5. La ecuación de Riccati en diferencias finitas es aplicable también a torres de destilación (de platos), a evaporadores múltiples, a series de filtros, a otros equipos comunes al ingeniero químico y a varios tipos de circuitos eléctricos conocidos en Ingeniería Eléctrica.

_____________________________
NOTAS
1 El autor ha sido por muchos años (más de 25) profesor de Ecuaciones Diferenciales en varias universidades del país y ha introducido allí el estudio de esta ecuación. Por eso sabe que en varias de ellas no se enseñaba antes; que en 10 de las 11 facultades colombianas de Ingeniería Química no se la enseña aún, y que esto mismo ocurre en la mayoría de los casi mil programas universitarios de ingeniería de distintas denominaciones que hay en el país. Este no es, pues, un tema fútil ni elemental.
2 Al hablar de "ácido fosfórico", en rigor, nos referimos al contenido del ion P₂O₅ en los líquidos.

BIBLIOGRAFÍA COMENTADA

Libros de matemáticas que tratan (poco o medianamente) sobre la ecuación en diferencias finitas de Riccati (son muy pocos).

Mickens, Ronald E. Difference Equations. Theory and Applications. New York: Van Nostrand Reinhold, 1990. 448 p.         [ Links ] Es el único que trata la ecuación de Riccati en diferencias finitas, la ordinaria y la de diferencias parciales entre los libros de 20 grandes bibliotecas en Colombia, varias de ellas universitarias. En las ecuaciones de Riccati ordinarias, distingue las generalizadas (inhomogéneas) de las reducidas (homogéneas). Presenta los dos únicos métodos conocidos para resolverlos. No muestra ninguna aplicación a la Ingeniería Química ni a ningún otro tema de tecnología. El autor ha consultado a 20 profesores universitarios de Matemáticas, de Circuitos Eléctricos y de Operaciones Unitarias (donde tiene aplicaciones posibles e importantes) y ninguno conoce este libro ni otro sobre la ecuación de Riccati en diferencias finitas, ni sobre sus aplicaciones tecnológicas, como la de este artículo.

Boole, George. A Treatise on the Calculus of Finite Differences. New York: Dover, 1960.         [ Links ] Dedica media página (p. 223) a esta ecuación sin llamarla "de Riccati". Solo da un método para resolverla; omite el otro; no da la solución general. No presenta ninguna aplicación tecnológica ni matemática; no trata la de varias variables.

Brand, Louis. Differential and Difference Equations. New York: Wiley, 1966.         [ Links ] Trata someramente la ecuación. Da sólo un método para resolverla; omite el otro método conocido; no da ejemplos técnicos.

Jenson. V. G. y Jeffreys, G. V. Métodos Matemáticos en Ingeniería Química. Madrid y Barcelona: Alhambra, 1979. 595 p.         [ Links ] En dos páginas (370 y 372) presenta la ecuación de Riccati en diferencias finitas y un método para resolverla (no el otro que hay) y da un ejemplo bien traído de una torre de destilación de platos. No trata la generalizada ni la de varias variables.

Marshall Jr., W. Robert and Pigford, Robert L. The Application of Differential Equations to Chemical Engineering Problems. Newark: University of Delaware Press, 1960. 170 p. En la página 79 presenta la ecuación y uno solo de los dos métodos que hay para resolverla. Resuelve un problema de absorción y otro de destilación fraccionada pero ninguno de extracción.         [ Links ]

Pearson, Carl. Handbook of Applied Matematics. New York: Van Nostrand Reinhold.         [ Links ] Es un libro casi enciclopédico en su tema, en un tomo, bastante extenso (1307 páginas). Dedica 5 renglones a esta ecuación. No da ejemplos técnicos.

Spiegel, Murray R. Calculus of Finite Differences and Difference Equations. New York: Mc Graw-Hill, 1971. 259 p.         [ Links ] En la página 181 resuelve un único problema de la ecuación de Riccati en diferencias finitas reducida, sin darle ese nombre, y por uno solo de los dos métodos conocidos (Problema 5.43). Es un problema analítico. No muestra aplicaciones; no trata el caso generalizado ni el de varias variables.

Página de Internet "Riccati Difference Equations".

http://www.math.uri.edu/kulenm/diffequaturi/chad442/project.htm. Visitada el 4 de noviembre de 2006.         [ Links ] Trata de aspectos puramente matemáticos de la ecuación; no menciona que tiene aplicaciones técnicas.

Artículos sobre aplicaciones técnicas de la ecuación de Riccati en diferencias finitas

Poveda Ramos, Gabriel. Las Ecuaciones en Diferencias Finitas en la Teoría de los Circuitos Eléctricos. En: Revista de la Academia Colombiana de Ciencias Exactas, Físicas y Naturales. Bogotá         [ Links ].

Libros sobre diferencias finitas o ecuaciones en diferencias finitas que no tratan sobre la ecuación de Riccati en diferencias finitas

Batchelder, Paul M. An Introduction to Linear Difference Equations. New York: Dover, 1967.         [ Links ]

Godounov, Sergei et Riabenki, Victor. Schemas aux Differences. Moscú: Mir, 1973. 357 p.         [ Links ]

Goldberg, Samuel. Introduction to Difference Equations. New York: John Wiley and Sons, 1968. 260 p.         [ Links ]

Jordan, Charles. Calculus of Finite Differences. New York: Chelsea, 1965.         [ Links ] Es ya un clásico en su tema. Muy extenso (654 páginas).

Levy, H. and Lessman, F. Finite Difference Equations. New York: The Macmillan, 1961. 277 p.         [ Links ] También muy conocido y extenso.

Miller, Keneth S. Difference Equations. New York: W. A. Benjamin, 1968.         [ Links ]

Miller, Keneth S. An Introduction to the Calculus of Finite Differences and Difference Equations. New York: Dover, 1960.         [ Links ]

Libros didácticos (renombrados) de operaciones unitarias que no tratan la ecuación de Riccati en diferencias finitas ni ninguna aplicación a estas tecnologías

Brown, George G. (Ed.). Unit Operations. New York: John Wiley and Sons, 1975. 609 p.         [ Links ]

Kirkbride, Charmel G. Chemical Engineering Fundamentals. New York: Mc. Graw-Hill, 1980.         [ Links ]

McCabe, Warren L. and Smith, Julian C. Unit Operations of Chemical Engineering. New York: Mc. Graw-Hill, 1967. 1007 p.         [ Links ]

Vilbrandt, Frank C. and Dryden, Charles E. Chemical Engineering Plant Design. New York: Mc. Graw-Hill, 1958.         [ Links ]

Walker, William H.; Lewis, Warren L. and McAdams, William H. (5 ed). New York and London: Mc Graw-Hill, 1978. 854 p.         [ Links ]