Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista EIA
Print version ISSN 1794-1237On-line version ISSN 2463-0950
Rev.EIA.Esc.Ing.Antioq no.11 Envigado Jan./June 2009
APLICACIÓN DEL DISEÑO DE EXPERIMENTOS PARA EL ANÁLISIS DEL PROCESO DE DOBLADO
DESIGN OF EXPERIMENTS APPLICATION FOR BENDING PROCESS ANALYSIS
APLICAÇÃO DO DESENHO DE EXPERIMENTOS PARA A ANÁ LISE DO PROCESSO DE DOBRA
GIOVANNI PÉREZ*, MARTÍN DARÍO ARANGO**, YULIANA AGUDELO***
* Ingeniero Administrador, Universidad Nacional de Colombia; Magíster en Desarrollo, Universidad Pontificia Bolivariana. Profesor Asociado e investigador del Grupo de Investigación y Consultoría Organizacional (GICO), Universidad Nacional de Colombia. Medellín, Colombia. gperez@unalmed.edu.co
** Ingeniero Industrial, Universidad Autónoma Latinoamericana. Doctor Ingeniero Industrial, Universidad Politécnica de Valencia, España. Profesor Asociado y director del Grupo GICO, Universidad Nacional de Colombia. Medellín, Colombia. mdarango@unalmed.edu.co
*** Ingeniera Industrial, Universidad Nacional de Colombia. Ingeniera, Melco de Colombia. Medellín, Colombia. yagudelr@unalmed.edu.co
Artículo recibido 13-XI-2008. Aprobado 27-VII-2009
Discusión abierta hasta diciembre de 2009
RESUMEN
El artículo expone un estudio realizado sobre el proceso de doblado en una empresa, para determinar qué factores tienen efecto sobre las dimensiones (longitud y ángulo de doblado) de las piezas de metal obtenidas. Acorde con la metodología de Diseño de Experimentos se desarrolla este estudio, para el cual se consideraron cuatro factores (operario, dobladora, material y grosor del material), cada uno con dos niveles que fueron seleccionados de manera aleatoria de una población de posibles niveles. Dos réplicas se tomaron para cada combinación de tratamientos. Las corridas experimentales se hicieron de modo aleatorio para garantizar la ausencia de sesgo en la recolección de los datos. Con lo anterior se realizaron en total 32 corridas experimentales, correspondientes a 32 datos de longitud y 32 datos de ángulo, considerando todas las posibles combinaciones. El análisis de los resultados muestra que las dimensiones de las piezas dobladas fluctúan. Para la longitud de doblado, se encontró que existe variabilidad en la población de niveles de los factores Dobladora y Grosor y en la interacción Dobladora*Operario; respecto al ángulo de doblado, se encontraron variaciones en la población de niveles de los factores Operario y Grosor y la interacción Operario*Grosor. En síntesis, el proceso de doblado presenta variaciones considerables que pueden ser preocupantes a la hora de requerir mucha precisión para un proceso de ensamble posterior.
PALABRAS CLAVE: proceso de doblado; longitud de doblado; ángulo de doblado; dimensiones; Diseño de Experimentos.
ABSTRACT
The paper shows a study made about the bending process in a company, to define which factors have an effect on the dimensions (bending length and bending angle) of the metal pieces obtained. The study develops according to Design of Experiments methodology. For this study, four factors were considered (operator, bending machine, sheet material, sheet thickness) at two levels each factor. Levels were chosen at random from a variety of possible levels; two replicates were taken for each treatment combination. Experimental runs were made at random to ensure absence of systematic error in data obtaining. There were made 32 experimental runs representing 32 bending length data and 32 bending angle data with all possible combinations of factor levels. The data analysis shows that dimensions of bended pieces change. Relating the bending length, there are variability in levels of the factors Bending Machine and Thickness, and in the interaction Bending Machine*Operator. Considering bending angle, there are variability in levels of the factors Operator and Thickness and the interaction Operator*Thickness. In brief, bending process presents considerable variations that can be worrying when requiring great accuracy for a later assembly process.
KEY WORDS: bending process; bending length; angle length; dimensions; Design of Experiments.
RESUMO
O artigo expõe um estudo realizado sobre o processo de dobra em uma empresa, para determinar os fatores que têm efeito sobre as dimensões (comprimento e ângulo de dobra) das peças de metal obtidas. Acorde com a metodologia de Desenho de Experimentos se desenvolve este estudo, para o qual se consideraram quatro fatores (operário, máquina de dobra, material e espessura do material), cada um com dois níveis que foram selecionados de maneira aleatória de uma população de possíveis níveis. Duas repetições se tomaram para cada combinação de tratamentos. As corridas experimentais se fizeram de modo aleatório para garantir a ausência de erro sistemático na colheita dos dados. Com o anterior se realizaram no total 32 corridas experimentais, correspondentes a 32 dados de comprimento e 32 dados de ângulo, considerando todas as possíveis combinações. A análise dos resultados amostra que as dimensões das peças dobradas oscilam. Para o comprimento de dobrado, se encontrou que existe variabilidade na população de níveis dos fatores Maquina de Dobra, Espessura e na interação Maquina de Dobra*Operário; respeito ao ângulo de dobra, se encontraram variações na população de níveis dos fatores Operário e Espessura e na interação Operário*Espessura. Em síntese, o processo de dobra apresenta variações consideráveis que podem ser preocupantes na hora de requerer muita precisão para um processo de montagem posterior.
PALAVRAS-CÓDIGO: processo de dobrado; comprimento de dobrado; comprimento do ângulo; dimens ões; Desenho de Experimentos.
1. INTRODUCCIÓN
El Diseño de Experimentos es una herramienta que permite planear una prueba o serie de pruebas para obtener conclusiones válidas y objetivas acerca de los procesos, a partir del análisis de los datos recolectados. En el campo de la ingeniería, el Diseño de Experimentos cumple un papel importante en los procesos de manufactura en diversos aspectos, incluyendo la mejora y desarrollo de procesos y el diseño de nuevos productos. En general, en la actualidad se requieren procesos óptimos en términos de la menor variabilidad, con el fin de garantizar calidad (Montgomery, 2001).
El Diseño de Experimentos que se presenta se aplica en una empresa manufacturera, con el fin de analizar el doblado de las láminas de metal que allí se procesan y determinar cuáles son los factores que influyen en sus dimensiones. Considerando que el proceso de doblado es el que genera más devoluciones de calidad en el nivel interno en la empresa estudiada, se realiza un análisis que permita posteriormente efectuar mejoras en dicho proceso y con ello disminuir los reprocesos de materia prima, el tiempo y los costos que ellos implica.
El estudio se realizó considerando los factores determinantes: el operario, la maquinaria y las caracter ísticas de la pieza para doblar (grosor y material), que resultaron del análisis causa-efecto y de una lluvia de ideas, en la que participaron los operarios, los supervisores y el jefe de Ingeniería responsables de dicho proceso.
2. PROCESO DE DOBLADO
En la manufactura de las piezas que componen el acabado de los ascensores, se requiere un proceso de laminado para conformar las láminas de metal. Éste es el proceso de doblado, que se efectúa, de acuerdo con las rutas de producción en la planta de la empresa considerada en el estudio, después del proceso de corte. De igual forma, las piezas que son dobladas, pasan a procesos posteriores como el de ensamble por medio de soldadura o pegado estructural.
El proceso de doblado puede definirse como la deformación plástica de una lámina de metal con respecto a una línea recta. En dicho proceso existen variables asociadas a las piezas procesadas (OSU, 2008):
Ri : radio interno de doblado
Ro: radio externo de doblado
Rm: radio de superficie media
Rp: radio de golpe o impacto
Rd: radio del dado o matriz
C: amplitud
Wd: amplitud media del dato
Rn: radio neutral de doblado circular
T: grosor de la lámina
El proceso de doblado se efectúa mediante prensas o dobladoras mecánicas y digitales, en las cuales pueden modificarse los datos empleados, a fin de variar las formas producidas. De igual manera, la preparación y calibración previa de los instrumentos de medición, como el goniómetro y pie de rey, son responsabilidad de los operarios, garantizando la precisión y exactitud en las mediciones. Para este caso fueron calibrados los diferentes instrumentos, antes de iniciar la fase experimental.
3. PLANTEAMIENTO DEL PROBLEMA
En la planta de producción las piezas de cada proceso se catalogan según cuatro grados de calidad.
Grado 1: Pieza que cumple con las especificaciones
Grado 2: Pieza que no cumple con las especificaciones, pero es útil funcionalmente
Grado 3: Pieza que no cumple con las especificaciones, pero puede ser reprocesada
Grado 4: Pieza que no cumple con las especificaciones.
El proceso de doblado es el que presenta mayores devoluciones en la planta por motivo de calidad, es decir, el que genera el mayor número de piezas grado 3 y grado 4.
De conformidad con los requisitos de algunas piezas para los procesos de ensamble, no se permiten ni las más mínimas variaciones. De otro lado, algunas piezas sí toleran pequeñas variaciones del orden de 1 mm como máximo.
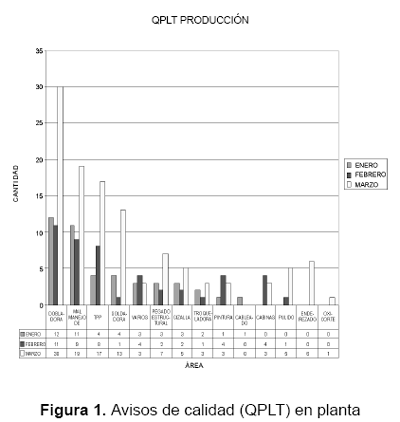
Según la información que suministra la figura 1, el proceso de doblado fue el responsable del 27,27 % de los avisos de calidad en el mes de enero, del 23,40 % en febrero y del 26,08 % en marzo.
Esto ocasiona gran impacto en la producción, debido a que se generan pérdidas de tiempo, dinero y materia prima. Tiempo en el caso de piezas catalogadas como grado 3, que requieren procesos adicionales para corregir los defectos dimensionales; dinero en términos de las horas-hombre que ello implica; materia prima en el caso de los rechazos definitivos o grado 4, que no pueden ser reprocesados.
3.1 Selección de factores y niveles
Para la ejecución del experimento se seleccionaron aleatoriamente dos niveles de cada factor, a saber:
- 2 prensas o dobladoras de tres posibles → Dobladora 2 y dobladora 3.
- 2 operarios de 9 posibles → Diego Parra (DP) y Libardo Oquendo (LO).
- 2 grosores de material de 12 posibles → 0,8 mm y 1 mm.
- 2 tipos de material de 5 posibles ® Acero laminado en frío o cold roll y acero galvanizado.
Factor A: Dobladora i=1, 2 a=2
Factor B: Operario j=1, 2 b=2
Factor C: Material k=1, 2 c=2
Factor D: Grosor del material l=1, 2 d=2
Se realizaron dos réplicas para cada combinación m=1, 2 n=2
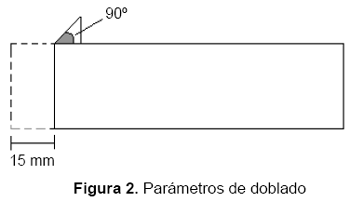
Para la recolección de los datos se estableció que las piezas fueran dobladas transversalmente una longitud de 15 mm a un ángulo de 90º, y según estos parámetros ambos operarios doblaron retales de láminas en los dos materiales seleccionados (acero cold roll y acero galvanizado) con los grosores especificados (0,8 mm y 1 mm) y en cada una de las dos dobladoras (2 y 3), tal como se muestra en la figura 2.
De esta forma se obtuvieron los datos para las dos variables respuesta medidas: longitud de doblado y ángulo de doblado, las cuales se midieron usando pie de rey y goniómetro.
3.2 Selección de la variable respuesta
Como se especificó, las dimensiones de las piezas dobladas se describen por la longitud y el ángulo de doblado. Luego, se tienen dos variables respuesta para analizar.
Yijklm = Longitud de doblado obtenida en la dobladora i, por el operario j, sobre la lámina de metal con material k y grosor l, en la réplica m.
Zijklm = Ángulo de doblado obtenido en la dobladora i, por el operario j, sobre la lámina de metal con material k y grosor l, en la réplica m.
3.3 Elección del diseño experimental
El objetivo del estudio es determinar si los factores elegidos para la experimentación realmente tienen efecto sobre las variables respuesta al igual que las interacciones entre éstas, pero el interés del estudio se centra en el análisis de la variabilidad del modelo para determinar los factores que ejercen mayor influencia sobre las variaciones dimensionales de las piezas dobladas.
Se plantea un diseño 24 con efectos aleatorios, es decir, un diseño con cuatro factores a dos niveles cada uno, en el cual los niveles de los factores fueron seleccionados aleatoriamente de una población de posibles niveles. Se cree conveniente el uso de un diseño 2k , debido a que proporciona el menor número de corridas experimentales en las que los cuatro factores pueden estudiarse en un diseño factorial completo. Además este tipo de diseño reduce los costos de la experimentación.
Modelo

Para i = 1, 2; j=1, 2; k=1, 2; l=1, 2; m=1, 2
Donde:
Yijklm: Variable aleatoria que representa la longitud de doblado de la pieza procesada en la i-ésima dobladora por el j-ésimo operario, correspondiente al k-ésimo material con el l-ésimo grosor para la m-ésima réplica.
Zijklm: Variable aleatoria que representa el ángulo de doblado de la pieza procesada en la i-ésima dobladora por el j-ésimo operario, correspondiente al k-ésimo material con el l-ésimo grosor para la m-ésima réplica.
μ: Media global para cada modelo.
τi: Efecto de la i-ésima dobladora sobre la media global.
βj: Efecto del j-ésimo operario sobre la media global.
δk: Efecto del k-ésimo material sobre la media global.
λl: Efecto del l-ésimo grosor sobre la media global.
(τβ)ij: Efecto combinado de la i-ésima dobladora y el j-ésimo operario sobre la media global.
(τδ)ik: Efecto combinado de la i-ésima dobladora y el k-ésimo material sobre la media global.
(τλ)il: Efecto combinado de la i-ésima dobladora y el l-ésimo grosor sobre la media global.
(βδ)jk: Efecto combinado del j-ésimo operario y el k-ésimo material sobre la media global.
(βλ)jl: Efecto combinado del j-ésimo operario y el l-ésimo grosor sobre la media global.
(δλ)kl: Efecto combinado del k-ésimo material y el l-ésimo grosor sobre la media global.
(τβδ)ijk: Efecto combinado de la i-ésima dobladora, el j-ésimo operario y el k-ésimo material sobre la media global.
(τβλ)ijl: Efecto combinado de la i-ésima dobladora, el j-ésimo operario y el l-ésimo grosor sobre la media global.
(βδλ)jkl: Efecto combinado del j-ésimo operario, el k-ésimo material y el l-ésimo grosor sobre la media global.
(τδλ)ikl: Efecto combinado de la j-ésima dobladora, el k-ésimo material y el l-ésimo grosor sobre la media global.
(τβδλ)ijkl: Efecto combinado de la i-ésima dobladora, el j-ésimo operario, el k-ésimo material y el l-ésimo grosor sobre la media global.
εijklm: Error experimental aleatorio asociado a la i-ésima dobladora, el j-ésimo operario, el k-ésimo material, el l-ésimo grosor en la m-ésima réplica.
3.4 Realización del experimento
Principios básicos
- Réplicas. Datos que fueron obtenidos al realizar el experimento con las mismas condiciones. En el estudio del proceso de doblado se tomaron dos réplicas para cada combinación de los niveles de los factores; esto para obtener una estimaci ón del error experimental.
- Aleatorización. Las corridas experimentales fueron realizadas de manera aleatoria para evitar sesgo por condiciones particulares en la experimentación.
- Bloqueo. En el experimento no se realizó bloqueo, debido a que el interés era obtener informaci ón acerca de todos los factores planteados y no se poseía suficiente información acerca de un factor particular que pudiera o debiera bloquearse para reducir el error experimental.
4. ANÁLISIS DE LOS DATOS
Para contar con conclusiones válidas en el análisis obtenido sobre los datos, es pertinente validar los modelos estadísticamente (W alpole y Myers, 1999). Con relación a los modelos, se cumplieron los supuestos de normalidad, independencia y varianza constante de los residuales para las variables respuesta longitud de doblado y ángulo de doblado. Los datos se analizaron con el softw are MIN ITAB (Viles, 2008) y se presentan en la tabla 1.
4.1 Variable respuesta longitud de doblado
- Análisis de varianza (tabla 1) ANOVA
Factores principales
Factor: Dobladora
Con una confianza del 95 %, se concluye que existe variabilidad en la población de niveles del factor Dobladora y que, por ende, es un factor determinante y que genera variaciones en las dimensiones de las piezas dobladas en la planta.
Factor: Operario
Como VP>α=0,05, no existe evidencia estadística suficiente para rechazar la hipótesis nula y concluir acerca de la variabilidad en la población de niveles del factor Operario.
Factor: Material
Como VP>α=0,05, no hay evidencia estadística suficiente para rechazar la hipótesis nula y concluir acerca de la variabilidad en la población de niveles del factor Material.
Factor: Grosor
Como VP< α=0,05, se rechaza la hipótesis nula y se concluye con una confianza del 95 % que existe variabilidad en la población de niveles del factor Grosor y que, por consiguiente, es un factor determinante y que genera variaciones en las dimensiones de las piezas dobladas en la planta.
INTERACCIÓN DOBLE
Factor: Dobladora*Operario
Como VP< α=0,05, se rechaza la hipótesis nula y se concluye con una confianza del 95 % que existe variabilidad en la población de niveles del factor combinado Dobladora*Operario, por lo que esta combinación de factores podría ejercer influencia en la longitud obtenida de las piezas dobladas.
Factor: Dobladora*Material
Como VP>α=0,05, no existe evidencia estadística suficiente para rechazar la hipótesis nula y concluir acerca de la variabilidad en la población de niveles del factor combinado Dobladora*Material.
Factor: Dobladora*Grosor
Como VP>α=0,05, no hay evidencia estadística suficiente para rechazar la hipótesis nula y concluir acerca de la variabilidad en la población de niveles del factor combinado Dobladora*Grosor.
Factor: Operario*Material
Como VP>α=0.05, no se tiene evidencia estadística suficiente para rechazar la hipótesis nula y concluir acerca de la variabilidad en la población de niveles del factor combinado Operario*Material.
Factor: Operario*Grosor
Como VP>α=0,05, no existe evidencia estadística suficiente para rechazar la hipótesis nula y concluir acerca de la variabilidad en la población de niveles del factor combinado Operario*Grosor.
Factor: Material*Grosor
Como VP>a=0.05, no existe evidencia estadística suficiente para rechazar la hipótesis nula y concluir acerca de la variabilidad en la población de niveles del factor combinado Material*Grosor.
INTERACCIÓN TRIPLE
Factor: Dobladora*Operario*Material
Como VP>α=0,05, no existe prueba estadística suficiente para rechazar la hipótesis nula y concluir acerca de la variabilidad en la población de niveles de la interacción triple Dobladora*Operario* Material.
Factor: Dobladora*Operario*Grosor
Como VP>α=0,05, no existe evidencia estadística suficiente para descartar la hipótesis nula y concluir acerca de la variabilidad en la población de niveles de la interacción triple Dobladora*Operario* Grosor.
Factor: Dobladora*Material*Grosor
Como VP>α=0,05, no hay prueba estadística suficiente para rechazar la hipótesis nula y concluir acerca de la variabilidad en la población de niveles de la interacción triple, Dobladora*Material*Grosor.
Factor: Operario*Material*Grosor
Como VP>α=0,05, no existe evidencia estadística suficiente para rechazar la hipótesis nula y concluir acerca de la variabilidad en la población de niveles de la interacción triple Operario*Material*Grosor.
INTERACCIÓN CUÁDRUPLE
Factor: Dobladora*Operario*Material*Grosor
Como VP>α=0,05, no hay evidencia estadística suficiente para rechazar la hipótesis nula, por lo cual no se puede concluir acerca de la variabilidad de la interacción de los cuatro factores analizados Dobladora*Operario*Material*Grosor.
4.2 Variable respuesta ángulo de doblado
- Análisis de Varianza (tabla 2) ANOVA
Factores principales
Factor: Dobladora
Como VP>α=0,05, no existe evidencia estadística suficiente para rechazar la hipótesis nula y concluir acerca de la variabilidad en la población de niveles del factor Dobladora.
Factor: Operario
Como VP< α=0,05, se rechaza la hipótesis nula y se concluye con una confianza del 95 % que existe variabilidad en la población de niveles del factor Operario y que, por tanto, es un factor determinante y que genera variaciones en el ángulo de las piezas dobladas en la planta.
Factor: Material
Como VP>α=0,05, no existe evidencia estadística suficiente para rehusar la hipótesis nula y concluir acerca de la variabilidad en la población de niveles del factor Material.
Factor: Grosor
Como VP< α=0,05, se rechaza la hipótesis nula y se concluye con una confianza del 95 % que existe variabilidad en la población de niveles del factor Grosor y que, por ende, es un factor determinante y que genera variaciones en el ángulo de las piezas dobladas en la planta.
INTERACCIÓN DOBLE
Factor: Dobladora*Operario
Como VP>α=0,05, no existe evidencia estadística suficiente para rechazar la hipótesis nula y concluir acerca de la variabilidad en la población de niveles del factor combinado Dobladora*Operario.
Factor: Dobladora*Material
Como VP>α=0,05, no hay evidencia estadística suficiente para rechazar la hipótesis nula y concluir acerca de la variabilidad en la población de niveles del factor combinado Dobladora*Material.
Factor: Dobladora*Grosor
Como VP>α=0,05, no existe evidencia estadística suficiente para rechazar la hipótesis nula y concluir acerca de la variabilidad en la población de niveles del factor combinado Dobladora*Grosor.
Factor: Operario*Material
Como VP>α=0,05, no se cuenta con evidencia estadística suficiente para rechazar la ótesis nula y concluir acerca de la variabilidad en la población de niveles del factor combinado Operario*Material.
Factor: Operario*Grosor
Como VP<α=0,05, se rechaza la hipótesis nula y se concluye con una confianza del 95 % que existe variabilidad en la población de niveles del factor combinado Operario*Grosor, por lo que esta combinación de factores podría ejercer influencia en la longitud obtenida de las piezas dobladas.
Factor: Material*Grosor
Como VP>a=0.05, no existe evidencia estadística suficiente para rechazar la hipótesis nula y concluir acerca de la variabilidad en la población de niveles del factor combinado Material*Grosor.
INTERACCIÓN TRIPLE
Factor: Dobladora*Operario*Material
Como VP>α=0,05, no existe evidencia estadística suficiente para rechazar la hipótesis nula y concluir acerca de la variabilidad en la población de niveles de la interacción triple Dobladora*Operario*Material.
Factor: Dobladora*Operario*Grosor
Como VP>α=0,05, no hay evidencia estadística suficiente para rechazar la hipótesis nula y concluir acerca de la variabilidad en la población de niveles de la interacción triple Dobladora*Operario*Grosor.
Factor: Dobladora*Material*Grosor
Como VP>α=0,05, no existe evidencia estadística suficiente para rechazar la hipótesis nula y concluir acerca de la variabilidad en la población de niveles de la interacción triple Dobladora*Material*Grosor.
Factor: Operario*Material*Grosor
Como VP>α=0,05, no se tiene evidencia estadística suficiente para rechazar la hipótesis nula y concluir acerca de la variabilidad en la población de niveles de la interacción triple Operario*Material* Grosor.
INTERACCIÓN CUÁDRUPLE
Factor: Dobladora*Operario*Material*Grosor
Como VP>α=0,05, no hay evidencia estadística suficiente para rechazar la hipótesis nula, así que no se puede concluir acerca de la variabilidad de la interacción de los cuatro factores analizados Dobladora*Operario*Material*Grosor.
Factor: Dobladora. Análisis de los gráficos de interacción
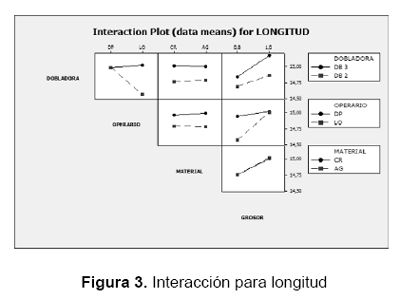
De la figura 3 puede concluirse que las interacciones dobles Dobladora*Operario y Operario*Grosor son significativas para la variable respuesta longitud de doblado, debido a que sus líneas se cortan.
De otro lado, la significación de la interacción Operario*Grosor debe analizarse con más detenimiento, debido a que mediante el análisis de varianza efectuado esta interacción resultó ser estadísticamente no significativa. También puede observarse que:
- El operario DP tiene un mejor desempeño en la dobladora 2, ya que se ajusta al valor de referencia asignado para el experimento (15 mm); el operario LO se desempeña mejor en la dobladora 3, aunque no existe una diferencia significativa respecto al valor obtenido en la dobladora 2.
- Respecto al material usado por los operarios, el mejor ajuste al valor de referencia (15 mm) lo obtiene el operario DP con ambos materiales: cold roll y acero galvanizado.
- Según el grosor empleado, el operario DP tambi én obtuvo el mejor desempeño para la longitud de doblado.
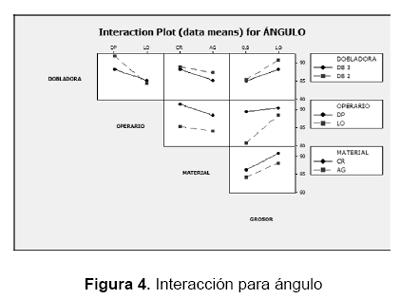
- De la figura 4 puede concluirse que las interacciones dobles Dobladora*Operario, Do bladora* Material y Dobladora*Grosor son significativas para la variable respuesta ángulo de doblado, debido a que sus líneas se cortan.
Sin embargo, la significación de estas interacciones debe ser soportada por pruebas analíticas como el análisis de varianza efectuado, en el que se concluyó que no era significativa de acuerdo con los valores P de la tabla ANOVA.
Analizando el gráfico de interacción Dobladora* Operario, se observa que el valor más aproximado al valor de referencia 90º se obtuvo en la dobladora 3 por el operario DP.
Respecto al operario y al material, se encuentra que el operario DP tiene mejor desempeño que LO con ambos materiales: cold roll y acero galvanizado.
5. CONCLUSIONES
- Según el análisis estadístico efectuado, puede concluirse que efectivamente existe variabilidad en el proceso de doblado de la empresa objeto de estudio, lo que es coherente con los altos porcentajes de avisos de calidad para el primer trimestre del año en la planta de producción.
- De los factores que participaron en el estudio (Dobladora, Operario, Material y Grosor), es importante considerar que, aunque todos ejercen influencia sobre las dimensiones obtenidas en el proceso de doblado, solo los niveles de los factores dobladora y operario podrían modificarse en la planta. El material y el grosor son características de la materia prima que no son susceptibles de ser modificadas.
- Para la variable respuesta longitud de doblado se encuentra que existe variabilidad en la poblaci ón de niveles de los factores Dobladora, Grosor y en la interacción Dobladora*Operario.
- Para la variable respuesta ángulo de doblado, se encuentra que existe variabilidad en la poblaci ón de niveles de los factores Operario y Grosor y en la interacción Operario*Grosor.
- Respecto al desempeño de los operarios comparado con los valores de referencia para las piezas para doblar (15 mm y 90º), puede concluirse que el operario DP obtuvo un mejor desempeño de acuerdo con el material y el grosor de las láminas de metal. Esto tanto para la longitud de doblado como para el ángulo de doblado.
- Garantizar un tamaño de muestra determinado acorde con el nivel de significación deseado muchas veces se ve limitado en el campo, debido a factores económicos y de tiempo, como la disponibilidad de materia prima para efectuar las pruebas experimentales y los paros en la producción para efectuar los ensayos y las mediciones.
- El proceso de doblado de la empresa objeto de esta experimentación debe someterse a un estudio detallado, para determinar los niveles de los factores controlables que permitan reducir la variabilidad al mínimo, debido a las exigencias de precisión del proceso de manufactura que exigen las piezas de los ascensores que se fabrican.
6. RECOMENDACIONES
En aras de modificar los niveles de los factores que influyen en la variabilidad del proceso de doblado y que efectivamente puedan controlarse se proponen las siguientes medidas correctivas:
- Inspeccionar las dobladoras en su mecánica, para asegurar que estén operando correctamente.
- Analizar la posibilidad de inversión de dobladoras digitales. La dobladora 3, por ejemplo, es muy antigua y todos los ajustes deben realizarse de manera manual.
- En el caso de los paños de cabina del ascensor, diseñar un soporte de la longitud del paño para evitar las variaciones que se generan en la actualidad en la longitud de estas piezas.
- El análisis de variabilidad efectuado señaló que el operario DP podría tener un mejor desempeño que LO, por lo que es recomendable analizar el método de cada uno de los 6 operarios que laboran en este proceso y compararlo con el método de trabajo de DP. De esta manera, podría identificarse y unificarse el mejor método y reducir las variaciones dimensionales de las piezas.
- Debido a que los operarios tienen un mejor desempeño en una determinada dobladora, analizar la distribución de turnos para asegurar que la persona que opere una u otra dobladora tenga pleno dominio del proceso en ella.
REFERENCIAS
(1) Montgomery, Douglas C. Design and analysis of experiments. John Wiley & Sons: U.S.A, 2001. [ Links ]
(2) Walpole, R. E. y Myers, R. H . Probabilidad y estadística para ingenieros. Prentice Hall Hispanoamérica, 6a ed., 1999. [ Links ]
(3) Ohio State University. OSU. Bending process overview. (Consulta: 15 abril 2008). Disponible en línea: <URL: http://nsmwww.eng.ohio-state.edu/BendingOverview / html/bending_system.html > [ Links ]
(4) Viles, Elizabeth. Guía de Minitab 4. Septiembre 2004. (Consulta: 16 abril 2008). Disponible en línea: <URL: http://www.tecnun.es/Asignaturas/Estad_ii/Archivos/ Practica/ManualdeMinitab.pdf [ Links ]