Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista EIA
Print version ISSN 1794-1237On-line version ISSN 2463-0950
Rev.EIA.Esc.Ing.Antioq no.12 Envigado July/Dec. 2009
RESOLUCIÓN DEL PROBLEMA DE ENRUTAMIENTO DE VEHÍCULOS CON LIMITACIONES DE CAPACIDAD UTILIZANDO UN PROCEDIMIENTO METAHEURÍSTICO DE DOS FASES
SOLVING THE CAPACITATED VEHICLE ROUTING PROBLEM USING A TWOPHASE METAHEURISTIC PROCEDURE
RESOLUÇÃO DO PROBLEMA DE ROTEAMENTO DE VEÍCULOS COM LIMITAÇÕES DE CAPACIDADE UTILIZANDO UM PROCEDIMENTO METAHEURÍSTICO DE DUAS FASES
Julio Mario Daza*, Jairo R. Montoya**, Francesco Narducci***
* Ingeniero Industrial, Magíster en Ingeniería Industrial. Profesor, Corporación Universitaria de la Costa, Barranquilla, Colombia. juliomariodaza@hotmail.com.
** Ingeniero Industrial. Master of Science in Industrial Engineering and Managment; Doctor en Ingenieria Industrial. Profesor Asociado, Escuela Internacional de Ciencias Económicas y Administrativas, Universidad de La Sabana, Chía (Cundinamarca), Colombia. jairo.montoya@unisabana.edu.co.
*** Ingeniero Industrial, Magíster en Ingeniería Industrial. Ingeniero consultor y docente catedrático, Departamento de Ingeniería Industrial, Universidad del Norte, Barranquilla, Colombia. fnarducci78@hotmail.com.
Artículo recibido 27-VI-2009. Aprobado 18-XI-2009
Discusión abierta hasta junio de 2010
RESUMEN
Este artículo presenta un procedimiento alternativo para resolver el problema de enrutamiento de vehículos con limitaciones de capacidad y flota homogénea (CVRP). Se propone un algoritmo metaheurístico que consta de la combinación de dos fases: diseño de rutas y planificación de la flota. La primera fase está compuesta de procedimientos heurísticos y metaheurísticos donde se construye una solución inicial que es mejorada mediante búsqueda tabú obteniendo soluciones no dominadas en tiempo de cálculo polinomial. Para la segunda fase, correspondiente a la planificación (scheduling) de la flota, se propone abordar el problema partiendo de una analogía con el problema de programación de máquinas paralelas idénticas. Este procedimiento tiene como función objetivo minimizar el costo fijo causado por la utilización de la capacidad instalada. Esta alternativa se aplicó sobre una instancia generada aleatoriamente y una instancia real arrojando resultados significativos al compararse con las heurísticas evaluadas.
PALABRAS CLAVE: problema de ruteo de vehículos; problema del agente viajero; optimización combinatoria; heurístico.
ABSTRACT
This paper presents an alternative procedure to solve the Capacitated Vehicle Routing Problem (CVRP) with homogeneous fleet. The paper proposes a two-phase metaheuristic algorithm: routes design and fleet scheduling. The first phase is based on heuristics and metaheuristics procedures in order to build an initial solution that is then improved using tabu search to obtain non-dominated solutions in polynomial computational time. For the second phase, corresponding to fleet scheduling, the problem is approached using an analogy with the identical parallel machine scheduling problem. This procedure looks for the minimization of the fixed cost of using installed capacity as the objective function. The proposed procedure was tested using both a random-generated instance and real data, giving competitive results in comparison with other heuristics tested.
KEY WORDS: vehicle routing problem; traveling salesman problem; combinatorial optimization; heuristic.
RESUMO
Este artigo apresenta um procedimento alternativo para resolver o problema de roteamento de veículos com limitações de capacidade e frota homogênea (CVRP). Propõe-se um algoritmo metaheurístico que consta da combinação de duas fases: desenho de rotas e planejamento da frota. A primeira fase está composta de procedimentos heurísticos e metaheurísticos onde se constrói uma solução inicial que é melhorada mediante busca tabu obtendo soluções não dominadas em tempo de cálculo polinomial. Para a segunda fase, correspondente ao planejamento (scheduling) da frota, se propõe abordar o problema partindo de uma analogia com o problema de programação de máquinas paralelas idênticas. Este procedimento tem como função objetivo minimizar o custo fixo causado pela utilização da capacidade instalada. Esta alternativa se aplicou sobre uma instância gerada aleatoriamente e uma instância real dando resultados significativos ao se comparar com as heurísticas avaliadas.
PALAVRAS CÓDIGO: problema de roteo de veículos; problema do agente viajante; otimização combinatória; heurístico.
1. INTRODUCCIÓN
El problema de enrutamiento o ruteo de vehículos (VRP, vehicle routing problem) data del año de 1959 y fue introducido por Dantzig y Ramser, quienes describieron una aplicación real de la entrega de gasolina a las estaciones de servicio y propusieron una formulación matemática. Cinco años después, Clarke y Wright propusieron el primer algoritmo que resultó efectivo para resolverlo. Y es así como se dio comienzo a grandes investigaciones y trabajos en el área de ruteo de vehículos.
Este problema puede entenderse como la intersección de dos conocidos problemas de optimización combinatoria. El primero, el del agente viajero (TSP, traveling salesman problem) considerando la capacidad de cada automóvil como infinita (Applegate et al., 2006) y el de empaquetamiento en compartimentos (BPP, bin packing problem) (Martello y Toth, 1990).
Por ende, el problema de enrutamiento de vehículos con limitaciones de capacidad y flota homogénea (CVRP-HF, capacitated vehicle routing problem with homogenous fleet) estudiado se considera un problema de optimización combinatoria y pertenece a la clase de problemas NP-completos, para los que no existe un algoritmo de tiempo polinomial que pueda resolverlos a optimalidad. Esto ha llevado a muchos investigadores a explorar diversos métodos para abordarlos. La mayoría de estos métodos puede ser ampliamente clasificados ya sea como algoritmos "exactos" o "de optimización" (Aarts y Lenstra, 2003).
Los algoritmos exactos son los que producen una solución óptima empleando varias técnicas que permitan explorar el espacio de búsqueda. Estos métodos exactos incluyen los que se basan en técnicas como ramificación y acotamiento, planos cortantes y programación lógica de restricciones. Estos algoritmos son razonablemente eficientes para problemas de tamaño modesto (Ignizio y Cavalier, 1994); aunque con ellos es posible en principio resolver los de cualquier tamaño, en la práctica no es así, debido al gran número de soluciones posibles para cualquier problema de tamaño razonable.
Durante los años sesenta, los investigadores trataban de responder la siguiente pregunta: ¿Existe un algoritmo de optimización con tiempo de ejecución polinomial para un problema como el TSP? Hasta ahora, nadie ha podido encontrar una respuesta a esta pregunta. Sin embargo, Karp (1972) mostró que si la respuesta es "sí" para el TSP, hay también otros problemas difíciles para los cuales podría hallarse un algoritmo polinomial. Como ningún algoritmo se ha encontrado para alguno de estos problemas, Reeves (1996) dice que esto sugiere categóricamente que la respuesta a la pregunta original es "no". Por ello mismo el área de optimización combinatoria resulta cada vez más atrayente para investigadores y académicos, ya que cualquier contribución en este ámbito tiene repercusiones directas en la industria.
En este artículo se propone un procedimiento eficiente basado en técnicas metaheurísticas para resolver el problema de enrutamiento de vehículos con limitaciones de capacidad y flota homogénea, denominado CVRP-HF.
Este artículo está organizado de la siguiente manera. La sección 2 presenta el VRP, sus variantes y su reducción a otros problemas de optimización combinatoria. La sección 3 presenta los métodos de solución utilizados para abordar esta clase de problemas. La sección 4 presenta el planteamiento de la alternativa diseñada para generar una solución factible al problema planteado. Finalmente, se presentan en las secciones 5 y 6 respectivamente la evaluación de desempeño del modelo planteado y las conclusiones.
2. ASPECTOS TEÓRICOS
2.1 Problema de ruteo de vehículos (VRP)
A grandes rasgos un problema de ruteo de vehículos (VRP) consiste en, dado un conjunto de clientes y depósitos dispersos geográficamente y una flota de vehículos, determinar un conjunto de rutas de costo mínimo que comiencen y terminen en los depósitos, para que los vehículos visiten a los clientes máximo una vez. Dentro de esta definición, el problema se ubica en un amplio conjunto de variantes:
CVRP (Capacitated VRP) (Ralphs, Hartman y Galati, 2001)
MDVRP (Multi-Depot VRP) (Hjorring, 1995)
PVRP (Periodic VRP) (Baptista, Oliveira y Zúquete, 2002)
SDVRP (Split Delivery VRP) (Dror, Laporte y Trudeau, 1994; Archetti, Mansini y Speranza, 2001)
SVRP (Stochastic VRP) (Laporte y Louveaux, 1998)
VRPB (VRP with Backhauls) (Ralphs, Hartman y Galati, 2001); Jacobs-Blecha y Goetschalckx, 1992)
VRPPD (VRP with Pick-Up and Delivering) (Righini, 2000)
VRPSF (VRP with Satellite Facilities) (Bard et al., 1997)
VRPTW (VRP with Time Windows) (Cordeau et al., 2002)
2.2 Problema del agente viajero (TSP)
El TSP constituye la situación general y de partida para formular otros problemas combinatorios más complejos, aunque más prácticos, como el ruteo de vehículos y la programación de tareas dependientes del tiempo de alistamiento. En el TSP se dispone de un solo vehículo que debe visitar a todos los clientes en una sola ruta y a costo mínimo. No suele haber un depósito (y si lo hubiera, no se distinguiría de los clientes), no hay demanda asociada a los clientes y tampoco hay restricciones temporales.
Denotaremos por Δ+(i) y Δ-(i) al conjunto de nodos adyacentes e incidentes al nodo i, es decir, Δ+(i) = 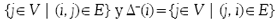 .De manera similar, el conjunto de arcos incidentes hacia el exterior e interior del nodo i se definen como
.De manera similar, el conjunto de arcos incidentes hacia el exterior e interior del nodo i se definen como 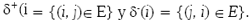
El problema puede formularse matemáticamente mediante programación lineal entera (PLE) como sigue (Clarke y Wright, 1964):
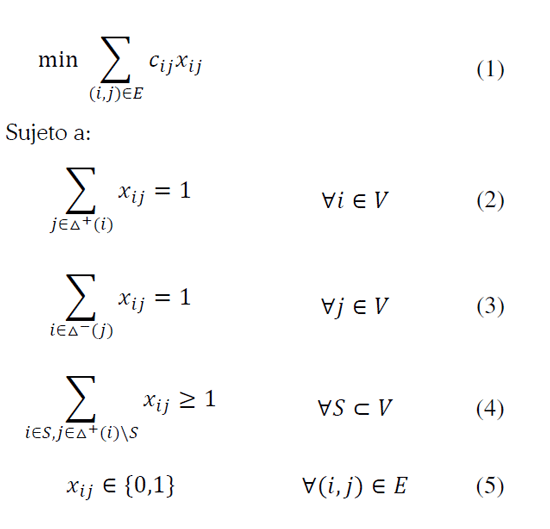
2.3 Complejidad del TSP y aproximaciones
La mayor parte de los problemas de ruteo de vehículos son generalizaciones del TSP. En ese sentido, puede considerarse el VRP más simple. No obstante, pertenece a la clase de problemas NP, debido a que tomando una secuencia cualquiera (certificado) ésta podría ser verificada en tiempo polinomial. Además, este problema puede considerarse del tipo NP-completo lo cual puede comprobarse reduciéndose el problema de optimización a uno de decisión mediante un ciclo hamiltoniano de la siguiente manera: dado un grafo G, ¿es posible determinar una ruta a través de todos los nodos de G una sola vez? (Garey y Johnson, 1979).
El tiempo de cálculo necesario para resolver el TSP se incrementa con rapidez a medida que aumenta el número de ciudades n. En un caso general el número de rutas factibles que debe considerarse es (n – 1)!/2, puesto que hay (n – 1) posibilidades para la primera ciudad después de la ciudad de residencia del agente, (n – 2) posibilidades para la siguiente ciudad y así sucesivamente. El denominador 2 surge porque cada ruta presenta una ruta inversa equivalente con la misma distancia (TSP simétrico). Así, mientras un TSP con 10 ciudades tiene no menos de 200.000 soluciones factibles que deben ser consideradas, un problema con 20 ciudades tiene alrededor de 1016 soluciones factibles, mientras que un problema con 50 ciudades tiene alrededor 1062 (Hillier y Lieberman, 2001).
Las soluciones óptimas a este problema para pequeñas instancias pueden ser encontradas en tiempo razonable (polinomial) mediante programación lineal entera (Nilsson, 2003). Sin embargo, el ser considerado NP-duro ocasiona que no se obtengan para grandes instancias algoritmos (exactos) que encuentren soluciones óptimas en un tiempo polinomial determinístico. Todos estos algoritmos crecen exponencialmente. Podemos disminuir el crecimiento polinómico al problema si establecemos tours cercanos al óptimo. Con esto ganamos velocidad, a costa de la calidad del tour, siendo la velocidad y el encierro una propiedad interesante de las heurísticas para este problema. Hay dos modos de encontrar el tamaño óptimo de una instancia para el TSP. El primero es resolverlo óptimamente encontrando así la longitud. El otro es el cálculo de la cota inferior de Held-Karp (HKLB), que produce un límite inferior para la solución óptima. Esta cota inferior es la norma que se juzga en el rendimiento de un algoritmo de aproximación para el problema (Nilsson, 2003). Además, la HKLB es en la actualidad la solución a la relajación a la PLE en la cual está formulado el TSP. La solución puede encontrarse en el tiempo polinómico usando el método simplex y un algoritmo de separación de restricciones polinomial (Johnson, McGeoch y Rothberg, 1996).
Para resolver el TSP normalmente se utilizan algoritmos de aproximación o heurísticos, la diferencia radica en que éstos nos dan una garantía de cómo podemos obtener malas soluciones. Normalmente especificada como un tiempo c del valor óptimo. El algoritmo de mejor solución existente es el de Arora (1998). El algoritmo garantiza una aproximación de (1+1/c) veces el valor óptimo, para todo c > 1. Esto se basa en partición geométrica y árboles de expansión. Aunque teóricamente c puede ser muy grande, esto tendrá un efecto negativo en su tiempo de corrida (O(n(log2n)O(c) para instancias bidimensionales).
2.3.1 Problema de empaquetamiento en compartimentos (BPP)
El problema consiste en embalar un conjunto de objetos en varias cajas o contenedores tal que el peso o el volumen total no exceda un valor máximo de las cajas. De una manera precisa, definimos un problema de empaquetamiento en compartimentos (BPP, bin packing problem) como sigue. Tenemos un conjunto finito de artículos e cada uno de los cuales tienen un peso w y una restricción de precedencia entre estos, incurriendo en un costo Cij (tal vez infinito). Posteriormente definimos un grupo ordenado para ser un subconjunto de artículos de modo que el peso total del grupo pedido no exceda la capacidad de la caja y ningún costo entre los artículos adyacentes en el grupo sea infinito.
La meta primaria es crear una solución factible con el número mínimo de grupos ordenados. Cuando dos soluciones tienen el mismo número de grupos ordenados, el que posea costo mínimo se escoge. Matemáticamente la formulación del problema puede ser así: dado un conjunto finito de elementos E={e1,…,en} con pesos asociados W={w1,…,wn} tales que 0≤wi≤w(Bin), se divide E en N subconjuntos, de forma que la suma de pesos en cada partición sea a lo sumo w(Bin), teniendo en cuenta que N sea mínimo.
2.3.2 Problema de m agentes viajeros, m-TSP
El problema de los m agentes viajeros o m-TSP es una generalización del TSP en la cual se tienen un depósito y m vehículos o agentes. El objetivo es construir exactamente m rutas, una para cada vehículo o agente, de modo que cada cliente sea visitado una vez por uno de los vehículos o agentes. Cada ruta debe comenzar y terminar en el depósito y puede contener a lo sumo p clientes, esto se determina mediante la solución de BPP. Una formulación mediante PLE, dada por Miller, Tucker y Zemlin (1960) es la siguiente:
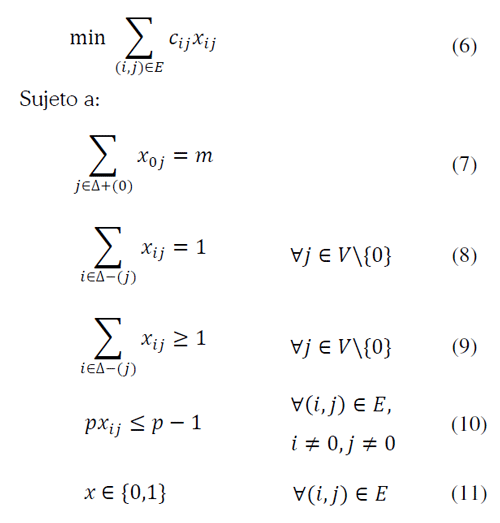
2.3.3 Problema de enrutamiento de vehículos con limitación de capacidades y flota homogénea (CVRP-HF)
Matemáticamente, una instancia I = (G, C, T, D, F) del CVRP-HF se puede definir como una extensión del m-TSP, dado un grafo dirigido G = (V, E), donde V es el conjunto de nodos que representan las ciudades o clientes y E es el conjunto de arcos que los conectan, relacionados con la matriz de costos C = (cij ), de tamaño N x N, de modo que cada arco tiene asignado un costo cij. D es un arreglo de la forma (pi) que especifica la información de demanda de cada cliente. F es un arreglo de la forma (Pk) que contiene los datos de capacidad máxima de los vehículos. La flota está compuesta por M vehículos, es decir, 1 ≤ k ≤ M.
El problema tiene el objetivo de encontrar una matriz X = (xijk), de tamaño N x N x M, donde las variables binarias xijk indican si el arco (i, j) se utiliza en la solución para ser visitado por k. El problema de PLE es como sigue:
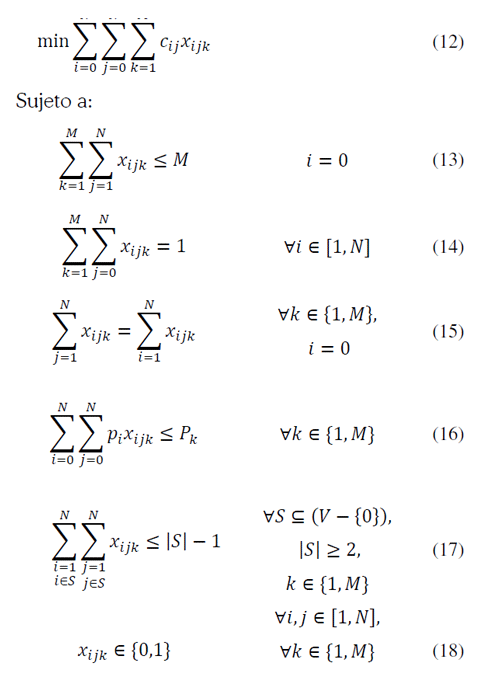
Las restricciones (13) indican que del centro de distribución deben partir máximo M vehículos. Las restricciones (14) y (15) garantizan que uno y solo un vehículo visite y abandone cada cliente formando por cada ruta un TSP. Las ecuaciones (16) muestran restricciones de capacidad vehicular en términos de peso, de acuerdo con lo sugerido por Dantzig y Ramser (1959); determinar el conjunto pi que no sobrepase pk se denomina problema de empaquetamiento en compartimentos (BPP por sus siglas en inglés). Finalmente los conjuntos de restricciones (17) y (18) establecen, respectivamente, la inexistencia de subrutas inconexas y los valores admisibles para las variables de decisión.
2.3.4 Métodos de solución
En la actualidad, la atención se ha centrado más y más en el uso de métodos de optimización combinatoria, debido a la complejidad de estos problemas en la obtención de soluciones óptimas en tiempo polinomial. Estas técnicas se dividen en técnicas de optimización local convencional (heurísticas) y técnicas de optimización local inteligente (metaheurísticas). A diferencia de un enfoque algorítmico "exacto", un método de optimización no tiene una base de matemática formal que lo sustente, es desarrollado más o menos por intuición (Ignizio y Cavalier, 1994).
La idea más genérica del término heurística está relacionada con la tarea de resolver inteligentemente problemas reales usando el conocimiento disponible (Narducci, 2005). Heurística proviene de una palabra griega con un significado relacionado con el concepto de encontrar y se vincula a la supuesta exclamación eureka de Arquímedes al descubrir su famoso principio (De la Cruz, 2003). Reeves (1996) define el término heurística de la siguiente forma: "Una técnica heurística (o simplemente una heurística) es un método que busca buenas soluciones (es decir, soluciones cercanas al óptimo) a un costo computacional razonable sin poder garantizar optimalidad".
Las técnicas heurísticas para el VRP, en general, pueden ser clasificadas dentro de cuatro categorías (Gaskell, 1967), así: constructivas, como el método de los ahorros de Clarke y Wright, con base en el ahorro generado por insertar nuevos clientes en cada vehículo hasta completar una solución final; métodos de agrupar primero, luego enrutar, que agrupan los clientes en varios subconjuntos, asignan cada subconjunto a un vehículo y luego resuelven cada TSP correspondiente (por ejemplo, el método de Fisher y Jaikumar, basado en el problema de asignación generalizado y el algoritmo de barrido de Gillet y Miller); métodos heurísticos de enrutar primero, luego agrupar, que empiezan resolviendo el TSP definido por todos los clientes y luego parten la ruta hallada para asignar un tramo a cada vehículo (como el método de curvas de llenado de Bowerman, Calamai y Brenthall, y el método de partición óptima de Beasley); y finalmente, los métodos de mejoramiento, como los intercambios Or–Opt.
Las metaheurísticas (también llamadas heurísticas modernas) han aparecido durante las últimas dos décadas (Yu, 1998) y tienen como función tomar inicialmente una solución factible, para luego mejorarla usando heurísticas de mejoramiento embebidas en una estructura más general. La característica común de estos enfoques es el uso de mecanismos para evadir óptimos locales (Moraga, 2002). Glover y Laguna (1997) definen el término "metaheurística" como
una estrategia maestra que guía y modifica otras heurísticas para producir soluciones más allá de aquéllas que son normalmente generadas en una solicitud por optimalidad local. Las heurísticas guiadas por tal metaestrategia pueden ser procedimientos de alto nivel o nada más que una descripción de movidas disponibles para transformar una solución en otra, junto con reglas de evaluación asociadas.
Por otra parte, entre las técnicas metaheurísticas para el VRP se encuentran las colonias de hormigas, búsqueda dispersa, algoritmos genéticos y la búsqueda tabú, entre otras. En la figura 1 se puede observar un compendio de las técnicas metaheurísticas utilizadas para resolver los problemas de optimización combinatoria. Se puede observar que se han empleado varias estrategias para resolver el problema, que se pueden agrupar en tres grandes categorías: búsqueda secuencial por entornos (o vecindarios), redes neuronales y algoritmos evolutivos. Dentro de cada categoría se encuentran subclasificaciones, con el fin de especificar las características de los procedimientos, según sean probabilistas o deterministas, con uno o varios operadores, constructivos, con perturbaciones, con cruzamiento de información o sin él, etc.
En esta investigación se optimizó la solución mediante la metaheurística llamada búsqueda tabú. Ésta es la más reconocida entre las metaheurísticas y ha sido extensamente aplicada a numerosos problemas combinatorios tales como VRP, TSP, el problema de asignación cuadrática (QAP) o el problema de la mochila 0-1 multidimensional (0-1 multidimensional knapsack problem). De acuerdo con Laporte et al. (2000), el procedimiento de búsqueda tabú ha sido la más exitosa metaheurística, en especial para resolver el VRP. En su libro, Glover y Laguna (1997) presentan una muy buena discusión sobre la aplicabilidad de búsqueda tabú en problemas de optimización reales.
3. METODOLOGÍA DE SOLUCIÓN PROPUESTA
La alternativa diseñada e implementada para resolver el CVRP-HF es una aproximación metaheurística que consta de la combinación de dos fases que son el ruteo y la planificación, como se muestra en la figura 2.
3.1 Fase I. Diseño de rutas
La primera fase es de búsqueda estratégica y se compone de procedimientos heurísticos que pueden subdividirse en dos partes. La primera parte es denominada de construcción y utiliza métodos de optimización local convencional (heurísticas), con el objetivo de acercar el proceso hasta una muy buena solución inicial. La segunda parte, llamada mejoramiento, emplea un método de búsqueda local inteligente (metaheurística) con características de memoria para mejorar así los resultados logrados en la primera parte y obtener soluciones no dominadas, esto con un tiempo polinomialmente razonable.
Método de asignar primero, rutear después. Los métodos asignar primero y rutear después (cluster first, route second) procede en dos fases. Primero se busca generar grupos de clientes, también llamados clusters, que estarían en una misma ruta en la solución final. Luego, para cada cluster se crea una ruta que visite a todos sus clientes. Las restricciones de capacidad se consideran en la primera etapa, asegurando que la demanda total de cada cluster no supere la capacidad del vehículo. Por lo tanto, construir las rutas para cada cluster es un TSP que, dependiendo de la cantidad de clientes en el cluster, se puede resolver en forma exacta o aproximada.
Heurística del barrido o sweep. En la heurística de barrido (Wren, 1971; Wren y Holliday, 1972; Gillett y Miller, 1974), los clusters se forman girando una semirrecta con origen en el depósito e incorporando los clientes "barridos" por dicha semirrecta hasta que se viole la restricción de capacidad. Cada cluster luego se rutea resolviendo un TSP.
El procedimiento se repite n veces, comenzando en cada ejecución por un cliente diferente a la forma en que se generan los clusters; las rutas obtenidas no se superponen, lo que puede ser bueno en algunos casos. Un posible resultado de la aplicación de este algoritmo se muestra en la figura 3 donde las líneas punteadas indican los límites de los clusters.
Este algoritmo puede aplicarse en problemas planos, es decir, en los que cada nodo se corresponde con un punto en el plano y las distancias entre ellos se definen como la distancia euclidiana o, en su defecto, distancia de Manhattan.
3.1.1 Heurística de inserción más próxima
Este es un método voraz (greedy, en inglés), que gradualmente construye un tour por la repetida selección de los arcos más cortos y los adhiere a un tour, con tal de que no cree un ciclo con menos de los N bordes, o aumentos el grado de cualquier nodo a más de 2. No se debe agregar el mismo borde dos veces durante el tour. La complejidad está dada por (O(n2log2(n)) y normalmente presenta entre el 15 y 20 % de la HKLB (Johnson y McGeoch, 1995).
3.1.2 Algoritmo k-Opt
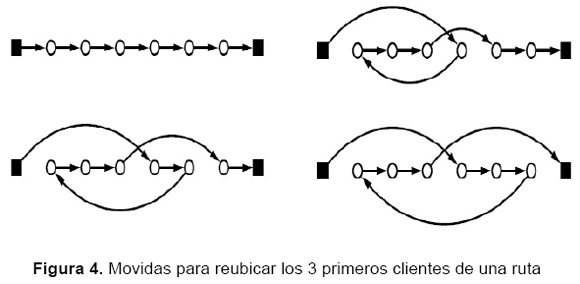
Una versión reducida del algoritmo 3-opt es el algoritmo Or-opt (Or, 1976), que consiste en eliminar una secuencia de k clientes consecutivos de la ruta y colocarlos en otra posición de la ruta, de modo que permanezcan consecutivos y en el mismo orden. Primero se realizan las movidas con k = 3, luego con k = 2 y finalmente con k = 1. En la figura 4 se muestra una ruta y todas las posibles maneras de reubicar los 3 primeros clientes a la manera de Or-opt. El tiempo de corrida del 2-opt producirá en el peor de los casos un tamaño de tour menor que el 5 % sobre la HKLB, mientras que el mejoramiento de la heurística 3-opt tendrá usualmente un tour de 3 % sobre la HKLB (Aarts y Lenstra, 2003). La complejidad en el peor de los casos es de O(log2(n)) para ambos movimientos (Fredman et al.,1995).
3.1.3 Búsqueda tabú (BT)
La búsqueda tabú es una técnica iterativa de búsqueda local inteligente que trata de evitar que las soluciones caigan en óptimos locales. Para esto se utilizan unas estructuras de memoria de corto y largo plazo, acompañadas de criterios de aspiración. En esta técnica en una iteración se pretende pasar de una solución a la mejor solución vecina, sin importar si esta es mejor o peor que la solución actual. El criterio de terminación puede ser un cierto número máximo de iteraciones o un valor de la función por optimizar. Entre las características relevantes que posee este método e implementadas en esta investigación se encuentran la denominada lista tabú y el criterio de aspiración. El objetivo más general de la lista tabú es continuar estimulando el descubrimiento de soluciones de alta calidad. En general, un tipo común de restricción opera seleccionando algún subconjunto de atributos y declarando un movimiento tabú un determinado número mínimo de veces. Otra característica de la BT son los criterios de aspiración que se introducen para determinar cuándo pueden ser reemplazadas las restricciones tabú, eliminando así una clasificación tabú aplicada a un movimiento en otro caso (Glover y Melian, 2003).
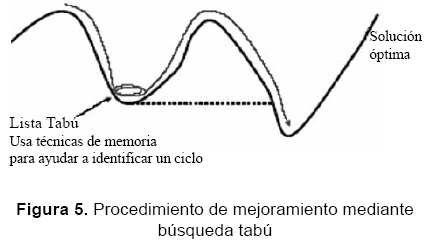
En esta investigación se tienen en cuenta dos tipos de criterios de aspiración. El primero es el criterio de aspiración por defecto, que se presenta si todos los movimientos disponibles están clasificados como tabú, entonces se selecciona el movimiento "menos tabú". El segundo criterio es el de aspiración por objetivo forma global, la cual consiste en eliminar una clasificación tabú de un movimiento cuando el movimiento conduce a una solución mejor que la mejor obtenida hasta ahora. Teniendo en cuenta las características anteriores, el procedimiento metaheurístico implementado permite guiar un algoritmo heurístico de búsqueda local para explorar el espacio de soluciones más allá de la simple optimalidad local, como se muestra en la figura 5.
3.2 Fase II. Planificación de la flota de vehículos
Para la segunda fase (planificación) se propone un procedimiento que tiene como función primordial minimizar el costo fijo causado por la utilización de la capacidad instalada. En otras palabras, se busca disminuir los costos en que incurre un operador logístico al definir una cantidad de vehículos en un ruteo determinado.
De forma genérica, Morton y Pentico (2003) afirman que "programar operaciones es el proceso de organizar, elegir y dar tiempos al uso de recursos para llevar a cabo todas las actividades necesarias, para producir las salidas deseadas en los tiempos deseados, satisfaciendo a la vez un gran número de restricciones de tiempo y relaciones entre las actividades y los recursos". La programación de operaciones se encarga de la localización de tareas a través del tiempo, en recursos que son siempre escasos debido a sus costos. Es un proceso de decisión, con la meta de optimizar uno o más objetivos (Narducci, 2005).
La planeación (scheduling) de transporte consiste en la asignación de un conjunto de vehículos en un orden y a ciertos instantes determinados, con el fin de completar una serie de tareas de carga/despacho para obtener ciertos resultados (función objetivo), como el mínimo tiempo libre de los vehículos, o incluso el tiempo de terminación más corto, bajo ciertas restricciones (Qiu y Hsu, 1999).
En la presente investigación se propone optimizar el uso de la capacidad instalada abordando un problema de secuenciación en máquinas paralelas idénticas, donde los recursos son los vehículos o transportadores, y los trabajos, las rutas a las cuales deben servir. En cuanto a los tiempos de procesamiento, estos son reemplazados por el tiempo que se tarda un transportador en abastecer todos los clientes de la ruta. Los tiempos son tomados de T, T = (Tij), una matriz de tamaño N x N que contiene los tiempos de ruta entre clientes, esto es, viajar desde el cliente i hasta j requiere Tij unidades de tiempo. En cuanto a las restricciones del modelo, encontramos primero las precedencias de las rutas y segundo el umbral de tiempo en el cual se debe realizar la programación de la jornada.
Una manera de extensa difusión para la presentación de planes operativos es el diagrama de Gantt, que en la programación de operaciones representa tiempo contra recursos. De esta manera es posible representar efectivamente información sobre asignación de tareas en recursos, secuenciación de trabajos y fechas de principio y fin de tareas parciales y totales. Se muestra el diagrama de Gantt realizado de esta investigación en la figura 6.
En la figura 7, es posible apreciar la manera en que la fase de planificación funciona. La mejor utilización de los tiempos inactivos produce una compresión del lapso, además permite disminuir los costos en que incurre un operador logístico al definir una cantidad de vehículos en un ruteo determinado, esto mediante la utilización de los tiempos inactivos de las rutas preconcebidas en las fases de construcción y mejoramiento, para reorganizar así estas tareas.
Lo anterior ocasiona una leve variación en la función objetivo de la formulación del CVRP-HF desplegada anteriormente; esta se encuentra expresada en términos de los costos Cij asociados a los arcos (i,j) entre clientes del grafo G=(V, E), en función de las distancias o tiempos de ruta entre ellos. En este caso, la solución óptima al CVRP-HF podría no ser la más conveniente en la práctica, si su valor objetivo corresponde a enrutar una gran cantidad de vehículos (por supuesto, el tamaño de flota representa un costo fijo asociado a la gestión, no contemplado en la formulación matemática).
Una metodología heurística podría manipularse para encontrar una solución más práctica que la óptima, aunque sacrifique el valor óptimo de la distancia (o el tiempo trascurrido), de hecho, esto es lo que se intenta hacer al ejecutar esta segunda fase denominada planificación. En el algoritmo propuesto, se implementó, por lo tanto, una función objetivo de la forma:
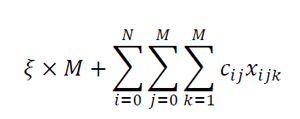
Donde M es el tamaño de la flota determinado en la fase de ruteo y ξ (representa el costo fijo asociado a la flota) es un valor de su costo, en caso de que se tuviera la necesidad de subcontratar vehículos.
Cabe afirmar que ésta es una variable muy usada en los sistemas reales, debido a que tercerizar es, por lo general, más económico que no hacerlo. En la implementación algorítmica, ξ es un parámetro adicional que depende exclusivamente del tipo de flota elegido para realizar el ruteo.
La reducción de la flota vehicular y, por ende, su costo consiste, entonces, en asignar el mayor número de rutas posibles a vehículos, sin sobrepasar las horas-hombre laborales del personal operativo (esto genera clusters de rutas o recorridos); aquellos clientes que no son asignados se asignan a un nuevo vehículo que parte de manera simultánea a este. Luego de haber asignado todas las rutas, se procede a cambiar en cada iteración el origen de las rutas para asignar (generando una vecindad en las rutas) y repetir el procedimiento para así explorar un nuevo espacio de solución que mejorará considerablemente el tamaño de la flota.
4. EVALUACIÓN DEL DESEMPEÑO
Este modelo se aplicó sobre dos instancias, una de ellas proveniente de una aplicación real. Por cuestiones de confidencialidad no es posible presentar los datos utilizados, puesto que refleja la aplicabilidad de una herramienta algorítmica en la realidad. Debido a la escala de la problemática, la evaluación del desempeño de CVRP-HF ha sido concentrada en las variables de transporte de un único tipo de productos en una flota homogénea. En la bibliografía existente se hace referencia a procedimientos heurísticos y metaheurísticos; es extenso el tratamiento del problema con las variables mencionadas, siendo al mismo tiempo escasa en cuanto al tratamiento de problemas relacionados con programación vehicular. Las instancias presentadas han sido evaluadas en las aplicaciones UN-Tech VRScheduler v1.0. El procedimiento propuesto fue comparado con otras herramientas disponibles para el enrutamiento de vehículos, como son BT for VRP, AAVRP y VRP Solver. BT for VRP (Cabarcas, 2002) propone un procedimiento basado en algunas características de memoria de búsqueda tabú y obtiene resultados satisfactorios. AAVRP (Filadelfo y Pérez, 2003) utiliza métodos de optimización local convencional como el barrido o sweeping y algunas características de la heurística de inserción, con lo que obtiene resultados satisfactorios en tiempo polinomialmente razonable. VRP Solver v1.3 (Snyder, 2004) es una aplicación que lleva a cabo una adaptación de algoritmo de ahorros en combinación con una versión reducida del algoritmo 3-opt, el cual construye rutas del vehículo que visitan cada ciudad precisamente una vez obedeciendo a la capacidad del vehículo especificado por el usuario y sus límites de distancia.
Las aplicaciones descritas fueron evaluadas en condiciones iguales en un computador Laptop marca Acer TravelMate 2423 WXCi, Intel Celeron M processor 370 (1.5 GHz, 400 MHz FSB, 1MB L2 cache), 40GB HDD, 256MB DDR2 (support dual-channel). Con estas condiciones se presentan a continuación, los resultados obtenidos de las instancias empleadas para evaluar el desempeño de la alternativa algorítmica diseñada e implementada.
Con el objetivo de evaluar el desempeño de los procedimientos heurísticos y metaheurísticos, lo comparamos con los siguientes métodos de optimización: algoritmo de ahorros (Snyder, 2004), búsqueda tabú sin criterios de aspiración (Cabarcas, 2002), inserción más próxima multipunto (Filadelfo y Pérez, 2003). Los resultados de las dos instancias evaluadas pueden observarse en la tabla 1.
Es notable el grado de optimización mostrado en la herramienta algorítmica propuesta, debido a que presentó un resultado alentador en lo que respecta a la distancia total recorrida ocupando el segundo lugar y solo siendo superada por el VRPSolver v1.3, pero en lo que respecta a la disminución de la capacidad instalada (mediante la planificación) presentó un desempeño mejor que todas las aplicaciones evaluadas. El resultado para la instancia real asciende a la utilización de 15 camiones, la herramienta estableció un total de 6 vehículos, lo que muestra ahorros significativos. Este resultado fortalece la validez y la pertinencia del procedimiento.
Es notable también el poco tiempo de corrida empleado para la obtención de resultados, con una calidad superior, en cuanto a optimización de la capacidad, a los obtenidos en periodos similares, por las heurísticas que se utilizaron como comparación. Cabe resaltar que, a diferencia de los procedimientos heurísticos existentes, la heurística propuesta presentó un comportamiento estable en cuanto a la pertinencia y calidad de la solución. Esto implica que, mediante la aplicación de un procedimiento heurístico suplementario innovador, se garantiza una solución con más calidad que la mejor solución posible de los procedimientos algoritmo de ahorros, búsqueda tabú sin criterio de aspiración e inserción más próxima multipunto.
5. CONCLUSIONES
Los resultados obtenidos con base en la alternativa metaheurística de dos fases para el problema de ruteo de vehículos, con restricciones de capacidad y flota homogénea, permiten concluir que la aplicación de procedimientos heurísticos que implementen un proceso de programación de operaciones vehiculares puede presentar un comportamiento homogéneo y confiable ante diversas instancias de situaciones problemáticas reales del ruteo de vehículos.
En general, se encontraron soluciones muy buenas al problema en lo que respecta al tiempo computacional Tc requerido, el cual es sorprendentemente menor de un minuto (Tc<1min), además se encontró una notable mejoría en la determinación del número óptimo de camiones para asignar a los clientes, esto mediante la planificación, llevando así a disminuir el costo fijo de la capacidad instalada de hasta en un 50 % menos que con las otras aplicaciones evaluadas en la presente investigación.
Los anteriores resultados pueden llevar a concluir que esta alternativa podría resultar muy conveniente en la práctica, si se cuenta con procesamiento de mediano a alto nivel. En esto radica su ventaja práctica y en la organización de las soluciones para una gestión provechosa. En consecuencia, se deduce también que el objetivo general de desarrollar una opción que permita mejorar la planeación y asignación de las rutas de transporte en las empresas de carga y mensajería se cumple a cabalidad.
Se evaluaron características de desempeño de varias metodologías de optimización en trabajos previos, justificando la escogencia de las heurísticas elegidas y la metaheurística búsqueda tabú para la propuesta; se diseñó e implementó el algoritmo en lenguaje Visual Basic 6.0, con una sencilla, agradable y didáctica interfaz gráfica para agilizar el análisis experimental.
AGRADECIMIENTOS
El trabajo presentado en este artículo hizo parte del curso "Teoría de la Complejidad" del programa de Maestría en Ingeniería Industrial (énfasis Métodos Cuantitativos) desarrollado durante la visita del segundo autor al Departamento de Ingeniería Industrial de la Universidad del Norte en julio de 2008. Este autor desea expresar sus agradecimientos a los doctores Carlos Paternina y Ángel González por la invitación y el apoyo prestado. El trabajo subsecuente de este artículo fue desarrollado como parte del proyecto CEA-24-2008 financiado por la Universidad de La Sabana, Colombia.
REFERENCIAS
Aarts, E. and Lenstra, J. Local search in combinatorial optimization. John Wiley & Sons. 2003. [ Links ]
Applegate, David L.; Bixby, Robert E.; Chvátal, Vasek and Cook, William J. "The traveling salesman problem: a computational study". Princeton University Press, 2006, 606 p. [ Links ]
Archetti, C.; Mansini, R. and Speranza M. G. "The split delivery vehicle routing problem with small capacity", Technical Report n. 201, Department of Quantitative Methods, University of Brescia, 2001. [ Links ]
Arora, S. "Polynomial time approximation schemes for euclidian traveling salesman and other geometric problems", Journal of the ACM, vol. 45, No. 5, September 1998, pp. 753-782. [ Links ]
Baptista, S.; Oliveira, R. C. and Zúquete, E. "A period vehicle routing case study", European Journal of Operational Research, 139:220-229, Elsevier, 2002. [ Links ]
Bard, J. F.; Huang, L.; Dror, M. and Jaillet, P. "A branch and cut algorithm for the VRP with satellite facilities", IIE Transactions 30, pp. 821-834. 1997. [ Links ]
Cabarcas, Juan. Desarrollo de una alternativa algorítmica para enrutamiento de vehículos con restricciones de capacidad. Barranquilla, 2002, 83 p. Trabajo de grado (Ingeniería Industrial). Universidad del Norte. [ Links ]
Clarke, G. and Wright, W. Scheduling of vehicles from a central depot to a number of delivery points. Operations Research, No. 12 (1964), pp. 568-581. [ Links ]
Cordeau, J.-F.; Desaulniers, G.; Desrosiers, J.; Solomon, M. M. and Soumis, F. "VRP with time windows". In P. Toth and D. Vigo (eds.): The vehicle routing problem, SIAM Monographs on Discrete Mathematics and Applications, vol. 9, Philadelphia, PA, 157-193. 2002. [ Links ]
Dantzig, G. B. and Ramser, J. H. The truck dispatching problem. En: Management Science 6, No. 1 (1959); p. 80-91. Citado por ARONSON, L. Algorithms for vehicle routing - A survey. Delft, 1995, p. 43. [ Links ]
De la Cruz, Jair. Alternativa heurística de dos fases para el problema de enrutamiento de vehículos con ventanas de tiempo, múltiples productos y flota heterogénea. Barranquilla, 2003, 155 p. Tesis de maestría (Ingeniería Industrial). Universidad del Norte. [ Links ]
Dror, M.; Laporte G. and Trudeau P. "Vehicle routing with split deliveries", Discrete Applied Mathematics 50, 239-254. 1994. [ Links ]
Filadelfo, Samuel y Pérez, Gina. Desarrollo de una alternativa para mejorar el enrutamiento actual de la empresa transportadora de carga y mensajería Colvanes Ltda. Barranquilla, 2003, 80 p. Trabajo de grado (Ingeniería Industrial). Corporación Universitaria de la Costa. [ Links ]
Fredman, M. L.; Johnson, D. S.; McGeoch L. A. and Ostheimer, G. "Data structures for traveling salesmen", Journal of Algorithms 18 (3), 1995, pp. 432-479. [ Links ]
Garey, Michael R. and Johnson, David S. Computers and intractability: a guide to the theory of NP-completeness. W. H. Freeman. 1979. [ Links ]
Gaskell, T. Bases for vehicle fleet scheduling. Operational Research Quarterly. No. 18 (1967), pp. 281-295. [ Links ]
Gillett, B. and Miller, L. A heuristic algorithm for the vehicle-dispatch problem. Operations Research, 22 (1974) 340-349. [ Links ]
Glover, F. and Laguna, M. (1997). Tabu search. Kluwer Academic Publishers. [ Links ]
Glover, Fred and Melian, Belen. Tabu search. Revista Iberoamericana de Inteligencia Artificial. No 19, (2003), pp. 29-48. [ Links ]
Hillier, F. S. and Lieberman, G. J. Introduction to operations research, 8th ed, McGraw-Hill, 2001, pp. 621-623. [ Links ]
Hjorring, C. "The vehicle routing problem and local search metaheuristics", Chapter 2. PhD thesis, Department of Engineering Science, The University of Auckland, 1995. [ Links ]
Ignizio, J. and Cavalier, T. Linear programming. Englewood Cliffs, NJ: Prentice Hall, 1994, 666 p. [ Links ]
Jacobs-Blecha, C. and Goetschalckx, M. "The vehicle routing problem with backhauls: properties and solution algorithms". Technical Report, School of Industrial and Systems Engineering, Georgia Institute of Technology, Atlanta, Georgia. Presented at the National Transportation Research Board, January 13-15, 1992, Washington DC. [ Links ]
Johnson, D. S. and McGeoch, L. A. "The traveling salesman problem: a case study in local optimization", November 20, 1995. [ Links ]
Johnson, D. S.; McGeoch L. A. and Rothberg, E. E. "Asymptotic experimental analysis for the Held-Karp traveling salesman bound". Proceedings of the Annual ACM-SIAM Symposium on Discrete Algorithms, 1996, pp. 341-350. [ Links ]
Karp, R. Reducibility among combinatorial problems. In: Miller R. and Thatcher J. (eds.). Complexity of Computer Communications. Plenum Press, New York. 1972. [ Links ]
Laporte, G.; Gendreau, M.; Potvin, J. and Semet, F. (2000). Classical and modern heuristics for the vehicle routing problem. International Transaction in Operational Research 7, 285-300. [ Links ]
Laporte, G. and Louveaux, F. V. "Solving stochastic routing problems with the integer L-shaped method". In: Fleet Management and Logistics, T.G. Crainic and G. Laporte (eds.), 159-167, Kluwer Academic Publishers, Boston, 1998. [ Links ]
Martello, S. and Toth, P. Knapsack problems. Wiley, Chichester 1990. [ Links ]
Miller, C.; Tucker, A. and Zemlin, R. Integer programming formulation of traveling salesman problems. Journal of the ACM No. 7 (1960), pp. 326-329. [ Links ]
Moraga, R. J. (2002). Meta-RaPS: an effective solution approach for combinatorial problems. Ph.D. thesis. Orlando, FL: University of Central Florida. [ Links ]
Morton, T. and Pentico, D. Heuristic scheduling systems. John Wiley & Sons, 1993. [ Links ]
Narducci, Francesco. Programación de talleres intermitentes flexibles, por medio de la heurística del margen de tolerancia. Barranquilla, 2005, 117 p. Tesis de maestría (Ingeniería Industrial). Universidad del Norte. [ Links ]
Nilsson, C. "Heuristics for the traveling salesman problem", Department of Computer Science, Linkoping University, 2003. [ Links ]
Ralphs, T.; Hartman, J. and Galati, M. "Capacitated vehicle routing and some related problems". Rutgers University, 2001. [ Links ]
Reeves, C. Modern heuristic techniques. In: Rayward- Smith, V. J.; Osman, I. H.; Reeves, C. R. and Smith, G. D. (eds.), Modern Search Methods, John Wiley & Sons, 1996. [ Links ]
Or, I. Traveling salesman-type combinatorial optimization problems and their relation to the logistics of regional blood banking (1976). [ Links ]
Qiu, L. and Hsu, W. J. (1999). Scheduling and routing for AGVs: a survey. Technical Report, CAISTR- 99-26, Center for Advanced Information Systems, Nanyang Technological University, Singapore. [ Links ]
Righini, G. "Approximation algorithms for the vehicle routing problem with pick-up and delivery", Note del Polo - Ricerca 33, Polo Didattico e di Ricerca di Crema, Università degli Studi di Milano, July 2000. [ Links ]
Snyder, Lawrence V. (2004). Adaptation of Clarke-Wright with Or-Opt for the vehicles route problems, Lehigh University, www.lehigh.edu/~lvs2. [ Links ]
Wren, A. Computers in transport planning and operation. Ian Allan (1971). [ Links ]
Wren, A. and Holliday, A. Computer scheduling of vehicles from one or more depots to a number of delivery points. Operational Research Quarterly 23 (1972) 333-44. [ Links ]
Yu, G. (1998). Industrial applications of combinatorial optimization. Boston: Kluwer Academic Publishers. [ Links ]