Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista EIA
Print version ISSN 1794-1237On-line version ISSN 2463-0950
Rev.EIA.Esc.Ing.Antioq no.13 Envigado Jan./June 2010
A NUMERICAL APPROACH FOR FAULT DETECTION IN BEAM-LIKE STRUCTURES USING MODAL STRAIN ENERGY
UN ENFOQUE NUMÉRICO PARA LA DETECCIÓN DE FALLAS EN ESTRUCTURAS TIPO VIGA CON USO DE LA ENERGÍA MODAL DE DEFORMACIÓN
UM ENFOQUE NUMÉRICO PARA A DETECÇÃO DE FALHAS EMESTRUTURAS TIPO VIGA COM USO DA ENERGIA MODAL DE DEFORMAÇÃO
Carlos Alberto Riveros*, Edwin Fabián García**, Manuel Alonso Builes***
* Ingeniero Civil, Universidad Industrial de Santander; Master of Engineering, The University of Tokyo; Doctor ofEngineering, Kyoto University. Profesor Asistente, Ingeniería Civil, Escuela Ambiental, Universidad de Antioquia.Medellín, Colombia. riveros@udea.edu.co
** Ingeniero Civil, Universidad Nacional de Colombia; Master of Engineering, The University of Tokyo; PhD. (c) ofEngineering, Kyoto University. Profesor Asistente, Ingeniería Civil, Escuela Ambiental, Universidad de Antioquia.Medellín, Colombia. egarcia@udea.edu.co
*** Ingeniero Civil, Universidad Nacional de Colombia; Master of Engineering, The University of Tokyo. Ingeniero Senior, Solingral S. A. Profesor de cátedra, Ingeniería Civil, Escuela Ambiental, Universidad de Antioquia. Medellín,Colombia. builes@udea.edu.co; mabuiles@integral.com.co
Artículo recibido 21-X-2009. Aprobado 15-VI-2010
Discusión abierta hasta diciembre de 2010
ABSTRACT
Vibration-based damage detection is based on the fact that measurements of changes in the vibration propertiesof a structure can be used to determine the occurrence of structural damage. Therefore, there is a strong needfor the development and implementation of fault detection and optimum sensor location methods that addressthe issue of limited instrumentation and its effect in predicting damage degradation. In this paper, the results of anumerical implementation of a previously developed sensor distribution method are presented. A finite elementmodel of a railway box-girder bridge is assembled. Then, the damage index method is numerically implementedin order to identify damage from the resulting sensor measurements. Both the optimum sensor placement and thedamage detection methods are based on the concept of modal strain energy. Finally, the numerical results showthat the proposed approach is suitable for continuous damage monitoring implementations and can be used as auseful tool for damage assessment in beam-like structures.
KEY WORDS: structural health monitoring; fault detection; optimum sensor location; modal strain energy;sensitivity matrix; curvature of the vibration mode shape.
RESUMEN
La detección de daño estructural usando vibraciones se fundamenta en el hecho de que pueden usarsemediciones de cambios en las propiedades de vibración de una estructura para determinar la ocurrencia de dañoestructural, por lo tanto, existe una fuerte necesidad de desarrollar e implementar métodos de detección de dañoy óptima localización de sensores que tengan en cuenta el uso de instrumentación limitada y su efecto en la predicciónde deterioro estructural. En este artículo se presentan los resultados de la implementación numérica deun método de óptima localización de sensores previamente desarrollado. Se ensambla un modelo en elementosfinitos con base en un modelo de un puente ferroviario de tipo viga-cajón. Luego, el método de índice de dañose emplea para la identificación de daño estructural, con base en las mediciones obtenidas de los sensores. Losmétodos de óptima localización de sensores y de detección de daño presentados en este artículo se basan en eluso de la energía modal de deformación. Los resultados numéricos muestran que la energía modal de deformaciónes apropiada para aplicaciones de seguimiento continuo de daño en estructuras y que puede usarse como unaherramienta útil para inspecciones de integridad estructural en estructuras tipo viga.
PALABRAS CLAVE: monitoreo de salud estructural; detección de daño; localización de sensor óptima;energía modal de deformación; matriz de sensibilidad; curvatura de los modos de vibración.
RESUMO
A deteção de dano estrutural usando vibrações se fundamenta no fato de que podem usar-se mediçõesde mudanças nas propriedades de vibração de uma estrutura para determinar a ocorrência de dano estrutural,portanto, existe uma forte necessidade de desenvolver e aplicar métodos de deteção de dano e ótima localizaçãode sensores que levem em conta o uso de instrumentação limitada e seu efeito no prognóstico de deterioraçãoestrutural. Neste artigo se apresentam os resultados da aplicação numérica de um método de ótima localizaçãode sensores previamente desenvolvido. Encaixa-se um modelo em elementos finitos com base em um modelo deuma ponte ferroviária de tipo viga-gaveta. Depois, o método de índice de dano se emprega para a identificaçãode dano estrutural com base nas medições obtidas dos sensores. Os métodos de ótima localização de sensorese de detecção de dano apresentados neste artigo estão baseados no uso da energia modal de deformação. Osresultados numéricos mostram que a energia modal de deformação é apropriada para aplicações de seguimentocontínuo de dano em estruturas e que pode usar-se como uma ferramenta útil para inspeções de integridadeestrutural em estruturas tipo viga.
PALAVRAS CÓDIGO: monitoração de saúde estrutural; deteção de dano; localização de sensor ótima;energia modal de deformação; matriz de sensibilidade; curvatura dos modos de vibração.
1. INTRODUCTION
Continuous damage monitoring of civil engineeringstructures is based on the premise thatdamage will cause changes in the measured modalparameters such as eigenfrequencies, mode shapes,and damping ratios. Therefore, vibration-baseddamage detection methods utilize measured modalparameters to assess the health condition of a structure(Kumar, Shenoi and Cox, 2009). Many of suchmethods have been developed for civil engineeringstructures due to their potential to enhance oreven eventually replace current visual inspectiontechniques resulting in significant economic savings.Nevertheless, there are several challenges yetremaining to optimally design a robust continuousdamage monitoring system. One of these challengesis the effective placement of sensors to achieve theobjectives of the structural health monitoring system(Li, 2010). Optimum sensor placement deals withboth the number of sensors needed for economicimplementation and the best location of those sensors;in addition, the resulting sensor configurationshould consider the modes of interest, the characteristicsof the excitation, including the source, typeand frequency range and the likelihood of damagein various regions of the structure, if this informationis available. Furthermore, the effectiveness of aplacement methodology will be strongly related tothe requirements and needs of the damage detectiontechnique that is to be employed in the system(Riveros et al., 2008).
On the other hand, although continuousdamage monitoring of civil engineering structureshas generated a lot of research over the past fewyears, there is still the debate on how the problemof test/analysis mismatch -in terms of degrees offreedom- can be tackled (Yang, 2009). It is knownfrom sensitivity studies using finite element modelsand from in-situ tests of artificially damaged bridgesthat the decrease of frequencies is relatively low. Eventhough the local stiffness drop at a local damage sitemay be high, the global stiffness results in relativesmall frequency changes, which can only be detectedwith very precise sensing systems and identificationprocedures. A well-known test program correspondsto the damage tests on the I-40 plate girder bridgelocated in New Mexico (USA). As reported by Farrarand Jauregui (1996), five modal-based methods fordamage detection were compared using data recordedfrom this bridge where damage was intentionallyinflicted. Damage detection results generally showedthat the damage index method performed the best.However, in two out of five levels of inflicted damage,the variation of temperature induced an increaseof the fundamental frequency of the bridge leadingto an undetectable reduction of stiffness. However,Limongelli (2010) used the previously mentionedI-40 plate girder bridge to study the sensitivity tochanging temperature of the interpolation damagedetection method (IDDM) showing that the IDDMprovides reliable results, almost not affected by temperaturechanges, in case of signals with a low levelof noise; for noisy signals, Limongelli (2010) proposeda threshold value in order to judge if the structurehad suffered damage.
Alvandi and Cremona (2006) reported goodagreement between the predicted damage locationand the actual ones for all experimental and simulateddamaged cases. They used a simple supportedbeam under various levels of noise in the appliedexcitation force and concluded that, regarding noisysignals, the strain energy-based method performedthe best. More recently, Li (2010) presented a damageidentification study using various strain-related indicators,such as strain (curvature) mode shape, strainenergy, strain frequency response function, etc.,and concluded that the strain energy-based indexdemonstrates an excellent anti-noise performance,and therefore improvement of damage identificationresults can be achieved by using embedding machinelearning techniques.
This paper presents a modal strain energybasedapproach for identification of structural damagein beam-like structures. A finite element (FE)model of a box-girder bridge is assembled based on data provided by Yang and Wu (2002). Then,an optimum sensor location algorithm is presentedand numerically implemented in the FE model. Thisalgorithm is based on the use of the sensitivity matrix,which is derived from mode shapes derivatives. Finally,a modal strain energy-based method is utilizedto locate damaged sites.
2. PROBLEM FORMULATION
Optimum sensor placement will be dependenton several factors, including: a) the damage detectionalgorithm employed; b) the location of damage andrelative likelihood of damage in the various locationsof the structure; c) excitation source; d) objectivesof the continuous damage monitoring system; ande) the selected mode shapes. Herein, we employthe damage index (DI) method for determinationof the existence of damage (Stubbs and Kim, 1994),and a previously proposed technique is additionallyconsidered to place sensors, known as the damagemeasurability (DM) method. The optimum sensorplacement method is described in the following section,and this discussion is followed by a descriptionof the DI method.
3. DAMAGE MEASURABILITY METHOD
Several researchers have made significantcontributions to the development of methods foroptimum sensor placement. One of these is the effectiveindependence method developed by Kammer(1991), which is based on the maximization of thedeterminant of the Fisher information matrix (FIM).Hemez and Farhat (1994) extended the effectiveindependence method by placing sensors based onthe strain energy contributions of the structure; theyproposed the use of the FIM as a distribution of strainenergy, which yields an array of sensors optimallylocated to detect structural damage. Udwadia (1994)proposed the optimum sensor location algorithm,which minimizes the covariance error between thestructural parameters that are to be identified andtheir estimate from the limited measurements; thismethod is rigorously founded on the FIM and isapplicable to both linear and nonlinear systems; additionally,it was also proved that the kinetic energycriterion for optimum sensor placement is inappropriateto develop such type of methods. Heredia-Zavoniand Esteva (1998) stated that the optimum sensorconfiguration should be chosen as the one that minimizesthe expected Bayesian loss function involvingthe trace of the inverse of the FIM. Cobb and Liebst(1996) developed the eigenvector sensitivity method,which employs the eigenvalue and eigenvector sensitivitiesfor the determination of the optimal sensorlocations. Shi, Law and Zhang (2000) presented amethod in which the sensor locations are selectedaccording to their ability to localize structural damagebased on the eigenvector sensitivity method. Xiaand Hao (2000) proposed measurement selectionin terms of two factors, namely, the sensitivity of aresidual vector to the structural damage using theapproach proposed by Shi, Law and Zhang (2000)and the sensitivity of the damage to the measurementnoise. Riveros et al. (2004) numerically implementedthe method developed by Xia and Hao (2000) incable-stayed bridges.
The DM method was developed by Xia andHao (2000), and is defined using two factors. The firstfactor is related to the fact that sensor locations mustbe optimized for the purpose of localizing structuraldamage sites and the second factor is the sensitivityof damage to measurement noise. The mathematicalderivation of the method is based on the sensitivitybasedelement-by-element (SB-EBE) model updatingmethod proposed by Hemez and Farhat (1994),which represents the relationship between themeasured eigenfrequencies and eigenvectors andthe structural stiffness parameters using a truncatedTaylor series expansion as shown in Eq. (1).
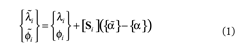
where λi, Φi and 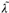 i
i 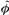 i, are the ith eigenfrequencyand eigenvector of the undamaged and damagedstructure, respectively, {α} and {
i, are the ith eigenfrequencyand eigenvector of the undamaged and damagedstructure, respectively, {α} and {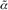 } are structuralelemental stiffness parameters (ESP) of the initial andupdated FE model after the occurrence of damagewith ne elements, and Si is the corresponding sensitivitymatrix defined in Eq. (2).
} are structuralelemental stiffness parameters (ESP) of the initial andupdated FE model after the occurrence of damagewith ne elements, and Si is the corresponding sensitivitymatrix defined in Eq. (2).

To estimate the elemental stiffness parameterchange according to Eq. (1), the covariance matrixof the estimation errors must be minimized. Udwadiaand Garba (1985) demonstrated that maximizing thedeterminant of the FIM as a distribution of strainenergy Bi given in Eq. (3) for the ith mode

leads to the minimization of the covariance matrixand, thus, the best estimate of {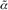 } - {α}. The FIMas a distribution of strain energy B is defined by thecontribution of the selected modes. Kammer (1991)showed that the diagonal terms of
} - {α}. The FIMas a distribution of strain energy B is defined by thecontribution of the selected modes. Kammer (1991)showed that the diagonal terms of
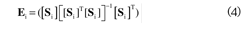
can be used to rank the importance of a particularDOF for the ith mode. Thus, if a particular DOF hasa small contribution to the diagonal terms of Ei, thissensor position can be eliminated from the selectedsensor locations, then the remaining sensor locationsmaximize the contribution to the FIM as a distributionof the strain energy Bi providing the most informationfor damage detection. The contribution of allthe selected modes for sensor placement is obtainedby adding the contribution of each mode using thediagonal terms of Ei. The second factor is the sensitivityof damage to measurement noise, defined in Eq. (5).
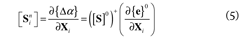
Where {Δα} is an elemental stiffness changegiven by {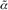 } - {α}, Xi is a noise vector correspondingto noise contributing to the selected modes, Sinis the sensitivity of change in {Δα} due to a unitmeasurement noise, and {e} is the modal datachange vector containing the differences betweenthe selected eigenfrequencies and mode shapes atthe corresponding instrumented degrees of freedom,np, of the structure before and after the occurrence ofdamage, the superscript "0" represents the noise-freevalue. The vector {e} can be obtained using Eq. (6).
} - {α}, Xi is a noise vector correspondingto noise contributing to the selected modes, Sinis the sensitivity of change in {Δα} due to a unitmeasurement noise, and {e} is the modal datachange vector containing the differences betweenthe selected eigenfrequencies and mode shapes atthe corresponding instrumented degrees of freedom,np, of the structure before and after the occurrence ofdamage, the superscript "0" represents the noise-freevalue. The vector {e} can be obtained using Eq. (6).

where the sensitivity matrix S is obtained by consideringthe contribution of the selected modes to thesensitivity matrix Si defined in Eq. (2). The first partialderivatives of the eigenfrequencies and mode shapeswith respect to the noise vector Xi were derived byXia and Hao (2000). For the selected mode shapes,Sin is a matrix having dimensions of np x ne, wherene is the number of elements of the structural model,therefore each row of the Sin matrix represents theinfluence of noise from the measured data at the kthdegree of freedom. The noise sensitivity is obtained by

The damage measurability for a structuralmodel is determinated as the ratio of F to Sn, wherethe vector F, defined in Eq. (8), is the summationof all measured modes nm of Ei defined in Eq. (4).
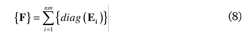
The first factor in the definition of the damagemeasurability is related to the contribution ofeach measured degree of freedom to the FIM as adistribution of strain energy, and the second factorquantifies the influence of the measurement noiseon each instrumented degree of freedom, therefore,damage measurability values with high damage sensitivityvalues and low measurement noise sensitivityvalues must be selected to optimally locate sensors.
4. DAMAGE INDEX METHOD
The selection criteria for this method are basedon previous research work that can be summarizedas follows. Tang and Leu (1991) showed that changesin the mode shapes of the structure were more sensitiveindicators of damage than natural frequencies.Pandey, Biswas and Samman (1991) demonstratedthe use of changes in the curvature of the modeshapes to detect and locate damage; they also foundthat both the modal assurance criterion (MAC) andthe coordinate modal assurance criterion (COMAC)were not sensitive enough to detect damage in itsearlier stages. Chance, Tomlinson and Worden (1994)found that measuring curvature directly using strainmeasurements gives very improved results than thoseof the curvature calculated from the displacements.Also, Chen and Swamidas (1994) found that strainmode shapes facilitated the location of a crack in acantilever plate using finite element method simulation.Yam et al. (1996) have found that the strainmode shape is more sensitive to structural localchanges than the displacement mode shape. Quanand Weiguo (1998) showed that, for the steel deckof a bridge, the curvature mode shapes are the bestamong three damage recognition indices based onmode shapes (the COMAC, the flexibility, and the curvature mode shape).
The DI method is adopted here for damagedetection. This method has been extensively used inprevious damage detection studies showing betterperformance over other existing damage detectionmethods (Farrar and Jauregui, 1996; Barroso andRodriguez, 2004; Li, 2010). The DI method wasdeveloped by Stubbs and Kim (1994) to detect theexistence and location of damage in a structure and isbased on the assumption that strain energy stored indamaged regions will decrease after the occurrenceof damage. The damage index βj is estimated by thechange of the curvature of a particular mode shape,which is related to mode strain energy changes atlocation j, βj is then defined in Eq. (9). The completederivation of the method can be found in Alvandiand Cremona (2006).
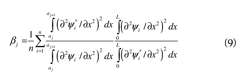
where ∂2ψi /∂x2 and ∂2ψi*/∂x2are the second derivativesof the ith mode shape before and after the occurrenceof damage, respectively, n is the numberof the selected mode shapes, L is the length of thebeam element in which damage is being evaluated,and aj and aj+1 are the limits of this beam element.The damage index for the selected mode shapes isobtained by adding the individual contribution tothe damage index from each of the selected modeshapes.
The damage index procedure can be summarizedas follows: (1) calculate the mode shapesamplitudes for the nodes where sensors are located;(2) estimate the amplitudes of the mode shapes forthe nodes where no sensors are located by interpolatingthe instrumented nodes using cubic-splinefunctions; and, (3) take a second derivative of theinterpolation function at each node. Finally, treatingβj as a realization of a normally distributed randomvariable β, a normalized damage index is computedas shown in Eq. (10).

where 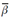 and õβ are the mean and standard deviationof the damage index, respectively. The jth substructureis defined as damaged when Zj>2, which correspondsto a hypothesis testing with 95 % confidencelevel. The DI method is implemented in this paperusing the graphical user interface DIAMOND developedat Los Alamos National Laboratory (Doebling,Farrar and Cornwell, 1997).
and õβ are the mean and standard deviationof the damage index, respectively. The jth substructureis defined as damaged when Zj>2, which correspondsto a hypothesis testing with 95 % confidencelevel. The DI method is implemented in this paperusing the graphical user interface DIAMOND developedat Los Alamos National Laboratory (Doebling,Farrar and Cornwell, 1997).
5. DESCRIPTION OF THE BRIDGE
The box-girder bridge used for this numericalstudy was presented by Yang and Wu (2002), and corresponds to a railway bridge. Having a bridgespan of 30 m, Young´s modulus of 28,25 GPa, perunit-length mass (including the mass of the ballastlayer) of 41,7 t/m, sectional area of 6,73 m2 andmoment of inertia of 7,84 m4. The FE model of thebridge is composed of 30 Euler-Bernoulli elements.Each element is 1 m length based on previous workconducted by Riveros et al. (2010) using very flexibleslender structures. The nodes at each end of thestructure have vertical and free rotational DOFs.In figure 1, optimum sensor locations are shownin the upper part of the model, elements selectedto perform damage detection are labeled in thesquared elements. Only one supporting node has afree horizontal DOF as depicted in figure 1.
6. NUMERICAL SIMULATION
It is still challenging to implement a damagedetection method using a few number of instrumentednodes; the FE model presented in this paper has90 DOFs and the maximum number of sensors thatwill be selected from optimum sensor placement toperform damage detection is 10, on the other hand,only vertical components of the vertical mode shapesare considered for this numerical implementation.The DI method can perform damage detection usingthis limited information, but for other damagedetection methods which require the use of stiffnessmatrix and mass matrix of the whole structure,thenumber of unmeasured DOFs makes this analysismore complicated, almost impossible, especiallywhen the measured information is used to assemblethe stiffness matrix for the damage state.
The number of modes that can be identifiedfrom the bridge should be considered when decidingthe final distribution of sensors. When continuousdamage monitoring is the main objective of themodal identification test, ambient vibration test,rather that forced vibration test or free vibration testis the most affordable and suitable test, especiallytraffic loading can be used as an ambient excitationsource for railway bridges. Traffic loading on railwaybridges has been studied at the University of Tokyoby Miyashita et al. (2005) showing that cyclic externalloads of the bogies generate forced vibration and thefrequency is proportional to the train velocity. Trafficloading can be modeled under some assumptions asa stationary broadband force leading to the possibilityto extract the free response of the structure, whichcan be used to extract its dynamic features.
Higher modes can also be extracted in astructure when forced vibration testing is used, but inreal applications, it is very difficult to apply sufficientartificial excitation to surpass the ambient vibrationforces acting on the bridge. The advantage of usingambient vibration sources is that not only theyare cheap, but also they are truly representative ofthe real excitation to which the bridge is subjectedduring its service life, but, on the other hand, theuse of ambient excitation sources for continuousmonitoring implies the use of limited information, asa result, only few low frequency modes can be usedfor damage detection. Because the main goal of thisstudy is the numerical implementation of a continuousdamage monitoring system for beam-like structures,we assume herein that traffic will be the mainexcitation source. This type of loading acts primarilyto excite the vertical modes of the bridge. Thus, inthis study we focus on a selected number of modesdominated by vertical motions in order to simulatethe use of sensors capable of measuring only verticalcomponents. Feng et al. (2004) developed a neuralnetwork-based system identification technique for model updating using traffic-induced vibrationscollected from a box-girder bridge located in Irvine,California. They emphasized that the determinationof input forces during an ambient vibration test aredifficult to estimate. Therefore, modal parametersare usually derived from vibration measurementswithout requiring information about input loads. Fivevertical modes using vibration data were identified by Feng et al. (2004).
Figure 1 depicts the resulting sensor configurationobtained from the numerical implementationof the DM method. The first 5 vertical modes areselected for this implementation based on the workpresented by Feng et al. (2004). The DI method isthen used to identify the occurrence of damage. Twolevels of damage are selected in this paper. Therefore,structural damage is modeled by 10 % (case 1)and 15 % (case 2) stiffness reduction of the elementsdefined in table 1.
Damage is considered to be successfully detectedif a sensor channel shows a large variation inthe strain energy before and after the occurrence ofdamage according to Eq. (10). The damage detectionresults are shown in figures 2, 3, 4 and 5. Damage issuccessfully identified if the normalized damage indexpresented in Eq. (10) is larger than 2. Figure 2 showsthat the sensor location 4 identifies the occurrence ofdamage for scenario DS1. It can be seen that all thescenarios presented in this paper for both cases arecorrectly identified. Actually, when damage occursin a simply supported bridge all mode shapes areaffected and therefore the damaged region inducesa reduction of the measured modal strain energyin other regions allowing the identification of theoccurrence of damage. It is also important to notethat negative values can be obtained during damageidentification. Basically, those cases represent largedifferences in the curvature of the mode shapesbetween healthy and damage states. The structurepresented in this paper corresponds to an isostaticstructure; it means that the occurrence of damagesignificantly modifies its mode shapes. For example,the fundamental mode shape of a simply supportedbeam corresponds to a half-cycle of a sinusoidalfunction with no inflection points in the mode shape,and considering that the proposed method is basedon modal strain energy, the detection of damageoccurrence is more challenging. On the other hand,a continuous beam or a frame structure, defined ashyperstatic structure, contains more inflection pointsin its mode shapes. The fact is that damage detectionbecomes more challenging for isostatic structures interms of collapse of the structure and transmissionof loads to the supports and therefore this study isoriented to that case. Failure in an element of anisostatic structure may disrupt significantly the paththat follows the load applied to the structure andeven cause the collapse of the structure. On the otherhand, failure of an element in a hyperstatic structuremay modify the way in which loads are transmittedto the supports, but the stability of the structure maynot be compromised. Finally, negative values canbe treated by using embedding machine learningtechniques.
An additional study is performed using anevenly distributed sensor configuration as shown in figure 6. The main objective of this final case (case3) is to show the advantages of using an optimumsensor placement method. The damage detectionresults for the case 3 are presented in figures 7 and 8. It is possible to observe that the quality of the damageidentification results is affected by the lack of anoptimum sensor placement method. The numberof non-identified cases is expected to increase if thenumber of sensors is reduced.
7. CONCLUSIONS
In this paper, a modal strain energy-basedapproach for fault detection in beam-like structureswas presented. An optimum sensor location methoddeveloped by Xia and Hao (2000) was numericallyimplemented in a FE model of a box-girder bridgeand a damage detection study was performed usingthe DI method. The basic assumption of vibrationbaseddamage detection is that structural damagewill significantly alter the stiffness, mass, or energydissipation properties of a system, which, in turn, alterthe measured dynamic response of that system. TheDI method could identify the occurrence of damagefor the damage scenarios presented in this paper.The results presented show the good performanceof the proposed strain energy-based approach andagree well with the results obtained by Li (2010).The use of the higher modes was avoided in orderto present more realistic results. In addition, damagedetection was conducted by considering onlyvertical contributions of the selected mode shapes.It was also numerically shown that optimum sensorplacement provides a significant improvement ofdamage detection results. The excellent anti-noiseperformance of modal strain energy-based methodswas already demonstrated by Alvandi and Cremona(2006). Therefore, the methodology presented in thispaper is a potential tool for structural health monitoringof beam-like structures, such as the group ofsimply supported bridges that compose the Metrosystem in Medellin.
Identification and damage detection techniquesthat are able to locate damage based on measureddata collected from real structures still seem along way from reality. A false positive (false alarmingof fault) is one of the main concerns when developinga robust damage detection methodology. Therefore,for practical applications of the method presentedin this paper it will be necessary to use embeddingmachine learning techniques in order to identify falsepositives. In addition, the development of low-costand rapid-to-deploy wireless structural monitoringsystems having embedded damage detectionalgorithms as proposed by Weng et al. (2008) willprovide robust and affordable solutions for vibrationbaseddamage detection implementations. Anotherpossible scenario is that damage location using lowfrequency vibration is undertaken to identify thoseareas where more detailed local inspection shouldbe concentrated.
NOMENCLATURE
B = determinant of the FIM as a distribution ofstrain energy
E = contribution to the FIM as a distribution ofstrain energy
F = summation of all measured modes
S = sensitivity matrix
X = noise vector
Z = normalized damage index
{e} = modal change vector
{α} = undamaged initial stiffness parameter
{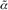 }= damaged initial stiffness parameter
}= damaged initial stiffness parameter
{Δα} = elemental stiffness change
β = damage index
λ = undamaged eigenfrequency
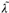 = damaged eigenfrequency
= damaged eigenfrequency
φ = undamaged eigenvector
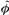 = damaged eigenvector
= damaged eigenvector
ψ = undamaged mode shape
ψ* = damaged mode shape
REFERENCES
Alvandi, A. and Cremona, C. (2006). "Assessment of vibration-based damage identification techniques". Journal of Sound and Vibration, vol. 292, No. 1-2 (April),pp. 179-202. [ Links ]
Barroso, L. R. and Rodriguez, R. (2004). "Damage detectionutilizing the damage index method to a benchmarkstructure". Journal of Engineering Mechanics ASCE, vol.130, pp. 142-151. [ Links ]
Chance, J.; Tomlinson, G. R. and Worden, K. A simplifiedapproach to the numerical and experimental modeling of the dynamics of a cracked beam. Proceedings of the 12th International Modal Analysis Conference. Honolulu,Hawaii, USA (1994), pp. 778-785. [ Links ]
Chen, Y. and Swamidas, A. S. J. Dynamic characteristicsand modal parameters of a plate with a small growingsurface cracks. Proceedings of the 12th InternationalModal Analysis Conference. Honolulu, Hawaii, USA.(1994), pp. 1155-1161. [ Links ]
Cobb, R. G. and Liebst, B. S. (1996). "Sensor location and structural damage localization using minimal sensorinformation". AIAA, vol. 32, pp. 369-374. [ Links ]
Doebling, S. W.; Farrar, C. R. and Cornwell, P. J. DIAMOND. A graphical user interface toolbox for comparativemodal analysis and damage identification. Proceedings of the Sixth International Conference on RecentAdvances in Structural Dynamics. Southampton, UK.(1997), vol. 2, pp. 399-412. [ Links ]
Farrar, C. R. and Jauregui, D. Damage detection algorithmsapplied to experimental and numerical modal data fromthe I-40 bridge. Los Alamos National Laboratory ReportLA-13074-MS (1996). [ Links ]
Feng, M. Q.; Kim, D. K.; Yi, J. H. and Chen, Y. (2004)."Baseline models for bridge performance monitoring".Journal of Engineering Mechanics ASCE, vol. 130, pp.562-569. [ Links ]
Hemez, F. M. and Farhat, C. An energy based optimumsensor placement criterion and its application to structuredamage detection. Proceedings of the 12th International Modal Analysis Conference. Honolulu (1994). [ Links ]
Heredia-Zavoni, E. and Esteva, L. (1998) "Optimal instrumentation of uncertain structural systems subjectto earthquake motions". Earthquake Engineering and Structural Dynamics, vol. 27, pp. 343-362. [ Links ]
Kammer, D. C. (1991). "Sensor placement for on-orbitmodal identification and correlation of large spacestructures". Journal of Guidance, Control, and Dynamics,vol. 14, pp. 251-259. [ Links ]
Kumar, M.; Shenoi, R. A. and Cox, S. J. (2009). "Experimental validation of modal strain energies based damageidentification method for a composite sandwichbeam". Composites Science and Technology, vol. 69,pp.1635-1643. [ Links ]
Li, Y. Y. (2010). "Hypersensitivity of strain-based indicators for structural damage identification: a review". Mechanical Systems and Signal Processing, vol. 24, pp.653-664. [ Links ]
Limongelli, M. P. (2010). "Frequency response functioninterpolation for damage detection under changingenvironment". Mechanical Systems and Signal Processing(in press). [ Links ]
Miyashita, T.; Ishii, H.; Fujino, Y.; Shoji, A. and Seki, M.Clarification of the effect of high-speed train induced vibrationson a railway steel box girder bridge using laserDoppler vibrometer. Proceedings of the InternationalConference on Experimental Vibration Analysis for CivilEngineering Structures. France (2005). pp. 349-357. [ Links ]
Pandey, A. K.; Biswas, M. and Samman, M. M. (1991)."Damage detection from changes in curvature modeshapes". Journal of Sound and Vibration, vol. 145, pp.321-332. [ Links ]
Quan, Q. and Weiguo, Z. Damage detection of suspensionbridges. Proc. the 16th International Modal Analysis Conference. Santa Barbara, California, USA. (1998).pp. 945-951. [ Links ]
Riveros, C. A.; Fujino, Y.; Xia, Y.; Dyke, S. and Caicedo, J.M. Sensor placement for continuous health monitoring incable-stayed bridges: comparative studies. Proceedings of the 7th International Conference on Motion and Vibration Control. St. Louis, MO, USA. (2004). pp. 255-269. [ Links ]
Riveros, C. A.; Utsunomiya, T.; Maeda, K. and Itoh, K.(2008) "Damage detection in flexible risers using statistical pattern recognition techniques". International Journal of Offshore and Polar Engineering, vol. 18 (1),pp. 35-42. [ Links ]
Riveros, C. A.; Utsunomiya, T.; Maeda, K. and Itoh, K.(2010) "Response prediction of long flexible risers subjectto forced harmonic vibration". Journal of Marine Science and Technology, vol. 15 (1), pp. 44-53. [ Links ]
Shi, Z. Y.; Law, S. S. and Zhang L. M. (2000) "Optimumsensor placement for structural damage detection".Journal of Engineering Mechanics ASCE, vol. 126, pp.1173-1179. [ Links ]
Stubbs, N. and Kim, J. T. Field verification of a nondestructive damage localization and severity estimation algorithm.Texas A&M University report for New Mexico State University (1994). [ Links ]
Tang, J. P. and Leu, K. M. (1991) "Vibration tests and damagedetection of P/C bridge". Journal of the ChineseInstitute of Engineers, vol. 14, pp. 531-536. [ Links ]
Udwadia, F. E. (1994) "Methodology for optimum sensorlocations for parameter identification in dynamicsystems". Journal of Engineering Mechanics ASCE, vol.102, pp. 368-390. [ Links ]
Udwadia, F. E. and Garba J. A. "Optimal sensor locationsfor structural identification". Proceedings of the JPL Workgroup on Identification and Control of Flexible Space Structures. San Diego, CA. (1985). [ Links ]
Weng, J. H.; Loh, C. H.; Lynch, J. P.; Lu, K. C.; Lin, P. Y. and Wang, Y. (2008) "Output-only modal identification of acable-stayed bridge using wireless monitoring systems". Engineering Structures, vol. 30 (7), pp. 1820-1830. [ Links ]
Xia, Y. and Hao, H. (2000) "Measurement selection forvibration-based structural damage identification".Journal of Sound and Vibration, vol. 236, pp. 89-104. [ Links ]
Yang, Q. W. (2009) "A numerical technique for structuraldamage detection". Applied Mathematics and Computation, vol. 215, pp. 2775-2780. [ Links ]
Yang, Y. B. and Wu, Y. S. (2002) "Dynamic stability of trainsmoving over bridges shaken by earthquakes". Journalof Sound and Vibration, vol. 258, pp. 65-94. [ Links ]
Yam, L. H.; Leung, T. P.; Li, D. B. and Xue, K. Z. (1996)"Theoretical and experimental study of modal strainenergy". Journal of Sound and Vibration, vol. 191, pp. 251-260. [ Links ]














