Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista EIA
Print version ISSN 1794-1237On-line version ISSN 2463-0950
Rev.EIA.Esc.Ing.Antioq no.14 Envigado July/Dec. 2010
ANÁLISIS DE SENSIBILIDAD ESPACIAL DE UN MODELO HIDRODINAMICO DEL EMBALSE PUNCHINÁ (ANTIOQUIA)
SPATIAL SENSITIVITY ANALYSIS OF A HYDRODYNAMIC MODEL OF THE PUNCHINÁ RESERVOIR (ANTIOQUIA)
ANÁLISE DE SENSIBILIDADE ESPACIAL DE UM MODELO HIDRODINÂMICO DO RESERVATÓRIO PUNCHINÁ (ANTIOQUIA)
Carlos Alejandro Escobar*
* Ingeniero Civil, Universidad Nacional de Colombia Sede Medellín; Doctor en Ciencias Naturales, Universidad Christian Albrechts, Alemania. Profesor Asociado, Universidad EAFIT. Medellín, Colombia. carloses@eafit.edu.co
Artículo recibido 11-VIII-2010. Aprobado 30-XI-2010
Discusión abierta hasta junio de 2011
RESUMEN
Se presenta en este artículo una metodología que permite cuantificar explícitamente el valor óptimo de los parámetros numéricos de un modelo hidrodinámico, tales como la resolución de la malla (en dirección horizontal y vertical) y el intervalo temporal de cálculo. El procedimiento se basa en un análisis de beneficio-costo, donde se busca obtener un balance entre la calidad de la solución numérica y el costo computacional requerido para lograrla. El carácter espacial del análisis de sensibilidad propuesto permite determinar en cada una de las celdas de la malla de cálculo la alteración en la solución numérica debida a variaciones en los parámetros físicos o numéricos que constituyen el modelo. Lo anterior posibilitó identificar en el interior del embalse Punchiná dónde y en qué grado son relevantes la resolución de la malla, el intervalo de cálculo temporal, la rugosidad del lecho y el coeficiente de viscosidad de remolino.
PALABRAS CLAVE: sensibilidad espacial; modelo hidrodinámico; embalse Punchiná; central hidroeléctrica San Carlos.
ABSTRACT
This paper presents a methodology to assess explicitly the optimal value of the numerical parameters in a hydrodynamic model, such as the grid resolution (horizontal and vertical direction) and the calculation time interval. The methodology is based on a cost-benefit analysis which seeks a desirable balance between the quality of the numerical solution and the required computational time. The spatial nature of the sensitivity analysis presented allows us to determine in each calculation grid cell the alteration of the numerical solution due to changes in the numerical or physical parameters in the model. According to this, it was possible to determine within the Punchiná reservoir where and to what extent are relevant the grid resolution, the time interval, the bed roughness, and the eddy viscosity coefficient.
KEY WORDS: spatial sensitivity; hydrodynamic model; Punchiná reservoir; San Carlos power station.
RESUMO
Apresenta-se neste artigo uma metodologia que permite quantificar explicitamente o valor ótimo dos parâmetros numéricos de um modelo hidrodinâmico, tais como a resolução da malha (em direção horizontal e vertical) e o intervalo temporal de cálculo. O procedimento baseia-se em uma análise de benefício-custo, onde se procura obter um balanço entre a qualidade da solução numérica e o custo computacional requerido para consegui-la. O caráter espacial da análise de sensibilidade proposta permite determinar em cada uma das células da malha de cálculo a alteração na solução numérica devida a variações nos parâmetros físicos ou numéricos que constituem o modelo. O anterior possibilitou identificar no interior do reservatório Punchiná onde e em que grau são relevantes a resolução da malha, o intervalo de cálculo temporário, a rugosidade do leito e o coeficiente de viscosidade de redemoinho.
PALAVRAS-CÓDIGO: sensibilidade espacial; modelo hidrodinâmico; reservatório Punchiná; usina hidreléctrica San Carlos.
1. INTRODUCCIÓN
El embalse Punchiná sirve a la central hidroeléctrica de San Carlos, cuya primera fase de 620 MW fue puesta en operación en 1984 (Gómez y Mejía, 1984) y la segunda, también de 620 MW en 1987. En la actualidad cuenta con una capacidad instalada de 1.240 MW, distribuidos en ocho unidades de 155 MW, que la convierte en una de las principales proveedoras de energía del país. No obstante, los estudios del comportamiento hidrodinámico del embalse son escasos, lo cual restringe la capacidad de predicción y la toma de decisiones en diversos aspectos de carácter ingenieril, ambiental, biológico, económico, etc.
En el marco del proyecto de investigación "Sedimentación en embalses, Evaluación de alternativas aplicadas al manejo de sedimentos, Caso Punchiná, Fase I", financiado por la Universidad EAFIT, se inició la construcción de un modelo hidrodinámico 3D para el embalse, que comprende el desarrollo de un análisis de sensibilidad. En este estudio preliminar, se pretende mejorar el conocimiento del comportamiento global del modelo y su respuesta a cambios en algunos parámetros físicos y numéricos (Toro, 2004) de los cuales en particular se carece de información, o es escasa o poco confiable; así se posibilita cuantificar la incertidumbre en la respuesta del modelo respecto a estos parámetros de entrada, tal como lo expresan Alemseged y Rientjes (2005). Por tanto, este estudio no llevará necesariamente a definir el valor de algunos parámetros, pero sí a definir con anticipación sobre qué parámetros es importante extremar precauciones (reducir incertidumbre), dada su relevancia en el comportamiento del modelo.
Entre un análisis de sensibilidad y los estudios posteriores de calibración y validación de un modelo hidrodinámico es posible reducir la incertidumbre sobre las variables físicas de mayor relevancia por medio de su observación en el campo. Infortunadamente, en muchos casos lo anterior no se concreta, debido a las limitaciones tecnológicas para determinar algunos parámetros o al alto costo económico implícito. Esto conduce a que en la fase de calibración del modelo se requiera considerar un número mayor de variables desconocidas, a las cuales se les impone, por lo general un valor inmodificable en espacio y tiempo, con el fin de acercar los resultados del modelo a algunos valores observados (WL/Delft Hydraulics, 2006), lo cual al final resulta en importantes limitaciones a la aplicabilidad del modelo.
En la actualidad existen diversos tipos de aproximaciones para llevar a cabo un análisis de sensibilidad, tales como: (i) métodos basados en la varianza: el de Sobol (Sobol, 1990; Homma y Saltelli, 1996; ), el FAST (Cukier et al., 1973), el extended FAST (Saltelli, Tarantola y Chan, 1999), etc.; (ii) métodos basados en análisis de regresión (Iman y Helton, 1988; Helton, 1993); y (iii) métodos tipo OAT (un parámetro a la vez). Se opta en este estudio por uno de los métodos tipo OAT, los cuales se usan ampliamente en ingeniería y física (Saltelli, Tarantola y Campolongo, 2000). Este método permite determinar el comportamiento de una variable de referencia respecto a cambios deliberados en algún parámetro (de a uno cada vez).
La metodología propuesta en este estudio se caracteriza por considerar la variabilidad espacial de la sensibilidad, con lo cual se permite identificar dónde y en qué grado son relevantes los distintos parámetros físicos y numéricos que considera el modelo. De esta forma, los recursos disponibles se pueden utilizar para obtener mayor información de los factores realmente significativos y sólo en las subáreas de influencia, maximizando así el aprovechamiento de los recursos con reducción en los costos computacionales y de las campañas de medición; es decir: (i) no se requiere medir en toda el área de estudio algunos parámetros que únicamente son relevantes en determinadas subáreas (v. gr. aguas someras o profundas); (ii) la resolución de la malla puede ampliarse o reducirse en algunas zonas del dominio, redundando en menores costos computacionales; (iii) se estima el error en que puede incurrirse si se pasa por alto la observación en campo de una variable hidrodinámica; (iv) se determinan las áreas donde una modelación 3D es justificable, etc.
2. ÁREA DE ESTUDIO
El embalse Punchiná está localizado en el noroeste de Colombia, sobre el ramal central de la cordillera de los Andes, en la cuenca del río Guatapé, a unos 80 km al oriente de la ciudad de Medellín (figura 1). El embalse se sitúa en la cota 750 msnm, latitud 6º14’ Norte y longitud 74º52’ Oeste. El proyecto hidroeléctrico tiene una caída media neta de 554 m (http://www.isagen.com.co) y un caudal promedio de 143 m3/s (Gómez y Mejía, 1984). La capacidad del embalse es de 58 Mm3 y aporta al sistema interconectado eléctrico nacional un promedio de 1.240 MW.
La dinámica de corrientes en el embalse es dominada ante todo por el aporte de sus tributarios principales, las corrientes de densidad y los efluentes (Escobar y Pérez, 2009). Los efluentes son afectados en gran medida por las reglas de operación del embalse, demandas energéticas y disponibilidad del líquido. La profundidad máxima del embalse se aproxima a los 45 m y se encuentra en el sureste del embalse. La tasa anual de acumulación de sólidos es de 0,94 Mm3 (ISA, 1989). El clima de la cuenca del río Guatapé se clasifica como subtropical, con precipitación promedio anual entre 2.000 y 3.000 mm y temperatura media de 25 ºC, que se caracteriza por una estación seca de 3-4 meses al comienzo del año y una lluviosa los meses restantes (Gómez y Mejía, 1984).
3. FORZAMIENTOS HIDROMETEOROLÓGICOS
Se presenta en la tabla 1 un resumen de los parámetros físicos y forzamientos externos (condiciones de frontera) utilizados en las simulaciones hidrodinámicas, los cuales ejercen una influencia característica sobre las corrientes del embalse Punchiná. Entre ellos se tienen: los tributarios principales (ríos Guatapé y San Carlos), las corrientes de densidad (gradientes térmicos) y los efluentes (vertedero y torres de captación). Los valores reportados corresponden a los valores medios observados en el embalse en el año 2006; mayores detalles pueden encontrarse en Escobar y Pérez (2009).
4. MODELO HIDRODINÁMICO
La plataforma de modelación Delft3D desarrollada por WL/Delft Hydraulics en los Países Bajos (Roelvink y van Banning, 1994) se usa en la determinación del flujo no estacionario en el embalse Punchiná. La posible estratificación térmica en el embalse exige la construcción de un modelo 3D que permita considerar su existencia y la variabilidad espacio-temporal de las corrientes. El modelo hidrodinámico resuelve las ecuaciones de Navier-Stokes sobre una malla curvilínea, en combinación con un grupo apropiado de condiciones iniciales y de frontera que resultan del forzamiento debido a factores meteorológicos, densidad variable, descarga de ríos y efluentes. Las fluctuaciones turbulentas las incluye el modelo por medio de los esfuerzos de Reynolds, definidos por medio del modelo de cierre de turbulencia κ−ε (Uittenbogaard, van Kester y Stelling, 1992). El transporte de calor se determina mediante la solución de la ecuación de advección-difusión en 3D, donde el intercambio de calor en la interfase aire-agua se define con la metodología propuesta por Octavia, Jirka y Harleman (1977).
5. METODOLOGÍA
El procedimiento utilizado en este análisis de sensibilidad retoma algunos conceptos presentados en Villegas, Toro y Vélez (2005), donde se determina una relación entre un coeficiente CV (que denota variaciones en la solución numérica debidas a cambios en el número de celdas), el tiempo de cómputo CPU y el número de celdas activas para la definición del tamaño óptimo de malla. La metodología que se presenta a continuación adopta estos conceptos y a partir de ellos construye curvas típicas de beneficio-costo, de las cuales se determina explícitamente el número óptimo de celdas, capas e intervalo de cálculo temporal requerido en las simulaciones hidrodinámicas, de tal forma que el costo computacional se justifique con la calidad de la solución numérica.
Esta calidad se cuantifica por medio del parámetro CV, que indica la discrepancia que tiene la solución del modelo (por el uso de distintas mallas/ parámetros) respecto a una solución "patrón", la cual se supone de mayor confiabilidad. El CV se define de acuerdo con la siguiente relación:
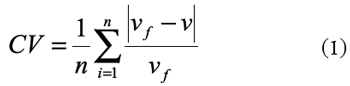
Donde v es la variable de referencia sobre la cual se quiere determinar la sensibilidad del modelo, en este caso la velocidad media del flujo (integrada en la vertical); vf es el valor de la variable de referencia en la simulación "patrón" y n es el número total de celdas de la malla. Es decir, la variable CV equivale al promedio de los coeficientes de variación local "CVL " calculados en todas las celdas del dominio. De esta forma, se da origen al análisis de sensibilidad espacial en que el coeficiente CVL permite determinar el efecto de algún parámetro físico o numérico en cualquier punto del embalse.
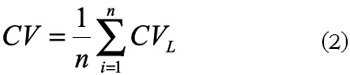
El costo computacional CPU equivale al tiempo de cálculo requerido por el equipo de cómputo. Por fin, se anota que las variables CV y CPU se normalizaron respecto a sus valores máximos, para luego confrontarlas en el análisis de beneficio-costo.
6. SENSIBILIDAD ESPACIAL DEL MODELO HIDRODINÁMICO RESPECTO A PARÁMETROS NUMÉRICOS
En esta sección se presenta la sensibilidad del modelo hidrodinámico respecto a las características de la malla de cálculo (horizontal y vertical) y al intervalo de tiempo usado en la integración temporal. Sin embargo, se anota sobre la existencia de otro número de parámetros numéricos que no se consideran en este análisis y que pueden afectar en algún grado las características de la solución, v. gr. aspectos relacionados con el secado e inundación de celdas, suavizado de las discrepancias entre las condiciones iniciales y las de frontera, selección del tipo de solución numérica, etc. (WL/Delft Hydraulics, 2006).
6.1 Malla de cálculo horizontal
La malla de cálculo que se superpone sobre el área de estudio está compuesta al principio por celdas cuyo número no se sabe a priori si es suficiente para describir en forma apropiada el flujo en el embalse. Por consiguiente, esta sección tiene como objetivo definir el número de celdas óptimo de la malla que permita determinar la batimetría y la solución del modelo hidrodinámico de manera adecuada.
El desarrollo del análisis de sensibilidad del modelo respecto a la malla horizontal contempla simulaciones con mallas de 45.620, 11.500, 3.104 y 771 celdas, de las cuales se espera definir el número de celdas óptimo para la malla. Adicionalmente y de acuerdo con las posibilidades que ofrece el análisis espacial, se determinarán las subáreas donde se debe modificar la resolución de la malla, con el fin de mejorar el desempeño del modelo.
A continuación se presentan los resultados de las simulaciones para los cuatro tipos de malla utilizados. La figura 2 muestra la variación en la calidad de la solución y el costo computacional respecto al número de celdas activas. El CVmax corresponde a la simulación cuyos resultados presentan la mayor discrepancia respecto a los obtenidos en la simulación "patrón" (malla de 45.620 celdas); esto ocurre para la simulación con una malla de 771 celdas. El CPUmáx ocurre para la malla "patrón", dado su mayor número de celdas. De la relación beneficio-costo en la figura 2 se infiere que la intersección representa el punto donde se logra un equilibrio entre el costo computacional y la calidad de la solución. En consecuencia, se determina que el número óptimo de celdas para la malla horizontal es de 11.009. En la tabla 2 se presenta para cada una de las simulaciones realizadas la discrepancia en la solución (en términos de velocidades) respecto a la obtenida con la malla "patrón". Esta discrepancia se cuantifica por medio del parámetro estadístico RMAE (relative mean absolute error).
Una vez determinado el número de celdas óptimo para la malla de cálculo, se procede a representar gráficamente la sensibilidad espacial del modelo respecto a la resolución de la malla. La figura 3 presenta el valor del CVL obtenido en cada una de las celdas, para las simulaciones con mallas de 11.500, 3.104 y 771 celdas. En esta figura se observa que la reducción del número de celdas incrementa el valor del CVL, lo cual es más notorio en tramos curvos, zonas de flujo muerto, desembocadura de tributarios menores y orillas; en cambio en el cauce principal del río, la solución numérica fue bastante homogénea en todas las simulaciones. En las zonas donde el CVL es alto se puede incrementar el refinamiento de las celdas a costa de reducirlo donde el CVL sea bajo; de esta forma es posible mejorar la calidad de la solución (reducir el CV) sin necesidad de incrementar el número de celdas.
Conocido el efecto que tiene la resolución de la malla horizontal en la solución numérica, se procede a modo de verificación a definir el número de celdas óptimo que permite representar la batimetría del embalse con la precisión adecuada. En este caso, el coeficiente de variación CVvol utiliza el volumen del embalse como variable de referencia.
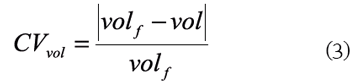
Donde, vol es el volumen del embalse y volf es el volumen del embalse determinado por medio de la malla más fina. La figura 4 presenta, con un criterio independiente al anterior, la evaluación del número de celdas óptimo para la malla de cálculo. Es decir, de una parte se analizó el efecto del número de celdas en la solución numérica y, de otra, su efecto en la representación de la batimetría.
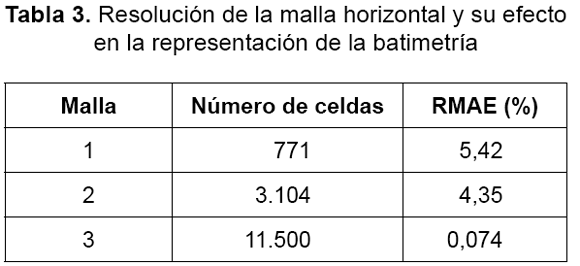
De este análisis se determina que el número óptimo de celdas para la malla es de 11.500, donde es distintivo el cambio repentino de pendiente del CVvol, indicando el poco aporte que las celdas adicionales a este valor tendría en la representación de la batimetría. Nótese que en este caso los coeficientes de variación CVvol no resultan de alguna simulación hidrodinámica (no se tiene costo computacional). De allí que no se utilice el criterio de la intersección, usado previamente para definir el número óptimo de celdas. La tabla 3 presenta un resumen de las discrepancias en la descripción de la batimetría con cada una de las mallas utilizadas (respecto a la malla patrón).
6.2 Malla de cálculo vertical
La plataforma de modelación Delft3D utilizada permite discretizar la dirección vertical por medio de una malla con sistema coordenado tipo sigma (Phillips, 1957) donde las capas están limitadas por dos planos, de los cuales uno se aproxima a la superficie libre del agua, y el otro, a la topografía del fondo. El número de capas en la vertical es constante para la totalidad del área de estudio. En este análisis de sensibilidad se consideraron 4 mallas verticales, caracterizadas por tener 20, 10, 5 y 3 capas. La discretización en la vertical por medio de 20 capas corresponde a la malla "patrón".
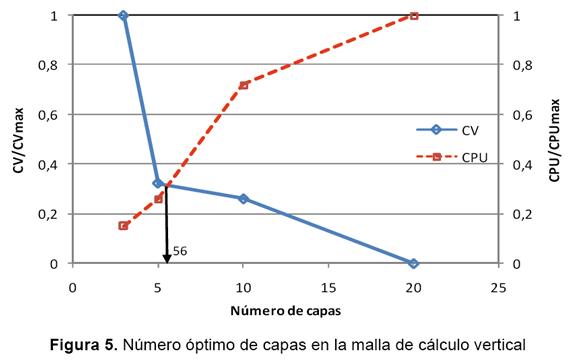
De acuerdo con la metodología planteada en la sección 6.1, se determina el número óptimo de capas en las cuales se recomienda dividir la malla. Igualmente, se procederá a determinar la sensibilidad espacial del modelo, indicando las zonas que pueden ser más afectadas por la discretización utilizada. La figura 5 muestra un análisis de beneficio (calidad de la solución numérica) y costo (tiempo de cómputo) con el cual se selecciona el número óptimo de capas (unas 6).
Después se procede a representar la sensibilidad espacial del modelo respecto al número de capas. La figura 6 presenta el valor de CVL para las mallas de 10, 5 y 3 capas. Es notorio el incremento del CVL con la reducción del número de capas. También el hecho de que en las zonas de aguas profundas, donde la estratificación térmica se vuelve relevante (Escobar y Pérez, 2009), el CVL es mucho mayor que el calculado en la cola del embalse, donde las profundidades son menores y el flujo se asimila al de un río. La tabla 4 presenta para cada una de las mallas utilizadas el valor del RMAE en la solución numérica respecto a la malla "patrón" de 20 capas.
6.3 Intervalo temporal de cálculo
La integración temporal usada por el esquema de solución numérica (método "Cyclic") se basa en el método ADI "alternating direction implicit", el cual no impone restricciones al intervalo temporal de cálculo (Stelling y Leendertse, 1991). De allí que la estabilidad numérica por lo regular, en consecuencia, no sea un problema y que prevalezca el criterio de precisión en la determinación del intervalo temporal. Sin embargo, éste se restringe a un intervalo de tiempo máximo de 2 minutos, de acuerdo con la recomendación de no exceder un valor de 10 en el número de Courant (WL/Delft Hydraulics, 2006). Por tanto, el desarrollo del análisis de sensibilidad consideró simulaciones con intervalos temporales de cálculo iguales a 2, 1 y 0,5 minutos.
Por medio de un análisis de beneficio-costo se determina el intervalo temporal de cálculo óptimo para utilizar en las simulaciones hidrodinámicas en el embalse. Este intervalo de cálculo temporal se escoge de acuerdo con un equilibrio entre la calidad de la solución y el costo computacional. El procedimiento utilizado es similar al presentado en la determinación del número óptimo de celdas y capas en la malla de cálculo, donde la velocidad media del flujo es la variable de referencia y a partir de ella se calcula el valor del parámetro CV. La simulación "patrón" considera un intervalo de cálculo temporal igual a 0,5 minutos.
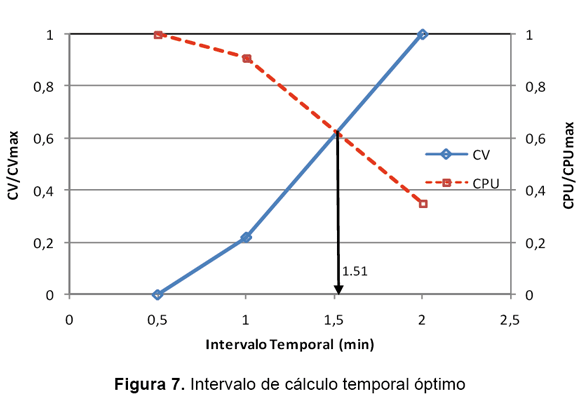
La figura 7 indica que el intervalo temporal de cálculo óptimo para la simulación hidrodinámica del embalse es de 1,5 minutos. La tabla 5 presenta para cada uno de los intervalos utilizados el valor del RMAE en la solución numérica respecto a la simulación "patrón".
A continuación se determina la sensibilidad espacial del modelo respecto a la variación del intervalo temporal de cálculo. En la figura 8 se muestran las subregiones del embalse que serán más afectadas al reducir el costo computacional.
7. SENSIBILIDAD ESPACIAL DEL MODELO HIDRODINÁMICO RESPECTO A PARÁMETROS FÍSICOS
Determinar en campo algunos parámetros físicos con la resolución espacio-temporal que permite la modelación numérica actual puede resultar una tarea bastante complicada si no imposible. Lo anterior, en algunos casos, se debe a que los costos de la medición son inaccesibles y en otros casos a la aleatoriedad y escalas de longitud micro de algunos parámetros que dificultan su observación. Aunque se anota que en la actualidad se dispone de la tecnología para medir con precisión aceptable la mayoría de parámetros físicos.
En caso de desconocerse algún parámetro en el modelo por una de estas razones, se recomienda inferir su efecto en la modelación con un análisis de sensibilidad. En esta sección se considera la sensibilidad del modelo hidrodinámico respecto a la rugosidad del lecho y la viscosidad de remolino. Un análisis de sensibilidad respecto a otros procesos y forzamientos externos como el viento, estratificación térmica, caudales de afluentes y efluentes puede encontrarse en Escobar y Pérez (2009).
7.1 Rugosidad
Determinar la rugosidad en el fondo de un cuerpo de agua implica decidirse por uno de los dos caminos siguientes: medición de perfiles de velocidad o medición de parámetros morfológicos (formas de lecho) y sedimentológicos (tamaño de granos). Sin excepción, las dos opciones demandarían un arduo trabajo de campo. Este trabajo en algunos casos no es factible, dada la alta variabilidad espacio-temporal que puede presentar la rugosidad y los altos costos que supondría su medición.
Al no contarse con un valor confiable de la rugosidad en el embalse, se procede a realizar un análisis de sensibilidad respecto a esta variable. En este caso se observará el efecto en las corrientes debido al uso de dos valores de la rugosidad. La discrepancia en las velocidades medias del embalse calculadas en estas dos simulaciones, cuya única diferencia fue el valor asignado al coeficiente de Chézy (32,5 y 97,5 m1/2/s), se utiliza para determinar el efecto que tiene la rugosidad en la modelación hidrodinámica.
La figura 9 presenta los cambios relativos en la velocidad media del flujo debidos al cambio de rugosidad e indica también las zonas que son más susceptibles de ser afectadas por variaciones en la rugosidad y, por ende, es una guía para seguir en el momento de llevar a cabo alguna medición de este parámetro.
El efecto de la rugosidad en las corrientes se hace notorio en: (i) los tramos curvos del cauce, dado el efecto que tiene la rugosidad en la formación y disipación de flujos secundarios (helicoidales); (ii) las zonas de aguas someras laterales al río San Carlos, donde la rugosidad relativa es mayor; y (iii) las cercanías a la captación, donde el aceleramiento del flujo en las capas inferiores, en que se localizan las tomas de agua, conlleva una mayor resistencia del lecho al flujo.
7.2 Viscosidad
La simulación hidrodinámica en el embalse Punchiná considera el modelo de cierre de turbulencia κ−ε (Launder y Spalding, 1972) para el cálculo de la viscosidad de remolino. Este es un modelo de turbulencia de segundo orden, donde la energía cinética turbulenta κ y la tasa de disipación viscosa ε se definen por medio de una ecuación de transporte. Una vez conocidos κ y ε, se pueden determinar la longitud de mezcla y la viscosidad.
El valor de la viscosidad de remolino horizontal depende del flujo y el tamaño de celdas usado en la malla. La viscosidad horizontal en mallas con tamaños finos de celdas (decenas de metros), donde la mayoría de los detalles del flujo pueden ser resueltos por la malla misma, oscila entre 1 y 10 m2/s. Las mallas con tamaños de celdas en el rango de cientos de metros o más presentan coeficientes de viscosidad que varían entre 10 y 100 m2/s (WL/Delft Hydraulics, 2006).
La viscosidad de remolino horizontal se asocia con forzamientos y movimientos turbulentos horizontales. Esta viscosidad podría no ser determinada adecuadamente por los modelos numéricos, debido al tamaño de las celdas o a los promedios implícitos en las ecuaciones de movimiento de Reynolds. Mayores detalles sobre el cálculo de los esfuerzos de Reynolds pueden encontrarse en Rodi (1993). Según lo anterior, se recomienda introducir en el modelo una viscosidad de remolino horizontal de referencia, con el propósito de compensar el posible déficit en el cálculo de esta variable.
Los flujos 3D en aguas someras presentan un tensor de esfuerzos anisotrópico. La viscosidad de remolino horizontal es mucho mayor que la viscosidad vertical (Uittenbogaard, van Kester y Stelling, 1992). El valor de la viscosidad de remolino vertical depende de la aplicación particular. La experiencia muestra que en estuarios y lagos estratificados un valor apropiado de la viscosidad vertical oscila entre 10-4 y 10-3 m2/s (WL/Delft Hydraulics, 2006). En flujos fuertemente estratificados, la viscosidad de remolino vertical calculada por el modelo puede ser baja y se requiere un valor de referencia adicional que le permita amortiguar pequeñas oscilaciones generadas por inundación-secado de celdas, condiciones de frontera, dragado del viento, etc., las cuales de otra forma sólo podrían ser amortiguadas en el fondo del embalse. Por ello, tanto la viscosidad de remolino horizontal como la vertical calculadas por el modelo pueden requerir ajustes mediante unos valores de referencia. Estos valores los determina el usuario del modelo por un proceso de calibración, dada la dificultad para conocer a priori el valor de esta variable.
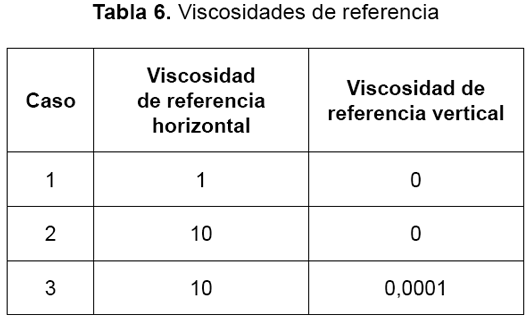
A continuación se desarrolla un análisis de sensibilidad respecto a la viscosidad de remolino. De acuerdo con este propósito se considera la simulación de tres casos (tabla 6), donde se varía de forma deliberada la viscosidad de referencia y se mira el efecto de este cambio en las velocidades medias del flujo. Ambas viscosidades de referencia (horizontal y vertical) se suman a las respectivas viscosidades calculadas por el modelo.
La figura 10 muestra el cambio relativo en las velocidades medias del flujo, si se considera un incremento de la viscosidad de referencia horizontal (derecha) y de la viscosidad de referencia vertical (izquierda). La diferencia relativa en las velocidades calculadas en los casos 1 y 2 (tabla 6) determina el efecto de la viscosidad horizontal. El efecto en la modelación por un incremento en la viscosidad vertical se determina de acuerdo con la discrepancia en las velocidades calculadas en los casos 2 y 3.
La variación de la viscosidad de remolino horizontal del modelo afecta más que todo las zonas del embalse donde las corrientes de densidad son notables; es decir, donde la velocidad del flujo es muy baja o en zonas profundas. En estas regiones el flujo de calor y los gradientes de temperatura asociados son relevantes y se ven afectados por el cambio en la viscosidad, que a su vez afecta los coeficientes de difusión.
8. DISCUSIÓN
Por lo general, en el desarrollo de un análisis de sensibilidad no se cuenta con información de campo suficiente para verificar si hay un buen desempeño del modelo. Por consiguiente, se supone en este estudio que las simulaciones tipo "patrón", aquellas con la mayor resolución espacio-temporal, son las más confiables y que los incrementos adicionales sobre esta resolución (espacio y tiempo) no deben conllevar cambios significativos en la solución del modelo.
La sensibilidad del modelo al tamaño de la malla de cálculo horizontal y vertical, al intervalo de cálculo temporal, a la rugosidad y a la viscosidad se definió considerando la velocidad de las corrientes como parámetro de referencia. En caso de que el interés de la modelación y el parámetro de referencia cambien (v. gr. la temperatura, concentraciones, transporte de sustancias, etc.) es de esperarse que los resultados del análisis de sensibilidad presenten a su vez variaciones respecto a los que se indican en este artículo.
El criterio para seleccionar el valor óptimo de las variables numéricas confronta dos parámetros que indican la calidad de la solución y el costo computacional. A ambos se les da el mismo peso, lo cual puede eventualmente modificarse; por consiguiente, la intersección de las curvas en las figuras 2, 5 y 7 representa el punto donde ambos parámetros coinciden y, por tanto, a diferencia de cualquier otro punto, no hay favorecimiento de un parámetro en detrimento del otro.
La necesaria adimensionalización del coeficiente de variación CV y del costo computacional CPU respecto a sus valores máximos puede implicar cierta confusión en la lectura de las figuras; en particular, el parámetro CV/CVmax fue de unos 30 y 60 % en la intersección de las curvas en las figuras 5 y 7 (valores y gradientes en apariencia altos). Sin embargo, la lectura conjunta de estas gráficas con las tablas 4 y 5 correspondientes permite evidenciar que los valores respectivos del CV difícilmente superarían el 3 % para las simulaciones con los parámetros numéricos óptimos.
La resolución óptima de la malla de cálculo horizontal cumple un doble criterio. El primero implica que la solución numérica de las ecuaciones de movimiento está próxima a una solución de referencia (obtenida con la malla "patrón"). El segundo criterio conlleva el aseguramiento de la calidad en la representación que hace el modelo de la batimetría. Finalmente se adopta el criterio más conservador y, por tanto, se determina que el número de celdas adecuado para la malla es de unas 11.500 (figura 4).
La calidad de la solución numérica obtenida con la malla horizontal que emplea el número de celdas óptimo puede mejorarse; en particular, si se refina el tamaño de celdas en las zonas que el CVL es alto (ver figura 3) y se incrementa donde el CVL es bajo. De esta manera puede lograrse una mayor eficiencia en la modelación buscando que en las zonas donde los detalles del flujo lo exigen se reduzca el tamaño de las celdas y, a su vez, se incremente en zonas con flujos más uniformes.
La necesidad de utilizar una modelación 3D en el embalse se explica fundamentalmente por la heterogeneidad en las temperaturas (estratificación térmica). Sin embargo, esta característica no se presenta en la totalidad del embalse y sólo es relevante en zonas de aguas profundas (Escobar y Pérez, 2009). Por consiguiente, se advierte que el procedimiento para determinar el número óptimo de capas (figura 5) considera la totalidad del embalse. Es decir, el resultado obtenido refleja un equilibrio entre dos zonas que presentan una mayor y menor exigencia de la modelación 3D.
9. CONCLUSIONES
De acuerdo con el análisis de sensibilidad realizado y las condiciones de flujo descritas en la tabla 1, se concluye lo que se expone enseguida.
El número óptimo de celdas en la malla horizontal de cálculo para el modelo hidrodinámico del embalse Punchiná es de 11.500, lo cual implica para el área del embalse un tamaño de celdas promedio de 17 m de lado. Sin embargo, el tamaño de las celdas en algunas zonas del embalse con flujos más complejos debe refinarse. Este es el caso de los tramos con curvas y las zonas donde desembocan los tributarios menores, donde este tamaño promedio de celdas no permite determinar con detalle la particularidad del flujo.
La resolución de la malla vertical en el embalse Punchiná debe considerar por separado dos regiones: la zona Norte del embalse con profundidades menores de 30 m y la zona Sur con profundidades mayores. El procedimiento realizado en este estudio consideró el embalse en su totalidad, lo cual resultó en una discretización óptima de la malla en 6 capas aproximadamente (figura 5). Por consiguiente, considerar 6 capas puede ser conservador en la zona Norte del embalse, mientras que en la zona Sur se puede comprometer la calidad de la solución.
El intervalo de cálculo temporal recomendado para la modelación hidrodinámica es de 1,5 minutos (figura 7). Sin embargo, debe anotarse que este resultado se restringe al esquema de solución, al tamaño de malla y a la condición de flujo utilizado en este estudio. El detrimento en la solución numérica del modelo debido a un incremento en el intervalo temporal se nota más en la zona Sur del embalse, donde es más profundo, y el criterio de estabilidad de Courant-Friedrichs-Levy puede comprometerse.
Un error en la determinación de la rugosidad del lecho que se implemente en el modelo hidrodinámico afectaría ante todo las corrientes del embalse localizadas en la zona externa de las curvas, en las zonas laterales al cauce del río San Carlos, en las desembocaduras de los tributarios y en las cercanías a la captación. Como consecuencia, en estas zonas debe hacerse énfasis en la determinación precisa de este parámetro.
AGRADECIMIENTOS
Esta investigación fue desarrollada dentro del marco del proyecto PUNCHINÁ, "Sedimentación en embalses, Evaluación de alternativas aplicadas al manejo de sedimentos, Caso Punchiná, Fase I". El autor quiere agradecer a la Universidad EAFIT por financiar el proyecto. Agradece al Departamento de Instrumentación de la Central San Carlos por facilitar la información de niveles, caudales de afluentes y efluentes en el embalse. El autor agradece también a la estudiante de Ingeniería Liliana Velásquez por su participación en la edición de este artículo.
REFERENCIAS
Alemseged, T. H. and Rientjes T. H. M. Effects of LIDAR DEM resolution in flood modeling: A model sensitivity study for the city of Tegucigalpa, Honduras. The Netherlands: ISPRS WG III/3, III/4, V/3 Workshop "Laser scanning 2005", Enschede, 2005. [ Links ]
Cukier, R. I.; Fortuin, C. M.; Shuler, K. E.; Petschek, A. G. and Schaibly, J. H. (1973). "Study of the sensitivity of coupled reaction systems to uncertainties in rate coefficients, I. Theory". Journal of Chemical Physics, vol. 59, No. 8, pp. 3873-3878. [ Links ]
Escobar, C. A y Pérez, J. (2009). "Aplicación del análisis de sensibilidad de un modelo hidrodinámico en la determinación de la relevancia de procesos físicos y forzamientos externos en las corrientes del embalse Punchiná (Antioquia)". Revista Universidad EAFIT, vol. 45, No. 156, pp. 73-89. [ Links ]
Gómez, A. y Mejía, O. (1984). "Proyecto hidroeléctrico de San Carlos". Revista SAI, vol. 1, No. 5, pp. 5-17. [ Links ]
Helton, J. C. (1993). "Uncertainty and sensitivity analysis techniques for use in performance assessment for radioactive waste disposal". Reliability Engineering & System Safety, vol. 42, No. 2-3, pp. 327-367. [ Links ]
Homma,T. and Saltelli, A. (1996). "Importance measures in global sensitivity analysis of nonlinear models". Reliability Engineering & System Safety, vol. 52, No. 1 (April), pp. 1-17. [ Links ]
Iman, R. L. and Helton, J. C. (1988). "An investigation of uncertainty and sensitivity analysis techniques for computer models". Risk Analysis, vol. 8, No. 1 (March), pp. 71-90. [ Links ]
ISA (Interconexión Eléctrica S.A). Informe de sedimentación Embalses Punchiná-San Lorenzo y Calderas. Gerencia de Operación. 1989. OSCJ-89-019-E, 100 p. [ Links ]
Launder, B. E. and Spalding, D. B. Mathematical models of turbulence. London: Academic Press, 1972. 169 p. [ Links ]
Octavia, K. A. H.; Jirka, G. H. and Harleman, D. R. F. Vertical heat transport mechanisms in lakes and reservoirs. Report no 227. Cambridge, MA: Massachusetts Institute of Technology, 1977. [ Links ]
Phillips, N. A. (1957). "A co-ordinate system having some special advantages for numerical forecasting". Journal of Meteorology, vol. 14, pp. 184-185. [ Links ]
Rodi, W. Turbulence models and their application in hydraulics: a state-of-the-art review. 3rd ed. Rotterdam: A. A. Balkema, 1993. 104 p. [ Links ]
Roelvink, J. A. and van Banning, G.K.F.M. (1994). "Design and development of DELFT3D and application to coastal morphodynamics". In: Verwey, Minns, Babovic, and Maksimovic (eds.). Hydroinformatics´ 94, Balkema, Rotterdam. [ Links ]
Saltelli, A.; Tarantola, S. and Chan K. (1999). "A quantitative model-independent method for global sensitivity analysis of model output". Technometrics, vol. 41, No. 1 (February), pp. 39-56. [ Links ]
Saltelli, A., Tarantola, S. and Campolongo F. (2000). "Sensitivity analysis as an ingredient of modeling". Statistical Science, vol. 15, No. 4, pp. 377-395. [ Links ]
Sobol, I. M. (1993). "Sensitivity analysis for nonlinear mathematical models". Mathematical and Computer Modelling, vol. 1, No. 4, pp. 407-414. [ Links ]
Stelling, G. S. and Leendertse J. J. (1991). "Approximation of convective processes by cyclic ACI methods". Proceedings of 2nd ASCE Conference on Estuarine and Coastal Modelling, Tampa, (27 February - 1 March). [ Links ]
Toro, F. (2004). "Sistemas de soporte de decisiones para la creación de modelos numéricos hidrodinámicos". Revista EIA, vol. No. 2 (agosto), pp. 53-65. [ Links ]
Uittenbogaard, R. E.; van Kester, J. A. T. M. and Stelling, G. S. Implementation of three turbulence models in 3D-TRISULA for rectangular grids. Report Z81, Delft Hydraulics. 1992. [ Links ]
Villegas, B.; Toro M. y Vélez, J. (2005). "Definición de los tamaños óptimos de malla e intervalo de cálculo en un modelo numérico: aplicación al caso del embalse de Porce II". Dyna, vol. 72, No. 147 (noviembre), pp. 23-32. [ Links ]
WL/Delft Hydraulics. Delft3D-FLOW, simulation of multidimensional hydrodynamic flows and transport phenomena, including sediments, User Manual. Delft, 2006. [ Links ]